1. Introduction
Cities in developing countries exhibit high levels of inequality in public infrastructure and services [
1], such as water scarcity [
2], limited accessibility [
3], and inadequate public health facilities [
4]. These inequalities arise from several factors, including limited resources, population growth, ineffective urban planning, or a combination of these factors [
5]. This context makes infrastructure planning challenging, as it is necessary to meet new demands and, as a priority, address unmet needs, thereby reducing inequalities in a scenario of scarce resources.
Urban public infrastructure comes in different forms [
6]. Public facilities, such as hospitals, police stations, and schools, are associated with the principle of universality, or unrestricted accessibility for the entire population [
7]. In turn, public goods such as streets, sidewalks, water, and sewage systems share the principle of universality and are characterized by indivisibility, which means that the good cannot be divided without losing its essential characteristics [
8]. This study examines a second form of urban public infrastructure that contributes to well-being but is not directly associated with physical infrastructure, such as garbage collection.
Planning public infrastructure in urban areas requires the simultaneous analysis of multiple factors [
9]. This simultaneous analysis requires considerable cognitive effort, which can limit and hinder decision-making [
10]. One solution to this problem is the adoption of an operational framework using composite indicators [
11,
12,
13].
Composite indicators are one-dimensional measures that result from aggregating weighted or unweighted normalized sub-indicators [
14]. These one-dimensional measures enable decision-makers to represent and understand complex, multidimensional phenomena, thereby facilitating informed decision-making across various areas of knowledge [
15,
16].
Scholars’ interest in improving methods for constructing composite indicators is growing [
17,
18,
19,
20]. This study contributes to these efforts by exploring new methods for constructing composite indicators that represent public infrastructure in urban areas, incorporating innovations into the Ordered Weighted Averaging operator.
The Ordered Weighted Averaging is an aggregation operator proposed by Yager [
21,
22] whereby sub-indicators are weighted according to their respective performance [
23]. Its weighing system allows for the construction of composite indicators with flexibility to emphasize the positive or negative aspects of the multidimensional phenomenon [
24]. Additionally, the Ordered Weighted Averaging weighing system allows for the adjustment of compensation levels between sub-indicators with poor and above-average performance [
25]. Finally, its weighting system considers the heterogeneity principle, in which the influence of a sub-indicator in the multidimensional phenomenon varies according to the decision-making unit [
7,
26].
However, despite these advantages, Ordered Weighted Averaging is little employed to construct composite indicators (see
Section 2) compared to other methods (e.g., [
27,
28]). Additionally, existing studies have concentrated on geography, where raster images are processed [
29,
30,
31,
32]. In contrast, studies that use Ordered Weighted Averaging to construct composite indicators based on vector data are fewer in number (e.g., [
33]). These studies do not comprehensively explore the different weighting systems of Ordered Weighted Averaging and their consequences in representing the multidimensional phenomenon. This gap leaves researchers in the dark about which weighting system to use or whether any weighting system should be avoided altogether.
This study aims to shed light on the repercussions of different weighting systems of Ordered Weighted Averaging on representing public infrastructures in urban areas, which are demonstrated through the case of the urban infrastructure of the city of São Sebastião do Paraíso, Brazil.
The study presents four points of originality. First, it offers a specific portrait of the literature on composite indicators constructed by Ordered Weighted Averaging. Second, the study examines the impact of different weighting systems on composite indicators, identifying which ones are suitable for representing public infrastructures in urban areas. Third, the study introduces a new set of weighting systems that simultaneously address the presence of outliers and compensate for poor and above-average performance sub-indicators. Fourth, the study proposes a mechanism for the balanced expansion of infrastructure in cities, assigning a higher property tax to areas that benefit most from urban infrastructure while prioritizing investment in areas with deficient urban infrastructure.
The findings obtained from these innovations contribute to expanding the literature on urban planning and composite indicators by offering alternatives for representing public infrastructures in urban areas and other multidimensional phenomena. Specifically, the composite indicator of urban infrastructure helps decision-makers understand a complex reality without losing generality. In turn, the new set of weighting systems enables the obtaining of reliable representations of urban infrastructure, thereby avoiding inaccurate or mistaken decisions.
In addition to this introduction,
Section 2 reviews the literature on public infrastructures in urban areas and composite indicators, with a particular emphasis on the low frequency of use of Ordered Weighted Averaging.
Section 3 explains how Ordered Weighted Averaging works, lists its most well-known weighting systems, and presents the weighting system proposed in this study. The data and methods are presented in
Section 4.
Section 5 presents an application example that compares the repercussions of different Ordered Weighted Averaging weighting systems on the representation of public infrastructures in urban areas. Finally,
Section 6 presents the final considerations, research limitations, and future lines of investigation.
3. Ordered Weighted Averaging
Firstly, explaining how the method proposed by Yager [
21,
22] works is opportune. Although quite peculiar, Ordered Weighted Averaging is very easy to implement. In short, the construction of a composite indicator using the method is carried out through the six steps below:
Normalize the data to the range [0, 1];
Transpose the data matrix, leaving the sub-indicators in the rows and the decision-making units in the columns;
Order the data in the transposed matrix from largest to smallest;
Define weights for each line, ensuring that the sum of the weights is equal to 1 (one);
Multiply the weights of each line by the values of the decision-making units in the same line;
Obtain the composite indicator scores by adding the weighted values of each column.
These steps emphasize the importance of defining the Ordered Weighted Averaging weights, as they are now associated with the row of the transport matrix and no longer with the sub-indicators [
8]. The method defines the weights based on the decision-making unit’s performance in each sub-indicator, generating scores that are sensitive to the local context [
25]. The weighting logic directed at the ordered sub-indicators operationalizes the concept of spatial heterogeneity, as the sub-indicator weights vary according to the decision-making unit [
7]. In short, Ordered Weighted Averaging enables the construction of composite indicators that are sensitive to the spatial context, highlighting positive or negative characteristics to varying degrees depending on the adopted weighting system.
3.1. Ordered Weighted Averaging Linguistic Operators
At this point, addressing the linguistic operators [
53] that enable the implementation of different weighting systems in Ordered Weighted Averaging is relevant. Linguistic operators are generally presented through their respective formulations [
54]. In the present case, these formulations are transcribed into text to facilitate their understanding.
Max operator: Assigns a weight of one to the first line (sub-indicators with the highest performance) and a weight of zero to the other lines, performing an utterly non-compensatory aggregation that skews the scores upward to the maximum.
Min operator: Assigns a weight equal to one to the last line (sub-indicators with the lowest performance) and a weight of zero to the other lines, performing an utterly non-compensatory aggregation, which skews the scores downwards to the maximum.
Simple average operator: Assigns equal weights to all lines, performing an utterly compensatory aggregation, not skewing the scores in any direction.
Note that these operators do not allow regulation of the compensation levels between sub-indicators or directing the bias of the scores, making it necessary to implement operators such as:
More than J criteria: Assigns a weight of one to the last j criteria defined by the decision-maker, performing a non-compensatory aggregation, which biases the scores downwards, with the compensation levels and the intensity of the bias controlled by the value of j.
At least J criteria: Assigns a weight of one to the first j criteria defined by the decision-maker, performing a non-compensatory aggregation, which biases the scores upwards, with the compensation levels and the intensity of the bias controlled by the value of j.
Although there are many other linguistic operators, the flexibility offered by the More than J and At least J criteria operators allows for representing a multidimensional phenomenon from different perspectives. Other weighting systems can be implemented with Ordered Weighted Averaging.
3.2. Goal-Based Ordered Weighted Averaging
Entropy weighting is a widely used weighting system [
55,
56], which is also applied in the literature on composite indicators [
57]. This weighting system assigns higher weights to data with greater informational diversity [
58]. Factor analysis is another standard weighting system in the literature on composite indicators [
27]. This weighting system has already been applied in the definition of weights for Ordered Weighted Averaging [
24]. It consists of finding a weight vector that maximizes the variance of the input data [
14]. In short, weighting systems frequently used in the construction of composite indicators can be adapted and implemented in Ordered Weighted Averaging as follows:
Entropy: Higher weights are assigned to lines with greater informational diversity, maximizing discrimination between decision-making units [
57];
Average variance extracted: Higher weights are assigned to the most correlated lines, maximizing the variance of the ordered data [
14,
59].
3.3. Extreme Values Reduction Ordered Weighted Averaging
Finally, the extreme values reduction weighting system prioritizes intermediate values to reduce the influence of divergent opinions on the results [
60,
61]. This weighting system prevents possible outliers from biasing the composite indicator scores or increasing the trade-off between poor and above-average performance sub-indicators. The extreme values reduction weighting system assigns zero weight to lines with higher or lower values, preventing outliers from being included in the aggregation and ensuring non-compensation between poor and above-average performance sub-indicators, which can be summarized as follows:
This study develops a new set of weighting systems that reconcile the core idea of extreme value reductions (EVR) in prioritizing intermediate values and statistical objectives such as variance maximization, phenomenon explanation, and informational diversity.
3.4. Novel Weighting Systems for Ordered Weighted Averaging
The new weighting systems introduced in this study define the intermediate weights of the EVR-Symmetric weights through data-driven methods. This combination enables the development of the following set of new weighting systems:
EVR-Factor Analysis: Greater weights are assigned to the intermediate lines in such a way as to maximize the correlations of the input data with the composite indicator.
EVR-Max link: Greater weights are assigned to the intermediate lines, with these weights defined based on a function that maximizes the correlation of the composite indicator with the reference indicator.
EVR-Entropy: Greater weights are assigned to lines that allow the construction of a composite indicator with the greatest possible informational diversity measured by the entropy index.
Subsequently, these new weighting systems are compared to the operator’s maximum, minimum, simple average, More than J, and At least J criteria in representing urban infrastructure.
3.5. Defining the Weights in Ordered Weighted Averaging and EVR Weighting Systems
Initially, it is necessary to point out that the Max and Min operators assign non-zero weights to only one row of the transposed matrix constructed in Step 3 (
Section 3). Therefore, these operators do not offer the decision-maker flexibility in defining the weights. In turn, the At least J and More than J criteria operators offer the decision-maker complete flexibility in defining the weights. This definition is entirely subjective and is associated with the trade-off between emphasis intensity and information in the model. In short, a greater emphasis intensity results in more information weighted with zero weight, and, consequently, less information in the model.
Table 2 exemplifies this logic for the More than J criteria operator.
In turn, EVR-based weighting systems define weights based on statistical objectives. The EVR-Factor Analysis is an adaptation of the function proposed by Santos et al. [
62]. These weighting systems set the
weights in (2) in such a way as to maximize the variance extracted from the input data of the composite indicator:
where
corresponds to the composite indicator as defined in (2).
EVR-Max link is an adaptation of the function proposed by Correa Machado et al. [
63]. These weighting systems set the
weights in (2) to maximize the correlation of the reference indicator income (
) with the composite indicator:
where
is the covariance,
is the standard deviation of
,
is the standard deviation of
.
EVR-Entropy is an adaptation of the function proposed by Libório et al. [
64]. These weighting systems define the weights
in (2) to maximize the entropy index of the indicator composed by the following function:
where
is the number of decision-making units,
is the
-th score of the composite indicator.
5. Results and Discussions
5.1. Strengths and Weaknesses of Weighting Systems in the Representation of Urban Infrastructure
The Max and At least J operators are similar. They assign greater weights to the first lines, increasing the composite indicator scores, as sub-indicators with higher values are positioned in these lines during the sorting step. Composite indicators constructed by these operators have average scores of 0.994 and 0.910.
Conversely, the Min and More than J operators are similar in that they assign greater weights to the last lines, where sub-indicators with lower values are located, thereby reducing the composite indicator scores. Biasing the composite indicator scores upwards or downwards helps the decision-maker highlight the positive or negative aspects of the multidimensional phenomenon. Composite indicators constructed by these operators have average scores of 0.010 and 0.503.
Table 6 shows that indicators constructed using the logic of extreme value reductions present intermediate average scores. This result indicates the presence of outliers that bias the scores in traditional weighting systems. In particular, the average score of the simple average operator composite indicator is 0.650. This average score is lower than that observed in the EVR-Symmetric weights composite indicator, which was 0.717. This example suggests the presence of poor performance sub-indicators between extreme values.
In addition to highlighting the positive and negative aspects of multidimensional phenomena, weighting by ordering prevents poor performance sub-indicators from being compensated by above-average performance sub-indicators [
25]. This non-compensatory approach is advantageous because it differentiates composite indicators with different data structures but with the same mean. In other words, composite indicators with the same mean are treated differently, where one aggregates sub-indicators with performance close to the mean and the other aggregates sub-indicators with performance far from the mean [
24].
At this point, it is important to note that the Max and Min operators do not offer flexibility in regulating the bias intensity or compensation levels between sub-indicators. Both construct a composite indicator with total bias (positive or negative) and zero compensation level, as indicated by their coefficient of variation in
Table 7.
The results in
Table 7 show that the highest compensation level is observed between sub-indicators in the composite indicator More than J criteria. This result reinforces previous evidence on poor performance sub-indicators, particularly those with extreme values, as they increase the coefficient of variation of the scores. This evidence is corroborated by the coefficients of variation of the composite indicator’s simple average operator and EVR-Symmetric weights. The compensation levels between sub-indicators in the EVR-Symmetric weights are 0.484 and 0.635 in the simple average operator. Naturally, this result is expected, as extreme values increase the compensation levels between sub-indicators, increasing the coefficient of variation of the scores.
Another repercussion of the critical weighting systems to be evaluated is the correlation of the composite indicator with the reference indicator of income. This correlation is significant because it enables us to evaluate the extent to which the composite indicator aligns with the concept of the multidimensional phenomenon.
Table 8 shows that the Max and Min operators do not capture the essence of urban infrastructure. The correlation coefficients of these composite indicators with the city areas’ urban infrastructure are 0.147 and 0.278. According to the rule of thumb of Hinkle et al. [
65], these correlations are negligible. The other seven composite indicators correlate with income between 0.412 and 0.343 and are more closely aligned with the urban infrastructure construct.
The average extracted variance informs how much sub-indicator data was retained in the composite indicator.
Table 9 shows that the constructed composite indicators extract about 20% of the information from the sub-indicators. However, the Max and Min composite indicators capture a much smaller percentage, 0.142 and 0.021, respectively.
These results prove that Max and Min operators can construct unreliable composite indicators. In particular, these operators also perform poorly in correlation with the reference indicator and show excessive bias in the scores.
Furthermore, composite indicators constructed by Max and Min operators show considerable deviations in urban infrastructure ranking.
Table 10 shows that the uncertainty associated with the Max and Min weighting systems is, on average, 3.045 and 3.658 times greater than the mean.
A relevant point to highlight is the zero ranking uncertainty observed in the composite indicators’ simple average and EVR-Symmetric weights. On the one hand, this result suggests that the weighting that favors intermediate values may not significantly impact the ranking of urban infrastructure. On the other hand, the results suggest that extreme values may underestimate urban infrastructure, as they increase the compensability between sub-indicators.
5.2. Visualization of the Repercussions of Weighting Systems in the Representation of Urban Infrastructures
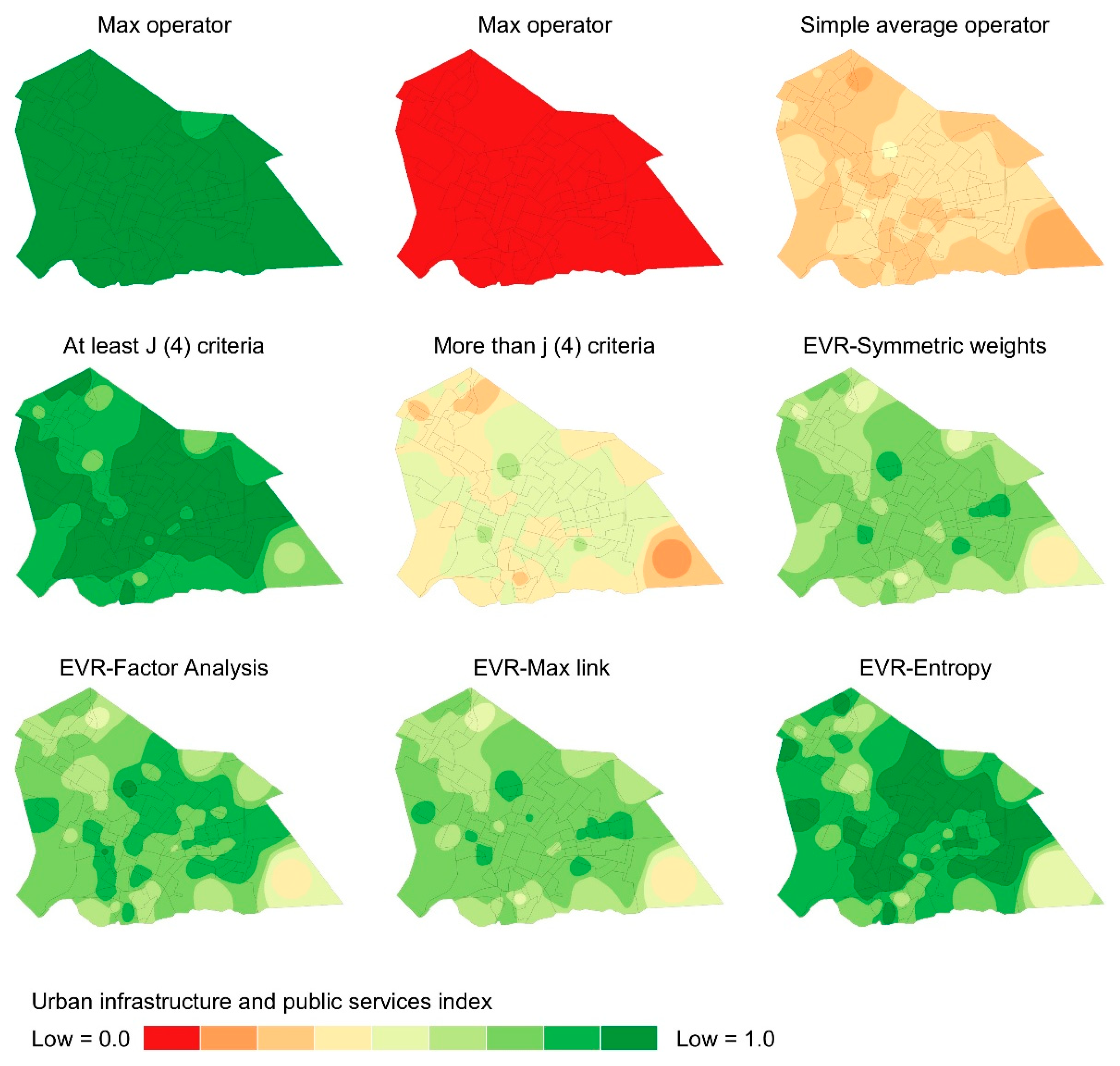
The Max and Min weighting systems are generally unsuitable for representing composite indicators, as they fail to capture the concept of multidimensional phenomena, resulting in significant information loss and high-ranking uncertainty.
Figure 1 illustrates that the Max and Min weighting systems also excessively bias the composite indicator scores, thereby creating difficulties in differentiating between decision-making units.
Weighting systems based on extreme value reduction logic are ideal for representing multidimensional phenomena for different reasons. These weighting systems avoid the aggregation of sub-indicators with extreme performance, avoiding excessive bias in the scores and reducing the compensation levels between sub-indicators. They also offer composite indicators with the highest degrees of correlation with the multidimensional phenomenon concept and representation concerning the input sub-indicators. Furthermore, they do not cause significant variations in the ranking of urban infrastructure, indicating a stable internal structure.
However, weighting systems implemented based on extreme value reduction logic fail to highlight the negative aspects of the multidimensional phenomenon. This limitation prevents public managers from identifying priority areas for investments in urban infrastructure. In this case, it is possible to consider using composite indicators constructed by the More than J (4) criteria and simple average weightings to overcome this limitation.
5.3. Strategies for a Balanced Expansion of Urban Infrastructure
Implementing different weighting systems provides an opportunity to develop strategies for the balanced expansion of urban infrastructure. On the one hand, implementing the More than j (4) weighting system enables the identification of areas in the city with the most deficient urban infrastructure. Prioritizing investments in these areas is a natural choice, as they reduce inequality in the distribution of urban infrastructure more significantly. On the other hand, EVR-Entropy allows the implementation of a second strategy for the balanced expansion of urban infrastructure. Governments can adjust property tax rates in consideration of the supply of urban infrastructure. Thus, the property tax would consider the welfare benefits and real estate appreciation that urban infrastructure generates. In short, higher rates are attributed to areas that benefit most from urban infrastructure.
The combination of the strategies mentioned above enables the implementation of a mechanism for balancing the city’s infrastructure. In this case, areas with the greatest deficiencies in urban infrastructure (those exceeding the J criteria) correspond to areas with the lowest property tax rates (as measured by EVR-Entropy) and vice versa. This mirroring enables the implementation of a mechanism for fiscal justice, directing investments in urban infrastructure to enhance the well-being of all citizens.
Figure 2 illustrates the areas of the city with the most significant deficiencies in urban infrastructure.
Figure 2 illustrates the areas of São Sebastião do Paraíso (MG) with the most significant deficiencies in urban infrastructure, revealing a clear center–periphery pattern typical of Latin American socio-spatial urban organization [
66]. In this structure, central areas tend to exhibit better living conditions and infrastructure provision, while peripheral zones face pronounced deficiencies, often equated with those of the underprivileged.
Under these circumstances, the combination of the More than J criteria and EVR-Entropy weighting systems provides valuable insights for public planners aiming to develop balanced infrastructure strategies. Specifically, the areas identified as most deficient by the More than J criteria align with those showing the lowest property tax rates under the EVR-Entropy system, and vice versa. This mirroring enables the implementation of a redistributive mechanism that promotes fiscal justice, in which revenue collected from wealthier, well-served areas can be reinvested in underserved neighborhoods. After all, better infrastructure increases property value and quality of life. Therefore, residents in these areas can contribute more through taxes, while inhabitants of vulnerable areas can be protected from excessive taxation and prioritized for infrastructure investment. Such an approach not only enhances social equity but also improves the efficiency and transparency of urban planning decisions.
5.4. External Validation
The external validation of the More than J criteria and EVR-Entropy weighting systems aims to ensure robust results and a balanced expansion of urban infrastructure.
Table 11 shows that the selected weighting systems are robust from both perspectives. First, the scores of the composite indicators constructed using the More than J criteria and EVR-Entropy weighting systems exhibit very strong correlations with the scores of the composite indicators constructed by the methods most frequently employed in the literature.
Secondly,
Table 12 shows that the ranking of census sectors in terms of infrastructure and urban services does not exhibit significant fluctuations due to changes in the weighting system of the More than J criteria or the EVR-Entropy method.
These results indicate that the priority areas for investment in public infrastructure or for adjusting the property tax rate, as indicated by the More than J criteria or EVR-Entropy weighting systems, are stable and do not present significant fluctuations in relation to the Principal Component Analysis, Entropy, and Benefit-of-the-Doubt methods.
6. Conclusions
This study highlights several significant findings on constructing composite indicators using the Ordered Weighted Average operator. First, composite indicators constructed using the Max and Min operators proved inadequate, as they presented high information loss and uncertainty, thereby compromising their usefulness in evaluating urban infrastructure. Second, weighting systems based on extreme value reduction logic are more effective in representing multidimensional phenomena, as they avoid aggregating sub-indicators with extreme performance and, thus, reduce bias in the scores of composite indicators.
These results have significant practical implications for urban planners, as they provide a solid basis for directing investments in urban infrastructure. The study suggests that adopting weighting systems that prioritize intermediate values can lead to more effective resource allocation, helping to identify areas with deficient infrastructure and promoting more equitable urban development. Furthermore, the correlation of composite indicators with reference indicators, such as average income, was significantly improved with the new weighting systems, indicating greater adherence to the concept of multidimensional phenomena.
The new weighting systems for the Ordered Weighted Average operator enable the consideration of heterogeneity in sub-indicators within each area, allowing for the planning of balanced urban infrastructure expansion that takes into account the characteristics of each area. Furthermore, the non-compensability between sub-indicators prevents one infrastructure from replacing another, preventing deficiencies in one type of infrastructure from being masked by the presence of other infrastructures. The capacity of the composite indicators to capture the multidimensional concept is another valuable piece of information for urban planners, as it signals whether the composite indicator is appropriate for use. Finally, the informational loss inherent in sub-indicator aggregation helps urban planners verify the compatibility between the conceptual and operational frameworks by revealing the transfer rate of the data defined in the conceptual framework to the composite indicator.
These novelties open up new directions for future investigations, particularly concerning the analysis of variation in the importance of sub-indicators across spatial units, which can further enrich our understanding of urban phenomena. Within this line of research, it is essential to note that the ordering of the transposed matrix presents considerable challenges in tracking the weights assigned to the sub-indicators within each decision-making unit. This limitation hinders the interpretation of spatial heterogeneity, such as identifying the most relevant sub-indicators by geographic context, and measuring the sensitivity levels of the weighting systems in the composite indicator scores. In this context, developing a mechanism for tracking the weights assigned to sub-indicators within each decision-making unit is also a promising line of future research.