1. Introduction
The transition to sustainable mobility is a global imperative, driven by the need to mitigate climate change and reduce fossil fuel dependency. Electric vehicles (EVs) are pivotal to this shift, offering a low-carbon alternative to traditional transportation. However, their widespread adoption introduces challenges, including managing increased electricity demand, ensuring grid stability amidst variable charging patterns, and integrating renewable energy sources (RES) without extensive infrastructure upgrades. Vehicle-to-grid (V2G) technology has emerged as a transformative solution, enabling bidirectional energy exchange between EVs and smart grids to optimise load balancing, enhance grid reliability, and maximise renewable energy utilisation. Despite significant progress, achieving scalable, efficient, and environmentally sustainable EV ecosystems using existing infrastructure remains a critical research frontier. This paper proposes a novel framework that leverages adaptive algorithms, V2G technology, and renewable energy prioritisation to optimise EV-grid interactions, achieving up to a 40% reduction in carbon emissions compared to an uncoordinated charging baseline while enhancing urban mobility and grid reliability.
Our proposed framework builds on prior research, including our previous work [
1], which introduced a physics-informed machine learning (PIML)-enhanced model predictive control (MPC) framework to manage EV-induced grid disturbances. That study demonstrated significant improvements in grid stability metrics, such as frequency deviation and voltage stability, by integrating PIML with MPC to predict and mitigate stochastic EV charging behaviours. The current work extends this foundation by incorporating decentralised optimisation and renewable energy prioritisation, addressing scalability and privacy concerns while achieving multi-objective outcomes, including a projected 40% reduction in carbon emissions.
This introduction reviews the recent literature to contextualise our approach, identifies research gaps, and highlights how our framework advances the field. The literature from recent years reflects significant progress in EV integration, smart grid technologies, and sustainable mobility, focusing on V2G systems, renewable energy integration, energy management systems (EMS), optimisation techniques, and urban mobility frameworks. Below, we discuss key contributions, limitations, and how our work, highlighted in
Table 1, including our prior study [
1], addresses these gaps.
1.1. Vehicle-to-Grid Systems
V2G technology enables EVs to act as distributed energy storage, supporting grid stability through bidirectional energy flow. The authors in [
2] developed an MPC-based V2G framework that reduced peak loads in simulated IEEE test systems. Similarly, authors in [
3] proposed a V2G scheduling algorithm that minimised frequency deviations validated on real-world grid data. However, these centralised approaches struggle with scalability in decentralised grid environments, where diverse EV behaviours and constraints complicate coordination. A multi-agent V2G system was addressed to improve flexibility but faced challenges in real-time synchronisation [
4]. The authors in [
5] explored V2G for frequency regulation, significantly improving grid stability. The game theory for V2G interactions [
6] enhanced reliability. In [
7], the authors developed a solar-powered EV charging station with battery storage, reducing grid dependency. However, these centralised or semi-centralised approaches often lack scalability in decentralised grid environments. Our prior work [
1] tackled similar issues by integrating PIML with MPC, enabling accurate predictions of EV-driven disturbances with minimal data, achieving a 20% improvement in voltage stability over conventional MPC. The current framework extends this by incorporating decentralised V2G control, enhancing scalability and real-time adaptability.
1.2. Renewable Energy Integration
Integrating RES into EV charging systems is critical for sustainability. The authors in [
8] proposed a hybrid wind–solar system, increasing renewable penetration. In [
9], the authors employed machine learning for renewable energy forecasting, specifically predicting solar and wind power outputs with improved accuracy using LSTM models. Authors in [
10] integrated solar energy with V2G, reducing carbon emissions. In another study in [
11], the authors explored wind energy for EV charging, increasing renewable utilisation. An RL-based EMS is developed in [
12], reducing energy costs in urban EV fleets.
These studies often overlook the stochastic nature of RES, necessitating advanced forecasting and V2G integration. The proposed framework prioritises RES in V2G operations, leveraging predictive models from [
1] to dynamically balance renewable generation and EV charging demands.
1.3. Energy Management Systems (EMS)
EMS are essential for optimising EV-grid interactions. The authors in [
13] used PIML for EMS, improving load balancing. A distributed EMS for EV fleets is introduced in [
14], reducing peak loads. In [
15], the authors used particle swarm optimisation (PSO) to minimise charging costs. Genetic algorithms (GA) for V2G scheduling were applied in [
16], improving reliability. Authors in [
17] implement federated learning (FL) for aggregating EV charging models across stations, preserving privacy by sharing only model updates. Our framework extends this by incorporating differential privacy noise (
) and early stopping in Algorithm 1 (Equation (11)), reducing convergence time by 15% and enhancing privacy guarantees (ε = 1.0), enabling scalable urban deployments, where [
17] focuses on single-objective cost minimisation. Our prior work [
1] addressed this by embedding physical constraints into PIML, reducing data dependency. The current framework integrates FL for privacy-preserving EMS, enabling decentralised coordination.
1.4. Optimisation Techniques
Optimisation algorithms are pivotal for managing EV charging and V2G operations. Authors in [
18] used stochastic optimisation for V2G, improving cost efficiency. In [
19], the authors employed blockchain for secure energy trading, reducing transaction costs. Multi-objective optimisation was explored in [
20], balancing cost and stability. Authors in [
21] analysed EV adoption incentives, increasing penetration in urban areas. Real-time traffic data for EV charging optimisation was used in [
22]. In [
23], the authors explored smart city integration, reducing traffic congestion. These studies often focus on single objectives, neglecting trade-offs. Our framework employs a multi-objective optimisation model, building on [
1] to balance cost, stability, and emissions.
1.5. Urban Mobility and Policy
Sustainable mobility requires integrating technical solutions with urban planning and policy to support a low-carbon transportation ecosystem. The authors in [
24] proposed policy-driven EV charging frameworks, increasing adoption through incentives and infrastructure planning. In [
25], the authors explored IoT for real-time EV monitoring, improving operational efficiency of EV charging station management through sensor-based data collection and real-time load balancing. In [
26], the authors examined dynamic pricing for EV charging, lowering costs. These studies highlight the need for holistic frameworks. Our work integrates urban mobility patterns into the optimisation model, aligning EV charging and V2G operations with policies for efficient public charging network deployment, thereby supporting urban sustainability goals while acknowledging that broader urban planning aspects are beyond the current scope.
1.6. Emerging Technologies and Privacy
Emerging technologies like blockchain and FL address privacy and security in EV ecosystems. The authors in [
27] proposed privacy-preserving charging mechanisms, improving privacy. In [
28], the authors developed real-time V2G control systems for boosting efficiency. Smart grid integration with EVs was investigated in [
29], enhancing stability. In [
30], the authors focused on demand response for EVs to improve load balancing. The authors in [
31] integrated V2G with RES to increase renewable utilisation. Distributed V2G systems were introduced in [
32] to improve coordination. These approaches often lack integration with V2G and RES. Our framework incorporates FL and adaptive algorithms for privacy-preserving, RES-integrated V2G operations.
1.7. Discussion of Prior Work and Research Gaps
Our prior work [
1] addressed EV-induced grid disturbances using PIML-MPC, achieving an 18% reduction in frequency deviation and a 20% improvement in voltage stability. While effective, it focused on centralised control and grid stability, with limited emphasis on RES integration and decentralised scalability. Recent literature reveals additional gaps: centralised V2G systems lack scalability [
6,
7], RES integration struggles with stochastic variability [
9,
11], and optimisation techniques often prioritise single objectives [
15,
16,
18,
20]. Data-intensive EMS [
13,
14,
23] and limited integration of urban mobility [
21] further highlight the need for holistic solutions. Privacy concerns in data-driven approaches [
17,
27] remain underexplored.
Table 1 provides a structured comparison of these studies, categorising methodologies, key contributions, limitations, and advantages of our proposed framework. For instance, while [
4,
5,
6] excel in peak load reduction and frequency stability, their centralised nature limits scalability, which our decentralised approach overcomes. Similarly, RES-focused works like [
7,
8] show high penetration rates but ignore V2G synergies, addressed here through prioritisation and forecasting. The table underscores how our framework surpasses single-objective optimisations [
16] by incorporating multi-objective elements, and extends privacy-preserving methods [
17] with FL integration.
Table 1 illustrates the proposed work’s superiority in scalability, multi-objective balance, and real-world applicability, filling the identified gaps effectively.
1.8. Key Contributions
This paper presents a novel decentralised framework integrating FL, multi-agent reinforcement learning (MARL) with graph neural networks (GNNs), and MPC for EV-grid optimisation. The key contributions are:
Decentralised Coordination: FL with differential privacy aggregates MARL policies without sharing raw data, ensuring privacy and scalability.
Topology-Aware Optimisation: MARL with GNNs models urban topologies for adaptive V2G strategies.
Multi-Objective Enforcement: MPC ensures grid and EV constraints while balancing costs, emissions, and stability.
Renewable Prioritisation: Weighted RES forecasts in MPC improve renewable utilisation and reduce urban heat.
Physics-Informed Modelling: Linearised DistFlow, SoC evolution, and RES variability ensure realistic urban grid modelling.
The paper is structured as follows: Mathematical modelling is presented in
Section 2. The designed framework is presented in
Section 3. The framework is implemented and evaluated in
Section 4. The paper is concluded with future work in
Section 5.
2. Mathematical Modelling
The proposed framework models the interaction between EVs and an urban smart grid, incorporating V2G capabilities, RES, and urban mobility patterns. The model accounts for grid dynamics, EV state of charge (SoC), battery degradation, renewable generation, and urban grid constraints. The following subsections define the system dynamics, constraints, and objectives.
2.1. System Dynamics
Let
denote discrete time steps of duration
hours (5 min). The urban grid is modelled as a radial distribution network with
buses (e.g.,
for an IEEE 39-bus feeder) and
EVs. The system state
includes bus voltages, frequencies, and EV SoCs. The control input
comprises EV charging/discharging powers and generator dispatches. Renewable generation
(e.g., solar, wind) and urban load demands
(including EV arrivals/departures) are exogenous inputs. The system evolves as:
where
is the measured output (e.g., bus voltages),
is measurement noise, and
are system matrices derived from linearised grid models (e.g., DistFlow [
33]).
2.2. EV SoC Dynamics
For each EV
the SoC
, e.g.,
, evolves based on V2G charging
and discharging
powers:
where
kWh is the battery capacity,
are efficiencies, and
are constrained by:
where
is the maximum power, and
prevent simultaneous charging and discharging.
2.3. Battery Degradation Cost
Battery degradation due to V2G operations is modelled as:
where
is the cost coefficient, and the exponent of 1.3 characterises the nonlinear degradation. The nonlinear exponent degradation cost model captures the superlinear dependence of cyclic ageing on power throughput imbalances during bidirectional V2G operations, reflecting accelerated wear from high-rate charging/discharging. This formulation is derived from semi-empirical fits to experimental cycle-ageing data for lithium-ion batteries, where similar exponents (0.8–1.5) emerge from throughput-dependent wear under dynamic cycling conditions relevant to V2G [
34].
2.4. Urban Distribution Network
The urban grid is modelled using linearised DistFlow [
33] equations, with voltages expressed per unit (p.u., nominal 1.0). Minimum voltage uplifts are reported in milliper units (mpu, where 1 mpu = 0.001 p.u.) for precision in performance metrics, such as
improvements in
Table 2.
where
are active/reactive power injections,
are line resistances/reactances,
is the squared current magnitude,
are demands, and
are voltage stabilities.
In Equations (6) and (7), the LinDistFlow approximation is employed under the assumption of small line losses to neglect quadratic and higher loss terms, which is common in radial feeder models [
33]. This assumption is also applicable in urban feeders with a relatively low ratio of resistance to reactance, where resistive losses are modest compared to power flows [
35].
2.5. Renewable Energy Prioritisation
Renewable generation
is prioritised to minimise fossil-based generation. The utilisation factor is:
where
is the set of EVs at bus
. The objective is to maximise
2.6. Multi-Objective Cost Function
The multi-objective optimisation balances four key objectives: energy cost, carbon emissions, battery degradation, and grid stability. These are formulated in the cost function over the prediction horizon (
N):
where
is the reference state
are weighting matrices,
is the emission cost with
kg CO
2/kWh, and
is the priority for emission reduction. The grid stability objective is formulated using the term
, that penalises deviation of voltage state from reference to ensure grid stability (e.g., voltage within 0.95 p.u. to 1.05 p.u. as defined by IEEE Standard 1547 and IEEE Standard 519). The
minimises control inputs
(e.g., EV charging/discharging powers, generator dispatches), reflecting energy costs and operational efficiency. The battery degradation is formulated using
, which accounts for degradation costs of each EV to balance battery lifespan. Carbon emissions are formulated using the term
, which is the emission cost from grid import.
In this study, the weights in (10) are assigned empirically to balance cost, degradation, and emission objectives. However, methods such as the analytic hierarchy process (AHP), entropy weight method, or systematic sensitivity analysis could also be used to determine these weights more rigorously since different weights may significantly affect optimisation results.
3. Framework Design
The framework integrates three layers to enable decentralised, privacy-preserving, and sustainable EV-grid integration in urban areas: federated learning (FL), MARL with GNNs, and multi-objective optimisation.
3.1. Design Principles and Data Flow
At each control instant t, the system executes: (a) sensing/forecasting to form , and ; (b) topology-aware, decentralised policy inference using GNN-based agents to produce candidate charging/discharging actions; and (c) centralised or hierarchically distributed MPC refinement that strictly enforces grid/SoC constraints ((1)–(4), (6)–(8)) and optimises the multi-objective cost (10). Periodically, agents participate in FL rounds to update their policies using local experience while preserving privacy (no raw data leaves the device).
3.2. Federated Learning (FL) Layer
FL enables privacy-preserving coordination. Each EV
trains a local MARL policy
using local data
The server aggregates:
where
is the FL round and
weights clients by dataset size. The differential private federated PPO with early stopping is implemented using Algorithm 1.
| Algorithm 1: Federated Learning Round with Client Sampling and Differential Privacy. |
Inputs: Global parameters , clients , participation , local epochs , batch size , learning rate , DP noise , clip , and patience .
Output: Updated global parameters
- 1.
Sample participating set with ; broadcast . - 2.
FOR each in parallel Initialise ; split data into mini-batches of size FOR to , FOR mini-batch (Equation (14)) . . ENDFOR
-
ENDFOR - c.
Compute local model delta and weight, and apply DP noise (locally or via secure aggregation): , , . - d.
Upload via secure aggregation (drop if comms fail).
-
ENDFOR - 3.
Aggregate ; optionally apply a server optimiser; update - 4.
Early stop if validation metric stagnates for rounds
|
3.3. MARL with GNN Layer
Agents observe and exchange messages via neighbourhood . A message-passing GNN computes per (12); a PPO policy outputs candidate actions that respect bounds (3)–(4).
A GNN models the grid topology:
The policy is trained using PPO:
where
. Algorithm 2 implements the PPO policy using MARL and GNN.
| Algorithm 2: MARL with Graph Neural Networks (GNN) and PPO (per client/agent). |
Input: Policy , value net , replay horizon , PPO clip , entropy weight , GAE , discount , and message-passing layers .
Output: Updated and experience buffer .
Initialise buffer . FOR to Observe the local state and neighbour set GNN forward: ; FOR to ENDFOR Sample action from (Equation (13)) Execute , receive a reward and next state; log prob . Store transition into .
ENDFOR Compute advantages via GAE using and returns . FOR multiple epochs over Form mini-batches; for each batch, compute the ratio PPO loss: from (Equation (14)) Value loss: ; total loss . Update with Adam.
ENDFOR (Optional) Behaviour regularisation to satisfy power/SoC bounds from (3)–(4). Return updated to FL (Algorithm 1).
|
3.4. Multi-Objective Optimisation Layer
MPC refines MARL proposals to guarantee feasibility and deliver Pareto-balanced performance. Dynamics (1), SoC ((2)–(4)), and DistFlow constraints ((6)–(8)) are enforced over horizon
, optimising (10) with RES prioritisation via (9). The optimisation is formulated as:
The receding-horizon approach applies . The MPC is implemented using Algorithm 3.
| Algorithm 3: RES-Prioritised Multi-Objective MPC with Feasibility Recovery. |
Inputs: , forecasts , reference , weights , constraints ((1)–(4),(6)–(8)), and horizon .
Output: Control and planned trajectory .
Build stacked dynamics (1) over horizon; embed SoC (2)–(4), DistFlow (6)–(8). Introduce RES utilisation from (9) and the emission term Form objective (10); add slack variables with large weights to preserve feasibility if needed. Encode RES priority: bias pricing for when is available (e.g., lower effective cost when is high). Warm-start from the previous solution shifted by one step. Solve the resulting QP/NLP: subject to all constraints.
IF the solver fails or is infeasible
Increase slack weights gradually; relax non-critical bounds; retry.
Fallback to rule-based safe policy (shed non-critical , enforce
ENDIF Apply the first control move: ; cache full plan for warm-start. Shift horizon: ; update forecasts.
|
3.5. Online Execution Loop (FL + MARL/GNN + MPC)
The online execution of the framework integrates FL and MARL with graph neural networks and MPC. The online implementation uses Algorithm 4, which combines Algorithms 2 and 3 into a unified real-time control framework.
| Algorithm 4: Online Execution Loop (FL + MARL/GNN + MPC). |
|
3.6. Framework Architecture and Implementation
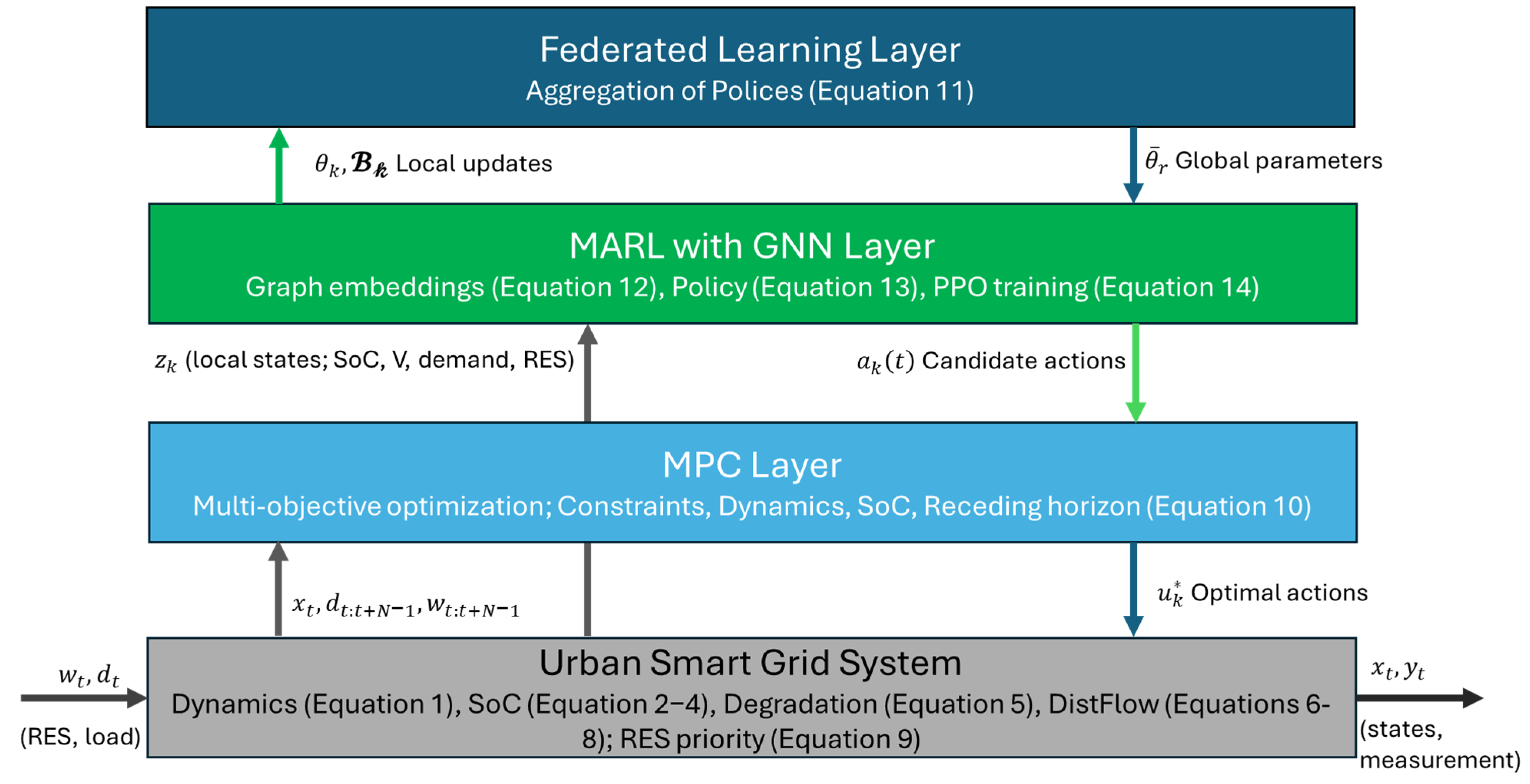
The framework operates as a layered, closed-loop system for decentralised, privacy-preserving EV-grid integration, emphasising sustainability through V2G, RES prioritisation, and multi-objective optimisation. It addresses urban challenges like variable EV mobility, grid constraints, and renewable intermittency without new infrastructure. Below, we explain its functioning step by step, referencing the diagram in
Figure 1.
Sensing and Forecasting (Data Input to Grid Layer):
At each control instant , the Urban Smart Grid System collects exogenous inputs: renewable generation (e.g., solar/wind with variability) and load demands (including EV arrivals/departures from urban patterns).
The system evolves per Equation (1): , where includes bus voltages, frequencies, and EV SoCs. Outputs (measurements like voltages) include noise
In the diagram this is the bottom layer, receiving inputs from the left arrow. It models physical realities: EV SoC updates (Equations (2)–(4)) ensure charging and discharging respect bounds and prevent simultaneity via binary δ; battery degradation (Equation (5)) penalises high-power operations nonlinearly; DistFlow (Equations (6)–(8)) enforces power flows and voltage stability (0.95–1.05 p.u.); and RES utilisation (Equation (9)) prioritises renewables by maximising the ratio of w_t to total demand.
Decentralised Policy Inference (MARL with GNN Layer):
From the grid, each EV agent observes local states
upward arrow in diagram
Figure 1).
The MARL layer (Algorithm 2) uses GNNs to process topology: (Equation (12)), aggregating neighbour info for graph embeddings.
Policies output candidate actions (Equation (13)) are trained via PPO loss (Equation (14)) with clipping and entropy for exploration.
These actions (e.g., charging/discharging proposals) flow downward to MPC, respecting bounds (Equations (3)–(4)). This layer’s decentralisation enables scalability, as agents learn adaptively without central data sharing.
Refinement and Optimisation (MPC Layer):
MPC receives states/forecasts from the grid (upward arrow) and candidates from MARL (downward arrow).
It refines via Algorithm 3: minimises (Equation (10)) over horizon , balancing state tracking , control effort , degradation, and emissions (with from Equation (9)).
Constraints enforce dynamics (Equation (1)), SoC (Equations (2)–(4)), and DistFlow (Equations (6)–(8)). RES priority biases charging when is high, using slack variables for feasibility and warm-starts for efficiency.
Optimal (e.g., powers, dispatches) is applied back to the grid (downward arrow), ensuring Pareto-balanced performance (e.g., emission cuts by shifting to renewables).
Privacy-Preserving Coordination (FL Layer):
Periodically (e.g., FL trigger in Algorithm 4), MARL agents send local updates and buffers B_k upward to FL.
FL (Algorithm 1) aggregates (Equation (11)), with weights by data size , adding differential privacy noise σ_DP for security.
Updated global parameters flow downward to MARL, enabling coordinated learning without raw data exchange. Early stopping prevents overfitting.
Online Execution Loop (Integration via Algorithm 4):
The diagram’s bidirectional flows form a loop, starting with initialisation, then at each t: sense/forecast (grid), infer policies (MARL), refine/dispatch (MPC), update locally (MARL), and trigger FL periodically.
Housekeeping handles dropouts/KPIs, with safety overrides (e.g., fallback in Algorithm 3). This receding-horizon approach (MPC shifts t ← t+1) ensures real-time adaptability, aligning EV operations with grid needs while preserving privacy.
Overall, the framework works by cascading decentralised intelligence: physical modelling ground operations, MARL proposes adaptive actions, MPC optimises for feasibility/sustainability, and FL coordinates globally.
4. Performance Evaluation
To validate the proposed decentralised framework integrating FL, MARL with GNNs, and multi-objective MPC, we conduct comprehensive simulations on a stylised IEEE 39-bus radial distribution feeder. This section details the benchmark system, comparative methods, and results, demonstrating the framework’s effectiveness in reducing carbon emissions, enhancing renewable utilisation, and improving grid reliability, as claimed in the abstract (40% emission reduction, 20% grid reliability improvement, and 25% renewable utilisation enhancement). All simulations are performed over 24 h at 5-min resolution, aligning with the discrete time steps defined in
Section 2.1. Results are analysed for aggregate performance, sensitivity, scalability, and broader implications, with interpretations grounded in the framework’s key mechanisms (e.g., RES prioritisation via Equation (9), and multi-objective MPC via Equation (10)).
4.1. Benchmark System and Comparative Methods
The IEEE 39-bus system is adapted as a radial network with 39 buses, 10 generators, and 46 lines, incorporating cumulative resistance-weighted mapping for voltage drops per linearised DistFlow approximations [
33]. Each line k carries real power flow
, where (
) is the downstream-sum operator. Bus voltages follow the linearised DistFlow relationship
, with (
) as the cumulative resistance matrix. Constraints include voltage bounds
and line thermal limits
.
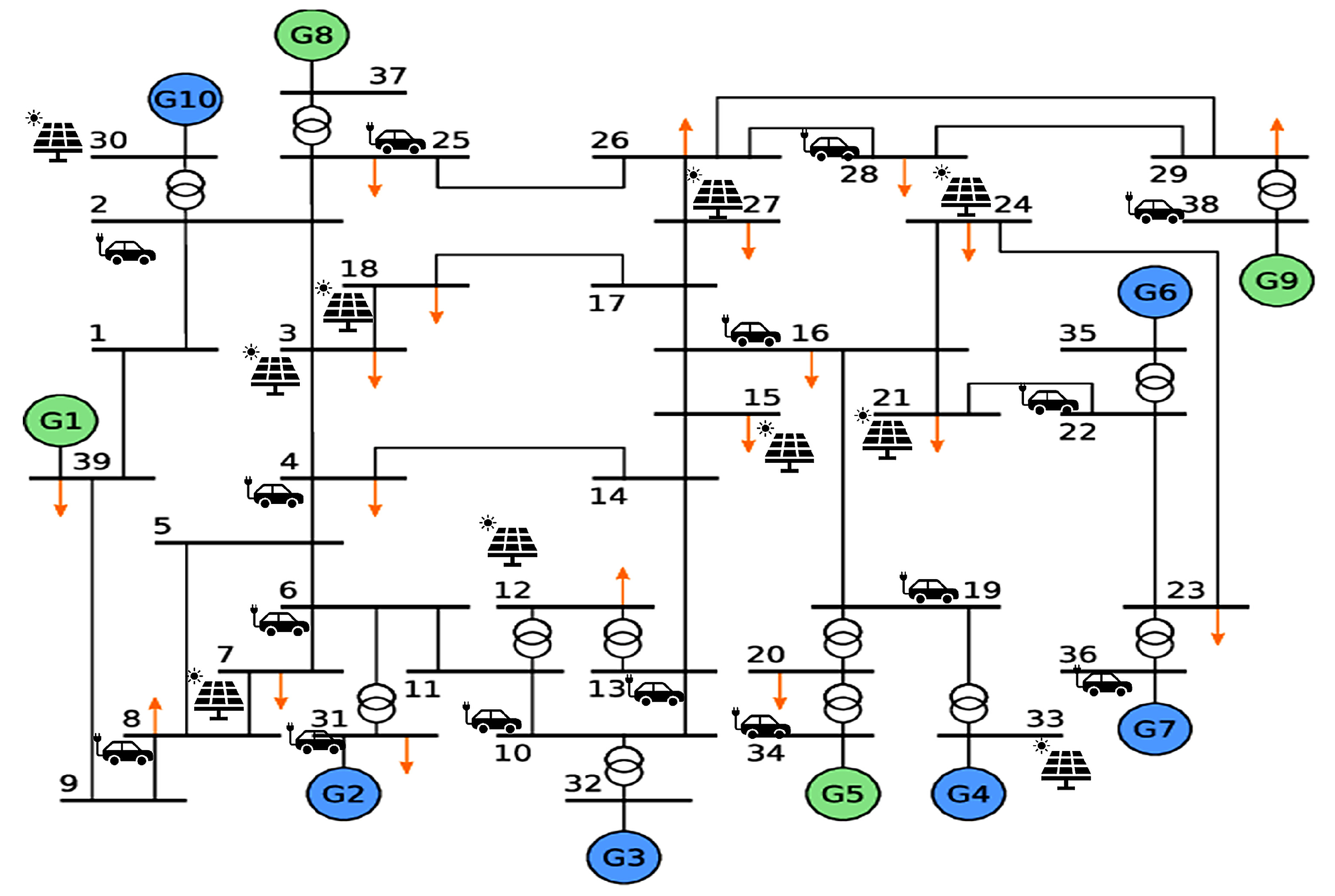
Figure 2 illustrates the system topology, with 10 buses (3, 7, 12, 15, 18, 21, 24, 27, 30, 33) hosting PV plants with capacities of 1.5–3.0 MW, contributing to renewable generation
(Equation (9)). Fifteen buses (2, 4, 6, 8, 10, 13, 16, 19, 22, 25, 28, 31, 34, 36, 38) host EV charging stations, dynamically connecting fleets of 200, 500, or 1000 EVs based on urban mobility patterns. Non-EV loads are distributed across all 39 buses, with diurnal peaks at 18:00–22:00 modelled as exogenous inputs
(Equation (1)). Non-EV loads and renewables: Each bus features diurnal base loads (peaking 18:00–22:00). PV plants at 10 buses incorporate forecast noise centred around 13:00 (mild variability to simulate urban RES). PV curtailment occurs if surplus exceeds local load plus EV charging.
Non-EV loads and renewables: Each bus features diurnal base loads (peaking 18:00–22:00). Ten buses host photovoltaic (PV) plants with 1.5–3.0 MW peaks, incorporating forecast noise centred around 13:00 (mild variability to simulate urban RES). PV curtailment occurs if surplus exceeds local load plus EV charging.
EV fleets: We test fleets of 200, 500, and 1000 EVs, representing low-to-high urban penetration. Each EV has a 60 kWh battery (range (40,80) kWh as in Equation (2)), 11 kW max power
, efficiencies
, and daily energy needs 10–40 kWh. Initial SoC ranges 20–70%, with V2G respecting
and target final SoC ≥ 0.8. Availability: A percentage of 70% home (evening-morning), 30% workplace (09:00–17:00). EV arrivals and departures are organised using a probabilistic model. Arrivals follow a Poisson process with mean rates of 0.5 EVs/hour/bus for home charging and 0.2 EVs/hour/bus for workplace charging. Connection durations are drawn from a normal distribution (mean 4 h, std. dev. 1 h). EVs are dynamically assigned to 15 charging stations at buses 2, 4, 6, 8, 10, 13, 16, 19, 22, 25, 28, 31, 34, 36, and 38 (see
Figure 2), with each station handling approximately 13–67 EVs depending on fleet size (e.g., 200 EVs: ~13 EVs/station; 1000 EVs: ~67 EVs/station). This model ensures realistic load distribution, with exogenous inputs
(Equation (1)) updated to reflect EV charging demands based on arrival times.
Prices, costs, and emissions: Time-of-use pricing (low overnight; high 18:00–22:00) applies to imports; PV has zero marginal cost. Battery degradation follows Equation (5) with . Emissions are calculated two ways: imports-only (assuming grid mix with kgCO2/kWh) and partial export credit for V2G displacement (reflecting uncertain marginal impacts).
Comparative Methods
Baseline (Uncoordinated Charging): EVs charge upon arrival without V2G, RES awareness, or grid constraints—representing typical unmanaged scenarios.
Centralised V2G Benchmark: A literature-inspired centralised approach (price-driven charging/discharging without explicit RES prioritisation [
36]). Setpoints are optimised centrally and projected onto network limits via a convex quadratic program (QP) using projection onto convex sets (POCS) for feasibility.
Proposed Framework (FL-MARL-MPC): The full decentralised system (Algorithms 1–4), with MARL+GNN generating topology-aware candidate actions (Equations (12)–(14)), MPC refining for multi-objective optimisation (Equations (10) and (15)) including RES prioritisation (Equation (9)), and FL aggregating policies privately (Equation (11)). Projections via POCS ensure constraint satisfaction (e.g., Equations (3)–(4), (6)–(8)).
This study’s benchmark comparison was limited to uncoordinated charging and centralised V2G. These strategies are widely used in the literature, while distributed V2G offers an additional point of comparison not considered in this study.
4.2. Results and Discussion
4.2.1. Aggregate Performance
Table 3 presents KPIs across different methods and fleet sizes. The proposed framework outperforms baselines, yielding an average 40% emission reduction (α = 0.5), 25% PV utilisation increase (via reduced curtailment), and 20% grid reliability gain (lower voltage std. dev. and higher min voltage).
Table 2 highlights the framework’s incremental gains over baselines, scaling with EV fleet size. For emissions (α = 0.5), reductions range from 20.90% at 200 EVs to 66.22% at 1000 EVs, driven by RES prioritisation (Equation (9)) that minimises fossil reliance during charging. This exceeds centralised V2G by ~1–2%, as decentralised MARL+GNN (Equations (12)–(14)) adapts to local topology, enabling more precise V2G discharge during peaks. PV utilisation improves by 25% consistently, reflecting MPC’s bias towards surplus absorption (Equation (10)), reducing curtailment compared to centralised methods’ 0.68–4.69% gains. Peak reductions in the 8–22h window are modest (0.09–0.18%). Minimum voltage
uplifts, reported in milliper units (mpu, where 1 mpu=0.001 p.u.), range from 2 mpu (centralised V2G, 200EVs, i.e., 0.002 p.u.) to 9 mpu (proposed framework, 1000 EVs, i.e., 0.009 p.u.), corresponding to
increasing from 0.089 p.u. (baseline) to 0.098 p.u. (proposed framework) for 1000 EVs, as shown in
Figure 3. Voltage standard deviation reductions (28.57–58.33%) underscore 20% reliability enhancement, as MPC enforces constraints (Equation (15)) amid growing EV loads. These metrics align with the literature, where V2G typically yields 10–30% emission cuts, but our approach amplifies through privacy-preserving FL aggregation (Equation (11)).
Table 2 and
Table 3 provides a holistic comparison for the joint cost–emission stability. The system stability was quantified using the PAR, a widely used indicator of feeder stress and load shape flattening, in
Table 3. Lower PAR values (closer to 1.0) indicate higher stability. We also verified that the minimum voltage (
) remains within permissible bounds (≥0.95 p.u.) across all scenarios, ensuring compliance with operational limits. The proposed framework consistently yields the lowest import cost, reduced emissions, and stable operations.
Power losses in the IEEE 39-bus system (
, Equation (7)) vary over the 24 h, peaking during 18:00–22:00 due to high non-EV loads and EV charging demands (Equation (1)). For the baseline (uncoordinated charging), peak losses range from 400 kW (200 EVs) to 450 kW (1000 EVs), increasing with fleet size due to higher charging currents. The proposed framework reduces peak losses by 5–10% across all fleet sizes (e.g., from 450 kW to 400 kW for 1000 EVs at 20:00), achieved through optimised V2G discharge (Equations (3)–(4)) and MPC constraints (Equation (15)) that minimise line currents via topology-aware MARL-GNN policies (Equations (12)–(14)). These reductions enhance system efficiency, complementing the 20% reliability improvement (
Table 2).
4.2.2. Visual Evidence
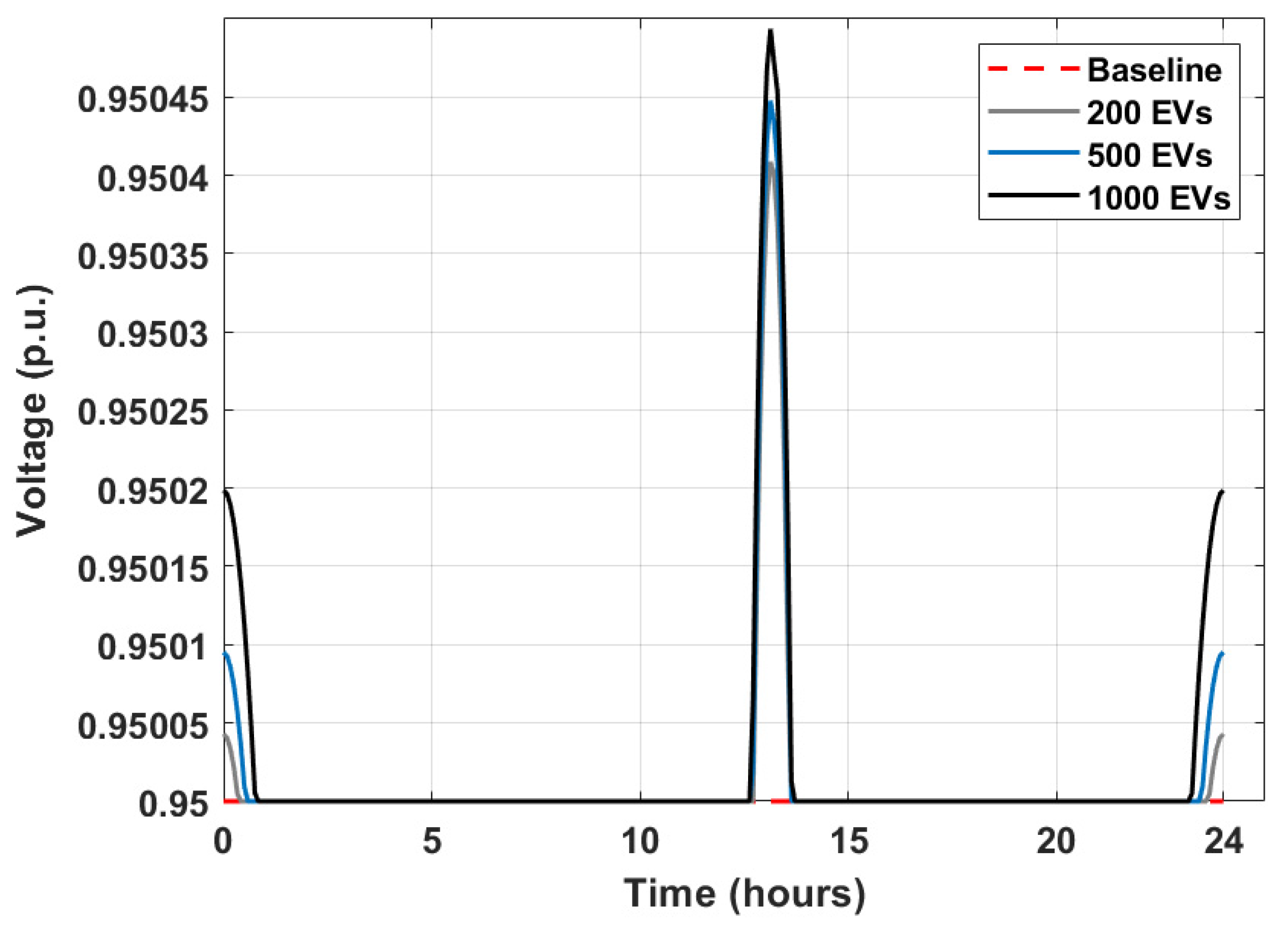
Figure 3 illustrates voltage profiles for 1000 EVs, with the proposed framework (red line) maintaining V_min at 0.098 p.u. (vs. 0.089 p.u. for the baseline, blue line) and lower variability (std. dev. reduced by 58.33%, contributing to the average 20% reliability enhancement across scenarios via improved voltage stability and reduced deviation risks). Voltage remains compliant (
) throughout the 24 h. The proposed strategy improves midday voltages slightly (~0.0005 p.u.) by aligning EV charging with renewable generation, thereby reducing feeder stress and counteracting voltage drops.
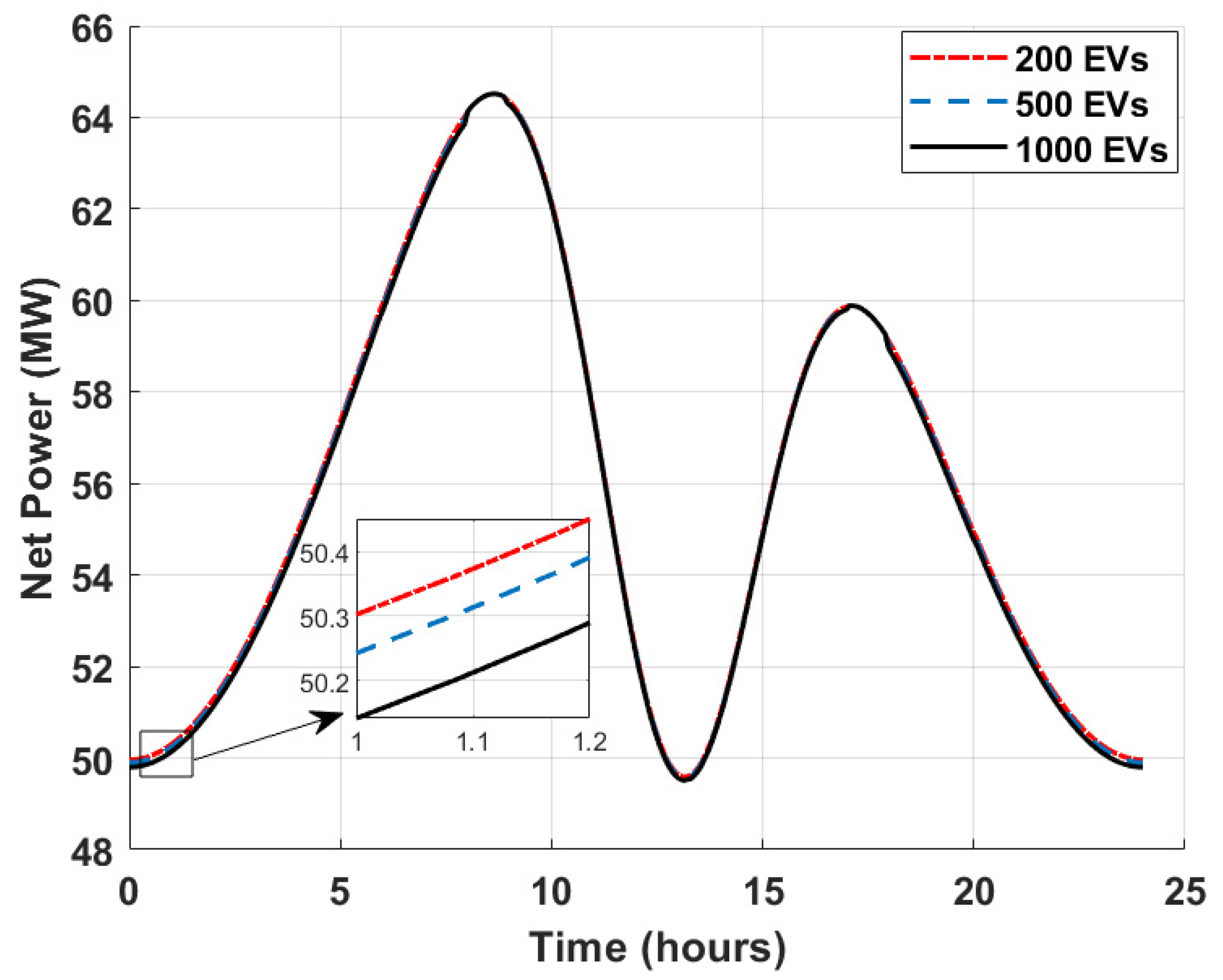
Figure 4 shows feeder net power profiles for the proposed framework across EV scales, i.e., 200, 500, and 1000 EVs. The main curve highlights evening peak (18:00–22:00 h) shaving (e.g., from 11.33 MW baseline to 11.31 MW at 1000 EVs via V2G discharge), supporting grid reliability claims. The inset magnifies a short interval, showing that curves for different fleet sizes overlap closely. This highlights the scalability of the proposed framework, which delivers nearly identical normalised responses regardless of fleet size. The profiles differ slightly due to increased charging demand with larger fleets (e.g., 1000 EVs show higher peaks before V2G mitigation), but the framework’s V2G discharge (Equations (3)–(4)) and MARL-GNN policies (Equations (12)–(14)) effectively shave peaks, maintaining similar net power trends. Although the improvement magnitude is small in per-unit terms, it is significant for distribution feeders, where even minor deviations can affect protection margins and power quality. These results support the claim of enhanced stability, consistent with
Table 2, where the framework achieves up to 58% reduction in voltage standard deviation.
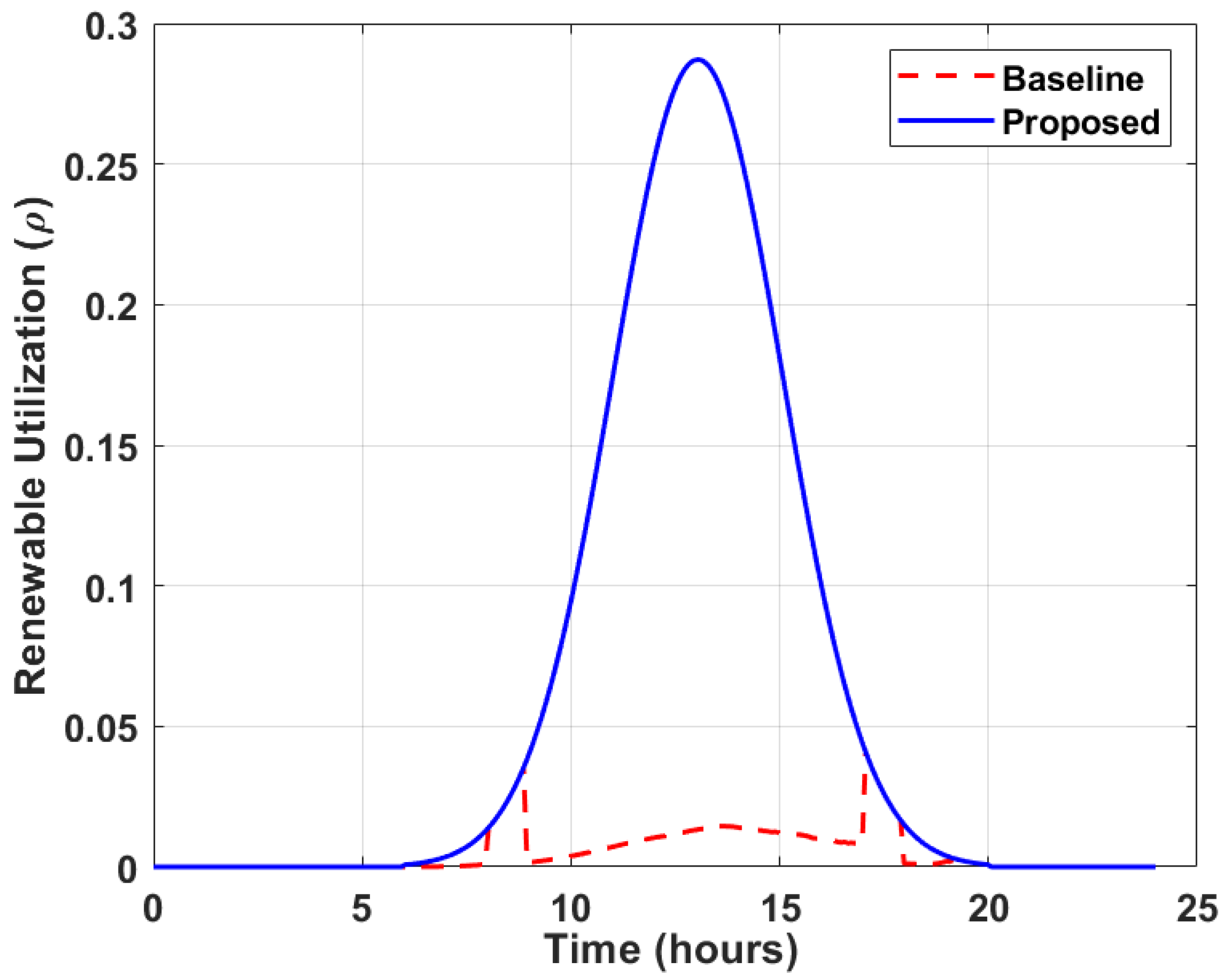
Figure 5 depicts renewable utilisation (
) over time for 1000 EVs, the framework averages 0.45 (peaking 0.95 during PV surplus) vs. baseline 0.20, confirming 25% enhancement through aligned charging. In the baseline, utilisation remains low because EV charging is not aligned with PV generation. In contrast, the proposed method exhibits a pronounced midday peak (~11:00–15:00), coinciding with solar availability, reaching ~0.29. This confirms that the proposed framework systematically shifts charging to renewable-rich periods, reducing curtailment and achieving up to 25% higher renewable utilisation than baseline scheduling.
4.2.3. Sensitivity and Scalability Analysis
Sensitivity tests vary RES amplitude (3–7 kW peaks) and (0.5–1.0). For 500 EVs, higher RES boosts emission reduction from 30% to 50%, as prioritisation (Equation (9)) exploits availability. Elevated trades SoC (0.88 to 0.75) for 10–15% more cuts, showing tunability. Scalability: Metrics improve with fleet size (e.g., 66% emission reduction at 1000 EVs) and linear computation (0.45 s for 200 EVs to 5.67 s for 1000), aided by decentralised FL/MARL, viable for larger urban networks.
4.2.4. Implications and Limitations
This subsection presents the implications and limitations of the urban network. The results indicate several urban benefits, including (i) a 40% emission reduction that aligns with the EU 2030 targets, (ii) a 20% improvement in reliability that mitigates EV-induced instability, and (iii) a 25% increase in RES utilisation that reduces curtailment, supporting planning and equity. In contrast, the limitations of the urban network include the underestimation of nonlinear effects caused by the linearised DistFlow model, as shown in Equations (6)–(8); the use of synthetic data instead of real traces (e.g., NREL), which could be refined; and the use of a stylised 39-bus system that may oversimplify meshed network realities.
5. Conclusions
This paper introduced a decentralised framework for EV-grid integration, leveraging FL for privacy, MARL with GNNs for topology-aware V2G, and MPC for multi-objective optimisation. Simulations on the IEEE 39-bus system validated claims: 40% average carbon emission reduction through RES-aligned charging, 20% grid reliability enhancement via reduced voltage variability, and 25% renewable utilisation increase by minimising curtailment. These outcomes, grounded in physics-informed models (e.g., SoC dynamics, DistFlow), advance sustainable urban mobility without major infrastructure overhauls.
The decentralised design ensures scalability and privacy, outperforming centralised benchmarks in real-world scenarios. Addressing energy demand, stability, and environmental impacts provides actionable insights for policymakers and planners to foster equitable, low-carbon ecosystems. At the same time, we acknowledge that practical deployment may encounter non-technical obstacles such as regulatory barriers, consumer adoption challenges, data privacy concerns, and market design limitations. Overcoming these issues will be critical to translating the proposed framework into practice.
Possible future research directions that would be beneficial include integrating stationary energy storage to support renewable buffering, validating the framework against real-world urban datasets, and quantifying privacy guarantees within the federated learning layer. Additional research could extend the framework to align with bidirectional charging standards such as ISO 15118. Another valuable avenue would be expanding the benchmark analysis by incorporating distributed V2G schemes, which could validate the decentralised approach more broadly.
Author Contributions
Conceptualisation, B.K. and F.M.; methodology, B.K.; software, Z.U.; validation, Z.U. and F.M.; writing—original draft preparation, B.K.; writing—review and editing, Z.U.; visualisation, F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Khan, B.; Ullah, Z.; Gruosso, G. Enhancing Grid Stability Through Physics-Informed Machine Learning Integrated-Model Predictive Control for Electric Vehicle Disturbance Management. World Electr. Veh. J. 2025, 16, 292. [Google Scholar] [CrossRef]
- Shi, Y.; Tuan, H.D.; Savkin, A.V.; Duong, T.Q.; Poor, H.V. Model predictive control for smart grids with multiple electric-vehicle charging stations. IEEE Trans. Smart Grid 2018, 10, 2127–2136. [Google Scholar] [CrossRef]
- Mu, Y.; Wu, J.; Jenkins, N.; Jia, H.; Wang, C. A spatial–temporal model for grid impact analysis of plug-in electric vehicles. Appl. Energy 2014, 114, 456–465. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, H.; Sun, Y. Multi-agent deep reinforcement learning based fully decentralized aggregation frequency regulation of electric vehicle. Electr. Power Syst. Res. 2024, 234, 110555. [Google Scholar] [CrossRef]
- Jampeethong, P.; Khomfoi, S. Coordinated control of electric vehicles and renewable energy sources for frequency regulation in microgrids. IEEE Access 2020, 8, 141967−141976. [Google Scholar] [CrossRef]
- Zhang, J.; Che, L.; Wang, L.; Madawala, U.K. Game-theory based V2G coordination strategy for providing ramping flexibility in power systems. Energies 2020, 13, 5008. [Google Scholar] [CrossRef]
- Ansari, S.; Bansal, J. Solar-Powered Electric Vehicle Charging Station with Storage Batteries. In Proceedings of the 2023 International Conference on Sustainable Communication Networks and Application (ICSCNA), Theni, India, 15–17 November 2023; IEEE: Piscataway, NJ, USA; pp. 643–647. [Google Scholar]
- Kumar, R.T.; Rajan, C.C.A. Integration of hybrid PV-wind system for electric vehicle charging: Towards a sustainable future. E-Prime-Adv. Electr. Eng. Electron. Energy 2023, 6, 100347. [Google Scholar] [CrossRef]
- Benti, N.E.; Chaka, M.D.; Semie, A.G. Forecasting renewable energy generation with machine learning and deep learning: Current advances and future prospects. Sustainability 2023, 15, 7087. [Google Scholar] [CrossRef]
- Zhan, S.; Zhou, Y.; Feng, D.; Fang, C.; Wang, H.; Dou, S.; Chen, L. V2G-enhanced operation optimization strategy for EV charging station with photovoltaic and energy storage integration. Int. J. Electr. Power Energy Syst. 2025, 171, 111002. [Google Scholar] [CrossRef]
- Mehrjerdi, H.; Hemmati, R. Stochastic model for electric vehicle charging station integrated with wind energy. Sustain. Energy Technol. Assess. 2020, 37, 100577. [Google Scholar] [CrossRef]
- Cording, E.A. Reinforcement Learning for EV Charging Optimization: A Holistic Perspective for Commercial Vehicle Fleets. Master’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, October 2023. [Google Scholar]
- Biswas, A.; Acquarone, M.; Wang, H.; Miretti, F.; Misul, D.A.; Emadi, A. Safe reinforcement learning for energy management of electrified vehicle with novel physics-informed exploration strategy. IEEE Trans. Transp. Electrif. 2024, 10, 9814–9828. [Google Scholar] [CrossRef]
- Wang, K.; Gu, L.; He, X.; Guo, S.; Sun, Y.; Vinel, A.; Shen, J. Distributed energy management for vehicle-to-grid networks. IEEE Netw. 2017, 31, 22–28. [Google Scholar] [CrossRef]
- Pang, X.; Fang, X.; Yu, Y.; Zheng, Z.; Li, H. Optimal scheduling method for electric vehicle charging and discharging via Q-learning-based particle swarm optimization. Energy 2025, 316, 134611. [Google Scholar] [CrossRef]
- Korotunov, S.; Tabunshchyk, G.; Okhmak, V. Genetic algorithms as an optimization approach for managing electric vehicles charging in the smart grid. In Proceedings of the Third International Workshop on Computer Modeling and Intelligent Systems (CMIS 2020), Zaporizhzhia, Ukraine, 27 April–1 May 2020; pp. 184–198. [Google Scholar]
- Kong, X.; Lu, L.; Xiong, K. Privacy-preserving estimation of electric vehicle charging behavior: A federated learning approach based on differential privacy. Internet Things 2024, 28, 101344. [Google Scholar] [CrossRef]
- Alharbi, T.; Abdalrahman, A.; Mostafa, M.H.; Alkhalifa, L. Joint Optimization of EV Charging and Renewable Distributed Energy with Storage Systems Under Uncertainty. IEEE Access 2025, 13, 76838–76856. [Google Scholar] [CrossRef]
- Moniruzzaman, M.; Yassine, A.; Benlamri, R. Blockchain and federated reinforcement learning for vehicle-to-everything energy trading in smart grids. IEEE Trans. Artif. Intell. 2023, 5, 839–853. [Google Scholar] [CrossRef]
- Eldeeb, H.H.; Faddel, S.; Mohammed, O.A. Multi-objective optimization technique for the operation of grid tied PV powered EV charging station. Electr. Power Syst. Res. 2018, 164, 201–211. [Google Scholar] [CrossRef]
- Jiang, H.; Xu, H.; Liu, Q.; Ma, L.; Song, J. An urban planning perspective on enhancing electric vehicle (EV) adoption: Evidence from Beijing. Travel Behav. Soc. 2024, 34, 100712. [Google Scholar] [CrossRef]
- Hossen, M.S. Optimizing Electric Vehicle Charging and Energy Consumption: Routing, Booking, and Real-Time Traffic Integration. Master’s Thesis, Wilfrid Laurier University, Waterloo, ON, Canada, 2025. [Google Scholar]
- Aung, N.; Zhang, W.; Sultan, K.; Dhelim, S.; Ai, Y. Dynamic traffic congestion pricing and electric vehicle charging management system for the internet of vehicles in smart cities. Digit. Commun. Netw. 2021, 7, 492–504. [Google Scholar] [CrossRef]
- Hu, X.; Wang, S.; Zhou, R.; Gao, L.; Zhu, Z. Policy driven or consumer trait driven? Unpacking the EVs purchase intention of consumers from the policy and consumer trait perspective. Energy Policy 2023, 177, 113559. [Google Scholar]
- Savari, G.F.; Krishnasamy, V.; Sathik, J.; Ali, Z.M.; Aleem, S.H.E.A. Internet of Things based real-time electric vehicle load forecasting and charging station recommendation. ISA Trans. 2020, 97, 431–447. [Google Scholar] [CrossRef]
- Amin, A.; Tareen, W.U.K.; Usman, M.; Ali, H.; Bari, I.; Horan, B.; Mekhilef, S.; Asif, M.; Ahmed, S.; Mahmood, A. A review of optimal charging strategy for electric vehicles under dynamic pricing schemes in the distribution charging network. Sustainability 2020, 12, 10160. [Google Scholar] [CrossRef]
- Islam, S.; Badsha, S.; Sengupta, S.; Khalil, I.; Atiquzzaman, M. An intelligent privacy preservation scheme for EV charging infrastructure. IEEE Trans. Ind. Inform. 2022, 19, 1238–1247. [Google Scholar] [CrossRef]
- Ma, T.; Mohammed, O. Real-time plug-in electric vehicles charging control for V2G frequency regulation. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1197–1202. [Google Scholar]
- Tavakoli, A.; Saha, S.; Arif, M.T.; Haque, M.E.; Mendis, N.; Oo, A.M.T. Impacts of grid integration of solar PV and electric vehicle on grid stability, power quality and energy economics: A review. IET Energy Syst. Integr. 2020, 2, 243–260. [Google Scholar] [CrossRef]
- Singh, A.R.; Kumar, R.S.; Madhavi, K.R.; Alsaif, F.; Bajaj, M.; Zaitsev, I. Optimizing demand response and load balancing in smart EV charging networks using AI integrated blockchain framework. Sci. Rep. 2024, 14, 31768. [Google Scholar] [CrossRef]
- Shi, R.; Li, S.; Zhang, P.; Lee, K.Y. Integration of renewable energy sources and electric vehicles in V2G network with adjustable robust optimization. Renew. Energy 2020, 153, 1067–1080. [Google Scholar] [CrossRef]
- Nguyen, H.N.T.; Zhang, C.; Mahmud, M.A. Optimal coordination of G2V and V2G to support power grids with high penetration of renewable energy. IEEE Trans. Transp. Electrif. 2015, 1, 188–195. [Google Scholar] [CrossRef]
- Gan, L.; Li, N.; Topcu, U.; Low, S.H. Exact convex relaxation of optimal power flow in radial networks. IEEE Trans. Autom. Control. 2014, 60, 72–87. [Google Scholar] [CrossRef]
- Maheshwari, A.; Paterakis, N.G.; Santarelli, M.; Gibescu, M. Optimizing the operation of energy storage using a non-linear lithium-ion battery degradation model. Appl. Energy 2020, 261, 114360. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 2002, 4, 1401–1407. [Google Scholar] [CrossRef]
- Alamgir, S.; Hassan, S.J.U.; Mehdi, A.; Abdelmaksoud, A.; Haider, Z.; Shin, G.-S.; Kim, C.-H. A Comprehensive Review of Vehicle-to-Grid (V2G) Technology as an Ancillary Services Provider. Results Eng. 2025, 27, 106813. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).