Abstract
Vehicular transportation is one of the most widely used modes in modern cities for reaching key destinations such as workplaces, healthcare facilities, recreational areas, and educational institutions, among others. However, the performance of vehicular traffic on these roads can vary significantly due to the influence of different environmental variables. In the literature, factors such as traffic incidents, weather conditions, road infrastructure, and driving habits, among others, have been identified as impacting vehicular traffic performance. In this context, predictive models have been developed to anticipate congestion at specific points in cities based on statistics, machine learning, simulation, and complex networks. This study proposes a novel index aimed at assessing the level of performance of vehicular traffic on streets based on the relationship among relevant urban environmental variables. This index is generated through Genetic Programming, considering a set of variables related to traffic, incidents, and services. The case study will focus on the streets of the Tlalpan Municipality in Mexico City.
1. Introduction
Vehicular transportation in current large cities contributes to reach services such as healthcare facilities, workplaces, culture services, and education institutions, among others, as described by the Center for Complexity Sciences [1]. City traffic includes multiple forms of mobility, such as walking, cycling, public transport, shared vehicles, private vehicles, motorcycles, and other means, according to the urban mobility pyramid [2].
Among these modes, private transportation has become the most commonly used for point-to-point travel. This is evidenced by the growing number of registered vehicles reported by state and municipal governments in Mexico—a trend historically documented by the National Institute of Statistics and Geography [3].
The increase in the number of vehicles in cities, combined with factors such as population density, poor urban planning, inadequate road infrastructure, and the unequal distribution of essential services, contributes to fluctuating levels of vehicular traffic on certain streets. As noted in the studies by Mondal [4] and Sun [5], the occurrence of traffic incidents in specific regions also exacerbates the situation. Furthermore, temporal and spatial factors, such as the increase in traffic accidents, influence the performance of vehicular traffic, as highlighted by Wang’s research [6].
Traffic policies, driving culture, and economic factors, according to Almeida [7], also influence vehicular traffic performance. Additionally, urban infrastructure plays a crucial role in shaping traffic patterns, as mentioned by Nian [8]. Various solutions have been proposed to enhance traffic performance in cities, with traffic modeling being one of the earliest approaches. According to Kushchenko [9], this type of modeling enables analysis of vehicle movement and identifying key variables, such as intersections, queue dynamics and lengths, speed, and other characteristics.
Sun’s analysis [10] highlights common variables in traffic models, such as speed, vehicle length, distances, number of vehicles per kilometer, flow rate, intersections, traffic signals, and road segment lengths. However, these models only allow the analysts to visualize vehicular flow under normal conditions. In situations when traffic density increases, the phenomenon of congestion arises, a situation that can also be attributed to other characteristics of the urban environment. Studies have addressed congestion through indicators or indices that characterize it, generally relating average speed to traffic density.
This research makes a significant contribution through the development of a novel mathematical model that introduces an index to evaluate vehicular traffic performance on urban streets. While Genetic Programming and symbolic regression are not entirely new techniques, their application in this specific context brings innovative value by enabling the discovery of complex relationships among multiple variables that impact traffic. These techniques are employed because they offer flexibility and the capacity to generate models that adapt to the nonlinear and dynamic nature of urban traffic, something that is not always achievable with traditional or exact approaches.
The need for a new indexing method arises from the limitations of existing approaches, which often fail to capture the complexity and variability of urban traffic environments. Current indices tend to oversimplify reality by focusing only on speed indicators, overlooking critical factors that truly affect traffic, such as incidents, infrastructure, and surrounding services. Although sets of variables that influence traffic flow have been identified in the literature, models associating these variables to adequately characterize vehicular traffic performance have not been developed. This lack of a comprehensive approach may lead to an inadequate assessment of traffic performance, especially in areas where multiple influences interact significantly.
The choice of Genetic Programming and symbolic regression addresses the need for an approach that does not rely on rigid assumptions about relationships between variables. Unlike exact methods such as numerical approaches or traditional regression techniques, which require predefined models and, in many cases, linearity, Genetic Programming enables the evolutionary generation of solutions by exploring a broader space of potential mathematical formulas that fit the data. This approach is particularly useful when variable interactions are not evident or when there is a need to simultaneously optimize multiple objective functions.
On the other hand, although artificial intelligence (AI) techniques such as neural networks or machine learning models can be effective in certain scenarios, they often act as “black boxes,” making it difficult to interpret the results. In this case, symbolic regression enables the generation of explicit models that not only predict traffic behavior but are also interpretable, facilitating the understanding of how variables related to traffic, incidents, and services interact.
The proposed index incorporates traffic, incident, and service (points of interest) variables, allowing for an index that more accurately characterizes the performance or equilibrium state of vehicular traffic on a street. This combination of factors is key to better capturing the changing and complex conditions of urban streets, providing a model that is not only predictive but also more attuned to the realities of urban mobility.
Thus, the proposed index offers an integral evaluation of traffic performance based on the interaction between the independent and dependent variables involved, providing a more accurate, interpretable, and adaptive solution to the fluctuating conditions of urban traffic.
2. Related Works
The works reviewed in the literature are grouped into two main approaches. (i) research that develops mathematical models to evaluate traffic congestion based on various variables and (ii) research that identifies the variables with the greatest impact on vehicular congestion and also analyzes how they affect mobility in urban environments.
Equations, functions, and mathematical models have been proposed in several studies to characterize traffic congestion through the relationship between different variables. For example, Mohan, He and Liponhay [11,12,13] proposes a Zone Speed Index (IVZ) aimed at classifying areas as fast or slow based on the relationship between those zones.
Pandey [14] addresses the heterogeneity of mixed traffic in road networks, proposing a Heterogeneity Index (HI) that quantifies the diversity of vehicle categories in the traffic flow. A high HI value reflects greater vehicular diversity, which favors mobility, based on Passenger Car Units (PCU) for different types of vehicles and their proportion within the flow.
On the other hand, Leitner [15] proposes a speed performance index to assess congestion in the road network, developing congestion indices for both individual road segments and the entire network. These indices are based on variables such as average travel speed, the proportion of non-congested time, and segment length.
Another relevant approach is the work of Seong [16], who introduces new metrics through Hägerstrand’s space–time cube to characterize traffic congestion, using distance and time as the key variables.
Wang [17] proposes three methods to calculate the congestion index: the first based on travel speed, the second on roadway saturation degree, and the third on integral parameters such as travel efficiency and low-speed proportion.
On the other hand, Arirja [18] develops an index to represent congestion density over time, introducing the occupancy variable, which combines speed and vehicle length to measure the time in which a road segment is occupied.
Liu [19] constructs a prediction model for congestion time through a multivariable equation that includes traffic density, average delay time, traffic flow, and peak hours as independent variables.
The analysis of the literature also identified variables influencing traffic congestion. For example, Chen [20] highlights traffic accidents and response time as key factors. Bian [21] identifies variables such as per capita street area and vehicle ownership, while Mahona [22] emphasizes the importance of continuous crossings, bus stops, and traffic lights. Yu [23], for his part, underscores intersections as one of the main causes of congestion.
Points of interest in cities, such as shopping centers and schools, also play an important role, according to Gullotta [24], as they attract vehicles during specific time periods, increasing congestion. Rahman [25] identifies income and employment clustering in specific areas as a factor exacerbating traffic, while Pi [26] mentions road design, incidents, and poor driving habits as contributing factors to congestion.
It is fascinating to explore the different indices and indicators, like the indicators in [27] that propose important metrics for evaluating alternative transportation systems—the Mode Efficiency Factor and the Passenger Transportation Supply Efficiency Index—that allow for the evaluation of traffic congestion. This research work presents an innovative proposal: an index that integrates variables from accessible sources, offering a more accurate visualization of mobility performance. This index aims to provide a more comprehensive understanding of the problem of congestion in urban environments and to provide a solid foundation for addressing it.
3. Methodology for the Creation of an Index to Assess the Performance Level of Vehicular Traffic on Urban Streets
The methodology proposed to create an index to evaluate vehicular traffic performance on urban streets is divided into three main phases. The first phase addresses the case study, providing a detailed description of the geographical area from which data on traffic, incidents, and services are collected. The second phase focuses on data acquisition, outlining the tools used to gather this information. Finally, the third phase describes the methodological approach used in designing the proposed mobility index.
3.1. Case Study Definition Phase
The case study defined for this research is the vehicular traffic in the area of Tlalpan Municipality, located in Mexico City, which covers the largest territorial expanse in the south-southwest part of the metropolis. Tlalpan is bordered to the north by the Municipalities of Álvaro Obregón and Coyoacán, to the east by Xochimilco and Milpa Alta, to the south by Huitzilac in Morelos, and to the west by Magdalena Contreras, as well as by the municipalities of Tianguistenco and Jalatlaco of the State of Mexico. With an area of 306.52 km2, Tlalpan represents 20% of the total area of Mexico City, ranking first compared to the other Mexico City Municipalities, as reported by the National Institute of Statistics and Geography [28]. This municipality is characterized by having both urban and rural areas, providing a diverse environment that facilitates making inferences and formulating conclusions regarding the findings of our research.
3.2. Data Acquisition Phase
The data collection consisted of obtaining the variables shown in Table 1, grouped into three categories: traffic, incidents, and services (points of interest), each of which plays an essential role in traffic performance on the streets. Traffic variables, such as jamFactor, describe the level of congestion, while Speed and Speed_Uncapped allow for a comparison between expected speed under optimal conditions and actual speed, providing a direct indicator of vehicle flow efficiency. Variables like Length and Number_Segments detail the capacity of the roadway, and temporal factors, such as Work_Day_Traffic, Traffic_Block_Type, and Traffic_Hour, facilitate the identification of congestion patterns associated with the time of day, day of the week, or whether it is a workday, enabling the assessment of traffic performance in different temporal contexts.

Table 1.
Detailed description of the number of records and variables in the traffic-incident-POIs dataset.
On the other hand, incident variables such as Type and Criticality reflect the type and severity of events, such as accidents or road closures, that directly affect circulation and decrease traffic speed in specific areas. Variables like Start_Time, End_Time, and Incident_Block_Type provide information on the duration and frequency of incidents, helping to predict their patterns and understand their impact on road accessibility. Finally, the points of interest (POIs) variables, represented by Name and Bbox_POI, identify the location of services and destinations that generate higher traffic in their surroundings. The concentration of POIs in an area increases the likelihood of congestion, as these sites attract a significant flow of vehicles at specific times.
To deepen the analysis of traffic congestion, it would be desirable to incorporate a broader range of critical factors, such as weather, road conditions, and driver behavior, which are highly likely to influence vehicle density and traffic flow. These elements can introduce significant variations in traffic, providing a richer and more accurate understanding of road dynamics in various scenarios. However, these factors were not included in this study due to limitations related to the availability and consistency of the necessary data. Historical and real-time information about weather or specific road conditions is not always available for each analyzed segment, and accurately obtaining these conditions would require exhaustive and continuous data collection, which is often impractical in many urban contexts. Furthermore, the variability of these factors over time and space makes their integration into the analysis complex and potentially biased, as homogeneous and replicable measurements cannot be guaranteed.
In line with these challenges, the methodology focused on high-impact variables whose collection and measurement are consistent over time, thus allowing for a robust and replicable analysis of vehicular congestion. This approach excludes personal and contextual factors that are difficult to measure, such as driver stress or the detailed weather conditions of each area, which, while critical, are challenging to obtain in representative and homogeneous volumes without affecting the viability of the study. By prioritizing variables whose influence is directly measurable on traffic performance, the study evaluates congestion without resorting to invasive or complex data acquisition methods. Thus, the relevance and feasibility of the analysis are optimized, maintaining the methodological rigor necessary to effectively assess the impact of traffic on road performance despite not encompassing all possible external factors.
Data acquisition on traffic and road incidents was carried out using the Here Maps Application Programming Interface (API), following the methodology proposed by De la Cruz-Nicolás [29]. There are other alternatives for acquiring traffic data, such as the one used in the work of [30]. Comprehensive traffic and incident data were collected from October 2023 to March 2024, covering 24 h a day with requests made every 5 min. The Geoapify API was used to obtain data related to points of interest. The datasets obtained on traffic, road incidents, and services are presented in Table 1.
The description of each variable in the Traffic-incident-POIs dataset is shown in Table 2.

Table 2.
Description of the variables in the Traffic-incident-POIs dataset.
3.3. Index to Evaluate the Performance of Vehicular Traffic Developing Phase
The proposed approach for developing an index to evaluate the performance level of vehicular traffic on urban streets has been divided into five stages. The process begins with the collection of data on traffic, traffic incidents, and points of interest, and they conclude with the generation of the index as a result, as illustrated in Figure 1.
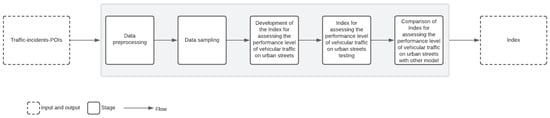
Figure 1.
Stages that allow for obtaining the index to evaluate the performance level of vehicular traffic on urban streets.
In the first stage, the preprocessing of traffic data, traffic incidents, and points of interest is carried out, which includes transformation, standardization, and selection of the most relevant variables. In the second stage, a sample is extracted from the preprocessed dataset of Traffic-Incidents-POIs to expedite the analysis and modeling of the index.
The third stage involves the development of a mathematical model that will represent the index. This is done by using genetic programming and the Traffic-Incidents-POIs dataset as input. The fourth stage consists of conducting tests of the index that evaluates traffic congestion, employing a new dataset and statistical metrics to measure the accuracy of the model in assessing the level of performance of vehicular traffic.
Finally, the fifth stage focuses on comparing the obtained index with other indices that can be found in the literature for assessing the performance of vehicular traffic. The following sections provide a detailed explanation of the proposed stages.
3.3.1. Stage 1: Data Preprocessing
Data preprocessing is established as the fundamental basis for ensuring the effectiveness and accuracy of the final results. In this research, the data preprocessing process was carried out through the following three steps: data transformation, standardization, and relevant variable selection
Step 1. Data Transformation: The primary objective of data transformation is to adjust the distributions of the data to resemble a normal form, which is essential in model construction. To assess whether the variables influencing traffic performance exhibit normal behavior, the Kolmogorov-Smirnov test was applied. Performing this test on the Traffic-Incidents-POIs Sample dataset provided valuable information about the distribution of variables related to traffic performance, revealing that these did not follow a normal distribution. This finding indicates the need to implement appropriate transformations to address this irregularity in the data and ensure the validity of subsequent analyses.
To determine the type of transformation to apply to the Traffic-Incidents-POIs dataset, an analysis was conducted on incidents across various streets. The data exhibited a right-skewed distribution, characterized by a higher number of streets with few incidents, while some streets had a significantly higher count. Additionally, vehicle speeds on most streets showed an asymmetric distribution, with low speeds prevailing but isolated cases of vehicles traveling at very high speeds, also resulting in a right-skewed distribution. On the other hand, points of interest (POIs) located on these streets are represented in different scales and units, adding an additional layer of complexity to the data analysis. In this context, the following transformations are justified: the square root, which is useful for count data with a right skew, such as traffic incidents, as it reduces variance and brings the distribution closer to normality; the cubic transformation, ideal for data with moderate skewness, such as vehicle speeds, which helps smooth the tails and improve distribution symmetry; and Z-score normalization, which is especially applicable when comparing variables on different scales, such as the performance scores of POIs, allowing data standardization and facilitating direct comparison between disparate variables. The applied transformation included the implementation of square root transformation, z-score normalization, and cubic transformation, using Equations (1)–(3) on the Traffic-Incidents-POIs dataset to normalize the data.
where:
It is the individual value of the variable,
It is the mean of the variable’s distribution,
It is the standard deviation of the variable’s distribution.
The result of normalizing the Traffic-Incidents-POIs dataset has demonstrated that applying the cubic transformation significantly improves the normality of this dataset.
Step 2. Standardization: For the Traffic-Incidents-POIs dataset, which has variables on different scales, a standardization was performed that adjusts the values within a range of 0 to 1. This process was carried out using Equation (4).
where
It is the original value that is to be normalized,
It is the minimum value in the original dataset,
It is the maximum value in the original dataset.
Standardization allowed all variables in the Traffic-Incidents-POIs dataset to be adjusted to a range between 0 and 1.
Step 3. Variable Selection: To identify the most significant variables in the Traffic-Incidents-POIs dataset, the rotation matrix from the Principal Component Analysis (PCA) was used. This approach allowed for the determination of variables that have a notable impact on vehicle traffic performance. The most relevant variables are presented in Table 3.

Table 3.
Most Relevant Variables from the Traffic-Incidents-POIs Dataset Tráfico-Incidencias-POIs.
3.3.2. Stage 2: Data Sampling
The dataset used in this research, named Traffic-Incidents-POIs, contains a total of 873,020,000 records. To obtain a representative sample of 1,000,000 records, we implemented simple random sampling, following these steps:
Step 1. Population Definition: The dataset of 873,020,000 records was defined as the population.
Step 2. Simple Random Sampling: To select the sample, we used the simple random sampling function from Python’s Random library. This method ensures that each record in the population has an equal probability of being selected, expressed in Equation (5):
where is the probability of selecting record , and is the total population size (873,020,000 in this case).
Step 3. Selection Process: Selection was performed by generating a random number that identifies the positions of records within the original dataset. Through this process, we extracted 1,000,000 records randomly, without replacement, meaning that once a record was selected, it could not be selected again. This approach is essential to avoid selection bias and ensure that the sample reflects the population’s variability.
Step 4. Sampling Equation: The selection probability for each record is expressed in Equation (6), which defines the sample size in relation to the total population:
In our case, the sample size (n) is 1,000,000, representing approximately 0.115% of the total population. This sample size is suitable for statistical analysis as, according to the Central Limit Theorem, a sufficiently large sample allows the distribution of the sample mean to approximate a normal distribution, facilitating statistical inference.
Step 5 Variance and Sampling Error: To address bias, we considered the sample variance. The population variance () was estimated from the sampled data, and the standard error of the mean () was calculated using Equation (7):
where is the population standard deviation, and is the sample size. The standard error of the mean was 0.00241, suggesting that the mean calculated from our sample is accurate and reliable for estimating the population mean.
Table 4 presents the composition of the obtained sample, which is used in the experiment to develop a mathematical model representing the index for evaluating vehicular traffic performance.

Table 4.
Description detailing the number of records and the number of variables in the sample used.
3.3.3. Stage 3: Development of the Index for Assessing the Performance Level of Vehicular Traffic on Urban Streets
The development of the index to evaluate the level of performance of vehicular traffic on urban streets involves creating a mathematical model that establishes a relationship between a dependent variable, specifically the jam factor (jamFactor) described in Table 2, and a set of independent variables that influence this factor. These independent variables encompass all those mentioned in the same table. The relationship between them is determined through the application of Genetic Programming (GP), a technique that falls within the framework of Evolutionary Computing.
According to Koza’s work [31], the Genetic Programming paradigm offers an approach to exploring the space of a set of symbolic expressions, seeking a highly fit individual expression to solve or approximate the solution to a specific problem. In this context, populations of symbolic expressions are generated through a genetic process based on the Darwinian principle of survival of the fittest. Additionally, an appropriate genetic crossover operator (sexual recombination) is used to mate symbolic expressions, as illustrated in Figure 2 and Algorithm 1 described in Langdon’s work [32].
| Algorithm 1 Abstract GP algorithm |
| 1. Randomly create an initial population of symbolic expressions from the available primitives 2. Repeat 3. Execute each symbolic expression and ascertain its fitness. 4. Select one or two symbolic expression(s) from the population with a probability based on fitness to participate in genetic operations. 5. Create new individual symbolic expression (s) by applying genetic operations with specified probabilities. 6. Until an acceptable solution is found or some other stopping condition is met (for example, reaching a maximum number of generations). 7. Return the best-so-far individual. |
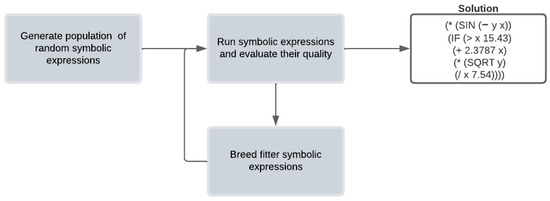
Figure 2.
Abstract evolutionary cycle to identify the most suitable symbolic expression, as described in Riccardo Poli’s work [33].
The parameters that are needed as input for Algorithm 1, which allow the generation of symbolic expressions relating independent variables to the dependent variable, are described in the following steps:
- Step 1. Identification of the set of terminals (variables and constants): Terminals are fundamental elements used in the construction of symbolic expressions, which aim to solve the posed problem.
- Step 2. Identification of the set of primitive functions: Primitive functions are operations performed on the data, such as COS, SIN, AND, OR, NOT, ADD, and SUB, and will be available to construct the symbolic expressions addressing the problem.
- Step 3. Identification of the reference variable: This is the variable that defines the behavior of the problem at hand.
- Step 4. Identification of the fitness measure: This refers to the fitness function used to evaluate the quality of an individual symbolic expression within the population. Examples of these functions include Mean Squared Error and the Coefficient of Determination, among others.
- Step 5. Assignment of values to the hyperparameters of the evolutionary program: This includes setting the population size, number of generations, crossover probability, and mutation probability, among others.
- Step 6. Implementation.
The development of the index that evaluates the level of performance of traffic in urban streets is carried out using Algorithm 1. This algorithm requires a series of parameters, as detailed in the previous steps, to obtain symbolic expressions. The steps are reiterated below, now incorporating the values from the latest experiment conducted, which led to the derivation of the symbolic expression that represents the mathematical model of the index for evaluating the performance of vehicular traffic in urban streets.
- Step 1. Identification of the set of terminals (variables and constants): The set of terminals is defined based on the variables listed in Table 2, which refer to traffic, traffic incidents, and points of interest. These variables interact with each other to reflect the state of traffic congestion.
- Step 2. Identification of a sufficient set of primitive functions: Considering the variability in traffic congestion behavior, as illustrated in Figure 3, the following primitive functions are selected: add, sub, mul, div, sqrt, log, abs, neg, inv, sin, cos, and tan.
- Step 3. Identification of the reference variable: An entropy analysis of the 32 variables described in Table 2 is conducted to determine which variable reflects the degree of disorder in vehicular traffic, considering traffic as a system. This analysis identified the variable “jam factor” (jamFactor) as the one that best represents congestion behavior. The jam factor, measured on a scale from 0 to 10 according to Here Maps [34], indicates low vehicular traffic flow (little congestion) with values close to 0, implying a high speed of movement. In contrast, a value close to 10 indicates high traffic flow, reflecting a reduced speed of movement (high congestion). Therefore, the jam factor is inversely proportional to speed, as illustrated in Figure 3 and detailed in Table 5.
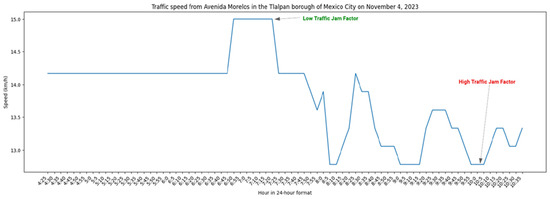
Figure 3.
Fragment of vehicular traffic records throughout a day on Avenida Morelos, located in the Tlalpan Municipality.

Table 5.
Scale of values for the jam factor developed by Here Maps [34], along with the performance criteria for vehicular traffic proposed in this research.
Table 5.
Scale of values for the jam factor developed by Here Maps [34], along with the performance criteria for vehicular traffic proposed in this research.
| Range of Congestion Factor | Traffic Congestion Level | Color | Performance Level |
|---|---|---|---|
| 0 <= jamFactor < 4 | Light congestion | Green | Excellent |
| 4 <= jamFactor < 8 | Moderate congestion | Yellow | Good |
| 8 <= jamFactor < 10 | Severe congestion | Red | Regular |
| jamFactor = 10 | Road closed | Black | Bad |
The performance of traffic congestion, known as the jam factor, reflects the level of vehicular traffic performance on urban streets related with the available speed. This information is detailed in Table 5 and visually illustrated in Figure 4.
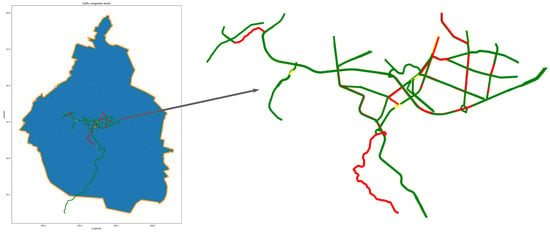
Figure 4.
Traffic levels in Tlalpan, Mexico City, using colors: green for light congestion (excellent), yellow for moderate (good), red for severe (fair), and black for road closed (poor), according to the jamFactor.
- Step 4. To select the symbolic expressions that optimally reflect the index evaluating vehicular traffic performance in urban streets, those with the highest fitness are chosen. The fitness functions of Mean Squared Error (MSE) and Mean Absolute Error (MAE) were used to evaluate the most prominent symbolic expressions in each generation.
- Step 5. The selection of hyperparameters in the Genetic Programming (GP) process was carefully considered to maximize the model’s ability to find a symbolic expression that aligns with the behavior of the jamFactor, a key indicator in traffic evaluation. The number of generations, set at 300, was chosen to balance solution space exploration while preventing overfitting. With this value, the model has sufficient iterations to improve solutions without risking noise memorization in the data. Additionally, selecting a population of 1 million individuals was essential to ensure a broad and diverse search within the space of symbolic expressions, which is crucial in complex problems like traffic modeling. A large initial set increases the likelihood of the algorithm discovering meaningful relationships among variables. Similarly, the number of GP runs, set at 30, ensures robustness in the results by minimizing the impact of inherent random variability in evolutionary algorithms. This approach ensures that the solutions found are not dependent on a single isolated run but are consistent and repeatable. Finally, the tournament size of 2000 participants was selected to ensure that the selection process within the algorithm favored the exploitation of the best solutions while retaining the ability to explore alternative options in the search space. Collectively, these hyperparameters, shown in Table 6, were designed to achieve an optimal balance between exploring the possible solution space and converging toward a model that accurately reflects the relationship between the jamFactor and the involved variables, thus providing a robust and mathematically valid result for traffic modeling.

Table 6.
Hyperparameters used in the evolutionary program.
Table 6.
Hyperparameters used in the evolutionary program.
| Parameter | Value |
|---|---|
| Dataset | Muestra_tráfico-incidencias-POIs |
| Number of generations | 300 |
| Population | 1,000,000 |
| Number of executions | 30 |
| Tournament size | 2000 |
- Step 6. Implementation: To implement Algorithm 1 using the data defined in Steps 1 to 5, the SymbolicRegressor class from the Gplearn library in Python was utilized. This tool enabled the execution of genetic programming and the generation of symbolic expressions that represent the mobility index.
Once the parameters in Algorithm 1 were configured, the experiment was conducted to obtain a set of symbolic expressions, from which the most suitable one for evaluating the performance of vehicular traffic on urban streets was selected. The experiment involved running Algorithm 1 a total of 30 times, and in each execution, the most optimal symbolic expression was chosen based on its fitness value. Table 7 and Table 8 present the symbolic expressions found during the experiment.

Table 7.
Symbolic expressions representing the index for evaluating the performance of vehicular traffic on urban streets, obtained in the experiment—Part 1.

Table 8.
Symbolic expressions representing the index for evaluating the performance of vehicular traffic on urban streets, obtained in the experiment—Part 2.
The symbolic expression identified in the experiment as the best representation of the index for evaluating the performance of vehicular traffic on urban streets was selected based on its lowest Mean Squared Error (MSE) value. A low MSE value is preferable, as it indicates that the model’s predictions are closer to the actual values in the dataset. In this case, the chosen symbolic expression is number 24, detailed in Table 8, which has an MSE of 0.980081. Therefore, the index evaluating the performance of vehicular traffic on urban streets is presented in Equation (8).
where
sqrt(log(X4*(X13*X30**(3/2)*X4 *(X13*sqrt(X13*X30)*(−X30 + X7**4) − X30) + X30) + X7 + sqrt(X13*X30)))
X4 = Length of the segment,
X7 = The speed may exceed the legal speed limit,
X12 = Day number of traffic monitoring (1=Monday, 2=Tuesday, … 7=Sunday),
X30 = Time block in which the incident was recorded.
The interpretation of the mobility index, expressed in Equation (8), is indeed complex; therefore, a simplification process is carried out, which is described below for Equation (8).
Step 1 Using the properties of logarithms, separate the terms in Equation (8) to obtain the following expression:
Step 2 Reorganize and group the terms related to and to obtain the following expression:
where and represent combinations of the other terms.
Step 3 Substitute logarithms, separating from , resulting in the following expression:
Step 4 Implement the series approximation to finally transform Equation (8) into Equation (9), as shown below:
Equation (9) results from processing the original Equation (8) in the proposed model for evaluating vehicular traffic performance on urban streets. This simplification not only optimizes the mathematical complexity of the model but also provides a clear and accessible interpretation of how different variables impact traffic performance, which is crucial for traffic planners.
First, the term represents the direct influence of the variable , which refers to the segment length associated with vehicle density on a road or even specific characteristics of the road type (such as capacity). The coefficient α provides a quantitative indicator of how variations in affect traffic performance. For example, if vehicle volume on a street increases, overall traffic performance is expected to decrease, as higher density tends to cause congestion. This relationship allows planners to anticipate potential congestion issues and adjust their strategies, such as implementing adaptive traffic signals or modifying recommended routes to optimize traffic flow.
The second term, , introduces a relationship between , which represents speeds exceeding the legal limit and may correlate with the number of traffic incidents or accidents, and , which refers to the time block in which incidents occur. Here, β acts as a multiplier that quantifies the influence of incidents on traffic performance, taking road capacity into account. This term indicates that the impact of traffic incidents is more significant when road capacity is limited. Therefore, if there is an increase in , there is a higher likelihood of incidents, which will result in greater congestion, especially on already saturated roads (under ). This insight is essential for planners, as it enables them to prioritize interventions in accident-prone areas or implement more effective prevention and response measures.
Finally, the constant term γ can encompass additional factors affecting traffic performance, such as weather conditions, roadwork, or special events that are not directly measured by or , such as traffic days. Including γ in the model allows planners to account for external variations that can influence traffic and are equally relevant to managing road infrastructure. By integrating these factors into planning, more robust strategies can be developed that consider not only typical traffic conditions but also atypical situations that may arise.
In this experiment, the lowest value of the Mean Absolute Error (MAE) also corresponded to symbolic expression number 24, detailed in Table 8, which showed a value of 0.580635, making it the best choice in terms of fitness and value adjustment.
3.3.4. Stage 4: Index for Assessing the Performance Level of Vehicular Traffic on Urban Streets Testing
The evaluation of the index that measures the performance of vehicular traffic in urban streets involves analyzing its effectiveness and ability to identify congestion on these roads. This is achieved by applying the model to an independent test dataset, followed by a comparison between the model’s estimates and the actual or expected values.
The validation of the proposed mobility index, represented in Equation (9), was conducted using a new dataset comprising 1152 records corresponding to four days of vehicular flow in the Tlalpan Municipality. The results obtained from the index in Equation (9) were compared with the jamFactor values provided by Here Maps as a reference. Table 9 and Table 10 present an excerpt of the results derived from the variables involved in the index proposed in this research.

Table 9.
Evaluation of the proposed index compared to the jamFactor value provided by Here Maps—Part 1.

Table 10.
Evaluation of the proposed index compared to the jamFactor value provided by Here Maps—Part 2.
The accuracy of the proposed index for evaluating vehicular traffic flow on urban streets was determined through the percentage representation of the Mean Squared Error using Equation (10).
where
The minimum value of the observed data set,
The maximum value of the observed data set.
An MSE of 30% was obtained, indicating that the model has an approximate deviation of 30% from the observed values. This result is significant, as it suggests that the model performs reasonably well in capturing the dynamics of vehicular traffic, adequately reflecting the overall trends in the data. Although there is room for improvement, this level of accuracy provides a solid foundation for the evaluation and management of traffic in urban streets, which can facilitate the implementation of effective strategies to mitigate congestion.
3.3.5. Stage 5: Comparison of Index for Assessing the Performance Level of Vehicular Traffic on Urban Streets with Another Model
The comparison of the traffic index proposed in this research with the INRIX congestion index is both relevant and necessary for various reasons, from theoretical to practical perspectives, in evaluating urban traffic performance.
The INRIX congestion index is one of the most widely used and recognized in the field of traffic analysis. Over the years, it has been validated in multiple studies and applied in various cities around the world, becoming a benchmark standard in traffic performance evaluation [35]. By contrasting our index with that of INRIX, not only is a solid reference framework established, but the effectiveness and applicability of the new model are also evaluated in comparison with a consolidated and prestigious approach.
This comparison provides the opportunity to evaluate the accuracy and robustness of the proposed model. By using standard metrics such as Mean Squared Error (MSE) and Mean Absolute Error (MAE), it is possible to quantify the differences between the indices, offering an objective view of how our index behaves in relation to an established model [36]. This type of analysis is crucial for identifying areas for improvement and validating whether our index can become a viable tool for traffic management.
Moreover, by comparing the results of our index with those of INRIX, we can better understand how each model responds to different conditions of the related variables. This not only helps place our index within the broader context of indicators but also provides valuable insights for developing more effective strategies for traffic management [20,37].
The comparison also allows us to identify limitations in the INRIX index that can be addressed by the new model. By analyzing how each index reacts to specific traffic situations, opportunities can be discovered to improve the proposed index, whether by incorporating new variables, adjusting its methodology, or adopting hybrid approaches that integrate elements from both models. Finally, by contrasting our index with that of INRIX, we contribute to the existing body of knowledge on urban traffic evaluation.
To compare the index obtained in Section 3.3.3, which evaluates the performance of vehicular traffic on urban streets, we contrast it with a model proposed by INRIX in the literature (see Table 11). The INRIX traffic congestion index establishes a relationship between the actual average travel speed and the free-flow speed. This comparison allows us to analyze the effectiveness of the proposed index in relation to a recognized model in the field of traffic analysis.

Table 11.
Vehicle congestion models documented in the literature.
The comparative analysis between the index proposed in this research and the INRIX index was conducted using a dataset of 2000 records, along with the jamFactor values provided by Here Maps. To evaluate the accuracy of each model, metrics such as Mean Squared Error (MSE) and Mean Absolute Error (MAE) were employed. The results of this accuracy evaluation are presented in Table 12.

Table 12.
Evaluation of model performance using MSE and MAE.
The proposed index has an MSE of 7.05548636, which is slightly lower than the INRIX congestion-based index, which has an MSE of 7.64142780. This suggests that the proposed index fits the data better according to this metric. However, it is important to note that the MAE for the INRIX index is lower, with a value of 1.72769129, indicating that the former may be slightly more accurate than the proposed index.
In the field of traffic management, it is essential not only to assess the overall accuracy of predictions but also to consider the model’s ability to identify trends and patterns at a macro level. The lower MSE obtained in the proposed model suggests that it adjusts more effectively to traffic variations, which is especially valuable for urban planning and decision-making. This research proposes a model that clearly relates the variables involved in analyzing traffic performance on city streets. The precise identification of congestion patterns can facilitate more efficient and optimized management of road resources.
Additionally, the practical applicability of the proposed model can be strengthened by integrating it with other traffic analysis and management systems. Although the MAE is higher, this does not reduce the model’s utility in contexts where understanding traffic dynamics and making forecasts based on historical trends is crucial. For example, if the model can anticipate critical congestion moments or traffic patterns that are not easily detectable through other metrics, its implementation could be highly beneficial, thus contributing to more proactive and effective urban traffic management.
4. Results
The analysis was conducted using a dataset of 1,000,000 records and 35 variables related to traffic, services, and incidents on the roads, employing the congestion factor as the reference variable. Through genetic programming, the relationship between these variables was explored with the aim of obtaining a symbolic expression that represents an index to evaluate the performance of vehicle traffic on urban streets. The resulting symbolic expression, presented in Equation (8), reveals a nonlinear relationship between the various variables that comprise the mobility index, where each variable contributes uniquely and specifically to the final value of the index.
For example, the variable X4, which represents the length of the segment, highlights the importance of the street segment size in traffic flow. As the length of a segment increases, traffic tends to be more fluid; in contrast, shorter segments often have multiple intersections, which can lead to higher density. Additionally, the variable X7, which indicates the current or real-time speed, is crucial for assessing the speed of vehicles at a given moment.
The day on which traffic occurs, represented by variable X12, also plays a fundamental role, as traffic behavior varies from Monday to Sunday. Variable X30, which denotes the time block in which vehicle flow is recorded, significantly impacts traffic performance. Together, these variables reflect key aspects of urban traffic that influence congestion. Equation (8) allows for the quantification and evaluation of these factors to estimate the level of congestion in a specific urban environment. Furthermore, mathematical operations such as square root, logarithm, and operators like addition, subtraction, multiplication, and division are incorporated to process some of the variables when calculating the final value of the index. This indicates that the model takes into account both the magnitude and nature of the variables in its assessment of vehicle traffic performance.
The proposal of the index with an adjustment treatment, represented by Equation (9) in this work, provides a tool that allows for a quantitative estimation of vehicle traffic performance on urban streets. Unlike other indices, the proposed index details the relationship between variables that are not reflected in other models, making it a highly descriptive index that clearly indicates which variables are associated with optimal or poor vehicle traffic. This index can be of great utility for traffic planners, municipal authorities, and others interested in understanding and managing traffic congestion in urban environments. The equation offers an objective and data-driven tool for assessing congestion, which can facilitate decision-making and the design of strategies aimed at improving urban mobility.
The comparison of the proposed index in this study with other indices present in the literature involves evaluating the accuracy of the developed model in relation to existing alternatives. This analysis allows us to determine the relative capacity of our model to assess vehicle traffic performance on urban streets, contrasting it with approaches used in previous research. To this end, we compare the index obtained in Section 3.3.3, which evaluates vehicle traffic performance on urban streets, with a model proposed by INRIX in the literature. The INRIX traffic congestion index establishes a relationship between the actual average travel speed and the free flow speed. This comparison enables us to analyze the effectiveness of the proposed index in relation to a recognized model in the field of traffic analysis.
The comparative analysis between the proposed index in this research and the INRIX index was conducted using a dataset of 2000 records, along with the jamFactor values provided by Here Maps. To assess the accuracy of each model, metrics such as Mean Squared Error (MSE) and Mean Absolute Error (MAE) were employed. The results of this accuracy evaluation indicate that the proposed index has an MSE of 7.05548636, which is slightly lower than the INRIX-based congestion index, which presents an MSE of 7.64142780. This suggests that the proposed index fits the data better according to this metric. However, it is important to note that the MAE for the INRIX index is lower, with a value of 1.72769129, indicating that the latter may be slightly more accurate than the proposed index.
Although the proposed index is superior to INRIX in MSE and INRIX is more accurate in terms of MAE, the proposed index offers significant advantages regarding the understanding of traffic performance on the streets. Unlike INRIX, which simply classifies the performance of a street on a scale, the proposed index not only evaluates whether traffic is good or bad but also identifies and relates various factors that influence these dynamics. This allows users to have a clearer perspective on what is affecting traffic, providing a greater expectation of understanding regarding the current conditions and the reasons behind the observed performance.
5. Discussion
The evaluation of traffic congestion in urban environments constitutes a complex challenge that requires consideration of multiple interrelated factors. In this study, a model referred to as the “index” is proposed, developed through genetic programming, to assess the performance of vehicular traffic on urban streets. Our research represents a significant contribution to addressing this issue, although it also raises various considerations that require deeper analysis and discussion.
The comparison of the results predicted by the proposed model with other types of traffic data, as well as evaluating its performance in different urban contexts and traffic conditions, would be a valuable approach to strengthening the model. A more thorough exploration of the influence of the selected variables in the mobility index equation may require additional manual adjustments. This would involve incorporating new variables empirically known to impact traffic congestion. Nevertheless, it will be necessary to reevaluate the model to determine its effectiveness with the newly added variables and to verify whether these improve its performance.
It is essential to detail how the index model could be applied in practice to address the evaluation of traffic congestion in urban environments. This involves exploring its potential use in specific urban planning and traffic management applications, as well as identifying the challenges and limitations that may arise during its implementation.
6. Conclusions
This study presents a comprehensive perspective on assessing the performance of vehicle traffic on urban streets, using an index derived through genetic programming and symbolic regression. The application of this model and the analysis of its results have led to significant conclusions that illuminate the nature and management of traffic congestion in urban areas.
The use of genetic programming to derive a symbolic expression that represents the index relating the most impactful variables of vehicle traffic performance on urban streets proves to be an effective strategy for capturing the complexity of congestion in urban environments. The variables selected in the equation, such as traffic origin, incident severity, expected speed on the road, and the number of segments, reflect important aspects that influence urban traffic congestion.
The evaluation of vehicle traffic performance through the proposed index offers a systematic and precise approach to measuring congestion. This model can be invaluable for informed decision-making in traffic management and urban mobility. Furthermore, the developed index has the potential to be applied in various areas of urban planning and transportation policy formulation, providing an objective, data-driven tool for assessing and addressing congestion in urban environments.
However, it is essential to discuss the broader implications of this research in the context of traffic planning and policy development. Understanding traffic congestion should not be limited to measurement; it must be integrated into a framework that considers the long-term effects on urban mobility and the well-being of citizens.
One of the main implications of this study is that integrating the proposed index into traffic planning can transform how urban congestion is addressed. Instead of simply identifying the most congested streets, urban planners can use the index to understand the underlying factors contributing to congestion. This allows for the development of more tailored solutions, such as modifying routes, optimizing traffic light timings, and redistributing traffic based on actual observed conditions.
Moreover, the index can be useful in prioritizing infrastructure investments. Areas that show poor performance in the index could be candidates for infrastructure improvements, such as lane expansions, the creation of exclusive public transport routes, and the implementation of more sophisticated traffic management systems. This not only contributes to improving traffic flow but can also have a positive impact on reducing pollution and enhancing the quality of life for residents.
In the realm of transportation policies, this study emphasizes the need for a holistic, data-driven approach to policy formulation. Decision makers can use the index to establish key performance indicators that guide traffic policies. This could include creating incentives for the use of sustainable mobility alternatives, such as public transport, cycling, or promoting shared mobility.
Furthermore, by providing accurate and up-to-date data on congestion, the index can be crucial in formulating policies that respond to the changing needs of urban communities. In periods of high demand, such as sports events or festivals, the index could help establish temporary management strategies that minimize the impact of increased traffic.
To further enrich the proposed mobility index model, future research should consider applying the index in different urban contexts and evaluating its effectiveness in various cities with distinct demographic and geographical characteristics. It would also be beneficial to explore the index’s ability to adapt to exceptional situations, such as emergencies or natural disasters, where traffic may be significantly affected. Additionally, the comparison of the proposed index in this work is only conducted against the INRIX model; therefore, strengthening the proposed model would involve including more diverse and relevant benchmarks. Incorporating metrics such as the Speed Performance Index and the Speed Reduction Index could provide a more comprehensive view of traffic performance. The Speed Performance Index measures the effectiveness of the average vehicle speed compared to the ideal speed, providing context on how traffic behaves concerning urban mobility objectives. Meanwhile, the Speed Reduction Index evaluates the decrease in speed compared to a free-flow scenario, allowing for the identification of critical areas where interventions are necessary to improve traffic flow. This would not only enhance the understanding of the relative performance of the proposed index but could also provide valuable insights into its robustness and applicability across a variety of traffic scenarios. Including multiple comparisons could facilitate a more thorough analysis and contribute to the validation of the index in practice, which, in turn, could guide the formulation of more effective traffic policies tailored to the specific realities of each urban context.
Similarly, as future work, a detailed methodology is proposed to integrate the mobility index into current traffic management systems, with the aim of optimizing its utility for urban planners and enhancing its impact on decision-making. This methodology would begin with a comprehensive evaluation of technical compatibility, ensuring that the index can be efficiently integrated into the already implemented traffic management systems. To achieve this, the most relevant variables of the index that provide significant value would be identified, and the desired outputs would be established, such as real-time alerts and congestion reports, that can be adapted to the operational functions of these systems. In the next phase, an integration infrastructure would be developed, likely through APIs and data visualization modules, to enable the real-time flow of index data to traffic systems. These tools would include accuracy and quality tests to ensure the reliability of the information, as well as the creation of visual interfaces that simplify the interpretation of the index in interactive maps and graphs, thereby improving strategic decision-making regarding traffic.
As an additional future work, a detailed methodology is proposed for integrating the mobility index into current traffic management systems, aiming to optimize its utility for urban planners and enhance its impact on decision-making. This methodology would begin with a comprehensive assessment of technical compatibility, ensuring that the index can be efficiently integrated into already implemented traffic management systems. To achieve this, the most relevant variables of the index that provide significant value would be identified, and desired outputs, such as real-time alerts and congestion reports, would be established to adapt to the operational functions of these systems. In the next phase, an integration infrastructure would be developed, likely through APIs and data visualization modules, allowing for the real-time flow of index data into traffic systems. These tools would include accuracy and quality testing to ensure the reliability of the information, as well as the creation of visual interfaces that simplify the interpretation of the index in interactive maps and graphs, thereby improving strategic decision-making regarding traffic.
To implement the proposed index in real-time traffic monitoring systems using technologies such as the Internet of Things (IoT) and Intelligent Transportation Systems (ITS), several computational and operational requirements are necessary. First, it is essential to have adequate processing capacity, including fast processing units (CPU/GPU) and high-performance servers capable of handling large volumes of data in real time. Additionally, an effective storage system is needed, which allows the use of real-time databases and distributed storage solutions to ensure data availability and scalability. Connectivity and bandwidth are equally critical; a robust network infrastructure must be established with sufficient capacity to transmit data from IoT devices to analysis servers, ensuring low latency. Furthermore, interoperability is essential, which implies implementing standardized communication protocols and APIs that facilitate the integration of various data sources. For data analysis, real-time analysis algorithms and visualization tools must be implemented to enable urban planners to easily interpret the information. Security protocols must also be considered to protect data integrity, along with a security monitoring system that alerts to potential threats. The system architecture should be scalable to accommodate future demands and the integration of new IoT devices, and finally, it is important to have trained personnel to manage and maintain the system, ensuring its proper functioning and updates. These requirements are essential for the proposed index to provide accurate and useful analyses of real-time traffic performance, facilitating informed decision-making to improve urban mobility.
Author Contributions
Conceptualization, E.D.l.C.-N. and A.M.-R.; methodology, E.D.l.C.-N.; software, E.D.l.C.-N.; validation, H.E.-E., A.M.-R. and E.D.l.C.-N.; formal analysis, E.D.l.C.-N.; investigation, O.A.P.-M.; resources, E.D.l.C.-N.; data curation, O.A.P.-M.; writing—original draft preparation, E.D.l.C.-N.; writing—review and editing, H.E.-E.; visualization, O.A.P.-M.; supervision, A.M.-R.; project administration, A.M.-R.; funding acquisition, O.A.P.-M. and E.C. Interpretation of Results, Analysis of the Hyperparameters of the Genetic Algorithm and Verification of Results. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The traffic and road incident dataset is available through the Here Maps API (https://developer.here.com/develop/rest-apis), while service data is obtained via the Geoapify API (https://www.geoapify.com/places-api/).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- The Complexity Science Center. Available online: https://www.c3.unam.mx/boletines/boletin5.html (accessed on 4 January 2024).
- IDEA. Movilidad Sostenible. Available online: https://www.idae.es/movilidad-sostenible/la-piramide-de-la-movilidad-urbana (accessed on 4 January 2024).
- National Institute of Statistics and Geography. Available online: https://www.inegi.org.mx/temas/vehiculos/ (accessed on 4 January 2024).
- Mondal, S.; Gupta, A. Speed distribution for interrupted flow facility under mixed traffic. Phys. A 2021, 570, 125798. [Google Scholar] [CrossRef]
- Sun, C.; Pei, X.; Hao, J.; Wang, Y.; Zhang, Z.; Wong, S.C. Role of road net-work features in the evaluation of incident impacts on urban traffic mobility. Transp. Res. Part B 2018, 117, 101–116. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, Z.; Yang, Y.; Yang, X.; Liu, Y. Factors influencing traffic accident frequencies on urban roads: A spatial panel time-fixed effects error model. PLoS ONE 2019, 14, e0214539. [Google Scholar] [CrossRef] [PubMed]
- Almeida, A.; Brás, S.; Sargento, S.; Oliveira, I. Exploring bus tracking data to characterize urban traffic congestion. J. Urban Mobil. 2023, 4, 100065. [Google Scholar] [CrossRef]
- Nian, G.; Sun, J.; Huang, J. Exploring the effects of urban built environment on road travel speed variability with a spatial panel data model. ISPRS Int. J. Geo-Inf. 2021, 10, 829. [Google Scholar] [CrossRef]
- Kushchenko, L.E.; Kushchenko, S.V.; Baranov, Y.N.; Dnistrenko, N.S. Traffic modeling. IOP Conf. Ser. Mater. Sci. Eng. 2019, 698, 066034. [Google Scholar] [CrossRef]
- Sun, J. Mathematical modeling of traffic. J. Phys. 2021, 2012, 012060. [Google Scholar] [CrossRef]
- Mohan Rao, A.; Ramachandra Rao, K. Measuring urban traffic congestion—A review. Int. J. Traffic Transp. Eng. 2012, 2, 286–305. [Google Scholar] [CrossRef]
- He, F.; Yan, X.; Liu, Y.; Ma, L. A traffic congestion assessment method for urban road networks based on speed performance index. Procedia Eng. 2016, 137, 425–433. [Google Scholar] [CrossRef]
- Liponhay, M.; Valenzuela, J.F.; Dorosan, M.; Dailisan, D.; Monterola, C. A dynamic urban mobility index from clustering of vehicle speeds in a tourist-heavy city. Appl. Sci. 2023, 13, 12763. [Google Scholar] [CrossRef]
- Pandey, A.; Sharma, M.; Biswas, S. Concept of heterogeneity index for urban mixed traffic. Int. J. Transp. Sci. Technol. 2023, 12, 354–372. [Google Scholar] [CrossRef]
- Leitner, D.; Meleby, P.; Miao, L. Recent advances in traffic signal performance evaluation. J. Traffic Transp. Eng. 2022, 9, 507–531. [Google Scholar] [CrossRef]
- Seong, J.; Kim, Y.; Goh, H.; Kim, H.; Stanescu, A. Measuring traffic congestion with novel metrics: A case study of six U.S. metropolitan areas. ISPRS Int. J. Geo-Inf. 2023, 12, 130. [Google Scholar] [CrossRef]
- Wang, W.-X.; Guo, R.-J.; Yu, J. Research on road traffic congestion index based on comprehensive parameters: Taking Dalian city as an example. Adv. Mech. Eng. 2018, 10, 168781401878148. [Google Scholar] [CrossRef]
- Arirja Gani, F.; Yoshii, T.; Kurauchi, S. The suitable index of flow and density in the mixed traffic. IOP Conf. Ser. Earth Environ. Sci. 2017, 71, 012015. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, C.; Zheng, Z. Traffic congestion and duration prediction model based on regression analysis and survival analysis. Open J. Bus. Manag. 2020, 08, 943–959. [Google Scholar] [CrossRef][Green Version]
- Chen, L.; Shi, J.; Cheng, M.; Zhu, H.; Sun, L. Characteristics of urban road non-recurrent traffic congestion based on floating car data. In Proceedings of the 4th International Conference on Electronic Information Technology and Computer Engineering 2020, Xiamen, China, 6–8 November 2020; pp. 120–126. [Google Scholar] [CrossRef]
- Bian, C.; Yuan, C.; Kuang, W.; Wu, D. Evaluation, classification, and influential factors analysis of traffic congestion in Chinese cities using the online map data. Math. Probl. Eng. 2016, 2016, 1693729. [Google Scholar] [CrossRef]
- Mahona, J.; Mhilu, C.; Kihedu, J.; Bwire, H. Factors contributing to traffic flow congestion in heterogenous traffic conditions. Int. J. Traffic Transp. Eng. 2019, 9, 238–254. [Google Scholar] [CrossRef]
- Yu, J.; Wang, L.; Gong, X. Study on the status evaluation of urban road intersections traffic congestion base on AHP-TOPSIS modal. Procedia Soc. Behav. Sci. 2013, 96, 609–616. [Google Scholar] [CrossRef]
- Gullotta, G.; Loret, E.; Stewart, C.; Sarti, F. Traffic attractors and congestion in the urban context, the case of the city of Rome. J. Geogr. Inf. Syst. 2020, 12, 545–559. [Google Scholar] [CrossRef]
- Rahman, M.M.; Najaf, P.; Fields, M.G.; Thill, J.-C. Traffic congestion and its urban scale factors: Empirical evidence from American urban areas. Int. J. Sustain. Transp. 2022, 16, 406–421. [Google Scholar] [CrossRef]
- Pi, M.; Yeon, H.; Son, H.; Jang, Y. Visual Cause Analytics for Traffic Congestion. IEEE Trans. Vis. Comput. Graph. 2019, 27, 2186–2201. [Google Scholar] [CrossRef] [PubMed]
- Owais, M.M.; Enieb, M.; Abbas, Y.A. Evaluation and Analysis of Urban Passengers Transport Modes Operation Performance Efficiency. JES J. Eng. Sci. 2011, 39, 283–299. [Google Scholar] [CrossRef]
- National Institute of Statistics, Geography, and Informatics. Available online: https://www.inegi.org.mx/contenidos/productos/prod_serv/contenidos/espanol/bvinegi/productos/historicos/920/702825920845/702825920845_1.pdf (accessed on 8 January 2024).
- De la Cruz-Nicolás, E.; Martínez-Rebollar, A.; Estrada-Esquivel, H.; Pliego-Martínez, O.A. Methodology to obtain traffic data and road incidents through maps applications. In Smart Cities; Springer Nature: Cham, Switzerland, 2023; Volume 1938, pp. 3–17. [Google Scholar] [CrossRef]
- Owais, M. Deep learning for integrated origin–destination estimation and traffic sensor location problems. IEEE Trans. Intell. Transp. Syst. 2024, 25, 6501–6513. [Google Scholar] [CrossRef]
- Koza, J. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Langdon, W.B.; Poli, R.; McPhee, N.F.; Koza, J.R. Genetic Programming: An Introduction and Tutorial, with a Survey of Techniques and Applications. Stud. Comput. Intell. 2008, 115, 927–1028. [Google Scholar] [CrossRef]
- O’Neill, M.; Poli, R.; William, B.; Langdon, N.F. Mcphee: A field guide to genetic programming. Genet. Program. Evolvable Mach. 2009, 10, 229–230. [Google Scholar] [CrossRef]
- Here Maps Developer. Available online: https://www.here.com/docs/bundle/sdk-for-ios-navigate-developer-guide/page/topics/routing.html#find-traffic-along-a-route (accessed on 12 January 2024).
- Pishue, B. INRIX Global Traffic Scorecard; Scorecard Rep.; INRIX: Washington, DC, USA, 2023; Available online: https://inrix.com/scorecard/ (accessed on 4 January 2024).
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- INRIX. Available online: https://inrix.com/press-releases/medidor-inrix-del-trafico-congestion-desploma/#:~:text=Para%20cada%20segmento%20de%20carretera,con%20libre%20circulaci%C3%B3n)%20%E2%80%93%201 (accessed on 20 February 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).