Abstract
Resilience-based decision-making for urban water distribution systems (WDSs) is a challenge when WDS sensing data contain incomplete or missing values. This study investigated the impact of missing data imputation on a WDS resilience evaluation depending on missing data percentages. Incomplete datasets for the nodal pressure of the C-town WDS were developed with 10%, 30%, and 50% missing data percentages by manipulating a true dataset for normal operation conditions produced using EPANET. This study employed multiple imputation methods including classification and regression trees, predictive mean matching, linear regression regarding model error, and linear regression using projected values. Then, resilience values were evaluated and compared using unimputed and imputed datasets. An analysis of performance indicators based on NRMSE, NMAE, NR-Square, and N-PBIAS revealed that higher missing-data percentages led to increased deviation between the true and imputed datasets. The resilience evaluation using unimputed datasets produced significant deviations from the true resilience values, which tended to increase as the missing data percentages increased. However, the imputed datasets substantially contributed to reducing the deviations. These findings underscore the contributions of data imputation to enhancing resilience evaluation in WDS decision-making and suggest insights into advancing a resilience evaluation framework for urban WDSs with more reliable data imputation approaches.
1. Introduction
As water distribution systems (WDSs) are adopting the concept of resilience, resilience measures have become decisive in developing recovery and responsive strategies against disruptive events [1]. A design framework based on resilience focuses on evaluating and identifying the performance of a system in terms of its persistence, adaptability, and transformability to address future uncertainty [2]. System functionality analysis, resilience evaluation, maintenance, response and recovery plans, and system monitoring are the main components in decision-making for WDS design and operation to ensure resilience [3,4,5]. From this perspective, the components in resilience-based decision-making require quantification, analysis, and evaluation of the physical and hydraulic state of WDSs. Thus, data for system states before, during, and after a disruptive event are necessary for resilience-based decision making.
There are various approaches to obtaining data on the physical and operational performance of WDSs. For instance, leakage detection was traditionally based on human experience, but advancements in signal-processing algorithms and affordable computers have led researchers to develop automatic leakage detection techniques [6]. In this context, various techniques using the analysis of acoustic wave and emissions, vibration sensing, ground-penetrating radar, hydrophone, and transient/wavelet analysis have been introduced and applied [7]. Advanced Metering Infrastructure (AMI) is also used to interconnect the flow meters connected at the customer premises, with the control center of the utility company allowing the proactive identification of any existing problem and solving them [8]. These days, water utilities have been employing the Supervisory Control and Data Acquisition (SCADA) system in WDSs, which facilitates real-time monitoring and control of efficient water distribution, management, and water losses/leaks and their prompt resolutions [8].
However, despite data availability from the various methods of obtaining system data, the observed data often contain missing or incomplete values and significant noise [9]. The missing data can be a challenge for quantifying and analyzing WDS performances under disruptions and thereby suggest unexpected or counterintuitive results from resilience evaluation in decision-making. The low quality and quantity of observed data frequently occur due to a range of reasons, such as sensor failures, data collection errors, equipment faults, communication network interruptions, calibration inaccuracies, environmental conditions, and natural hazards [10]. Another growing threat to the quality of observed datasets is cyber-attacks [11]. With the advances in information and communication technology (ICT), a smart system approach incorporating sensors, communication, and controllers into existing WDSs—or water cyber-physical systems—has received great worldwide attention for its effective, sustainable, and resilient operations [12]. As smart WDSs monitor and control their performance based on real-time data observations through complicated networks of cyber components (e.g., data loggers, PLC), communication, and information, they become easy targets for cyber-attacks [13]. One of the cyber-physical attack actions is manipulating, removing, or falsifying sensing data—i.e., the distortion of the original dataset, compromising critical system operations. Thus, data reliability problems coming from missing, incomplete, and manipulated data can significantly affect the performance of modeling, analysis, and evaluation in resilience-based decision making [14].
Missing or manipulated data problems are recognized as a common challenge encountered in the analysis of real-world datasets [15]. Typically adopted ways to address the missing or incomplete data are deleting or imputing the data. The deletion method eliminates all observations, including missing or incomplete data. It is a simple and rapid method. However, as the percentage of missing data in a dataset increases, simple deletion can lead to a lack of data, biased results, and unreliable performance in modeling and analysis [16]. The data imputation method, reconstructing and filling in missing data, has been widely adopted in the fields of engineering and non-engineering [17]. These techniques range from traditional methods (e.g., single imputation using mean, mode, and media) to more advanced methods such as multivariate imputation and machine learning techniques [18,19]. Traditional approaches such as mean, median, or mode are limited in handling variability in the data and cause significant bias in data imputation [20]. The linear interpolation method has been widely used due to its simplicity; however, it is not recommended for datasets with a large number of missing values [21]. Also, least squares is one of the most widely used data imputation methods, in which linear regression is used to predict the missing values [22]. However, this method also results in bias as it is sensitive to outliers and data variability [23].
Single imputation methods, such as mean, median, or regression-based substitution, create and replace missing data with reasonable values based on similar observed variables [24]. They provide reliable point estimates; however, they do not effectively capture the uncertainty and standard errors and variance of data [24]. Regression-based imputation correctly estimates covariances but still underestimates variances, whereas mean and median imputations bias correlations and covariances [25].
Multiple imputation approaches are widely used in various fields and generate numerous plausible values for missing data while accounting for the randomness and variability of data [26,27]. These consist of model-based (e.g., regression), distance-based (e.g., k-nearest neighbor), and covariance-based techniques [28,29]. Harder et al. (2024) [30] created a structured methodology for clustering complex medical data using multiple imputation, ensuring fairness and the unbiased identification of illness subgroups, even when missing data. Their method effectively handled missing data, supporting robustness in medical diagnosis. Nguyen and Matthews (2024) [31] used the multiple imputation method to estimate player performance during missing seasons and build aging curves using imputed datasets. This analysis results in a better understanding of performance dynamics across time. Ni and Leonard (2005) [32] proposed an enhanced imputation approach designed for Intelligent Transportation Systems, which allows for repeated imputations and statistical inference to improve decision-making processes. Meanwhile, Kofman et al. (2003) [33] dealt with incomplete data issues with financial applications by employing multiple imputation approaches, which are particularly useful when the missing data meets precise requirements, ensuring reliable financial analysis.
Based on the review of the available scientific literature, it has emerged that the application of data imputation techniques in the fields of water resources and systems has primarily focused on hydrological variables such as stream flow data [34], water quality data [16,35], and groundwater data [36,37], as well as demand forecasting [14]. However, it has been noted that there have been few studies addressing the imputation of missing data in WDSs and investigating the effects of data imputation on resilience-based decision-making. A lack of understanding of the impacts of imputed data can suggest misinterpretation about the resilience effects of responsive and recovery options for a WDS. Thus, this study investigates the impacts of the use of missing and imputed data on resilience evaluation for WDSs, considering various ranges in missing data percentages. Here, the missing data percentage is defined as the ratio of the number of missing or manipulated values to the total number of observations.
This study will contribute to the understanding of data recovery and restoration in the context of missing data on WDS resilience evaluation and provide insights into the selection of appropriate imputation methods, the impact of imputed data on water infrastructure management, and improving resilience-based decision-making and planning processes.
2. Methods
Figure 1 shows a summary of the method of this study: (1) creating datasets for normal operating conditions for a WDS, (2) introducing missing values into the datasets with various missing data percentages, (3) imputing the missing values using multiple imputation approaches, (4) checking the accuracy of the imputation approaches, and (5) evaluating the resilience of the WDS depending on various missing data percentages.
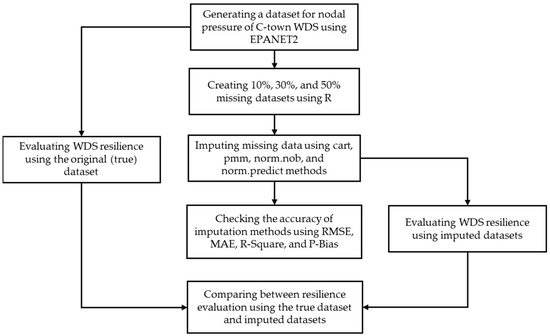
Figure 1.
Summary of methodology.
2.1. Creating the Datasets for Normal Operating Conditions
This study selected the C-town WDS to create datasets with missing values and apply data imputation (Figure 2). The C-town WDS, as a real-world, medium-sized network, has been widely used in various studies (including battle competitions) for the purposes of hydraulic simulation model calibration, leakage/attack detection, resilience evaluation, and design and operation optimization [13,38,39]. The C-town WDS consists of 388 nodes, 429 pipelines, 4 valves, 7 tanks, 11 pumps, 9 PLCs, and a SCADA system, which gathers data from all PLCs and coordinates system operations [13].
This study used a hydraulic simulation model—U.S. EPANET to produce a thorough 24-h dataset for the hydraulic performance of the C-town WDS under normal operating conditions. EPANET has been widely used for the analysis and design of WDSs by academics and practitioners. It places no limit on the size of the network, allows for time-varying simulations, and models pressure-dependent flow [40]. The nodal pressure of 18 demand nodes in the C-town WDS was considered as the hydraulic performance used to produce incomplete and imputed datasets in the following sections, which were also used to evaluate resilience (see Section 2.5). This dataset contains no data that were manipulated or missed. Thus, this dataset can be used as a baseline for the hydraulic performance of the C-town WDS, which was also manipulated to create incomplete datasets with missing values.
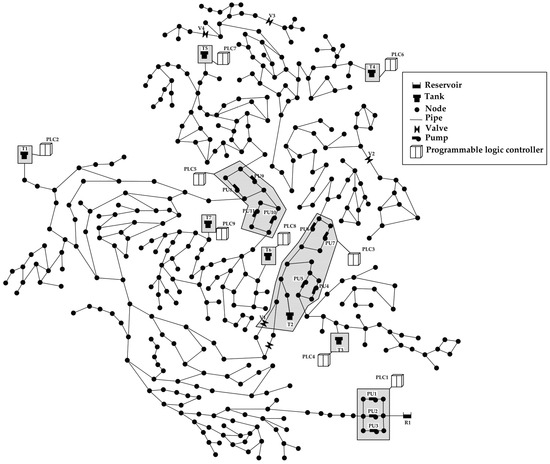
Figure 2.
C-town WDS (adopted from [41]).
2.2. Introducing Missing Values into the Dataset with Data Missing Percentage
This study considered the missing data percentages of 10%, 30%, and 50%. Thus, randomly selected data points (of nodal pressure) depending on the missing data percentages were eliminated from the previously produced dataset. For example, for the 10% missing-data percentage, 10% of the pressure values of the 18 demand nodes were removed from the 24-h dataset.
In general, missing values in a dataset can be produced based on the assumption of Missing Completely at Random (MCAR), Missing at Random (MAR), or Missing Not at Random (MNAR) [42]. MCAR is the highest level of randomness, where missing values occur entirely at random and independent of any variables considered. MAR involves missing data probabilities that depend on observed information in the dataset. On the other hand, MNAR occurs when the probability of missing data is dependent on unobserved values of the variable due to the sensitivity of the response variable. In this context, this study adopted the assumption of MCAR to produce datasets with missing values, considering the randomness and uncertainty of the missing data. Production of the datasets with missing values in different missing percentages was carried out using the `prodNA` function in RStudio, which has been widely used to artificially introduce missing values into a dataset [43]. Thus, a total of four datasets were produced: original (true), 10% missing, 30% missing, and 50% missing, as shown in Figure 1.
2.3. Imputing Missing Data Using Multiple Imputation Approaches
This study adopted the multiple imputation approach, which can address the uncertainty of imputed missing values and suggest a more reliable estimation of missing values than the single imputation approach [44]. Multiple imputation generates multiple complete datasets that are separately imputed from a missing dataset by statistical analysis and by repeating a single imputation process [21]. Thus, the multiple datasets contain a different set of imputed values of missing data, respectively.
Multivariate Imputation by Chained Equations (MICE) is an increasingly popular algorithm among the multiple imputation algorithms, which can implement multiple imputation using the Fully Conditional Specification [45]. Fully Conditional Specification iteratively imputes the missing values for a variable in an incomplete dataset by applying conditional distributions based on the other variables [46]. Thus, this study used the MICE algorithm, which is built in the mice package in R [47]. The mice package includes multiple imputation methods. The imputation methods used in this study were classification and regression trees (cart), predictive mean matching (pmm), linear regression ignoring model error (norm.nob), and linear regression with predicted values (norm.predict), assuming MCAR.
The cart method uses decision trees to impute missing values by dividing the data based on the values of other variables [48]. It builds a decision tree for each variable with missing data and predicts the missing values using the known values of other variables. The cart method provides a robust and flexible approach for coping with missing data by repeatedly constructing multiple imputed datasets and integrating uncertainty, allowing the achievement of reliable estimates on the missing data [49]. The pmm method fills in missing data by identifying known values from the dataset that have the closest mean distance with predictive values to the missing data [50]. The method of linear regression ignoring model error (norm.nob) fills in missing data by predicting the missing values using a linear regression model. It generates imputed values based on the variability from the linear regression line fitted on the dataset by ignoring model error [51]. The method of linear regression with predicted values (norm.predict) also adopts the predicted value using a linear regression model to impute the missing data. This method assumes that the data follow a normal distribution. Thus, unlike the method of linear regression ignoring the model error, it incorporates the imputation process’s inherent uncertainty by imputing the missing values by selecting random samples from a predicted normal distribution [52]. With this method, the variability and uncertainty present in the missing data are preserved, allowing for more precise and reliable statistical analysis.
2.4. Checking the Accuracy of Imputation Methods
This study evaluated the data imputation performance of multiple imputation methods using the following statistical indicators: mean of normalized root mean square error (Mean N-RMSE), mean of normalized mean absolute error (Mean N-MAE), mean of normalized root mean square error (Mean N-RSQUARE), and mean of normalized percent bias (Mean N-PBIAS) [53,54]. By normalizing the disparities between the original (true) values of the dataset and the imputed values, these indicators allowed the evaluation and comparison of the overall accuracy of the multiple imputation methods. The normalized RMSE, MAE, RSQUARE, and PBIAS were estimated using the normalized imputed and true values of the missing data through the min-max normalization. The performance indicators are mathematically represented as follows:
where is the total number of data points, is the normalized imputation value for missing data, is the normalized true value for missing data, and is the normalized mean of true value. After obtaining the values of N-RMSE, N-MAE, NR-SQUARE, and N-PBIAS for each of the 18 nodes, the mean value of each indicator for the 18 nodes was calculated.
2.5. Evaluating the Resilience of the WDS with Imputed Data
For the WDS resilience evaluation, this study used an energy-surplus-based resilience metric (Equation (5)) that was introduced by Todini (2000) [55]. This metric has been widely used to evaluate the resilience of WDSs against the uncertainty of system disruptions [1]. It is defined as the fraction of available energy surplus at the nodes, which can be internally dissipated to meet demand and head requirements during a physical failure event over the maximum energy surplus provided to the WDS. Physical and hydraulic disruptions in WDSs can lead to significant energy (pressure or head) losses. This can result in a drop in nodal pressure (head) and a failure to meet the required pressure, which in turn causes failures in water delivery. In this context, the resilience metric (Equation (5)) provides higher resilience values when the system has sufficient surplus energy to overcome the energy loss during disruptions:
where and are the design demand and head required at node ; is the available head at node ; is the flow from th reservoir; is the total head in th reservoir; is the energy supplied to the WDS from th pump; is the specific weight of water; and , , and are the number of nodes, reservoirs, and pumps, respectively, in the WDS.
Using Todini (2000)’s resilience metric, this study evaluated and compared the resilience evaluation for various missing data percentages and imputed data generated through the multiple imputation methods. This comprehensive investigation aims to understand the efficacy of imputation approaches in improving resilience evaluation as compared to the cases in which incomplete datasets remain unimputed.
3. Results and Discussion
3.1. The Performance of Data Imputation Methods
The dataset created using the EPANET2 model for the C-town WDS consisted of total 1728 datapoints for the nodal pressure of 18 demand nodes. The missing values were randomly introduced to 10%, 30%, and 50% of the total data points. Figure 3 shows the performance of multiple data imputation methods including cart, pmm, norm.nob, and norm.predict in MICE for the different missing-data percentages. Overall, it is observed that the performance of all imputation methods decreases as the missing data percentage increases. As noted in Figure 3a–c, the cart method demonstrates the lowest data imputation performance across all levels of missing data percentages. On the other hand, the linear regression methods (i.e., norm.nob and norm.predict) show relatively higher performances in data imputation, as compared to other methods. However, it is also noted that the performance of the norm.nob and norm.predict methods varies depending on the missing data percentage. The norm.nob method shows better performance at a relatively lower missing-data percentage, while the norm.predict method provides higher accuracy at higher missing-data percentages. Thus, the varying performances depending on the missing data percentages suggest ensemble methods that combine various data imputation methods into an integrated data imputation framework to demonstrate better performances across various ranges of missing data percentages, as compared to a conventional multiple imputation method [56].
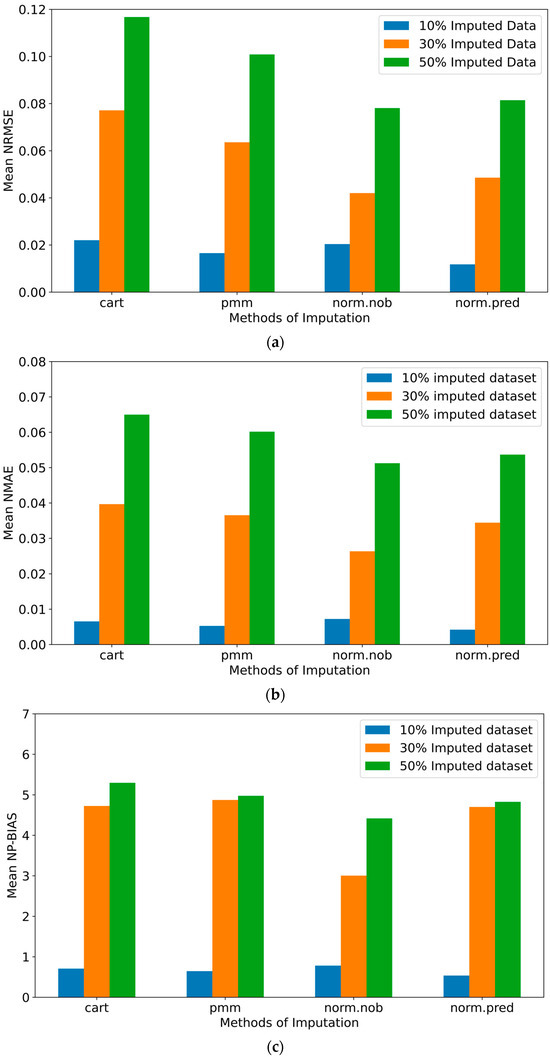
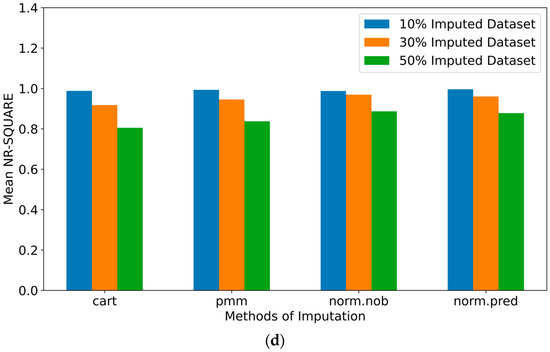
Figure 3.
Performance evaluation of the different imputation methods for different missing-data rates using (a) Mean N-RMSE, (b) Mean N-MAE, (c) Mean N-PBIAS, and (d) Mean NR-SQUARE.
Meanwhile, as observed in Figure 3, the performance differences among the imputation methods are relatively small at lower missing-data percentages. However, as the missing data percentages increase, Figure 3 shows an evident increase in the differences in their data imputation performances. In this context, it is noted that the performance of the cart and pmm methods rapidly degrades with increasing missing-data percentages. However, the relatively high performance based on the NR-SQUARE (Figure 3d) indicates that the four imputation methods can produce imputed datasets capturing the overall patterns of the datapoints, as compared to their increasing errors (Figure 3a–c) in the imputation of individual missing values.
In summary, the performance evaluation of the data imputation methods concludes that, as the missing data percentages increase, their accuracy performances in data imputation decrease. Additionally, the choice of an imputation method and the missing data (imputation) percentage affect the data imputation performance. This suggests the need to emphasize the importance of careful consideration in handling missing data in WDS datasets—e.g., through an ensemble method of multiple data imputation techniques.
Table 1, Table 2, Table 3 and Table 4 present the ranks of the imputation methods for 10%, 30%, and 50% missing-data percentages, considering the imputation performance based on the Mean N-RMSE, Mean N-MAE, Mean NP-BIAS, and Mean NR-SQUARE, respectively. The imputation methods are ranked higher if they have lower values for the Mean NRMSE, Mean NMAE, and Mean NPBIAS and higher values for the Mean NR-Square. The ranks by mean and mode in the tables represent the average and mode of the ranks. Using the ranks, Kendall’s W test was carried out to test the consistency of each imputation method’s performance [53]. It measures the agreement among the raters when they rank multiple options, and the degree of consistency in their rankings—Kendall’s W of zero indicates no agreement among the judges, implying that their ratings or assessments are fully independent of one another. Conversely, when the judges’ Kendall’s W value is one, it means that there is absolute agreement among them, meaning that everyone agrees entirely on their ratings or assessments [53]. As observed in Table 1, Table 2, Table 3 and Table 4, the Kendall’s test statistics for the ranks based on the four performance indicators are close to one, and the p-value is significant at a 5% level of significance, implying substantial agreement in the ranks in the tables. Thus, it is noted that the imputation method’s ranking remains consistent, regardless of the performance indicators or the missing data percentages in the dataset. This similarity in rankings across various imputation methods aligns with the findings proposed by [53].

Table 1.
Rank of imputation methods for different missing-data percentages using Mean N-RMSE.

Table 2.
Rank of imputation methods for different missing-data percentages using Mean N-MAE.

Table 3.
Rank of imputation methods for different missing-data percentages using Mean N-PBIAS.

Table 4.
Rank of imputation methods for different missing-data percentages using Mean NR-SQUARE.
3.2. The Impacts of Imputed Data on Resilience Evaluation
The energy-surplus-based resilience of the C-town WDS was evaluated using the datasets that were imputed by multiple imputation methods—cart, pmm, norm.nob, and norm.predict in MICE. Figure 4 illustrates the RMSE between the C-town WDS resilience values evaluated using the original (true) datasets and both unimputed (incomplete) and imputed datasets across 10%, 30%, and 50% missing-data percentages. The RMSE was calculated by taking the square root of the average squared difference between the resilience values evaluated using the true dataset and the unimputed and imputed datasets. Overall, Figure 4 shows a significant difference (RMSE) between the resilience values evaluated using the unimputed, imputed, and true datasets. However, the resilience evaluation using the imputed datasets demonstrated a significant reduction in the deviations from the true resilience levels, regardless of the imputation methods. Thus, it can be noted that implementing appropriate imputation methods can significantly contribute to the reliable evaluation of system resilience in the presence of missing values in an incomplete dataset. In addition, it is also inferred that a resilience evaluation using unimputed and incomplete datasets can suggest inadequate and inappropriate options in WDS design and operation to enhance system resilience.
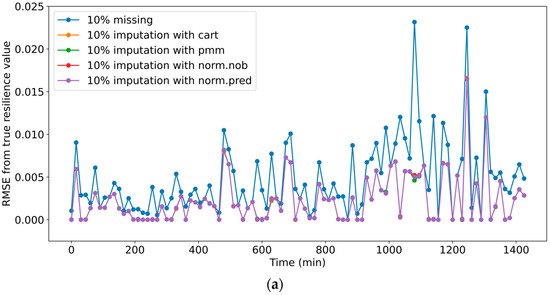
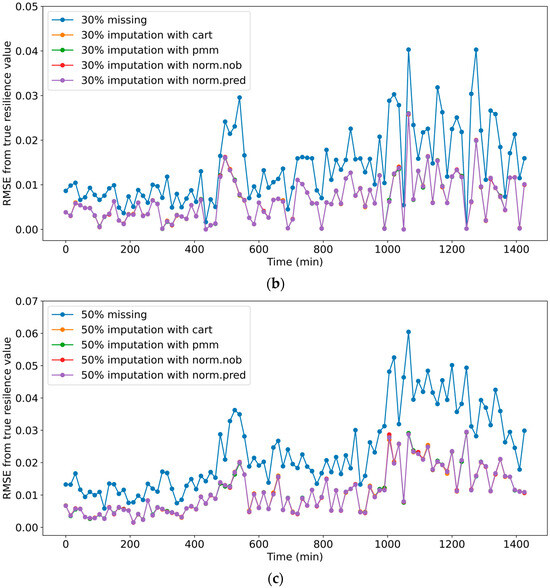
Figure 4.
The comparison between the resilience evaluation through the RMSE from true resilience levels: (a) 10% missing and imputed datasets, (b) 30% missing and imputed datasets, and (c) 50% missing and imputed datasets.
Figure 4 also shows that, as the missing data percentage increases, the resilience evaluation using both the imputed and unimputed datasets produces increasing deviations from the true resilience levels. However, the increase in the deviation along the missing data percentages was found to be significantly greater when the resilience was evaluated using the unimputed datasets as compared to the imputed datasets. This result suggests that the imputation of missing data can contribute to improving the capability of resilience evaluation in a decision-making process with incomplete datasets.
Meanwhile, Figure 4 shows an increasing deviation from true resilience values over time. The nodal demand (supplied demand) was observed to be higher during the period from 15 to 24 h, which produced greater deviations in the resilience values than other time periods. This result notes that missing data or imputation (slightly under- or over-estimated) during periods of higher demand can result in greater deviations among resilience values calculated using true, unimputed, and imputed datasets. It is also considered that this impact will be more significant for resilience measures that include nodal pressure (or head) as a critical parameter. Thus, the reliable monitoring of WDS performance during peak demand periods, combined with imputation methods tailored to multiple ranges of nodal demand, is suggested to enhance the overall accuracy of resilience evaluation using imputed datasets.
4. Conclusions
Recent advancements in ICT have significantly enhanced the efficiency and convenience of acquiring data on the performance of water infrastructure systems. In this context, data reliability is becoming increasingly essential for informed decision-making in designing, operating, and managing WDSs. The data obtained through sensors and meters are used in validating decision-supporting tools (e.g., hydraulic simulation models) and evaluating the effects of water-engineering options on the reliability, resilience, and vulnerability of the WDSs against various physical, operational, and cyber failures. However, the observed or sensed datasets frequently include missing or incomplete values due to various causes, such as sensor errors and malfunctions and malicious manipulations. In this regard, various data imputation methods have been developed and applied; however, no studies have addressed the impact of missing data and imputation on resilience evaluation, especially for WDSs. Resilience evaluation using incomplete or imputed data derived from poorly performing imputation methods can suggest inadequate responsive or recovery options for system disruptions. In this regard, this study investigated the question: how do unimputed and imputed values in an incomplete dataset that includes missing data impact the results of a resilience evaluation for a WDS? This study created incomplete datasets for the C-town WDS with 10%, 30%, and 50% missing-data percentages by manipulating a true dataset for the WDS performance in normal operation conditions. Then, this study compared the energy-surplus-based resilience values evaluated using unimputed and imputed datasets through multiple imputation methods—cart, pmm, norm.nob, and norm.predict—in MICE.
The investigation of the performance of the multiple imputation methods underscores a growing deviation between the imputed data and the original true data as the missing data percentage increased. The main findings of this study are as follows:
- (1)
- The results showed differences in the performance of the imputation methods depending on the data missing percentages. Thus, rather than relying on a single imputation method, an ensemble set of multiple imputation methods is suggested in a decision-making framework for a more reliable imputation of missing data in a wide range of missing data percentages.
- (2)
- The investigation of the resilience evaluation highlighted that significant deviations from the true resilience values were produced in the evaluation using unimputed datasets, while the imputed datasets effectively contributed to reducing the deviations.
- (3)
- The evaluation using the unimputed datasets that included missing values suggested lower performances than the imputed datasets, as the missing data missing percentage increased.
- (4)
- Resilience evaluation using incomplete or inaccurately imputed datasets for the periods of high demand can produce significant deviations from true resilience values evaluated using true datasets.
- (5)
- The imputation of missing data can enhance the reliability of resilience-based decision-making by improving the results of a resilience evaluation.
This study focused on the resilience of a WDS as a system performance. However, various perspectives on system performance such as vulnerability, reliability, and sustainability (e.g., energy use, operating costs, and social impacts) can be considered in decision-making for WDS design and management. In this context, the insights from this study can extend to the impacts of missing or imputed data on evaluating these various performances. This study identified that the multiple imputation methods, effectively addressed the imputation of missing data in WDS, and, in turn, enhanced the accuracy of resilience evaluation. In this regard, it is believed that data imputation will help improve the capability for not only resilience evaluation but also the evaluation of vulnerability, reliability, and sustainability in a decision-making process with incomplete datasets.
This study used true and incomplete datasets that represent a limited aspect of system performance (nodal pressure or head). Nodal pressure (head) is one of the critical components in designing, operating, and managing WDSs and evaluating energy-surplus-based resilience. As the prominence of resilience-based strategies increases, a lot of resilience measures have been developed to evaluate system resilience across various aspects of system performance. Components such as water flow, unmet demand, energy consumption, and contamination can be considered in resilience measures. Thus, investigating the impacts of missing data and imputation on the evaluation, using diverse resilience measures, will suggest insights for enhancing the capability of resilience evaluation across various aspects of system performance.
Meanwhile, this study randomly selected missing data points depending on the missing data percentages. Although random selection can result in the inclusion of consecutive data points, it has limitations for understanding the impacts of data imputation depending on missing data continuity. Expanding this study by addressing consecutive missing values in data imputation with various missing data percentages for the performance of WDSs will enable a more comprehensive understanding of its impacts on the reliable evaluation of the reliability, resilience, and vulnerability of the WDSs.
Also, in addition to the four multiple imputation methods in this study, more advanced imputation methods such as machine learning and ensemble methods have been introduced in recent years. Comparing the performance of these imputation methods and their contributions to resilience evaluation will provide engineering insights into establishing a robust framework with data imputation to enhance decision-making capabilities.
Author Contributions
Conceptualization, S.S. and A.B.G.; methodology, S.S. and A.B.G.; software, A.B.G.; validation, B.A.M., U.P. and A.B.G.; formal analysis, S.S. and A.B.G.; writing—original draft preparation, A.B.G. and B.A.M.; writing—review and editing, S.S. and A.B.G.; supervision, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding authors.
Acknowledgments
The authors thank the editor and the reviewers for their insights to enhance the quality of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Shin, S.; Lee, S.; Judi, D.; Parvania, M.; Goharian, E.; Mcpherson, T.; Burian, S. A Systematic Review of Quantitative Resilience Measures for Water Infrastructure Systems. Water 2018, 10, 164. [Google Scholar] [CrossRef]
- Brown, C.; Boltz, F.; Freeman, S.; Tront, J.; Rodriguez, D. Resilience by Design: A Deep Uncertainty Approach for Water Systems in a Changing World. Water Secur. 2020, 9, 100051. [Google Scholar] [CrossRef]
- Schramm, E.; Felmeden, J. Towards More Resilient Water Infrastructures. In Resilient Cities 2; Springer: Dordrecht, The Netherlands, 2012; Volume 2, pp. 177–186. ISBN 978-94-007-4223-9. [Google Scholar]
- Pamidimukkala, A.; Kermanshachi, S.; Adepu, N.; Safapour, E. Resilience in Water Infrastructures: A Review of Challenges and Adoption Strategies. Sustainability 2021, 13, 2986. [Google Scholar] [CrossRef]
- Khatri, K.B. Current State and Future Direction for Building Resilient Water Resources and Infrastructure Systems. Eng 2022, 3, 175–195. [Google Scholar] [CrossRef]
- Hunaidi, O.; Chu, W.; Wang, A.; Guan, W. Detecting Leaks in Plastic Pipes. J. Am. Water Work. Assoc. 2000, 92, 82–94. [Google Scholar] [CrossRef]
- Islam, M.; Azam, S.; Shanmugam, B.; Mathur, D. A Review on Current Technologies and Future Direction of Water Leakage Detection in Water Distribution Network. IEEE Access 2022, 10, 107177–107201. [Google Scholar] [CrossRef]
- Gopi, C.; Vidyanandan, L. Sensor Network Infrastructure for AMI in Smart Grid. Procedia Technol. 2016, 24, 854–863. [Google Scholar] [CrossRef]
- Shuang, Q.; Liu, H.; Porse, E. Review of the Quantitative Resilience Methods in Water Distribution Networks. Water 2019, 11, 1189. [Google Scholar] [CrossRef]
- Krishnamurthi, R.; Kumar, A.; Gopinathan, D.; Nayyar, A.; Qureshi, B. An Overview of IoT Sensor Data Processing, Fusion, and Analysis Techniques. Sensors 2020, 20, 6076. [Google Scholar] [CrossRef]
- Clark, R.M.; Panguluri, S.; Nelson, T.D.; Wyman, R.P. Protecting Drinking Water Utilities from Cyberthreats. J. AWWA 2017, 109, 50–58. [Google Scholar] [CrossRef]
- Cahn, A. An Overview of Smart Water Networks. J. AWWA 2014, 106, 68–74. [Google Scholar] [CrossRef]
- Shin, S.; Lee, S.; Burian, S.; Judi, D.; Mcpherson, T. Evaluating Resilience of Water Distribution Networks to Operational Failures from Cyber-Physical Attacks. J. Environ. Eng. 2020, 146, 04020003. [Google Scholar] [CrossRef]
- Zanfei, A.; Menapace, A.; Brentan, B.M.; Righetti, M. How Does Missing Data Imputation Affect the Forecasting of Urban Water Demand? J. Water Resour. Plan. Manag. 2022, 148, 04022060. [Google Scholar] [CrossRef]
- Hernández-Pereira, E.M.; Álvarez-Estévez, D.; Moret-Bonillo, V. Automatic Classification of Respiratory Patterns Involving Missing Data Imputation Techniques. Biosyst. Eng. 2015, 138, 65–76. [Google Scholar] [CrossRef]
- Rodríguez, R.; Pastorini, M.; Etcheverry, L.; Chreties, C.; Fossati, M.; Castro, A.; Gorgoglione, A. Water-Quality Data Imputation with a High Percentage of Missing Values: A Machine Learning Approach. Sustainability 2021, 13, 6318. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, F.; Wu, L.; Xie, N.; He, Z. Semantic Understanding and Prompt Engineering for Large-Scale Traffic Data Imputation. Inf. Fusion 2024, 102, 102038. [Google Scholar] [CrossRef]
- Gómez-Carracedo, M.P.; Andrade, J.M.; López-Mahía, P.; Muniategui, S.; Prada, D. A Practical Comparison of Single and Multiple Imputation Methods to Handle Complex Missing Data in Air Quality Datasets. Chemom. Intell. Lab. Syst. 2014, 134, 23–33. [Google Scholar] [CrossRef]
- Rahman, M.M.; Davis, D.N. Machine Learning-Based Missing Value Imputation Method for Clinical Datasets. In IAENG Transactions on Engineering Technologies: Special Volume of the World Congress on Engineering 2012; Yang, G.-C., Ao, S., Gelman, L., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 245–257. ISBN 978-94-007-6190-2. [Google Scholar]
- Khan, S.I.; Hoque, A.S.M.L. SICE: An Improved Missing Data Imputation Technique. J. Big Data 2020, 7, 37. [Google Scholar] [CrossRef]
- Aguilera, H.; Guardiola-Albert, C.; Serrano-Hidalgo, C. Estimating Extremely Large Amounts of Missing Precipitation Data. J. Hydroinform. 2020, 22, 578–592. [Google Scholar] [CrossRef]
- Lin, W.-C.; Tsai, C.-F. Missing Value Imputation: A Review and Analysis of the Literature (2006–2017). Artif. Intell. Rev. 2020, 53, 1487–1509. [Google Scholar] [CrossRef]
- Pan, S.; Chen, S. Empirical Comparison of Imputation Methods for Multivariate Missing Data in Public Health. Int. J. Environ. Res. Public Health 2023, 20, 1524. [Google Scholar] [CrossRef]
- Little, R.J.A.; Rubin, D.B. Single Imputation Methods. In Statistical Analysis with Missing Data; Wiley Series in Probability and Statistics; John and Wiley and Sons: Hoboken, NJ, USA, 2014; pp. 59–74. ISBN 978-1-119-01356-3. [Google Scholar]
- Graham, J.W.; Van Horn, M.L.; Taylor, B.J. Dealing with the Problem of Having Too Many Variables in the Imputation Model. In Missing Data; Springer: New York, NY, USA, 2012; pp. 213–228. ISBN 978-1-4614-4017-8. [Google Scholar]
- Rubin, D. An Overview of Multiple Imputation. In Proceedings of the Survey Research Methods Section; American Statistical Association: Alexandria, VA, USA, 1988. [Google Scholar]
- Schafer, J.L.; Olsen, M.K. Multiple Imputation for Multivariate Missing-Data Problems: A Data Analyst’s Perspective. Multivar. Behav. Res. 1998, 33, 545–571. [Google Scholar] [CrossRef]
- Honaker, J.; King, G.; Blackwell, M. Amelia II: A Program for Missing Data. J. Stat. Softw. 2011, 45, 1–47. [Google Scholar] [CrossRef]
- Templ, M.; Kowarik, A.; Filzmoser, P. Iterative Stepwise Regression Imputation Using Standard and Robust Methods. Comput. Stat. Data Anal. 2011, 55, 2793–2806. [Google Scholar] [CrossRef]
- Harder, A.A.; Olbricht, G.R.; Ekuma, G.; Hier, D.B.; Obafemi-Ajayi, T. Multiple Imputation for Robust Cluster Analysis to Address Missingness in Medical Data. IEEE Access 2024, 12, 42974–42991. [Google Scholar] [CrossRef]
- Nguyen, Q.; Matthews, G.J. Filling the Gaps: A Multiple Imputation Approach to Estimating Aging Curves in Baseball. J. Sports Anal. 2024, 10, 77–85. [Google Scholar] [CrossRef]
- Ni, D.; Leonard, J.D.; Guin, A.; Feng, C. Multiple Imputation Scheme for Overcoming the Missing Values and Variability Issues in ITS Data. J. Transp. Eng. 2005, 131, 931–938. [Google Scholar] [CrossRef]
- Kofman, P.; Sharpe, I.G. Using Multiple Imputation in the Analysis of Incomplete Observations in Finance. J. Financ. Econom. 2003, 1, 216–249. [Google Scholar] [CrossRef]
- Oriani, F.; Borghi, A.; Straubhaar, J.; Mariethoz, G.; Renard, P. Missing Data Simulation inside Flow Rate Time-Series Using Multiple-Point Statistics. Environ. Model. Softw. 2016, 86, 264–276. [Google Scholar] [CrossRef]
- Nieh, C.; Dorevitch, S.; Liu, L.C.; Jones, R.M. Evaluation of Imputation Methods for Microbial Surface Water Quality Studies. Environ. Sci. Process. Impacts 2014, 16, 1145–1153. [Google Scholar] [CrossRef]
- Evans, S.; Williams, G.P.; Jones, N.L.; Ames, D.P.; Nelson, E.J. Exploiting Earth Observation Data to Impute Groundwater Level Measurements with an Extreme Learning Machine. Remote Sens. 2020, 12, 2044. [Google Scholar] [CrossRef]
- Sarma, R.; Singh, S.K. A Comparative Study of Data-Driven Models for Groundwater Level Forecasting. Water Resour Manag. 2022, 36, 2741–2756. [Google Scholar] [CrossRef]
- Pournaras, E.; Taormina, R.; Thapa, M.; Galelli, S.; Palleti, V.; Kooij, R. Cascading Failures in Interconnected Power-to-Water Networks. ACM SIGMETRICS Perform. Eval. Rev. 2019, 47, 16–20. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E.; Ormsbee, L.; Uber, J.G.; Bros, C.M.; Kalungi, P.; Burd, R.; Zazula-Coetzee, B.; Belrain, T.; Kang, D.; et al. Battle of the Water Calibration Networks. J. Water Resour. Plan. Manag. 2012, 138, 523–532. [Google Scholar] [CrossRef]
- Arunkumar, M.; Mariappan, V.N. Water Demand Analysis of Municipal Water Supply Using Epanet Software. Int. J. Appl. Bioeng. 2011, 5, 9–19. [Google Scholar]
- Taormina, R.; Galelli, S.; Tippenhauer, N.O.; Salomons, E.; Ostfeld, A. Characterizing Cyber-Physical Attacks on Water Distribution Systems. J. Water Resour. Plan. Manag. 2017, 143, 04017009. [Google Scholar] [CrossRef]
- Umar, N.; Gray, A. Comparing Single and Multiple Imputation Approaches for Missing Values in Univariate and Multivariate Water Level Data. Water 2023, 15, 1519. [Google Scholar] [CrossRef]
- Thurow, M.; Dumpert, F.; Ramosaj, B.; Pauly, M. Imputing Missings in Official Statistics for General Tasks—Our Vote for Distributional Accuracy. Stat. J. IAOS 2021, 37, 1379–1390. [Google Scholar] [CrossRef]
- Kaplan, D.; Yavuz, S. An Approach to Addressing Multiple Imputation Model Uncertainty Using Bayesian Model Averaging. Multivar. Behav. Res. 2020, 55, 553–567. [Google Scholar] [CrossRef]
- Zhang, Z. Multiple Imputation with Multivariate Imputation by Chained Equation (MICE) Package. Ann. Transl. Med. 2016, 4, 30. [Google Scholar] [CrossRef]
- Bartlett, J.W.; Seaman, S.R.; White, I.R.; Carpenter, J.R. Multiple Imputation of Covariates by Fully Conditional Specification: Accommodating the Substantive Model. Stat. Methods Med. Res. 2015, 24, 462–487. [Google Scholar] [CrossRef]
- Van Buuren, S.; Groothuis-Oudshoorn, K. Mice: Multivariate Imputation by Chained Equations in R. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar] [CrossRef]
- Burgette, L.F.; Reiter, J.P. Multiple Imputation for Missing Data via Sequential Regression Trees. Am. J. Epidemiol. 2010, 172, 1070–1076. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Taylor & Francis: New York, NY, USA, 2017; ISBN 9781315139470. [Google Scholar]
- Yang, S.; Kim, J.K. Predictive Mean Matching Imputation in Survey Sampling. arXiv 2018, arXiv:1703.10256. [Google Scholar]
- Seyyed Nezhad Golkhatmi, N.; Farzandi, M. Enhancing Rainfall Data Consistency and Completeness: A Spatiotemporal Quality Control Approach and Missing Data Reconstruction Using MICE on Large Precipitation Datasets. Water Resour. Manag. 2024, 38, 815–833. [Google Scholar] [CrossRef]
- Kim, H.-R.; Soh, H.Y.; Kwak, M.-T.; Han, S.-H. Machine Learning and Multiple Imputation Approach to Predict Chlorophyll-a Concentration in the Coastal Zone of Korea. Water 2022, 14, 1862. [Google Scholar] [CrossRef]
- Jadhav, A.; Pramod, D.; Ramanathan, K. Comparison of Performance of Data Imputation Methods for Numeric Dataset. Appl. Artif. Intell. 2019, 33, 913–933. [Google Scholar] [CrossRef]
- Loh, W.S.; Ling, L.; Chin, R.J.; Lai, S.H.; Loo, K.K.; Seah, C.S. A Comparative Analysis of Missing Data Imputation Techniques on Sedimentation Data. Ain Shams Eng. J. 2024, 15, 102717. [Google Scholar] [CrossRef]
- Todini, E. Looped Water Distribution Networks Design Using a Resilience Index Based Heuristic Approach. Urban Water 2000, 2, 115–122. [Google Scholar] [CrossRef]
- Ding, Y.; Street, W.N.; Tong, L.; Wang, S. An Ensemble Method for Data Imputation. In Proceedings of the 2019 IEEE International Conference on Healthcare Informatics (ICHI), Xi’an, China, 10–13 June 2019; pp. 1–3. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).