Interaction between Development Intensity: An Evaluation of Alternative Spatial Weight Matrices
Abstract
1. Introduction
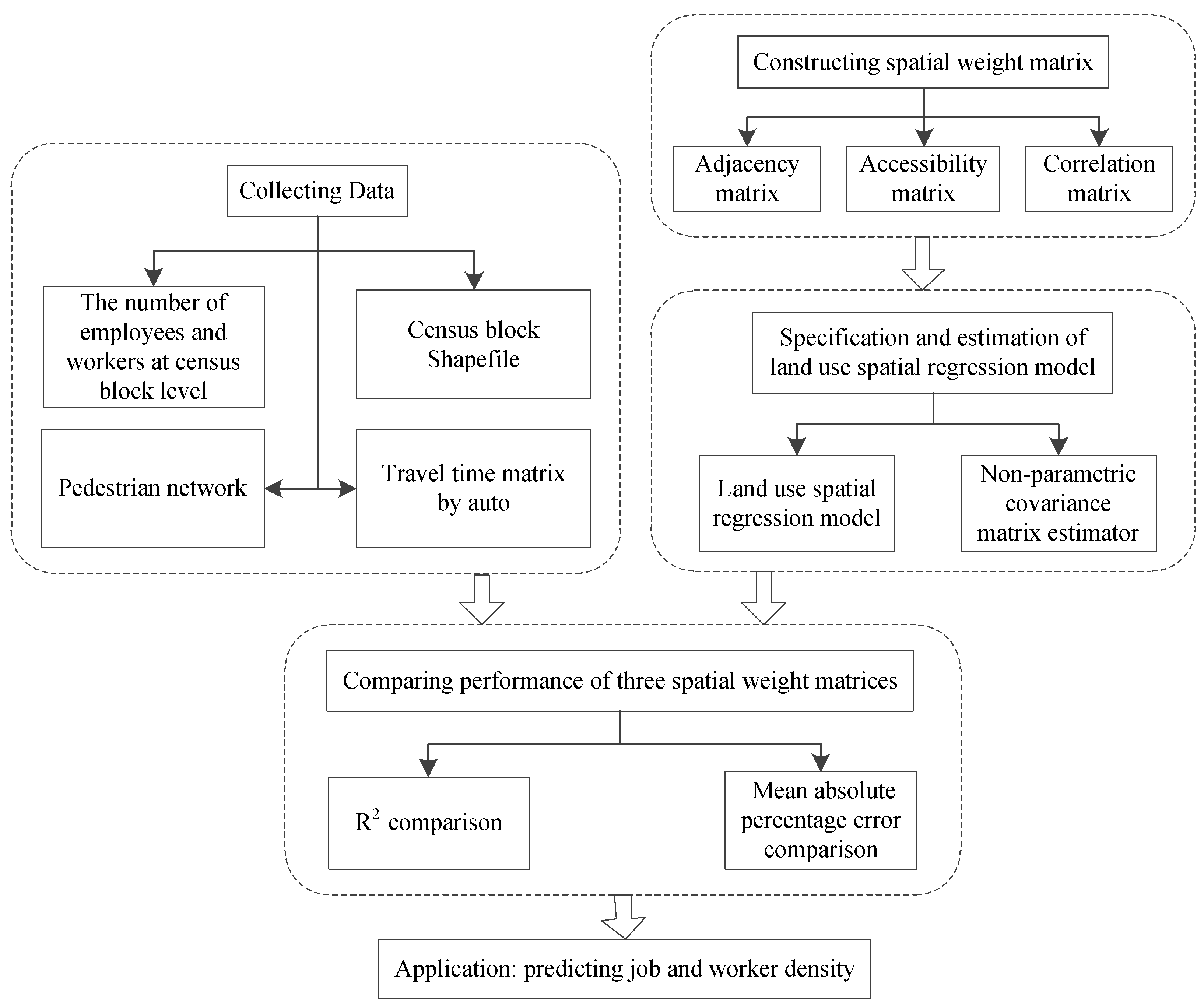
2. Spatial Weight Matrix
2.1. Adjacency Matrix
2.2. Accessibility Matrix
2.3. Correlation Matrix
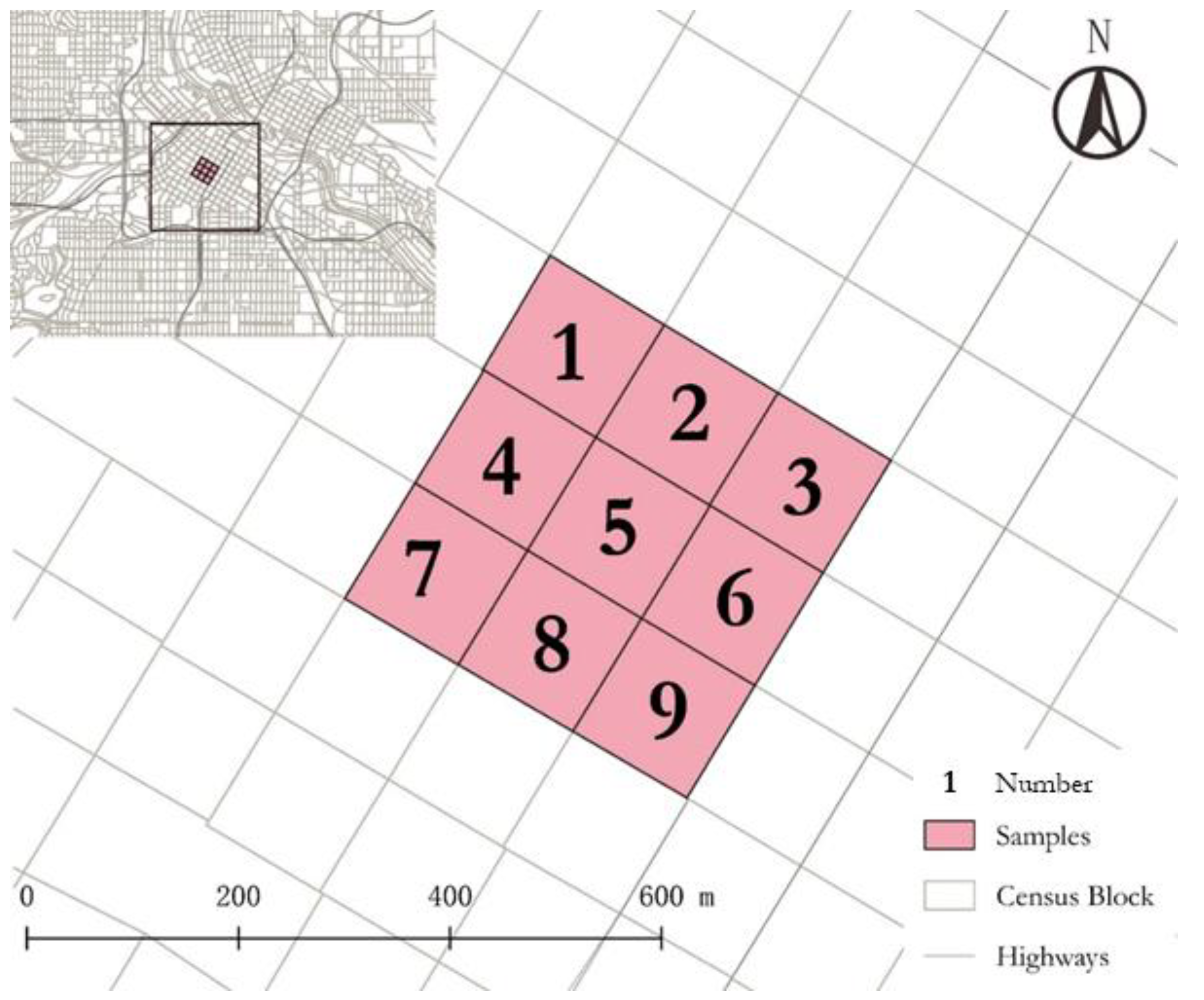
2.4. An Illustration of Three Spatial Weight Matrices
3. Model Specification and Statistical Technique
3.1. Model Specification
3.2. Statistical Technique
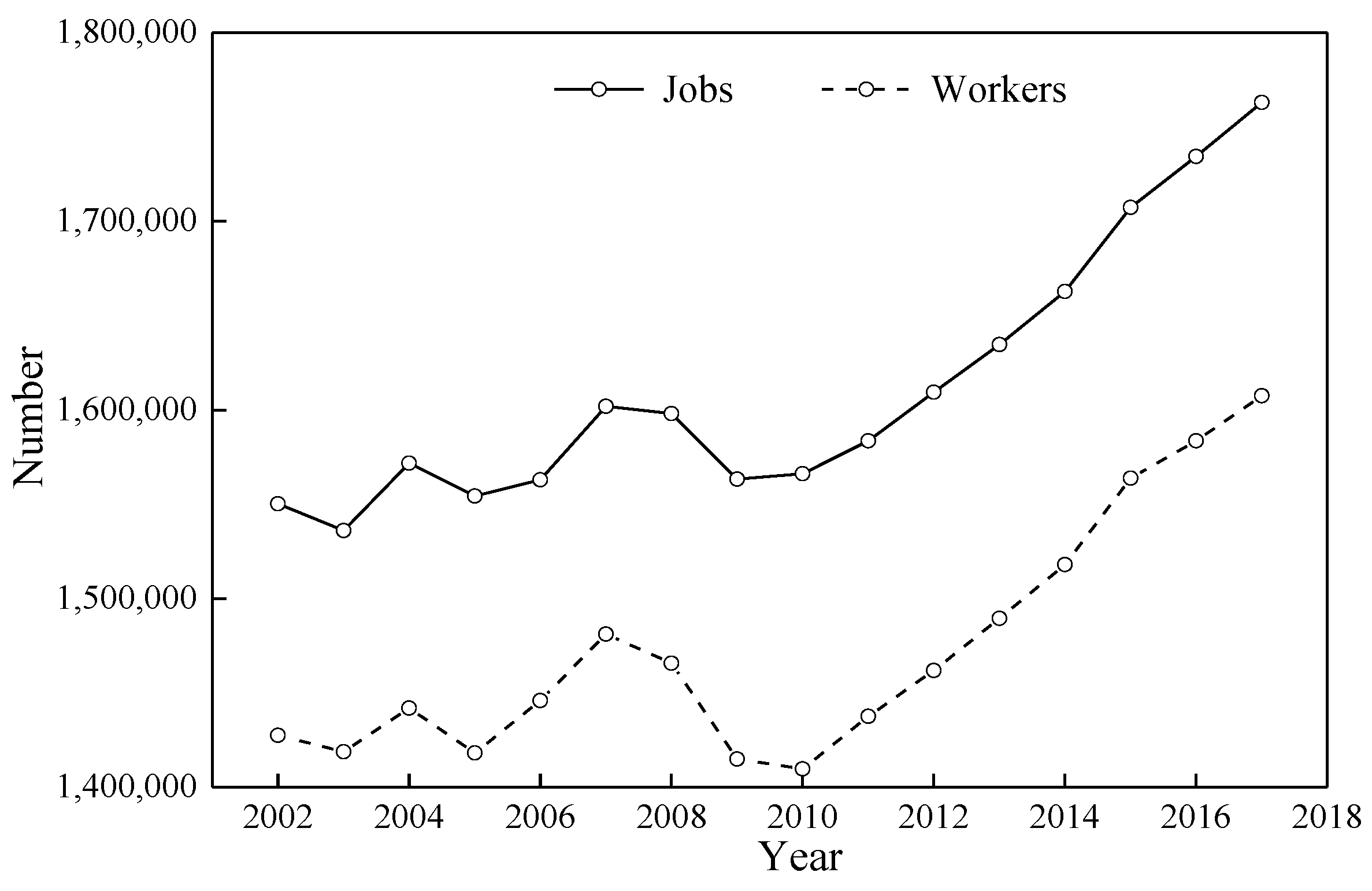
4. Data
5. Results
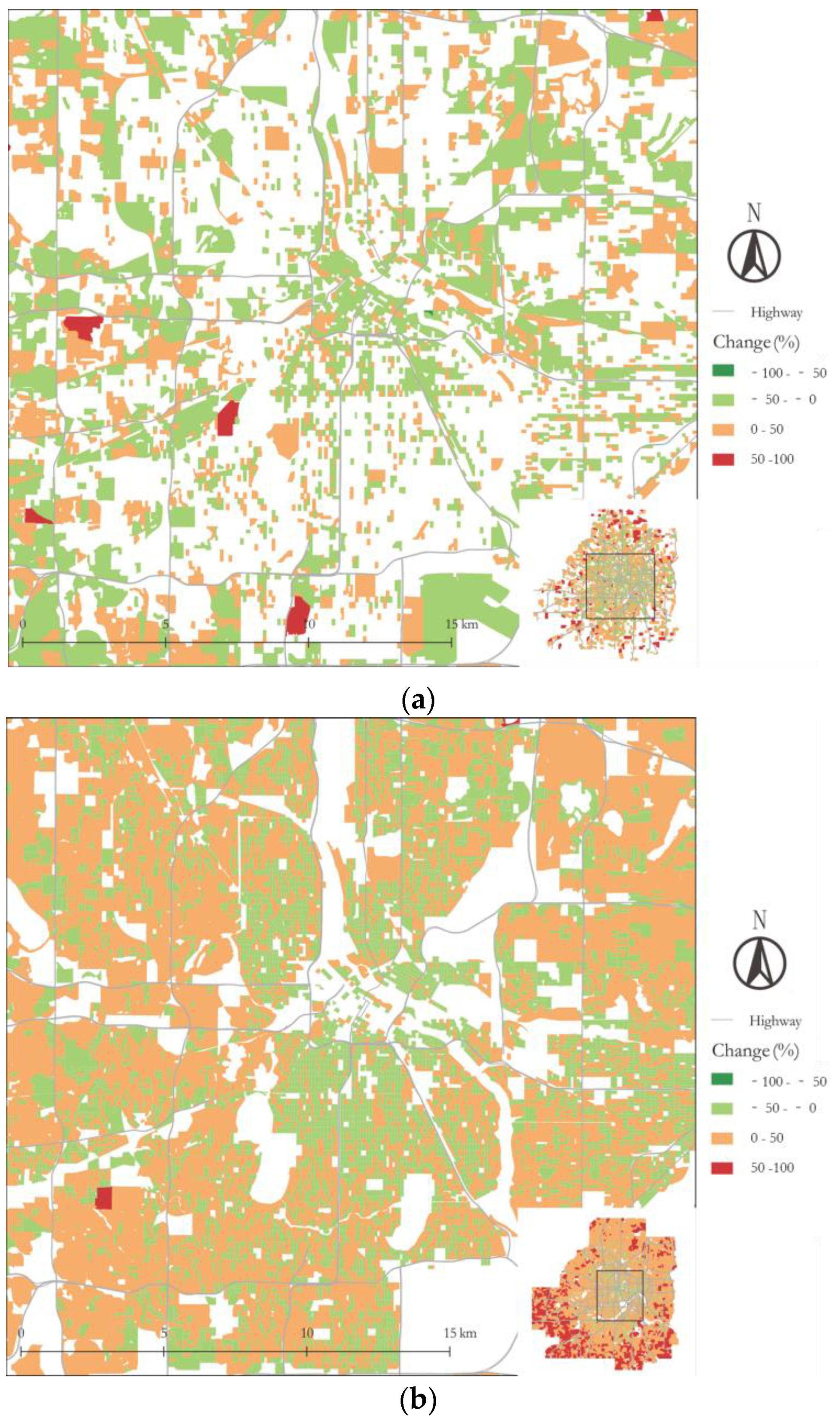
6. Application
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Torrens, P.M. Simulating sprawl. Ann. Assoc. Am. Geogr. 2006, 96, 248–275. [Google Scholar]
- Fujita, M.; Krugman, P.; Mori, T. On the evolution of hierarchical urban systems. Eur. Econ. Rev. 1999, 43, 209–251. [Google Scholar] [CrossRef]
- Yeh, A.G.-O.; Li, X. A Cellular Automata Model to Simulate Development Density for Urban Planning. Environ. Plan. B Plan. Des. 2002, 29, 431–450. [Google Scholar] [CrossRef]
- Feng, Y.; Tong, X. Calibration of cellular automata models using differential evolution to simulate present and future land use. Trans. GIS 2018, 22, 582–601. [Google Scholar] [CrossRef]
- Broitman, D.; Koomen, E. Residential density change: Densification and urban expansion. Comput. Environ. Urban Syst. 2015, 54, 32–46. [Google Scholar] [CrossRef]
- Wang, X.; Kockelman, K.M.; Lemp, J.D. The dynamic spatial multinomial probit model: Analysis of land use change using parcel-level data. J. Transp. Geogr. 2012, 24, 77–88. [Google Scholar] [CrossRef]
- Shen, Y.; Silva, J.D.A.E.; Martínez, L.M. Assessing high-speed rail’s impacts on land cover change in large urban areas based on spatial mixed logit methods: A case study of Madrid Atocha railway station from 1990 to 2006. J. Transp. Geogr. 2014, 41, 184–196. [Google Scholar]
- Zheng, Q.; He, S.; Huang, L.; Zheng, X.; Pan, Y.; Shahtahmassebi, A.R.; Shen, Z.; Yu, Z.; Wang, K. Assessing the Impacts of Chinese Sustainable Ground Transportation on the Dynamics of Urban Growth: A Case Study of the Hangzhou Bay Bridge. Sustainability 2016, 8, 666. [Google Scholar] [CrossRef]
- Wrenn, D.H.; Sam, A.G. Geographically and temporally weighted likelihood regression: Exploring the spatiotemporal determinants of land use change. Reg. Sci. Urban Econ. 2014, 44, 60–74. [Google Scholar] [CrossRef]
- Lambin, E.F.; Geist, H.J.; Lepers, E.; Meyer, W.B.; Turner, I.B.L.; Meyfroidt, P.; Alix-Garcia, J.; Wolff, H.; Bentley, J.W.; Innes, R.; et al. Dynamics of Land-Use and Land-Cover Change in Tropical Regions. Annu. Rev. Environ. Resour. 2003, 28, 205–241. [Google Scholar] [CrossRef]
- Verburg, P.H.; Schot, P.P.; Dijst, M.J.; Veldkamp, A. Land use change modelling: Current practice and research priorities. GeoJournal 2004, 61, 309–324. [Google Scholar] [CrossRef]
- Zhou, B.; Kockelman, K.M. Neighborhood impacts on land use change: A multi-nomial logit model of spatial relationships. Ann. Reg. Sci. 2008, 42, 321–340. [Google Scholar] [CrossRef]
- Waddell, P.; Borning, A.; Noth, M.; Freier, N.; Becke, M.; Ulfarsson, G. Micro-simulation of urban development and loca-tion choices: Design and implementation of urbanism. Netw. Spat. Econ. 2003, 3, 43–67. [Google Scholar] [CrossRef]
- Batty, M. Cities and Complexity: Understanding Cities with Cellular Automata, Agent-Based Models and Fratals; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Verburg, P.H.; van Eck, J.R.R.; de Nijs, T.C.M.; Dijst, M.J.; Schot, P. Determinants of Land-Use Change Patterns in the Netherlands. Environ. Plan. B Plan. Des. 2004, 31, 125–150. [Google Scholar] [CrossRef]
- de Nijs, T.; Pebesma, E. Estimating the Influence of the Neighbourhood in the Development of Residential Areas in the Netherlands. Environ. Plan. B Plan. Des. 2010, 37, 21–41. [Google Scholar] [CrossRef]
- Levinson, D. Density and dispersion: The co-development of land use and rail in London. J. Econ. Geogr. 2007, 8, 55–77. [Google Scholar] [CrossRef]
- Conway, T.M. Current and Future Patterns of Land-Use Change in the Coastal Zone of New Jersey. Environ. Plan. B Plan. Des. 2005, 32, 877–893. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Jensen-Butler, C. Estimation of the spatial weights matrix under structural constraints. Reg. Sci. Urban Econ. 2013, 43, 617–634. [Google Scholar] [CrossRef]
- Chung, S.; Hewings, G. Competitive and Complementary Relationship between Regional Economies: A Study of the Great Lake States. Spat. Econ. Anal. 2015, 10, 205–229. [Google Scholar] [CrossRef]
- Ermagun, A.; Levinson, D.M. Development and application of the network weight matrix to predict traffic flow for congested and uncongested conditions. Environ. Plan. B Urban Anal. City Sci. 2018, 46, 1684–1705. [Google Scholar] [CrossRef]
- Getis, A.; Aldstadt, J. Constructing the spatial weight matrix using a local statistic. Geogr. Anal. 2004, 36, 90–104. [Google Scholar] [CrossRef]
- Feld, L.P.; Köhler, E.A.; Wolfinger, J. Modeling fiscal sustainability in dynamic macro-panels with heterogeneous effects: Evidence from German federal states. Int. Tax Public Financ. 2019, 27, 215–239. [Google Scholar] [CrossRef]
- Asumadu, S.S.; Vladimir, S. Effect of foreign direct investments, economic development and energy consumption on greenhouse gas emissions in developing countries. Sci. Total Environ. 2019, 646, 862–871. [Google Scholar]
- Iacono, M.; Levinson, D.; El-Geneidy, A. Models of Transportation and Land Use Change: A Guide to the Territory. J. Plan. Lit. 2008, 22, 323–340. [Google Scholar] [CrossRef]
- Anselin, L. Spatial econometrics: Methods and models. J. Am. Stat. Assoc. 1988, 85, 905–907. [Google Scholar]
- Alijani, Z.; Hosseinali, F.; Biswas, A. Spatio-temporal evolution of agricultural land use change drivers: A case study from Chalous region, Iran. J. Environ. Manag. 2020, 262, 110326. [Google Scholar] [CrossRef]
- Wyman, M.S.; Stein, T.V. Modeling social and land-use/land-cover change data to assess drivers of smallholder defor-estation in Belize. Appl. Geogr. 2010, 30, 329–342. [Google Scholar] [CrossRef]
- Iacono, M.; Levinson, D. Predicting land use change: How much does transportation matter. Transp. Res. Rec. 2009, 2119, 130–136. [Google Scholar] [CrossRef]
- Cui, M.; Levinson, D. Accessibility and the Ring of Unreliability. Transp. A Transp. Sci. 2016, 14, 4–21. [Google Scholar] [CrossRef]
- Vickerman, R.W. Accessibility, Attraction, and Potential: A Review of Some Concepts and Their Use in Determining Mobility. Environ. Plan. A Econ. Space 1974, 6, 675–691. [Google Scholar] [CrossRef]
- Wachs, M.; Kumagai, T. Physical accessibility as a social indicator. Socio-Econ. Plan. Sci. 1973, 7, 437–456. [Google Scholar] [CrossRef]
- Abdi, H. The kendall rank correlation coefficient. In The Concise Encyclopedia of Measurement and Statistics; Springer: New York, NY, USA, 2008. [Google Scholar]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Aldstadt, J.; Getis, A. Using AMOEBA to Create a Spatial Weights Matrix and Identify Spatial Clusters. Geogr. Anal. 2006, 38, 327–343. [Google Scholar] [CrossRef]
- Jönsson, K. Cross-sectional and serial correlation in a small-sample homogeneous panel data unit root test. Appl. Econ. Lett. 2005, 12, 899–905. [Google Scholar] [CrossRef]
- Hoechle, D. Robust Standard Errors for Panel Regressions with Cross-Sectional Dependence. Stata J. Promot. Commun. Stat. Stata 2007, 7, 281–312. [Google Scholar] [CrossRef]
- Driscoll, J.C.; Kraay, A.C. Consistent Covariance Matrix Estimation with Spatially Dependent Panel Data. Rev. Econ. Stat. 1998, 80, 549–560. [Google Scholar] [CrossRef]
- Longitudinal Employer-Household Dynamics. Available online: https://lehd.ces.census.gov/data/#lodes.html (accessed on 19 September 2017).
- Census 2010 Geography—Blocks, Block Groups, Tracts, Tazs, Counties, County Subdivisions and Water. Available online: https://gisdata.mn.gov/dataset/us-mn-state-metc-society-census2010tiger (accessed on 8 September 2011).
- Geofabrik. Minnesota, 2012. Available online: http://download.geofabrik.de/north-america/us/minnesota.html (accessed on 18 July 2019).
- Murphy, B.; Levinson, D.; Owen, A. Accessibility and Centrality Based Estimation of Urban Pedestrian Activity. Working Papers: 2015, Minneapolis, USA. Available online: https://hdl.handle.net/11299/179834 (accessed on 18 July 2019).
- Accessibility Measures to Population, Employment and Labour by Auto and Transit for the Period of 1995, 2000, 2005, 2010 for the Twin Cities Region. Available online: https://conservancy.umn.edu/handle/11299/200792 (accessed on 9 November 2018).
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Storper, M. Why do regions develop and change? The challenge for geography and economics. J. Econ. Geogr. 2010, 11, 333–346. [Google Scholar] [CrossRef]
- Ermagun, A.; Levinson, D. An Introduction to the Network Weight Matrix. Geogr. Anal. 2017, 50, 76–96. [Google Scholar] [CrossRef]
| Variables | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 4 | |||||||||
| Coef. | Drisc/Kraay Std. Err. | Sig. | Coef. | Drisc/Kraay Std. Err. | Sig. | Coef. | Drisc/Kraay Std. Err. | Sig. | Coef. | Drisc/Kraay Std. Err. | Sig. | |
| 9.12 × 10−01 | 2.61 × 10−03 | *** | 9.12 × 10−01 | 2.32 × 10−03 | *** | 9.11 × 10−01 | 2.81 × 10−03 | *** | 9.42 × 10−01 | 1.13 × 10−02 | *** | |
| 3.68 × 10−03 | 5.46 × 10−03 | |||||||||||
| 1.32 × 10−03 | 1.22 × 10−02 | |||||||||||
| 3.22 × 10−03 | 4.59 × 10−04 | ** | ||||||||||
| −1.00 × 10−03 | 8.26 × 10−04 | |||||||||||
| 4.08 × 10−04 | 1.29 × 10−05 | *** | ||||||||||
| 2.98 × 10−05 | 2.88 × 10−05 | |||||||||||
| Const. | 9.12 × 10−01 | 2.61 × 10−03 | *** | 9.12 × 10−01 | 2.32 × 10−03 | *** | 9.11 × 10−01 | 2.81 × 10−03 | *** | 9.42 × 10−01 | 1.13 × 10−02 | *** |
| Obs. | 49,260 | 49,260 | 49,260 | 49,260 | ||||||||
| Group | 8210 | 8210 | 8210 | 8210 | ||||||||
| Prob > F | 0.000 | 0.000 | 0.000 | 0.000 | ||||||||
| R2 | 0.7943 | 0.7943 | 0.7944 | 0.8969 | ||||||||
| Variables | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model 5 | Model 6 | Model 7 | Model 8 | |||||||||
| Coef. | Drisc/Kraay Std. Err. | Sig. | Coef. | Drisc/Kraay Std. Err. | Sig. | Coef. | Drisc/Kraay Std. Err. | Sig. | Coef. | Drisc/Kraay Std. Err. | Sig. | |
| 8.94 × 10−01 | 1.54 × 10−02 | *** | 8.93 × 10−01 | 1.67 × 10−02 | *** | 8.84 × 10−01 | 1.33 × 10−02 | *** | 9.36 × 10−01 | 8.70 × 10−03 | *** | |
| 9.75 × 10−03 | 3.68 × 10−03 | * | ||||||||||
| −2.82 × 10−02 | 4.33 × 10−03 | ** | ||||||||||
| 2.18 × 10−03 | 3.60 × 10−04 | ** | ||||||||||
| −3.86 × 10−03 | 1.64 × 10−04 | *** | ||||||||||
| 2.80 × 10−04 | 1.97 × 10−05 | *** | ||||||||||
| 1.26 × 10−05 | 3.86 × 10−05 | |||||||||||
| Const. | −8.36 × 10−01 | 1.52 × 10−01 | ** | −8.53 × 10−01 | 1.59 × 10−01 | ** | −9.46 × 10−01 | 1.26 × 10−01 | ** | −4.45 × 10−01 | 8.08 × 10−02 | ** |
| Obs. | 49,260 | 202,230 | 202,230 | 202,230 | ||||||||
| Group | 8210 | 33,705 | 33,705 | 33,705 | ||||||||
| Prob > F | 0.000 | 0.000 | 0.000 | 0.000 | ||||||||
| R2 | 0.8035 | 0.8045 | 0.8058 | 0.9027 | ||||||||
| Variables | ||||||
| 25 Percentile | 50 Percentile | 75 Percentile | ||||
| −9.730 | −7.764 | −6.453 | ||||
| Value | Elasticity | Value | Elasticity | Value | Elasticity | |
| 2.631 | 0.003 | −0.087 | 2.796 | 0.003 | −0.116 | |
| −1274.180 | 0.000 | 5.344 | −1752.130 | 0.000 | 9.210 | |
| Variables | ||||||
| 25 Percentile | 50 Percentile | 75 Percentile | ||||
| −8.113 | −7.437 | −6.974 | ||||
| Value | Elasticity | Value | Elasticity | Value | Elasticity | |
| 0.061 | 0.010 | −0.007 | −0.182 | 0.010 | 0.024 | |
| −0.132 | −0.028 | −0.046 | −0.389 | −0.028 | −0.147 | |
| −0.058 | 0.002 | 0.002 | 3.309 | 0.002 | −0.097 | |
| −1.091 | −0.004 | −0.052 | −0.055 | −0.004 | −0.003 | |
| −826.985 | 0.000 | 2.856 | −5.490 | 0.000 | 0.021 | |
| Spatial Matrices | Job Density | Worker Density | ||||
|---|---|---|---|---|---|---|
| MAPE | Variance | Friedman Test | MAPE | Variance | Friedman Test | |
| Adjacency | 8.10 | 190.48 | 0.000 | 4.27 | 15.22 | 0.000 |
| Accessibility | 8.09 | 190.82 | 4.16 | 15.00 | ||
| Correlation | 6.46 | 127.79 | 4.06 | 12.19 | ||
| Change (%) | −100–−50 | −50–0 | 0–50 | 50–100 | |
|---|---|---|---|---|---|
| Density | |||||
| Job | 0.000 | 0.563 | 0.422 | 0.015 | |
| Worker | 0.000 | 0.312 | 0.671 | 0.017 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Cui, M.; Levinson, D. Interaction between Development Intensity: An Evaluation of Alternative Spatial Weight Matrices. Urban Sci. 2023, 7, 22. https://doi.org/10.3390/urbansci7010022
Li M, Cui M, Levinson D. Interaction between Development Intensity: An Evaluation of Alternative Spatial Weight Matrices. Urban Science. 2023; 7(1):22. https://doi.org/10.3390/urbansci7010022
Chicago/Turabian StyleLi, Manman, Mengying Cui, and David Levinson. 2023. "Interaction between Development Intensity: An Evaluation of Alternative Spatial Weight Matrices" Urban Science 7, no. 1: 22. https://doi.org/10.3390/urbansci7010022
APA StyleLi, M., Cui, M., & Levinson, D. (2023). Interaction between Development Intensity: An Evaluation of Alternative Spatial Weight Matrices. Urban Science, 7(1), 22. https://doi.org/10.3390/urbansci7010022







