1. Introduction
Humankind is involved in a civilizational crisis derived from human activity and an economic model that has been dominant up to now. The environmental degradation of natural resources and ecosystems coupled with climate change have the potential to destabilize entire regions. In this context, the rapid shifting to a sustainable development model is crucial in order to mitigate the potential crisis derived from the current human relationship with natural resources. Within the key changes in the parading of sustainable development, the change and improvement of critical infrastructure such as energy and transport are key elements in this transition. In the case of transport, there are multiples approaches with which to shift to a sustainable mobility system (understanding a sustainable mobility system as a one which minimizes the environmental impact, its energy demand, and that is competitive and economically viable). Some of these approaches include: Supporting infrastructure for non-motorized trips; land use plans which increase city density and improve the variety of land uses (15-min city); Increasing the competitiveness of public transport; Car management, to reduce its attractiveness (reducing parking spaces, zone restrictions, fuel prices, taxes, etc.); Acceleration of the electrification of the transport sector, and the migrating to a sharing economy paradigm of the transport sector.
Transit planning involves the integration of several fields of analysis, such as mobility dynamics, land use, and transit systems, to mention a few. In the case of the transit system, key conventional elements must be integrated into the analysis, such as the operation cost, emissions, energy demand, and general structure proprieties such as headway, the distance between stops, spatial coverage, the capacity of the lines, etc. [
1,
2].
However, there are some other key elements to analyze that help notoriously with the decision-making process and the evaluation of the performance of a transport network that is related to the physical and structural efficiency of the transport system. To measure these physical and structural features, transport planners have resorted to network sciences and the measure of network properties derived from this field. Network proprieties are rarely taken into consideration in transport planning, despite the remarkable information that can be generate related to the performance of a transport network [
3].
Network science is an academic field that uses discrete mathematics in order to understand the structural proprieties of a network. To do this, there is a necessity to have a network representation of the phenomena of study. This representation materializes in nodes and links that represent the dynamics and relations of a specific phenomenon [
4]. Network science has become popular, especially since the 1990s, due to the improvement in computational power and the development of Geographical Information Systems (GIS) [
5]. However, the difficulties in creating large datasets of networks have historically been a challenge in the field.
Nevertheless, the integration of complex transport networks is very recent [
6]. In overall terms, these approaches have had a strong emphasis on routing optimization and transport costs [
7]. To evaluate the proprieties of the transport system, a network representation must be done, this representation changes over time and over the kind of transport network subject to analysis. This characterization is generally a static representation; this allows the analysis of the structural or topological features of the transport system [
8].
In the case of a transit system, most of the studies focus on a static approach, which tries to highlight the general features of the network in terms of topology, geometry, morphology, and traffic flows [
6]. In terms of representation, transport networks can be represented as nodes and links where the nodes are the stops of the transport system and the links are the paths among each stop. This conception is the base of the representation of the transit system’s configuration into a network, and is the baseline in order to analysis its structural features.
Figure 1 shows this concept.
Within this field of network science applied to transport networks, there are many network proprieties that can be measured in a transit system, such as the Diameter, Detour index, Network density, Pi index, Eta index, Theta index, Beta index, Alpha index, Gamma index, Koening number, Shimbel index, and Hub dependence, among others [
9]. However, this paper measures three network properties, which are the Shimbel index, Detour index, and Hub dependence.
The Shimbel index is bond to the grade of accessibility which measures the structural efficiency in terms of travel time through the network [
9]. On the other hand, the Detour index represents the spatial efficiency of the network, comparing the travel distance and the Euclidean distance among the origin and destination. Finally, the Hub dependence is a set of structural indicators bond with the resilience and vulnerability of the network [
9]. The importance of measuring the network properties of a transit system relies on the premise that every main aspect of the performance of the transit system is bonded with its structure. Aspects such as operational cost, pollution, energy demand, and travel time, among others, are linked with the technology and structure of the transit network. This relation can be visualized in
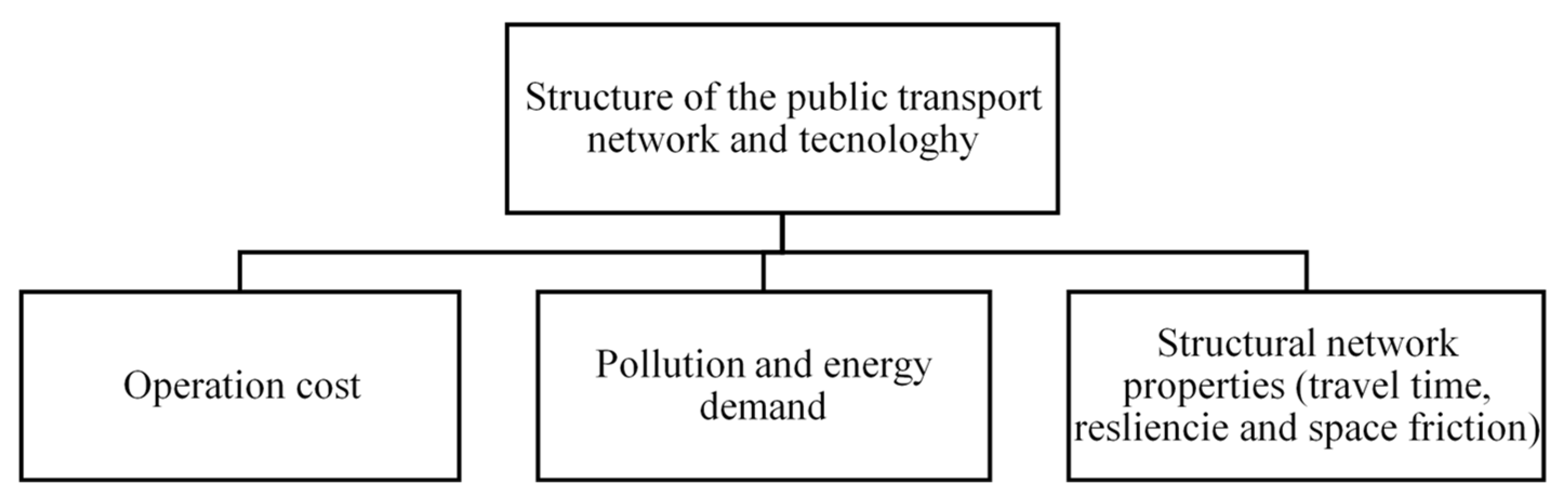
Figure 2 that represents the relationship that the structure and technology of the transit system have with other main aspects, such as operation cost, pollution, energy demand, and structural proprieties. As can be seen, the structure and technology of the network are the main aspects that influence the performance of the rest of the relevant aspects of the transit system. If the transit system has efficient structure and technology, the operation cost is going to reduce, as well as the environmental impact and the energy demand. This influences network properties such as travel time, resiliency, and space friction. For this reason, transport planners must integrate the process of planning the network proprieties of the transit.
In this sense, the objective of this paper is to analysis some of the main structural features that should be taken into consideration in the planning process of a transits system and to generate a framework and a digital tool with which to carry out this analysis (accessibility, spatial friction, and vulnerability). This structural evaluation was taken into consideration as an alternative transit network proposed for Guadalajara, Mexico [
10]. The network representation of this alternative transit system was made mainly using the general transit feed specification (GTFS). The GTFS is an accurate network representation, as it integrates the location of stops, the bond between stops in a route, and the travel time of the buses along each route [
11]. To use and exploit the GTFS properly, a set of software tools were used. These tools mainly included the open route engine tool Open Trip Planner (OTP) and R as a programming platform.
Finally, this paper is divided into four sections:
Section 1 gives a little introduction to the applications of network science in transit analysis,
Section 2 addresses the methodology and the materials used, and
Section 3 contains the results and discussion. Finally,
Section 4 concludes of the work.
3. Results
3.1. Shimbel Index and Grade of Accessibility
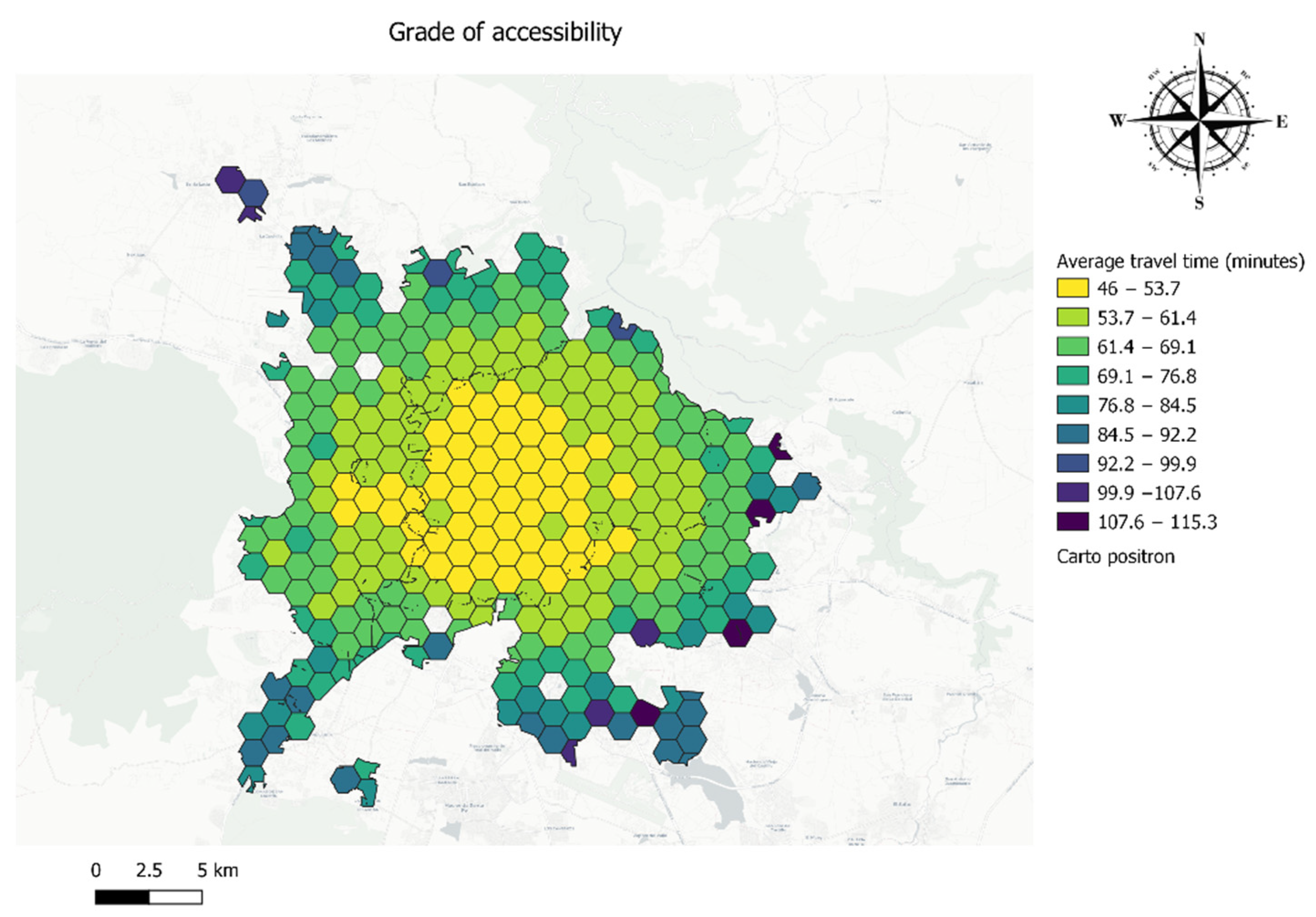
As was mentioned before, the Shimbel index and the grade of accessibility in a network indicates the travel time efficiency that the transit system gives. To have a spatial visualization of this propriety, the
Figure 7 shows the grade of accessibility of each of the node (represented by a hexagon) each node contains a certain value of the average travel time that ranges from 45 min to 115 min.
The average travel time is affected mainly by two factors. The first factor is due to its spatial location (the centroids that are more central have a lower average travel time), and the second factor is the features of the transport network. The features of the transport network, such as the geometry of the lines, the commercial speed, the headway, and the connectivity of the lines, have a significant impact on the efficiency of the reported travel time.
As it can be seen, the average travel time ranges from 46 min in some central areas of the city to 115 min in the periphery of the city.
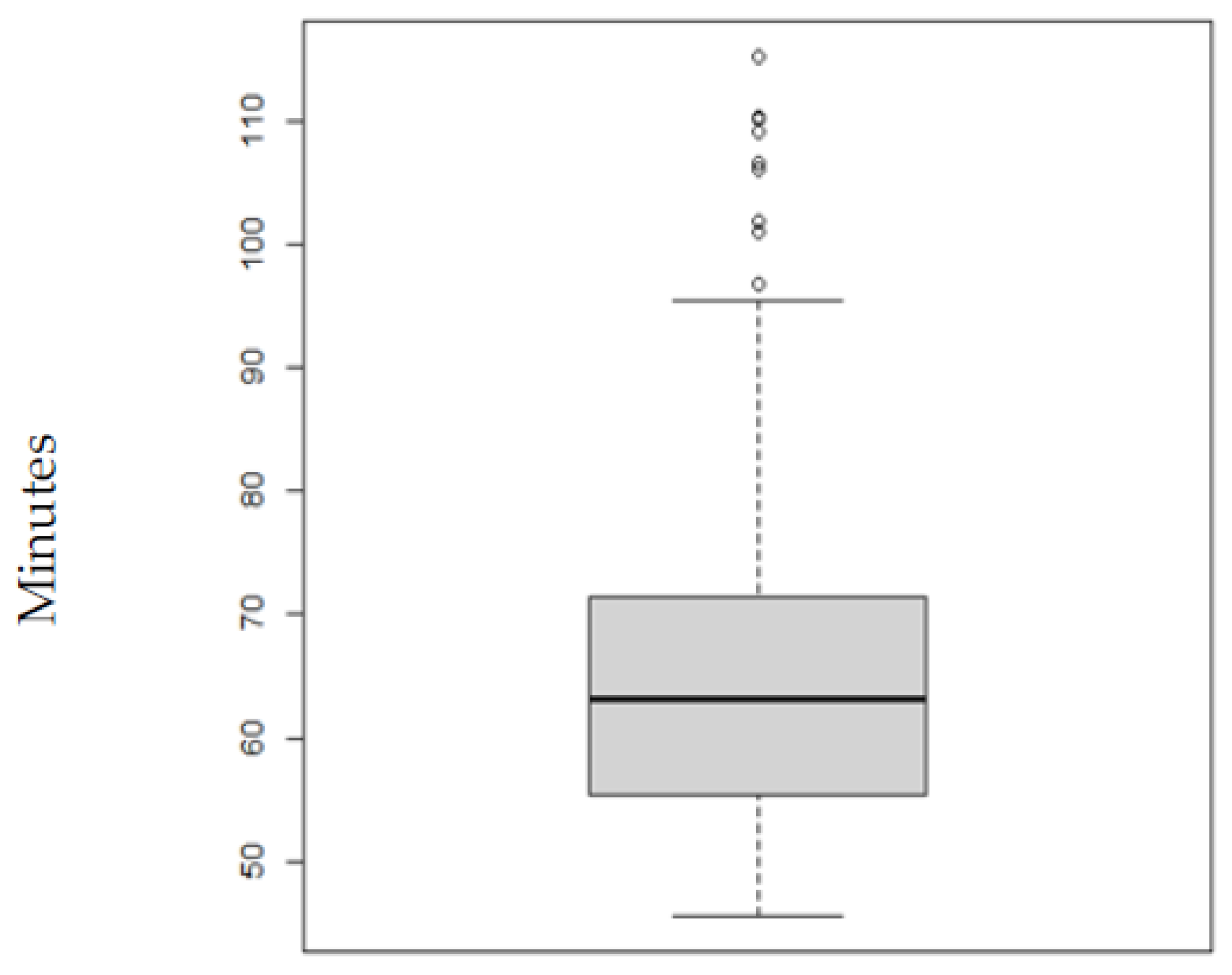
Figure 8 shows a box plot of the total travel time of every OD pair within the service area. 50% of the average travel time of all the centroids ranges from around 55 min to 70 min. Additionally, it can be observed that 75% of the trips have a travel time under 70 min.
Finally,
Table 2 contains the Shimbel index of the hole network, as well as the breakdown of average travel time. In the case of the average travel time, the value is 70 min composed by 52 min in vehicle travel time, 12 min of walking time and 6 min of waiting time. On the other hand, the Shimbel index has a value of 0.015. It is important to mention that, in order to compare the Shimbel index with another network, they have to contain the same number of nodes. If this does not happen, the Shimbel index is not compatible, and therefore able, to compare directly.
3.2. Deuter Index and Distance Friction
In the case of the Deuter index, after the data processing, it was possible to generate a table that contains the distance of every trip using the transit system and the Euclidian distance for every origin and destination.
Figure 9 shows a box plot of the distribution of the travel distance using the transit system and the Euclidian distance. The left side indicates the travel distance distribution on the transit system. As it can be seen, 75% of the trips are under 25 km. On the other hand, the Euclidian travel distance distribution has a travel distance of less than 15 km in the 75% of the trips.
Additionally,
Table 3 shows the final result of the Deuter index, the average travel distance using the transit system, and the average Euclidean distance. In the case of the Deuter index, it has a value of 0.63 (higher values means trips more direct in spatial terms), which was generated by dividing the Euclidian travel distance of 11.91 km and the regular travel distance using the transit system with a value of 18.81 km.
3.3. Hub Dependence and Resilience of the Network
The transformation of the GTFS into a graph object allowed us to measure the set of resilience and vulnerability indicators expressed previously. These indicators are betweenness centrality, central point dominance, and average path length. In the case of the set of indicators proposed for this section, the nodes are represented as a stop or a cluster of stops, and the links remain as the path that follows a route among each stop.
Table 4 shows the results for the set of indicators. As can be observed, there are three measures of betweenness centrality, which are the highest, the average, and the lowest. The highest value reaches 746,551, which is the number of times a specific node was used as a bridge among the optimal path of an OD pair. The average value is of the betweenness centrality, and was 65,824. Meanwhile, the lowest was 0. These is a significant difference between each of the indicators. On the other hand, the average path length in typical conditions is 36.27. Finally, the spectral gap has a value of 0 which is a very low number that indicates a low level of robustness in the network.
Additionally,
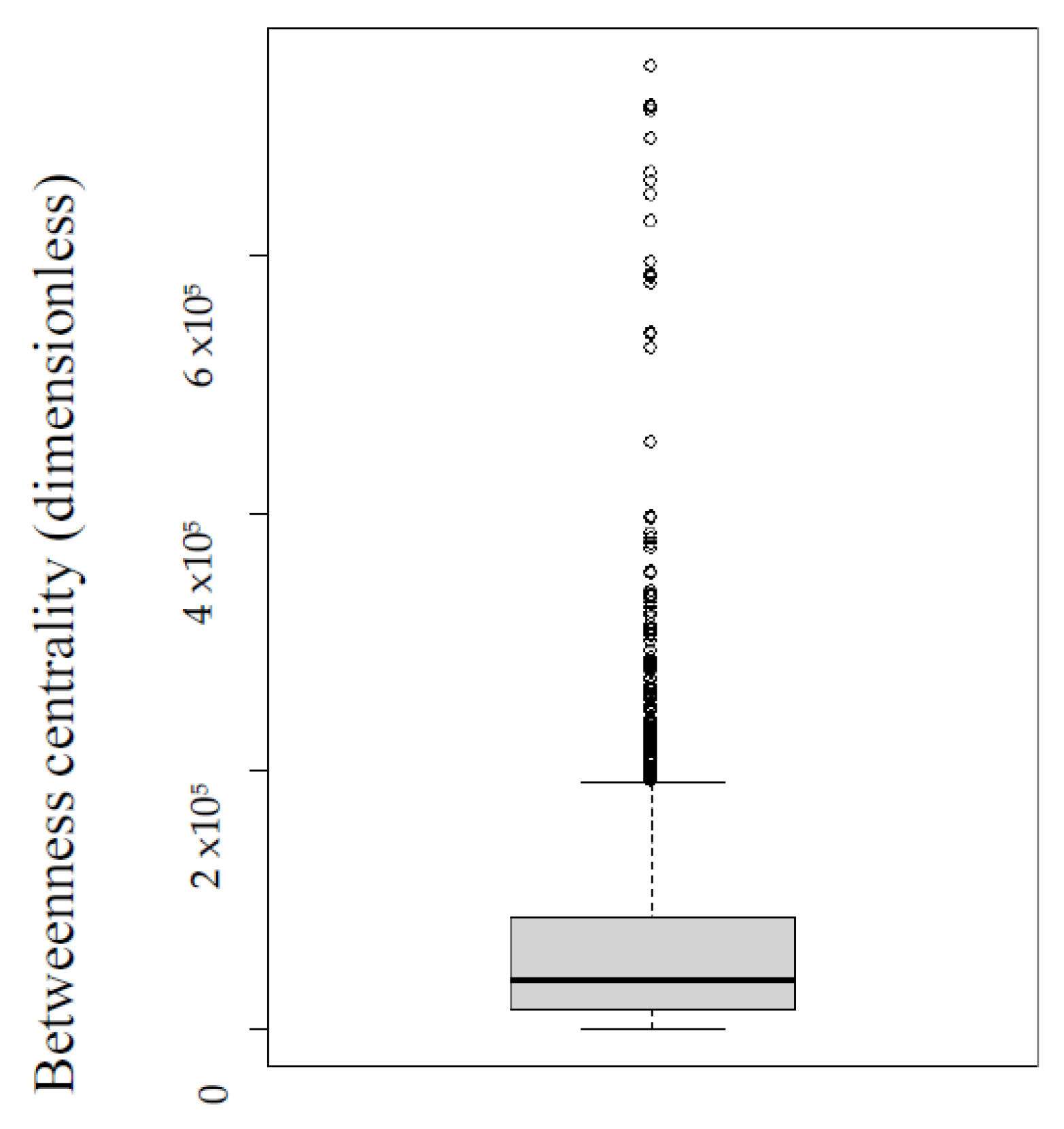
Figure 10 shows the boxplot of the distribution of the value of the betweenness centrality of all the nodes. As can be observed, 75% of the values in the betweenness centrality distribution are under around 75,000 units. The compact shape of the box indicates a highly similar distribution in the values of the betweenness centrality. However, as can be seen, the box plot has long whiskers that represent outliers in the value distribution. This means a much higher centrality in a few nodes compared with the rest of the nodes.
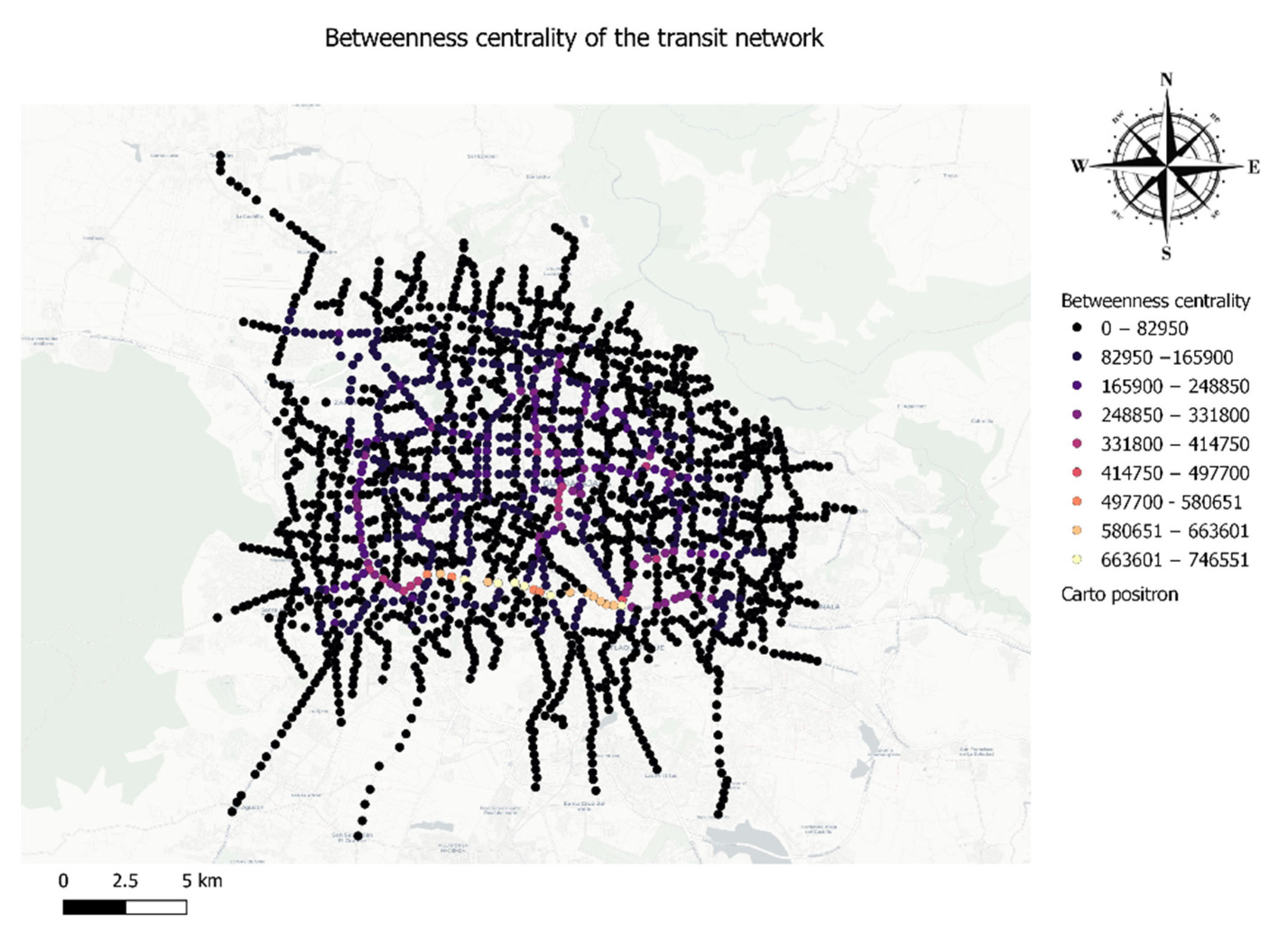
On the other hand, the value of the betweenness centrality can be visualized spatially in
Figure 11. The figure shows some key areas of the network. One of the most interesting is the segments of lines that cross the city horizontally in the south part of the service area. This specific area of the city is used as a bridge in so many trips. Other key areas can be identified in the center of the city and, as indicated by vertical line, in the western area. As a whole, these three areas are used very frequently as a bridge among the optimal trips within the service area.
The spatial visualization of the betweenness centrality allows the identification of key areas that can compromise the performance of the network (any perturbation in this area such as traffic, an accident, etc., can largely compromise the functionality of the transit system). On the other hand, the significant difference in the distribution value showed by the boxplot in
Figure 10 indicates a great polarization of values.
In the case of the average path length, there were several scenarios of measurements. The first scenario of the average path length was performed in typical conditions (that is to say, all the nodes, stops, or areas of the city worked well without affecting the flow of trips among any stop), and has a value of 36.27 stops. On the other hand, different scenarios were done by randomly removing nodes from 0% to 70% of the nodal remotion (every one of these scenarios was measurement within a cycle of 1000 times in order to get the mean magnitude of the average path length in each scenario).
Finally, as was mentioned in
Section 2, another set of scenarios were performed, removing strategic nodes (in this case, the nodes with the highest magnitude of closeness centrality and highest betweenness centrality results are presented in
Figure 12.
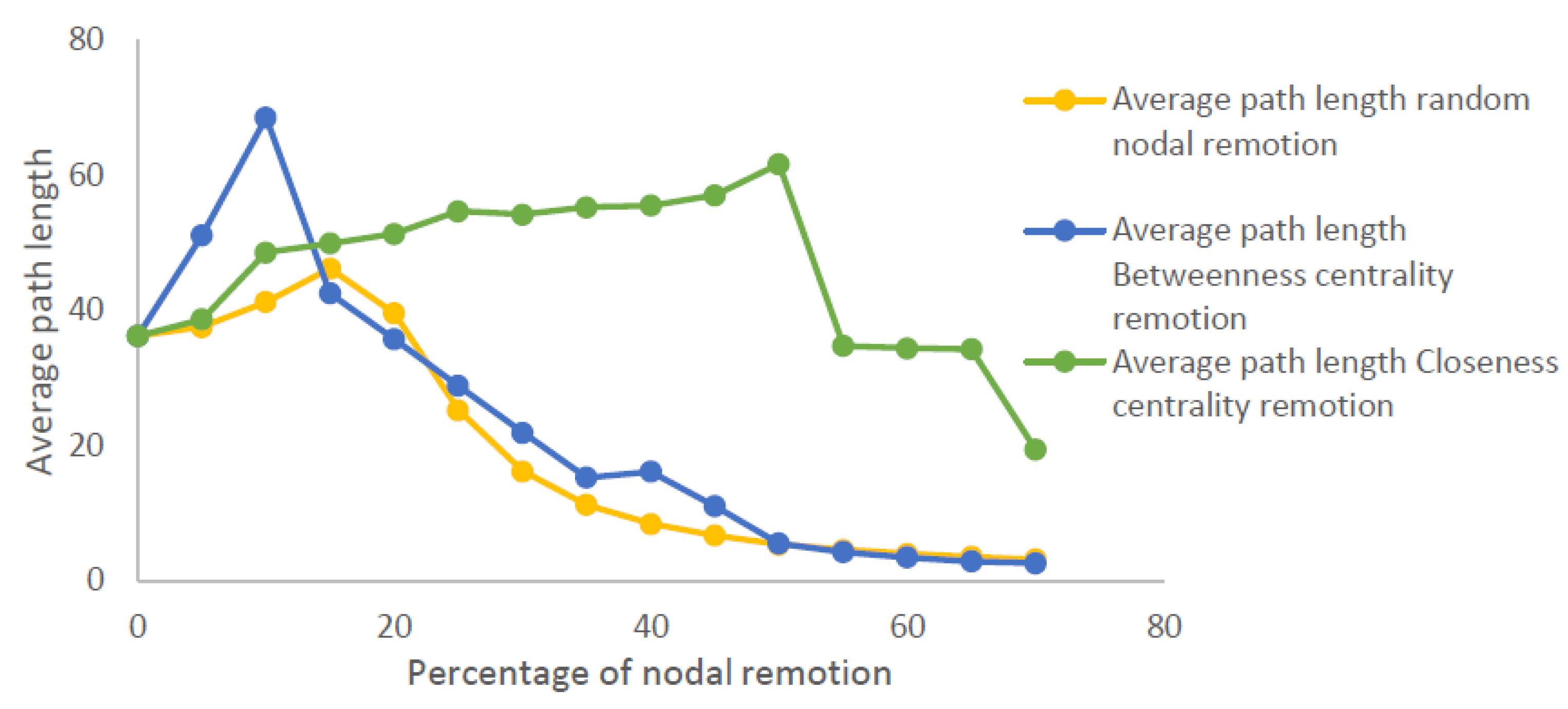
Figure 12 integrates three different scenarios. The first scenario is the average path length (connectivity) under random nodal remotion, the second scenarios is under strategic remotion affecting the nodes with highest values in betweenness centrality and the third scenario is strategic nodal remotion for highest values in closeness centrality.
The data used for built the
Figure 12 can be seen in
Table 5. As it can be observed in
Table 5 the critical point under random remotion happened until the remotion of 15% of the nodes of the network in that point the connectivity passed from an average path length of 36 to 46 which is and affectation of 27%, this can be translated to travel time affectation which passed from an average of 70 to 89 min.
On the other hand, in the scenarios of strategic remotion using the nodes with highest betweenness centrality the critical point was reached at 10% of nodal remotion with a higher affectation passing from an average path length of 36 to 69 which means an affectation of 91%.
Finally, the critical point remotion the closeness centrality nodes was reached until the remotion of 50% of the nodes passing from an average path length of 36 to 62 which means an affectation of 72%. Under these scenarios can be visualized the most import affectation is done under scenarios of betweenness centrality remotion. This data showed the importance of identification the nodes with highest betweenness centrality, due to these nodes are the most used within the shortest trips the affectation in these nodes have remarkable affectation in the connectivity of the network.
In addition to this analysis, as was mentioned in
Section 2, the measurement of the total nodes connected was conducted using the Dijkstra algorithm for the different scenarios.
Figure 13 illustrates the total number of connected nodes. All the scenarios (random remotion, and both strategic remotion) present numbers of total connected nodes very similar. All of them start in 3.48 million of possible connection. In the case of the random remotion, it ends with 877,032 connected nodes. On the other end, the scenario of Betweenness centrality remotion ends with 884,540 nodes and 478,172 for the scenario of Closeness centrality. In general terms there is not a significant different in the total possible connection among all the scenarios. In this sense, the network has a notable difference in the performance of its connectivity under the different scenarios but all of them still are able to connected about the same number of nodes.
As it can be observed in this section, the variety of results of network proprieties indicators give a good overall view of the structural performance of the network in terms of travel time (grade of accessibility), spatial friction (Deuter index), and vulnerability.
4. Conclusions
The methodology presented in this work is a robust framework, able to be applied to any transit network using the code developed for this work. The aspects for measurement proposed (accessibility, spatial friction, and vulnerability) are some of the main relevant aspects that a planner must take into consideration in order to compare the performance of different transit network scenarios within a planning process. In this sense, the work done here is a solid framework and a tool that can be used widely.
The results presented here show a clear panorama of the performance of the structural aspects of the transit system. In the case of accessibility, it showed a better performance in the center of the city. This follows a basic principle of centrality: the areas of the city in the center will have better connectivity to the rest of the area of interested due to its location. However, other variables get into account which are the commercial speed of the buses, the geometry of the lines, the headway and the connectivity among the routes. However, in order to take this as a real indicator for decision-making, a comparison between transit system or modes of transport should take place, in order to see understand the performance among different scenarios or modes of transport and select generate a decision towards the best scenario. In the case of the alternative network examined in this study, the average travel time was 70 min, and it showed a travel time distribution close to a normal distribution. In general terms, this distribution and the magnitude of the travel time are good indicators of the performance of the network in this aspect.
In the case of spatial friction, due to the fact that the alternative network was based on a grid layout, that is to say, a network based on transfers that allows the user go from and to anywhere with one transfer, the spatial friction was low. In this case, the Deuter index was 0.63. Finally, the vulnerability analysis was the most significant. In the case of the vulnerability analysis, it showed a poor performance with a great polarization to some of the nodes (stops) of the network.
This was very visible with the shape of the box plot in
Figure 10 and with the central point dominance that had a value of 680,726 when the mean of the betweenness centrality was 65,824. This polarization paved the way for affectation in the connectivity. The impact in the connectivity was visible in
Table 5. This analysis showed the key relevance that has the nodes with highest betweenness centrality to the connectivity of the network. The remotion in these nodes trigger the most remarkable impacts to the connectivity passing from an average of 70 min to 133 min in the critical point which was at 10% of nodal remotion. As a conclusion from this analysis in order to keep the performance of the transit system transport planners must identify the key nodes of the network and generates policies dedicated to keep the optimal flow of the transit system in those zones. As it was seem in this work little perturbations on these nodes can led to deep impacts in the average travel time for users.
While it is true that the results are solid numbers for the alternative transit network used in this work, it is difficult to make a general judgment about the network’s efficiency due to the fact that there is no other network with which to compare it to, as a consequence of a lack of data (GTFS) related the actual transit network within the service area. This lack of data made it impossible to do these full analyses by comparing two transit networks in the same area of service.
For this reason, it is hard to generate a final judgment of the performance of this alternative network. However, some elements of this work must be highlighted, such as the fact that an open-source tool in R was generated in order to have a solid framework with which to analyze the structural features of transit networks [
21].