Abstract
Over the last two decades, a growing number of works in urban studies have revealed how micro-retail distribution is significantly related to specific properties of the urban built environment. While a wide variety of urban form measures have been investigated using sophisticated analytical approaches, the same attention has not equally been found in statistical procedures. Several essential features of micro-retail statistical distribution and modelling assumptions are frequently overlooked, compromising the statistical robustness of outcomes. In this work we focus on four main aspects: (i) the discrete, non-negative and highly skewed nature of store distribution; (ii) its zero-inflation; (iii) assessment of the contextual effect; and (iv) the multicollinearity generated by the inclusion of highly related urban descriptors. To overcome these limitations, we propose an integrated methodological framework for both modelling and variable selection assessment based on generalized linear models (GLMs) and elastic-net (Enet) penalized regression (PR), respectively. The procedure is tested via a real case study of the French Riviera, which is described using a large dataset of 105 street-based urban form measures. The outcomes of this procedure show the superiority of the zero-inflate negative binomial count regression approach. A restricted number of urban form properties are found to be related to the micro-retail distribution depending on the specific scale and morphological context under analysis.
1. Introduction
Stores represent one of the most important elements of the urban environment. Their presence engenders human interaction, socioeconomic vibrancy, cohesion and sense of place from the street to the neighborhood level, ultimately affecting the attractiveness of a whole city [1,2]. In the last two decades, the increasing availability of micro-store data has stimulated a growing body of research investigating the different location factors underlying store distribution [3]. More particularly, quantitative urban geography and urban form studies have explored the relationship between micro-retail distribution and the physical properties of urban form, also named “the morphological sense of commerce” [4]. The goal underlying these works is to investigate if and how the spatial organizations of urban form elements (streets, building and plots) influence the human perception and usages of urban spaces, and, subsequently, whether this effects the distribution of socio-economic activities such as traditional brick and mortar micro-retailers. These works might provide academics and practitioners with evidence on how urban systems work and nourish discussion about how to improve life quality in urban areas through their design and planning.
Among the forerunners of this specific research stream, we find Hillier’s Movement Economy Theory (MET) [5,6,7]. MET explains how the spatial configuration of public spaces influences movement patterns and, indirectly, the localization of stores. Several protocols and modelling approaches have highlighted the importance of different street-network configurational properties on micro-retail distribution. Micro-retail patterns have proven to be significantly correlated with integration (to-movement) and betweenness (through-movement) centrality measures defined within the Space Syntax-SSx [7] and Multiple Centrality Assessment (MCA) [8,9] methodological frameworks, respectively.
Although there is a general agreement about the importance of street-network properties, one main limitation concerns the absence of other essential features of urban morphology such as building distribution and height, site morphology, built-up density, and so on. Integrating these aspects might provide a more holistic description of urban form and, therefore, of its relationship with micro-retail distribution [10]. Together with configurational approaches, researchers have gradually introduced additional urban form descriptors evaluating both their individual and combined effects on micro-retail distribution, including street-based urban design qualities [11], street-block typologies and built-up density [12,13] and plot systems [14], among others. Moreover, other researchers have started investigating how the importance of each urban form variable might play different roles in micro-retail distribution depending on the relative morphological context defined as, for instance, city size, central/peripheral sectors [15] or underlying planned/spontaneous urban grids [16,17].
While sophisticated approaches have been developed for the identification, conceptualization and description of urban form, the same attention has not been equally found in modelling and statistical analysis. In this work, the implementation of well-established urban form analytical approaches provides us with a large number of street-based descriptors and allows us to focus on the statistical and modelling procedures implemented to describe the relationship between urban form and micro-retail distribution.
The first part of this paper is devoted to a critical review of the methodological procedures developed in previous works; the discussion is organized around four traditionally overlooked aspects:
- (i)
- the discrete, non-negative and highly skewed nature of micro-retail distribution, which is incompatible with the assumptions underlying traditional statistical approaches;
- (ii)
- the store absence, which characterizes urban spaces, is represented by a highly zero-inflated statistical distribution; store absence has both theoretically and methodologically been excluded from analysis;
- (iii)
- the role of contextual descriptors and their inclusion in traditional regression approaches;
- (iv)
- the presence of high multicollinearity when considering a large set of urban descriptors, which has been an issue in several methodological and theoretical approaches.
To overcome these limitations, an integrated methodological framework based on generalized linear models (GLMs) is herein proposed and implemented in order to study the relationship between micro-retail distribution and urban form in the French Riviera metropolitan area.
We begin by showing the superiority of the Zero-Inflated Negative Binomial (ZINB) model when applied to several regressive approaches. Beyond the ability of ZINB regressions to handle both skewness and an over-representation of zeroes, this outcome also supports the hypothesis of a double generative process describing two main aspects of micro-retail distribution in urban environments: presence/absence on one side, and the number/density of stores on the other. Moreover, the implementation of penalized regression (PR) as a built-in solution for variable selection procedures within the GLM framework allows the identification of specific subsets of urban morphological indicators depending on the urban typo-morphological context under investigation.
This work is part of a wider research project studying the relationship between urban form and the retail system, developing innovative methodologies for their study and producing new knowledge about the French Riviera urban system. This paper focuses on methodological developments and proposes an innovative procedure to model the relationship between retail distribution and urban form.
This paper is organized as follow: Section 2 provides a critical review of the statistical procedures developed in previous works, wherein the four aforementioned limitations are individually discussed. Section 3 describes the modelling and variable selection procedures based on GLM and PR, respectively. This protocol is then tested using a case study of the French Riviera, with outcomes discussed in Section 4. Limitations and future research perspectives conclude the paper.
2. Methodological Literature Review
2.1. Analysing the Relationship between Urban Form and Micro-retail Distribution
As presented above, several studies have explored the role played by different urban morphological aspects on micro-retail distribution. Table A1 presents a non-exhaustive collection of recent works investigating micro-retail locational factors related to the physical urban environment; for each paper, the column “analytical approach” highlights the statistical analytical/modelling approach implemented.
Three groups might be recognized: visual exploration of spatial co-occurrences, bivariate statistical tests and simple/multiple linear regressions (MLR).
Despite valuable observations highlighted in those works based on a visual exploration of spatial co-occurrences [13], weak and non-reproducible outcomes prevent both theoretical and methodological inferences or comparative analysis. Confirmation biases might also affect conclusions outlined through this approach.
Pearson’s correlation represents the most implemented analytical procedure [8,9,10,18,19,20]. This approach allows the presence of a linear relationship between two continuous variables to be evaluated. Nonetheless, when considering micro-retail distribution, the normality assumption underlying Pearson’s correlation test is not met: micro-retail measures can only assume positive values within the interval [0, +∞). Moreover, the presence of outliers and the high presence of zeroes (absence of stores) might further increase the distribution skewness. Similar characteristics can be associated with urban form descriptors (i.e., network centralities, building coverage ratios). Consequently, the statistical significance of correlation tests might result in biased outcomes.
Three main solutions might be considered: (i) implementation of a rank correlation test (i.e., Spearman, Kendall); (ii) evaluation of the non-linear fit between micro-retail and urban form properties [16,21]; and (iii) manipulations of the original data to meet a normality assumption such as log-transformation or, similarly, smoothing approaches [8,9,10,18,19,20]. Independently from the specific solution, these procedures propose simple bivariate analysis, assessing strength and direction of the relationship between each morphological variable and micro-retail measures. However, multivariate effects occur at the same time; stores might be detected through correspondence of a particular combination of variables. The simple bivariate correlation should not be implemented when the goal of the study (as in this work) is the evaluation of the combined importance of a set of explanatory variables.
MLR evaluates the combined effects of several independent descriptors, disentangling and examining their separate effects and assessing both partial and semi-partial correlations with target variables. To analyze the relationship between micro-retail and urban form, several works have implemented this modelling approach [17,22,23,24,25]. Although MLR is considered to be a powerful technique, it might not always represent the best solution. As previously discussed for statistical correlation tests, strong assumptions are also required for the implementation of MLR. The main assumption of homoscedasticity (normal distribution of residuals) is often not respected when a response variable is skewed (e.g., store count/density per street). In this case, residuals almost always correlate positively with the predictors and, consequently, the estimated standard errors of the regression coefficients are smaller than their true values. However, “heteroscedasticity is a problem with the model, not the data” [26].
Instead of discussing possible violations and subsequent data manipulations, the choice of a statistical modelling approach adapted to the nature of the data under analysis might be considered a simpler and much more effective solution. Although several retail distribution measures have been used as response variables (i.e., store floor space, sales volume, workforce, frontage length) when studying the spatial distribution of stores, the simple number of establishments within a given region represents the most adopted solution. Individual stores represent the natural level of the analysis as well as the legal and functional unit for most businesses [27,28]. “Counting values represent the natural, obvious, and meaningful scale to describe discrete occurrences/distribution, and one should retain these virtues if possible” [26]. In this case, the dependent variable can only take discrete non-negative values, and it does not necessarily follow a normal distribution. In such cases, a conventional linear regression cannot be applied; instead of proposing ad-hoc transformations, count regression approaches should be preferred [29,30].
Count regression approaches have been developed since the end of the 1980s in different domains of study, including retail geography [27,31,32]. Nonetheless, among the academic community investigating urban form, only recent works have proposed the implementation of count regression approaches; for instance, Ye et al. [12] considered negative binomial regression when studying the relationship between street-block properties with catering-related stores. However, the superiority of this model to the more traditional MLR approach has not yet been evaluated. Therefore, the first goal of this work is to propose such an assessment for the modelling of the relationship between micro-retail distribution and urban form through the implementation of a robust model selection procedure.
2.2. Stores Absence and the Survivorship Bias
Beyond the choice of the most adapted analytical approach, a second aspect should be highlighted. The attention of academics is traditionally captured by those spaces where stores are observed, whereas absence is usually ignored or considered in the same way as missing data. Few works have tackled this specific feature. For instance, while correlating micro-retail presence and street-network configurational indicators, Omer and Goldblatt [17] compared values obtained from the overall study area to those observed in the subset of streets with a micro-retail presence different from zero.
The absence of stores in urban spaces has never been considered as an integral part of the process defining micro-retail spatial distribution, leading to what several disciplines have recognized as survivorship bias [33]. This bias is explained as the tendency of (statistic) studies to draw conclusions considering a subset of “successful” individuals who might not be representative of the overall population.
In our context, the emphasis on a specific subset of spatial units might be explained by the high heterogeneity characterizing micro-retail distribution in an urban space, which becomes even more evident when using fine-grained spatial units such as street segments. Micro-retail is found only in a small percentage of the total number of street-based units. Hence, academics traditionally apply a manual reduction of the zero overrepresentation [9,14,20,22]. Selecting and analyzing spatial units based on a specific criterion is not a bias in itself, although biases might arise in the interpretation of its results. This selection might be considered to be a legitimate choice under the condition that interpretations and conclusions of results highlight this background constraint underlying the statistical analysis. Thus, the same statistical relationships might or might not be verified when extending the analysis to the whole dataset. In other terms, outcomes explain the necessary but not sufficient conditions by which to observe the phenomena.
The exclusion of spatial units from the statistical analysis are not only a possible source of bias, but also represent a significant loss of knowledge. The absence of micro-retail should be considered just as predictive and informational as its presence. Integrating this aspect into the analysis would require limiting data manipulation procedures that lead to the manifestation of survivorship bias. Beyond the manual removal of zeros, smoothing/interpolation procedures such as kernel density estimation (KDE) [8,9,10,18,19,20] also result in similar conclusions. In this case, the relationship between the variables under analysis is overstated [24] (p. 63), valuable and detailed information such as an absence of stores might be omitted or diluted and the autocorrelation component of micro-retail distribution is artificially amplified.
Additionally, an important role is played by the spatial unit choice: precise and sharp information about store absence can be diluted depending on partition size (Modifiable Area Unit Problem-MAUP [34]). Two main strategies have been proposed when studying human-related phenomena: the use of behavioral-based scales [35] and reduction of the aggregation scale [36]. In this work, the use of street counts on street-based spatial units addresses both these requirements, allowing the investigation of both the presence and absence of stores.
Analyzing micro-retail absence also requires specific analytical/modelling procedures. Within the count regression methodological framework, explicit approaches have been proposed by which to evaluate zero-inflation in the target variable [37]. The hypothesis underlying these approaches is that two processes might generate the distribution of micro-retail activity: the first is responsible for its absence/presence, while the second explains its intensity. Therefore, we can investigate whether different combinations of urban morphological parameters underlie the two processes.
While zero-inflated procedures have been largely investigated in several domains, the appropriateness of these approaches still need to be assessed within the aforementioned urban form literature. Thus, the second goal of this work is to test the hypothesis regarding the presence of a double process that describes micro-retail presence/absence and magnitude through zero-inflated GLM approaches.
2.3. The Contextual Effect
So far we have discussed how specific modelling approaches should be considered when studying the relationship between micro-retail distribution and urban form. However, their statistical distribution and subsequent statistical relationship might vary depending on the specific urban context under analysis.
The contextual effect (also called the neighborhood, integral or landscape effect, depending on the discipline [38,39]) has previously been investigated only by a limited number of authors among the aforementioned studies. Among urban form literature, several works have integrated urban morphological context descriptors that have been defined using different approaches: expert-based knowledge incorporating urban and architectural data [16], official land-use zoning [24], center–periphery subsystem definitions [15], historical urban planning growth (planned/spontaneous) [17] and density types [14].
The spatial context represents a fundamental component of urban systems under study, especially when studying large regions encompassing heterogeneous urban forms. Overlooking this aspect might impact the model outcomes with a systematic over/underestimation effect and spurious correlations between dependent and independent variables [40,41]. Therefore, morphological-based partitions are included among the descriptor of the urban form in this work.
Several approaches have been developed to integrate contextual variables in statistical modelling. When referring to urban form literature, three main approaches have been considered. Scoppa [24] implemented both least square means and disaggregated approaches. Least square means is considered an aggregated data analysis approach, assessing latent differences in a scale-level dependent variable using a nominal-level variable described by two or more categories. As for correlation and MLR, these approaches also rely on a normal distribution assumption of variables within groups, all described by equal standard deviations. To overcome this limitation, other non-parametric alternatives might be implemented such as the Kruskal–Wallis H test proposed in [14]. Nonetheless, every aggregation technique describes whether a contextual partition is significantly correlated to a specific variable losing fine-grain description at the individual level, ultimately leading to interpretational ecological fallacy biases [42]. On the contrary, in disaggregation techniques [43] each feature under analysis is labelled using n dummy variables that describe the association to the region in which the individual is located; however, the linear relationship between the dependent variable and the regressors is not affected. This technique only allows the intercept value to be adjusted, and assumes the same relationship exists between variables in every group.
To overcome these limitations, regressions should be separately replicated for each sub-region under analysis, allowing the different variable relationships occurring in different regions to be explored. Some of the aforementioned works adopted regression via subgroup solutions [16]; however, separation approaches lack an assessment of inter-class variability.
A fourth approach that should be mentioned here is multilevel linear modelling (MLM). This approach, traditionally implemented in social studies, allows variables defined at different aggregation levels (often administrative units) with a nested structure to be investigated [38]. When considering our research design, contextual partitions identified areas of similar morphological properties, but no descriptors were associated with these higher-level aggregations.
Bearing in mind the aforementioned observations, individual regressions were implemented that allowed specific solutions for both model and variable selection procedures to be explored for each sub-region.
2.4. Multicollinearity and Variable Selection Procedure
The proliferation of studies investigating different urban form features and methodological approaches in relation to micro-retail distribution has resulted in a rich yet fragmented literature. Despite evidence about the individual importance of specific aspects of urban form on micro-retail distribution, an overall picture of the role of the urban built environment is still missing. This same observation might be found in the origin of a recent trend in urban form literature (beyond the specific case of the micro-retail) interested in bridging and analyzing the combined effect of several urban form aspects and measures [44]. However, assessing the combined and relative importance of a large number of strongly correlated urban form descriptors comes into conflict with the assumption of independent variables underlying traditional regression approaches. This limitation is even more evident in the current work, where several variables are specifically conceived for the detection of aspects of urban form that are different but still correlated.
Although multicollinearity does not influence overall model precision, its main consequences concern the analysis and interpretation of individual regression coefficients, preventing isolation of the individual contribution of each explanatory variable [45,46]. In order to detect and reduce multicollinearity issues, several approaches have been proposed and traditionally applied.
Bivariate correlation coefficients and tolerance-based diagnosis (i.e., variance inflation factor-VIF) represent two traditional approaches that allow the regressors at the origin of multicollinearity issues to be identified. Bivariate correlation coefficients require an expert-based selection, with subsequent concerns about the robustness/reproducibility of the procedure; moreover, the evaluation of every couple of variables becomes a highly time-consuming procedure with large datasets. On the contrary, stepwise routines have been elaborated for tolerance-based diagnosis. Although these procedures support and automatize the process of variable selection [47], they also have been demonstrated to be sensitive to small perturbations in initial data [48], and to produce biased regression coefficients [49]. Both correlation and tolerance-based approaches do not consider dependent variables to be a targets of the selection process, and only explore the intercorrelation between regressors [50]. To overcome this limitation, Sevtsuk [23] implemented a variable selection based on a statistical significance threshold that was applied to each predictor regression coefficient.
A second approach to dimensionality reduction includes procedures such as factor analysis, linear discriminant analysis and principal component analysis. These approaches identify lower numbers of unobserved variables called factors, which are expressed as linear combinations of higher numbers of correlated variables. In the specific case of micro-retail distribution, factor analysis is implemented (e.g., [26]). Despite the mathematical similarities between several available methods, different results might arise with possible complications in the interpretation of each factor [51]. The main issue here is that the direct interpretation of original features is lost; moreover, different variable aggregations in each sub-region hinder any intra- and inter-level comparative analysis within our partition.
In the present work, we prioritized the identification of variables that are objectively measured and individually observable in their disaggregated forms, rather than subjective/latent/composite factors, in order to facilitate both the interpretation of each individual indicator (or group of indicators) and comparative analyses of the different sub-regions of the study area.
To meet these goals, we implemented penalized regression (PR) [49] procedures in the present work. PR is a recent feature-selection approach that allows identification of the most significant subsets of features of a targeted variable by removing features characterized by low relevance and high redundancy [52]. Using a computationally efficient procedure, PR reduces the original model complexity to a simpler, final model that encompasses the most significant variables.
Although PR has recently been applied in micro-retail-related studies [53,54,55], to the best of our knowledge it has not been implemented and assessed within urban morphology. Implementing PR in our case study allowed us to deal with multicollinearity in our dataset, and to achieve our third goal of outlining the subset of individual urban morphological variables most related to micro-retail spatial distribution within each sub-region under analysis.
2.5. Objective
In the previous sections, we discussed the main analytical approaches for analyzing the relationship between micro-retail distribution and urban form. To summarize, a simple bivariate correlation analysis is the most adopted approach used in urban studies when investigating the individual relationships of single variables with micro-retail distributions. However, when the focus of analysis combines several urban environment indicators, MLR has been proposed as a superior alternative.
The intrinsic statistical characteristics of our variables might represent an important restriction affecting the underlying assumptions of both bivariate correlation and MLR and, consequently, the validity of their outcomes. We highlighted their conceptual and methodological limitations when modelling the discrete, non-negative, highly skewed nature of micro-retail distribution. While the absence of stores should be considered an integral part of the process describing store distribution, the resulting zero-inflation is traditionally overlooked or manually removed. Increases in the number of urban variable descriptors and the spatial extents needed to deal with multicollinearity among a large set of independent regressors require different values depending on the morphological context under study. These two aspects are still overlooked or discussed individually without a common methodological framework; nonetheless, only their combined evaluation can reveal important information on the roles played by each urban form aspect on micro-retail distribution.
Based on these observations, the following sections will show how the combination of GLM and PR approaches represents a better alternative to MLR models. This well-established modelling approach is able to deal with the four aforementioned aspects within a coherent, robust and innovative methodological framework.
3. Materials and Methods
In this section, we present the study area and databases underlying both urban and micro-retail descriptors. Next, the spatial unit of analysis and different families of street-based urban form descriptors are briefly defined. Finally, the model and variable selection procedures are described.
3.1. Case Study and Data Sources
The analytical protocol proposed in this work was tested on a real case study of the French Riviera metropolitan area in southern France. This polycentric coastal settlement comprises 88 municipalities that are structured around six main urban centers. From west to east we find: the Cannes–Grasse–Antibes conurbation, with 74,200, 51,000 and 73,800 inhabitants in their central cities, respectively; Nice, with 343,000 inhabitants, representing the largest municipality of the French Riviera and its administrative center; and the enclave of Monaco and the border city of Menton, with 38,000 and 28,000 inhabitants, respectively. Within these six municipalities about 70% of all micro-retail businesses is found. Spread around these main centers, 295,000 people live in smaller cities, villages and hamlets surrounded by vast residential areas, according to the morphological properties of the site. All these differently sized centers are interconnected by a pervasive, discontinuous and car-dependent residential fabric. With a total of more than 1 million inhabitants, the French Riviera is the seventh most populated metropolitan area in France.
The combination of all these elements produces a sequence of urban centers and peripheral areas of different sizes that encompass a large variety of urban forms. Previous studies have disentangled the high heterogeneity of the study region, identifying typo-morphological regions both at district and neighborhood scales [56,57]. These sub-regions correspond to different urban morphological contexts characterized by specific combinations and distributions of urban configurational and morphological descriptors; moreover, for each of these regions, different zero-inflation and overdispersion properties of the micro-retail distribution are also observed. These characteristics allow the present work to overcome the limitations of traditional works that have investigated only individual core regions of medium- or large-sized monocentric cities [10], and to assess the current analytical procedure under different contextual and statistical conditions.
Two sources of data are considered in this work. The official data about micro-retail distribution is provided by the local Chamber of Commerce of Nice Cote-d’Azur (CCINCA), counting about 50,000 businesses and services active as of 1 January 2017. (More recently, this same information has been made available at the national level by the national statistics agency (INSEE).)The address information allowed us to geocode the database and provide a spatial representation of the phenomena under study. This process was realized through the National Open Addresses Database (Base d’Adresses Nationale Ouverte (BANO)). The BANO geolocation tool associated a score of the geocoding results describing the localization precision at four levels: null, municipality, street and house number. From our original dataset: (i) 7% of the data presented missing information, or fell outside of our study area, and was thusly excluded from our analysis; (ii) 2% of information was geo-localized at the municipality level and 13% was at the street level—the cause of these mis-localisations was often a result of incomplete address information in the original database such as missing civic number, misspelt street name, incorrect name of an isolated hamlets and so on, and a manual correction was carried out when the correct retail activity address was available from other online sources; (iii) 78% of data were correctly located at the house-number level. We obtained a final dataset of 45,726 stores distributed across 33,221 locations (several activities shared the same addresses), 82% with a precise civic number and 18% at the street level (positioned at street segment midpoints). In 135 locations, large planned centers were found with retail surfaces higher than 2000 square meters. This specific retail format does not possess the same combinations of locational factors as smaller activities [58], however its presence has the potential to profoundly modify the surrounding urban morphology and flow, making these centers an attractive element for smaller activities (i.e., retail locomotives). For this reason, these activities (from now on named “anchor stores”), were excluded from the original dataset and considered as a locational factor for smaller commercial activities (see Section 3.2).
Urban form descriptors were based on the geographic databases (BD TOPO, 2017) from the French National Institute of Geographical and Forest Information (IGN). Four layers of urban morphological elements were used: building, street-network, parcel and digital terrain model (DTM).
Based on these data sources, well-established GIS-based protocols were implemented for the elaboration of the different urban morphological descriptors, while statistical procedures were implemented with R libraries [59]. The use of relatively simple data and available analytical/statistical protocols make this work reproducible for future comparative studies.
3.2. The Variables under Investigation
The spatial unit of analysis was the street segment. Streets represent one of the most used spatial units, and have been attracting attention in the last 20 years from urban designers, configurational studies, morphologists and urban geographers [60]. Streets are considered to be the bridging element between different methodological and theoretical approaches [44].
The street segment is here defined as the centerline between two street-junctions. Four reasons motivate this choice, the first of which being that “the dominant network model is the one that represents the street junctions as vertices in the graph and the linear street segments as its edges” [61]. Secondly, by using street network centerlines, the primary approach allows the independent identification of configurational properties according to the physical shapes and sizes of built forms surrounding street segments (isolating configurational properties of the network from morphometric measures of the streetscape and fabrics). Thirdly, the use of a centerline permits a geometrical reference when studying streetscapes from the street point of view (measures of setback, parallelism of facades and so on are used as reference street edges and/or street centerlines). The street segment therefore becomes both a geometrical (streetscape measures, the geometry of retail agglomerations, etc.) and metric (local configurational properties, local morphological patterns, etc.) reference [62], and the use of visual axes as in SSx or alternative street-like representations of the street network provide a distorted reference system for streetscape descriptors. Finally, the street segment represents a behaviorally oriented partition of space, which is better suited for socioeconomic phenomena such as the distribution of retail businesses in urban space [35].
To describe different aspects of urban form, several computer-aided procedures from established scientific literature were implemented for our study region. Each street segment was characterized by more than 100 street-based descriptors of urban form (further details about urban form indicators are described in Appendix B).
Four main subsets of indicators can be recognized: the first comprises 40 indicators that have been defined to describe street network configurational properties using the MCA protocol [8,9]. Local Reach, Straightness, Closeness and Betweenness centralities are assessed at different scales and impedances on pedestrian and vehicular modelled street-networks (300-, 600- and 1200-meter radii and 5- and 20-minute radii, respectively. Their normalized versions are obtained following a two-step floating catchment area procedure (2SFCA) [63].
The second subset of indicators is made up of 36 indicators describing the street-network accessibility towards public squares, coastline and anchor stores, which are considered influential components of an urban form on micro-retail distribution. As with the previous metrics, several scales and impedances were considered.
From the urban design and urban morphological literature, 30 indicators describing the built form layout along the street edges have been defined (also named skeletal streetscapes [64]). Several GIS protocols have been proposed in recent urban form literature [64,65,66,67]. and indicators such as façade alignment, building set-back, average building height and so on are calculated while considering building distribution within a 50-meter distance from street edges through the definition of street-based proximity bands (PBs) and sightlines [56,67].
Finally, street-based contextual variables/partition have been obtained through the implementation of the Multiple Fabric Assessment procedure [56], wherein each street segment is associated with nine values, with each one describing the probability of association with different urban fabric types. In more central and compact regions, historical centers, traditional planned fabrics with adjoining buildings and discontinuous fabrics of buildings and houses are found (respectively, UF1–3). Semi-peripheral and peripheral regions are prevalently composed of modernist urban fabrics and suburban areas with lower/higher natural constraints (respectively, UF4–6). Finally, the least dense regions are described by connective artificial fabrics and natural spaces of hills and mountains (respectively, UF7–9). This urban fabric partition is illustrated in Figure 1 and further described in [57]. The study of the spatial organization of these nine urban fabrics allows the identification of three morphological macro-regions within a metropolitan area: First-, Second-Age City (following the morphological categories of [68]) and Natural Space. These two typo-morphological partitions of the study area, illustrated in Figure 1, define the sub-regions where count regression approaches are individually applied; the limited number of streets with stores within the Natural Space and UF7–9 prevent the implementation of our analytical procedures in these specific morphological regions.
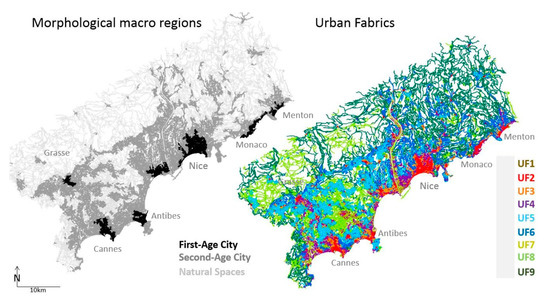
Figure 1.
The French Riviera study region: the three morphological regions (First-/Second-Age City and Natural Spaces (left)) and the nine urban fabrics (UF1–9 (right)). Source: [56,57].
Of the almost 100,000 street segments composing the whole street network of the French Riviera, we focused on those where built-up elements were found within 50 meters from street edges. Streets crossing natural areas, large public parks and small connective segments were excluded, reducing our dataset to 63,071 units. Each street segment was defined by the number of small stores representing the target variable of our models. Different values of zero-inflation, street density and overdispersion were observed in each morphological sub-region (Table 1).

Table 1.
Micro-retail distribution, variance and zero-inflation values for the overall study region and within each morphological context.
Before proceeding with a description of the modelling protocol, two further aspects should be underlined. Firstly, the same four limitations presented in Section 2 still persist when using other fine-grained spatial unit definitions and urban form descriptors. As such, the modelling solution presented in this paper might also be tested and implemented with other street-based spatial unit definitions (i.e., axial streets, named streets, raster-based solutions, plots, etc.). Nonetheless, the combination of several urban form analytical procedures, each one based on ad hoc spatial unit definitions, would require a supplementary artificial manipulation of the variables, which would lead to the introduction of a statistical bias and compromise both the modelling and variable selection procedure performances and outcomes.
Secondly, this work focuses on the study of the physical properties of urban form, and does not take into consideration any socioeconomic and land-use regulation aspects. It is fully recognized that such aspects play an important role as locational factors in retail distribution, and are each related to urban form in different ways. For this reason, both modelling performance measures and variable selection procedure could be strongly dependent on these variables, confounding the role of other urban descriptors. Their exclusion from the modelling procedure allows the roles of different properties of the urban built environment to be explored and pointed out. Further research would be needed to disentangle the roles of urban form, socioeconomic aspects and planning constraints.
3.3. Modelling Micro-retail Distribution: From Linear to Count Regression Approaches
As discussed in the previous section, count regression approaches seem to be best suited to our case study. These methods have been widely developed over the last 50 years [30,69,70,71,72]. GLMs have been specifically developed to handle count data: a mathematical transformation on the dependent variable is operated, considering the true distribution of errors and assuming a distribution from an exponential family (i.e., binomial, Poisson, multinomial, etc.). A linear relationship is then investigated between the independent variables and the transformed response rather than its raw values. A maximum likelihood estimation (MLE) procedure is implemented for the estimation of the model parameters.
When the distribution of the dependent variables (and errors) follows a Gaussian (G) distribution, the identity function describes the transformation and, subsequently, the GLM results in the same estimates as the traditional MLR [72]. When the variable to be analyzed is represented by a count variable, the random component assumes the form of a Poisson distribution and the corresponding transformation is usually a log function. The resulting model is called a log-linear or Poisson regression model (P). However, the main assumption of a Poisson model is that the mean and standard deviations of the observed dependent variable are equivalent, an assumption that is not met when the dependent variable is characterized by high heterogeneity. Negative binomials (NBs) might be considered an alternative to the Poisson model, and this specific form provides a built-in solution to account for overdispersion. P and NB represent two interesting alternatives to G/MLR overcoming the restrictive assumption of homoscedasticity while considering the true distribution of errors.
Despite being able to handle discrete non-negative and skewed distributions, the models presented so far cannot handle overdispersion due to zero-inflation (heuristic rules suggest a presence of zeroes not higher than 20% of the expected values, which is far less than what was observed in our target variable). In such situations, the GLM approach proposes alternative solutions that are able to integrate and model an excessive presence of zeroes.
With zero-inflated (ZI) regression models [37], zeros originate according to two simultaneous processes. The probability distribution of zero-inflated models are defined as the combination of a logistic part modelling the structural zeros (or true zeros) and a count part assuming a P (ZIP) or NB (ZINB) form from which random zeros (or false zeros) are produced.
Zero-alternated (ZA, or hurdle) approaches [73,74] model all zeros as one part, while the non-zero part is modelled with zero-truncated count regressions. The implementation of the P or NB forms into the zero-truncated part of the model result in zero-alternated Poisson (ZAP) and negative binomial (ZANB) models.
Implementing ZI and ZA models allowed us to explore the possibility that two processes might determine the observed zero and non-zero values instead of considering that these values come from the same data-generating process. Both ZI and ZA are described by the combination of logistic regression and Poisson (ZIP-ZAP) or negative binomial (ZINB-ZANB) models. The main difference among these approaches is that the former considers the observed distribution of values to be the result of the combined processes with a possibility of distinguishing between structural and random zeros, while the latter supposes two separate generating processes producing zero and non-zero values. Finally, the opportunity to use P and NB both in ZI and ZA allows us to control for the combined overdispersion of count and zero parts.
For the three models previously described (G, P, NB), four additional models were implemented and compared (ZIP, ZAP, ZINB, ZANB). The seven models here presented were performed on the overall study area and eight aforementioned sub-regions.
GLM is a powerful technique that enables a wide number of modelling approaches beyond the traditional MLR to investigate different aspects of the dependent variable statistical distribution. While the implementation and comparison of these approaches have been already discussed in several disciplines, no work has investigated this specific aspect in the case of micro-retail distribution and urban form. The implementation of a comparative analysis of seven regression models allowed us to understand whether specific processes should be considered when describing the relationship between urban form and micro-retail distribution. Goodness-of-fit measures are described in the next section as support for the model selection procedure.
Before proceeding with further specifications, another observation should be made. Micro-retail distribution is frequently measured as a density; one might argue that the raw count of stores might be strongly biased by the size of the underlying spatial unit. A specific approach to handle density variables is possible when implementing GLM. Density might be seen as a rate between a count value (the store number) and the underlying spatial unit size (street length), also named the exposure variable. GLM handles exposure variables using simple algebra, changing the dependent variable from a rate into a count by simply multiplying both sides of the equation according to the exposure variable and moving it to the right side of the equation. In the final model, the exposure variable becomes a term of the regression coefficients, also called the offset variable. With this solution, GLM permits the preservation of the natural form of the counting data, which accounts for the variabilities determined by the underlying spatial unit dimension.
3.4. Modelling Selection: Goodness-of-fit Measures
Defining a common procedure by which to assess and compare the different models is a task of paramount importance when identifying the most adapted modelling approach.
Since the traditional coefficient of determination R2 requires a homoscedastic distribution of error, extensive scientific literature has focused on pseudo-R2 for count regression models [75,76,77,78]. Nonetheless, there is no consensus on which measure should be preferred, and each choice might lead to certain drawbacks [79]. For example, goodness-of-fit measures have been specifically conceived for each type of GLM regression, preventing their application in a large variety of models with the final goal of supporting the model selection phase.
To overcome this limitation, measures based on information criteria (IC) have become increasingly popular. The notion behind IC approaches is the need to find a compromise between likelihood maximization and the principle of parsimony, which favors simpler models [72]. The Akaike information criterion (AIC) [80] is obtained as , where K is the number of estimable parameters that correspond to the degree of freedom, and is the maximum value of the likelihood function for the model M. In other words, the AIC score is an estimate of a constant based on the degrees of freedom of a model, plus the negative log-likelihood of the model knowing the data. A lower AIC score reflects models that are closer to reality. AIC scores do not have a specific meaning when independently considered, but a comparison of AIC scores from different models can help an analyst rank and select the best solutions from a finite set of models. An AIC can only be obtained from GLM approaches that allow non-nested models to be compared, which ordinary statistical tests cannot do.
The implementation of likelihood ratio-based tests (LR-test) provides an analyst with further evidence highlighting statistically significant differences between IC scores. The null hypothesis of an LR-test is whether both compared models are equally close to the true model. If the null hypothesis is not verified, one of the two models should be considered as having a better performance. The Vuong test [81] for non-nested models is so far the most applied LR-test among the different domains of the scientific literature without any restrictions on GLMs. In this work, AIC scores and the non-nested Vuong testing were used to quantify and rank our model performances and, ultimately, guide the model selection. As we were aware of possible biases when considering ZI models [82], rootgrams [83] were also implemented as a graphic solution to support the model assessment.
While the aforementioned procedure assessed and supported the model selection procedure, two additional aspects should be outlined. Firstly, loglikelihood-based measures allowed comparison only if models shared the same underlying dataset (both in terms of variables and records). Therefore, the same approach was not suitable when comparing global model outcomes with those obtained from the subgroup regressions approach. Secondly, AIC is a global measure, and does not allow to appreciate the roles of overdispersion and zero-inflation on model performance outcomes.
Other parameters were also implemented, allowing the description of different aspects of the model outcomes. Count pseudo-R2 [84] was implemented as the proportion of correct estimates on the overall number of predictions; similarly, weighted accuracy, recall and F1 scores were also provided. Traditional measures of dispersion of the residuals (mean absolute and standard deviation) for each model completed the model outcome description. These measures were applied while considering zero and count parts of each model separately, thus revealing their relative impacts on the overall goodness-of-fit measures.
3.5. Feature Selection.
In the previous sections we defined a model selection procedure to identify the most adapted approach to describing micro-retail distribution, which we based on overall goodness-of-fit measures, without considering the specific combination of regressors. Nonetheless, as outlined in Section 2.4, non-experimental studies are nearly always characterized by the presence of multicollinearity; this was even more true in this work, where different facets and metrics of the same phenomenon—the urban physical form—were studied and combined. Another goal of this work was to outline the subsets of individual urban morphological variables related to micro-retail spatial distribution within each sub-region under analysis.
In order to achieve this objective, a specific category of feature selection—penalized regression (PR)—provided a built-in solution for GLM count regression approaches. While the goal of traditional selection procedures is to remove predictors from a model that are not considered significant and thus set their regressor coefficients to zero, the idea underlying PR is to penalize them toward zero without forcing them to be exactly zero (for this reason, these methods are also known as shrinkage or regularization methods). In this way, the complexity of the model is reduced while keeping all or part of the variables in the model. PR traditionally requires the choice of a shrinkage value of lambda to define the magnitude of the penalization.
Three main penalized regression procedures are most commonly used: ridge, least absolute shrinkage selection operator (LASSO) and elastic net (Enet). In ridge PR, the loss function underlying the regression models is augmented to minimize the sum of the squared residuals while taking into account and penalizing the size of the parameter estimates, with the final goal of shrinking them toward zero. In LASSO PR [49], the regression coefficient to be shrunk toward zero as well as those with a minor contribution might be forced to be exactly equal to zero. Two different penalization functions are considered in ridge and LASSO approaches. While ridge seems to be more frequently adapted when coefficient parameters are of a similar size, LASSO regression is typically adapted when a model presents a subset of variables with high coefficient parameters while the remaining have very small coefficients [85].
Finally, Enet regression combines both Ridge and LASSO penalization approaches, allowing both the coefficient to shrink toward zero while also setting some variables to equal zero precisely, producing simpler and more interpretable models. Implementing Enet regression in our case study enabled us to outline the subset of urban morphological variables most related to the spatial distribution of retail.
In order to find the optimal values for the shrinkage parameters, specific iterative processes were implemented from a large number of possibilities using optimization procedures based on IC such as AIC or, similarly, the Bayesian Information Criterion (BIC, [86]). For each study region, we asked the Enet algorithm to explore 20 values of lambda. The regression coefficients reported in this work correspond to the penalized model for which the lowest BIC scores were observed.
4. Results: Application to the French Riviera Case Study
The outcomes of the procedure previously described are herein presented as follows. First, we focus on the model selection outcomes. Since the overall model selection criteria and predictions are not influenced by multicollinearity problems, the role of individual regressors is temporarily overlooked. Once the most adapted modelling procedure is defined, the second part of this section is dedicated to the results of the variable selection procedure.
4.1. Model Selection
Seven regression models (G, P, NB, ZIP, ZINB, ZAP, ZANB) were implemented on the overall space, on two sub-regions at the district scale (First/Second-Age City) and on six urban fabrics (UF1–6). Each of the 63 models is described in Table 2 according to the following set of four descriptors: AIC, -2loglikelihood, number of features (streets) and number of parameters c (variable number + number of parameters of the model). The best model was found to correspond with the lowest AIC value.

Table 2.
Model selection for the overall study area and each morphological region.
Higher values of AIC were found, as expected, corresponding to the linear (G) and Poisson (P, ZIP, ZAP) regression models. The inappropriateness of these models is here empirically confirmed independent of the spatial region under analysis. Lower AIC scores were found for the NB, ZINB and ZANB models. Despite small differences among these three approaches, ZINB always presented the lowest AIC values.
As can be observed in Table 3 where non-nested Vuong test results are reported, the statistically significant superiority of ZINB was confirmed in every region with the exception of UF5 and UF6. In these two specific cases, p > 0.05 when comparing the AIC values of ZINB and ZANB. These outcomes provide solid evidence regarding the presence of a double process defining micro-retail distribution.

Table 3.
Results of the Vuong LR-test between our seven models for the overall study area and each morphological region.
These observations are further confirmed when plotting the relative rootgrams. In Figure 2 we might observe rootgrams for the seven models implemented on the overall study area, and similar behaviors can be observed for every morphological sub-region. Linear (G) and Poisson regression models (P, ZIP, ZAP) did not account for overdispersion, contrary to all negative binomial regression models (NB, ZINB, ZANB).
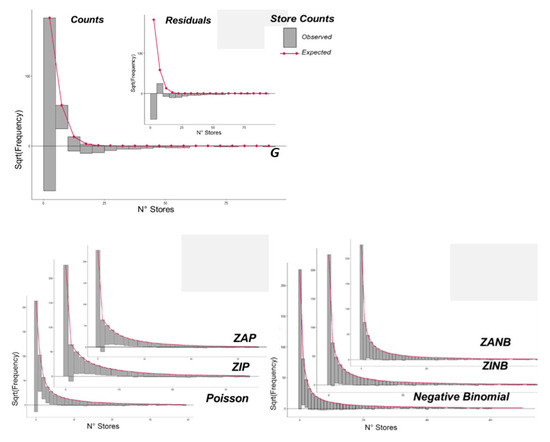
Figure 2.
Rootgram of the global model (overall space study and variables) for: linear model G (top), Poisson regressions P-ZIP-ZAP (bottom-left) and negative binomial regressions NB-ZINB-ZANB (bottom-right). The last group of models showed a better fit between expected and observed values.
Having determined ZINB to be the modelling approach that best fit our study case, we can now observe the impact of regression according to the different subgroups: Table 4 gathers the set of 13 measures previously described using the count and zero outcomes for each sub-region under analysis. The lowest accuracy and sensitivity values were found in the more central compact fabrics. Inversely, peripheral urban fabrics showed higher values. Precision relatively to the count parts dropped in peripheral urban fabrics where higher zero-inflation was observed.

Table 4.
Comparison of the results of ZINB models when global and sub-regions are evaluated for the same subgroup of features.
When implementing ZINB models separately on the First- and Second-Age City partitions, the accuracy of the overall model improved +0.38% and +0.98%, respectively, while the accuracy level grew by +0.52% when using the six UFs. The decomposition of the overall study area showed minor improvements on the overall predictability of the model. However, different levels of improvement were observed when considering each sub-region individually: the accuracy of UF1–3 substantially improved by +4.66%, +12.29% and +2.55%, respectively, and the F1 score improved by +7.38%, 2.89% and 5.50%, respectively. As for UF5 and UF6, the accuracy was similar between the global and local models, while the F1 scores were higher in the latter. Only for UF4 did both accuracy and F1 scores show small variations between global and local models.
When observing the separate sensitivity and precision values for the count and zero parts, an overall growth in precision could be observed, as well as a loss in sensitivity in the counting parts. Moreover, both accuracy and sensitivity improved for the zero parts, with the exception of UF5 and UF6. We might conclude that the decomposition of the study area in morphological subspaces (both UF and morphological macro-regions) improved the goodness-of-fit for traditional central areas, while semi-peripheral and peripheral regions seemed to be penalized. Since street elements in peripheral regions outnumbered those of more central areas, the model improvements achieved in central areas were diluted and reduced to modest values when evaluating the combined results of sub-models (First-/Second-Age City and UF1–6). These outcomes might support the hypothesis that urban form plays an important role in defining store distributions in compact traditional areas, while other locational factors should be considered for less dense, peripheral regions.
Projecting model outcomes in a geographical space allows the analyst to observe the spatial characteristics of the predictive power of the models. Ignoring these spatial representations of the model outcomes might hinder the detection of eventual model limitations, precluding important observations for future research developments. Specific patterns of residuals might suggest the omission of essential variables. In Figure 3, we illustrate the observed distribution of micro-retail, along with the predicted values and their errors, zoomed in on the city of Nice. From the left to the right we can compare the global model, the First/Second-Age City and the urban fabric composite models. Despite the set of goodness-of-fit measures previously described indicating higher performance values associated with the combined models, these differences were hardly detectable in the geographical space. An overall underprediction was observed for hilly neighborhoods surrounding the city center, and underprediction was also observed along the coastline, despite the inclusion of a specific set of indicators. Only expert-based knowledge of the study area might allow us to better understand and explain the underlying reasons for specific hyper-local over/under prediction values. For instance, underprediction was observed in correspondence with pedestrian areas or along those streets characterized by specific retail functional agglomeration issues resulting from historical/commercial inertia of the street/neighborhood [22] (p. 120).
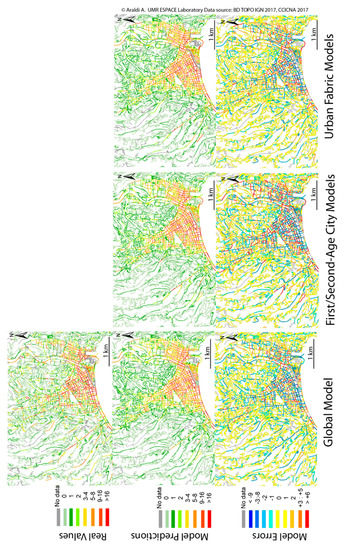
Figure 3.
Projection in the geographical space of the observed, predicted and residual values for the global model, First/Second-Age City and urban fabric composite models.
4.2. Variable Selection
In this section, the results of the variable selection are presented. This second phase of the analysis allows us to identify and describe which combinations of indicators underlied the spatial distribution of micro-retail in the global study area as well as in each morphological region. A specific geographical/urban discussion of the individual roles of each urban form indicator goes beyond the goals of this paper. However, we provide some observations about the methodological procedures and an overall presentation of the selected variables.
In the global model as well as in the local models UF1, UF5 and UF6, the zero part was completely erased, resulting in an NB model. The reasons for this difference can most likely be traced to the model selection procedure of Enet algorithms based on the minimization of BIC as well as the higher penalizing factor for a larger number of regressors. These results might support the idea that an NB model is, in certain cases, a simpler and more efficient solution. On the contrary, the ZINB approach, despite being the most performant solution when the full model was studied, became too complex when a smaller number of variables was investigated.
The variable selection procedure allows the importance of a restricted number of variables between 27 (for compact urban regions) and 11/13 (for suburban and less dense urban fabrics) to be highlighted. From the initial 105 variables, 54 appeared in at least one model, with half of them found in at least three models. The left column of Table 5 enumerates the 27 most recurrent indicators in descending order of the number of models, while the right column provides the variable ranks when considering the importance of each variable assessed as the sum of the absolute increase/decrease of the odds ratios observed in every model.

Table 5.
Outcomes of feature selection procedures. Selection frequencies of the most recurrent descriptors of urban form in relation to micro-retail spatial distribution
Table 6 presents all the selected indicators within each morphological region; variables selected for the count and zero parts are detailed in the upper and lower, respectively. Based on this table, we might observe how the built-up coverage ratio (PB50m), local betweenness (1200 m) and street acclivity represent the three aspects of urban form most related to the store distribution. This first outcome is in line with the results discussed in the urban form and micro-retail literature by [14], [8] and [87], respectively. The outcomes of this analysis show how micro-retail distribution might be explained by the combined effect of these three aspects (almost) independently according to the spatial partition under study (scale and contextual invariance). The built-up coverage ratio does not play a significant role in historical centers, UF1, where it has reached a certain homogeneity of high values (last phase of the burgage cycle [88]) and other urban form properties become more significant in defining favorable conditions for retail presence.

Table 6.
Outcomes of the variable selection procedure (Enet-PR ZINB) implemented on the overall space of the French Riviera (global) and its contextual partitions (First-/Second-Age City, UF1–6).
Skeletal streetscape morphometric descriptors such as the built-up coverage ratio, the corridor effect, built-up fragmentation, average building height, open space, street acclivity and length have a higher importance as locational factors in micro-retail distribution. These indicators are the most frequently selected, showing higher odd ratios compared to street-network configurational properties.
Indicators always negatively associated with micro-retail distribution are street acclivity, average and standard deviations of building setback and prevalence of small houses (footprint surface < 150 m2).
The procedure implemented in this paper highlights the twofold role played by contextual descriptors. The first role is the direct influence of urban fabrics, morphological regions and their combinations on the definition of the retail presence; for example, both artificial connective and modernist fabrics (UF7 and UF4, respectively) were negatively correlated with micro-retail distribution when found within compact regions (First-Age City); on the contrary, they become positively associated with store distribution when located in car-oriented peripheral regions (Second-Age City). This observation supports the hypothesis of a double urban system that has been traditionally described by both urban form and micro-retail geographer researchers. The second role is the indirect effect on the variable selection procedure implemented within each region. While some streetscape and street-network configurational descriptors showed high values in every sub-region (i.e., built-up coverage ratio, local betweenness and street acclivity), others showed a high dependency on morphological context. In particular, some variables showed a significant role only in specific regions (i.e., corridor effect and building height were positively related to retail count only in compact fabrics, while the average set-back was negatively related to retail count only in suburban fabrics; Table 6), while others showed a divergent effect (i.e., parcel frequency showed positive/negative values for compact/open fabrics, respectively; Table 6). The identification of these regionalized behaviors would not have been possible with traditional global approaches. Moreover, these specific outcomes suggest the presence of more complex, non-linear relationships, with retail distribution requiring the exploration of more sophisticated modelling approaches.
When focusing on zero parts, we might notice how regression coefficients showed lower absolute values, and their impacts were always negatively related to an absence of micro-retail. Five indicators were selected: corridor effect, built-up fragmentation, parcel frequency, 5-min reach and 1200-m betweenness, each one utilized in different sub-regions.
5. Discussion and Conclusions
This paper presented and discussed some methodological aspects that researchers should consider when analyzing the relationship between micro-retail distribution and urban form from a street-based perspective.
In the first part of the paper, we highlighted how analytical approaches should account for the discrete, non-negative, highly skewed and zero-inflated nature of store distribution. Overlooking these aspects might affect modelling outcomes with both statistical and survivorship biases. Thus, identifying and implementing adapted modelling procedures becomes of paramount importance. Moreover, multicollinearity issues might arise from the assessment of a large number of urban form descriptors differently combined depending on their relative morphological contexts. Innovative modelling approaches are required to allow the evaluation of the combined effects of a large number of variables and to highlight their individual/relative contributions to an understanding of retail distribution. The final goal is to overcome the fragmented knowledge, providing a wider and holistic description of urban form and its relationship with micro-retail distribution.
To overcome these limitations, in the second part of this work we proposed the implementation of modelling and variable selection procedures within an integrated methodological framework. Seven count regression approaches were implemented (G, P, NB, ZIP, ZINB, ZAP, ZANB) in the real-world case study of the French Riviera metropolitan conurbation. The goal of these models was to estimate the number of stores per street segment from a dataset of 105 street-based descriptors of urban form (including street-network configurational properties, morphological skeletal streetscape and urban morphological contextual descriptors). A specific modelling selection procedure based on AIC and LR tests allowed us to assess the performance levels of these seven models and highlight the superiority of the ZINB solution. The same conclusion was also reached when implementing the same model selection procedure separately in different morphological contexts defined at different scales. These outcomes confirm the hypothesis about the presence of a double-generating process at the origin of retail distribution that described the presence/absence and total number of stores observed along street segments.
Finally, the implementation of penalized regression procedures allowed us to select a reduced subset of urban form descriptors for each morphological region. Some indicators were significantly related to the retail distribution independent of the scale/context definition, while others assumed a specific role within given morphological subspaces. This outcome highlights the importance of the morphological context in the study of micro-retail distribution in metropolitan areas. This same outcome might also be interpreted from an urban planning and design perspective, as the need to study intrinsic properties of the urban form (i.e., streetscapes) depends on the general patterns/context within a multiscale/multilevel approach.
From an analytical perspective, this work provided a robust methodological framework for the study of retail distribution and urban form. Further works will examine the geographical and urban significance of these results as well as their contributions to the established theoretical framework of both urban form and retail geography.
The same methodological framework presented in this paper might also be implemented (with few adaptations) in the follow ways: (i) considering different/new urban form properties, with other functional and socioeconomic descriptors being included for a wider definition of the urban environment beyond the form of a physical city; (ii) considering specific retail categories, formats (i.e., franchise/independent stores) and surface-based categories; (iii) to assess the relative importance of urban descriptor categories (i.e., configurational, morphological and streetscape descriptors) or assess the capacity of different urban form protocols (i.e., SSx, MCA, etc.); (iv) for synchronic/diachronic comparative analysis; and (v) in conjunction with other human-based phenomena characterized by a discrete pattern of occurrences and measured on a fine-grained partition of the urban space.
Finally, future works could explore three main methodological aspects that are still overlooked in this work. Firstly, as regards the possible between-class variability of the hierarchical nested organization of the urban form (street, neighborhood, morphological regions), one solution might consider the implementation of MLM [44] combined with the GLM and PR procedures discussed in this work. Secondly, researchers might be interested in non-linear behaviors in data; indeed, the only downside of GLM procedures is the underlying hypothesis of a (generalized) linear relationship between the target variable and regressors. Machine learning modelling procedures should be tested both for modelling and variable selection procedures. Finally, a third aspect that could also be integrated with the four aspects discussed in this paper is the role of the spatial organization of stores; applying methodological approaches such as semivariograms and correlograms to both observed distribution and model errors [89].
Funding
This research was funded by Chambre du Commerce et d’Industrie Nice Côte d’Azur, CIFRE-EPACE Agreement N° 2015/1478.
Acknowledgments
The author of this paper would like to thank Giovanni Fusco, research fellow at ESPACE laboratory, for the valuable insights and the support in every phase of this research project.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AIC | Akaike Information Criteria |
| BIC | Bayesian Information Criteria |
| MCA | Multiple Centrality Assessment |
| MFA | Multiple Fabric Assessment |
| Enet | Elastic Net Penalized Regression |
| GLM | Generalized Linear Model |
| MLR | Multiple Linear Regression |
| NB | Negative Binomial |
| P | Poisson |
| PR | Penalized Regression |
| SSx | Space Syntax |
| ZA | Zero Altered |
| ZANB | Zero Altered Negative Binomial |
| ZAP | Zero Altered Poisson |
| ZI | Zero Inflated |
| ZINB | Zero Inflated Negative Binomial |
| ZIP | Zero Inflated Poisson |
Appendix A. Urban Form and Retail Distribution Literature Review

Table A1.
Literature review: papers investigating the relationship between urban form (mainly street-network configuration properties) and micro-retail distribution. E/NC-KDE, Euclidean/network-constrained Kernel Density Estimation; CDF, cumulative distribution function; MLR/BLR, muliple/bivariate linear regression; ExpR, exponential regression; P-corr, Pearson correlation; NBR, negative binomial regression; K-W H-test, Kruskal–Wallis H test.
Table A1.
Literature review: papers investigating the relationship between urban form (mainly street-network configuration properties) and micro-retail distribution. E/NC-KDE, Euclidean/network-constrained Kernel Density Estimation; CDF, cumulative distribution function; MLR/BLR, muliple/bivariate linear regression; ExpR, exponential regression; P-corr, Pearson correlation; NBR, negative binomial regression; K-W H-test, Kruskal–Wallis H test.
| Urban Form and Micro-retail Distribution | |||||
|---|---|---|---|---|---|
| Authors | Year | Dependent Variable | Phenomena | Space Study | Analytical Approach |
| Hillier | 1999 | N° Stores/street | Micro-retail pattern | Camden London, UK | MLR |
| Cutini | 2001 | N° Stores/25 m (100 streets) | Micro-retail pattern | 3 small-medim sized Italian towns | ExpR |
| Van Nes | 2005 | - | Micro-retail aggl. | Amsterdam, Netherland | Visual |
| Joosten and Van Nes | 2005 | - | Catering businesses | Berlin, Germany | Visual |
| Sarma | 2006 | N° Stores/aggl. | Micro-retail aggl. | New Delhi, India | BLR |
| Porta | 2006 | E-KDE: 100m-cells, bandwidth 100–300) | Micro-retail pattern | Bologna, Italy | P-Corr |
| Ortiz-Chao | 2008 | N° Stores/street | Micro-retail (land use) | Mexico City, Mexico | CDF |
| Porta | 2012 | E-KDE (300-mt BW) on a 10m-size cell raster | Micro-retail Pattern | Barcelona, Spain | P-Corr |
| Tsou, Chen | 2013 | Micro-retail density within traffic zones | Micro-retail Pattern | Taipei city, taiwan | MlogLR |
| Van Nes | 2014 | - | Micro-retail Pattern | Pompeii, Rome | Visual |
| Wang et al. | 2014 | E-KDE (1.5-km BW on 100-m cell-side raster) | Micro-retail pattern | ChangChun, China | P-corr |
| Sevtsuk | 2014 | Presence/absence micro-retail building level | Micro-retail pattern | Cambridge and Sommerville, USA | MLR-Spatial Lag and Error |
| Sevtsuk | 2010 | ||||
| Cui and Han | 2015 | E-KDE (1.5-km BW, 100-m size cell) | Micro-retail (Point of Interest) | Zhengzhou, China | P-corr |
| Omer and Goldblatt | 2015 | N° Build. with micro-retail 50m street-buffer | Micro-retail pattern (comm.build.) | 8 Israeli Cities (3 types) | P-corr MLR |
| Scoppa | 2013 | Micro-retail frontage/ street length | Micro-retail pattern (comm.parcels) | Buenos Aires, Argentina | BLR, PCA-MLR |
| Peponis Scoppa | 2015 | ||||
| Ye et al. | 2017 | N° Stores/street block | Catering businesses | Shenzhen, China | NBR |
| Lin et al. | 2018 | E-KDE (3.5-km BW, 100-m size cells) | Micro-retail pattern (POI) | Guangzhou, China | |
| Cutini et al. | 2018 | N° Stores/ street (30 streets) | Micro-retail pattern | Milan, Italy | Exp-Corr |
| Saraiva et al. | 2019 | E-KDE (20-m size cells) | Micro-retail vacancy | 4 medium-sized Portuguese cities | P-corr |
| Bobkova et al. | 2019 | N° Stores/ plot | Micro retail pattern | London, Amsterdam Stockholm | K-W H-test |
Appendix B. Street-based Urban Form Measures
Appendix B.1. Street Network Configurational Indicators
Following the definition by Porta et al. [8,9] of street network centrality indicators, for each street midpoint i lying on the network G, we implement:
where:
- d[i, j] represents the distance of the shortest path between the reference midpoint i and each destination midpoint j within the sub-network identified by the radius r;
- δ[i, j] represents the relative Euclidean distance between each midpoint i and each destination midpoint j within the same distance;
- is the number of minimum paths from node j to node k on network G passing through point i, with j and k at a distance less than or equal to r.
Following the definition by Luo and Wang [63] of a two-step floating catchment area (2SFCA), we implement the normalization (N) of Equations (A1)–(A4) as:
where is the of each street midpoint j within the sub-network identified by the radius r (as defined in Equation (A1)).

Table A2.
Summary table of the 40 street-network configurational indicators. r, radius; n, normalized.
Table A2.
Summary table of the 40 street-network configurational indicators. r, radius; n, normalized.
| Pedestrian r [meters] | Vehicle [minutes] | |||||
|---|---|---|---|---|---|---|
| 300 | 600 | 1200 | 5 | 20 | ||
Equations (A1)–(A4) are implemented considering a specific weight matrix associating each midpoint j with the presence/absence of a given urban features (such as squares, coastline and anchor stores). This approach would allow the directional centrality measures summarized in the following table to be obtained.

Table A3.
Summary table of the 36 directional centrality indicators. r, radius; S, squares; C, coastline, AS, anchor stores.
Table A3.
Summary table of the 36 directional centrality indicators. r, radius; S, squares; C, coastline, AS, anchor stores.
| Towards Squares r [metres] | Towards Coastline r [meters] | Towards Anchor Stores r [meters] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 300 | 600 | 1200 | 600 | 1200 | 2400 | 300 | 600 | 1200 | |
Appendix B.2. Skeletal Streetscape Descriptors
Figure A1 proposes a schematic illustration of the two GIS protocols implemented for the description of the skeletal streetscape. While the sightline approach (on the left) describes the façade disposition along the street centerline (Table A4), the proximity band approach (on the right) allows the description of the building masses surface/volumetric distribution (Table A5).
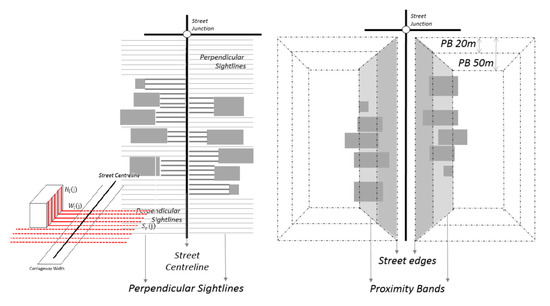
Figure A1.
Graphical representation of the two skeletal streetscape GIS protocols. On the left: building façade described through sightlines perpendicular to the street centerline, homogeneously distributed (3 m). On the right: building footprint and volumes captured by the proximity band approach (source: [89]).

Table A4.
Summary table of the 36 directional centrality indicators. r, radius; S, squares; C, coastline; AS, anchor stores.
Table A4.
Summary table of the 36 directional centrality indicators. r, radius; S, squares; C, coastline; AS, anchor stores.
| Streetscape Indicator from Street Sightlines | ||
|---|---|---|
| Urban Streetscape Component | Indicator | Implementation Formulae |
| Open Space | Openness | |
| Openness Roughness | ||
| Facades-Street Network-Parcels Relationship | Building Setback * | |
| Facades Misalignment | ||
| Average Building Height | ||
| Building Height Misalignment | ||
| Facades Cross-sectional Ratio | Cross-sectional proportion | |
| Variability of Cross-sectional proportion | ||

Table A5.
Streetscape indicators implemented through the proximity band procedure (source: [56]).
Table A5.
Streetscape indicators implemented through the proximity band procedure (source: [56]).
| Streetscape Indicator from Proximity Bands | ||||
|---|---|---|---|---|
| Urban Fabric Component | Indicator | Definition and Implementation Formulae | Proximity Band Width | |
| Network Morphology | Street Length | Street segments length between two intersections | / | |
| Windingness | 1−(Euclidean distance/network distance) between two intersections | / | ||
| Local connectivity | Average of the presence nodes of degree 1 (ND1) | / | ||
| Average presence nodes of degree 4 (ND4) | / | |||
| Average presence nodes of degree 3, 5 + (ND35+) | / | |||
| Built-up Morphology | Prevalence of Building types | (0:125] m2 building surf./total built-up surf. | 50 | |
| (125:250] m2 building surf./total built-up surf. | ||||
| (250:1000] m2 building surf./total built-up surf. | ||||
| (1000:4000] m2 building surf./total built-up surf. | ||||
| (4000: max] m2 building surf./total built-up surf. | ||||
| PB coverage ratio | Built-up Surface/PB Surf. | |||
| Building Contiguity | Weighted average of buildings frequency on built-up units | |||
| Specialization of Building Types | Specialized Building surf./PB surf. | |||
| Network-Building Relationship | Street corridor effect | Parallel façades length/street length | 10 | |
| PB building height H | Building volume/PB surface | 20 | ||
| Open Space Width W | (PB surf.-built surf.)/street length | |||
| Height/Width Ratio | PB Building Height/Open Space Width | |||
| Building frequency along SN | N. of Buildings/Str. length | |||
| Network-Plot Relationship | Parcel Frequency | N. of Plots/Street length | 50 | |
| Site Morphology | Surface slope | High sloped surf. (S > 30%)/PB Surface | 50 | |
| Network-Site Relationship | Street acclivity | Avg. arct(slope) along the street centerline | E [arct(slope)i] | / |
Appendix B.3. Urban Fabrics

Figure A2.
Aerial and street view images of the nine urban fabrics (UFs) of the French Riviera as defined by the MFA protocol (source: Google Map and Google Street view 2017, [56,57,89]).
References
- Smith, A.; Sparks, L. The role and function of the independent small shop: The situation in Scotland. Int. Rev. Retail Distrib. Consum. Res. 2000, 10, 205–226. [Google Scholar] [CrossRef]
- Chiaradia, A.; Hillier, B.; Schwander, C.; Wedderburn, M. Spatial Centrality, Economic Vitality/Viability. In Proceedings of the 7th International Space Syntax Symposium; KTH Royal Institute of Technology: Stockholm, Sweden, 2009. [Google Scholar]
- Aversa, J.; Doherty, S.; Hernandez, T. Big Data Analytics: The New Boundaries of Retail Location Decision Making. Pap. Appl. Geogr. 2018, 4, 390–408. [Google Scholar] [CrossRef]
- Saraiva, M.M. The Morphological Sense of Commerce: Symbioses between Commercial Activity and the Form and Structure of Portuguese Medium-Sized Cities. Ph.D. Thesis, Univ. do Porto, Porto, Portugal, 2013. [Google Scholar]
- Hillier, B. Space is the Machine; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Hillier, B.; Iida, S. Network and Psychological Effects in Urban Movement. In Spatial Information Theory; Cohn, A., Mark, D., Eds.; Springer: Berlin, Germany, 2005; pp. 475–490. [Google Scholar]
- Hillier, B. Centrality as a process. Urban Des. Int. 1999, 4, 107–127. [Google Scholar] [CrossRef]
- Porta, S.; Strano, E.; Iacoviello, V.; Messora, R.; Latora, V.; Cardillo, A.; Scellato, S. Street centrality and densities of retail and services in Bologna, Italy. Environ. Plan. B Plan. Des. 2009, 36, 450–465. [Google Scholar] [CrossRef]
- Porta, S.; Latora, V.; Wang, F.; Rueda, S.; Strano, E.; Scellato, S.; Latora, L. Street centrality and the location of economic activities in Barcelona. Urban Stud. 2012, 49, 1471–1488. [Google Scholar] [CrossRef]
- Saraiva, M.; Marques, T.S.; Pinho, P. Vacant Shops in a Crisis Period—A Morphological Analysis in Portuguese Medium-Sized Cities. Plan. Pract. Res. 2019, 34, 255–287. [Google Scholar] [CrossRef]
- Remali, A.M.; Porta, S.; Romice, O. Correlating street quality, street life and street centrality in Tripoli, Libya. 2014. Available online: https://strathprints.strath.ac.uk/50265/ (accessed on 23 March 2020).
- Ye, Y.; Li, D.; Liu, X. How block density and typology affect urban vitality: An exploratory analysis in Shenzhen, China. Urban Geogr. 2018, 39, 631–652. [Google Scholar] [CrossRef]
- Joosten, V.; Van Nes, A. How block types influence the natural movement economic process: Micro-spatial conditions on the dispersal of shops and Café in Berlin. In Proceedings of the 5th International Space Syntax Symposium, Delft, The Netherlands, 13–17 June 2005; Volume 13. [Google Scholar]
- Bobkova, E.; Marcus, L.; Berghauser Pont, M.; Stavroulaki, I.; Bolin, D. Structure of plot systems and economic activity in cities: Linking plot types to retail and food services in London, Amsterdam and Stockholm. Urban Sci. 2019, 3, 66. [Google Scholar] [CrossRef]
- Saraiva, M.; Pinho, P. Spatial modelling of commercial spaces in medium-sized cities. GeoJournal 2017, 82, 433–454. [Google Scholar] [CrossRef]
- Cutini, V. Centrality and land use: Three case studies on the configurational hypothesis. Cybergeo 2001, 10. [Google Scholar] [CrossRef]
- Omer, I.; Goldblatt, R. Spatial patterns of retail activity and street network structure in new and traditional Israeli cities. Urban Geogr. 2016, 37, 629–649. [Google Scholar] [CrossRef]
- Wang, F.; Antipova, A.; Porta, S. Street centrality and land use intensity in Baton Rouge, Louisiana. J. Transp. Geogr. 2011, 19, 285–293. [Google Scholar] [CrossRef]
- Cui, C.; Han, Z. Spatial patterns of retail stores using POIs data in Zhengzhou, China. In Proceedings of the 2015 2nd IEEE International Conference on Spatial Data Mining and Geographical Knowledge Services (ICSDM), Fuzhou, China, 8–10 June 2015. [Google Scholar]
- Wang, S.; Xu, G.; Guo, Q. Street centralities and land use intensities based on points of interest (POI) in Shenzhen, China. Int. J. Geo-Inf. 2018, 7, 425. [Google Scholar] [CrossRef]
- Cutini, V.; Farese, D.; Rabino, G. Milan: The Configuration of a Metropolis. In Smart Planning: Sustainability and Mobility in the Age of Change; Springer: Cham, Switzerland, 2018; pp. 343–357. [Google Scholar]
- Sevtsuk, A. Path and Place: A Study of Urban Geometry and Retail Activity in Cambridge and Somerville. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2010. [Google Scholar]
- Sevtsuk, A. Location and agglomeration: The distribution of retail and food businesses in dense urban environments. J. Plan. Educ. Res. 2014, 34, 374–393. [Google Scholar] [CrossRef]
- Scoppa, M.D. Towards a Theory of Distributed Attraction: The Effects of Street Network Configuration Upon the Distribution of Retail in the City of Buenos Aires. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2013. [Google Scholar]
- Scoppa, M.D.; Peponis, J. Distributed attraction: The effects of street network connectivity upon the distribution of retail frontage in the City of Buenos Aires. Environ. Plan. B Plan. Des. 2015, 42, 354–378. [Google Scholar] [CrossRef]
- Gardner, W.; Mulvey, E.P.; Shaw, E.C. Regression analyses of counts and rates: Poisson, overdispersed Poisson, and negative binomial models. Psychol. Bull. 1995, 118, 392. [Google Scholar] [CrossRef]
- Pipkin, J.S. A Partitioning Model of Urban Retail Structure. Geogr. Anal. 1993, 25, 179–198. [Google Scholar] [CrossRef]
- Lebrun, N. Centralités Urbaines et Concentrations de Commerces. Ph.D. Thesis, Université de Reims-Champagne Ardenne, Reims, France, 2002. [Google Scholar]
- Cameron, A.C.; Trivedi, P.K. Regression Analysis of Count Data; Cambridge Univ. Press: Cambridge, UK, 2013; Volume 53. [Google Scholar]
- Hilbe, J.M. Negative Binomial Regression; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Guy, C.M. Recent advances in spatial interaction modelling: An application to the forecasting of shopping travel. Environ. Plan. A 1987, 19, 173–186. [Google Scholar] [CrossRef]
- Shonkwiler, J.S.; Harris, T.R. A Non-Gaussian Time Series Analysis of Rural Retail Business Counts. J. Reg. Sci. 1993, 33, 37–48. [Google Scholar] [CrossRef]
- Taleb, N.N. The Black Swan: The Impact of the Highly Improbable; Random House: New York, NY, USA, 2007; Volume 2. [Google Scholar]
- Heywood, I. Introduction to Geographical Information Systems; Addison Wesley Longman: New York, NY, USA, 1998. [Google Scholar]
- Zhang, M.; Kukadia, N. Metrics of urban form and the modifiable areal unit problem. Transp. Res. Rec. 2005, 1902, 71–79. [Google Scholar] [CrossRef]
- Holt, D.; Steel, D.G.; Tranmer, M.; Wrigley, N. Aggregation and ecological effects in geographically based data. Geogr. Anal. 1996, 28, 244–261. [Google Scholar] [CrossRef]
- Lambert, D. Zero-inflated Poisson regression, with an application to defects in manufacturing. Technometrics 1992, 34, 1–14. [Google Scholar] [CrossRef]
- Oakes, J.M.; Andrade, K.E.; Biyoow, I.M.; Cowan, L.T. Twenty years of neighborhood effect research: An assessment. Curr. Epidemiol. Rep. 2015, 2, 80–87. [Google Scholar] [CrossRef] [PubMed]
- Jenks, C.; Mayer, S. The Consequences of Growing up in a Poor Neighborhood. In Inner City Poverty in the United States; Lynn, M., Ed.; McGeary: Washington, DC, USA, 1990; pp. 111–186. [Google Scholar]
- Kaufman, J.S.; Cooper, R.S. Seeking causal explanations in social epidemiology. Am. J. Epidemiol. 1999, 150, 113–120. [Google Scholar] [CrossRef]
- Greenland, S.; Morgenstern, H. Confounding in health research. Annu. Rev. Public Health 2001, 22, 189–212. [Google Scholar] [CrossRef]
- Robinson, W.S. Ecological correlations and the behavior of individuals. Am. Sociol. Rev. 1950, 15, 351–357. [Google Scholar] [CrossRef]
- Nezlek, J.B. Multilevel Modeling for Social and Personality Psychology, 1st ed.; SAGE: London, UK, 2011. [Google Scholar]
- Kropf, K. Bridging configurational and urban tissue analysis. In Proceedings of the 11th Space Syntax Symposium, Lisbon, Portugal, 3–7 July 2017. [Google Scholar]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J.; Li, W. Applied Linear Statistical Models; McGraw-Hill Irwin: Boston, MA, USA, 2005; Volume 5. [Google Scholar]
- Cohen, J.; Cohen, P.; West, S.G.; Aiken, L.S. Applied Multiple Correlation/Regression Analysis for the Social Sciences, 3rd ed.; Erlbaum: Hillsboro, NJ, USA, 2003. [Google Scholar]
- Craney, T.A.; Surles, J.G. Model-dependent variance inflation factor cutoff values. Qual. Eng. 2002, 14, 391–403. [Google Scholar] [CrossRef]
- Judd, C.M.; McClelland, G.H.; Ryan, C.S. Data Analysis: A Model Comparison Approach; Harcourt Brace Jovanovich: San Diego, CA, USA, 2011. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Maddala, G.S.; Lahiri, K. Introduction to Econometrics, 4th ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Lee, C.; Moudon, A.V. The 3Ds+ R: Quantifying land use and urban form correlates of walking. Transp. Res. Part D Transp. Environ. 2006, 11, 204–215. [Google Scholar] [CrossRef]
- Wei, H.L.; Billings, S.A. Feature subset selection and ranking for data dimensionality reduction. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 162–166. [Google Scholar] [CrossRef]
- Roth Tran, B. Blame It on the Rain: Weather Shocks and Retail Sales. 2016. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3381302 (accessed on 23 March 2020).
- Vakhutinsky, A.; Mihic, K.; Wu, S.M. A Prescriptive Analytics Approach to Markdown Pricing for a in E-Commerce Retailer. J. Pattern Recognit. Res. 2019, 1, 1–21. [Google Scholar]
- Verstraete, G.; Aghezzaf, E.H.; Desmet, B. A data-driven framework for predicting weather impact on high-volume low-margin retail products. J. Retail. Consum. Serv. 2019, 48, 169–177. [Google Scholar] [CrossRef]
- Araldi, A.; Fusco, G. From the built environment along the street to the metropolitan region. Human scale approach in urban fabric analysis. Environ. Plan B Urban Anal. City Sci. 2019, 46, 1243–1263. [Google Scholar] [CrossRef]
- Fusco, G.; Araldi, A. The Nine Forms of the French Riviera: Classifying Urban Fabrics from the Pedestrian Perspective. In 24th ISUF International Conference. Book of Papers (1313–1325); Editorial Universitat Politècnica de València: Valencia, Spain, 2017. [Google Scholar]
- Ortiz-Chao, C.G. Land use patterns and access in Mexico City. In Proceedings of the ACSP-AESOP Fourth Joint Congress, Chicago, IL, USA, 6–11 July 2008. [Google Scholar]
- Wang, Z. Regularized Linear Models. 2020. Available online: https://cran.r-project.org/web/packages/mpath/index.html (accessed on 23 March 2020).
- Fleury, A. La rue: Un objet géographique? Tracés. Revue Sci. Hum. 2004, 5, 33–44. [Google Scholar] [CrossRef]
- Marshall, S.; Gil, J.; Kropf, K.; Tomko, M.; Figueiredo, L. Street network studies: From networks to models and their representations. Netw. Spat. Econ. 2018, 18, 735–749. [Google Scholar] [CrossRef]
- Batty, M. Agents, cells, and cities: New representational models for simulating multiscale urban dynamics. Environ. Plan. A 2005, 37, 1373–1394. [Google Scholar] [CrossRef]
- Luo, W.; Wang, F. Spatial accessibility to primary care and physician shortage area designation: A case study in Illinois with GIS approaches. In Geographic Information Systems and Health Applications; Skinner, R., Khan, O., Eds.; Idea Group Publishing: Hershey, PA, USA, 2003; pp. 260–278. [Google Scholar]
- Harvey, C.; Aultman-Hall, L.; Troy, A.; Hurley, S.E. Streetscape skeleton measurement and classification. Environ. Plan. B Urban Anal. City Sci. 2017, 44, 668–692. [Google Scholar] [CrossRef]
- Purciel, M.; Neckerman, K.M.; Lovasi, G.S.; Quinn, J.W.; Weiss, C.; Bader, M.D.; Rundle, A. Creating and validating GIS measures of urban design for health research. J. Environ. Psychol. 2009, 29, 457–466. [Google Scholar] [CrossRef]
- Vialard, A.A. Typology of Block-Faces. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2013. [Google Scholar]
- Araldi, A.; Perez, J.; Fusco, G.; Fuse, T. Multiple Fabric Assessment: Focus on Method Versatility and Flexibility. In Computational Science and Its Applications—ICCSA2018. Proceedings, Part III, Lecture Notes in Computer Science; Springer: Berlin, Germany, 2018; Volume 10962, pp. 251–267. [Google Scholar]
- Portzamparc, C. L’âge III; Projet urbain, n° 3; La ville Hors la Ville: Paris, UK; Minist. Équipement: Paris, France, 1995; pp. 4–6. [Google Scholar]
- McCullagh, P. Generalized Linear Models, 2nd ed.; Chapman and Hall/CRC: Horsham, PA, USA, 2018. [Google Scholar]
- Agresti, A.; Kateri, M. Categorical Data Analysis; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- St-Pierre, A.P.; Shikon, V.; Schneider, D.C. Count data in biology—Data transformation or model reformation? Ecol. Evol. 2018, 8, 3077–3085. [Google Scholar] [CrossRef]
- Kutner, M.H.; Neter, J.; Nachtsheim, C.J.; Li, W. Applied Linear Regression Models, 4th ed.; McGraw-Hill: New York, NY, USA, 2004. [Google Scholar]
- Mullahy, J. Specification and testing of some modified count data models. J. Econom. 1986, 33, 341–365. [Google Scholar] [CrossRef]
- King, G. Variance specification in event count models: From restrictive assumptions to a generalized estimator. Am. J. Political Sci. 1989, 33, 762–784. [Google Scholar] [CrossRef]
- Cameron, A.C.; Windmeijer, F.A. An R-squared measure of goodness of fit for some common nonlinear regression models. J. Econom. 1997, 77, 329–342. [Google Scholar] [CrossRef]
- Long, J.S.; Freese, J. Regression Models for Categorical Dependent Variables Using Stata; Revised Edition; Stata Press: College Station, TX, USA, 2003. [Google Scholar]
- Mittlböck, M.; Schemper, M. Explained variation for logistic regression. Stat. Med. 1996, 15, 1987–1997. [Google Scholar] [CrossRef]
- Menard, S. Coefficients of determination for multiple logistic regression analysis. Am. Stat. 2000, 54, 17–24. [Google Scholar]
- Tjur, T. Coefficients of determination in logistic regression models—A new proposal: The coefficient of discrimination. Am. Stat. 2009, 63, 366–372. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. In Selected Papers of Hirotugu Akaike; Springer: New York, NY, USA, 1974; pp. 215–222. [Google Scholar]
- Vuong, Q.H. Likelihood ratio tests for model selection and non-nested hypotheses. Econom. J. Econom. Soc. 1989, 57, 307–333. [Google Scholar] [CrossRef]
- Wilson, P. The misuse of the Vuong test for non-nested models to test for zeroinflation. Econ. Lett. 2015, 127, 51–53. [Google Scholar] [CrossRef]
- Kleiber, C.; Zeileis, A. Visualizing count data regressions using rootograms. Am. Stat. 2016, 70, 296–303. [Google Scholar] [CrossRef]
- Gujarati, D.N. Basic Econometrics, 5th ed.; Tata McGraw-Hill Education Private Ltd.: New Delhi, India, 2009. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013; Volume 112, pp. 3–7. [Google Scholar]
- Gideon, S. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar]
- Parkins, A.E. Profiles of the Retail Business Section of Nashville, Tenn., and Their Interpretation. Ann. Assoc. Am. Geogr. 1930, 20, 164–175. [Google Scholar] [CrossRef]
- Conzen, M.R.G. Alnwick, Northumberland: A study in town-plan analysis. Trans. Pap. Inst. Br. Geogr. 1960, 27, iii-122. [Google Scholar] [CrossRef]
- Araldi, A. Retail Distribution and Urban Form: Street-Based Models for the French Riviera. Ph.D. Thesis, Université Côte d’Azur, Nice, France, 2019. [Google Scholar]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).