1. Introduction
As an adolescent, Christopher Alexander wished for himself a career in the fine arts, with its concomitant obsession with beauty and keen observation. Paternal pressure, however, was for something more ‘serious’—such as mathematics with its concomitant devotion to precision and veracity. His education consisted of an advanced degree in mathematics from Trinity College at Cambridge sandwiched between a BA (Trinity) and PhD (Harvard) in Architecture [
1]. He was then armed with both his original abiding concern for the aesthetic and an equally abiding concern for the verifiable.
In this essay, we hone our understanding of Beauty as we go, just as Alexander did. We encounter our cognitive handicaps just as Alexander did—but chronology yields to a few nods forward and backward in order to highlight the continuity of our main themes. As for complexity, our core reference is the classic material of scientist Warren Weaver and urban critic Jane Jacobs outlined in
Life and Death of American Cities [
2]. We have (a)
disorganized complexity, which arises in systems where many elements interact apparently randomly, but whose properties as a whole can be understood by using statistics and probabilities. We have (b)
simpler complexity involving few variables. In the far more difficult middle range, we have (c)
organized complexity which entails nonlinear, non-random interactions of variables, dynamic unfolding, and emergent properties. In a sense, a system with organized complexity presents as a coherent whole even before statistical analysis is performed—the system appears as if purposes were behind the interactions. Life sciences, understandings of negentropy, creative acts in art, poetry, music, architecture, and the functioning of natural cities—all of these have their home in organized complexity. Tools to understand such systems include modeling and simulation.
2. Intellectual History: Sixties, Early Material
Précis: As a young man, Christopher Alexander’s initial conception of Beauty revolves around appropriateness or ‘a just rightness of fit.’ Complexity, he believes, can be partially tamed with set theory. As this first decade of work harvests new insights, Beauty becomes an emergent property of organized complex systems and Alexander deepens his appreciation of overlap, ambiguity, and multiplicity of meaning. Main early publications: NOTES ON A SYNTHESIS OF FORM [
3], A CITY IS NOT A TREE [
4], BART [
5].
Remark One
Notes on the Synthesis of Form [
3], Alexander’s Ph.D. thesis, was an attempt to bring to heel the complexity of a village in India—his tools: force analysis, set theory, clustering, modularization, cohesion, coupling, strong and weak links. Beauty was, more than anything else, about ‘good fit,’ a lack of mistakes, and the appropriateness of a built object to its context and purpose. Design was, perforce, a somewhat humble activity of recognizing ‘misfits’ and correcting them while leaving in place that which worked well. It had to be that way because anything else was hubris, the taking on of more complexity than one could assimilate.
Alexander came home from India with an unshakeable certitude in the superiority of natural systems and long-standing building traditions grounded in soil and history. Why? Because they had a demonstrable superiority in dealing with organized complexity: distributed intelligence across a network, redundancy of information, multiple means of embedding information throughout the network, deep knowledge of variables such as local geography, weather patterns, multiple cultural demands, effective and economical use of local materials. Such a natural and unselfconscious process entailed gentle abstraction by generalization. Forms were local, buildable, purposeful, economic. Form did not follow function as in an abstract edict; function followed the concrete potentiality in the available forms. A field was cleared of rocks and the rocks offered their particular affordances for building, right there in situ. All interconnected within a complex whole.
Modern professionals, Alexander believed, with no choice but a self-conscious process which divorces them from such rich reality and limits them to arbitrary simplifications (often made far from the actual building site and inhabitants) are condemned to failure. When the Indian government offered Alexander a job designing a new town from scratch, he stuck with these convictions and turned down the opportunity—the task was too complex.
This theme of natural limitations in handling complex decisions never disappears. Decades later, in
The Nature of Order [
6,
7,
8,
9], Alexander returns to the impossibility of success with self-conscious
fabricated building. The number of likely mistakes is astronomical compared to the more natural or unself-conscious
generated building where manageable phases unfold in sequence. For example, in Book Two of
The Nature of Order [
7], Alexander estimates that a typical American house, constructed to blueprint, requires about 2000 carpenter-hours of work, with several decisions—of dimension and placement—made per hour. Since it’s nearly impossible to get any of them right, each house starts out with around 5000 carpenter mistakes—meaning a deliberate choice made incorrectly in retrospect. Let’s understand this: When a choice can be made in the context of the real world, where that thing will exist and where people are able to see and feel how they will interact with it, the choice can be made purposefully. When the choice is made at the drawing table by a designer, it is likely to be based on irrelevant ideas (such as a pre-existing image the designer has) or to be random, and, therefore, unlikely to contribute meaningfully to the whole.
Remark Two
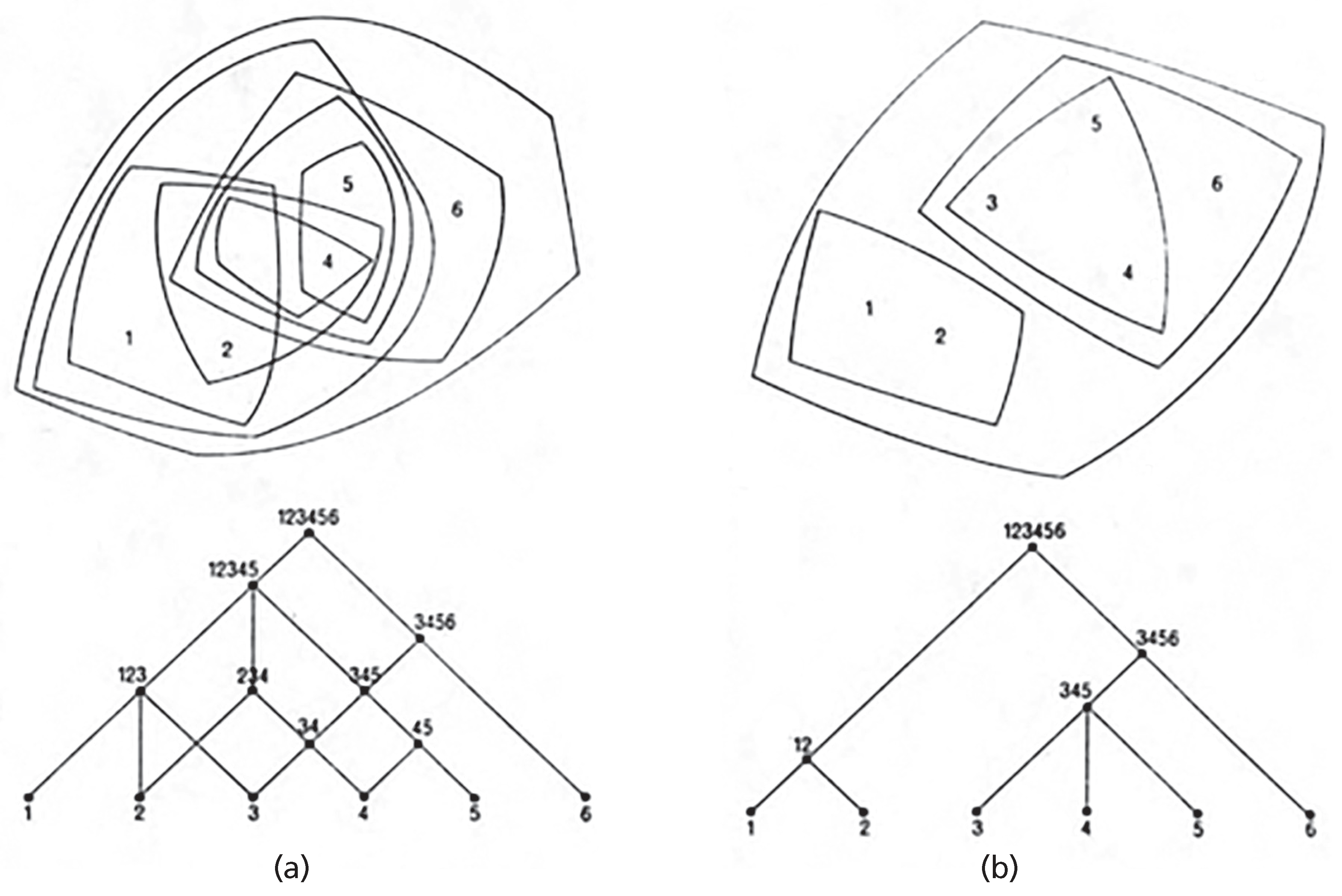
His now classic essay,
A City is Not a Tree [
4], brought Alexander into direct confrontation with his peers in urban planning. The job of the professional is to understand the organizing principles underpinning natural lively cities. Alas, we fall into our cognitive handicap trap of preferring models we can fathom over more difficult ones with a better chance of serving our needs. ‘Designed’ towns are set up as trees (
Figure 1b) (Alexander reviews a number of examples), but semilattices (
Figure 1a) are a better model for natural cities.
Alexander uses these definitions: A collection of sets is a tree if and only if for any two sets that belong to the collection, either one is fully contained in the other or else they are disjoint; a collection of sets is a semilattice if and only if whenever two overlapping sets belong to the collection, then the intersection of those sets also belongs.
To get an idea of the difference in complexity between tree and semilattice models, consider that a tree model based on 20 elements can maximally contain 19 subsets of the 20 elements (here they are for a balanced binary tree with 20 leaves: [a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t], [a, b, c, d, e, f, g, h, i, j], [k, l, m, n, o, p, q, r, s, t], [a, b, c, d, e], [f, g, h, i, j], [k, l, m, n, o], [p, q, r, s, t], [c, d, e], [h, i, j], [m, n, o], [r, s, t], [a, b], [d, e], [f, g], [i, j], [k, l], [n, o], [p, q], [s, t]), while a semilattice based on the same 20 elements makes room for over 1,000,000 subsets (the power set of 20 elements contains 1,048,576 subsets). If it were 50 instead of 20, the number would start ‘one quadrillion ….’
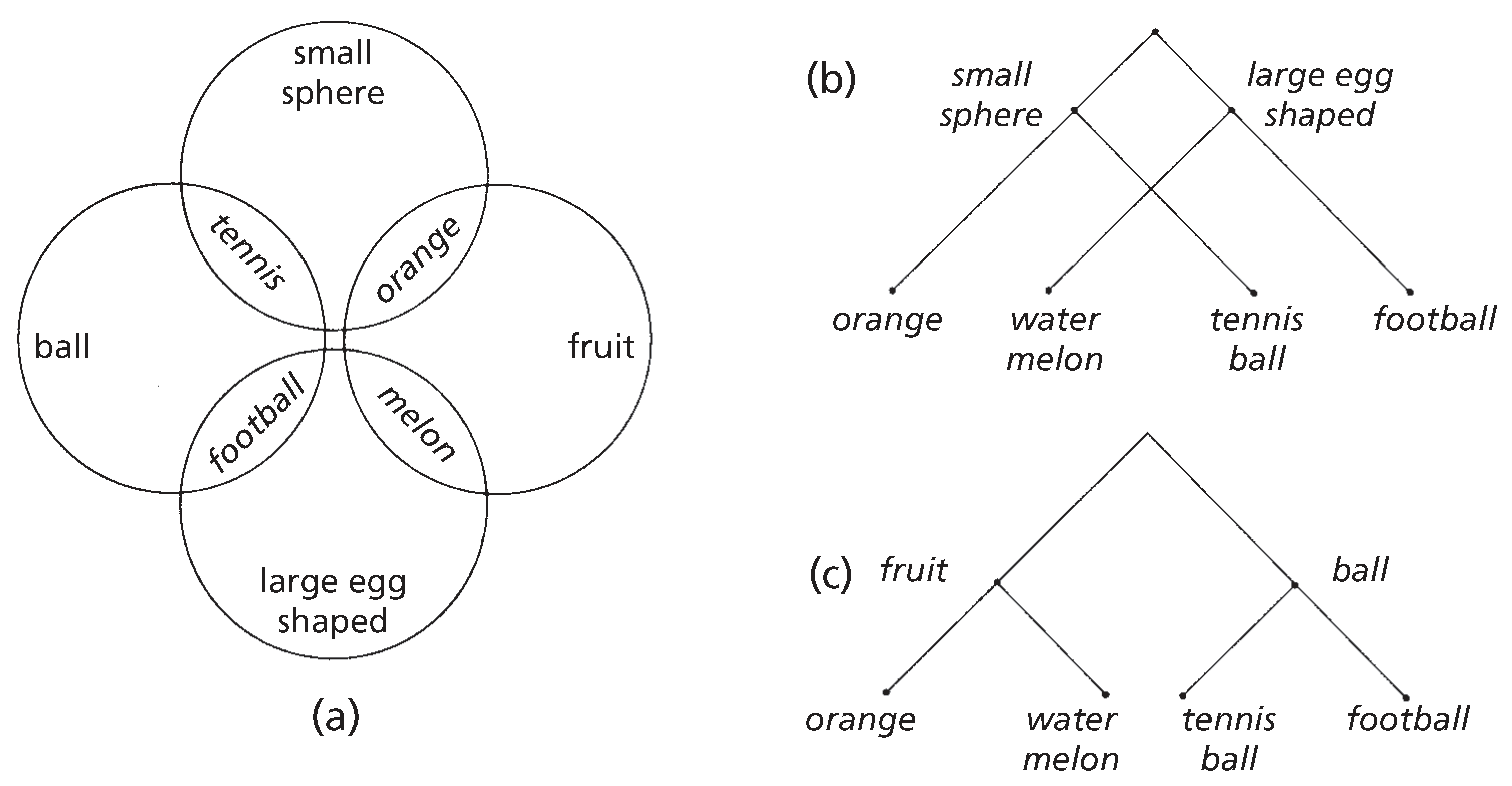
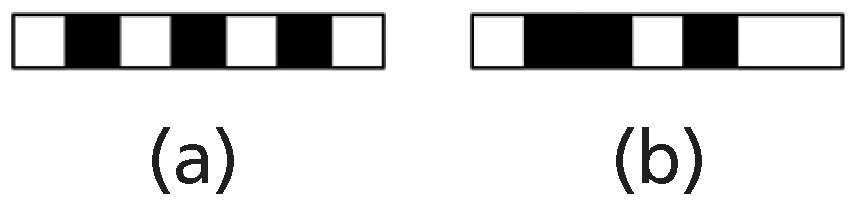
In his essay, Alexander patiently works out the cognitive difficulty of thinking in terms of overlapping subsets with an embarrassingly simplistic example. Given an orange, a watermelon, a football, and a tennis ball, we can group them as fruit and sports balls (
Figure 2a,b) or as small spheres and large oblong objects (
Figure 2a,c); we can visualize individual groupings in a tree structure, but because they overlap, it is beyond us to visualize four sets simultaneously in one simple move. We have to decompose and then re-compose. Alas, even with just an orange, watermelon, football, and tennis ball, we are but Pooh Bears of little brain, we can’t trivially do it.
Optimizing a tree is relatively simple—just optimize each node; the nodes are guaranteed to be independent. Optimizing a semilattice might require a metaheuristic approach because the search space is too big or too ill-structured. A metaheuristic approach samples a search space to find, generate, or select a sufficiently good optimization, but it does not guarantee a globally optimal solution. Many metaheuristic approaches use some form of stochastic optimization based on a set of generated random variables.
Jane Jacobs’ place ballet, a theater metaphor which initially seems quite limited, is really about the ability of an urban hardscape (as theater stage) to accommodate multiple choreographies acted out simultaneously. A single-use prop, say, a fancy street bench where one can only sit, does us little good. We’re better off with a low wide wall that can operate in multiple subsets: protect a bed of tulips, let grandpa sit in the sun, invite little Johnny to pretend he is on a tightrope, mark a boundary for neighborhood gangs, and accommodate a teenager who needs to put down schoolbooks to text a friend.
Beauty is part and parcel of all this. Overlapping subsets gives us ambiguity, multiple possibilities, slowly revealing meanings, and complexity in an urban environment. It is this complexity which enlivens us. The experience of Beauty lies partly in the half-hidden or deeply hidden relationships we can only dimly perceive or intuit. To illustrate this point, Alexander chose a painting by Simon Nicholson—chosen because it has no content other than overlap—and in the essay works out just a couple of the various overlaps, partially reconstructing the underlying semilattice (
Figure 3). He explains our intrigue and aesthetic appreciation of the painting: we relish the opportunity to intuit the higher complexity. Beauty is not simple. It is not the result of tree-thinking; it is complex, and perhaps in the direction of organized complexity.
Overlap and ambiguity would remain in Alexander’s conceptual arsenal until the end of his career. In a later book,
The Nature of Order [
6], Alexander will argue that DEEP INTERLOCK AND AMBIGUITY must be one of the fifteen essential geometric properties creating wholeness—and therefore Beauty. In
Battle [
10], his latest book, Alexander writes:
The principal features of a complex configuration are always created by overlap. Although this overlap may seem trivial, when we examine the overall design of the Persian carpet [in question], you will see that this kind of overlap, and ambiguity, is essential and pervasive…. This is the glue in any system of wholes. Wholeness itself is directly created by this apparent overlap, or ambiguity. The greater the number of overlapping wholes, the more tightly bound the configuration is, and the more deeply the wholeness of the object shows itself to be.
Overlap is not purely geometric—it can be semantic as well. For an example of overlap and organized complexity in literature, consider the novel,
Moby Dick [
11]. Ahab and the white whale (Moby Dick) are similarly described: Ahab:
bleached bone, ribbed and dented brow, wrinkled brow, snow-white ivory leg, wrinkling his brow; Moby Dick:
wrinkled brow and a crooked jaw, his wrinkled brow, the peculiar snow-white brow of Moby Dick. These form a descriptive overlap and hence gives rise to an existential ambiguity between Ahab and his obsession, Moby Dick, the white whale.
Remark Three
The study of BART [
5]—the San Francisco Bay Area Rapid Transit system—also instructs about Beauty, design, and complexity. Alexander was still in his young phase of system analysis, system requirements, misfits, hierarchical decomposition of parts. His study of the forces around a ticket booth lists 390 requirements (get tickets, get change, limit waiting time, the wait line can’t interfere with other traffic flows, and so on).
Even this relatively thorough model-through-requirements of a ticket booth didn’t cooperate with reality—other forces step forward out of the system itself; they act on their own behalf to come to their own balance. The designer is not in control of their creation. For example, one traveler simply pauses to chat with another traveler and confounds the traffic plan. Of course, there was a requirement that there not be congestion, but there was nothing the designers could do to prevent it with a designed mechanism. Alexander describes his thoughts:
So it became clear that the free functioning of the system did not purely depend on meeting a set of requirements. It had to do, rather, with the system coming to terms with itself and being in balance with the forces that were generated internal to the system, not in accordance with some arbitrary set of requirements we stated. I was very puzzled by this because the general prevailing idea at the time [1964] was that essentially everything was based on goals. My whole analysis of requirements was certainly quite congruent with the operations research point of view that goals had to be stated and so on. What bothered me was that the correct analysis of the ticket booth could not be based purely on one’s goals, that there were realities emerging from the center of the system itself and that whether you succeeded or not had to do with whether you created a configuration that was stable with respect to these realities.
We have with the BART study a first inkling of emergent properties of a complex system—a property lying somewhere just beyond reach. Alexander got his first hint that some emergent properties surprise. Complexity has a mind of her own. This temporality and, shall we say, independence of complex systems would slowly command more attention.
3. Intellectual History: Seventies to Mid-Eighties, a Prolific Period
Précis: Now teaching at Berkeley, Christopher Alexander is working with various groups of colleagues, and can institutionally muster project participants and students as research aids. The themes from his early work continue and evolve. Modularity with strong and weak links, now formulated as
patterns, is explored as a possible way to regain unself-conscious building. The subtle ineffability of Beauty warrants an entire book (
Timeless Way), and yet Beauty is also pegged as an exacting discipline of reckoning with each and every design constraint. Standard practices in urban development are seen as hopelessly wrong-headed. Fact and humanistic values must both figure in our decision-making. Major projects include Mexicali, which fails, and the Eishin campus in Japan, which succeeds. Main publications: A PATTERN LANGUAGE [
13], THE TIMELESS WAY OF BUILDING [
14], THE OREGON EXPERIMENT [
15], A NEW THEORY OF URBAN DESIGN [
16], THE GRASS ROOTS HOUSING PROCESS [
17].
Remark One
The book,
A Pattern Language [
13], was the outcome of a Request for Proposal (RFP) posted by the American Government. The National Institutes of Health (NIH) wanted to know if there was a relationship between the built environment and human well-being. They would pay for research. Alexander and colleagues responded to this RFP in a curious way: not only did they not know the answer, they admitted that they had no idea about how to find out. That said, it was an interesting question and they were willing to give it a try. They got the job.
Many ‘walkabouts’ and discussions later, the team formulated the concept of
pattern and catalogued 253 instances of spatial configurations that supported well-being in everyday, ordinary life. For example, a narrow ledge on the side of a building feels precarious, and the most that people do with it is put out laundry. A SIX-FOOT BALCONY (Pattern #167 [
13]), however, affords a sense of ease and safety, room for a small table and chairs, an invitation to connect life inside the building with life on the street, integrating the urban fabric both socially and physically. As another example, take the pattern, ENTRANCE TRANSITION (Pattern #112 [
13]): the problem space and
force resolution of a simple door—
ingress,
regress, and
closure—are changed and enlarged to include
transition and
threshold. The pattern recognizes not only our physically coming home after a day in the office, but our psychological need for time and space to shed our public persona and prepare for our domestic selves. This re-evaluation of function as well as form carries forward a concern seen earlier in
Notes.
To summarize the essentials: a pattern language is a set of abstract instructions, called “patterns,” which address recurring problems and tell people what they need to do in order to resolve those problems, along with a set of sequences—the order in which to consider the patterns. Each implementation will be different and finely adjusted to its context.
The word “pattern” refers (ambiguously) both to a configuration in the real world and the text which presents the problem-solution bundle to a designer/builder. A well-described pattern includes a set of forces, which are the overlapping relationships and other considerations the designer/builder must keep in mind when applying the pattern in situ. Forces and their resolution are essential to a pattern. In the ENTRANCE TRANSITION pattern, the forces are as follows:
provide ways to do the following:
- -
enter and leave the building,
- -
isolate inside from outside (protection from the weather, for example),
provide a transitional zone from the outside style of “public behavior” to an “intimate spirit,”
the transition zone must be large enough to take the time needed to “destroy the momentum of the closedness, tension, and ‘distance’ which are appropriate” to the outside world,
the transition zone can be, for example:
- -
outside the house,
- -
inside the house but outside the innermost parts of the house (an entry court),
- -
within a garden or hidden by a gate or bushes,
- -
around a bend that shelters the entrance from the street,
- -
a difference in texture along the path.
Because this zone might support other purposes—for example, because it is a garden—the forces appropriate to those other purposes must enter the balancing and resolution. Alexander worked with forces from the very beginning of his career and theorized about them until the end.
Although
A Pattern Language is generally considered to be his most important book, Alexander personally gave more weight to its philosophical companion, a long musing on the ineffability of Beauty—
The Timeless Way of Building [
14]:
The great traditional buildings of the past, the villages and tents and temples in which man feels at home, have always been made by people who were very close to the center of this way. It is not possible to make great buildings, or great towns, beautiful places, places where you feel yourself, places where you feel alive, except by following this way. And, as you will see, this way will lead anyone who looks for it to buildings which are themselves as ancient in their form, as the trees and hills, and as our faces are.
To understand the Timeless Way and to know how to design and build toward Beauty and well being, one has to know the
Quality Without a Name (QWAN):
There is a central quality which is the root criterion of life and spirit in a man, a town, a building, or a wilderness. This quality is objective and precise, but it cannot be named.
The mysterious way in which Alexander speaks of the Quality Without a Name reflects the paradoxical nature of Beauty as he saw it. Consider these statements:
The first place I think of when I try to tell someone about this quality is a corner of an English country garden where a peach tree grows against a wall. The wall runs east to west; the peach tree grows flat against the southern side. The sun shines on the tree and, as it warms the bricks behind the tree, the warm bricks themselves warm the peaches on the tree. It has a slightly dozy quality. The tree, carefully tied to grow flat against the wall; warming the bricks; the peaches growing in the sun; the wild grass growing around the roots of the tree, in the angle where the earth and roots and wall all meet.
It [QWAN] is a subtle kind of freedom from inner contradictions.
Alexander tried very very very hard to convey the mystery. The mystery that enables us to live. It means something like “alive,” but it isn’t metaphorical; “whole” captures part of the meaning—a thing that is whole is free from inner forces that can tear it apart, but “whole” implies enclosure and separation; “comfortable” captures some of the coziness of
QWAN, like the Danish concept of
hygge (a quality of coziness and comfortable conviviality that engenders a feeling of contentment or well-being), but “comfortable” has too many other meanings, like having too much money; “free” helps define the quality by implying that things that are not completely perfect or over-planned or precise can have the quality too, but “free” can imply wild abandon; “egoless” gets at it because a thing with
QWAN doesn’t seem planned precisely as if by a mastermind trying to fulfil an abstract image, but “egoless” misses because the personality of the designer and builder can shine through; “eternal”—
“something with the quality is so strong, so balanced, so clearly self-maintaining that it reaches into the realm of eternal truth, even if it lasts for only an instant” {
Timeless} [
14], but “eternal” implies mysteriousness, and
QWAN is ordinary; and finally there is “exact”—which, as we will see, is paradoxical in its own way.
For Alexander, a pattern language was simply an artificial crutch we can use to help us recall, reinvent, or rediscover our connection to the Quality Without a Name:
To reach the quality without a name we must then build a living pattern language as a gate.
This quality in buildings and in towns cannot be made, but only generated, indirectly, by the ordinary actions of the people, just as a flower cannot be made, but only generated from the seed.
Many scientists and mathematically inclined folks—practical people, computer scientists—shy away from this strange formulation. Alexander, though, believed that QWAN was something out there in an objective sense—possibly definable mathematically, something that could be recognized by an algorithm, or at least something that people can recognize because our cognition evolved to do so.
Remark Two
With this NIH research assignment—resulting in A Pattern Language and Timeless Way—humanistic values reached center stage and crisper definition. It all built upon earlier work.
Cultural forces had already been included in
Notes where Alexander had begun his investigation into how the texture and ambiguity of human life figure into the creation of homes and towns with the ‘clarity of form’ and ‘clarity of conception’ that underlie the unselfconscious approach to design. Building structures are made a particular way because that is how such structures are made in the local culture, from local materials because those are the only ones available, and they are made to be repaired by the same hands that built them. They conform to the land, weather, and climate because they must be able to survive there. Alexander writes of the Mousgoun African tribesmen:
[E]ach hut nestles beautifully in the dips and hollows of the terrain. It must, because its fabric is as weak structurally as the earth it sits on, and any foreignness or discontinuity caused by careless siting would not have survived the stresses of erosion. The weather-defying concrete foundations which we rely on, and which permit the arbitrary siting of our own houses, are unknown to the Mousgoum.
Legends, myths, rituals, and social order contribute to the nature of form and structure:
Each man’s hut is surrounded by the huts of his wives and his subservients, as social customs require—and in such a way, moreover, that these subsidiary huts also form a wall round the chief’s hut and thereby protect it and themselves from wild beasts and invaders.
In the BART study, Alexander learned that designers would need to come to terms with the unpredictability of ordinary people. Overlapping subsets were already valued as ways to arrange hardscape support for the dense texture, changeability, and complexity of human interactions.
Three aspects of Alexandrian Beauty became more salient as these humanistic values (cultural appropriateness, well-being, and QWAN) become inextricably linked to Beautiful solutions.
First, Beauty requires exquisite exactness. We had already seen that the structure of a design solution must match the structure of the problem. The exactness of Beauty means an adaption to all the forces and a solution which allows all those forces freedom to flow through.
Imagine, for example, that you are a ornithophile and would like to enjoy bird watching from both your kitchen window and your study. You decide to put out winter bird seed for blackbirds in your back garden. Even a bird feeder is complex. Blackbirds don’t like to swoop close to the ground so the feeder has to be high enough, but not too high or the wind will interfere, and you can’t put the feeder near other objects (like a clothesline) that will frighten them, and you can’t expose the birds to predators, and, of course, you want to enjoy them from comfortable spots inside your home. Almost every location and every form of feeder will be slightly wrong and, to be beautiful, it has to be exactly right. This insistence on reckoning with
all forces is non-negotiable. Even really tough problems—Alexander’s much later criticism regarding sustainable building comes to mind—must be worked through to perfection. It is not good enough to have premier solar panels and water catchments if that comes at the cost of ignoring other factors {
Sustainability} [
18].
Second, Beauty, which emerges on its own terms and embodies freedom from inner contradictions, can come only from designs that include human experience in the equation. Alexander was adamant about this. Traditionally, scientists, to keep their work tight and controllable, have insisted on eliminating personal experience. They seek repeatable experiments. They seek to understand what is, not what makes something Beautiful. Alexander understood both math and science, so that is not the point. Alexander, increasingly phenomenological, sought to illuminate experience and he started with his own experiences. As he steadfastly observed the object—what is ‘not him’ (bird feeders, low wide walls, town traffic, solar panels)—he became increasingly aware of the boundary with what is ‘him’—the subject—his own presence and existence.
Third, a recognition of Beauty emerges from the play between subject (you) and object (not you). This is core to
The Timeless Way of Building and, more directly, to Alexander’s life as a practitioner and teacher. Alexander exhorted us and himself onward in the following manner: you—the subject, the student, the doer—must work work work on your object—the not you, the city plan, the masonry wall. You must work in such a way (intensely, egolessly) that your work (the object, the plan, the wall) takes on qualities that evoke in you (the subject) a recognition of
QWAN in the object. For Alexander, this
QWAN, this Beauty, contained a certain sadness. It had, he said, the power to remind him of his own fleeting existence.
“It has a slightly bitter quality.” {
Timeless} [
14].
“I try to make the building so that it carries my eternal sadness.” {
Nature of Order Book Four} [
9]. This kind of work effort has, in his words,
“a goal of tears” [
9]. If you succeed, then your
œuvre evokes in others such deep feeling. The subject/object divide starts to blur towards non-duality.
This non-duality has the status of Value. Here is how Alexander expressed his hope that there could be unification of the classic distinction between
Fact and
Value—that is, between
what is and
what ought to be, or between scientific Truth and (perhaps moralistic) Beauty:
Myself, as some of you know, originally a mathematician, I spent several years, in the early sixties, trying to define a view of design, allied with science, in which values were also let in by the back door. I too played with operations research, linear programming, all the fascinating toys, which mathematics and science have to offer us, and tried to see how these things can give us a new view of design, what to design, and how to design.
Finally, however, I recognized that this view is essentially not productive, and that for mathematical and scientific reasons, if you like, it was essential to find a theory in which value and fact are one, in which we recognize that here is a central value, approachable through feeling, and approachable by loss of self, which is deeply connected to facts, and forms a single indivisible world picture, within which productive results can be obtained.
Alexander is saying he needs to find mathematical and scientific explanations for his intuitions in order for them to be taken seriously outside the arts. He wants Value to be a scientific fact—a statement that can be true or false, not one that is just opinion. Perhaps Alexander’s greatest legacy—and, so far, as a larger community, we have failed to take up the challenge—is to fully recognize that progress in urban sciences, and design and building of any sort, must include the qualitative, qualities, the experiential, Values as well as Facts.
Remark Three
The other important publications from this period—
The Oregon Experiment [
15] and
A New Theory of Urban Design [
16]—cover a lot of ground, but we mention just two themes critical for the making of urban fabrics.
Large lump development is a fool’s errand. Alexander writes:
Large lump development hinges on a view of the environment which is static and discontinuous; piecemeal growth hinges on a view of the environment which is dynamic and continuous …. According to the large lump point of view, each act of design or construction is an isolated event which creates an isolated building—“perfect” at the time of its construction, and then abandoned by its builders and designers forever …. Large lump development is based on the idea of replacement. Piecemeal growth is based on the idea of repair.
Our only prayer for coping with change is via incremental, in situ growth where we stringently limit decision-making to a stage-by-stage process—where we need to keep things in a semi-stable equilibrium, always whole, always livable, always learning. With piecemeal growth—and especially when the growth and learning take place after initial construction—there is time to get the decisions right. To see this, the Reader may try this simple experiment. Take ten pennies. Count the number of times you need to flip the coins one by one until all of them show heads. That is, flip the first coin until it shows heads—count how many times that took; then, flip the second coin until it shows heads and add that count to what you have so far. Do that until they all show heads. Now, count the time it takes you to flip all ten at once until they all simultaneously show heads. On average, it takes 20 flips to get all of them to show heads when you flip one coin at a time. On average, it takes 1024 flips to get them to all show heads when you flip them as a group: ; .
Large lump development spends in large lumps. Alexander believed that a gradient of spending is far healthier than a few fat envelopes. For every expenditure of 1000, there should be ten expenditures of 100, and, for every expenditure of 100, there should be ten expenditures of ten and, for every expenditure of ten, there should be ten expenditures of one. Repair and constant adaptation to change carry on from the broken flower pot to the roof to the roadway.
Agency surfaced as another critical theme. Who is to make or implement any given decision? The line of thinking originating in
Notes on the Synthesis of Form remains unbroken. In the unselfconscious process, the inhabitant of the house knows, better than anyone, about the misfits and knows, better than anyone, what the appropriate fix would be and needs no special permission to execute that fix. Keep the power of analysis and repair right there. Don’t move it up or sideways. When we get to the modern world of the Oregon university campus [
15] or renewal of the San Francisco waterfront [
20], things are more difficult, but the emphasis is the same. Those directly involved know the most and have mastered the most local complexity. Designers must work with that. The exactness which Beauty requires has a better chance if they do.
Alexander coalesced these ideas into a building process called the “Grassroots Housing Process” [
17].
Practices:
an architect-builder is in charge,
each site has its own builder’s yard for materials and tools,
common land between houses and the array of lots is handled by the community itself in groups small enough for face-to-face meetings,
families design their own homes,
construction is based on a standard process, not on standard components.
Principles:
Organic Order is achieved when there is a perfect balance between the needs of the parts and the needs of the whole: planning and construction will be guided by a process which allows the whole to emerge gradually from local acts;
Participation: all decisions about what and how to build will be in the hands of the users;
Piecemeal Growth: the construction undertaken in each budgetary period will be weighted overwhelmingly toward small projects;
Patterns: all design and construction will be guided by a collection of communally adopted patterns;
Diagnosis: the well being of the whole will be protected by an annual diagnosis which explains, in detail, which spaces are alive and which ones are dead;
Coordination: the slow emergence of organic order in the whole will be assured by a funding process which regulates the stream of individual projects.
Remark Four
Two significant larger scale building projects mark these years: Mexicali and the Eishin Campus. In 1975, Alexander got the opportunity to try his ideas—the practices and the principles—
in toto. Based on the strong recommendation of the University of Mexico, the Mexican government hired him to construct low cost self-designed housing for 30 families and to do things as he saw fit. There is no other way to put it: the project failed. Dismayed and alarmed, the government pulled the plug when only five houses had been built. A few excerpts from Alexander’s reflections:
The almost naïve, childish, rudimentary outward character of the houses disturbed them [the Mexican government] extremely.
…The buildings …are very nice, and we are very happy that they so beautifully reflect the needs of different families. But they are still far from the limpid simplicity of traditional houses, which was our aim …. The freedom of the pattern language, especially in the hands of our apprentices, who did not fully understand the deepest ways of making buildings simple, occasionally caused a kind of confusion ….
The word “simplicity” is obviously not the relevant word. There is something which in one instance tells you to be simple and which in another tells you to be more complicated. It’s the same thing which is telling you those two things.
But even assuming that you have got the technical part clear, the creation of this quality [QWAN] is a much more complicated process of the most utterly absorbing and fascinating dimensions. It is in fact a major creative or artistic act—every single little thing you do.
{
Production of Houses} [
21]
In 1985, Alexander got a second chance when invited to design and build a school campus in Japan. In his latest book,
Battle [
10], Alexander offers his embittered retelling of the blow-by-blow combat with standard industrial processes which stood in the way of achieving the Beauty he craved. However fraught, the project was completed. Hiroshi Ichikawa, professor of philosophy and aesthetic criticism wrote about Eishin in 1989:
When I first visited the campus, I found it rather strange and uncomfortable; I left soon after seeing it. The next day, I kept on thinking about what I had seen, and went back to see the campus again. A few days later, still having the picture of the campus in my mind, I could not let it go, and went back to see it once again.
During the next months, I found myself drawn back to it, again and again and again. The place and the buildings have a hidden depth, not present in contemporary, 20th-century works of architecture.
4. Intellectual History: Nineties, Perceived Failure and Begin Again
Précis: The collegial groups have now disbanded. Alexander is working mostly solo. In spite of the sales success of
A Pattern Language, Alexander is disappointed. Pattern aficionados build funky. It all lacks coherence and profundity. Where did he go wrong? What did he not say? Alexander opts to go back to the drawing board—and in a radical fashion. His previous attempts to bring mathematics to bear on complexity is held in abeyance. Persistent and disciplined observation comes to the fore. Complexity is dealt with intuitively. New tools and concepts are required and slowly forged. Beauty will now find roots in geometry, although the mathematics thereof will remain elusive. God becomes part of the discussion. Building project: West Dean Visitor Center. Major publication: A FORESHADOWING OF 21st CENTURY ART [
22].
Remark One
Alexander’s profound sense of dismay finds expression in these quotes:
Bootleg copies of the pattern language were floating up and down the West Coast and people would show me projects they had done and I began to be more and more amazed to realize that, although it worked, all of these projects basically looked like any other buildings of our time. They had a few differences. They were more like the buildings of Charles Moore or Joseph Esherick, for example, than the buildings of S.O.M. or I. M. Pei; but basically, they still belonged perfectly within the canons of mid-twentieth century architecture. None of them whatsoever crossed the line.
They thought the buildings were physically different. In fact, the people who did these projects thought that the buildings were quite different from any they had designed before, perhaps even outrageously so. But their perception was incredibly wrong; and I began to see this happening over and over again—that even a person who is very enthusiastic about all of this work will still be perfectly capable of making buildings that have this mechanical death-like morphology, even with the intention of producing buildings that are alive.
So there is the slightly strange paradox that, after all those years of work, the first three books are essentially complete and, from a theoretical point of view, do quite a good job of identifying the difference but actually do not accomplish anything. The conceptual structures that are presented are just not deep enough to actually break down the barrier. They actually do not do anything.
Alexander had a hunch about where he went most wrong. Geometry:
The point is that I was aware of some sort of field of stuff—some geometrical stuff—which I had actually had a growing knowledge of for years and years, had thought that I had written about or explained, and realized that, although I knew a great deal about it, I had never really written it down ….
In a diagnostic sense, I can say that if this geometrical field is not present in something then there is something wrong there and I can assess that fact within a few seconds.
To summarize, patterns are about spatial configurations but he hadn’t been very clear about how to put them together. A pattern is one thing. A pattern language is something else. He had spoken in the preface to
A Pattern Language (
APL) about the deeper Beauty, the poetry that comes from overlapping and densely packed patterns versus mundane more linear prose, but that had not given people much traction. He hadn’t been very clear about volumes of space:
…the majority of people who read the work, or tried to use it, did not realize that the conception of geometry had to undergo a fundamental change in order to come to terms with all of this. They thought they could essentially graft all the ideas about life, and patterns, and functions on to their present conception of geometry. In fact, some people who have read my work actually believe it to be somewhat independent of geometry, independent of style—even of architecture.
Remark Two
At this point, our protagonist began a long investigation to find water from a deeper well—something more profound. Alexander had always been an observer extraordinaire, a noticer par excellence, and epistemology, knowledge, can only begin with noticing and organizing personal experiences. It always precedes science.
It so happens that in the early 1970s Alexander had begun an infatuation with Turkish carpets. He spent a lot of money—even getting into financial trouble—and became a rug dealer for a while:
I was extremely innocent when I started out. I simply liked them. My main concern was actually in their color. I was completely absorbed by the question of color but never thought it would have any serious connection to my work. Also, I never thought of my interest in these rugs as having to do with geometry.
These very early Turkish carpets from centuries past (Alexander’s collection spans the 12th to 17th centuries) became his preferred objects of study and his teachers. He not only looked intently at them but copied again and again their shapes and interplay (
Figure 4).
The carpet years focused deeply on geometric configurations. For example, he noticed that it is the fine structure—structure down to
inch—
“the detailed organization of matter—that controls the macroscopic level in a way that architects have hardly dreamed of.” {
Foreshadowing} [
22] Alexander elaborates:
“twentieth century art has been very bad at handling this level. We have become used to a ‘conceptual’ approach to building, in which like cardboard, large superficial slabs of concrete, or glass, or painted sheetrock or plywood create very abstract forms at the big level. But they have no soul, because they have no fine structure at all ….” [
22] (
Figure 5).
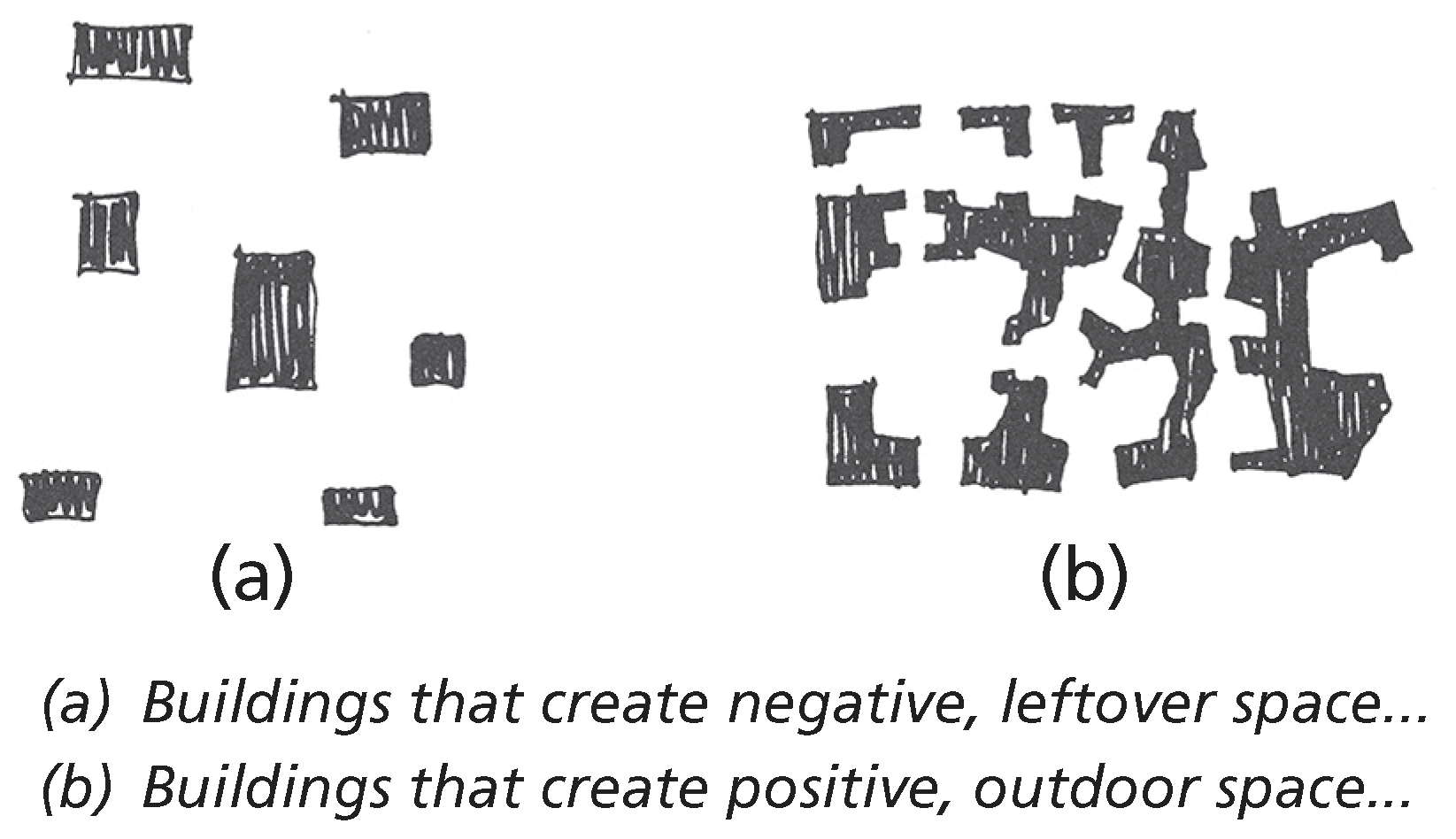
The careful reader will recognize in
Foreshadowing tentacles reaching back into the past and others feeling their way into the future. From the past we can revisit, for example, positive space seen in
APL in the pattern, POSITIVE OUTDOOR SPACE (Pattern #106 [
13],
Figure 6):
We can also revisit an earlier exploration of local symmetries and our cognitive abilities to pick up on coherence and how we—ever so dimly—perceive that
“coherent patterns …contain …local symmetries or ‘sub-symmetries.’” That exploration was an experiment Alexander conducted with Bill Huggins at Harvard University in the early 1960s [
6,
22]. They asked subjects to rank-order a set of strips from most to least coherent and simple. There were 35 strips, each consisting of three black squares and four white ones. Here are two examples (
Figure 7):
If there
was good agreement among the subjects about which were simpler and more coherent, then there would probably be some truth to the conjecture that there is an objective quality of wholeness or coherence or simplicity. It turned out that there was excellent agreement:
First, Huggins and I established that the relative coherence of the different patterns—operationally defined as ease of perception—was an objective quality, that varied little from person to person. In other words, the perceived coherence is not an idiosyncratic subjective thing, seen differently by different people. It is seen roughly the same by everyone.
Here (
Figure 8) are the 35 strips ordered according to the test subjects from most coherent at the top left, moving down the first column and then down each column from left to right, with the least coherent at the bottom right.
Next, Alexander asked whether there was some way to explain this ranking. Oddly, there is a way. It has to do with counting what Alexander called “sub-symmetries.” A sub-symmetry is a symmetrical sub-segment. Coherence is strongly correlated with the number of sub-symmetries. Here’s how you calculate this number: consider all the subsegments of sizes 2, 3, 4, 5, 6, and 7. There is one subsegment of length 7, 2 of length 6, 3 of length 5, and so forth—21 in all. Here are the subsegments of length 3 (
Figure 9):
Now, we simply count the number of subsegments that are symmetric—that is, we compute sub-symmetry counts for each strip. A subsegment is symmetric if it looks the same reversed. The numbers in
Figure 8 are the sub-symmetry counts of the strips to their left.
That there is such a correlation is remarkable. It seems that people prefer symmetries that appear on all levels—so, in Alexander’s formula, small symmetries count as much as large ones. The first strip (upper left) has symmetries all over the place, and it is pleasant to look at, but is it really more coherent than the one at the bottom of the first column? That one seems more regular in some ways, and it is certainly more interesting—it seems more complex, but it seems easier to remember, since there is a simple alternation rather than the 1-2-1-2-1-2-1 of the other. Maybe it is more coherent. The idea of sub-symmetries seems to take this into account, perhaps a little too simplistically. Alexander writes:
Thus, apparently, the perceived coherence of the different patterns depends almost entirely on the number of symmetrical segments which they contain. Since each of the segments which is symmetrical is a local symmetry I summarize this whole result, by saying that the most coherent patterns are the ones which contain the largest number of local symmetries or “sub-symmetries.”.
We can counter Alexander’s findings: with some exploration it is possible to do a little better at creating an algorithmic way—a finer net—to account for the test subjects’ assignment of coherence—not much better, but about 14% better; moreover, Alexander’s counting algorithm partitions the 35 strips into five buckets, and ours into 17.
In explaining the experimental ordering of the strips, Alexander writes
“it took me three or four years to find the right answer” [
6]. This was, he hinted, because, in the 1960s,
“lumpiness and symmetry were two of the main explanations for cognitive simplicity” [
6]. One might say this was because complexity was taken as chaos and near-total disorder, and simplicity was taken as pure order. The place in the middle was left out: an interesting locale in complex systems—the border between order and chaos. Chaos is unpredictability: combinations that might have lasting value or interest don’t last because the energy pushing change is too high. Order is total predictability: the only combinations that exist are the ones that always have because the energy maintaining stability is too high. And organized complexity is in the border of order and chaos.
Years later, in
The Nature of Order, while again discussing sub-symmetries, Alexander brought up the Alhambra (
Figure 10), a palace and fortress in Granada, Spain. It is at this stage that Alexander seemed to come upon one of the most interesting parts of his thinking about organized complexity: the paradoxical interplay between symmetry and asymmetry, or between simplicity and complexity. In the case of the Alhambra, the overall asymmetry comes from it spilling over an uneven hilltop, but its inner parts contain a tremendous concentration of symmetries. That is, the Alhambra is symmetrical where it could be, and asymmetrical where it needed to be; the places where it is rough are the places where the nature of the hilltop spoke loudly.
One way to think about how to design a building is to build where the site seems to be striving to create something itself. A harmonious structure is one whose internal similarities and differences reflect the ones that exist in its conditions. Good structure arises because the living process creates the right symmetries asymmetrically on the backs of other symmetries.
“Everything in nature is symmetrical unless there is a reason for it not to be …. Within the living cases, we know there is always a balance of symmetry and asymmetry. But we do not know a way to formulate this balance …. For the moment, we must just declare [it]
an enigma.” {
Nature of Order Book Two} [
7].
Remark Three
Alexander’s foray into the geometries of carpets—their symmetries and positive space—as a way to begin anew, generally followed the strip-research vein, but on a far less scientific basis. There were no studies, there were no numbers (though he did talk about the number of “centers” in a carpet correlating with its “wholeness”—we’ll see these concepts later in the essay). And in general the results were less compelling as a formal argument but much more compelling in Beauty.
Alexander’s rugs were not in any sort of neat category of geographical origin or type of weave. They were chosen because they had something special. Because he had so little money, he spent a lot of time looking at them before buying. He wasn’t particularly aware of the special quality that set some carpets apart but:
When people started telling me this (that my rugs had a special something) I began to look more carefully to discover that there was indeed something I was attracted to in a half-conscious way. It seemed to me that the rugs I tended to buy exuded or captured an incredible amount of power which I did not understand but which I obviously recognized.
In the course of buying so many rugs I made a number of discoveries. First, I discovered that you could not tell if a rug had this special property—a spiritual quality—until you had been with it for about a week …. So, as a shortcut, I began to be aware that there were certain geometrical properties that were predictors of this spiritual property. In other words, I made the shocking discovery that you could actually look at the rug in a sort of superficial way and just see if it had certain geometrical properties, and if it did, you could be almost certain that it had this spiritual property as well.
Alexander developed a new and strange shortcut for evaluating the quality and density of geometric configurations into an epistemological tool: the Mirror of Self Test. The test subject considers two carpets; in
Foreshadowing, he used the two carpets in
Figure 11 and asked the following question:
If you had to choose one of these two carpets, as a picture of your own self, then which one of the two carpets would you choose? …
In case you find it hard to answer the question, let me clarify by asking you to choose the one which seems better able to represent your whole being, the essence of yourself, good and bad, all that is human in you.
Note to the Reader: if you’ve not seen this test before, take a few minutes now to answer for yourself.
In many ways, Alexander’s project to understand Beauty, complexity, and how to overcome our cognitive handicaps depends on almost everyone answering the same way. Here is how he puts it:
I believe that almost everyone, after careful thought, will choose the left-hand example [a]. Even though the two are of roughly equal importance, and of comparable age, I believe most people will conclude that the left-hand one is more profound: that one feels more calm looking at it; that one could look at it, day after day, for more years, that it fills one more successfully, with a calm and peaceful feeling. All this is what I mean by saying that, objectively, the left-hand carpet is the greater—and the more whole, of the two.
What does the Mirror of Self test tell us about wholeness? We have spoken about organized and disorganized complexity, terms introduced many years ago by Jane Jacobs to talk about cities. Alexander was beginning to see that these terms apply to much smaller things, and that the Mirror of Self is really just a way for people to be able to discern the degree of order in organized complexity. To see this, let’s consider a slightly different version of the test (
Figure 12). The left-hand carpet is the Waving Border carpet, which is the original right-hand one above (
Figure 11a), but the right-hand one is that same Waving Border carpet randomized about 75%.
The randomized image was produced by choosing a set of random pairs of pixels from the left-hand image, and swapping the pixels referenced in each pair. No pixel appears twice in the set of pairs. The number of pairs was such that 75% of the pixels were out of order in the modified image.
Because of the manner this image was produced, we can be sure that it is disorganized (significantly randomized), but we can still see hints of the original organized structure. Someone might choose the right-hand one because it is more uniform, but everyone will see that there is “more going on” in the left-hand one. And perhaps people who would choose the left-hand one are thereby able to discern differences in degree of organization, and hence the ‘more profound,’ deeper organized complexity.
In
Foreshadowing, Alexander was upfront in saying that the power of these carpets comes (at least in part) from the intention and need of these early artists to portray their religious feelings. In the first paragraph of Chapter 1:
A carpet is a picture of God. That is the essential fact, fundamental to the people who produced the carpets, and fundamental to any proper understanding of these carpets ….
The Sufis, who wove most of these carpets, tried to reach union with God. And, in doing it, in contemplating this God, the carpet actually tries, itself, to be a picture of the all seeing everlasting stuff. We may also call it the infinite domain or pearl-stuff.
In the 1989 documentary,
“Places For The Soul: A Man Tries To Heal The World By Transforming The Way We Build” [
24], Alexander says of his own work:
…we’re trying to do something that no one else has ever tried to do in the 20th century … make God appear in the middle of a field [24].
5. Intellectual History: Turn of the Century, the Nature of Reality
Précis: Christopher Alexander may end up qualifying as what John Maynard Keynes might have called a ‘mad scribbler of a few years back’ [
25]. Few people have read Alexander’s book on Turkish carpets (see Amazon’s rankings of Alexander’s books). At the formidable sight of four volumes containing two thousand pages, many have also failed to tackle his opus magnum. For those who do buckle down to the reading, it is clear that Alexander never abandons initial inquiries: How to make sense of complexity. How to make Beauty. How to overcome cognitive limitations. How to find the proper mathematical expression. With this last period of investigation, not only Beauty but Life and the nature of Order (natural and man-made) lie in the geometries of space. Beauty in buildings and urban forms can come only from unfolding geometric properties. We desperately need to get past Descartes and put the experimenter back in the experiment. It is at our peril that we continue to separate Fact and Value. Veracity and verifiability of Value are ours to embrace. Alexander becomes increasingly
“drunk with God” [
26]. Major publication: THE NATURE OF ORDER [
6,
7,
8,
9].
Remark One
Alexander tells us that the
method René Descartes devised to understand reality somehow, and, most unfortunately, became the assumed
nature of reality:
The mechanistic idea of order can be traced to Descartes, about 1640. His idea was: If you want to know how something works, you can find out by pretending that it is a machine. You completely isolate the thing you are interested in from everything else, and you just say, suppose that thing, whatever it happens to be—the rolling of a ball, the falling of an apple, anything you want, in isolation—can you invent a mechanical model, a little toy, a mental toy, which does this and this and this, and which has certain rules, which will then replicate the behavior of that thing? It was because of this kind of Cartesian thought that one was able to find out how things work in the modern sense.
{
Nature of Order Book One} [
6]
Alexander claims that in the 20th century, architects and people in general came to take these machines as more literal—that reality
was a set of machine-like things behaving according to rules, and with this came the separation of Fact and Value. Certain statements became the only ones that could be true or false—statements of facts such as a doorway is three feet wide—while others became statements of opinions—such as a door painted light yellow has more life than one painted gray.
In the world-view I am presenting, a second kind of statement is also considered capable of being true or false. These are statements about the relative degree of life, degree of harmony, or degree of wholeness—in short, statements about value. In the view I hold, these statements about relative wholeness are also factual, and are the essential statements. They play a more fundamental role than statements about mechanisms.
{
Nature of Order Book One} [
6]
Alexander had a very different reality to propose. In
The Nature of Order, Alexander lays out an underlying order of, well, everything:
What we call “life” is a general condition which exists, to some degree or other, in every part of space: brick, stone, grass, river, painting, building, daffodil, human being, forest, city. And further: The key to this idea is that every part of space—every connected region of space, small or large—has some degree of life, and that this degree of life is well-defined, objectively existing, and measurable.
{
Nature of Order Book One} [
6]
Order (the nature thereof and ‘life’), be it the geometry in natural systems, or good artifacts (such as prayer carpets made by people) can be organized around fifteen fundamental geometric properties. These properties concern what Alexander called “centers.” Roughly speaking, a center is a thing that is noticed: a noticeable configuration, something distinct. Alexander writes:
[Centers] are those particular identified sets, or systems, which appear within the larger whole as distinct and noticeable parts. They appear because they have noticeable distinctness, which makes them separate out from their surroundings and makes them cohere, and it is from the arrangements of these coherent parts that other coherent parts appear.
{
Nature of Order Book One} [
6]
A simple way to begin to understand this concept is in
Figure 13.
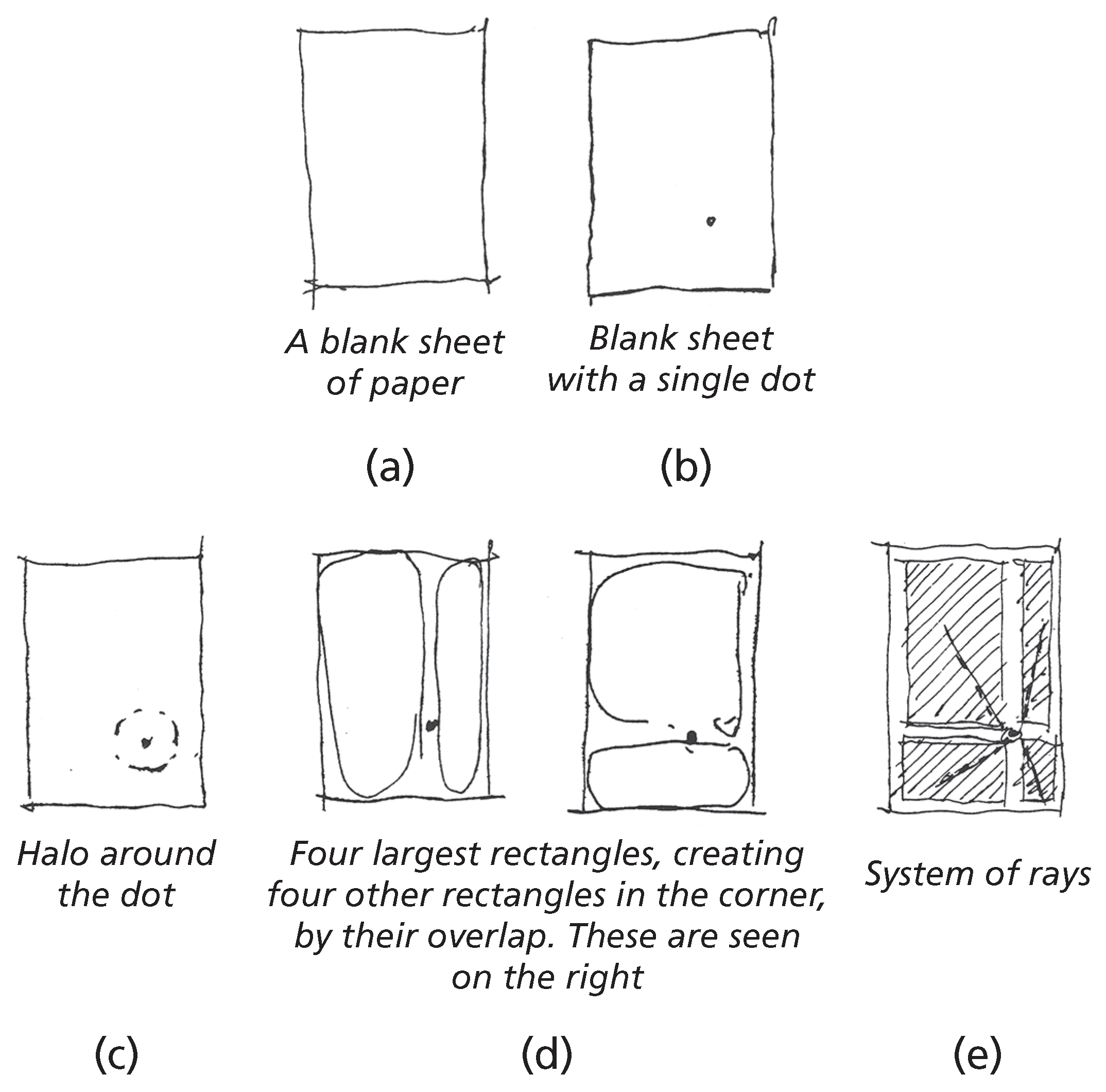
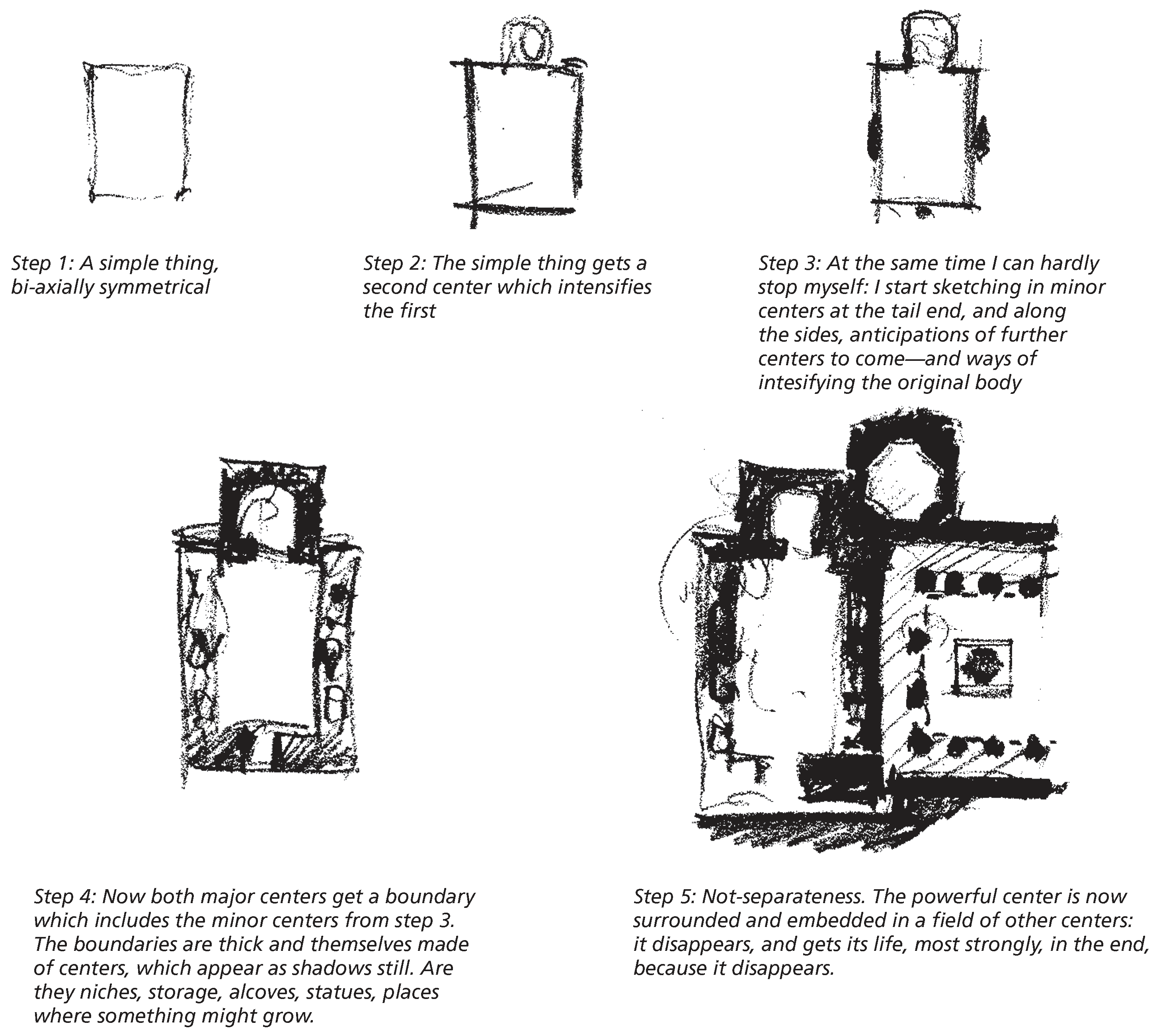
Figure 13a is a simple blank piece of paper, and
Figure 13b shows the placement of a dot. This dot is the first center—it is an explicit center, but it creates some latent ones as well, as we’ll see. Alexander writes:
Then I place one dot on [the blank sheet]. Although the dot is tiny, its impact on the sheet of paper is very great. The blank sheet of paper is one whole, one kind of wholeness. With the introduction of the tiny dot, the wholeness changes dramatically. Its gestalt changes. We begin to experience a subtle and pervasive shift in the whole. The space changes throughout the sheet of paper (and not only where the dot is), vectors are created, differentiations reaching far beyond the dot itself occur within the space. As a whole, an entirely new configuration has come into being, and this configuration extends across the sheet of paper as a whole.
{
Nature of Order Book One} [
6]
Alexander goes on to describe these “latent” centers (
Figure 13):
1. The sheet itself. 2. The dot. 3. The halo around the dot. 4. Bottom rectangle trapped by dot. 5. Left-hand rectangle trapped by dot. 6. Right-hand rectangle trapped by dot. 7. Top rectangle trapped by dot. 8. Top left corner. 9. Top right corner. 10. Bottom left corner. 11. Bottom right corner. 12. The ray going up from the dot. 13. Ray going down from the dot. 14. Ray going left from the dot. 15. Ray going right from the dot. 16. The white cross formed by these four rays. 17. Diagonal ray from dot to nearest corner. 18. Diagonal ray from dot to next corner. 19. Ray from dot to third corner. 20. Ray from dot to furthest corner.
{
Nature of Order Book One} [
6]
Importantly, a center is made of other centers, recursively—this can make the concept hard to grasp. Moreover, although Alexander spoke of geometrically distinct sets and parts, geometry doesn’t seem essential to the concept of centers. The essentials concern “conceptual structures”—identified sets or systems, a larger whole, distinct and noticeable parts, and coherence, all abstract notions having nothing to do with geometry or even physicality. When a center is made of others, recursively, the center can be quite complex and dense—it becomes “alive.” Alexander writes the following about the density of centers in the carpets:
The essential point …is that the most dense systems of centers, the oldest and most original, and the ones where the thing is so forcefully and archaically constructed, actually lead in some way to the emergence of a being in the carpet ….
…The density of centers creates a being. There are apparently certain configurations of centers, certain centers themselves, which have a more profound significance than others, because they somehow give rise to a “being”—which, like an individual human being, is distinct, autonomous—a creation unto itself—and which somehow rises from the dross of its component centers, and becomes magnificent ….
This being arises from the configuration of the centers, geometrically, but recognizing it as a being requires more than geometry—it takes a being that is alive to notice a being that is alive. This is the mystery of complexity in the vicinity of order.
Remark Two
Alexander theorized that a region of space increases in life as its centers unfold and display the fifteen properties. Each property is both a verb (a transformation that alters spatial order) as well as a descriptive name of a more static configuration. Here are their names:
| Levels of Scale | Good Shape | Roughness |
| Strong Centers | Local Symmetries | Echoes |
| Boundaries | Deep Interlock and Ambiguity | The Void |
| Alternating Repetition | Contrast | Simplicity and Inner Calm |
| Positive Space | Gradients | Not-Separateness |
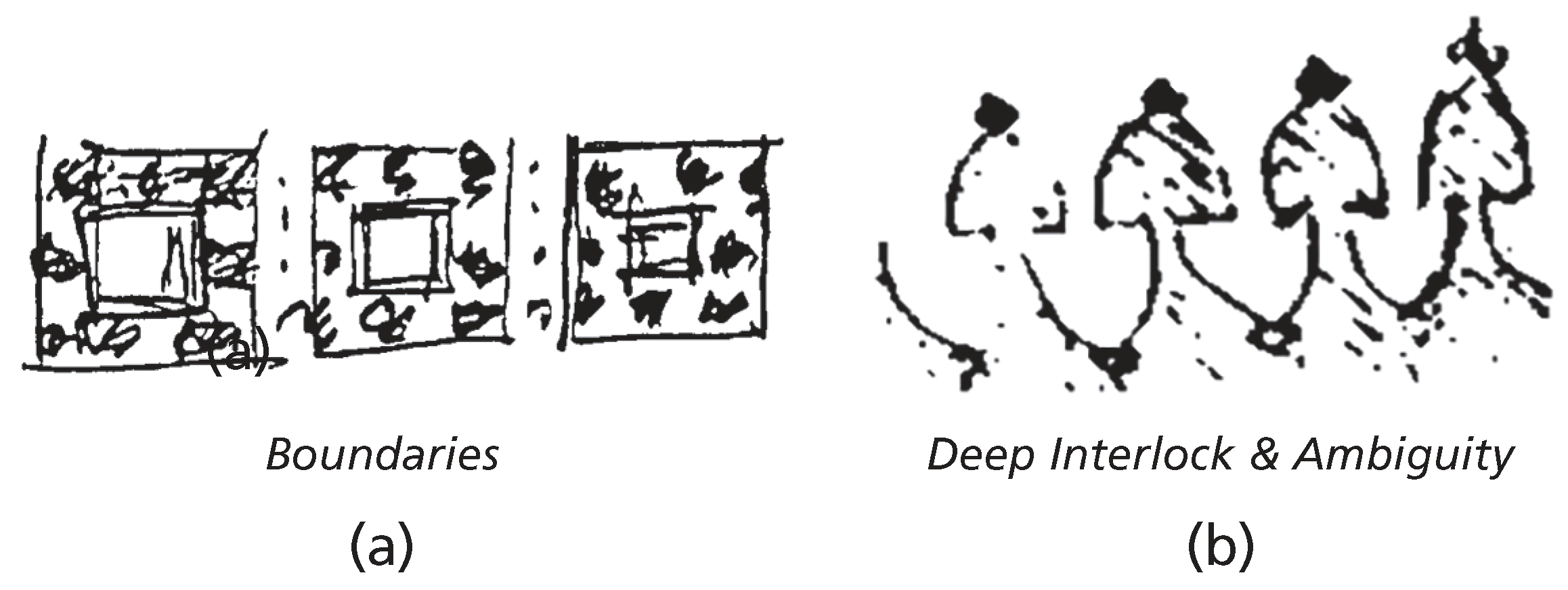
The following are descriptions of two of the properties: BOUNDARIES and DEEP INTERLOCK AND AMBIGUITY.
Boundaries: A boundary separates a center from other centers; it focuses attention on the center; a boundary is itself made of centers (
Figure 15a).
Deep Interlock and Ambiguity: Centers are sometimes “hooked” into their surroundings. It is sometimes difficult to disentangle a center from its surroundings through actual interlock or through an ambiguous zone which belongs both to the center and to its surroundings (
Figure 15b).
Remark Three
With Alexander’s work on unfolding, we have his strongest contribution to the discussion on organized complexity. In general, what can be called “unfolding order” emerges from a process integral to the thing being created. The process is one of differentiation. We start with a whole and differentiate it. Each differentiation is a structure-preserving transformation, which strengthens existing (“good”) centers by doing one or several of the following:
adding new centers that reinforce existing ones,
strengthening or developing one or several existing centers,
removing weak or dysfunctional centers.
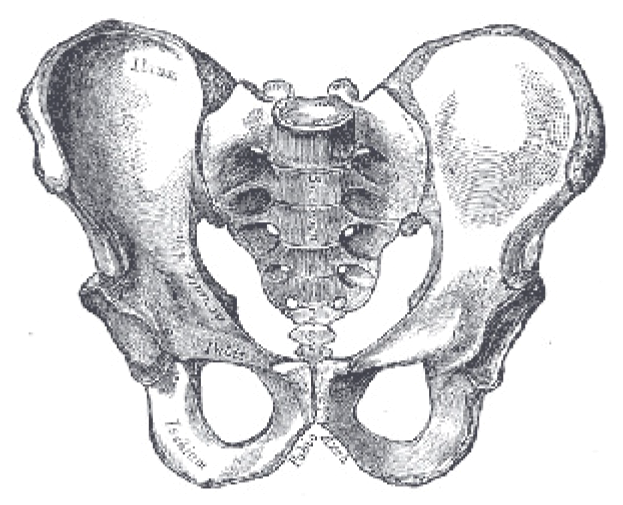
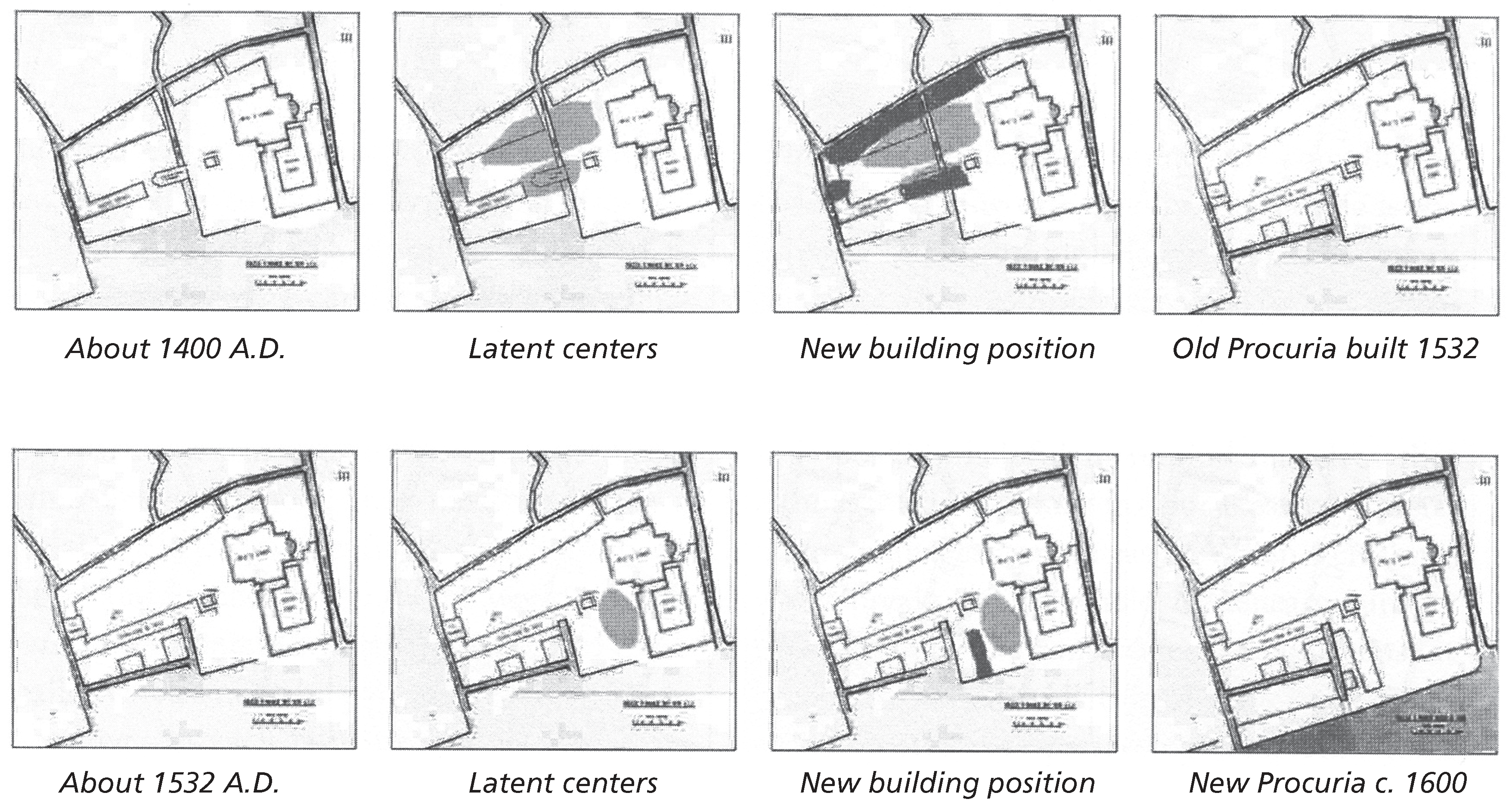
Consider two illustrations of structure-preserving transformations: human bones (
Figure 16) and a city plaza (
Figure 17). In the case of bones designed by Evolution, we can admire the subtle and complex shape of the human hip and pelvic bones, which enable us to run, bend, swivel, and sit and which come into being following a simple and elegant general rule: calcium will be deposited in the area where stress is greatest, and this over time.
In the case of a city plaza, we can see how, over 200 years, St. Mark’s Square in Venice intensified its presence by adding new centers, strengthening these centers through BOUNDARIES, increasing GOOD SHAPE, CONTRAST, POSITIVE SHAPE, and so on.
Along with unfolding geometry comes the theme of time. The shape (geometry) of a place (St. Mark’s) or thing (pelvic bone) can result only from a specific process: it is the trace of time. Alexander comments on the evolution of shapes in species studied by D’Arcy Thompson (
Figure 18):
What (D’Arcy) Thompson insisted on was that every form is basically the end result of a certain growth process. When I first read this I felt that of course the form in a purely static sense is equilibrating certain forces and that you could say that it was even the product of those forces—in a nontemporal, non-dynamic sense, as in the case of a raindrop, for example, which in the right here and now is in equilibrium with the air flow around it, the force of gravity, its velocity, and so forth—but that you did not really have to be interested in how it actually got made. Thompson however was saying that everything is the way it is today because it is the result of a certain history—which of course includes how it got made. But at the time I read this I did not really understand it very well; whereas I now realize that he is completely right.
There are four Conditions Necessary for Unfolding in the man-made world:
Step-by-Step Adaptation: Each adaptation is about ‘good fit,’ things get fitted closely to a harmonious whole.
Feedback: Continuous and relatively immediate feedback about whether what has been done is a living structure in sufficient degree. In human society, this requires a shared understanding of what “life” is all about.
Unpredictability: Unfolding cannot occur except in a framework which allows the whole to go where it must go. The dire modern passion for planning and advanced control must be replaced by an attitude which recognizes that openness to the future, and lack of predictability, is a condition for success.
Awareness of the Whole: Fourth, the most difficult for us, there must be an ever-present awareness of the whole, throughout the process. {
Nature of Order Book Two (1997 draft)} [
28].
Alexander posits a Fundamental Differentiation process for the man-made, as follows:
At any given moment in a process, we have a partially evolved state of a structure. This state is described by the wholeness: the system of centers, and their relative nesting and degrees of life.
We pay attention as profoundly as possible to this wholeness—its global, large-scale order, both actual and latent.
We identify the sense in which this structure is weakest as a whole, weakest in its coherence, most deeply lacking in feeling.
We look for the latent centers in the whole. Not those centers which are robust and exist strongly already; rather, centers which are dimly present in a weak form, but which seem to contribute to the current absence of life in the whole.
We then choose one of these latent centers to work on. It may be a large center, or middle-sized, or small.
We use one of more of the fifteen structure-preserving transformations to differentiate and strengthen the structure in its wholeness.
As a result of the differentiation which occurs, new centers are born.
In particular, as we shall have increased the strength of certain larger centers we shall also have increased the strength of smaller centers. The structure will now, as a result of this differentiation, be stronger and have more coherence and definition.
We test to make sure that this is actually so.
We also test that what we have done is the simplest differentiation possible.
When complete, we go back to the beginning of the cycle, and apply the same process again. {
Nature of Order Book Two (1997 draft)} [
28].
What exactly does it mean to use one or more of the fifteen structure-preserving transformations to differentiate and strengthen the structure in its wholeness? As noted earlier, each of the fifteen properties has an associated transformation that “creates” the corresponding property while retaining the existing structure. For example, if we perceive a center to be weak, we can strengthen it by creating a BOUNDARY around it. We can embolden a structure by adding a real center where we perceive a latent center, perhaps also creating a small symmetry; by creating an ambiguous interlock between two centers (which have already been elaborated by this process) (DEEP INTERLOCK and AMBIGUITY); or by adding centers that form a GRADIENT.
Here are the five steps in a series of structure-preserving transformations (
Figure 19, captions originally written by Alexander):
Two of the structure-preserving transformations are interesting because they don’t exactly preserve structure—they “preserve” the “good” structure and can be viewed as cleanup operations:
The VOID transformation is at work getting rid of garbage. Areas which are relatively undifferentiated, and which do not need their differentiation, are cleaned out and made more homogeneous, and defined by a boundary zone which is attached, surrounded, by more differentiated structure. The transformation also preserves an imitation of the greater undifferentiated void.
The SIMPLICITY transformation, like the void transformation, also cleans, simplifies. However, it works by removing unwanted centers, differences, and other kinds of complexity, throughout the structure, whereas the void does it by creating a single homogeneous zone in one place. The simplicity transformation gets rid of unnecessary structure by reducing it.
{
Nature of Order Book Two} [
7]
The ROUGHNESS transformation points to something that is less precisely, less mathematically defined, and hints that the required complexity (or deep simplicity we will see later) is a difficulty hard to pin down.
The ROUGHNESS transformation. In the course of making positive space, strong centers, local symmetries, or alternating repetition, it is often necessary to introduce or pack in irregular variants of repeating centers, to make things work out. The roughness transformation uses intentional irregularity to find the most regular fit possible for a given configuration, and one which permits things to work out successfully and simply in the large. It is of enormous importance. Wholeness would not be possible without it.
{
Nature of Order Book Two} [
7]
Remark Four
Because the unfolding process is totally general, it can be used to create anything at all. Alexander explored a few ways to provide more specific direction:
pattern languages,
sequences,
form languages.
Each project requires its own pattern language (sometimes called a “project language”), which takes into account local conditions, the requirements suggested by its future inhabitants and neighbors, and the culture.
A
sequence is the ordering of an unfolding and critical to the outcome. Early formulations of sequencing can be found in
A New Theory of Urban Design [
16]. Consider (on pages 61–75 of
A New Theory) the argument that the objective of positive urban space requires a sequencing of pedestrian space first, buildings second, and roads third. Note that this is the opposite of standard planning which puts roads first, buildings second, and pedestrian space last.
A
“form language…is a box of tricks, the elements, rules, ways of making roofs, edges, windows, steps, the ceiling of a room. The way to make a wall, the way to make a column. The shape of the edge where the building meets the sky. The ways which will not only make a coherent and beautiful work, but one which can be built, in our time, by means we understand, control, and can execute for not impossible amounts of money.” {
Nature of Order Book Two} [
7] For example, when we visit New England and look at houses built before 1750, we are looking at examples of ‘sentences’ in the form language of early New England homes. It is the same sort of thing when we visit Shetland and see the crofts, when we visit Porto and see the buildings wedged in the side streets, when we visit Hopi Second Mesa.
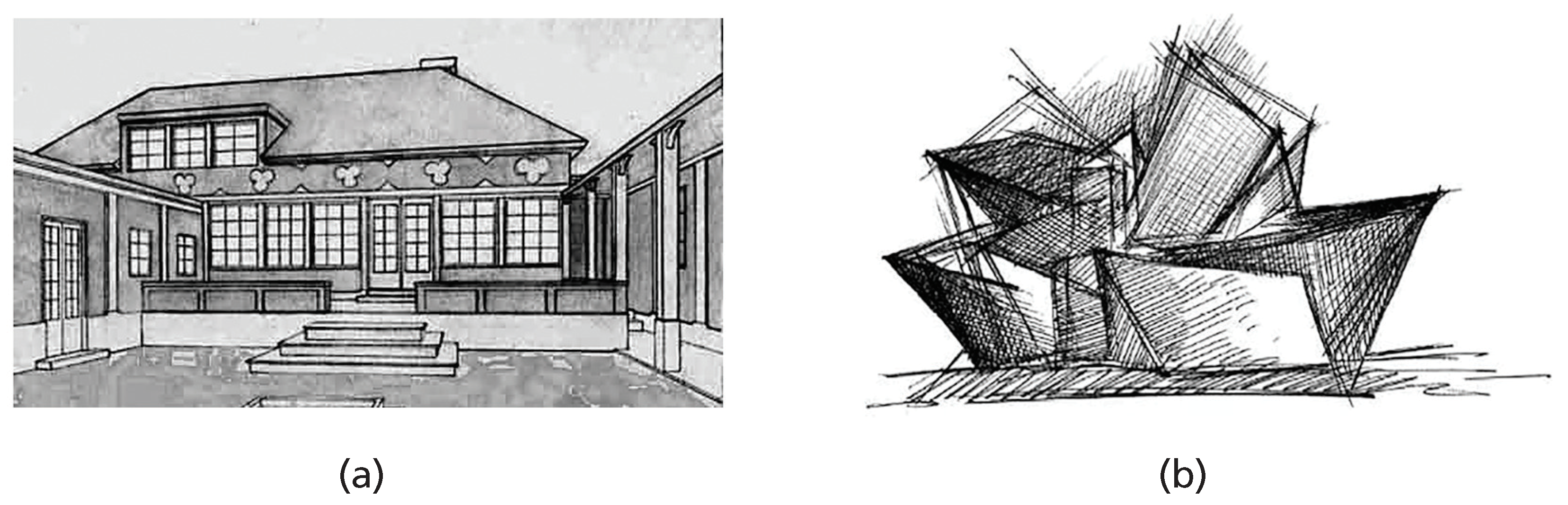
In these ways, Alexander layered process on top of process—we could call them scaffolding—to make building easier, but no process can supplant a designer’s innate sense of Beauty and wholeness. Beauty in buildings and urban forms can come only from an initial whole developing through progressive differentiations (geometric transformations). For example, with the house sketched in
Figure 20a, we could retrace those progressive differentiations, i.e., which centers had to be in position before a subsequent center could be formed. As a contrasting example, we cannot derive a generative sequence of forms in the Libeskind fabrication (
Figure 20b).
6. The Crux: Organized Complexity
In the most basic terms, Alexander’s search for Beauty was confounded by the essential need for complexity in the built world. What Alexander admired is complex but organically so: ancient city plans, rustic buildings, stave churches, Japanese gardens, classical music, how people interact socially, and nature.
In coming to terms with this tension between Beauty and complexity, Alexander makes it abundantly clear that
“all the well-ordered complex systems we know in the world, all those … that we view as highly successful are GENERATED structures, not fabricated structures.” {
Nature of Order Book Two} [
7] Moreover, such well-ordered complex structures arise because adaptations
can be and
are made according to the reality of context. Asymmetry and roughness result from required local adaptations. With patterns, it is adapting to the local forces; with the fundamental process, it is adapting to the centers that exist at the building site.
Alexander attributes some of the failure of fabricated, 20th century building to modular parts:
In order for the building to be alive, its construction details must be unique and fitted to their individual circumstances as carefully as the larger parts …. The details of a building cannot be made alive when they are made from modular parts.
Why is this? If we are trying to build on a site which is irregular, and if we have only crude hand tools, we need to find the place on the site where the house we want to build can be built using those tools. Therefore, we look for places where the adaptations we are able to make to the site meshes with the adaptations we are able to make to the house we have in mind. Nothing is modular. But at some point, people invented very powerful tools—the bulldozer, for example. Such tools enabled us to put all the adaptations on the shoulders of the site. If the site’s local forces present difficulties, we simply bulldoze those forces away. The house becomes the modular part. A modular part (generally) is not made to be adapted. It is fabricated—typically based on a plan made beforehand—and, hence, there is no reality to force itself into the equation—when you’re at the drafting table, drawing a straight line is just drawing a straight line. In other words, there is small opportunity for the experience of living there to enter the design, repair, and revision process. Instead of a whole resulting from organized and complex decisions, we have a death-like structure resulting from dumbed down decisions and no sense of coherence between building and context. Instead of a lovely stone croft nestled in the most serene and still part of the rocky, steep hill close by the voe—it’s a double-wide on a flat spot bulldozed halfway up.
The icing on the cake is that in many such situations, modern modular parts and structures created are too hardened and immutable—steel and glass instead of brick and wood, which can be repaired locally as needed.
However, what of simplicity? Alexander expressed disdain for the
“mechanical idea of simplicity as the geometrically banal.” {
Nature of Order Book Two} [
7]. Throughout his writings we see density of centers, overlap, ambiguity, roughness, imperfection, unfolding, ornament, generated complexity, asymmetry, sub-symmetries, and elaboration, along with complicated methods and processes, slow fanatical attention to detail, and a focus on adaptation. Alexander found simplicity in these; he says:
I shall argue, now, that living process, in its very nature, may, in a certain special sense, be called deeply simple—that it may be characterized by the idea that it is the simplest process which exists in any given set of circumstances. What has appeared all along, the idea that complexity is a manifestation of a deeper, more intricate structure created by structure-preserving unfolding, may be understood better yet when we appreciate that it is always the simplest step which governs: And that the drive provided by the SIMPLICITY AND INNER CALM transformation is, necessarily, at the very root of living process.
{
Nature of Order Book Two} [
7]
Alexander is saying that simplicity (in the good sense) arises during unfolding when one tries to resolve, complete, elaborate, and underpin the structure and wholeness that already exist in the place. That is, at every step, one tries to cause the least disturbance to existing structures. Complexity (in the bad sense) consists of distinctions which unnecessarily complicate a structure—and which sometimes need to be removed.
Alexander’s “well-ordered complexity” is what Weaver and Jacobs called “organized complexity.” Alexander was describing the edge of chaos—a place balanced between order and chaos, or between simplicity and complexity. When we look too deeply into chaos, we find only disorder; when we look too deeply into order, we find only the botfly of boredom; when we look in between, we find Beauty, poetry, life.
7. Evocative Art or Mathematical Precision?
Alexander, coming into his professional life with both an artistic and a mathematical bent, stayed the course by working in a strangely zigzag manner.
On one hand, his best writing is highly evocative—as in that
“slightly dozy quality” of the peach tree
“carefully tied to grow flat against the wall; warming the bricks ….” Let’s highlight what we mean by this evocative power by comparing the following two paragraphs. Describing the same scene, the first paragraph transfers information as simply as possible, while the second brings in greater sentience, many complexities:
The summer homes on Long Island were closed. Those homes were large. Those homes were on the shore. A ferry was crossing to Connecticut. It had lights. The moon was rising. I paid less attention to the houses. I paid more attention to the island. Early Dutch sailors came here. The island was covered in vegetation. The island was something new to them.
(written by the author R.P.G. for this essay)
Then, this—the same word count.
Most of the big shore places were closed now and there were hardly any lights except the shadowy, moving glow of a ferryboat across the Sound. And as the moon rose higher the inessential houses began to melt away until gradually I became aware of the old island here that flowered once for Dutch sailors’ eyes—a fresh, green breast of the new world.
In the first paragraph, the sentences are mostly simple declaratives—therefore, uniform. The simplicity is stark. Banal. Facts are stated. In its way, it gets the job done.
In the second paragraph, the words paint a vivid picture, almost a realistic dream. The first half uses ripples of light and dark—”hardly any lights,” “shadowy,” “glow,” and the moon showing, then hiding, the “inessential buildings.” The pace of the scene is slow—the “shadowy moving glow” of the boat, the buildings that “melt away,” the gradual awareness of the old island; the “now” and the “old.” Echoes between “rose,” “flowered,” and “fresh, green breast.” Notice the variety of word lengths, and how the natural is told with few syllables (“a fresh, green breast of the new world”) and the artificial with long (“shadowy, moving glow,” “ferryboat,” “inessential houses”). You can almost feel the subtle texture of the paragraph’s complexity. In this second paragraph, it is possible to identify many of the fifteen properties—translated to text from geometry. Like poetry, the real significance is at the margins of understanding, in the fractures of our reality, in the space between order and chaos.
To further illustrate the idea that unfolding order emerges from a process integral to the thing being created, consider this passage by Harold Pinter revealing how most playwrights—and most artists—work:
The thing germinated and bred itself. It proceeded according to its own logic. What did I do? I followed the indications. I kept a sharp eye on the clues I found myself dropping. The writing arranged itself with no trouble into dramatic terms. The characters sounded in my ears—it was apparent to me what one would say and what would be the other’s response, at any given point. It was apparent to me what they would not, ever, say, whatever one might wish …. When the thing was well cooked I began to form certain conclusions. The point is, however, that by that time the play was now its own world. It was determined by its own engendering image.
On one hand, as a writer and builder, Alexander conveyed meaning by evocation and works by unfolding—by creating centers and life. It is the artist in him.
On the other hand, what about all that mathematical training at Cambridge? From his early work to the carpet years, Alexander brought mathematics to bear wherever he felt it could help. A harsh critic might be underwhelmed by his mathematics and that same harsh critic might even wonder if there is anything deeply interesting there to be had. For example, even if we, say, devised simulations of wholeness or algorithms that approximate it, what would we learn?
In general, mathematics is the idealized language which describes reality; it can be used to explain things, and to predict them. However, in Alexander’s world of making things, it is the artist Alexander who takes over. We don’t have symmetry, but “rough symmetry.” Alexander disdained harsh, geometric simplicity. And he said that it was of enormous importance that one needed “irregular variants of repeating centers, to make things work out.”
In his later writings, where Alexander strikes out into a territory of new geometries, mathematics, as he knows it, fails him. A careful reader must work through the tiny print of footnotes and appendices to follow the tracks. Paraphrasing here from Appendix 4 of Book One of
The Nature of Order:
The life of any given center depends on the whole field of centers in which this center exists. Possibly viewed as a generalization of Mach’s Principle, we see that the behavior of any one particle is affected by the field. It cannot be measured by itself and therefore requires an entirely different view of the physical substance we call space or matter.
This new view is the essence of the recursive definition of a center, but we do not currently possess any convenient mathematical representation of such a recursive field. Classical fields have a field strength which is always dependent on something else—for example, gravitational space or electromagnetic fields. However, the intensities which occur in the field of centers as I see them depend on the field’s own values, so that the field is somehow self-dependent.
There is no field of classical physics which is self-dependent in this fashion. I have not yet been successful in my own attempts to create a mathematical model of such a self-dependent field. I am fairly sure that the field must be some kind of hierarchical structure in which different field strengths are nested. I also guess that it is associated with local symmetries. But, so far, I have failed.
The current mathematical descriptions of space assume that causal effects are local and this results from the neutral geometrical structure of the mathematics which we use to describe space. I am challenging this. Space itself must have a different mathematical structure.”
{
Nature of Order Book One} [
6]
Alexander was intent on explaining his observations of wholeness as being objective in the real world; and that means expressing them as mathematical statements. We might engage/counter Alexander’s declared failure by suggesting that autopoiesis comes close to this (and is a sort of definition of a living system), the steady state of a heat field does as well (as a computational system), and also the fixed point of a recursive function in lambda calculus (at least at a metaphorical level). One way to interpret Alexander’s efforts is that he was struggling for a way to express his intuitions, the way a scientifically inclined poet might try to express why one line of poetry is “more poetic” than another. Whether this has anything to do with the elusive Mach’s Principle doesn’t matter, but it would matter if a computationally effective method could be found to produce a strong field of centers.
Earlier, we described a center as “something that is noticed: a noticeable configuration, something distinct.” One problem with computationally effective methods is to mechanize “noticing,” which is complicated by the requirement to notice what people would notice—for instance, noticing “beings.” The closest we have come (as of 2019) is machine-learned algorithms using recurrent neural networks and convolutional neural networks. These techniques require training sets, and though in some cases labeled training sets are not required, somehow cultural and experiential facets need to be taken into account—some noticeable structures are noticeable because they are familiar or important in the culture because they are prototypical in the perceiver’s experience, because the perceiver is well-trained or skillful in some manner (artistry, for example), or because the effort required to perceptually process the structure is less than expected (sometimes called “processing fluency” [
31]).
There are other problems, which generally have to do with mimicking well the way people think and judge in a much deeper way than artificial intelligence is currently able to do.
When Weaver and Jacobs wrote of organized complexity, there were no computers capable of doing the computational work needed to simulate or understand the ideas. For now, the most we can hope for is a metaheuristic approach in which we search a space of candidates for the strongest, but would that get at the question of Value properly?
8. Mystery, Beauty, Urban Science, …
Pattern 7.7of the Eishin Campus: There is also one garden, so secret, that it does not appear on any map. The importance of the pattern is that it must never be publicly announced, must not be in [the] site plan; except for a few, nobody should be able to find it.
Alexander considered design to be more like resolving a mystery than solving a puzzle, the experience is more like slowly dawning insights than aha! moments and the process can take a long time. That mystery kept him alive, pulling him ever forward in his search. Something with QWAN (or wholeness or life or “beings”) needs some other thing—a tension, a strangeness, a stillness, a sadness, a complexity leaning against order—to make it special. After we find such a thing, we can explain it maybe with centers, patterns, sequences, and form languages—explain why. But not how. That’s important: why but not how. The mystery always eludes us.
The Beautiful is not trivially simple or ‘pretty,’ but attracts our attention in an almost obsessive way; that much seems clear. We are drawn to it, we come back to it over and over, we notice new things each time or notice them differently. All good art has this quality. Alexander strove to attain it and occasionally came close—Hiroshi Ichikawa’s comment on Eishin Campus suggests that he did. And that we cannot create Beauty without some grasp (explicit or intuitive) of the requisite complexity involved also seems clear.
… Complexity
The complexity of cities, as Jane Jacobs so famously suggested, is that of organized complexity. If true, then emergent phenomenon will not be predictable. We cannot blueprint out our plans for an urban built environment. Dare we say then that urban planning is an oxymoron? If so, we need a major and qualitative shift in thinking.
Alexander was courageous in confronting complexity and dogged in his pursuit of Beauty. He was firm in asking ought to be questions and including Values as well as Facts in debates and decision-making. His work remains wanting and incomplete, but that is not the point. Any of us who seriously engage intellectual pursuits will ultimately be proven wrong. The question is, can we be wrong in ways interesting enough to spur and inspire those who follow? Alexander, in interesting ways, may have scouted out a direction for urban science to make a great move forward. This would be particularly true with his later work on unfolding and design processes which allow for unpredictability, emergent Beauty, local adaptation to context, and the nonlinear interaction of variables. Also, not to be minimized was Alexander’s realization that organized complexity—the kind of complexity that exists at the boundary of order and chaos—applies not only at a large scale (such as cities), but at a small scale and even at a very small scale.
We cannot turn back the clock to the unselfconscious process of tribesmen constructing their huts, nor can we undo fundamentally bad geometries that can be neither repaired nor subsequently unfolded. Is there an urban development possible that has only a minimum backbone, is dynamic, is resilient through being redundant, self-repairing, self-correcting, and is governed by adaptive structure preservation? We are here in our overly simple, self-conscious blueprinted plan and standard operating procedures, but there is a better there, with more life and soul, over there.
Where is the gate?
Epilogue:Writing requires choosing. We chose a biographical focus. We chose to have Alexander speak his own expansive and emotion-revealing narrative. By so choosing, we have not addressed other topics. For example, Alexander’s intellectual debt to Alfred North Whitehead is absent [32]. We have ignored the whole raft of complexity scholars. We made no mention of those who, like mathematician Nikos Salingaros, have done much to further develop Alexander’s work [33]. We ignored urban scientists such as Luis Bettencourt who saw Alexander’s recursive, patterned, extendable, compositions as a template for open-ended urban design [34]. On the core themes of the essay, we did not investigate Bin Jiang’s computational methods for Alexandrian Beauty using PageRank and other techniques [35,36]. We paid no mind to Sergio Porta, Yodan Rofè, and MariaPia Vidoli who pragmatically took up the point where we end this essay by suggesting that the Gate from here to there lies in the interstices of System A [37]. Choices, all, for another day.