Urban Landscape Structure of a Fast-Growing African City: The Case of Niamey (Niger)
Abstract
1. Introduction
2. Materials and Methods
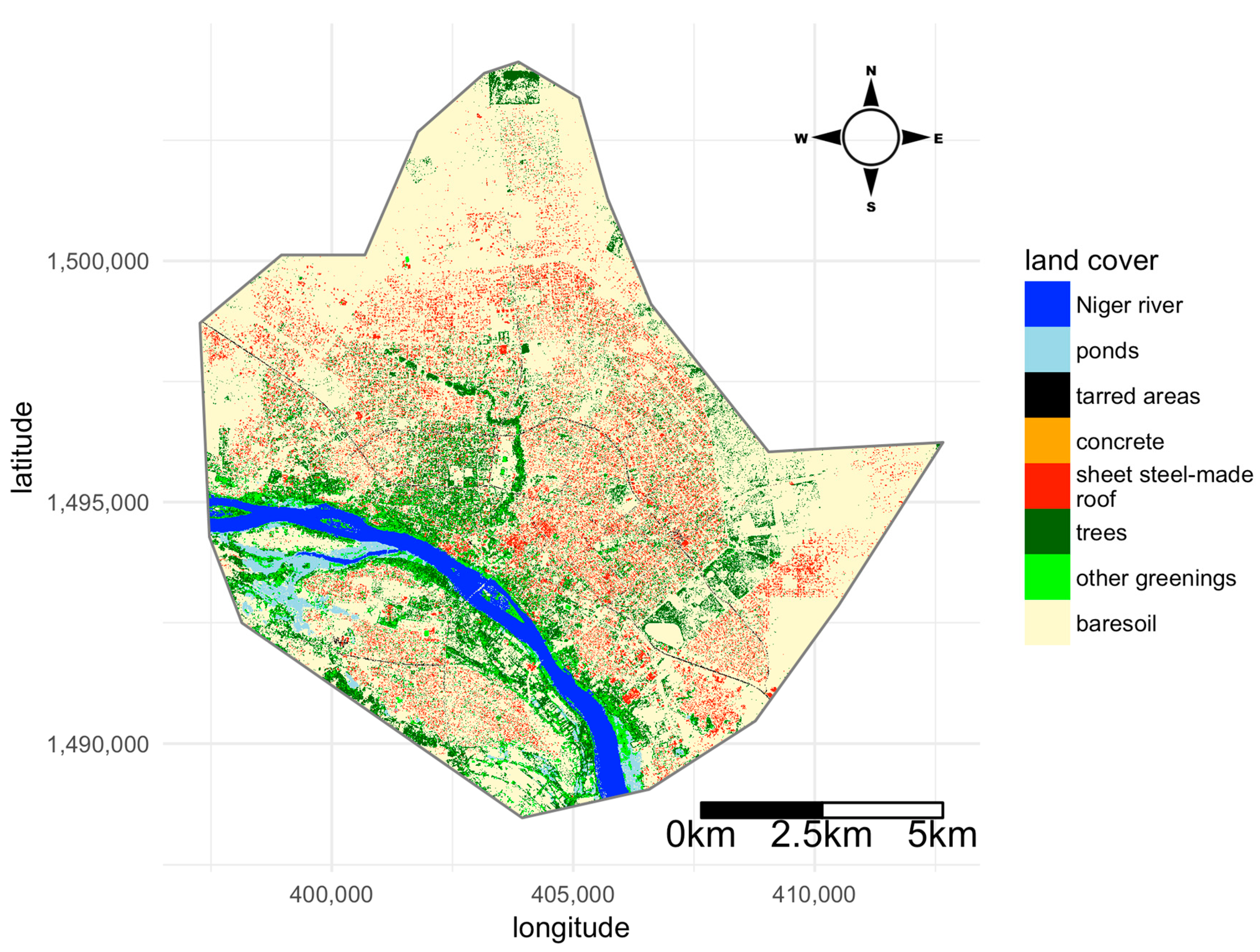
2.1. Study City: Niamey
2.2. Landscape Metrics
2.3. Multivariate Analysis Using the Principal Component Analysis (PCA)
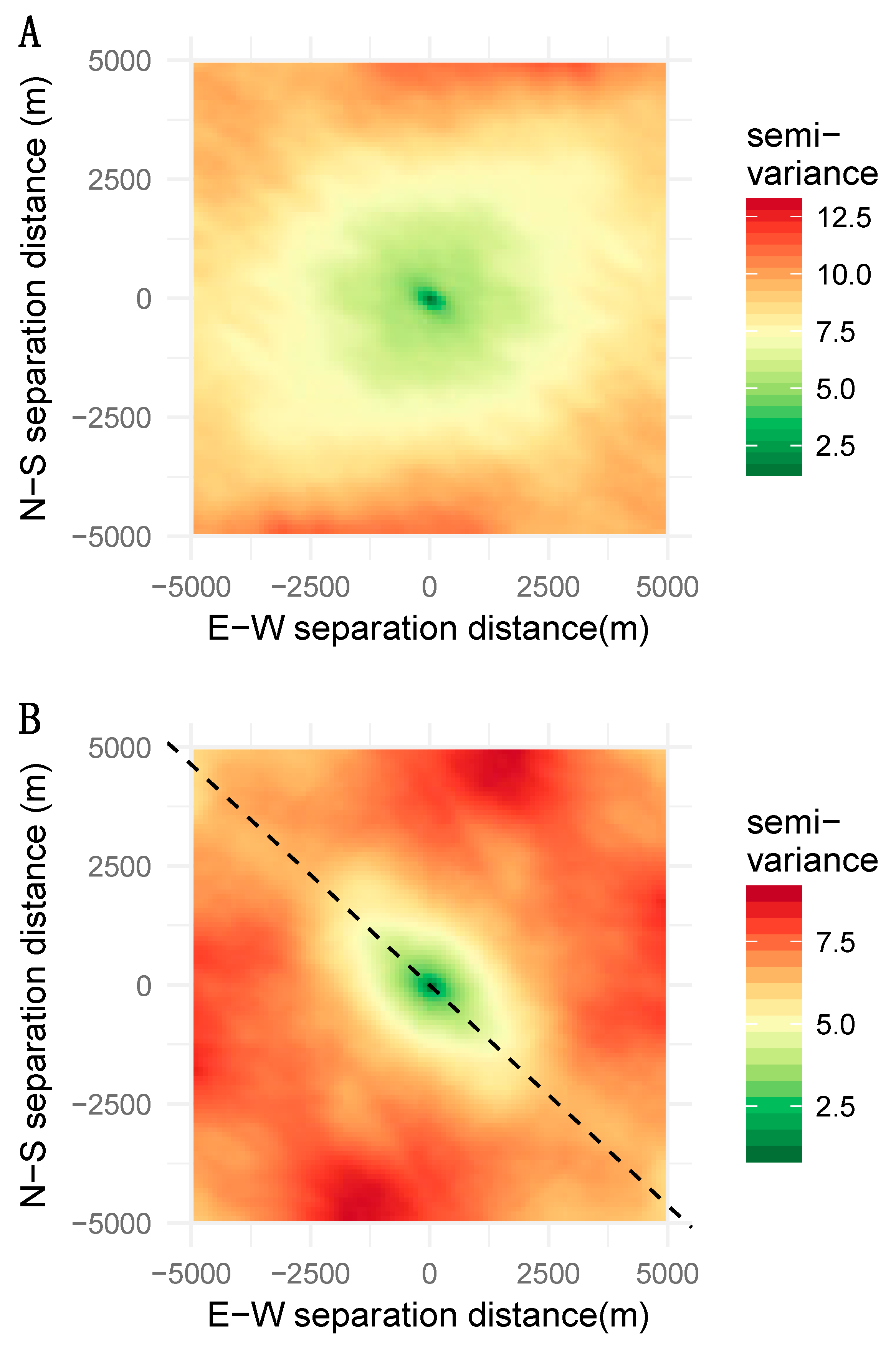
2.4. Variograms
3. Results
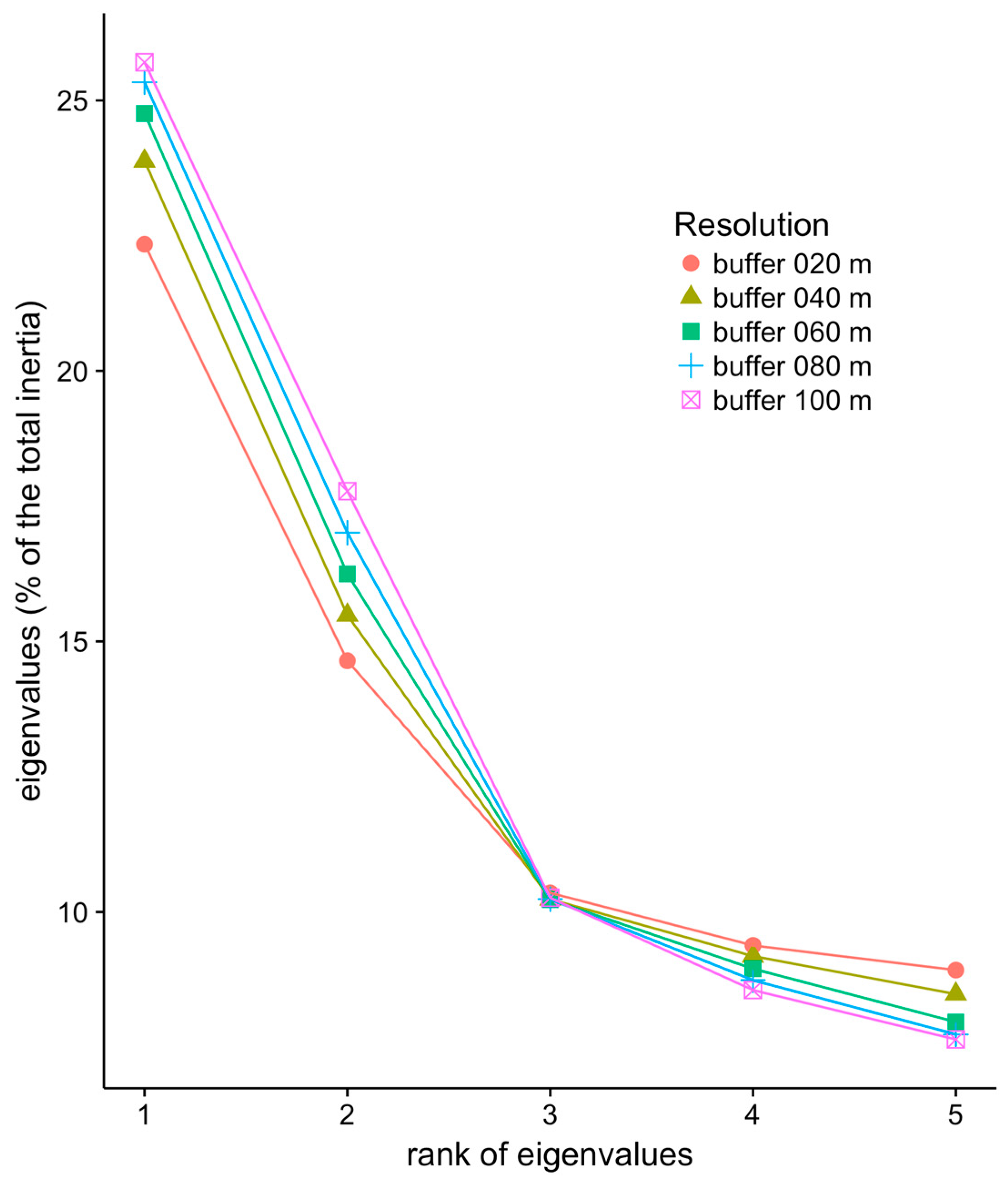
3.1. PCA Eigenvalues According to Buffer Sizes
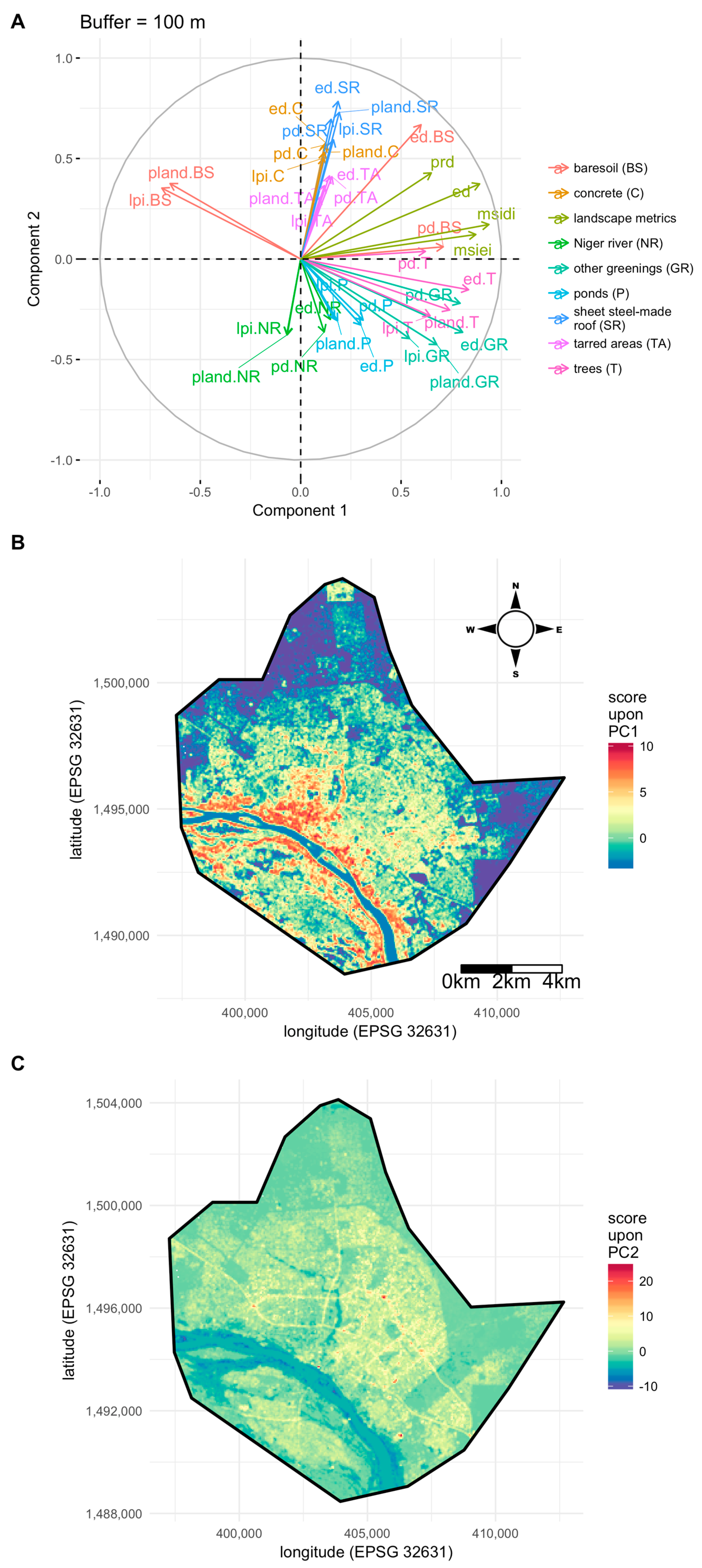
3.2. Citywide Variation of Landscape Features
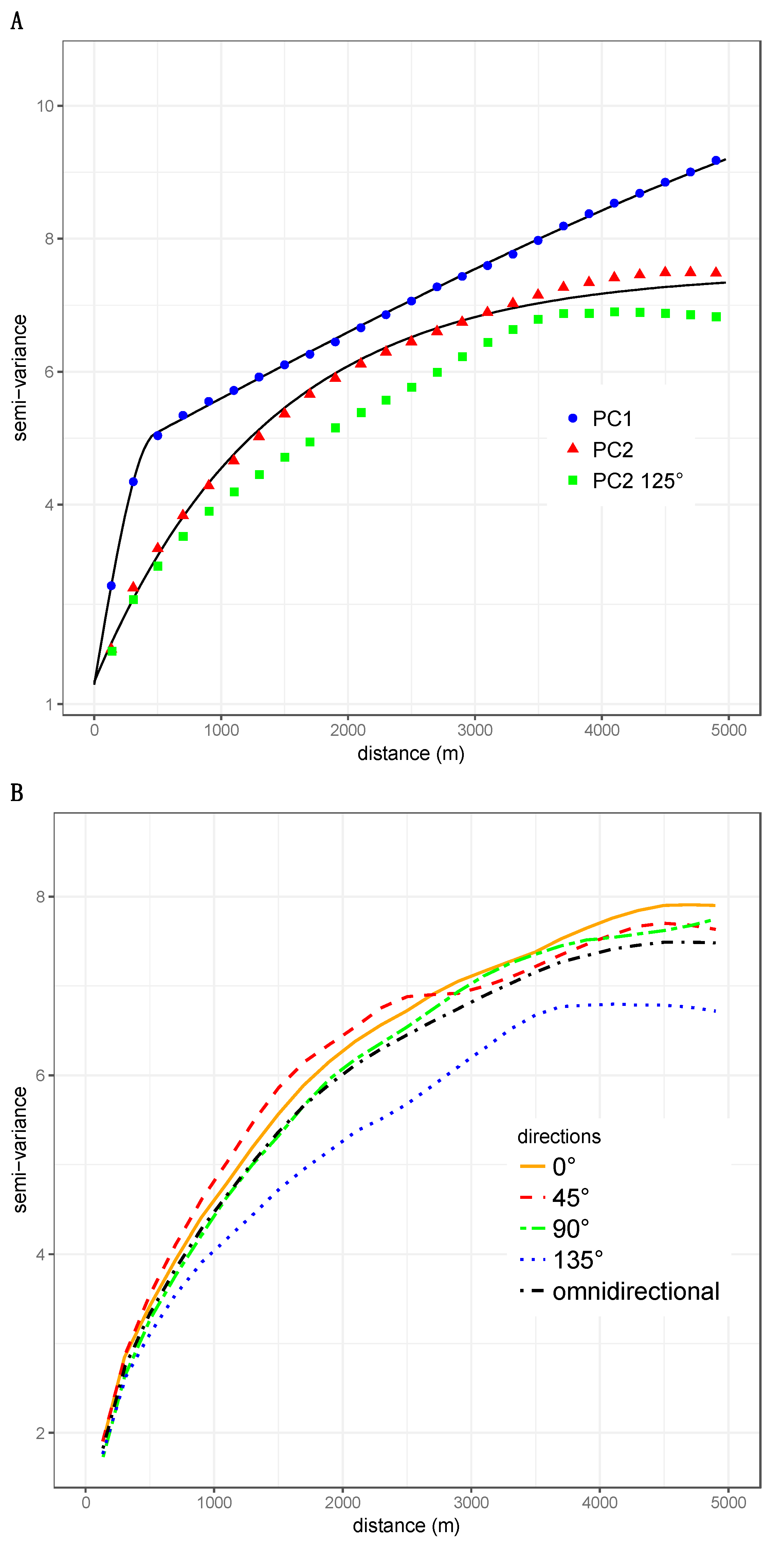
3.3. Variography of PCA First Components
4. Discussion
4.1. Niamey
4.2. Multivariate Analysis
4.3. Structural Analysis
4.4. Feeding Models, Refining Sampling Strategies and Setting Up Experimental Designs
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mohajerani, A.; Bakaric, J.; Jeffrey-Bailey, T. The urban heat island effect, its causes, and mitigation, with reference to the thermal properties of asphalt concrete. J. Environ. Manag. 2017, 197, 522–538. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.-C.; Fan, C.; Huang, T.; Wang, C.-F.; Chen, Y.-H. Urban Metabolic Analysis of a Food-Water-Energy System for Sustainable Resources Management. Int. J. Enviorn. Res. Public Health 2019, 16, 90. [Google Scholar] [CrossRef] [PubMed]
- Keairns, D.L.; Darton, R.C.; Irabien, A. The energy-water-food nexus. Annu. Rev. Chem. Biomol. Eng. 2016, 7, 239–262. [Google Scholar] [CrossRef] [PubMed]
- Naidja, L.; Ali-Khodja, H.; Khardi, S. Sources and levels of particulate matter in North African and Sub-Saharan cities: A literature review. Environ. Sci. Pollut. Res. 2018, 25, 12303–12328. [Google Scholar] [CrossRef] [PubMed]
- Pauleit, S.; Breuste, J.H. Land use and surface cover as urban ecological indicators. In Urban Ecology. Pattern, Processes, and Applications; Niemelä, J., Ed.; Oxford University Press: Oxford, UK, 2011; pp. 19–30. [Google Scholar]
- Luck, M.; Wu, J. A gradient analysis of urban landscape pattern: A case study from the Phoenix metropolitan region, Arizona, USA. Landsc. Ecol. 2002, 17, 327–339. [Google Scholar] [CrossRef]
- Seto, K.C.; Fragkias, M. Quantifying Spatiotemporal Patterns of Urban Land-use Change in Four Cities of China with Time Series Landscape Metrics. Landsc. Ecol. 2005, 20, 871–888. [Google Scholar] [CrossRef]
- McDonnell, M.J.; Hahs, A.K. The use of gradient analysis studies in advancing our understanding of the ecology of urbanizing landscapes: Current status and future directions. Landsc. Ecol. 2008, 23, 1143–1155. [Google Scholar] [CrossRef]
- Turner, M.G.; Gardner, R.H.; O’Neill, R.V. Landscape Ecology in Theory and Practice; Springer: New York, NY, USA, 2001. [Google Scholar]
- Anderson, P.M.L.; Okereke, C.; Rudd, A.; Parnell, S. Regional Assessment of Africa. In Urbanization, Biodiversity and Ecosystem Services: Challenges and Opportunities; Elmqvist, T., Fragkias, M., Goodness, J., Güneralp, B., Marcotullio, P.J., McDonald, R.I., Parnell, S., Schewenius, M., Sendstad, M., Seto, K.C., et al., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 453–459. [Google Scholar]
- United Nations. World Urbanization Prospects: The 2014 Revision: Highlights; United Nations: New York, NY, USA, 2014. [Google Scholar]
- McGarigal, K.; Cushman, S.A.; Ene, E. FRAGSTATS v4: Spatial Pattern Analysis Program for Categorical and Continuous Maps. Computer Software Program Produced by the Authors at the University of Massachusetts, Amherst. 2012. Available online: http://www.umass.edu/landeco/research/fragstats/fragstats.html (accessed on 12 June 2019).
- Manly, B.F.J.; Alberto, J.A.N. Multivariate Statistical Methods: A Primer; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Isaaks, E.H.; Srivastava, R.M. Applied Geostatistics; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016; Available online: https://www.R-project.org (accessed on 12 June 2019).
- Dray, S.; Dufour, A.-B. The ade4 Package: Implementing the Duality Diagram for Ecologists. J. Stat. Softw 2007, 22, 1–20. [Google Scholar] [CrossRef]
- Pebesma, E.; Heuvelink, G. Spatio-temporal interpolation using gstat. RFID J. 2016, 8, 204–218. [Google Scholar]
- Dobigny, G.; Garba, M.; Tatard, C.; Loiseau, A.; Galan, M.; Kadaouré, I.; Rossi, J.-P.; Picardeau, M.; Bertherat, E. Urban Market Gardening and Rodent-Borne Pathogenic Leptospira in Arid Zones: A Case Study in Niamey, Niger. PLoS Negl. Trop Dis. 2015, 9, e0004097. [Google Scholar] [CrossRef] [PubMed]
- Herold, M.; Scepan, J.; Clarke, K.C. The use of remote sensing and landscape metrics to describe structures and changes in urban land uses. Environ. Plan. A 2002, 34, 1443–1458. [Google Scholar] [CrossRef]
- Mahamane, M. Croissance urbaine et politique de peuplement au Niger. In Proceedings of the Colloque de l’AIDELF, Rabat, Morroco, 15–17 May 1990; pp. 379–388. [Google Scholar]
- Rossi, J.-P.; Kadaouré, I.; Godefroid, M.; Dobigny, G. Landscape epidemiology in urban environments: The example of rodent-borne Trypanosoma in Niamey, Niger. Infect. Genet. Evol. 2018, 63, 307–315. [Google Scholar] [CrossRef] [PubMed]
- Rossi, J.P.; van Halder, I. Towards indicators of butterfly biodiversity based on a multiscale landscape description. Ecol. Indic. 2010, 10, 452–458. [Google Scholar] [CrossRef]
- Buyantuyev, A.; Wu, J. Effects of thematic resolution on landscape pattern analysis. Landsc. Ecol. 2007, 22, 7–13. [Google Scholar] [CrossRef]
- Buyantuyev, A.; Wu, J.; Gries, C. Multiscale analysis of the urbanization pattern of the Phoenix metropolitan landscape of USA: Time, space and thematic resolution. Landsc. Urban. Plan. 2010, 94, 206–217. [Google Scholar] [CrossRef]
- Goovaerts, P.; Sonnet, P.; Navarre, A. Factorial kriging analysis of springwater contents in the Dyle river basin, Belgium. Water Resour. Res. 1993, 29, 2115–2125. [Google Scholar] [CrossRef]
- Legendre, P.; Legendre, L. Numerical Ecology; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Li, H.; Reynolds, J.F. On definition and quantification of heterogeneity. Oikos 1995, 73, 280–284. [Google Scholar] [CrossRef]
- Li, H.; Wu, J. Landscape pattern analysis: Key issues and challenges. In Key Topics in Landscape Ecology; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Wu, J.; Buyantuyev, A.; Jenerette, G.D.; Litteral, J.; Neil, K.; Shen, W. Quantifying spatiotemporal patterns and ecological effects of urbanization: A multiscale landscape approach. In Applied Urban Ecology: A Global Framework; Wiley Online Library: Hoboken, NJ, USA, 2011; pp. 33–53. [Google Scholar]
- De Gruijter, J.; Brus, D.J.; Bierkens, M.F.P.; Knotters, M. Sampling for Natural Resource Monitoring; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
| Name | Acronym | Description | Unit |
|---|---|---|---|
| Class metrics | |||
| Edge density | ED | ED quantifies the edge length on a per unit area basis | Meters per hectare |
| Largest patch index | LPI | LPI is a measure of dominance that quantifies the proportion of total landscape area occupied by the largest patch | Percent |
| Patch density | PD | PD expresses the number of patches on a per unit area basis | Number per 100 hectares |
| Percentage of landscape | PLAND | PLAND is a measure of landscape composition: how much of the landscape is comprised of a particular land-cover | Percent |
| Landscape metrics | |||
| Edge density | ED | ED is a measure of the total edge length in the landscape on a per unit area basis | Meters per hectare |
| Modified Simpson’s diversity index | MSIDI | MSIDI quantifies landscape diversity. It increases as the number of different patch types increases and the coverage of each patch type becomes equitable. | None |
| Modified Simpson’s evenness index | MSIEI | MSIEI measures how close the coverage area is distributed among the different land-covers | None |
| Patch richness density | PRD | PRD measures richness as the number of different land-covers in a landscape in a per area basis. | Number per 100 hectares |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rossi, J.-P.; Dobigny, G. Urban Landscape Structure of a Fast-Growing African City: The Case of Niamey (Niger). Urban Sci. 2019, 3, 63. https://doi.org/10.3390/urbansci3020063
Rossi J-P, Dobigny G. Urban Landscape Structure of a Fast-Growing African City: The Case of Niamey (Niger). Urban Science. 2019; 3(2):63. https://doi.org/10.3390/urbansci3020063
Chicago/Turabian StyleRossi, Jean-Pierre, and Gauthier Dobigny. 2019. "Urban Landscape Structure of a Fast-Growing African City: The Case of Niamey (Niger)" Urban Science 3, no. 2: 63. https://doi.org/10.3390/urbansci3020063
APA StyleRossi, J.-P., & Dobigny, G. (2019). Urban Landscape Structure of a Fast-Growing African City: The Case of Niamey (Niger). Urban Science, 3(2), 63. https://doi.org/10.3390/urbansci3020063





