Stochastic Techno-Economic Assessment of TSC Sizing in Distribution Networks

Abstract

This paper introduces a novel stochastic optimization framework for the optimal sizing of thyristor-switched capacitors (TSCs) in medium-voltage distribution networks. Unlike conventional deterministic approaches, the proposed model explicitly incorporates load demand variability through multiple probabilistic scenarios, thereby enhancing the robustness and reliability of reactive power compensation. The methodology employs advanced nonlinear programming techniques, i.e., the IPOPT solver within a scenario-based framework, in order to determine the TSC sizes that minimize the expected total system costs, including those associated with energy losses and investments. According to extensive simulations on a standard 33-bus distribution system, our stochastic approach yields cost savings of approximately 12.3–12.4% while significantly improving voltage stability and operational efficiency under various load conditions. Assessments regarding voltage profile performance and average processing times, as well as a comparative analysis considering deterministic results, were also conducted in order to validate the effectiveness and computational efficiency of the approach. This study underscores the importance of probabilistic modeling for a smarter, more resilient grid operation, laying a solid foundation for integrating adaptive reactive power devices to support sustainable and reliable power distribution in evolving smart grid environments.

1. Introduction

1.1. Background and Motivation

Reactive power compensation plays a crucial role in enhancing the efficiency, voltage stability, and reliability of medium-voltage distribution networks (MVDNs) [1,2]. Traditionally, utilities have employed fixed or stepwise-switched capacitor banks to meet reactive power demands, but these static solutions often struggle to adapt to the dynamic load variations observed throughout the day [3,4]. As a result, fixed capacitors can lead to suboptimal performance, causing voltage deviations and inefficient reactive power utilization, especially during peak or low-demand periods [5,6,7].

To overcome these limitations, modern distribution systems are increasingly turning towards flexible and adaptive reactive compensation devices, e.g., flexible AC transmission systems (FACTS), including static VAR compensators (SVCs), static synchronous compensators (STATCOMs), and thyristor-switched capacitors (TSCs) [8,9]. Among these, TSCs stand out for their cost-effectiveness, simplicity, rapid switching capabilities, and modular design, which makes them particularly suitable for medium-voltage applications [10,11].

While the deployment of TSCs offers significant operational advantages over more complex power electronic devices, their optimal sizing and siting remain a challenge due to the uncertainties in load patterns and system conditions [12]. Properly determining the optimal capacity of TSCs is vital for maximizing their benefits, minimizing operating costs, and ensuring reliable voltage regulation.

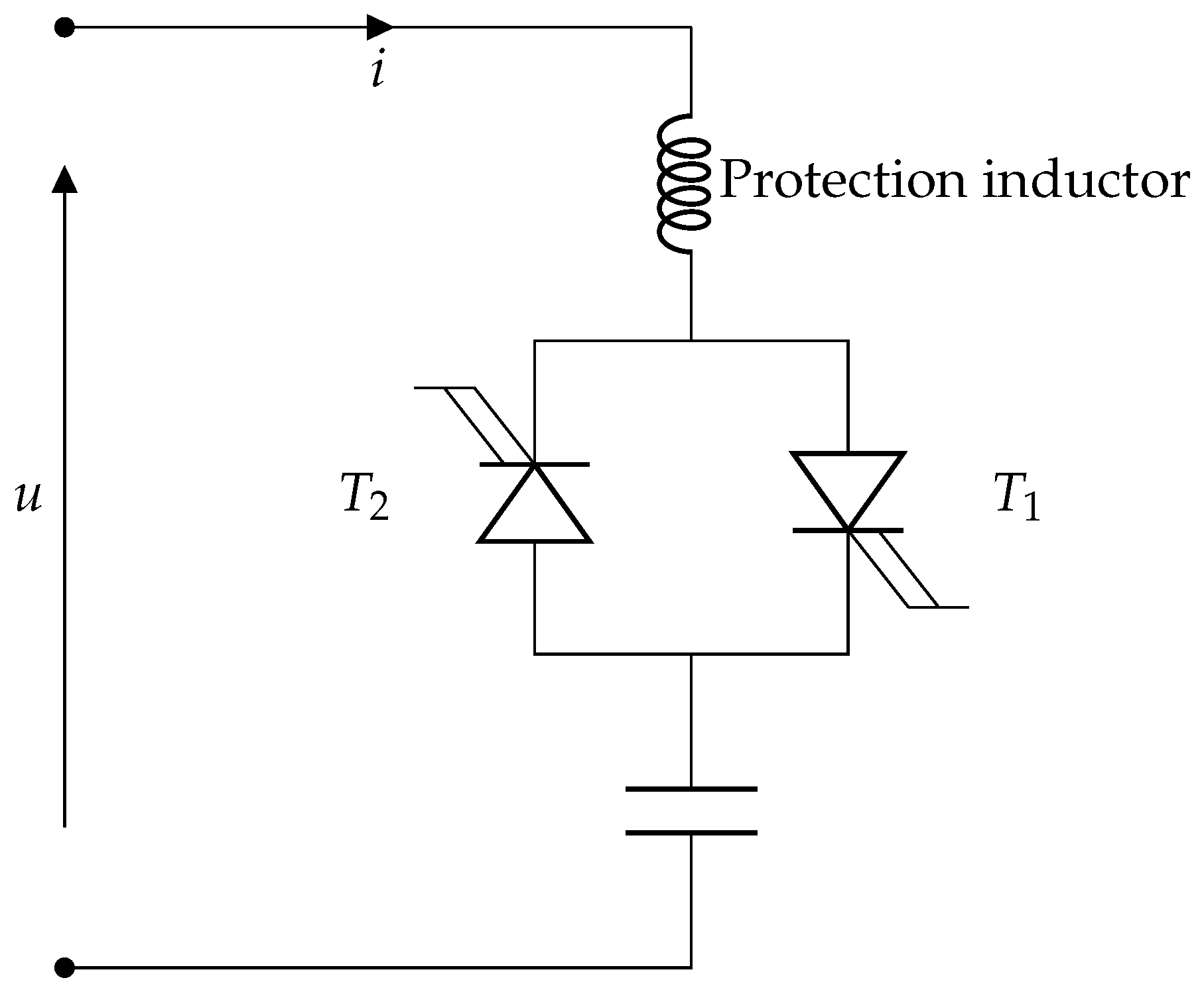
1.2. Principles of Operation and Configuration of TSCs

Figure 1 depicts the single-phase equivalent circuit of a TSC, a widely recognized tool for discrete reactive power compensation in electrical distribution systems. This configuration consists of a capacitor bank connected in series with a pair of thyristors ($T_1$ and $T_2$) arranged in anti-parallel, allowing for precise and controlled switching operations [13]. Moreover, a protection inductor is incorporated within the circuit in order to restrict the inrush current and mitigate transient phenomena during switching events, thereby safeguarding the power electronic components and enhancing the overall reliability of the system.

This configuration constitutes an effective and dependable solution for reactive power regulation amid the variable load conditions inherent to distribution systems [14]. In comparison with continuously controllable devices such as STATCOMs, TSCs are characterized by their simpler structural architecture and reduced initial capital expenditure, which makes them particularly advantageous for stepwise reactive power compensation in radial distribution feeders. The use of a thyristor-based switching mechanism obviates the need for mechanical contactors, resulting in faster response times and enhanced operational longevity [15]. Such features are aligned with the objectives established in smart grid paradigms, as they enable a digitally controlled, modular reactive power support that contributes to improved voltage stability and power factor correction. Within the broader context of advanced smart distribution networks, TSCs serve as an intermediate modality that bridges static capacitor banks and fully dynamic FACTS [16]. Their straightforward control logic and inherent scalability render them particularly suitable for integration into hybrid optimization strategies—such as the one proposed herein—aiming to minimize operating costs while strictly adhering to technical constraints under realistic, time-varying load profiles.

1.3. Problem Statement and Research Gap

While fixed-capacitor banks are preferred for their simplicity and low cost, they lack the adaptability needed to respond to the dynamic conditions of modern distribution networks. As advanced FACTS, TSCs provide significant advantages, given their ability to dynamically adjust reactive power support, thus improving voltage regulation, reducing losses, and enhancing the overall power quality of MVDNs [10]. Despite these benefits, the existing literature on TSC integration predominantly focuses on heuristic or deterministic approaches, often considering fixed demand conditions. Such methods do not adequately address the inherent uncertainties stemming from renewable energy sources and load variability, which limits their effectiveness in real-world applications.

Recent research efforts to optimize FACTS siting and sizing include:

• Transmission systems. The application of metaheuristic algorithms such as particle swarm optimization (PSO) [17] and seeker optimization [18] has shown improvements in voltage profiles and operating costs.
• Distribution networks. Hybrid strategies combining fuzzy logic and ant colony algorithms [19], heuristic approaches based on voltage and loss indices [20], and analytical–heuristic hybrid frameworks [21,22] have been explored for FACTS allocation.
• Advanced methodologies. Recent studies have incorporated metaheuristics within hybrid optimization models, but many still assume deterministic load profiles, neglecting stochastic variations.

Furthermore, some recent works have begun to explicitly incorporate uncertainty:

• The authors of [10] employed a master–slave framework combining black widow optimization (BWO) with hybrid encodings and approximate power flow models for optimal FACTS placement, including TCSCs and SVCs.
• In [11], the artificial hummingbird algorithm (AHA) was employed for TSC siting and sizing, focusing on minimizing annual costs and outperforming several metaheuristics on 33- and 69-bus systems.
• The contribution presented in [23] involved a hybrid approach combining the sine-cosine algorithm (SCA) for candidate TSC locations and sizes with the IPOPT solver for power flow optimization, achieving a 12.43% reduction in operating costs under variable reactive power injection conditions.

Table 1. Summary of existing methods for TSC siting and sizing.

Methodology	Optimization Strategies	Key Features
Metaheuristic algorithms (PSO, SCA, Chu & Beasley genetic algorithm, BWO)	Heuristic/metaheuristic	Suitable for complex, nonlinear problems; limited stochastic considerations
Hybrid approaches with power flow models	Hybrid deterministic/stochastic	Incorporates system constraints; often assumes fixed demand profiles
Stochastic-based optimization with interior point optimization (IPOPT)	Exact/mathematical programming	Handles large-scale, nonlinear problems; capable of integrating uncertainty through scenario-based planning

summarizes the currently employed methodologies for the siting and sizing of TSCs in distribution systems. It highlights the predominant approaches, their optimization strategies, and key characteristics, providing a clear overview of the state of the art and identifying potential areas for development, especially regarding the incorporation of uncertainty through stochastic methods.

This overview highlights the diversity of existing methods. However, a common limitation is their reliance on deterministic or overly simplified demand profiles. As distribution systems increasingly incorporate renewable energy sources and experience higher variability, the adoption of stochastic methodologies becomes essential.

1.4. Contributions and Scope

This paper presents a comprehensive stochastic optimization framework for the optimal sizing of TSCs in MVDNs which explicitly accounts for load demand uncertainties. Unlike traditional deterministic methods, the proposed approach incorporates multiple probabilistic active and reactive power demand scenarios, ensuring solutions that are robust, reliable, and adaptable to daily fluctuations. Our core contribution is the formulation of a scenario-based nonlinear programming model, solved efficiently with the IPOPT solver in Julia, which determines the TSC sizes that minimize the expected total cost, encompassing energy losses and capital investments, across diverse demand profiles.

Additionally, the methodology generates representative demand scenarios that capture load variability over different days of operation, providing a realistic basis for system planning. Numerical results demonstrate that this stochastic approach substantially enhances system resilience and cost-effectiveness when compared to conventional deterministic models, establishing a solid foundation for advanced reactive power management in smart grids. Although the current focus is on sizing, the framework paves the way for future extensions into optimal placement and real-time adaptive control, supporting a holistic, uncertainty-aware system optimization.

To complement the analysis, a comparative evaluation was conducted for the deterministic scenario, which involved integrating the IPOPT solver with the SCA [23] to determine the optimal nodal placement of reactive power compensators. The results confirmed the high efficiency of the proposed nonlinear formulation in defining the optimal operation of distribution networks equipped with reliable compensation devices, leading to improved voltage regulation and reduced operating costs.

Note that this methodology was developed and executed using Julia, version 1.9.2 [24], running on a personal computer equipped with an AMD Ryzen 7 3700 processor running at 2.3 GHz, complemented by 16 GB of RAM and a 64-bit version of Windows 10 Single Language. Julia was selected for its exceptional ability to deliver high computational performance, combining execution speeds comparable to low-level programming languages with the ease of development associated with their higher-level counterparts. This combination significantly enhances efficiency and scalability in solving complex optimization problems, making it an ideal platform for conducting extensive stochastic analyses in power systems applications [25].

This work assumed fixed TSC locations based on heuristic or prior studies, focusing solely on the optimal sizing problem. The authors recognize that this simplification limits the solution’s flexibility and may not capture the full potential of optimal device placement. Additionally, the current model does not incorporate certain operational constraints or dynamic factors such as transient stability, equipment aging, or network reconfiguration. These limitations are acknowledged within the scope of our study and will be addressed in future research with the aim of enhancing the practical applicability and robustness of the proposed framework. Despite these assumptions, the results demonstrate the potential of our scenario-based stochastic approach for delivering cost-effective and resilient reactive power solutions within the defined scope.

1.5. Document Structure

This paper is organized into several key sections. Initially, it presents a deterministic optimization model for the placement and sizing of TSCs in MVDNs, focusing on minimizing the total annualized costs by balancing energy losses and capital investments, subject to power flow and operational constraints (Section 2). This is followed by the development of a stochastic optimization framework that incorporates demand uncertainties through multiple scenarios, ensuring that the solutions are robust against load variability (Section 3). The approach (Section 4) employs scenario generation and probabilistic demand modeling to realistically capture demand fluctuations, as well as a sample average approximation method to efficiently handle multiple operational scenarios. Afterwards, the test system, a 33-node radial distribution network, is described in detail (Section 5), including its system parameters and load profiles. This feeder was used to evaluate the effectiveness of the proposed method. The simulation results demonstrate significant cost savings (around 12%), which were obtained through optimal TSC sizing across various operational scenarios, further highlighting the robustness and practicality of our approach. This document concludes with insights on future directions (Section 7), emphasizing the integration of real-time adaptive control, strategic TSC placement, and the adoption of hybrid optimization techniques to enhance system resilience, particularly considering the increasing integration of renewable sources.

2. Deterministic Optimization Model

This section presents the mathematical formulation for the optimal sizing of TSCs in MVDNs, with an emphasis on stochastic optimization analysis. This research specifically addresses the continuous problem of determining optimal TSC sizes while assuming predetermined locations. The problem is modeled so as to incorporate the nonlinear power flow equations and to consider the costs related to investments, along with various operational constraints inherent to distribution networks. The primary objective is to minimize the total annualized operating costs, which include energy losses and the capital expenditure associated with TSC integration [10,11].

2.1. Objective Function

The primary goal of this optimization framework is to minimize the total annualized cost associated with reactive power planning. This total cost, denoted by f, is expressed as the sum of two primary components, i.e., the costs of energy losses $f_1$ and the capital investment $f_2$. Formally, the objective function is formulated as follows:

$$f=f_1+f_2.$$

(1)

The first component, $f_1$, represents the cost incurred due to electrical energy losses across the network over a typical year. It is calculated as the summation of the instantaneous losses, weighted by the energy price, over all relevant time intervals, buses, and lines. Specifically, $f_1$ is expressed as follows:

$$f_1=C_{\mathrm{kWh}}\times T\times \sum _{h\in \mathcal{H}}\sum _{k,m\in \mathcal{N}}{v}_{kh}{v}_{mh}{Y}_{km}cos({\theta }_{kh}-{\theta }_{mh}-{\varphi }_{km}){\mathrm{\Delta }}_h,$$

(2)

where $C_{\mathrm{kWh}}$ indicates the unit energy cost, T the total number of days considered, $\mathcal{H}$ the set of time intervals (such as hours), and $\mathcal{N}$ the set of buses. The quantities $v_{kh}$ and ${\theta }_{kh}$ denote the voltage magnitude and phase angle at bus k during the interval h. The terms $Y_{km}$ and ${\varphi }_{km}$ correspond to the magnitude and phase angle of the admittance between buses k and m, while ${\mathrm{\Delta }}_h$ stands for the duration of the interval.

The second component, $f_2$, accounts for the capital costs associated with installing TSCs at various nodes. It is modeled based on a cubic cost function that captures the increasing marginal costs as the sizes of the TSCs increase. The expression for the investment cost reads:

$$f_2=T\times {\displaystyle \frac{k_1}{k_2}}\sum _{k\in \mathcal{N}}{q}_k^{\mathrm{TSC}}\left({\omega }_1{\left(q_k^{\mathrm{TSC}}\right)}^2+{\omega }_2{q}_k^{\mathrm{TSC}}+{\omega }_3\right),$$

(3)

where $q_k^{\mathrm{TSC}}$ symbolizes the capacity of the TSC installed at bus k. The coefficients ${\omega }_1,{\omega }_2,$ and ${\omega }_3$ define the quadratic and linear contributions to the cost, reflecting the economic impact of sizing. The factor $k_1/k_2$ represents the annuity spread over the entire planning horizon, transforming the capital investment into an equivalent annualized expense.

Overall, this cost function encapsulates a strategic balance: minimizing energy losses while controlling the capital expenditure related to reactive power compensation devices, resulting in a cost-efficient and sustainable reactive power management scheme.

2.2. Constraints

To maintain a consistent energy flow within the network, the active and reactive power injection at each bus must satisfy the steady-state power balance equations. These can be expressed as presented below. For each bus k and time period h, the active power balance is

$$p_{kh}^g-p_{kh}^d=\sum _{m\in \mathcal{N}}{v}_{kh}{v}_{mh}{Y}_{km}cos({\theta }_{kh}-{\theta }_{mh}-{\varphi }_{km}),\forall k\in \mathcal{N},h\in \mathcal{H},$$

(4)

while the reactive power balance accounts for TSC injections:

$$q_{kh}^g-q_{kh}^d+q_{kh}^{\mathrm{TSC}}=\sum _{m\in \mathcal{N}}{v}_{kh}{v}_{mh}{Y}_{km}sin({\theta }_{kh}-{\theta }_{mh}-{\varphi }_{km}),\forall k\in \mathcal{N},h\in \mathcal{H}.$$

(5)

Ensuring that the line flows are within thermal limits, the current magnitude flowing through each branch $(k,m)$ at time h must not exceed the rated capacity. The real and imaginary components of the current are computed as follows:

$$\begin{array}{c}\hfill i_{kmh}^r=y_{km}\left(v_{kh}cos({\theta }_{kh}-{\varphi }_{km})-v_{mh}cos({\theta }_{mh}-{\varphi }_{km})\right),\forall k,m\in \mathcal{N},h\in \mathcal{H}\end{array}$$

(6)

$$\begin{array}{c}\hfill i_{kmh}^i=y_{km}\left(v_{kh}sin({\theta }_{kh}-{\varphi }_{km})-v_{mh}sin({\theta }_{mh}-{\varphi }_{km})\right),\forall k,m\in \mathcal{N},h\in \mathcal{H}\end{array}$$

(7)

Thus, the limit on the lines’ current magnitude is

$$\sqrt{{\left(i_{kmh}^r\right)}^2+{\left(i_{kmh}^i\right)}^2}\le I_{km}^{max},\forall k,m\in \mathcal{N},h\in \mathcal{H}.$$

(8)

To keep the bus voltages within acceptable operating levels, the voltage magnitude $v_{kh}$ must satisfy the following:

$$V_{min}\le v_{kh}\le V_{max},\forall k\in \mathcal{N},h\in \mathcal{H}.$$

(9)

These bounds are typically selected based on standards and operational practices in order to ensure system reliability and safety.

Regarding the placement and capacity of TSCs, the binary variable $x_k\in \{0,1\}$ indicates whether there is one such unit at bus k. The sizing constraints enforce that the TSC capacity $q_k^{\mathrm{TSC}}$ is zero if not installed and bounded by the maximum capacity $q_{max}^{\mathrm{TSC}}$:

$$0\le q_k^{\mathrm{TSC}}\le x_k{q}_{max}^{\mathrm{TSC}},\forall k\in \mathcal{N}.$$

(10)

The reactive power injection $q_{kh}^{\mathrm{TSC}}$ can vary within the installed capacity:

$$-q_k^{\mathrm{TSC}}\le q_{kh}^{\mathrm{TSC}}\le q_k^{\mathrm{TSC}},\forall k\in \mathcal{N},h\in \mathcal{H}.$$

(11)

The total number of installed TSCs is limited by

$$\sum _{k\in \mathcal{N}}{x}_k\le x_{max}^{\mathrm{TSC}}.$$

(12)

In scenarios where reactive power support from TSCs is assumed to be constant over time, the reactive power injection simplifies to

$$q_{kh}^{\mathrm{TSC}}=q_k^{\mathrm{TSC}},\forall k\in \mathcal{N},h\in \mathcal{H},$$

(13)

ensuring a fixed reactive power contribution at each bus throughout the period of analysis.

3. Stochastic Optimization Model

In the real-world operation of electrical distribution networks, the active and reactive power demands at each node exhibit variability across different days. The optimal sizing of TSCs must account for these uncertainties to avoid unnecessary increases in investment costs or, conversely, to avoid under-sizing reactive power injection capacities. Incorporating stochastic considerations into the optimization process ensures that the solutions are robust and better aligned with actual system behavior under diverse operating conditions.

3.1. Mathematical Reformulation

To reformulate the deterministic optimization model shown in Equations (2)–(13), a new set encompassing all studied scenarios—denoted by $s\in \mathcal{S}$—was introduced. Although most of the model variables were adapted as functions of the scenario under analysis, the main objective of this research was to identify the optimal daily profile dispatch while considering all uncertainties arising from active and reactive power demand variations.

To this effect, two scenarios regarding TSC operation were tested: the first assumed fixed reactive power injection, while the second incorporated daily variations in reactive power. The proposed stochastic optimization model is presented below.  

• Objective functions:

$$minf=f_1+f_2,$$

(14)

$$f_1=C_{\mathrm{kWh}}\times T\times \sum _{s\in \mathcal{S}}\sum _{h\in \mathcal{H}}\sum _{k,m\in \mathcal{N}}{v}_{khs}{v}_{mhs}{Y}_{km}cos({\theta }_{khs}-{\theta }_{mhs}-{\varphi }_{km}){\Delta }_h{\lambda }_s,$$

(15)

$$f_2=T\times {\displaystyle \frac{k_1}{k_2}}\sum _{k\in \mathcal{N}}{q}_k^{\mathrm{TSC}}\left({\omega }_1{\left(q_k^{\mathrm{TSC}}\right)}^2+{\omega }_2{q}_k^{\mathrm{TSC}}+{\omega }_3\right),$$

(16)

• Set of constraints

$$p_{khs}^g-p_{khs}^d=\sum _{m\in \mathcal{N}}{v}_{khs}{v}_{mhs}{Y}_{km}cos({\theta }_{khs}-{\theta }_{mhs}-{\varphi }_{km}),\forall k\in \mathcal{N},h\in \mathcal{H},s\in \mathcal{S}$$

(17)

$$q_{khs}^g-q_{khs}^d+q_{kh}^{\mathrm{TSC}}=\sum _{m\in \mathcal{N}}{v}_{khs}{v}_{mhs}{Y}_{km}sin({\theta }_{khs}-{\theta }_{mhs}-{\varphi }_{km}),\forall k\in \mathcal{N},h\in \mathcal{H},s\in \mathcal{S}$$

(18)

$$i_{kmhs}^r=y_{km}\left(v_{khs}cos({\theta }_{khs}-{\varphi }_{km})-v_{mhs}cos({\theta }_{mhs}-{\varphi }_{km})\right),\forall k,m\in \mathcal{N},h\in \mathcal{H},s\in \mathcal{S}$$

(19)

$$i_{kmhs}^i=y_{km}\left(v_{khs}sin({\theta }_{khs}-{\varphi }_{km})-v_{mhs}sin({\theta }_{mhs}-{\varphi }_{km})\right),\forall k,m\in \mathcal{N},h\in \mathcal{H},s\in \mathcal{S}$$

(20)

$$\sqrt{{\left(i_{kmhs}^r\right)}^2+{\left(i_{kmhs}^i\right)}^2}\le I_{km}^{max},\forall k,m\in \mathcal{N},h\in \mathcal{H},s\in \mathcal{S}$$

(21)

$$V_{min}\le v_{khs}\le V_{max},\forall k\in \mathcal{N},h\in \mathcal{H},s\in \mathcal{S}$$

(22)

$$0\le q_k^{\mathrm{TSC}}\le x_k{q}_{max}^{\mathrm{TSC}},\forall k\in \mathcal{N}$$

(23)

$$-q_k^{\mathrm{TSC}}\le q_{kh}^{\mathrm{TSC}}\le q_k^{\mathrm{TSC}},\forall k\in \mathcal{N},h\in \mathcal{H}$$

(24)

$$\sum _{k\in \mathcal{N}}{x}_k\le x_{max}^{\mathrm{TSC}}.$$

(25)

$$\sum _{s\in \mathcal{S}}{\lambda }_s=1.$$

(26)

By incorporating multiple scenarios $(s\in \mathcal{S})$, this stochastic optimization framework explicitly captures the inherent uncertainties associated with active and reactive power demands. In addition, as it includes a variety of possible demand profiles, the model searches for solutions that are robust and effective across different operating conditions, rather than being optimized solely for a single deterministic scenario. This approach enhances the system design’s resilience in the face of fluctuations and unforeseen variations in the load, ensuring that the sizing and operation of TSCs remain reliable and economically efficient under diverse future scenarios. Ultimately, the stochastic formulation provides a comprehensive and practical basis for decision-making with regard to the planning and operation of power distribution networks.

Note that the parameter ${\lambda }_s$ represents the weight or probability assigned to scenario s within the set of all considered demand profiles $\mathcal{S}$. In the context of this stochastic optimization framework, each ${\lambda }_s$ indicates the relative importance or likelihood of scenario s. The sum of all weights equals one, ensuring a proper probability distribution. This allows the model to obtain a weighted average of costs and performance metrics, capturing the inherent uncertainties in the active and reactive power demand, providing solutions that are robust and effective across a range of possible future operating conditions.

Remark 1.

Both the deterministic and stochastic optimization models were implemented and solved in the Julia programming language, employing the interior-point method to efficiently handle the nonlinearities and constraints of the problem. This approach ensures reliability and computational efficiency in obtaining the optimal solutions for system planning and operation.

3.2. Stochastic Optimization Approach

In the context of TSC sizing within an electrical distribution system, it is crucial to recognize that the system operates under multiple states due to variability in renewable generation and load demand. Consequently, it is necessary to define a finite set of representative scenarios that capture the range of possible operating conditions.

To address this issue, the expected value of the objective functions $f_1$ and $f_2$ can be approximated through sample average approximation (SAA) [26]. This involves replacing the stochastic expectation with a weighted average over a finite set of scenarios, which yields the following formulation [27]:

$$\begin{array}{c}\hfill \underset{\mathrm{decision}\mathrm{variables}}{min}E\left[f_1,f_2,{\lambda }_s\right]\approx \sum _{s\in \mathcal{S}}{\lambda }_s\left(f_1^{\left(s\right)}+f_2^{\left(s\right)}\right),\end{array}$$

(27)

where $\mathcal{S}$ denotes the finite set of scenarios; ${\lambda }_s$ is the probability associated with scenario s, satisfying ${\sum }_{s\in \mathcal{S}}{\lambda }_s=1$; and $f_1^{\left(s\right)}$ and $f_2^{\left(s\right)}$ are the objective function components evaluated under scenario n.

This approach provides a tractable framework for incorporating uncertainty in renewable generation and load demand into the TSC sizing problem, enabling the derivation of solutions that are robust across a representative set of operating conditions. Increasing the number of scenarios improves approximation accuracy but also increases computational complexity, so a balance must be maintained which considers the system’s characteristics and the available computational resources [28].

4. Mathematical Framework for Probabilistic Demand Modeling

To appropriately account for demand uncertainty, the active and reactive power demands were modeled as stochastic variables. For each demand period $h=1,2,\dots ,H$, the demands $P_h^d$ and $Q_h^d$ were treated as realizations from normal distributions, characterized by their historical mean values and associated variability [29].

4.1. Stochastic Demand Distributions

Let ${\widehat{P}}_{hs}^d$ and ${\widehat{Q}}_{hs}^d$ denote the active and reactive demands, respectively, for the s-th scenario. These are modeled as Gaussian random variables [30]:

$${\widehat{P}}_{hs}^d\sim \mathcal{N}\left(P_h^d,{\sigma }_{Ph}^2\right),$$

(28)

$${\widehat{Q}}_{hs}^d\sim \mathcal{N}\left(Q_h^d,{\sigma }_{Qh}^2\right),$$

(29)

where the standard deviations are proportional to the mean demands:

$${\sigma }_{Ph}=P_h^d\times \eta ,{\sigma }_{Qh}=Q_h^d\times \eta ,$$

(30)

with $\eta >0$ representing the coefficient of variation (e.g., $\eta =0.10$ for 10% variability).

4.2. Scenario Generation Procedure

A set of N demand scenarios $\left\{({\widehat{P}}_{hs}^d,{\widehat{Q}}_{hs}^d):s=1,\dots ,S\right\}$ is generated by sampling independently from the above-defined Gaussian distributions for each period h:

$${\widehat{P}}_{hs}^d\sim \mathcal{N}\left(P_h^d,{\sigma }_{Ph}^2\right),{\widehat{Q}}_{hs}^d\sim \mathcal{N}\left(Q_h^d,{\sigma }_{Qh}^2\right),$$

(31)

for all $h=1,\dots ,H$.

4.3. Estimating the Probabilities of Each Scenario and Identifying the Most Probable Demand Profiles

To identify the demand scenarios with the highest likelihood, the probability density functions $f_P$ and $f_Q$ of the active and reactive demands are obtained using kernel density estimation (KDE):

$$f_P\left(p\right)\approx {\displaystyle \frac{1}{S}}\sum _{s\in \mathcal{S}}{K}_h\left(p-{\widehat{P}}_{hs}^d\right),$$

(32)

$$f_Q\left(q\right)\approx {\displaystyle \frac{1}{S}}\sum _{s\in \mathcal{S}}{K}_h\left(q-{\widehat{Q}}_{hs}^d\right),$$

(33)

where $K_h(·)$ is a kernel function (e.g., a Gaussian kernel) with bandwidth h. Assuming independence between the active and reactive demands, the joint density for scenario s is approximated as follows:

$${\pi }_s\propto f_P\left({\widehat{P}}_{hs}^d\right)\times f_Q\left({\widehat{Q}}_{hs}^d\right).$$

(34)

The $s^{*}$-th scenario that maximizes ${\pi }_s$ corresponds to the most probable demand realization. These scenarios serve as representative profiles for subsequent system planning and analysis.

4.4. Selecting the Most Representative Scenarios

To select the most representative scenarios, a statistical approach based on density estimation was employed. Initially, multiple demand scenarios (Pd and Qd) were generated for a full year (e.g., 365 days) based on the average daily demand values, assuming a normal distribution with a standard deviation proportional to each mean. Subsequently, KDE was applied separately to Pd and Qd, assuming independence between the active and reactive demands. The joint density of each scenario was then computed as the product of the individual densities, which indicates the likelihood of occurrence. The n scenarios with the highest joint density were selected as the most probable representative load profiles.

This process involved generating demands with random sampling $\mathrm{rand}\left(Normal\right(\mu ,\sigma \left)\right)$, followed by density estimation to evaluate the probability of each scenario. The scenarios with the highest estimated joint densities were chosen to effectively capture the demand variability while reducing the number of scenarios for analysis. This approach allows for a focused assessment of the demand profiles that are most likely to occur in real-world conditions, optimizing computational resources and improving the robustness of the planning and operational models.

5. Test System Information

A well-known radial distribution test system consisting of 33 nodes was utilized to evaluate the effectiveness of the proposed optimization method. The system’s topology is illustrated in Figure 2, while its electrical parameters—including line impedances and peak load values—are provided in

Table 2. Main parameters for the 33-node grid.

Node i-j	${\mathit{R}}_{\mathit{ij}}$ ($\mathbf{\Omega }$)	${\mathit{X}}_{\mathit{ij}}$ ($\mathbf{\Omega }$)	${\mathit{P}}_{\mathit{j}}$ (kW)	${\mathit{Q}}_{\mathit{j}}$ (kvar)	Node i-j	${\mathit{R}}_{\mathit{ij}}$ ($\mathbf{\Omega }$)	${\mathit{X}}_{\mathit{ij}}$ ($\mathbf{\Omega }$)	${\mathit{P}}_{\mathit{j}}$ (kW)	${\mathit{Q}}_{\mathit{j}}$ (kvar)
1-2	0.0922	0.0477	100	60	17-8	0.7320	0.5740	90	40
2-3	0.4930	0.2511	90	40	2-19	0.1640	0.1565	90	40
3-4	0.3660	0.1864	120	80	19-20	1.5042	1.3554	90	40
4-5	0.3811	0.1941	60	30	20-21	0.4095	0.4784	90	40
5-6	0.8190	0.7070	60	20	21-22	0.7089	0.9373	90	40
6-7	0.1872	0.6188	200	100	3-23	0.4512	0.3083	90	50
7-8	1.7114	1.2351	200	100	23-24	0.8980	0.7091	420	200
8-9	1.0300	0.7400	60	20	24-25	0.8960	0.7011	420	200
9-10	1.0400	0.7400	60	20	6-26	0.2030	0.1034	60	25
10-11	0.1966	0.0650	45	30	26-27	0.2842	0.1447	60	25
11-12	0.3744	0.1238	60	35	27-28	1.0590	0.9337	60	20
12-3	1.4680	1.1550	60	35	28-29	0.8042	0.7006	120	70
13-14	0.5416	0.7129	120	80	29-30	0.5075	0.2585	200	600
14-15	0.5910	0.5260	60	10	30-31	0.9744	0.9630	150	70
15-16	0.7463	0.5450	60	20	31-32	0.3105	0.3619	210	100
16-17	1.2860	1.7210	60	20	32-33	0.3410	0.5302	60	40

. Operating at a nominal line-to-ground voltage of 12.66 kV, the system maintains voltage regulation within a range of 0.90 p.u. to 1.10 p.u., which is consistent with common utility standards [13]. This test system is a widely accepted benchmark in the research community for testing power flow algorithms and optimization strategies in distribution networks, allowing for meaningful comparisons with prior work such as [11]. In this study, the IPOPT solver was used to address both the deterministic and the stochastic formulations of the models, leveraging its strength in managing the nonlinearities and constraints that characterize this type of problem.

The data employed to compute the expected TSC-related expenses are summarized in

Table 3. Parameter details of the $f_2$ cost function (TSC investment analysis).

Parameter	Value	Unit	Parameter	Value	Unit
${\omega }_1$	1.50	USD/Mvar3	${\omega }_2$	−713.00	USD/Mvar2
${\omega }_3$	153,750	USD/Mvar	T	365	days
$k_1$	${\displaystyle \frac{6}{2190}}$	1/day	$k_2$	10	years
${\mathrm{\Delta }}_h$	${\displaystyle \frac{1}{2}}$	hour	$C_{\mathrm{kWh}}$	0.1390	USD/kWh

. These values encompass the key technical and economic details necessary for assessing performance based on costs, and they were adapted from the study conducted by [10]. This information provides the foundation for evaluating the financial implications of installing TSCs within the analyzed distribution system.

To evaluate the performance of the TSCs within the 33-bus test feeder, a dynamic load profile was employed to emulate realistic demand fluctuations. The baseline demand at each bus was determined by the peak power consumption values listed in Table 2. These baseline figures were subsequently modulated across different time periods using the load factor percentages depicted in Figure 3. These load factors illustrate the temporal variations in power demand that occur throughout the day, facilitating a more accurate representation of the network’s dynamic loading conditions. This methodology provides a robust framework to assess the TSCs’ responsiveness and effectiveness under the realistic, time-varying load scenarios encountered in contemporary distribution systems.

6. Simulation Results

As previously mentioned, this methodology was developed and executed using Julia v1.9.2 [24] on a personal computer configured with an AMD Ryzen 7 3700 processor running at 2.3 GHz, complemented by 16 GB of RAM and a 64-bit version of Windows 10 Single Language. Julia was chosen for its ability to deliver high computational performance, combining execution speeds similar to those of low-level programming languages with the ease of development offered by their higher-level counterparts. This combination is particularly advantageous for efficiently solving complex optimization problems [25]. Note that all monetary values presented in the tables—including the total costs and the expenses associated with energy losses—are expressed in US dollars ($) to maintain consistency and clarity in the economic analysis.

6.1. Analysis Considering Uncertainties

For mathematical modeling and optimization, the JuMP package was employed because of its expressive syntax and extensive solver compatibility. Nonlinear subproblems were solved using the IPOPT solver [24], which is well-suited for large-scale, sparse, and non-convex optimization tasks. Furthermore, the placement of the TSCs was predefined by a distribution company that provided the data. The continuous sizing variables were also optimized with IPOPT.

Our analysis focused on identifying the TSC sizes while considering a variable reactive power dispatch, thereby enabling the mitigation of uncertainties in active and reactive power demands throughout the spectrum of expected operating conditions.

Remark 2.

The main contribution of this approach is its ability to identify the optimal TSC sizes for a variable reactive power injection scenario, without the need for daily adjustments to the reactive power dispatch. The resulting optimized curves are designed to operate effectively across all expected demand variations throughout the year. This eliminates the need for communication links in order to dynamically modify reactive power injections, which significantly reduces the installation, operating, and maintenance costs.

It should be noted that the selection of the locations for the TSCs was based on the numerical results reported by the authors of [13], which correspond to specific nodes in the 33-bus grid—namely, nodes 14, 30, and 32.

Table 4. Operating costs and TSC sizes for different scenarios in the 33-bus system, showing the cost reductions obtained from optimized sizing.

Dispatch	TSC Sizes (Mvar)	${\mathit{f}}_1$ (USD)	${\mathit{f}}_2$ (USD)	$\mathit{f}={\mathit{f}}_1+{\mathit{f}}_2$ (USD)	Reduction (%)
Deterministic operation scenario
Benchmark	—	112,740.8789	—	112,740.8789	—
Variable	$[0.1786,0.4022,0.1366]$	87,713.8749	11,015.3346	98,729.2096	12.4282
Reduced operation scenario (10 curves)
Benchmark	—	111,893.2259	—	111,893.2259	—
Variable	$[0.1775,0.3996,0.1361]$	87,076.4051	10,949.9381	98,026.3432	12.3929
Annual operation scenario (365 curves)
Benchmark	—	113,756.1792	—	113,756.1792	—
Variable	$[0.1788,0.4023,0.1366]$	88,706.8246	11,019.2002	99,726.0249	12.3335

summarizes the key results obtained from applying the proposed optimization framework to the 33-bus distribution system under different operational scenarios. This analysis compares the costs associated with the deployment of TSCs of varying sizes under three distinct sets of operating conditions: deterministic, reduced, and annual scenarios. For each scenario, economic performance was evaluated through three primary metrics: the fixed costs of TSCs ($f_1$), the operating costs associated with system violations or other penalties ($f_2$), and the total combined cost ($f=f_1+f_2$). These results proved instrumental in understanding the economic trade-offs involved in TSC placement and sizing, as well as in assessing the effectiveness of our approach in minimizing the overall costs.

The results reveal consistent and significant cost savings, achieved through the optimized sizing of TSCs in the 33-bus distribution system. In the deterministic scenario, the total cost decreases by approximately 12.43% with respect to the benchmark value: from about $112,740.88 to around $98,729.21. This reduction is primarily driven by a substantial decrease in fixed TSC deployment costs ($f_1$), which drops from the benchmark level to roughly $87,713.87. This indicates that a well-designed, smaller set of optimally sized TSCs can effectively mitigate system violations and enhance voltage control, leading to lower operational penalties ($f_2$), which were recorded at approximately $11,015.33—significantly less than the benchmark case, whose operating costs were not explicitly modeled.

Under the reduced operation scenario, which considered ten load variation curves to emulate typical demand fluctuations, the overall cost savings remained at around 12.39%. The total system cost decreased from roughly $111,893.23 (benchmark) to $98,026.34 when employing the optimized TSC sizes. The operating costs ($f_2$) declined notably to approximately $10,949.94, confirming that the benefits of our optimal control strategy persist under varying load conditions. This scenario underscores the robustness of the optimization approach in dynamically adapting to demand changes without substantial cost increases.

In the annual operation scenario, where 365 load curves modeled the year-round variability, the total cost experienced a slight increase compared to the reduced scenario, reaching approximately $113,756.18. Despite this, the cost reduction remained substantial, at around 12.33% with respect to the benchmark case. The operating costs rose marginally to about $11,019.20 but were still significantly lower than those of the benchmark case, illustrating the method’s effectiveness in managing long-term load fluctuations and providing a sustained system performance.

Overall, these findings demonstrate that optimized TSC sizing consistently yields ∼12.3–12.4% savings in total system costs across all operational scenarios. Most of these savings derive from reducing fixed investment expenses and operational penalties thanks to strategic placement and sizing. This approach enhances system reliability, voltage regulation, and operational efficiency under diverse and variable load conditions. These results emphasize the importance of incorporating dynamic optimization strategies for modern distribution systems in order to reap their economic and technical advantages over static or fixed configurations.

6.1.1. Voltage Profile Performance

To evaluate the performance of the voltage profiles across different operational scenarios, all nodal voltages are depicted over time for each period. The number of curves corresponding to each scenario under analysis is illustrated in Figure 4.

It is noteworthy that, across all tested scenarios, the voltages remained within a ∼10% bandwidth relative to the nominal value. However, the scenario with reduced curves—i.e., the analysis considering ten curves—exhibited the worst voltage profile, with a minimum voltage of about 0.9028 p.u. This behavior is expected, as the reduced number of curves is meant to approximate the most important cases within the entire dataset, introducing some variations to capture the stochastic nature of the problem.

In contrast, the deterministic case showed the best voltage profile, reaching approximately 0.9241 pu. This is due to the fact that this scenario considers the average model curves, reflecting an expected load that is moderate relative to the extreme cases represented in the reduced case.

6.1.2. Processing Time Behavior

To evaluate the computational efficiency of the proposed stochastic optimization approach for the optimal sizing of TSCs in MVDNs, the average processing time across different scenarios was analyzed, as summarized in

Table 5. Behavior of the processing times.

Case	Mean Time (s)	Max. Time (s)	Min. Time (s)
Deterministic	1.723	1.845	1.695
Reduced	19.128	22.089	16.373
Annual	6546.268	6845.698	6201.772

. These time values were obtained by performing 100 consecutive simulations for each case and then calculating the mean, maximum, and minimum process durations to ensure statistical reliability in the results.

The time analysis highlighted that the computational effort increases significantly when moving from deterministic to probabilistic scenarios. The deterministic case reported an average processing time of approximately 1.72 s. For the reduced scenario, the average time rose to around 19.13 s, reflecting the increased complexity of handling multiple load profiles. The annual scenario, which incorporates a full year of demand variations, required a substantially greater computational effort, with an average time exceeding 6.5 thousand seconds (approximately 1.82 h). These results illustrate the scalability of the approach and the importance of efficient optimization tools like IPOPT for managing large and complex stochastic problems.

6.2. Comparative Analysis vs. Deterministic Approaches

To compare the proposed approach against existing methodologies, a metaheuristic optimization method for the optimal placement of TCSs was considered. This combined approach employs the SCA [23] and is complemented by IPOPT refinement. Additionally, a comparative analysis against other methods from the literature is presented in

Table 6. Comparison of TSC sizing methods in the 33-bus system, showing costs and reductions.

Method	Location (Node)	Size (Mvar)	Objective Function (USD/Year)	Expected Reduction (%)
BONMIN	[6, 18, 30]	[0.0000, 0.1138, 0.4551]	100,221.38	11.10
CBGA	[13, 30, 31]	[0.1528, 0.3227, 0.1157]	100,139.21	11.18
PSO	[14, 30, 31]	[0.1486, 0.3244, 0.1157]	100,107.24	11.21
BWO	[14, 30, 32]	[0.1486, 0.3337, 0.1064]	100,093.29	11.22
AHA	[14, 30, 32]	[0.1486, 0.3337, 0.1064]	100,093.29	11.22
SCA-IPOPT	[14, 30, 32]	[0.1486, 0.3337, 0.1064]	100,093.29	11.22

.

The comparison presented in Table 6 clearly demonstrates the effectiveness of the SCA-IPOPT approach for the optimal placement of TCSs in a 33-bus grid. Notably, this method achieves the lowest objective function value (USD 100,093.29), matching the results of other advanced metaheuristic techniques, which converge to similar cost levels. Despite this, the key advantage of the SCA-IPOPT approach lies in its efficiency; it attains these optimal costs with a reliable and systematic methodology that leverages the strengths of both the SCA and IPOPT refinement.

Furthermore, the expected reduction in operating costs (approximately 11.22%) aligns with the improvements reported by other methods such as BWO and AHA, indicating that SCA-IPOPT provides comparable—if not superior—economic benefits. Its ability to produce these results consistently and with high precision underscores its robustness and effectiveness in addressing the placement problem’s nonlinearities and complexities. This performance validates its potential as a powerful and practical tool for strategic planning in power systems.

In conclusion, the results confirm that the SCA-IPOPT approach is highly effective in achieving optimal solutions, combining the exploration power of metaheuristics with the convergence efficiency of interior-point algorithms. Its performance not only matches the best existing methods in terms of cost reduction but also offers a structured and computationally reliable framework. This makes it a particularly attractive option for deployment in the management and planning of modern power systems, where both accuracy and computational efficiency are critical.

7. Conclusions and Future Work

This work aimed to develop and validate a stochastic optimization framework for the optimal sizing of TSCs in MVDNs, with the objective of minimizing the total operating and capital costs under demand uncertainty. The proposed method combined scenario-based stochastic modeling with advanced nonlinear programming, implementing the IPOPT solver in Julia to determine the most cost-effective TSC sizes that enhance system performance and resilience. According to the results, obtained through extensive simulations on a 33-bus distribution system, the stochastic approach achieved significant cost savings of approximately 12.3–12.4% while improving voltage stability and operational efficiency across various load scenarios. These findings confirmed the effectiveness of integrating probabilistic demand profiles into the sizing process, providing a robust and practical tool for modern power distribution planning.

Furthermore, the results highlighted the potential of this approach to support decision-making amid load variability, the integration of renewable sources, and changing system conditions. Furthermore, the methodology’s flexibility allowed for future improvements, such as the integration of placement strategies, real-time adaptive control, and the incorporation of renewable energy forecasting uncertainties. These avenues for further research were well documented and represent promising directions to extend the robustness and applicability of the framework in increasingly complex and dynamic power systems.

Future research should explore the incorporation of real-time adaptive control mechanisms that can further refine the deployment of TSCs against dynamically changing demand profiles and the penetration of renewable energy technologies. Additionally, extending the stochastic optimization model to include the strategic placement of TSCs alongside their sizing would be beneficial, as it would offer a comprehensive approach that not only addresses capacity but also optimizes the physical integration of TSCs within complex grid architectures, improving efficiency in both operational and economic terms.

Our findings bolster the case for using advanced optimization algorithms in smart grid technologies, enhancing grid resilience and flexibility. As the integration of renewable energy sources continues to grow, future work should include the development of hybrid optimization strategies, combining data-driven insights with machine learning to refine predictive capabilities. Such initiatives would ensure the robust management of power quality and supply under increasing grid complexity, ultimately advancing the transition towards more sustainable, intelligent power distribution systems.