Geometric Optimization of Savonius Vertical-Axis Wind Turbines Using Full Factorial Design and Response Surface Methodology
Abstract
1. Introduction
2. Materials and Methods
2.1. Vertical-Axis Wind Turbines (VAWTs)
2.2. Rotor Design
2.3. Optimization Methodology
2.4. Wind Tunnel and Data Acquisition System
2.5. Rotor Manufacturing via 3D Printing
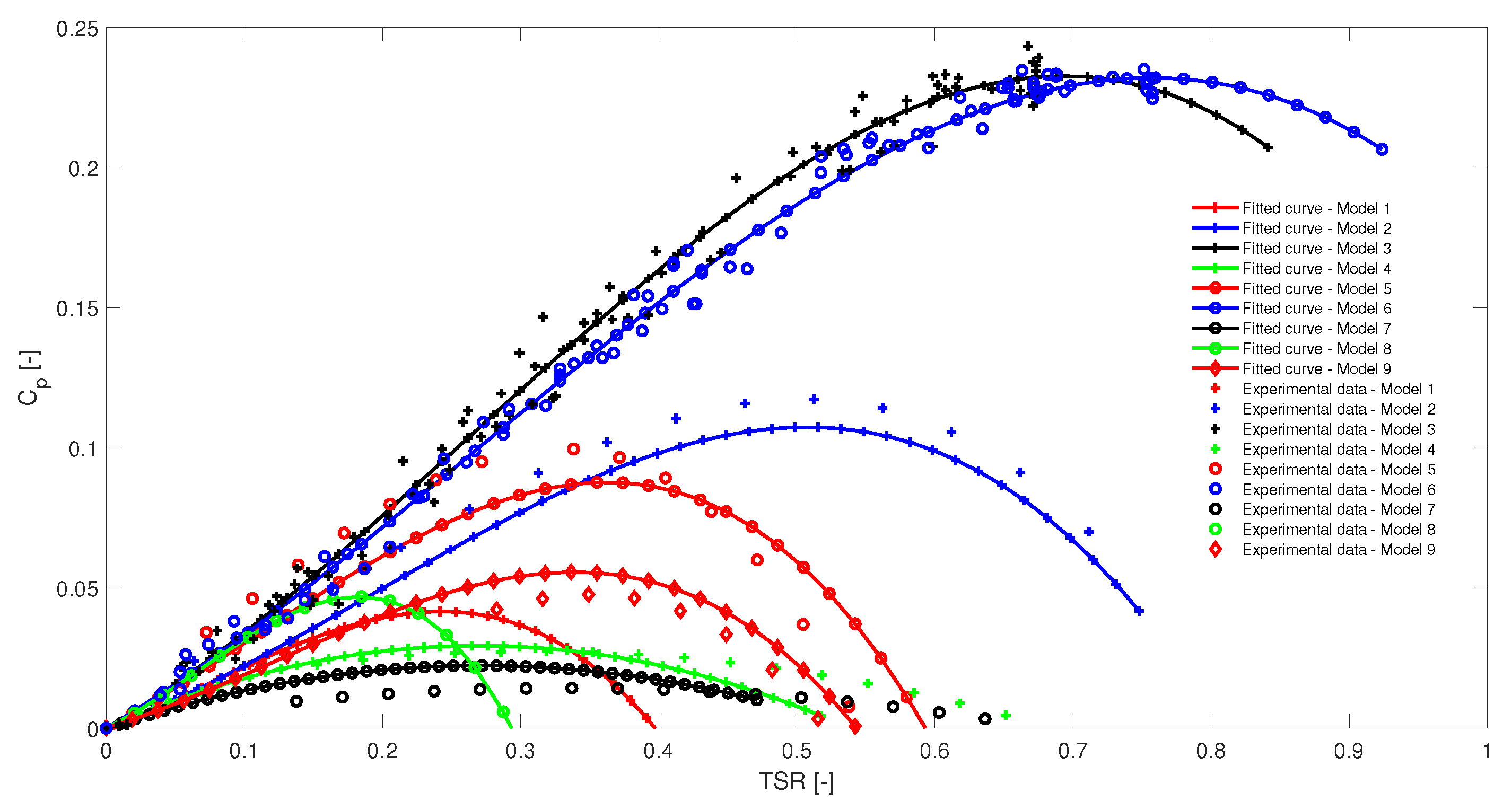
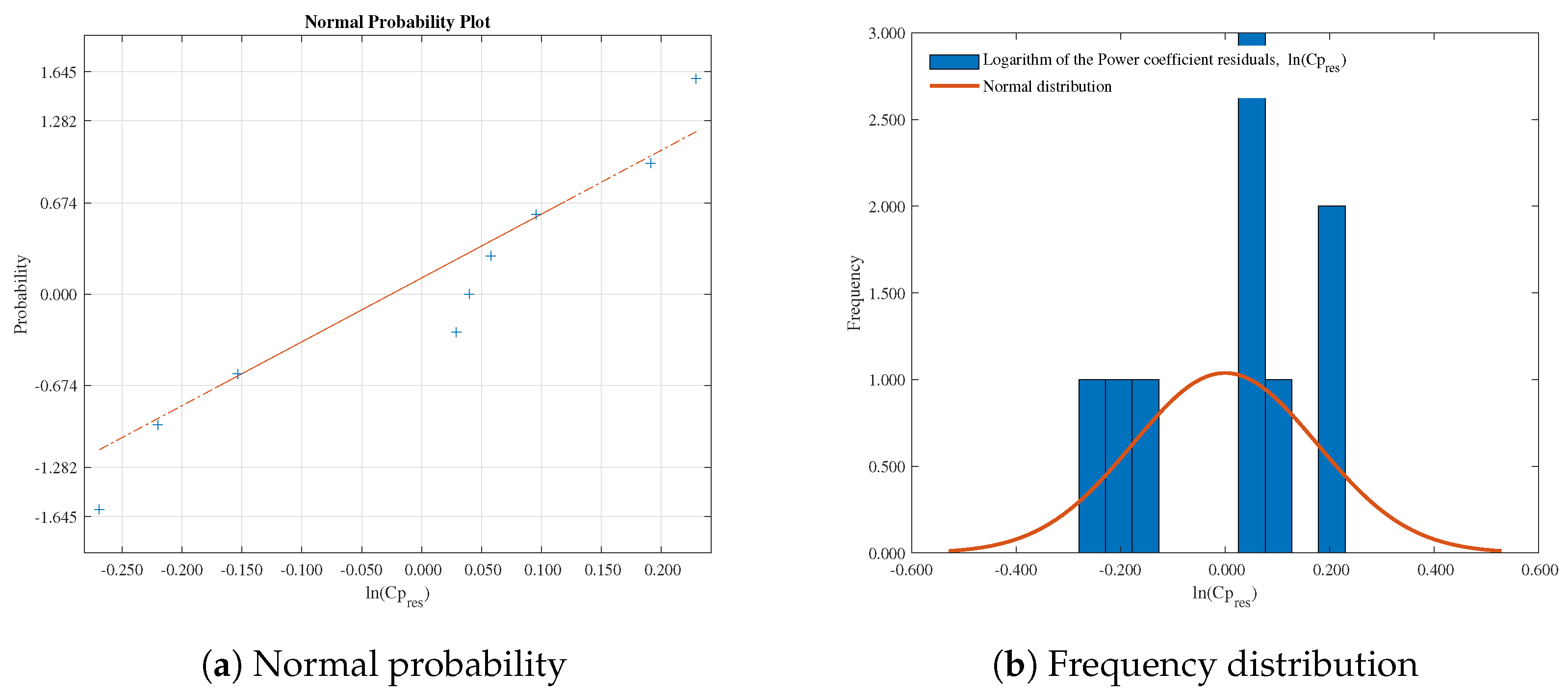
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Newman, P.; Beatley, T.; Boyer, H. Resilient Cities: Overcoming Fossil Fuel Dependence; Island Press: Washington, DC, USA, 2017. [Google Scholar]
- Mayer, A. Fossil fuel dependence and energy insecurity. Energy Sustain. Soc. 2022, 12, 27. [Google Scholar] [CrossRef]
- Backhouse, M.; Rodríguez, F.; Tittor, A. From a Fossil Towards a Renewable Energy Regime in the Americas? Socio-Ecological Inequalities, Contradictions and Challenges for a Global Bioeconomy; Friedrich-Schiller-University: Jena, Germany, 2019. [Google Scholar]
- Saleh, H.M.; Hassan, A.I. The challenges of sustainable energy transition: A focus on renewable energy. Appl. Chem. Eng. 2024, 7, 2084. [Google Scholar] [CrossRef]
- Balakrishnan, P. Global Renewable Energy Transition Challenges and Strategic Solutions. In Geopolitical Landscapes of Renewable Energy and Urban Growth; IGI Global Scientific Publishing: Hershey, PA, USA, 2025; pp. 63–96. [Google Scholar]
- Adewumi, A.; Olu-lawal, K.A.; Okoli, C.E.; Usman, F.O.; Usiagu, G.S. Sustainable energy solutions and climate change: A policy review of emerging trends and global responses. World J. Adv. Res. Rev. 2024, 21, 408–420. [Google Scholar]
- Kumar, A. Global warming, climate change and greenhouse gas mitigation. In Biofuels: Greenhouse Gas Mitigation and Global Warming: Next Generation Biofuels and Role of Biotechnology; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–16. [Google Scholar]
- Singh, S. Energy crisis and climate change: Global concerns and their solutions. In Energy: Crises, Challenges and Solutions; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 1–17. [Google Scholar]
- Kumar, S.; Rathore, K. Renewable energy for sustainable development goal of clean and affordable energy. Int. J. Mater. Manuf. Sustain. Technol. 2023, 2, 1–15. [Google Scholar] [CrossRef]
- Firoozi, A.A.; Firoozi, A.A.; Hejazi, F. Innovations in wind turbine blade engineering: Exploring materials, sustainability, and market dynamics. Sustainability 2024, 16, 8564. [Google Scholar] [CrossRef]
- Firoozi, A.A.; Hejazi, F.; Firoozi, A.A. Advancing wind energy efficiency: A systematic review of aerodynamic optimization in wind turbine blade design. Energies 2024, 17, 2919. [Google Scholar] [CrossRef]
- Afridi, S.K.; Koondhar, M.A.; Jamali, M.I.; Alaas, Z.M.; Alsharif, M.H.; Kim, M.K.; Mahariq, I.; Touti, E.; Aoudia, M.; Ahmed, M. Winds of progress: An in-depth exploration of offshore, floating, and onshore wind turbines as cornerstones for sustainable energy generation and environmental stewardship. IEEE Access 2024, 12, 66147–66166. [Google Scholar] [CrossRef]
- Simoes, M.G.; Farret, F.A.; Khajeh, H.; Shahparasti, M.; Laaksonen, H. Future renewable energy communities based flexible power systems. Appl. Sci. 2021, 12, 121. [Google Scholar] [CrossRef]
- Cai, Y.; Bréon, F.M. Wind power potential and intermittency issues in the context of climate change. Energy Convers. Manag. 2021, 240, 114276. [Google Scholar] [CrossRef]
- Teff-Seker, Y.; Berger-Tal, O.; Lehnardt, Y.; Teschner, N. Noise pollution from wind turbines and its effects on wildlife: A cross-national analysis of current policies and planning regulations. Renew. Sustain. Energy Rev. 2022, 168, 112801. [Google Scholar] [CrossRef]
- Nazir, M.S.; Ali, N.; Bilal, M.; Iqbal, H.M. Potential environmental impacts of wind energy development: A global perspective. Curr. Opin. Environ. Sci. Health 2020, 13, 85–90. [Google Scholar] [CrossRef]
- Rinaldi, G.; Thies, P.R.; Johanning, L. Current status and future trends in the operation and maintenance of offshore wind turbines: A review. Energies 2021, 14, 2484. [Google Scholar] [CrossRef]
- Shields, M.; Beiter, P.; Nunemaker, J.; Cooperman, A.; Duffy, P. Impacts of turbine and plant upsizing on the levelized cost of energy for offshore wind. Appl. Energy 2021, 298, 117189. [Google Scholar] [CrossRef]
- Das, A.; Chimonyo, K.B.; Kumar, T.R.; Gourishankar, S.; Rani, C. Vertical axis and horizontal axis wind turbine-A comprehensive review. In Proceedings of the 2017 International Conference on Energy, Communication, Data Analytics and Soft Computing (ICECDS), Chennai, India, 1–2 August 2017; pp. 2660–2669. [Google Scholar]
- Johari, M.K.; Jalil, M.; Shariff, M.F.M. Comparison of horizontal axis wind turbine (HAWT) and vertical axis wind turbine (VAWT). Int. J. Eng. Technol. 2018, 7, 74–80. [Google Scholar] [CrossRef]
- Al-Rawajfeh, M.A.; Gomaa, M.R. Comparison between horizontal and vertical axis wind turbine. Int. J. Appl. Power Eng. 2023, 12, 13–23. [Google Scholar] [CrossRef]
- Kumar, R.; Raahemifar, K.; Fung, A.S. A critical review of vertical axis wind turbines for urban applications. Renew. Sustain. Energy Rev. 2018, 89, 281–291. [Google Scholar] [CrossRef]
- Liu, J.; Lin, H.; Zhang, J. Review on the technical perspectives and commercial viability of vertical axis wind turbines. Ocean Eng. 2019, 182, 608–626. [Google Scholar] [CrossRef]
- Ahmad, M.; Shahzad, A.; Qadri, M.N.M. An overview of aerodynamic performance analysis of vertical axis wind turbines. Energy Environ. 2023, 34, 2815–2857. [Google Scholar] [CrossRef]
- Roy, S.; Saha, U.K. Review on the numerical investigations into the design and development of Savonius wind rotors. Renew. Sustain. Energy Rev. 2013, 24, 73–83. [Google Scholar] [CrossRef]
- Anbarsooz, M. Aerodynamic performance of helical Savonius wind rotors with 30 and 45 twist angles: Experimental and numerical studies. Proc. Inst. Mech. Eng. Part A J. Power Energy 2016, 230, 523–534. [Google Scholar] [CrossRef]
- Kothe, L.B.; Möller, S.V.; Petry, A.P. Numerical and experimental study of a helical Savonius wind turbine and a comparison with a two-stage Savonius turbine. Renew. Energy 2020, 148, 627–638. [Google Scholar] [CrossRef]
- Jeon, K.S.; Jeong, J.I.; Pan, J.K.; Ryu, K.W. Effects of end plates with various shapes and sizes on helical Savonius wind turbines. Renew. Energy 2015, 79, 167–176. [Google Scholar] [CrossRef]
- Zadeh, M.N.; Pourfallah, M.; Sabet, S.S.; Gholinia, M.; Mouloodi, S.; Ahangar, A.T. Performance assessment and optimization of a helical Savonius wind turbine by modifying the Bach’s section. SN Appl. Sci. 2021, 3, 739. [Google Scholar] [CrossRef]
- Damak, A.; Driss, Z.; Abid, M. Optimization of the helical Savonius rotor through wind tunnel experiments. J. Wind Eng. Ind. Aerodyn. 2018, 174, 80–93. [Google Scholar] [CrossRef]
- Kamoji, M.; Kedare, S.B.; Prabhu, S. Performance tests on helical Savonius rotors. Renew. Energy 2009, 34, 521–529. [Google Scholar] [CrossRef]
- Lajnef, M.; Mosbahi, M.; Abid, H.; Driss, Z.; Amato, E.; Picone, C.; Sinagra, M.; Tucciarelli, T. Numerical and experimental investigation for helical savonius rotor performance improvement using novel blade shapes. Ocean Eng. 2024, 309, 118357. [Google Scholar] [CrossRef]
- Lajnef, M.; Mosbahi, M.; Chouaibi, Y.; Driss, Z. Performance improvement in a helical Savonius wind rotor. Arab. J. Sci. Eng. 2020, 45, 9305–9323. [Google Scholar] [CrossRef]
- Damak, A.; Driss, Z.; Abid, M.S. Experimental investigation of helical Savonius rotor with a twist of 180. Renew. Energy 2013, 52, 136–142. [Google Scholar] [CrossRef]
- Rosato, A.; Perrotta, A.; Maffei, L. Commercial small-scale horizontal and vertical wind turbines: A comprehensive review of geometry, materials, costs and performance. Energies 2024, 17, 3125. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Datta, R.; Kumar, M.P.; Davim, J.P.; Pramanik, S. Energy conversion strategies for wind energy system: Electrical, mechanical and material aspects. Materials 2022, 15, 1232. [Google Scholar] [CrossRef]
- Bello, S.F.; Lawal, R.O.; Ige, O.B.; Adebayo, S.A. Optimizing vertical axis wind turbines for urban environments: Overcoming design challenges and maximizing efficiency in low-wind conditions. GSC Adv. Res. Rev. 2024, 21, 246–256. [Google Scholar] [CrossRef]
- Micallef, D.; Van Bussel, G. A review of urban wind energy research: Aerodynamics and other challenges. Energies 2018, 11, 2204. [Google Scholar] [CrossRef]
- Dewan, A.; Gautam, A.; Goyal, R. Savonius wind turbines: A review of recent advances in design and performance enhancements. Mater. Today Proc. 2021, 47, 2976–2983. [Google Scholar] [CrossRef]
- Laws, P.; Saini, J.S.; Kumar, A.; Mitra, S. Improvement in Savonius wind turbines efficiency by modification of blade designs—A numerical study. J. Energy Resour. Technol. 2020, 142, 061303. [Google Scholar] [CrossRef]
- Alom, N.; Saha, U.K. Evolution and progress in the development of savonius wind turbine rotor blade profiles and shapes. J. Sol. Energy Eng. 2019, 141, 030801. [Google Scholar] [CrossRef]
- Chen, L.; Chen, J.; Zhang, Z. Review of the Savonius rotor’s blade profile and its performance. J. Renew. Sustain. Energy 2018, 10, 013306. [Google Scholar] [CrossRef]
- Talukdar, P.K.; Kulkarni, V.; Saha, U.K. Performance estimation of Savonius wind and Savonius hydrokinetic turbines under identical power input. J. Renew. Sustain. Energy 2018, 10, 064704. [Google Scholar] [CrossRef]
- Alom, N.; Saha, U.K.; Dewan, A. In the quest of an appropriate turbulence model for analyzing the aerodynamics of a conventional Savonius (S-type) wind rotor. J. Renew. Sustain. Energy 2021, 13, 023313. [Google Scholar] [CrossRef]
- Gallo, L.A.; Chica, E.L.; Flórez, E.G. Numerical optimization of the blade profile of a savonius type rotor using the response surface methodology. Sustainability 2022, 14, 5596. [Google Scholar] [CrossRef]
- Saeed, H.A.H.; Elmekawy, A.M.N.; Kassab, S.Z. Numerical study of improving Savonius turbine power coefficient by various blade shapes. Alex. Eng. J. 2019, 58, 429–441. [Google Scholar] [CrossRef]
- Gallo, L.A.; Chica, E.L.; Flórez, E.G.; Obando, F.A. Numerical and experimental study of the blade profile of a Savonius type rotor implementing a multi-blade geometry. Appl. Sci. 2021, 11, 10580. [Google Scholar] [CrossRef]
- Peng, H.; Lam, H.; Liu, H. Power performance assessment of H-rotor vertical axis wind turbines with different aspect ratios in turbulent flows via experiments. Energy 2019, 173, 121–132. [Google Scholar] [CrossRef]
- Shamsoddin, S.; Porté-Agel, F. Effect of aspect ratio on vertical-axis wind turbine wakes. J. Fluid Mech. 2020, 889, R1. [Google Scholar] [CrossRef]
- El-Askary, W.; Saad, A.S.; AbdelSalam, A.M.; Sakr, I. Investigating the performance of a twisted modified Savonius rotor. J. Wind Eng. Ind. Aerodyn. 2018, 182, 344–355. [Google Scholar] [CrossRef]
- Zakaria, A.; Ibrahim, M. Effect of twist angle on starting capability of a Savonius rotor–CFD analysis. IOP Conf. Ser. Mater. Sci. Eng. 2020, 715, 012014. [Google Scholar] [CrossRef]
- Anderson, V.L.; McLean, R.A. Design of Experiments: A Realistic Approach; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Jankovic, A.; Chaudhary, G.; Goia, F. Designing the design of experiments (DOE)—An investigation on the influence of different factorial designs on the characterization of complex systems. Energy Build. 2021, 250, 111298. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, Y.T.; Lim, H.C. Effect of twist angle on the performance of Savonius wind turbine. Renew. Energy 2016, 89, 231–244. [Google Scholar] [CrossRef]
- Farozan, I.; Soelaiman, T.A.F.; Soetikno, P.; Indartono, Y.S. The effect of rotor aspect ratio, stages, and twist angle on Savonius wind turbine performance in low wind speeds environment. Results Eng. 2025, 25, 104041. [Google Scholar] [CrossRef]
- Bouvant, M.; Betancour, J.; Velásquez, L.; Rubio-Clemente, A.; Chica, E. Design optimization of an Archimedes screw turbine for hydrokinetic applications using the response surface methodology. Renew. Energy 2021, 172, 941–954. [Google Scholar] [CrossRef]
- Romero-Menco, F.; Betancour, J.; Velásquez, L.; Rubio-Clemente, A.; Chica, E. Horizontal-axis propeller hydrokinetic turbine optimization by using the response surface methodology: Performance effect of rake and skew angles. Ain Shams Eng. J. 2024, 15, 102596. [Google Scholar] [CrossRef]
- Fox, J. Regression Diagnostics: An Introduction; Sage Publications: Thousand Oaks, CA, USA, 2019. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Fraiman, D.; Fraiman, R. An ANOVA approach for statistical comparisons of brain networks. Sci. Rep. 2018, 8, 4746. [Google Scholar] [CrossRef]
- Potvin, C. ANOVA: Experiments in controlled environments. In Design and Analysis of Ecological Experiments; Chapman and Hall/CRC: Hoboken, NJ, USA, 2020; pp. 46–68. [Google Scholar]
- Ware, J.H.; Mosteller, F.; Delgado, F.; Donnelly, C.; Ingelfinger, J.A. P values. In Medical Uses of Statistics; CRC Press: Hoboken, NJ, USA, 2019; pp. 181–200. [Google Scholar]
- Di Leo, G.; Sardanelli, F. Statistical significance: P value, 0.05 threshold, and applications to radiomics—Reasons for a conservative approach. Eur. Radiol. Exp. 2020, 4, 18. [Google Scholar] [CrossRef]
- Saada, K.; Amroune, S.; Zaoui, M. Prediction of mechanical behavior of epoxy polymer using Artificial Neural Networks (ANN) and Response Surface Methodology (RSM). Fract. Struct. Integr. 2023, 17, 191–206. [Google Scholar] [CrossRef]
- Prabhahar, M.; Athitya, M.P.; Chitrambalam, M.T.; Prabhu, L.; Prakash, S. Experimental investigation of MS material in laser cutting machine using Taguchi method. AIP Conf. Proc. 2022, 2426, 020019. [Google Scholar] [CrossRef]
- Zhang, W. p-value based statistical significance tests: Concepts, misuses, critiques, solutions and beyond. Comput. Ecol. Softw. 2022, 12, 80. [Google Scholar]
- Valvez, S.; Silva, A.P.; Reis, P.N. Optimization of printing parameters to maximize the mechanical properties of 3D-printed PETG-based parts. Polymers 2022, 14, 2564. [Google Scholar] [CrossRef] [PubMed]
- Hsueh, M.H.; Lai, C.J.; Wang, S.H.; Zeng, Y.S.; Hsieh, C.H.; Pan, C.Y.; Huang, W.C. Effect of printing parameters on the thermal and mechanical properties of 3D-printed pla and petg, using fused deposition modeling. Polymers 2021, 13, 1758. [Google Scholar] [CrossRef] [PubMed]
- Prabowoputra, D.M.; Prabowo, A.R. Effect of geometry modification on turbine performance: Mini-review of Savonius rotor. Int. J. Mech. Eng. Robot. Res. 2022, 11, 777–783. [Google Scholar] [CrossRef]
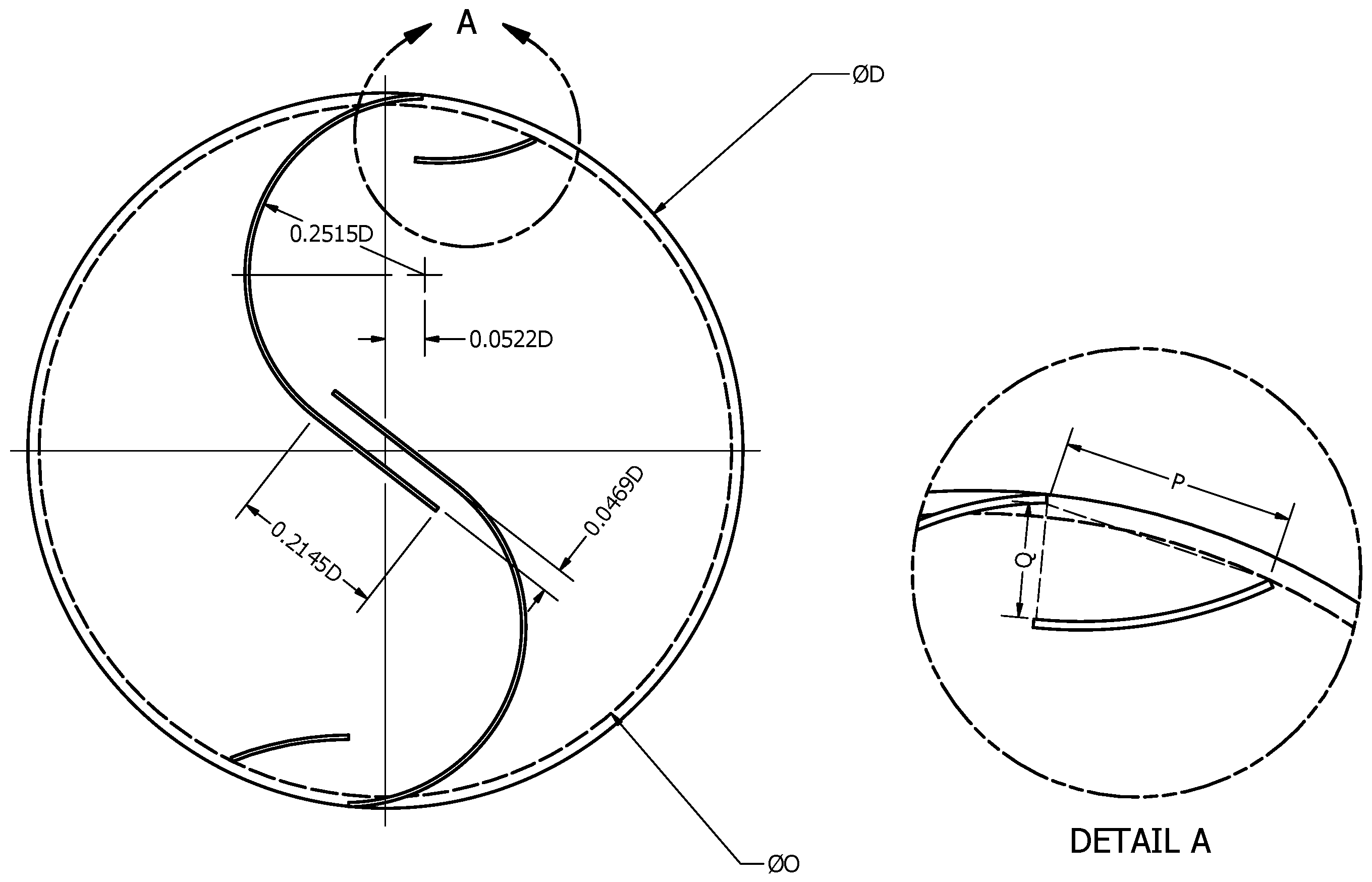
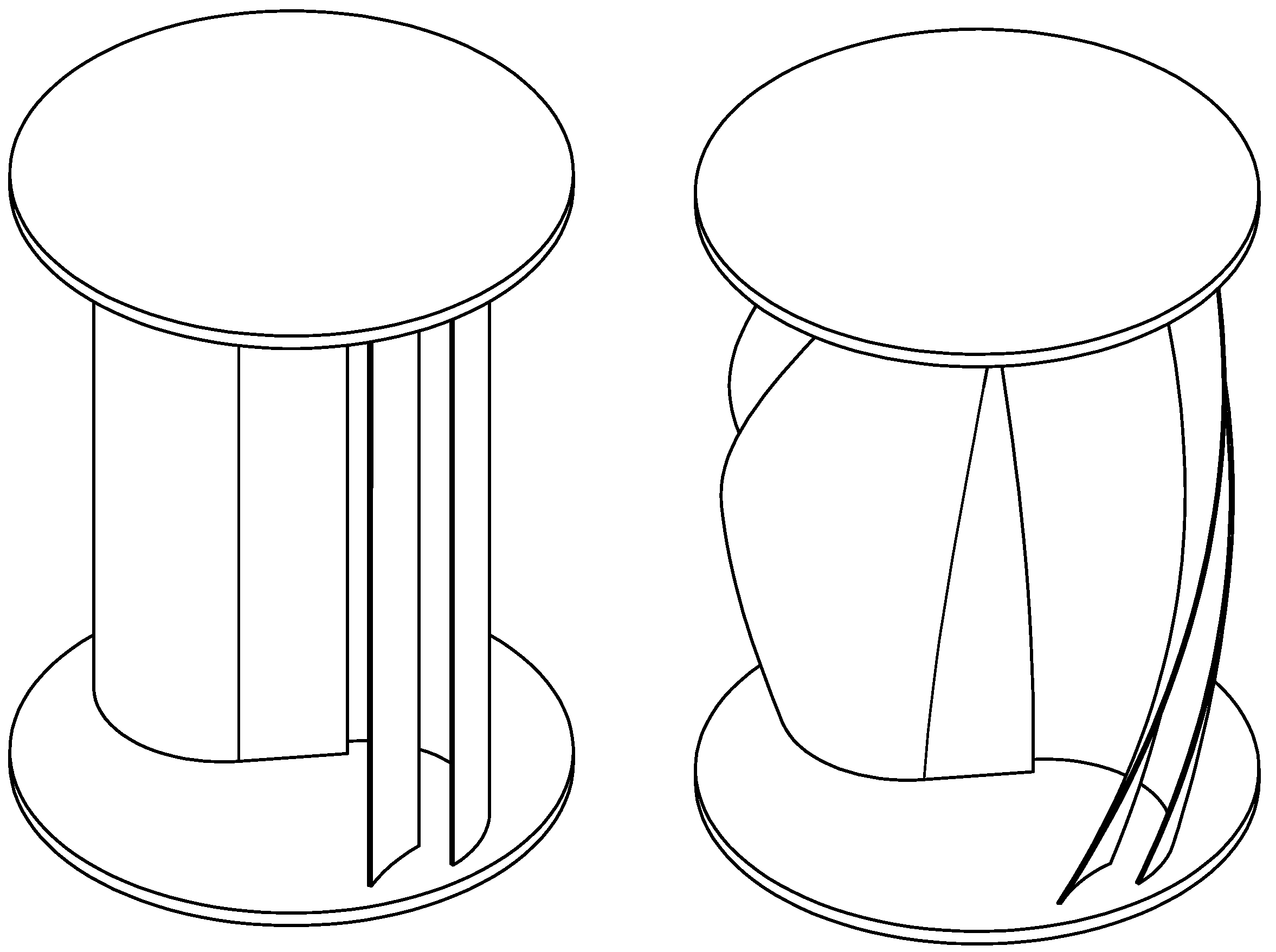


| Model | (Deg) | AR (-) |
|---|---|---|
| 1 | 30.0 | 0.70 |
| 2 | 30.0 | 1.35 |
| 3 | 30.0 | 2.00 |
| 4 | 105.0 | 0.70 |
| 5 | 105.0 | 1.35 |
| 6 | 105.0 | 2.00 |
| 7 | 180.0 | 0.70 |
| 8 | 180.0 | 1.35 |
| 9 | 180.0 | 2.00 |
| Model | Creality CR-M4 |
| Printing volume | 45 cm × 45 cm × 47 cm |
| Print layer thickness | 0.05–0.35 mm |
| Platform temperature | ∼100 °C |
| Nozzle diameter | 0.4 mm |
| Printing accuracy | ±0.1 mm |
| Nozzle printing temperature | ∼300 °C |
| Model | Creality K1C |
| Printing volume | 22 cm × 22 cm × 25 cm |
| Print layer thickness | 0.1–0.35 mm |
| Platform temperature | ∼100 °C |
| Nozzle diameter | 0.4 mm |
| Printing accuracy | ±0.1 mm |
| Nozzle printing temperature | ∼300 °C |
| Material | PETG |
| Color | Red |
| Wire diameter | 1.75 ± 0.05 mm |
| Elongation at break | 6.8 ± 0.9 (%) |
| Young’s modulus | 1.48 ± 0.27 (GPa) |
| Tensile strength | 31.9 ± 1.1 (MPa) |
| Weight | 1000 g |
| Recommended printing temp | 215–235 °C |
| Recommended printing speed | 30–150 mm/s |
| Model 1 | Model 2 | Model 3 |
 |  |  |
| Model 4 | Model 5 | Model 6 |
 |  |  |
| Model 7 | Model 8 | Model 9 |
 |  |  |
| Model | (Deg) | AR | Exp. | Exp. | Pred. | Residual |
|---|---|---|---|---|---|---|
| 1 | 30.0 | 0.70 | 0.04167 | −3.17797 | −3.27413 | 0.09615 |
| 2 | 30.0 | 1.35 | 0.10736 | −2.23148 | −2.28996 | 0.05848 |
| 3 | 30.0 | 2.00 | 0.23260 | −1.45844 | −1.30580 | −0.15264 |
| 4 | 105.0 | 0.70 | 0.02942 | −3.52577 | −3.25727 | −0.26850 |
| 5 | 105.0 | 1.35 | 0.08772 | −2.43359 | −2.47444 | 0.04085 |
| 6 | 105.0 | 2.00 | 0.23200 | −1.46102 | −1.69161 | 0.23060 |
| 7 | 180.0 | 0.70 | 0.02233 | −3.80168 | −3.83160 | 0.02992 |
| 8 | 180.0 | 1.35 | 0.04700 | −3.05749 | −3.25011 | 0.19262 |
| 9 | 180.0 | 2.00 | 0.05570 | −2.88739 | −2.66862 | −0.21877 |
| Term | Df | SS | MS | F-Value | p-Value |
|---|---|---|---|---|---|
| 1 | 1.381 | 1.381 | 22.209 | 0.00922 | |
| 1 | 3.679 | 3.679 | 59.167 | 0.00154 | |
| 1 | 0.175 | 0.175 | 2.811 | 0.16896 | |
| 1 | 0.162 | 0.162 | 2.607 | 0.18171 | |
| Residuals | 4 | 0.249 | 0.062 | – | – |
| Normality Test Name | Test Statistic | p-Value |
|---|---|---|
| KS Marsaglia Method | 0.6957 | 0.6384 |
| Jarque–Bera Test | 0.7027 | 0.7037 |
| Cramer–Von Mises Test | 0.0660 | 0.3157 |
| KS Limiting Form | 0.6957 | 0.7184 |
| Shapiro–Wilk Test | 0.9229 | 0.4470 |
| KS Lilliefors Modification | 0.2319 | 0.1778 |
| Shapiro–Francia Test | 0.9387 | 0.5244 |
| KS Stephens Modification | 0.7591 | 0.1500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velásquez, L.; Rengifo, J.; Saldarriaga, A.; Rubio-Clemente, A.; Chica, E. Geometric Optimization of Savonius Vertical-Axis Wind Turbines Using Full Factorial Design and Response Surface Methodology. Sci 2025, 7, 154. https://doi.org/10.3390/sci7040154
Velásquez L, Rengifo J, Saldarriaga A, Rubio-Clemente A, Chica E. Geometric Optimization of Savonius Vertical-Axis Wind Turbines Using Full Factorial Design and Response Surface Methodology. Sci. 2025; 7(4):154. https://doi.org/10.3390/sci7040154
Chicago/Turabian StyleVelásquez, Laura, Juan Rengifo, Andrés Saldarriaga, Ainhoa Rubio-Clemente, and Edwin Chica. 2025. "Geometric Optimization of Savonius Vertical-Axis Wind Turbines Using Full Factorial Design and Response Surface Methodology" Sci 7, no. 4: 154. https://doi.org/10.3390/sci7040154
APA StyleVelásquez, L., Rengifo, J., Saldarriaga, A., Rubio-Clemente, A., & Chica, E. (2025). Geometric Optimization of Savonius Vertical-Axis Wind Turbines Using Full Factorial Design and Response Surface Methodology. Sci, 7(4), 154. https://doi.org/10.3390/sci7040154








