Analysis of Marginal Expansion in Existing Pressurised Water Installations: Analytical Formulation and Practical Application
Abstract
1. Introduction
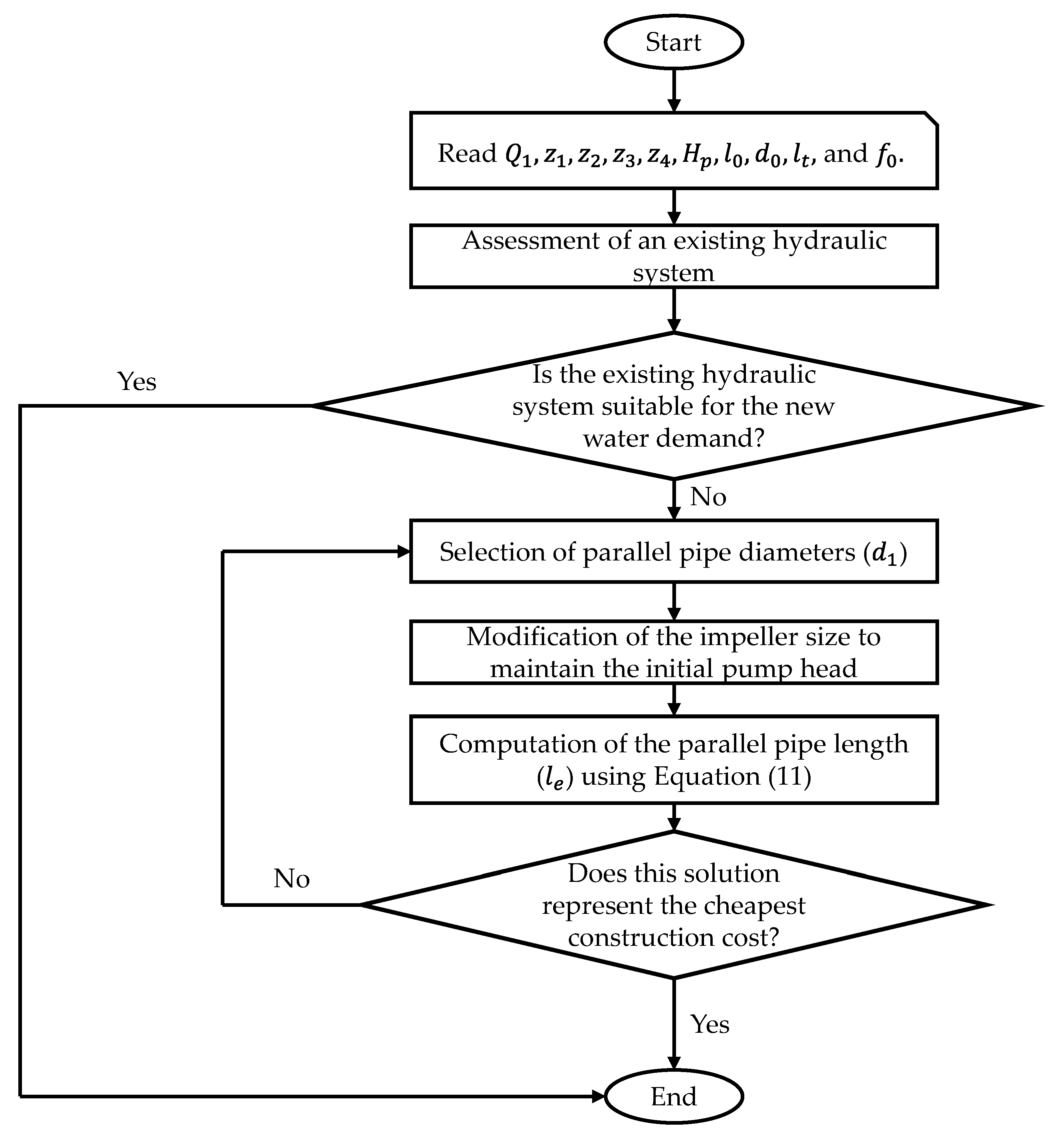
2. Proposed Methodology
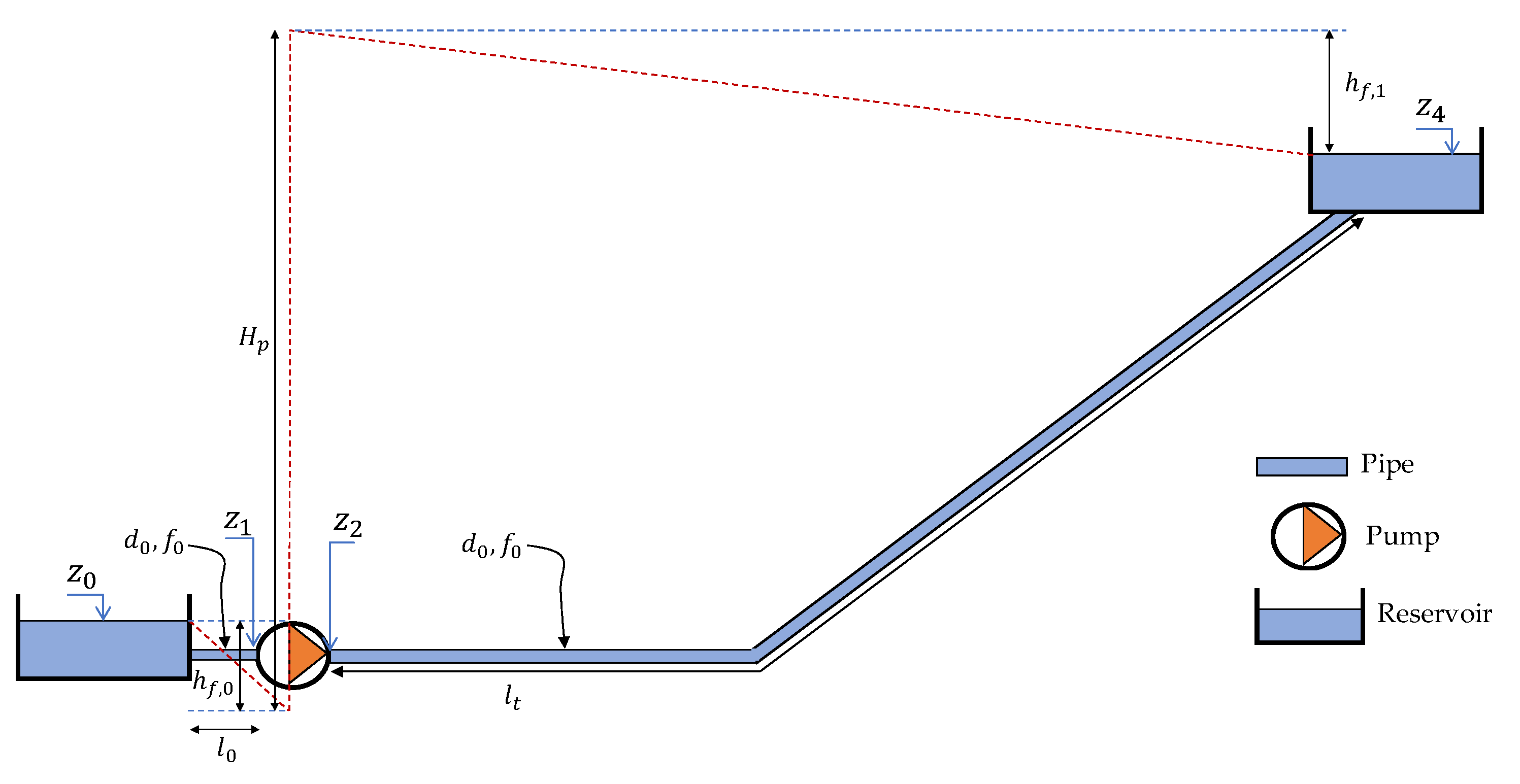
2.1. Hydraulic Modelling
2.1.1. Assumptions
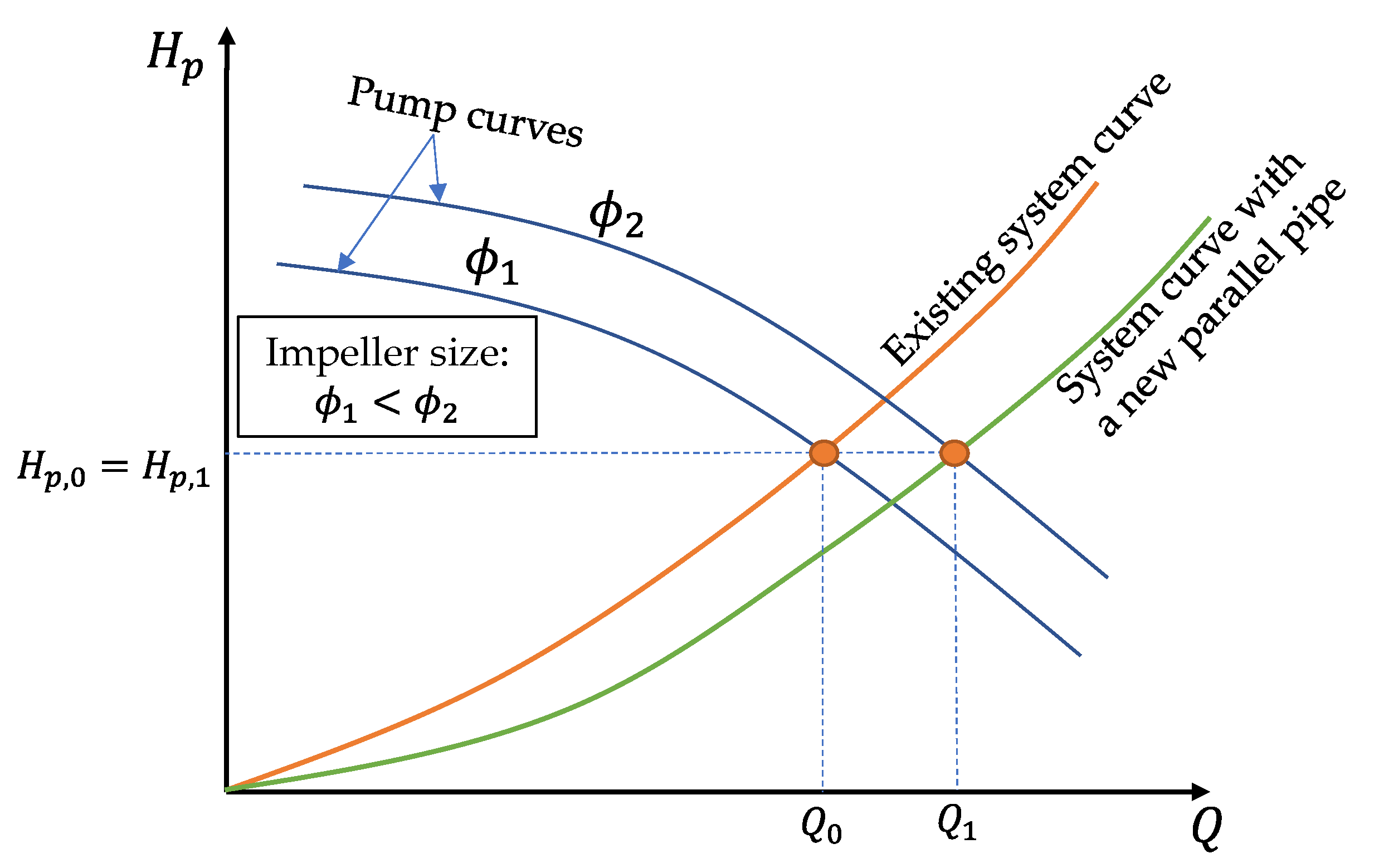
- The pump head of the pumping system is preserved considering a higher impeller size (ϕ2) [23].
- The installed parallel pipe will have resistance characteristics similar to the existing one.
- Friction losses in each pipeline section will be estimated using the Darcy–Weisbach equation [24].
- Water demand has increased.
2.1.2. Governing Equations
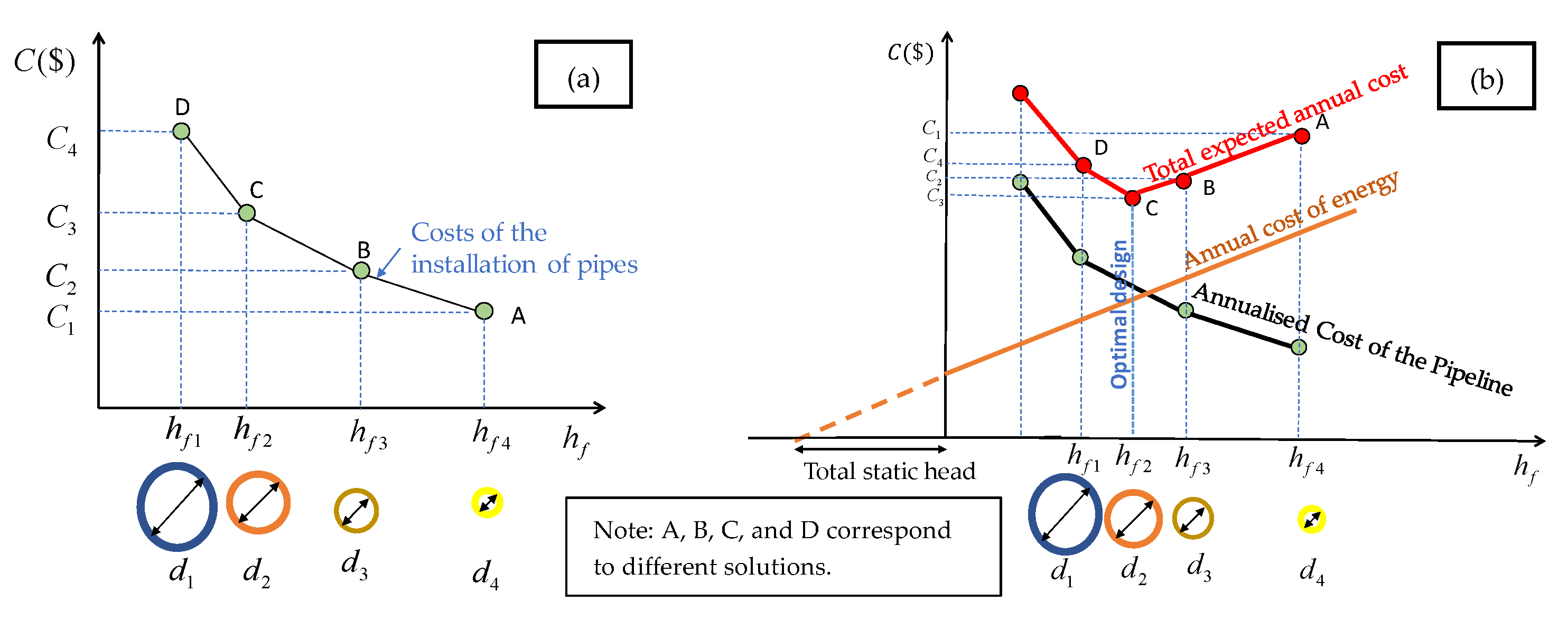
2.2. Computation of Construction Costs
3. Results and Discussion
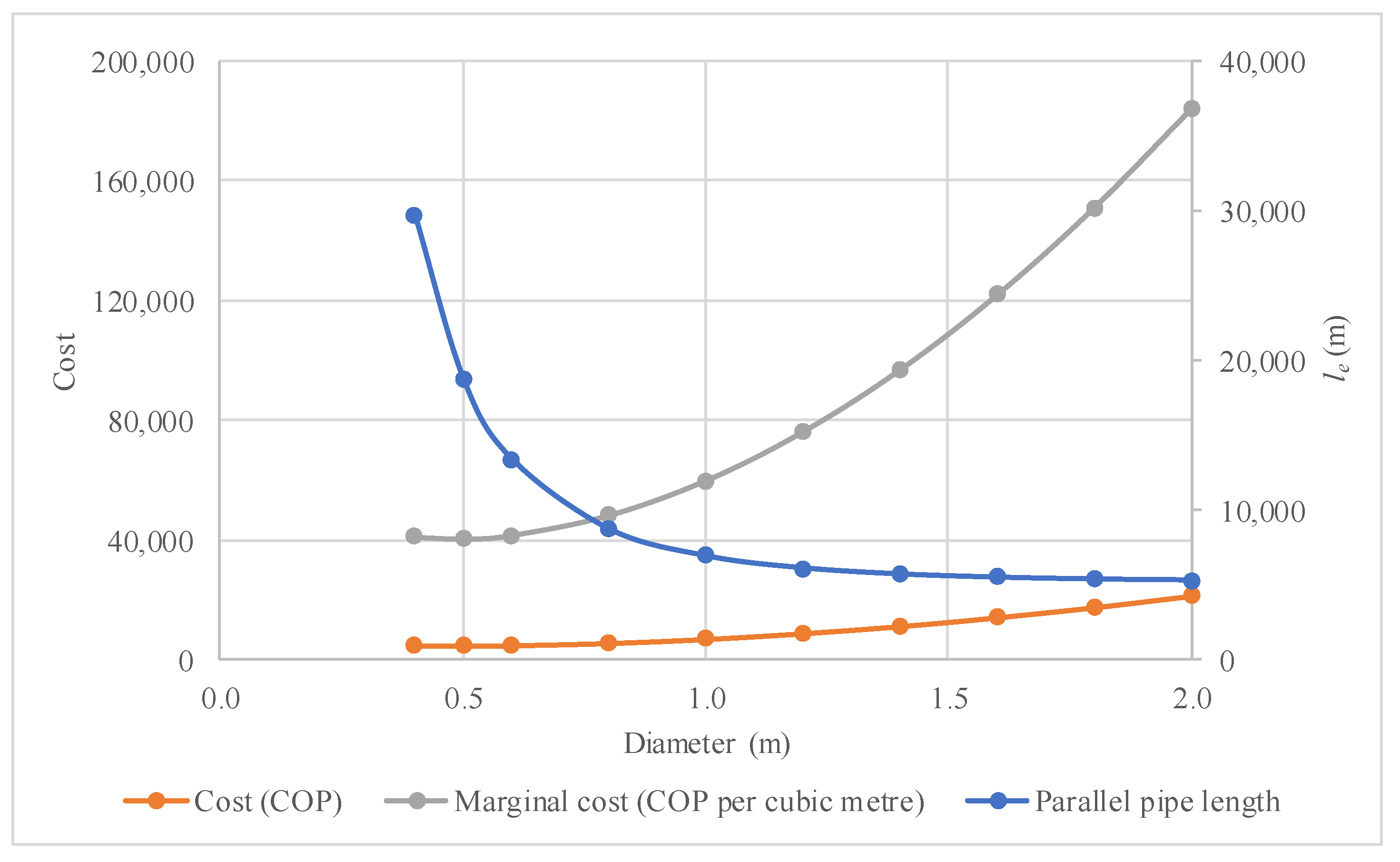
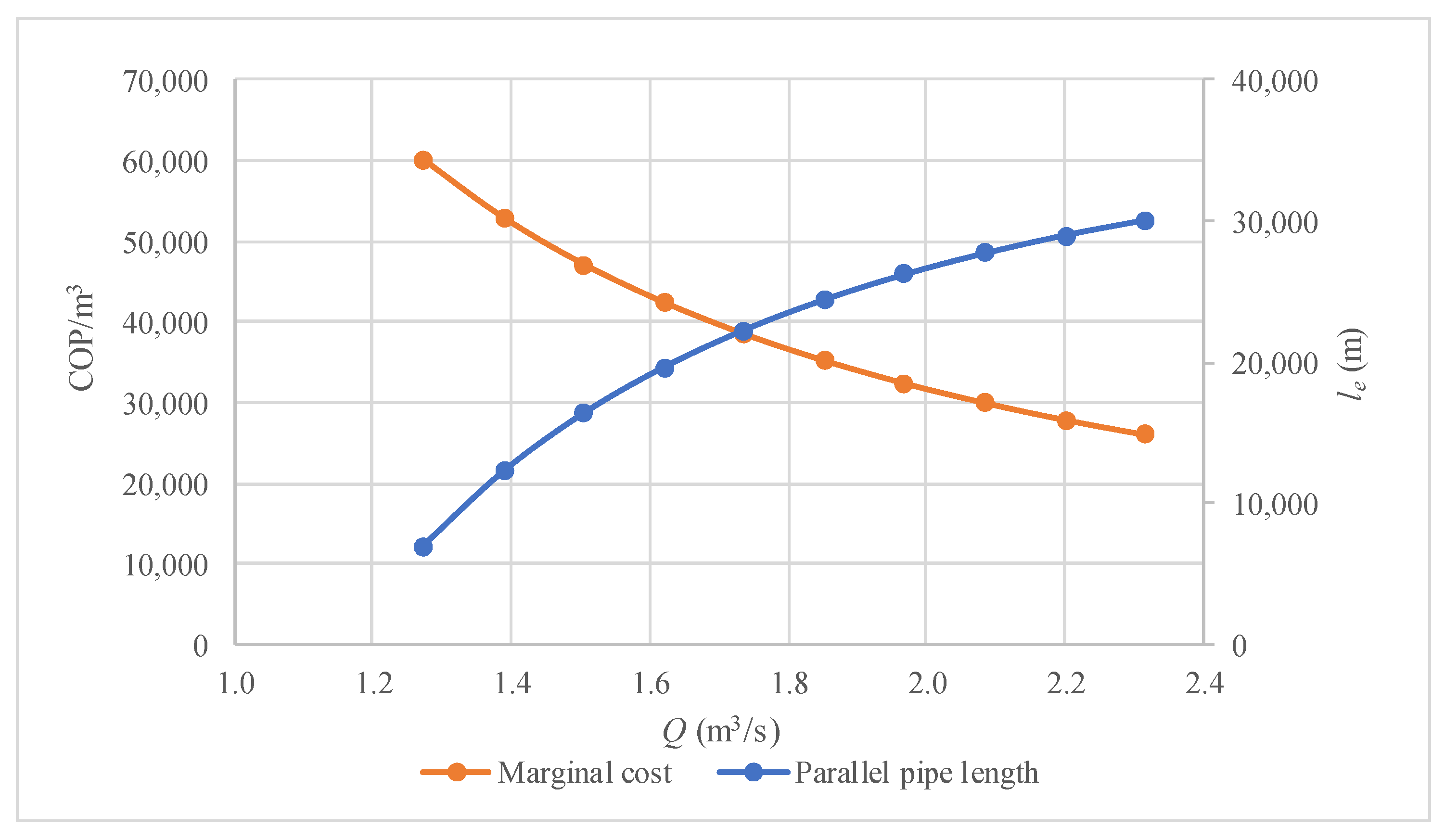
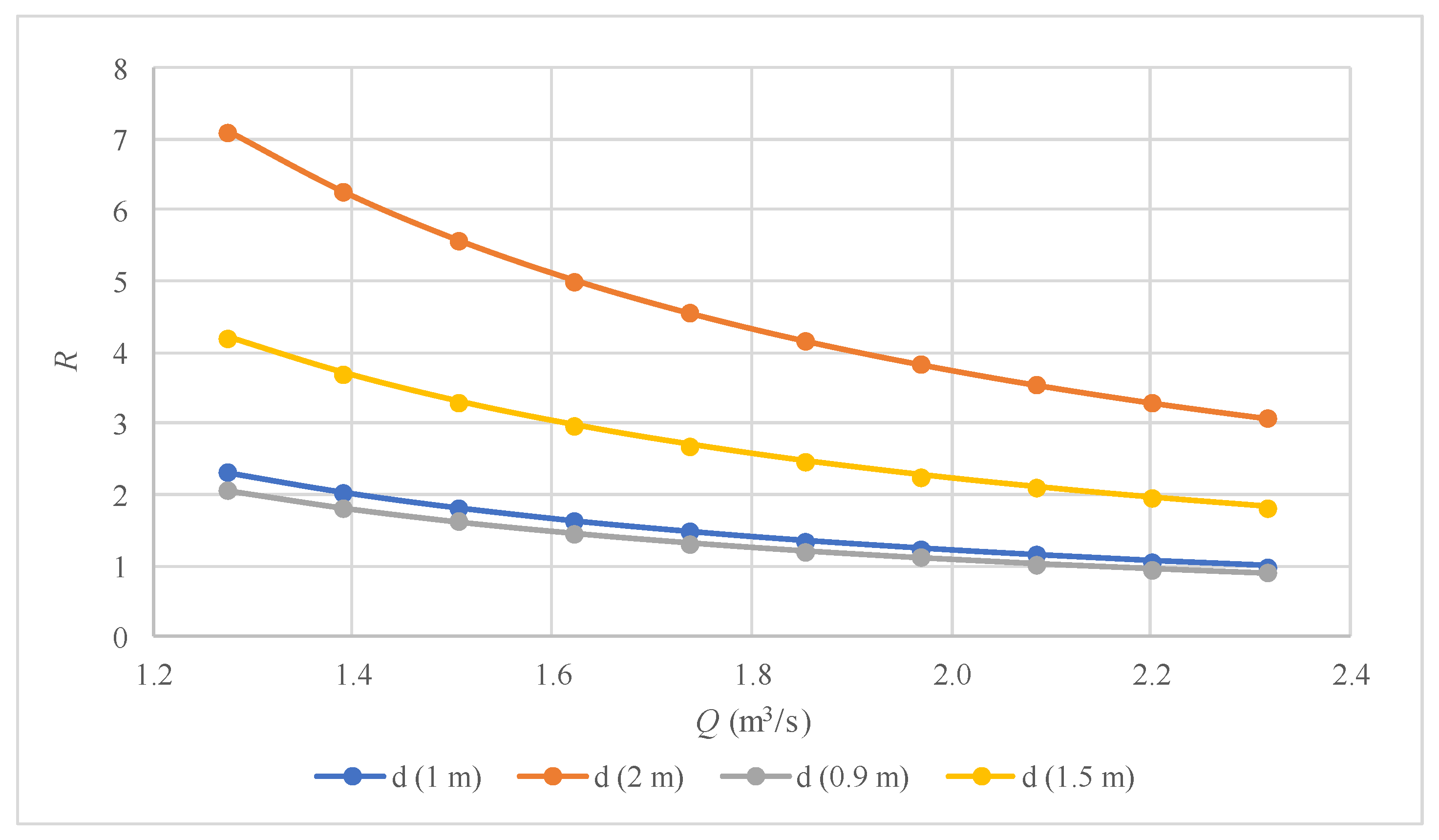
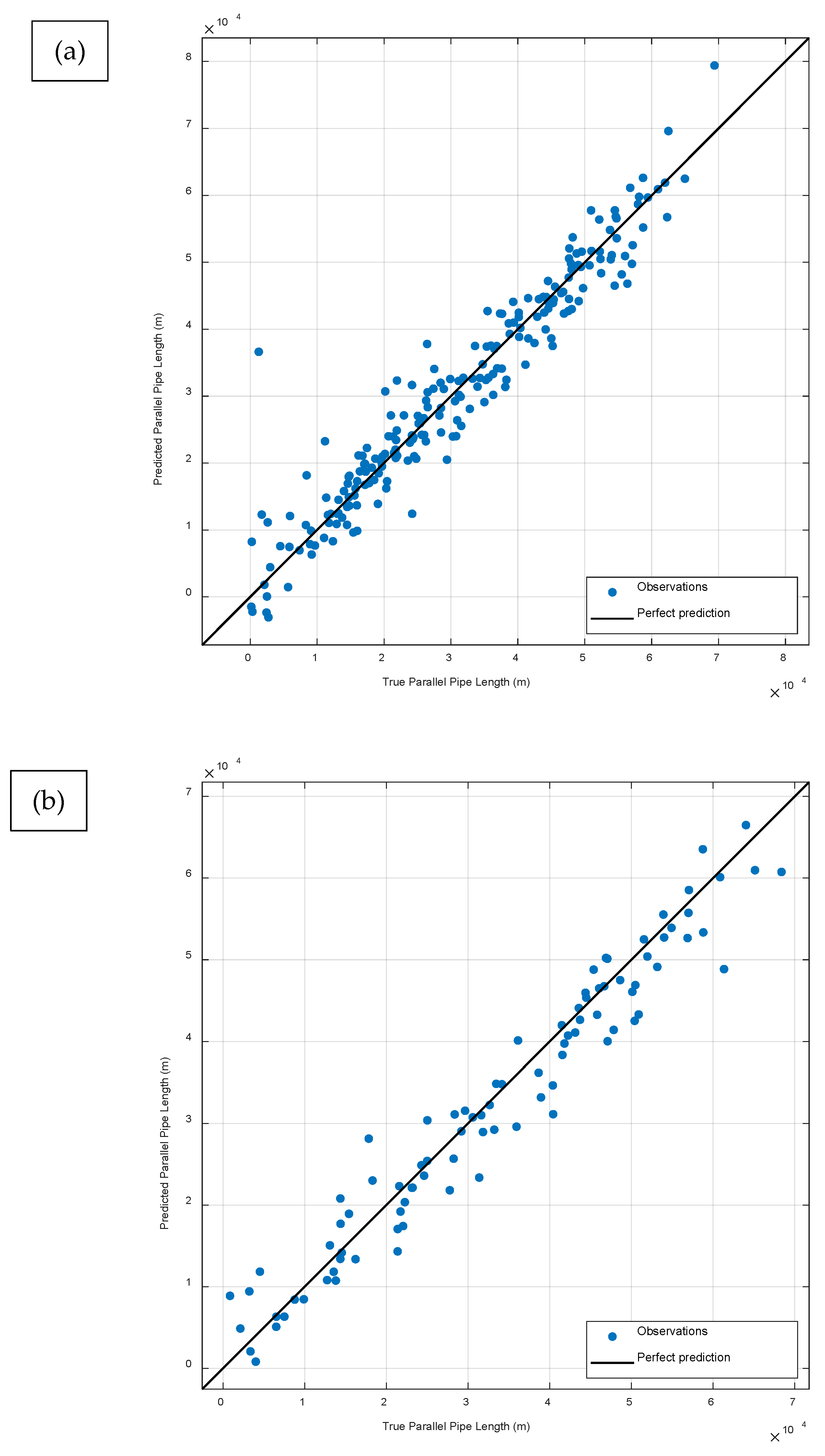
3.1. Practical Application
3.2. Discussion
- Addition of a new parallel pipe: To accommodate additional water demand, any new pipe must have resistance characteristics comparable to those of the existing pipeline (e.g., PN 6, PN 10, PN 16, PN 20, PN 25, PN 32 or other). This ensures adequate protection against water hammer effects. Good practice guidelines generally recommend increasing the design pressure of pipes by 10% for systems operating under gravity flow and by 30% for pumping systems, to account for maximum surge pressures. Such considerations are commonly applied in practical engineering design.
- Pipe roughness: The absolute roughness of existing pipes is assumed to remain constant over time. This implies that the hydraulic design must ensure flow velocities high enough to prevent biofilm development within the pipeline. The proposed methodology can be used to evaluate both the existing and the new friction losses.
- Pump performance curves: The pump curves for the two impeller sizes (see Figure 3) assume the same power input, meaning that both configurations operate close to their best efficiency point with similar efficiencies.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Internal pipe diameter for the existing installation (m); | |
| Internal pipe diameter for the projected parallel pipe (m); | |
| Friction factor for the existing installation (-); | |
| Friction factor for the projected parallel pipe (-); | |
| Friction losses (m); | |
| Pump head (m); | |
| Coefficient that depends on pipe diameter and friction factor (-); | |
| Proportionality constant (-); | |
| Projected parallel pipe length (m); | |
| Upstream pipe length (m); | |
| Downstream pipe length (m); | |
| Total numbers of observations (-); | |
| Unit cost (COP); | |
| Pipe resistance (s2/m5); | |
| Coefficient of determination (-); | |
| Constant standard dimension ratio (-); | |
| Existing water demand (m3/s); | |
| New water demand (m3/s); | |
| Pipe wall thickness (m); | |
| Invert elevation (m a.s.l.); | |
| Impeller size (m) | |
| Volume of material required (m3 per linear meter of pipe); | |
| Subscripts | |
| Pipe; | |
| Predicted value; | |
| True value | |
| Superscripts | |
| ̄ | Average value |
References
- Ghannam, S.; Hussain, F. Short-Term Water Demand Forecasting: A Review. Aust. J. Water Resour. 2024, 1–19. [Google Scholar] [CrossRef]
- Donkor, E.A.; Mazzuchi, T.A.; Soyer, R.; Alan Roberson, J. Urban Water Demand Forecasting: Review of Methods and Models. J. Water Resour. Plan. Manag. 2014, 140, 146–159. [Google Scholar] [CrossRef]
- Ministry of Housing, City, and Development (MinVivienda); Republic of Colombia. Resolution 0977 of 9 December 2021, Technical Guidelines for the Sector of Potable Water and Basic Sanitation (RAS). 2021. Available online: https://www.minvivienda.gov.co/normativa/resolucion-0799-2021 (accessed on 15 August 2025).
- Liu, H.; Xing, R.; Davies, E.G.R. Forecasting Municipal Water Demands: Evaluating the Impacts of Population Growth, Climate Change, and Conservation Policies on Water End-Use. Sustain. Cities Soc. 2025, 130, 106581. [Google Scholar] [CrossRef]
- Akuoko-Asibey, A.; Nkemdirim, L.C.; Draper, D.L. The Impacts of Climatic Variables on Seasonal Water Consumption in Calgary, Alberta. Can. Water Resour. J. 1993, 18, 107–116. [Google Scholar] [CrossRef]
- Amisigo, B.A.; McCluskey, A.; Swanson, R. Modeling Impact of Climate Change on Water Resources and Agriculture Demand in the Volta Basin and Other Basin Systems in Ghana. Sustainability 2015, 7, 6957–6975. [Google Scholar] [CrossRef]
- Dawadi, S.; Ahmad, S. Evaluating the Impact of Demand-Side Management on Water Resources under Changing Climatic Conditions and Increasing Population. J. Environ. Manag. 2013, 114, 261–275. [Google Scholar] [CrossRef] [PubMed]
- Dang, C.; Zhang, H.; Yao, C.; Mu, D.; Lyu, F.; Zhang, Y.; Zhang, S. IWRAM: A Hybrid Model for Irrigation Water Demand Forecasting to Quantify the Impacts of Climate Change. Agric. Water Manag. 2024, 291, 108643. [Google Scholar] [CrossRef]
- Ashofteh, P.-S.; Bozorg-Haddad, O.; Loáiciga, H.A. Development of Adaptive Strategies for Irrigation Water Demand Management under Climate Change. J. Irrig. Drain. Eng. 2017, 2, 143. [Google Scholar] [CrossRef]
- Eekhout, J.P.C.; Delsman, I.; Baartman, J.E.M.; van Eupen, M.; van Haren, C.; Contreras, S.; Martínez-López, J.; de Vente, J. How Future Changes in Irrigation Water Supply and Demand Affect Water Security in a Mediterranean Catchment. Agric. Water Manag. 2024, 297, 108818. [Google Scholar] [CrossRef]
- Gagliardi, F.; Alvisi, S.; Franchini, M.; Guidorzi, M. A Comparison between Pattern-Based and Neural Network Short-Term Water Demand Forecasting Models. Water Supply 2017, 17, 1426–1435. [Google Scholar] [CrossRef]
- González Perea, R.; Camacho Poyato, E.; Montesinos, P.; Rodríguez Díaz, J.A. Optimisation of Water Demand Forecasting by Artificial Intelligence with Short Data Sets. Biosyst. Eng. 2019, 177, 59–66. [Google Scholar] [CrossRef]
- Wu, I. pai Design of Drip Irrigation Main Lines. J. Irrig. Drain. Div. 1975, 101, 265–278. [Google Scholar] [CrossRef]
- Alperovits, E.; Shamir, U. Design of Optimal Water Distribution Systems. Water Resour. Res. 1977, 13, 885–900. [Google Scholar] [CrossRef]
- Choi, Y.H.; Lee, H.M.; Choi, J.; Yoo, D.G.; Kim, J.H. Development of Practical Design Approaches for Water Distribution Systems. Appl. Sci. 2019, 9, 5117. [Google Scholar] [CrossRef]
- Ramani, K.; Rudraswamy, G.K.; Umamahesh, N.V. Optimal Design of Intermittent Water Distribution Network Considering Network Resilience and Equity in Water Supply. Water 2023, 15, 3265. [Google Scholar] [CrossRef]
- Parvaze, S.; Kumar, R.; Khan, J.N.; Al-Ansari, N.; Parvaze, S.; Vishwakarma, D.K.; Elbeltagi, A.; Kuriqi, A. Optimization of Water Distribution Systems Using Genetic Algorithms: A Review. Arch. Comput. Methods Eng. 2023, 30, 4209–4244. [Google Scholar] [CrossRef]
- Mekonnen, Y.A. Evaluation of Current and Future Water Demand Scenario and Hydraulic Performance of Water Distribution Systems, a Case Study for Addis Kidam Town, Ethiopia. Appl. Water Sci. 2023, 13, 40. [Google Scholar] [CrossRef]
- Wang, K.; Meng, J.; Wang, Z.; Zhao, K.; Liu, B. Robust Adaptive Optimization for Sustainable Water Demand Prediction in Water Distribution Systems. Sci. Rep. 2025, 15, 4039. [Google Scholar] [CrossRef] [PubMed]
- Robak, A.; Bush, S.; Bjornlund, H. Advancing the Impact Identification Step of Benefit-Cost Analysis of Potable Water Infrastructure Investments: A Systems Method for Identifying Important Impacts Pre-Monetisation. Water Res. 2023, 239, 120058. [Google Scholar] [CrossRef]
- Napolitano, J.; Di Francesco, M.; Sechi, G.M. Decision Trees in Cost–Benefit Analysis for Flood Risk Management Plans. J. Hydroinform. 2024, 26, 762–778. [Google Scholar] [CrossRef]
- Varouchakis, E.A.; Palogos, I.; Karatzas, G.P. Application of Bayesian and Cost Benefit Risk Analysis in Water Resources Management. J. Hydrol. 2016, 534, 390–396. [Google Scholar] [CrossRef]
- Mays, L. Hydraulic Design Handbook, 1st ed.; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Chaudhry, M.H. Applied Hydraulic Transients; Van Nostrand Reinhold Company: New York, NY, USA, 1987. [Google Scholar]

| (m) | (m) |
|---|---|
| 2.0 | 5332 |
| 1.8 | 5401 |
| 1.6 | 5519 |
| 1.4 | 5732 |
| 1.2 | 6135 |
| 1.0 | 6949 |
| 0.8 | 8751 |
| 0.6 | 13,413 |
| 0.5 | 18,756 |
| 0.4 | 29,724 |
| (-) | (m) |
|---|---|
| 0.008 | 6341 |
| 0.009 | 6439 |
| 0.010 | 6531 |
| 0.011 | 6621 |
| 0.012 | 6707 |
| 0.013 | 6790 |
| 0.014 | 6871 |
| 0.015 | 6949 |
| 0.016 | 7025 |
| 0.017 | 7099 |
| 0.018 | 7172 |
| (m) | (m3/s) | (m) |
|---|---|---|
| 100 | 1.274 | |
| 95 | 1.209 | |
| 90 | 1.140 | |
| 85 | 1.066 | |
| 80 | 0.980 | 6949 |
| 75 | 0.901 | |
| 70 | 0.806 | |
| 65 | 0.698 | |
| 60 | 0.570 | |
| 55 | 0.403 |
(m) | (m) | Marginal Cost (COP/m3) |
|---|---|---|
| 0.10 | 18,756 | 66,009 |
| 0.15 | 9513 | 75,334 |
| 0.20 | 6949 | 97,826 |
| 0.25 | 6008 | 132,154 |
| 0.30 | 5610 | 177,678 |
| 0.35 | 5424 | 233,859 |
| 0.40 | 5332 | 300,254 |
| 0.45 | 5283 | 376,532 |
| 0.50 | 5256 | 462,465 |
| 0.55 | 5240 | 557,900 |
| 0.60 | 5231 | 662,734 |
| Variable | Unit | Range | |
|---|---|---|---|
| From | To | ||
| m3/s | 0.29 | 6.00 | |
| m a.s.l. | 1.0 | 4.0 | |
| m a.s.l. | 1.0 | 4.0 | |
| m a.s.l. | 5.0 | 10.0 | |
| m a.s.l. | 10.0 | 50.0 | |
| m | 50.0 | 220.0 | |
| m | 20.0 | 50.2 | |
| m | 0.26 | 1.96 | |
| m | 10,220 | 59,968 | |
| - | 0.010 | 0.024 | |
| - | 0.010 | 0.024 | |
| m | 0.32 | 2.88 | |
| m3/s | 0.02 | 5.71 | |
| Preset | R2 (Validation) | R2 (Test) | Preset | R2 (Validation) | R2 (Test) |
|---|---|---|---|---|---|
| Linear | 0.85 | 0.87 | Efficient Linear SVM | 0.00 | 0.18 |
| Interactions Linear | 0.89 | 0.91 | Boosted Trees | 0.84 | 0.89 |
| Robust Linear | 0.83 | 0.87 | Bagged Trees | 0.81 | 0.86 |
| Stepwise Linear | 0.92 | 0.95 | Squared Exponential GPR | 0.92 | 0.92 |
| Fine Tree | 0.72 | 0.86 | Matern 5/2 GPR | 0.92 | 0.92 |
| Medium Tree | 0.74 | 0.79 | Exponential GPR | 0.89 | 0.88 |
| Coarse Tree | 0.62 | 0.61 | Rational Quadratic GPR | 0.92 | 0.92 |
| Linear SVM | 0.84 | 0.87 | Narrow Neural Network | 0.77 | 0.85 |
| Quadratic SVM | 0.92 | 0.92 | Medium Neural Network | 0.45 | 0.67 |
| Cubic SVM | 0.92 | 0.92 | Wide Neural Network | 0.40 | 0.78 |
| Fine Gaussian SVM | 0.00 | −0.02 | Bilayered Neural Network | 0.79 | 0.84 |
| Medium Gaussian SVM | 0.85 | 0.85 | Trilayered Neural Network | 0.66 | 0.85 |
| Coarse Gaussian SVM | 0.83 | 0.85 | SVM Kernel | −0.01 | −0.06 |
| Efficient Linear Least Squares | 0.06 | 0.16 | Least Squares Regression Kernel | 0.81 | 0.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arrieta-Pastrana, A.; Coronado-Hernández, O.E.; Saba, M. Analysis of Marginal Expansion in Existing Pressurised Water Installations: Analytical Formulation and Practical Application. Sci 2025, 7, 140. https://doi.org/10.3390/sci7040140
Arrieta-Pastrana A, Coronado-Hernández OE, Saba M. Analysis of Marginal Expansion in Existing Pressurised Water Installations: Analytical Formulation and Practical Application. Sci. 2025; 7(4):140. https://doi.org/10.3390/sci7040140
Chicago/Turabian StyleArrieta-Pastrana, Alfonso, Oscar E. Coronado-Hernández, and Manuel Saba. 2025. "Analysis of Marginal Expansion in Existing Pressurised Water Installations: Analytical Formulation and Practical Application" Sci 7, no. 4: 140. https://doi.org/10.3390/sci7040140
APA StyleArrieta-Pastrana, A., Coronado-Hernández, O. E., & Saba, M. (2025). Analysis of Marginal Expansion in Existing Pressurised Water Installations: Analytical Formulation and Practical Application. Sci, 7(4), 140. https://doi.org/10.3390/sci7040140







