Cost Reduction in Power Systems via Transmission Line Switching Using Heuristic Search
Abstract
1. Introduction
1.1. General Context
1.2. Motivation
1.3. Literature Review
1.4. Contribution, Scope and Limitations
1.5. Paper Structure
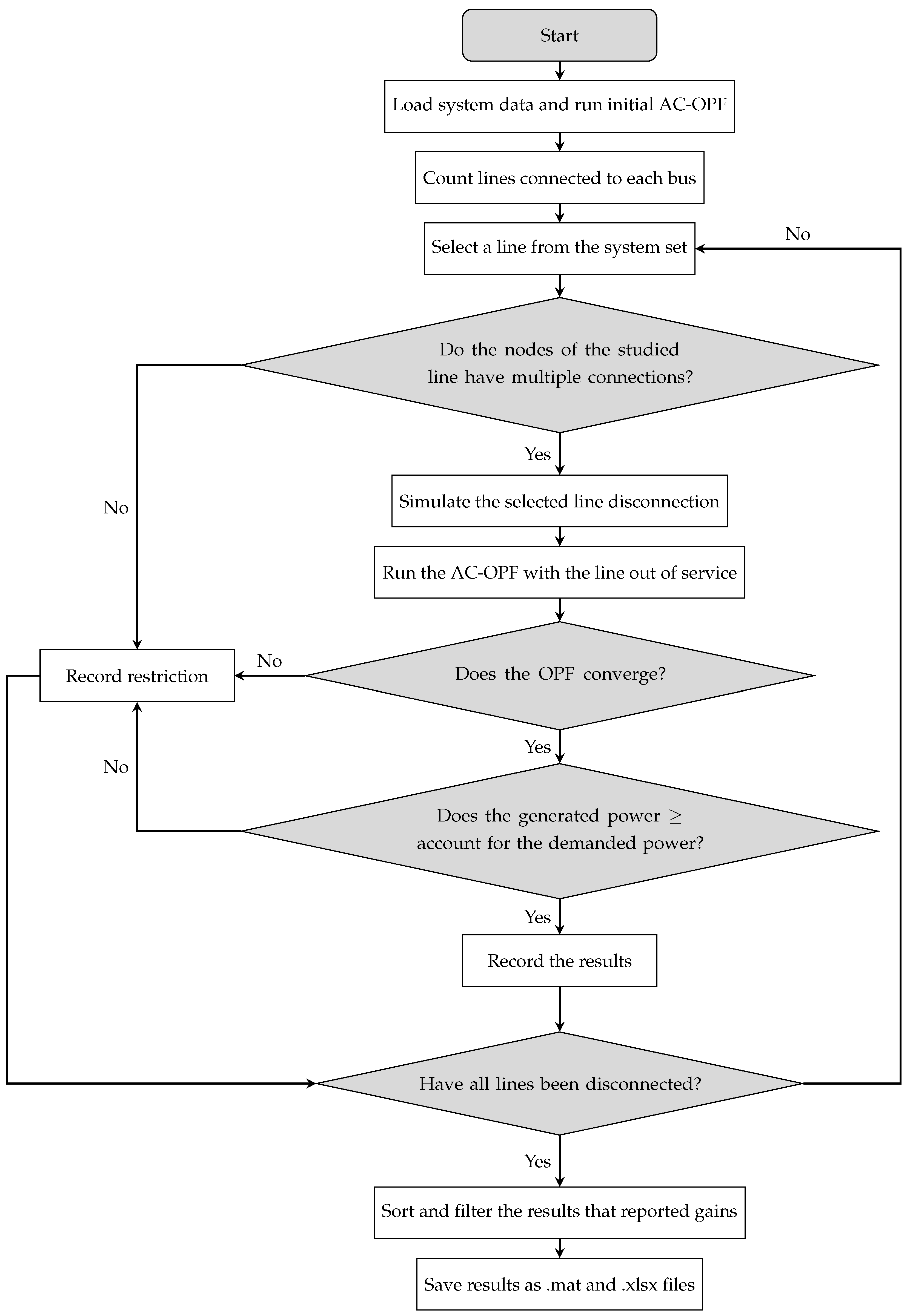
2. Methodology
2.1. Heuristic Solution Algorithm
2.1.1. Initialization and Base Case
2.1.2. Iterative Simulation and Feasibility Criterion
2.1.3. Consolidation and Optimal Configuration Selection
2.1.4. Objective Function
2.1.5. Problem Constraints
2.1.6. Model Characterization
2.2. Solution Strategy
3. Results and Discussion
3.1. Test Feeder Characterization
- With 3374 buses modeled in MATPOWER, this meshed and realistic electrical system integrates 596 generators, 4161 transmission lines, and 2434 loads, ensuring high redundancy and DG availability [33].
- It features two operating areas that facilitate the analysis of interzonal power flows, constituting a large-scale environment for assessing the methodology’s robustness and scalability. The fundamental parameters are summarized in Table 6.
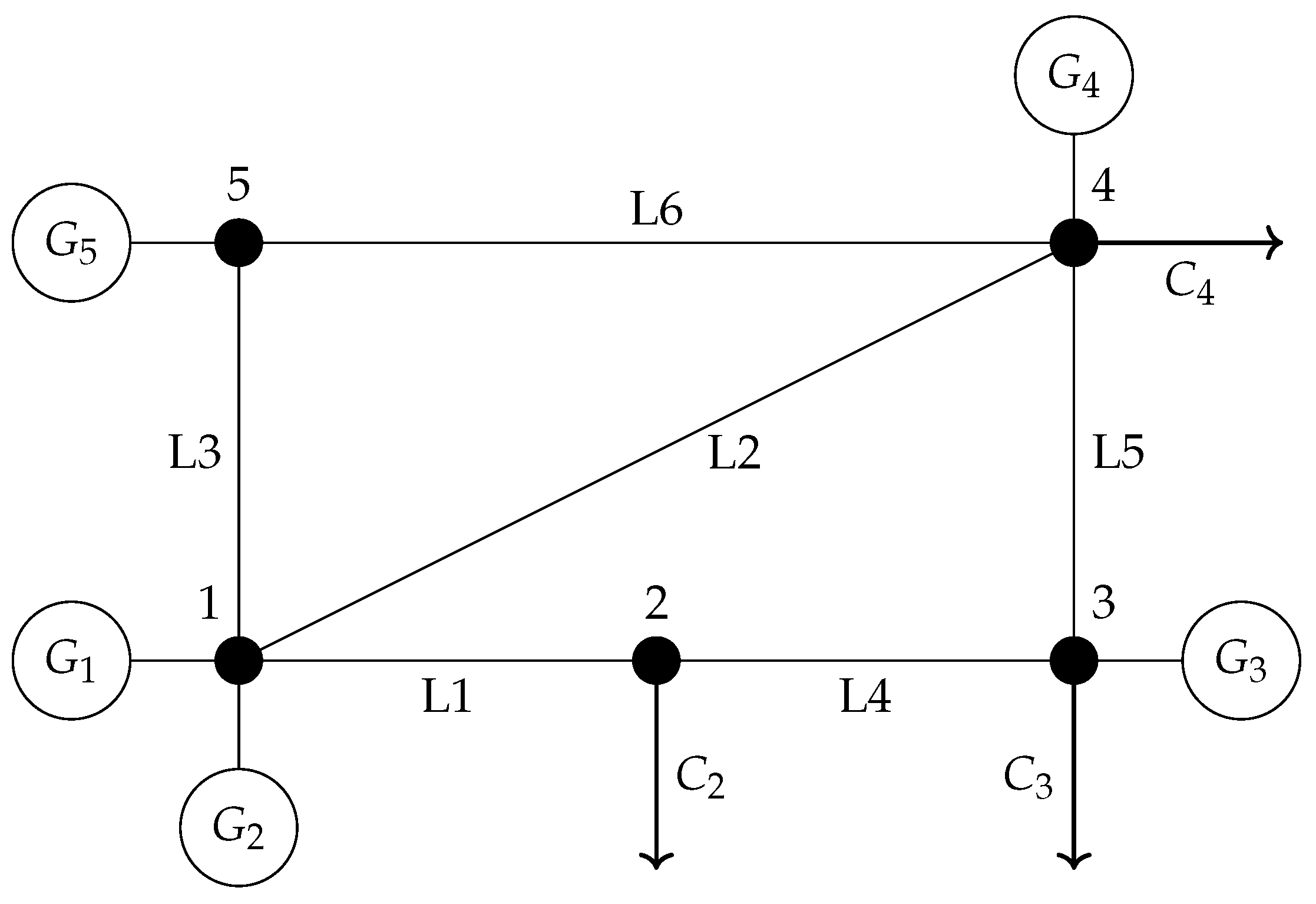
3.2. Numerical Validation, Analysis and Discussion Regarding the PJM 5-Bus Test System
3.3. Numerical Validation, Analysis and Discussion Regarding the 3374-Bus Feeder
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rashid, M.H.; Abed, N.Y.; Hussien, Z.F.; Rahim, A.A.; Abdullah, N. Electric Power System. In Power Electronics Handbook, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2024; pp. 845–863. [Google Scholar] [CrossRef]
- Zhang, N.; Yan, J.; Hu, C.; Sun, Q.; Yang, L.; Gao, D.W.; Guerrero, J.M.; Li, Y. Price-Matching-Based Regional Energy Market With Hierarchical Reinforcement Learning Algorithm. IEEE Trans. Ind. Inform. 2024, 20, 11103–11114. [Google Scholar] [CrossRef]
- Patrick, D.R.; Fardo, S.W.; Fardo, B.W. Electrical Power Systems Technology; River Publishers: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Vo, D.H.; Vo, A.T.; Ho, C.M. Urbanization and renewable energy consumption in the emerging ASEAN markets: A comparison between short and long-run effects. Heliyon 2024, 10, e30243. [Google Scholar] [CrossRef] [PubMed]
- El-Sayed, E.I.; Al-Gazzar, M.M.; Seif, M.S.; Soliman, A.M.A. Energy management of renewable energy sources incorporating with energy storage device. Int. J. Power Electron. Drive Syst. 2022, 13, 883–899. [Google Scholar] [CrossRef]
- Paul, B.; Sarker, A.; Abhi, S.H.; Das, S.K.; Ali, M.F.; Islam, M.M.; Islam, M.R.; Moyeen, S.I.; Rahman Badal, M.F.; Ahamed, M.H.; et al. Potential smart grid vulnerabilities to cyber attacks: Current threats and existing mitigation strategies. Heliyon 2024, 10, e37980. [Google Scholar] [CrossRef]
- Moran, L.; Espinoza, J.; Burgos, R. Voltage regulation in mine power distribution systems: Problems and solutions. In Proceedings of the 2014 IEEE Industry Application Society Annual Meeting, IAS 2014, Vancouver, BC, Canada, 5–9 October 2014. [Google Scholar] [CrossRef]
- Atul, D.; Singh, M. A Brief Review For Power Quality Problems Evaluation, Reliability, Concerns And Various Mitigation. Int. Sci. J. Eng. Manag. 2024, 3, 1–7. [Google Scholar] [CrossRef]
- Bosupally, D.; Muniyamuthu, V.; Muktevi, C. Congestion Management of Power Systems by Optimal Allocation of FACTS devices using Hybrid Techniques. Int. J. Electr. Electron. Res. 2023, 11, 299–307. [Google Scholar] [CrossRef]
- Hasan, M.M.; Chen, X.C. Business strategies and carbon emissions. Energy Econ. 2025, 141, 108092. [Google Scholar] [CrossRef]
- Mousavi, R.; Mousavi, A.; Mousavi, Y.; Tavasoli, M.; Arab, A.; Kucukdemiral, I.B.; Alfi, A.; Fekih, A. Revolutionizing solar energy resources: The central role of generative AI in elevating system sustainability and efficiency. Appl. Energy 2025, 382, 125296. [Google Scholar] [CrossRef]
- Lu, W.M.; Le, T.T. From Technology to Strategy: The Evolving Role of Smart Grids and Microgrids in Sustainable Energy Management. Energies 2025, 18, 4609. [Google Scholar] [CrossRef]
- Yadav, A.K.; Mahajan, V. Transmission line switching for loss reduction and reliability improvement. In Proceedings of the 2019 International Conference on Information and Communications Technology, ICOIACT 2019, Yogyakarta, Indonesia, 24–25 July 2019; pp. 794–799. [Google Scholar] [CrossRef]
- Andrés, P.; Almeida, M.; Francisco, D.; Galarza, C. Estado del Arte de conmutación de líneas de transmisión con análisis de contingencias. Rev. I+D Tecnol. 2019, 15, 98–106. (In Spanish) [Google Scholar] [CrossRef]
- Agarwal, A.; Pandey, A.; Pileggi, L. Continuous Switch Model and Heuristics for Mixed-Integer Nonlinear Problems in Power Systems. IEEE Trans. Power Syst. 2024, 39, 5780–5791. [Google Scholar] [CrossRef]
- Khanabadi, M.; Ghasemi, H. Transmission congestion management through optimal transmission switching. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar] [CrossRef]
- Numan, M.; Abbas, M.F.; Yousif, M.; Ghoneim, S.S.; Mohammad, A.; Noorwali, A. The Role of Optimal Transmission Switching in Enhancing Grid Flexibility: A Review. IEEE Access 2023, 11, 32437–32463. [Google Scholar] [CrossRef]
- Fisher, E.B.; O’Neill, R.P.; Ferris, M.C. Optimal transmission switching. IEEE Trans. Power Syst. 2008, 23, 1346–1355. [Google Scholar] [CrossRef]
- Tabatabaei Khorram, S.A.; Fotuhi-Firuzabad, M.; Safdarian, A. Optimal transmission switching as a remedial action to enhance power system reliability. In Proceedings of the 2016 Smart Grids Conference, SGC 2016, Kerman, Iran, 20–21 December 2016; pp. 7–12. [Google Scholar] [CrossRef]
- Jagadeesan Nair, V. Optimal Transmission Switching and Grid Reconfiguration for Transmission Systems via Convex Relaxations. Electricity 2025, 6, 37. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, L.; Liu, J.; Deng, X.; Wu, K. Multi-Period Optimal Transmission Switching with Voltage Stability and Security Constraints by the Minimum Number of Actions. Sustainability 2024, 16, 8272. [Google Scholar] [CrossRef]
- Masache, P.; Carrión, D.; Cárdenas, J. Optimal Transmission Line Switching to Improve the Reliability of the Power System Considering AC Power Flows. Energies 2021, 14, 3281. [Google Scholar] [CrossRef]
- Toctaquiza, J.; Carrión, D.; Jaramillo, M. An Electrical Power System Reconfiguration Model Based on Optimal Transmission Switching under Scenarios of Intentional Attacks. Energies 2023, 16, 2879. [Google Scholar] [CrossRef]
- Díaz González, C. Economic Load Dispatch in an Electric Power System: Modeling, Simulation, and Analysis. Master’s Thesis, University of Oviedo, Oviedo, Spain, June 2017. (In Spanish). [Google Scholar]
- Capitanescu, F.; Wehenkel, L. An AC OPF-based heuristic algorithm for optimal transmission switching. In Proceedings of the 2014 Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER’s extensible optimal power flow architecture. In Proceedings of the 2009 IEEE Power and Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar] [CrossRef]
- Wang, H.; Murillo-Sánchez, C.E.; Zimmerman, R.D.; Thomas, R.J. On computational issues of market-based optimal power flow. IEEE Trans. Power Syst. 2007, 22, 1185–1193. [Google Scholar] [CrossRef]
- Agarwal, A.; Pandey, A.; Pillegi, L. Continuous Switch Model and Heuristics for Mixed-Integer Problems in Power Systems. arXiv 2022, arXiv:2206.14510. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
- Oviedo, M.; Rios, D.; Baum, G.; Blanco, G. Optimal Transmission Switching for cost reduction in the Interconnected System of Paraguay. In Proceedings of the 2020 IEEE Congreso Bienal de Argentina, Resistencia, Argentina, 1–4 December 2020. [Google Scholar] [CrossRef]
- Fang, X.; Li, F.; Wei, Y.; Cui, H. Strategic scheduling of energy storage for load serving entities in locational marginal pricing market. IET Gener. Transm. Distrib. 2016, 10, 1258–1267. [Google Scholar] [CrossRef]
- Li, F.; Bo, R. Small test systems for power system economic studies. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010. [Google Scholar] [CrossRef]
- Fattahi, S.; Lavaei, J.; Atamturk, A. A bound strengthening method for optimal transmission switching in power systems. IEEE Trans. Power Syst. 2019, 34, 280–291. [Google Scholar] [CrossRef]
- Matpower. Description of case3375wp. 2025. Available online: https://matpower.org/docs/ref/matpower5.0/case3375wp.html (accessed on 3 July 2024).
- Matpower. Description of case5. 2025. Available online: https://matpower.org/docs/ref/matpower5.0/case5.html (accessed on 9 November 2024).
| Ref. | Proposed Methodology | Test System | Objective Function |
|---|---|---|---|
| [13] | Transmission line switching for losses reduction and reliability improvement | IEEE 24-bus | Minimizing active power losses and improving reliability |
| [14] | OTS as DC-OPF with binary variables, MILP | IEEE 5-bus, 14-bus | Minimizing total generation costs |
| [13] | OTS for enhancing transmission system reliability | IEEE 24-bus | Minimizing unserved demand and loss of load probability |
| [18] | MILP model based on DC-OPF for topology and dispatch optimization | IEEE 118-bus | Minimizing generation dispatch cost |
| [20] | OTS and grid reconfiguration via convex relaxations (SOCP, MISOCP), comparing DC, AC, and convexified OPF against novel relaxations for realistic grid physics | IEEE 9-bus, 39-bus, 118-bus | Minimizing generation costs, losses, and system congestion (locational marginal prices) with improved feasibility and computational efficiency |
| [21] | Multi-period OTS with voltage stability and security constraints; two-stage solution (prescreening + MILP/NLP rolling horizon) | IEEE 118-bus, 662-bus | Minimizing the number of switching actions while ensuring voltage stability and security margins over multiple periods |
| [22] | OTS considering AC power flows, reliability and contingency analysis (N-1, N-2, N-3), loadability and ranking; formulated as a MINLP with an AC-OPF | Ecuador, 230 kV system | Minimizing total generation cost and ensuring reliability/security under multiple contingencies and operating limits |
| [23] | OTS-based reconfiguration in the face of intentional attacks using a DC-OPF; contingency ranking and index analysis for vulnerability and mitigation; topology reconfiguration to optimize security | IEEE 30-bus | Minimizing generation cost and maintaining reliability/security when facing intentional attacks (N-1), reducing line overload and angle deviation after contingencies |
| Symbol | Definition | Symbol | Definition |
|---|---|---|---|
| Total operating cost ($/h) | Generator i cost ($/MWh) | ||
| Quadratic cost coeff. ($/MWh2) | Linear cost coeff. ($/MWh) | ||
| Constant cost coeff. ($/h) | Active power by gen i (MW) | ||
| Max. active power gen i (MW) | Min. active power gen i (MW) | ||
| Reactive power gen i (Mvar) | Max. reactive power gen i (Mvar) | ||
| Min. reactive power gen i (Mvar) | Demand at node i (MW) | ||
| Reactive demand at node i (Mvar) | Active power i-j (MW) | ||
| Reactive power i-j (Mvar) | Max. active power i-j (MW) | ||
| Min. active power i-j (MW) | Max. reactive power i-j (Mvar) | ||
| Min. reactive power i-j (Mvar) | Number of generators | ||
| Number of buses | Number of transmission lines | ||
| x | Binary matrix for line status | Line conductance () | |
| Line susceptance () | Voltage angle node i (°) | ||
| Voltage angle node j (°) | Min. system voltage angle (°) | ||
| Max. system voltage angle (°) | Voltage at node i (V) | ||
| Voltage at node j (V) | Max. voltage at node i (V) | ||
| Min. voltage at node i (V) | Max. system voltage (V) | ||
| Min. system voltage (V) |
| Node | (MW) | (Mvar) | (MW) | (Mvar) | (p.u) | (p.u) |
|---|---|---|---|---|---|---|
| 1 | 210 | 0 | 0 | 0 | 1.1 | 0.9 |
| 2 | 0 | 0 | 300 | 98.61 | 1.1 | 0.9 |
| 3 | 323.49 | 0 | 300 | 98.61 | 1.1 | 0.9 |
| 4 | 0 | 0 | 400 | 131.47 | 1.1 | 0.9 |
| 5 | 466.51 | 0 | 0 | 0.00674 | 1.1 | 0.9 |
| Line | Node i | Node j | () | ||
|---|---|---|---|---|---|
| L1 | 1 | 2 | 0.00281 | 0.0281 | 0.00712 |
| L2 | 1 | 4 | 0.00304 | 0.0304 | 0.00658 |
| L3 | 1 | 5 | 0.00064 | 0.0064 | 0.03126 |
| L4 | 2 | 3 | 0.00108 | 0.0108 | 0.01852 |
| L5 | 3 | 4 | 0.00297 | 0.0297 | 0.00674 |
| L6 | 4 | 5 | 0.00297 | 0.0297 | 0.00674 |
| Generator i | Cost ($/MWh) | P Limit (MW) | Q Limit (Mvar) |
|---|---|---|---|
| 1 | 14 | 40 | ±30 |
| 2 | 15 | 170 | ±127.5 |
| 3 | 30 | 520 | ±390 |
| 4 | 40 | 200 | ±150 |
| 5 | 10 | 600 | ±450 |
| Component | Description |
|---|---|
| Number of buses | 3374 |
| Number of generators | 596 |
| Number of lines | 4161 |
| Number of transformers | 383 |
| Number of loads | 2434 |
| Number of areas | 2 |
| Total generation capacity | 71,095.0 MW |
| Actual generated active power in the reference case | 49,193.3 MW |
| Actual generated reactive power in the reference case | 10,800.7 Mvar |
| Total active power demand | 48,363.0 MW |
| Total reactive power demand | 19,527.4 Mvar |
| Line | Node i | Node j | Final Cost ($/h) | Cost Reduction ($/h) | Cost Reduction (%) |
|---|---|---|---|---|---|
| Reference case | - | - | 17,551.89 | - | - |
| Line 6 | 4 | 5 | 15,163.03 | 2388.86 | 13.61 |
| Line 5 | 3 | 4 | 15,174.03 | 2377.86 | 13.55 |
| Line 4 | 2 | 3 | 16,587.95 | 963.94 | 5.49 |
| Line | ($/MWh) | ($/MWh) |
|---|---|---|
| Reference case | 10.00 | 39.71 |
| Line 6 | 14.90 | 32.55 |
| Line 5 | 10.00 | 40.00 |
| Line 4 | 11.82 | 30.00 |
| Line | (p.u.) | (p.u.) | (°) | (°) |
|---|---|---|---|---|
| Reference case | 1.064 | 1.100 | −0.73 | 3.59 |
| Line 6 | 1.088 | 1.100 | −0.05 | 7.73 |
| Line 5 | 1.082 | 1.100 | −3.65 | 3.47 |
| Line 4 | 1.063 | 1.100 | −1.71 | 3.39 |
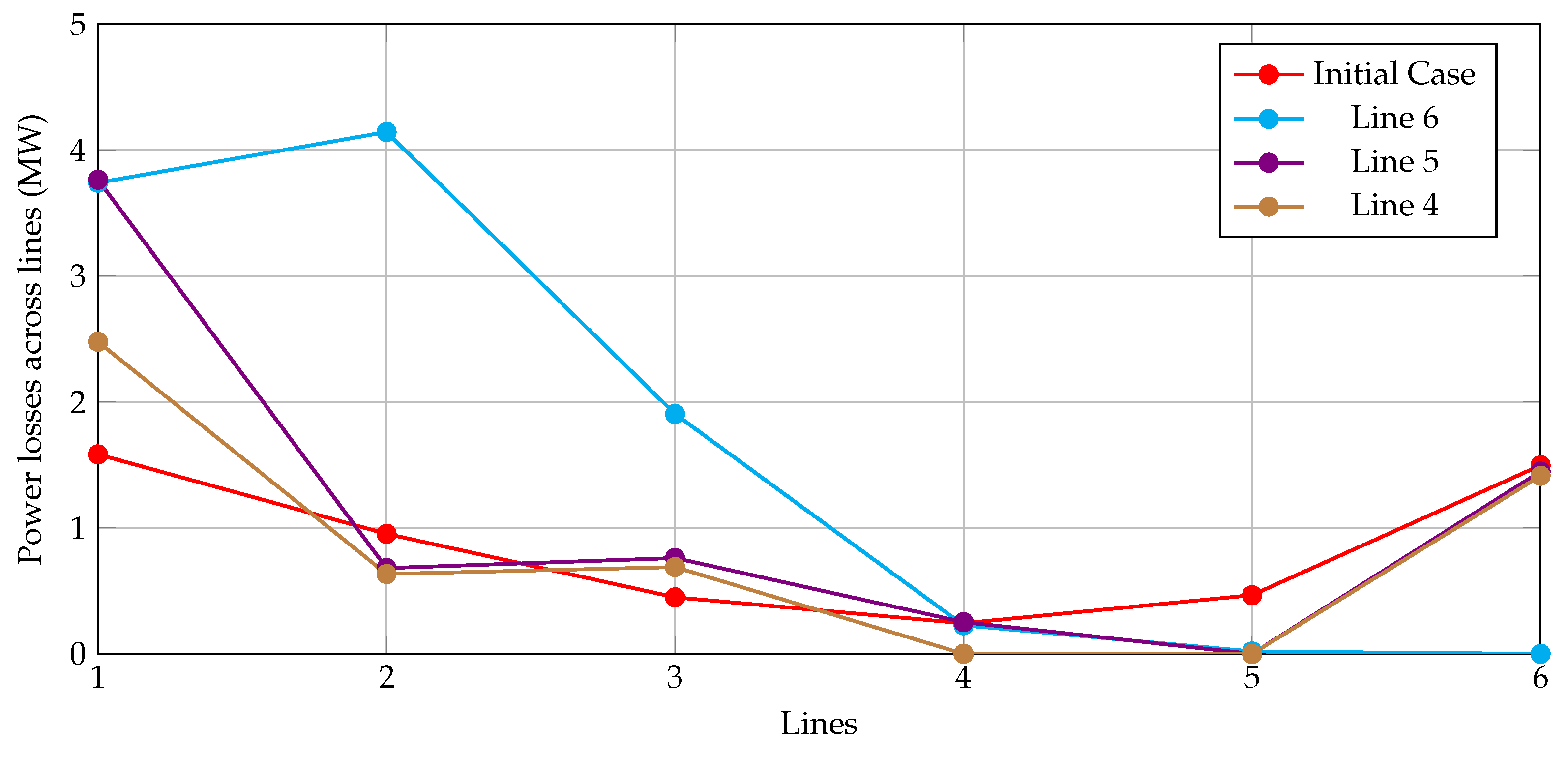
| Line | Generated Power (MW) | Demanded Power (MW) | Final Power Losses (MW) |
|---|---|---|---|
| Reference case | 1005.19 | 1000.00 | 5.19 |
| Line 6 | 1010.04 | 1000.00 | 10.04 |
| Line 5 | 1006.91 | 1000.00 | 6.91 |
| Line 4 | 1005.21 | 1000.00 | 5.21 |
| Line | Node i | Node j | Final Cost ($/h) | Cost Reduction ($/h) | Cost Reduction (%) |
|---|---|---|---|---|---|
| Reference case | - | - | 7,412,072.20 | - | - |
| Line 1116 | 665 | 657 | 7,406,667.60 | 5404.60 | 0.0729 |
| Line 1083 | 678 | 665 | 7,407,373.66 | 4698.54 | 0.0634 |
| Line 834 | 498 | 30 | 7,407,522.44 | 4549.76 | 0.0614 |
| Line 813 | 425 | 10 | 7,407,935.38 | 4136.82 | 0.0558 |
| Line 812 | 10 | 8 | 7,408,422.47 | 3649.73 | 0.0492 |
| Line 3520 | 9 | 8 | 7,408,473.04 | 3599.16 | 0.0485 |
| Line 1075 | 691 | 439 | 7,408,658.21 | 3413.99 | 0.0461 |
| Line | ($/MWh) | ($/MWh) |
|---|---|---|
| Reference case | −0.02 | 466.57 |
| Line 1116 | 0.00 | 338.97 |
| Line 1083 | −0.02 | 417.03 |
| Line 834 | 0.00 | 340.89 |
| Line 813 | 0.00 | 359.59 |
| Line 812 | 0.00 | 811.60 |
| Line 3520 | 0.00 | 473.84 |
| Line 1075 | −0.02 | 485.39 |
| Line | (p.u.) | (p.u.) | (°) | (°) |
|---|---|---|---|---|
| Reference case | 0.942 | 1.120 | −37.07 | 3.17 |
| Line 1116 | 0.942 | 1.120 | −35.68 | 3.16 |
| Line 1083 | 0.942 | 1.120 | −37.02 | 3.17 |
| Line 834 | 0.942 | 1.120 | −35.72 | 3.16 |
| Line 813 | 0.942 | 1.120 | −35.70 | 3.18 |
| Line 812 | 0.942 | 1.120 | −35.62 | 3.17 |
| Line 3520 | 0.942 | 1.120 | −35.67 | 3.19 |
| Line 1075 | 0.942 | 1.120 | −36.98 | 3.16 |
| Line | Total Generated Power (MW) | Total Demanded Power (MW) | Total Active Power Losses (MW) |
|---|---|---|---|
| Reference case | 49,193.3 | 48,363 | 830.26 |
| Line 1116 | 49,178.1 | 48,363 | 815.08 |
| Line 1083 | 49,192.6 | 48,363 | 829.62 |
| Line 834 | 49,179.4 | 48,363 | 816.37 |
| Line 813 | 49,183.9 | 48,363 | 820.92 |
| Line 812 | 49,179.9 | 48,363 | 816.86 |
| Line 3520 | 49,190.1 | 48,363 | 827.13 |
| Line 1075 | 49,192.7 | 48,363 | 829.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vera-Zambrano, J.C.; Álvarez-Arévalo, M.A.; Montoya, O.D.; Sánchez-Céspedes, J.M.; Giral-Ramírez, D.A. Cost Reduction in Power Systems via Transmission Line Switching Using Heuristic Search. Sci 2025, 7, 141. https://doi.org/10.3390/sci7040141
Vera-Zambrano JC, Álvarez-Arévalo MA, Montoya OD, Sánchez-Céspedes JM, Giral-Ramírez DA. Cost Reduction in Power Systems via Transmission Line Switching Using Heuristic Search. Sci. 2025; 7(4):141. https://doi.org/10.3390/sci7040141
Chicago/Turabian StyleVera-Zambrano, Juan Camilo, Mario Andres Álvarez-Arévalo, Oscar Danilo Montoya, Juan Manuel Sánchez-Céspedes, and Diego Armando Giral-Ramírez. 2025. "Cost Reduction in Power Systems via Transmission Line Switching Using Heuristic Search" Sci 7, no. 4: 141. https://doi.org/10.3390/sci7040141
APA StyleVera-Zambrano, J. C., Álvarez-Arévalo, M. A., Montoya, O. D., Sánchez-Céspedes, J. M., & Giral-Ramírez, D. A. (2025). Cost Reduction in Power Systems via Transmission Line Switching Using Heuristic Search. Sci, 7(4), 141. https://doi.org/10.3390/sci7040141







