Design of Experiments Applied to the Analysis of an H-Darrieus Hydrokinetic Turbine with Augmentation Channels
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
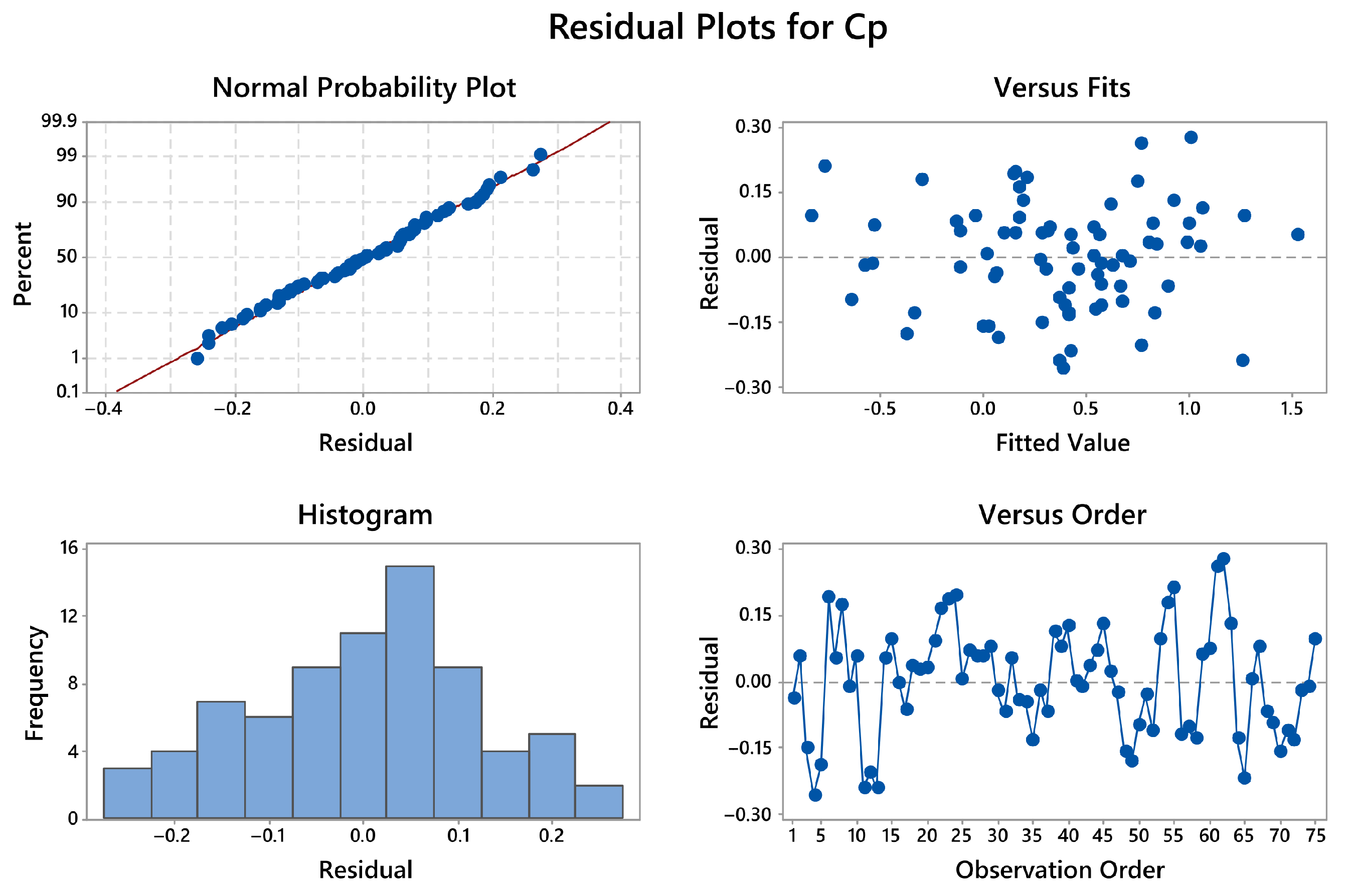
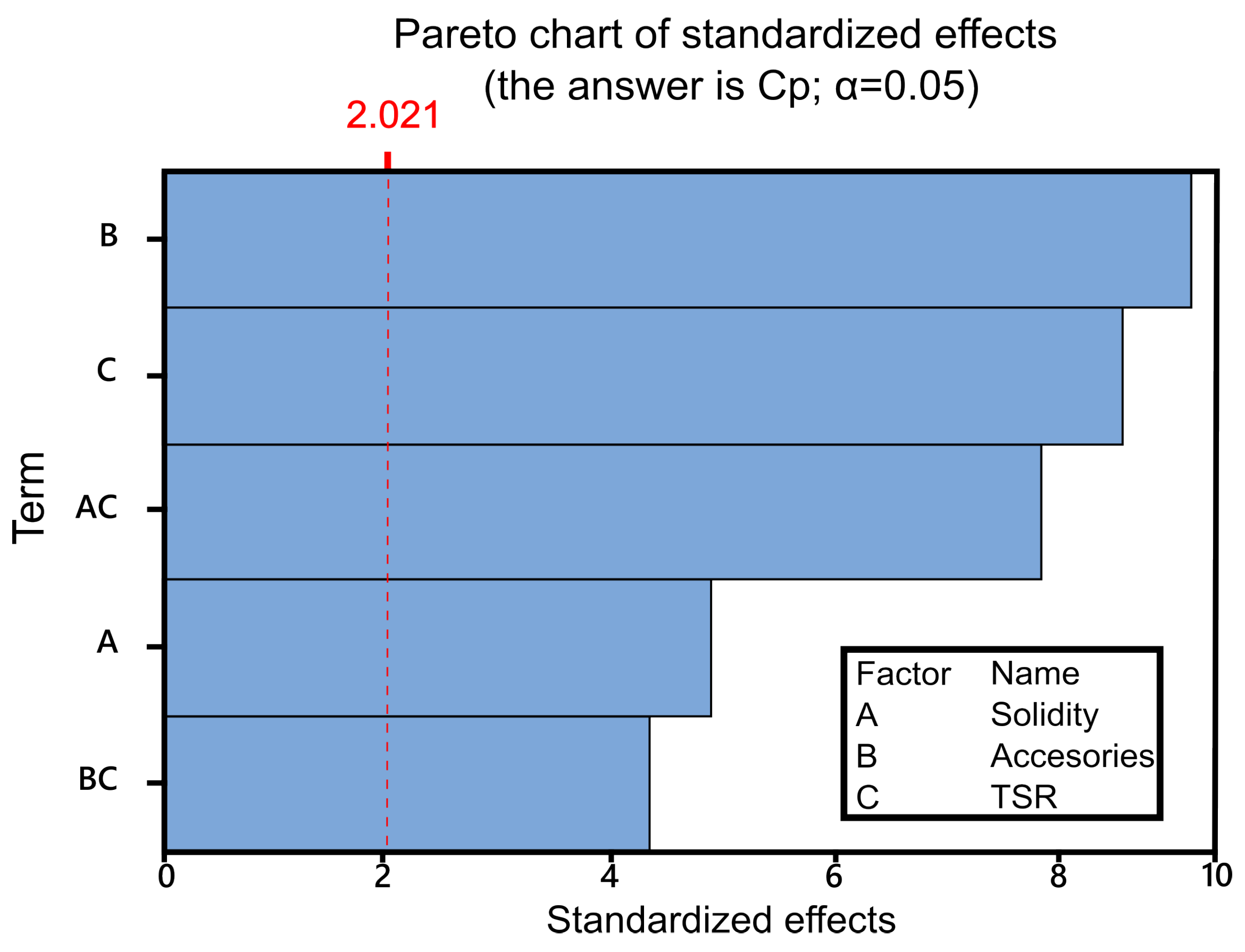
3.1. ANOVA
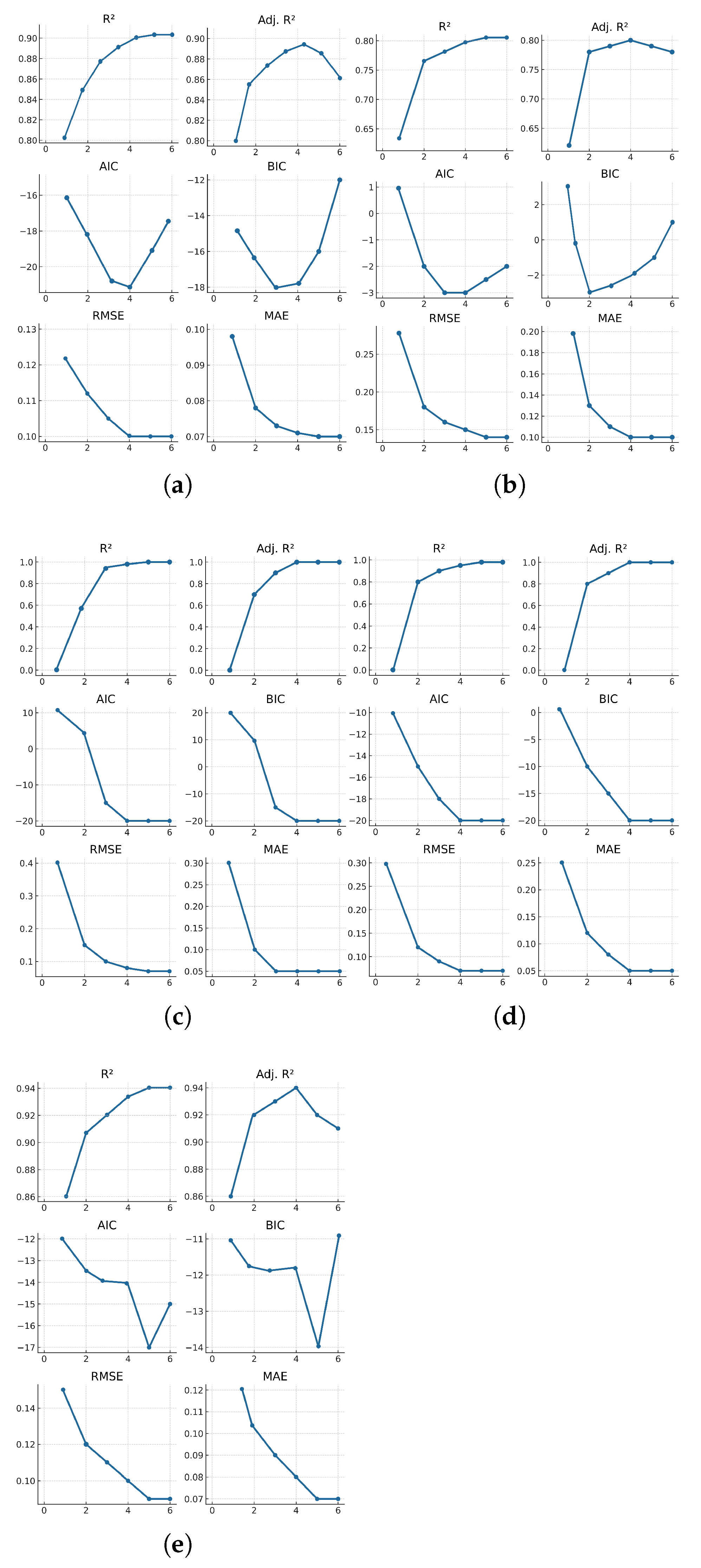
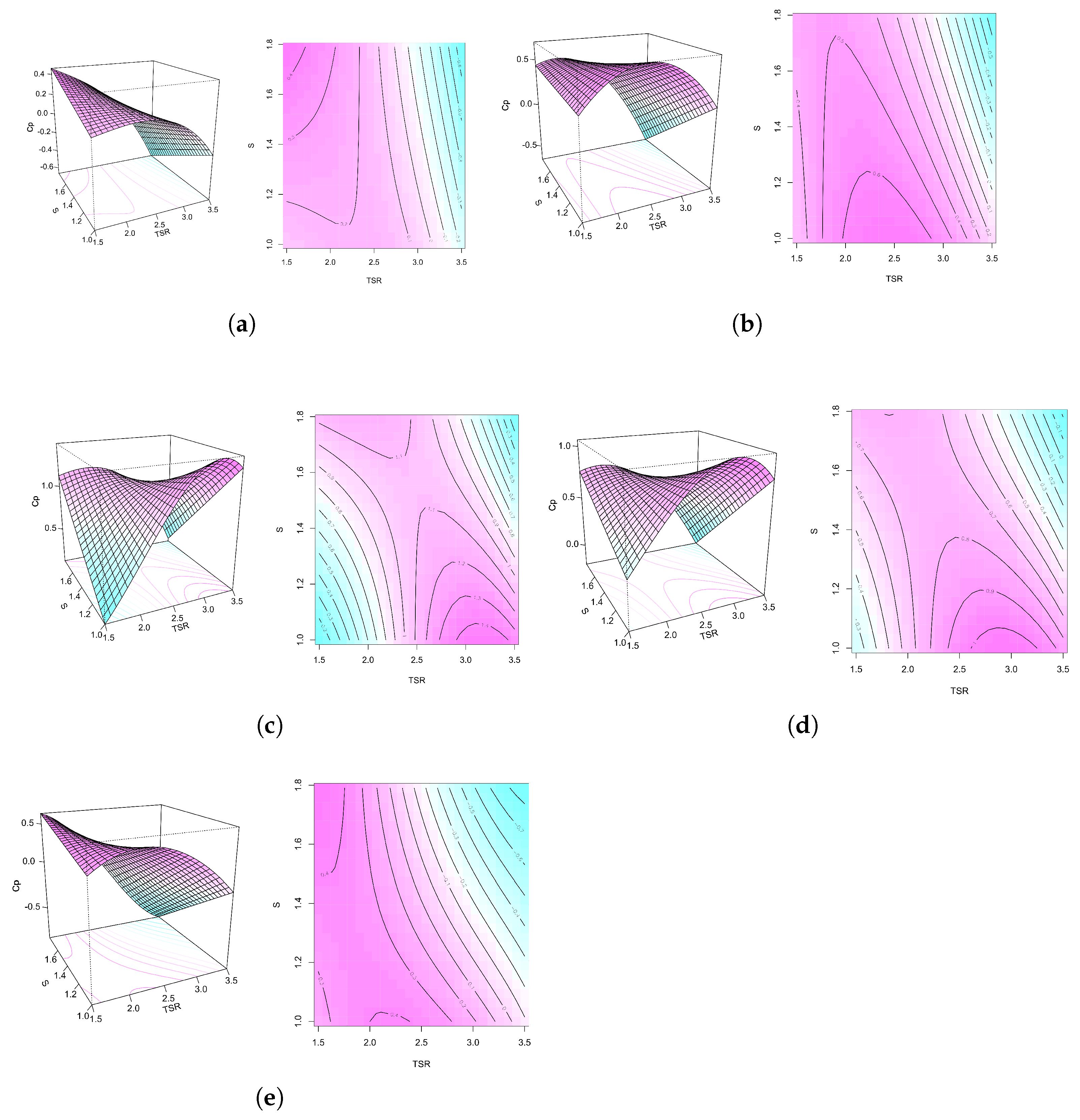
3.2. Linear Regression Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational fluid dynamics |
| VAWT | Vertical Axis Water Turbines |
| HAWT | Horizontal Axis Water Turbines |
| TSR | Tip-Speed Ratio |
| Cp | Power Coefficient |
| DoE | Design of Experiments |
| OVAT | One Variable at a Time |
| RSM | Response Surface Methodology |
| ANOVA | Analysis of Variance |
| BIC | Bayesian Information Criterion |
| AIC | Akaike Information Criterion |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Square Error |
References
- Vermaak, H.J.; Kusakana, K.; Koko, S.P. Status of micro-hydrokinetic river technology in rural applications: A review of literature. Renew. Sustain. Energy Rev. 2014, 29, 625–633. [Google Scholar] [CrossRef]
- Furukawa, A.; Watanabe, S.; Matsushita, D.; Okuma, K. Development of ducted Darrieus turbine for low head hydropower utilization. Curr. Appl. Phys. 2010, 10, S128–S132. [Google Scholar] [CrossRef]
- Gosselin, R.; Dumas, G.; Boudreau, M. Parametric study of H-Darrieus vertical-axis turbines using CFD simulations. J. Renew. Sustain. Energy 2016, 8, 053301. [Google Scholar] [CrossRef]
- Del Rio, J.A.S.; Sánchez, A.R.; Villa, D.S.; Quintana, E.C. Numerical Study of H-Darrieus Turbine as a Rotor for Gravitational Vortex Turbine. CFD Lett. 2022, 14, 1–11. [Google Scholar] [CrossRef]
- Du, L.; Ingram, G.; Dominy, R.G. Experimental study of the effects of turbine solidity, blade profile, pitch angle, surface roughness, and aspect ratio on the H-Darrieus wind turbine self-starting and overall performance. Energy Sci. Eng. 2019, 7, 2421–2436. [Google Scholar] [CrossRef]
- Arrieta-Gomez, M.; Vélez-García, S.; Zuluaga, D.H.; Tejada, J.C.; Sanin-Villa, D. Efficiency optimization of a hybrid Savonius-Darrieus hydrokinetic turbine via regression modeling and CFD-based design of experiments. Results Eng. 2025, 27, 105751. [Google Scholar] [CrossRef]
- chol Nam, M.; Dechun, B.; Xiangji, Y.; Mingri, J. Design optimization of hydraulic turbine draft tube based on CFD and DOE method. IOP Conf. Ser. Earth Environ. Sci. 2018, 136, 012019. [Google Scholar] [CrossRef]
- Moraes, R.C.; Dias, M.A.; Neto, L.J.M. Gas turbine combustor CFD study and single-objective DoE optimization. Numer. Heat Transf. Part A Appl. 2022, 82, 700–715. [Google Scholar] [CrossRef]
- Park, J.; Knight, B.G.; Liao, Y.; Mangano, M.; Pacini, B.; Maki, K.J.; Martins, J.R.R.A.; Sun, J.; Pan, Y. CFD-based design optimization of ducted hydrokinetic turbines. Sci. Rep. 2023, 13, 17968. [Google Scholar] [CrossRef]
- Khan, R.; Kumar, A. Performance enhancement of hydrokinetic turbine using augmentation techniques: A review. Int. J. Green Energy 2024, 21, 1667–1694. [Google Scholar] [CrossRef]
- Singh, E.; Roy, S.; Yam, K.S.; Law, M.C. Numerical analysis of H-Darrieus vertical axis wind turbines with varying aspect ratios for exhaust energy extractions. Energy 2023, 277, 127739. [Google Scholar] [CrossRef]
- Ghiasi, P.; Najafi, G.; Ghobadian, B.; Jafari, A.; Mamat, R.; Fairusham Ghazali, M. CFD-Study of the H-Rotor Darrius wind turbine performance in Drag-Lift and lift Regime: Impact of Type, thickness and chord length of blades. Alex. Eng. J. 2023, 67, 51–64. [Google Scholar] [CrossRef]
- Korukçu, M. Impact of Blade Modifications on the Performance of a Darrieus Wind Turbine. Processes 2024, 12, 732. [Google Scholar] [CrossRef]
- Patel, V.; Rathod, V.; Patel, C. Optimal utilization of hydrokinetic energy resources through performance improvement of the darrieus turbine using concave and flat blocking plates. Ocean Eng. 2023, 283, 115099. [Google Scholar] [CrossRef]
- Muñoz, A.G.; Rodriguez-Cabal, M.A.; Zuluaga, D.H. Assessment of H-Darrieus Hydrokinetic Turbines by Configuration with a Blocking Plate Using a Design of Experiment Approach. Math. Model. Eng. Probl. 2025, 12, 9–16. [Google Scholar] [CrossRef]
- Tunio, I.A.; Shah, M.A.; Hussain, T.; Harijan, K.; Mirjat, N.H.; Memon, A.H. Investigation of duct augmented system effect on the overall performance of straight blade Darrieus hydrokinetic turbine. Renew. Energy 2020, 153, 143–154. [Google Scholar] [CrossRef]
- Chen, W.H.; Lam, T.T.; Chang, M.H.; Jin, L.; Chueh, C.C.; Augusto, G.L. Optimizing H-Darrieus Wind Turbine Performance with Double-Deflector Design. Energies 2024, 17, 503. [Google Scholar] [CrossRef]
- Guevara-Muñoz, A.J.; Hincapie-Zuluaga, D.A.; Ángel Rodríguez-Cabal, M.; Sierra-Del-rio, J.A.; Colmenares-Quintero, R.F.; Torres-Lopez, E. 2D Numerical Analysis of an H-Darrieus Hydrokinetic Turbine with Passive Improvement Mechanisms. Eng. Trans. 2023, 71, 553–569. [Google Scholar] [CrossRef]
- Morrison, D.E.; Henkel, R.E. Significance Tests Reconsidered. In The Significance Test Controversy; Routledge: London, UK, 2017; pp. 182–198. [Google Scholar] [CrossRef]
- Gutierrez, H.; De la Vara, R. Análisis y Diseño de Experimentos, 3rd ed.; Editorial Mcgraw-hill: Mexico City, Mexico, 2008; pp. 1–489. [Google Scholar]
- Hansen, M.O.L.; Sørensen, N.N.; Flay, R.G.J. Effect of Placing a Diffuser around a Wind Turbine. Wind Energy 2000, 3, 207–213. [Google Scholar] [CrossRef]
- Jamieson, P.M. Beating Betz: Energy Extraction Limits in a Constrained Flow Field. J. Sol. Energy Eng. 2009, 131, 031008. [Google Scholar] [CrossRef]
- Ohya, Y.; Karasudani, T.; Sakurai, A.; Inoue, M. Development of a High-Performance Wind Turbine Equipped with a Brimmed Diffuser Shroud. Trans. Jpn. Soc. Aeronaut. Space Sci. 2006, 49, 18–24. [Google Scholar] [CrossRef][Green Version]
- Lam, R.; Allaire, D.L.; Willcox, K.E. Multifidelity Optimization using Statistical Surrogate Modeling for Non-Hierarchical Information Sources. In Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 5–9 January 2015; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2015. [Google Scholar] [CrossRef]
- Dziak, J.J.; Coffman, D.L.; Lanza, S.T.; Li, R.; Jermiin, L.S. Sensitivity and specificity of information criteria. Brief. Bioinform. 2020, 21, 553–565. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, M.M.A.; Nordgren, R.; Kjellsson, M.C.; Karlsson, M.O. Model-Based Residual Post-Processing for Residual Model Identification. AAPS J. 2018, 20, 81. [Google Scholar] [CrossRef]
- Lucas, J.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 3rd edition. J. Qual. Technol. 2010, 42, 228–230. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 10th ed.; Wiley: Hoboken, NJ, USA, 2019; pp. 1–688. [Google Scholar]
- Minitab. Soporte Técnico de Minitab-Minitab. 2025. Available online: https://www.minitab.com/es-mx/support/ (accessed on 15 February 2025).
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 4th ed.; Wiley: Hoboken, NJ, USA, 2016; pp. 1–856. [Google Scholar]
- Patel, V.; Eldho, T.; Prabhu, S. Performance enhancement of a Darrieus hydrokinetic turbine with the blocking of a specific flow region for optimum use of hydropower. Renew. Energy 2019, 135, 1144–1156. [Google Scholar] [CrossRef]
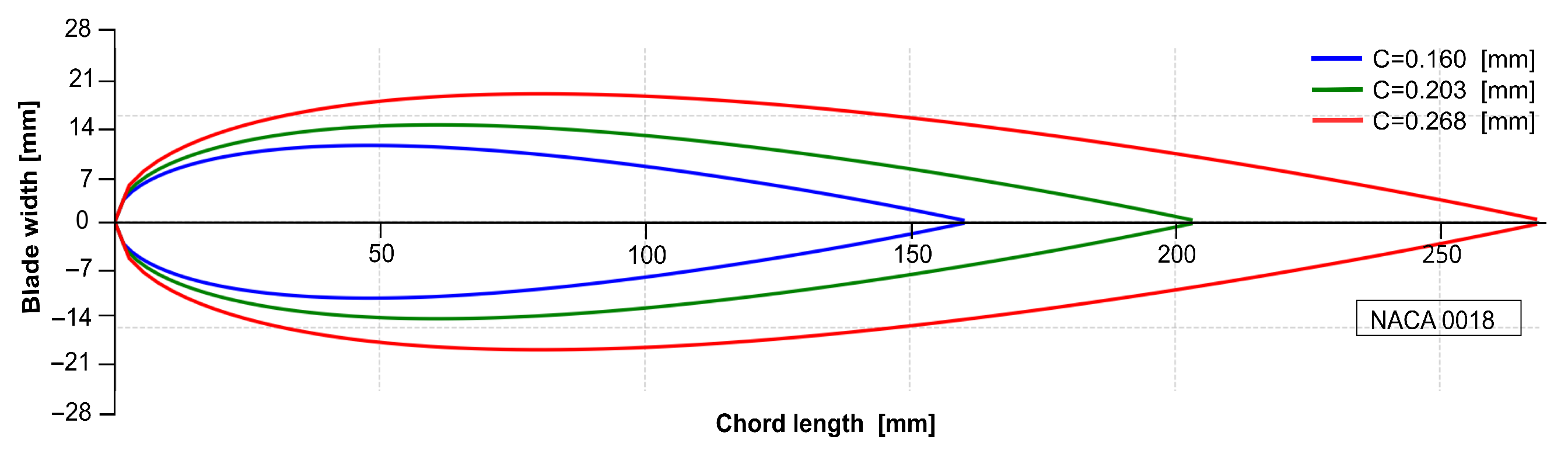
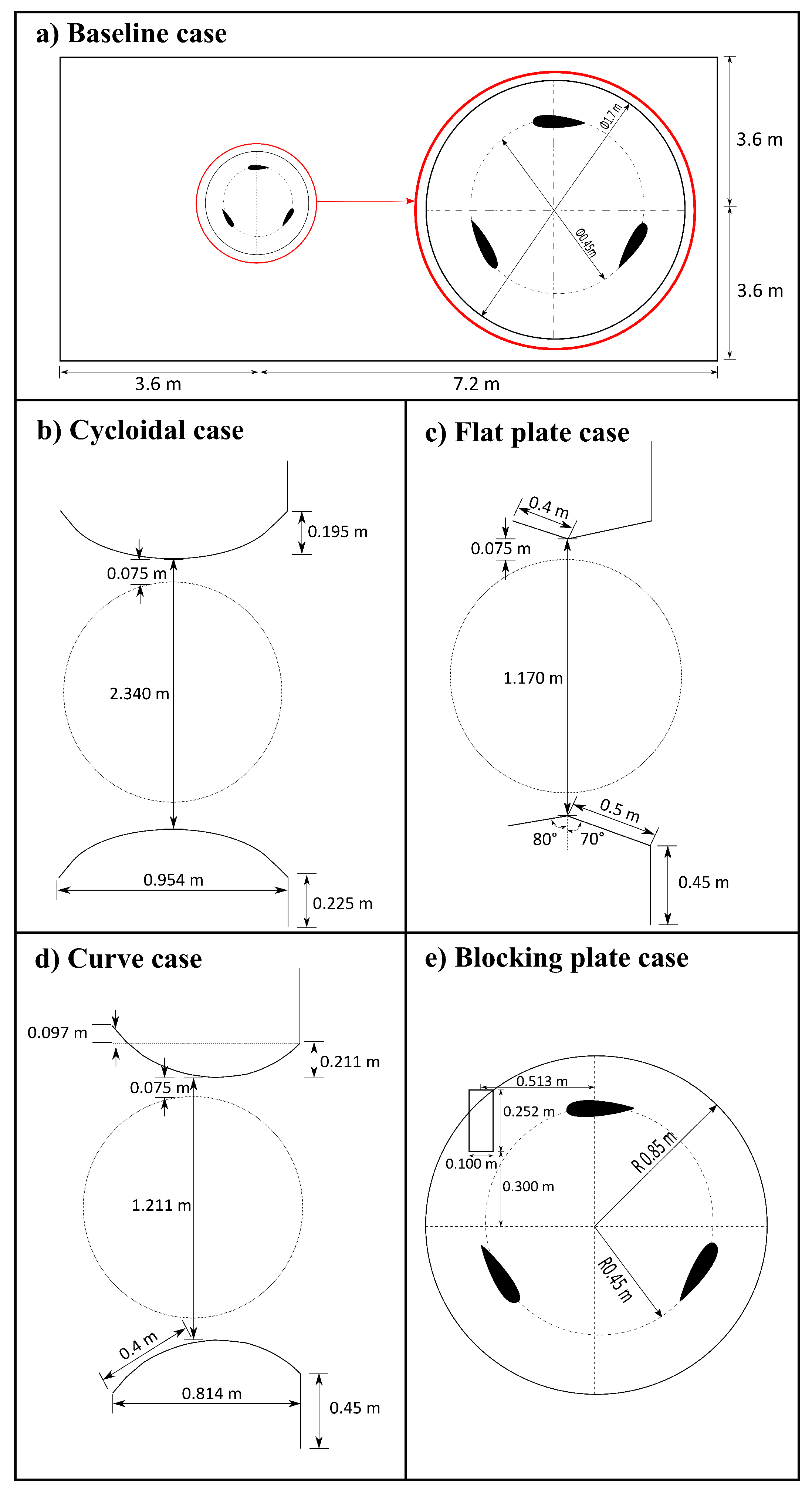
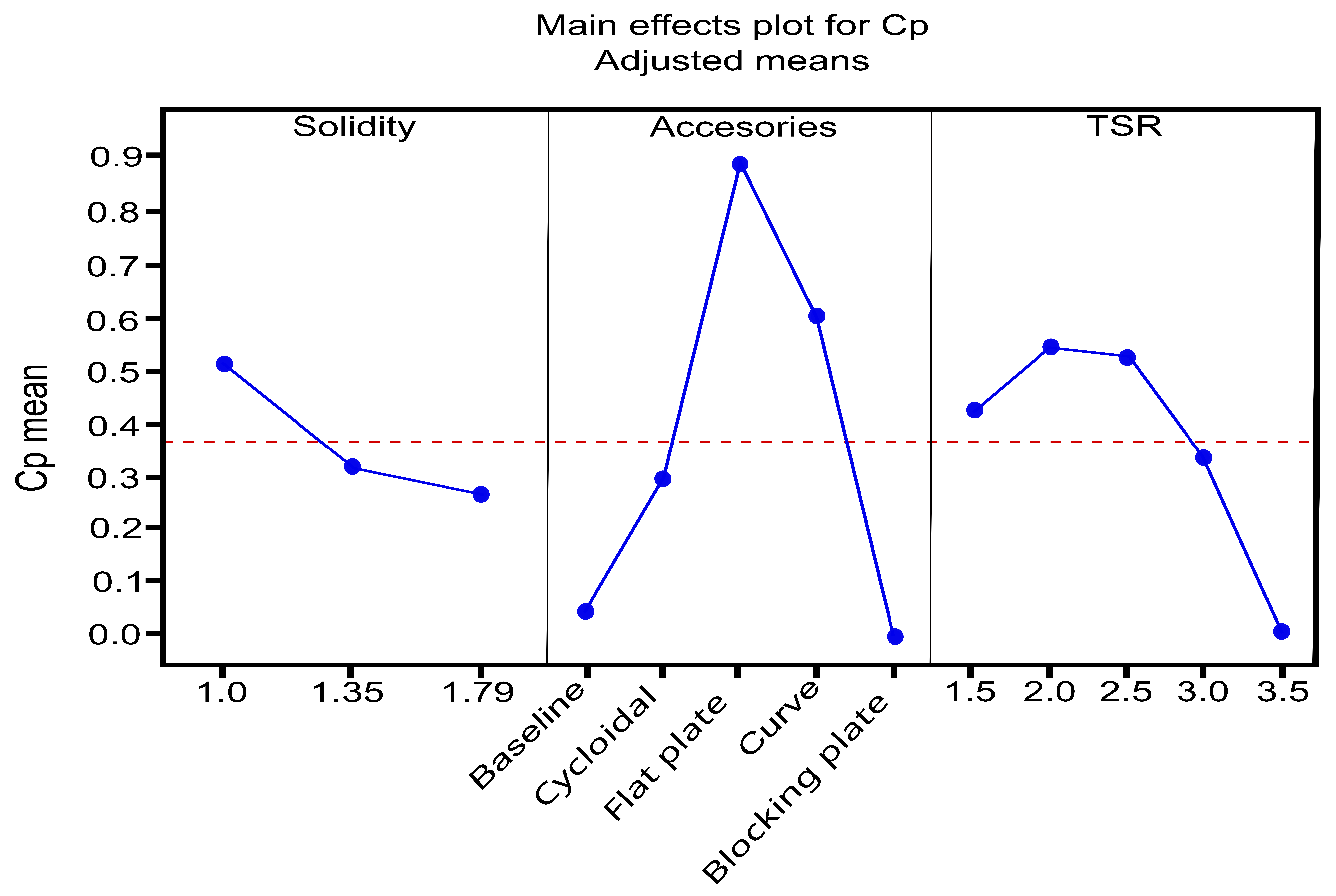

| Factors | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 |
|---|---|---|---|---|---|
| Solidity | 1.0 | 1.35 | 1.79 | – | – |
| Accessories | Standard | Cycloidal | Flat plate | Curve | Blocking plate |
| TSR | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
| Solidity | Accessories | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
|---|---|---|---|---|---|---|
| 1.0 | Standard | 0.021 | 0.207 | 0.136 | 0.126 | −0.117 |
| Cycloidal | 0.338 | 0.477 | 0.920 | 0.555 | 0.367 | |
| Flat plate | 0.128 | 0.555 | 1.014 | 1.576 | 1.364 | |
| Curve | 0.268 | 0.510 | 1.026 | 1.079 | 0.871 | |
| Blocking plate | 0.264 | 0.330 | 0.397 | 0.345 | 0.014 | |
| 1.35 | Standard | 0.392 | 0.342 | 0.153 | −0.060 | −0.643 |
| Cycloidal | 0.338 | 0.614 | 0.513 | 0.001 | −0.472 | |
| Flat plate | 0.610 | 0.831 | 1.180 | 1.079 | 0.741 | |
| Curve | 0.536 | 0.699 | 0.835 | 0.683 | 0.322 | |
| Blocking plate | 0.387 | 0.375 | 0.063 | −0.253 | −0.651 | |
| 1.79 | Standard | 0.427 | 0.281 | 0.054 | −0.127 | −0.564 |
| Cycloidal | 0.423 | 0.565 | 0.285 | −0.060 | −0.463 | |
| Flat plate | 1.026 | 1.280 | 1.055 | 0.703 | 0.202 | |
| Curve | 0.672 | 0.895 | 0.592 | 0.270 | −0.166 | |
| Blocking plate | 0.456 | 0.276 | −0.140 | −0.553 | −0.741 |
| Source | Degrees of Freedom | Sum of Squares | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 34 | 17.557 | 0.516 | 18.278 | |
| Lineal | 10 | 12.356 | 1.236 | 43.736 | 0 |
| Solidity | 2 | 0.832 | 0.416 | 14.733 | |
| Accessories | 4 | 8.612 | 2.153 | 76.205 | 0 |
| TSR | 4 | 2.912 | 0.728 | 25.768 | |
| 2-term interactions | 24 | 5.201 | 0.217 | 7.670 | |
| Solidity × TSR | 8 | 3.254 | 0.407 | 14.397 | |
| Accessories × TSR | 16 | 1.947 | 0.122 | 4.307 | |
| Error | 32 | 1.130 | 0.028 | ||
| Total | 74 | 18.687 |
| Sd | R-Squared [%] | R-Squared (Adjusted) [%] | R-Squared (Predicted) [%] |
|---|---|---|---|
| 0.168 | 93.95 | 88.81 | 78.74 |
| Case | Features | RMSE | MAE | AIC | BIC | Adj. | |
|---|---|---|---|---|---|---|---|
| Standard | [’S’, ’S T’, ’T⌃2’, ’T⌃3’] | 0.910 | 0.091 | 0.073 | −19.381 | −15.841 | 0.874 |
| Cycloidal | [’S’, ’T’, ’S T’, ’T⌃2’] | 0.852 | 0.144 | 0.105 | −5.492 | −1.952 | 0.793 |
| Flat plate | [’T’, ’S T’, ’T⌃2’, ’S T⌃2’, ’T⌃3’, ’S T⌃3’] | 0.966 | 0.073 | 0.064 | −22.070 | −17.114 | 0.941 |
| Curve | [’T’, ’S T’, ’T⌃2’, ’S T⌃2’, ’T⌃3’, ’S T⌃3’] | 0.962 | 0.062 | 0.052 | −26.651 | −21.694 | 0.934 |
| Blocking plate | [’S T’, ’T⌃2’, ’S T⌃2’, ’T⌃3’, ’S T⌃3’] | 0.949 | 0.090 | 0.070 | −17.739 | −13.491 | 0.921 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñoz, A.J.G.; Rodriguez-Cabal, M.A.; Chica, E.; Villa, D.S.; Hincapié Zuluaga, D. Design of Experiments Applied to the Analysis of an H-Darrieus Hydrokinetic Turbine with Augmentation Channels. Sci 2025, 7, 121. https://doi.org/10.3390/sci7030121
Muñoz AJG, Rodriguez-Cabal MA, Chica E, Villa DS, Hincapié Zuluaga D. Design of Experiments Applied to the Analysis of an H-Darrieus Hydrokinetic Turbine with Augmentation Channels. Sci. 2025; 7(3):121. https://doi.org/10.3390/sci7030121
Chicago/Turabian StyleMuñoz, Angie J. Guevara, Miguel. A. Rodriguez-Cabal, Edwin Chica, Daniel Sanin Villa, and Diego Hincapié Zuluaga. 2025. "Design of Experiments Applied to the Analysis of an H-Darrieus Hydrokinetic Turbine with Augmentation Channels" Sci 7, no. 3: 121. https://doi.org/10.3390/sci7030121
APA StyleMuñoz, A. J. G., Rodriguez-Cabal, M. A., Chica, E., Villa, D. S., & Hincapié Zuluaga, D. (2025). Design of Experiments Applied to the Analysis of an H-Darrieus Hydrokinetic Turbine with Augmentation Channels. Sci, 7(3), 121. https://doi.org/10.3390/sci7030121







