Potential Vulnerabilities of Cryptographic Primitives in Modern Blockchain Platforms

Abstract

Today, blockchain technologies are a separate, rapidly developing area. With rapid development, they open up a number of scientific problems. One of these problems is the problem of reliability, which is primarily associated with the use of cryptographic primitives. The threat of the emergence of quantum computers is now widely discussed, in connection with which the direction of post-quantum cryptography is actively developing. Nevertheless, the most popular blockchain platforms (such as Bitcoin and Ethereum) use asymmetric cryptography based on elliptic curves. Here, cryptographic primitives for blockchain systems are divided into four groups according to their functionality: keyless, single-key, dual-key, and hybrid. The main attention in the work is paid to the most significant cryptographic primitives for blockchain systems: keyless and single-key. This manuscript discusses possible scenarios in which, during practical implementation, the mathematical foundations embedded in the algorithms for generating a digital signature and encrypting data using algorithms based on elliptic curves are violated. In this case, vulnerabilities arise that can lead to the compromise of a private key or a substitution of a digital signature. We consider cases of vulnerabilities in a blockchain system due to incorrect use of a cryptographic primitive, describe the problem, formulate the problem statement, and assess its complexity for each case. For each case, strict calculations of the maximum computational costs are given when the conditions of the case under consideration are met. Among other things, we present a new version of the encryption algorithm for data stored in blockchain systems or transmitted between blockchain systems using elliptic curves. This algorithm is not the main blockchain algorithm and is not included in the core of modern blockchain systems. This algorithm allows the use of the same keys that system users have in order to store sensitive user data in an open blockchain database in encrypted form. At the same time, possible vulnerabilities that may arise from incorrect implementation of this algorithm are considered. The scenarios formulated in the article can be used to test the reliability of both newly created blockchain platforms and to study long-existing ones.

1. Introduction

The aim of this manuscript reflects the authors’ desire to draw the attention of blockchain system developers to the importance of understanding the mathematical foundations underlying cryptography in order to obtain correct implementations of blockchain applications. In particular, the cases proposed by the authors can be used by developers at the stage of testing their implementations.

Blockchain technologies are a special case of building distributed ledger systems. A distinctive feature of blockchain technologies is the construction of a single linked list, in which each subsequent entry depends on the previous one. This means that it is impossible to change any entry in the database without changing all the other entries linked to it [1,2]. A distinctive feature of the blockchain is the fact that the blockchain database is decentralized and can be stored by all users who work with it. The construction of a single linked chain is made possible by the mechanisms of cryptographic primitives. By “cryptographic primitives” we mean basic cryptographic methods, such as hash functions and encryption/decryption, used in the protocols of modern blockchain systems. As a rule, the main elements of any blockchain system are based on asymmetric cryptography on elliptic curves (ECC) and hash functions.

Chains between data blocks are established using consensus mechanisms. Consensus is understood as a formalized algorithm that allows the correctness of the blockchain construction to be checked. The most well-known consensus mechanisms include PoW, PoS, PBFT, and others. For example, with the PoW consensus mechanism, the user who works on creating a block (miner) adds a meaningless nonce value to the data block and generates a hash, trying to find such a hash, which will have zeros in the most significant bits. The number of zeros determines the complexity of the blocks generated and depends on the number of users in the system and their computing capabilities. In addition, hash functions are used to verify the integrity of individual records in the system, verify the integrity of blocks, and pack transactions into a block.

Asymmetric cryptography on elliptic curves, ECC, is used to form addresses in the network, form a signature, and confirm the right to perform certain operations in the network, etc. It should be noted that ECC is not a specific algorithm, but characterizes the general principle of constructing cryptographic algorithms. Various blockchain platforms use elliptic curve cryptography, including such platforms as Bitcoin, Ethereum, Polkadot, Solana, Litecoin, and many others. At the same time, as a rule, each user of the system is given a public–private key pair upon registration. And an account in the blockchain system is generated based on the public key. For example, the public key is hashed and a part of its hash value is taken, after which the result is presented in some encoding. It turns out that, knowing the user’s account, you cannot find out information about the user. But if you know the user’s public key, you can easily check whether the account belongs to them. Using their private key, users can manage transactions (confirm the legitimacy of the transfer) or put in their digital signature to confirm that these transactions were generated by a specific user of the system. For example, Bitcoin, Litecoin, and Ethereum use the ECDSA algorithm to sign transactions and manage accounts. Polkadot uses the ECDSA algorithm to generate digital signatures. That is why the ECDSA algorithm and the parameters of the elliptic curves used for Ethereum and Bitcoin are discussed further in the article.

Researchers are already wondering how sustainable the use of classical cryptography is to ensure the strength of blockchain systems, given the development of modern quantum technologies [3,4]. In 1997, Peter Shor presented an algorithm for factoring a number into prime factors, which allows a number M to be factorized using O(log M) logical qubits in O(log³ M) time [5]. Since a number of asymmetric cryptography algorithms are based on the factorization problem, the existence of a fast factorization algorithm for large numbers may eventually lead to vulnerabilities in existing systems. To date, IBM has made significant progress in producing quantum logic processors. As of mid-2024, they have established the production of chips with 133 physical qubits, and they also have one demonstration chip with more than a thousand qubits [6]. At the same time, there are certain technical problems with the density of qubits and the creation of gates for controlling sets of qubits [7]. In 2001, the efficiency of Shor’s algorithm was confirmed by IBM; the number 15 was factorized using Shor’s algorithm. IBM presented the results of factoring in the number 21 only in 2021 [8]. Ragavan et al. state in [9] that about 20 million qubits are required to factor in a 2048-bit number (about 600 digits in size). In 2023, a group of researchers published a new quantum factorization algorithm, which is more efficient than the previously known Shor’s algorithm [9]. In 2024, there was a leap in the practical application dynamics of factorization algorithms; Chinese researchers presented the results of factoring a 50-bit number using a quantum computer [10].

In anticipation of the improvement of quantum computers, cryptographers all around the world are working on post-quantum cryptography creation. Post-quantum cryptography refers to cryptographic algorithms that will be resistant to Shor’s algorithm. And in this context, we are talking primarily about asymmetric cryptography algorithms. In 2022, the US National Institute of Standards and Technology (NIST) announced the completion of the post-quantum cryptography competition. Five algorithms became finalists of the competition. Two algorithms (CRYSTALS-KYBER and NTRU) are designed for encryption and key exchange. Three algorithms (CRYSTALS-DILITHIUM, FALCON, SPHINCS+) are designed to generate and verify a digital signature. The CRYSTALS-DILITHIUM and FALCON algorithms are based on lattice theory, while the SPHINCS+ algorithm is constructed on the hash functions. At the same time, the recommended parameters for these encryption algorithms are currently critically large in terms of their focus on blockchain technologies. It is known that one of the blockchain’s problems is the problem of the constant growth of the stored database. And when choosing cryptographic primitives, it is important to use primitives that provide reliable protection with small sizes. Elliptic cryptography in modern blockchain platforms (for example, in Bitcoin, Litecoin and Ethereum) operates with keys of 32 bytes and produces a digital signature with a total size of 64 bytes. While the CRYSTALS-DILITHIUM algorithm has a public key of 1.1 KB (1024 bytes), a private key of about 2.7 KB (or 2700 bytes) and produces a signature of about 2.5 KB (or 2440 bytes). The FALCON algorithm has a public key of 1 KB (800–1000 bytes), a private key of about 1.6 KB (or 1600 bytes), and produces a signature of about 887 bytes. In the SPHINCS+ algorithm, the public key size can vary from 5 to 20 KB depending on the selected parameters, the private key can be from 20 to 100 KB depending on the configuration. The signature size for the SPHINCS+ algorithm varies depending on the selected parametrization, but is usually about 20 KB for the standard security level. As can be seen from the comparison, the parameters of the developed algorithms are many times larger than similar parameters of asymmetric cryptography on elliptic curves. And if we consider that one blockchain block can contain several thousand transactions, each of which contains a signature, then the blockchain volumes will increase many times over.

Thus, the current state of affairs shows that at the moment the threat of quantum computing is more a future threat than a threat of the present. At the same time, attempts are already being made to counter quantum threats. Developments are being carried out in two directions: the creation of post-quantum cryptography, which will be resistant to hacking using quantum computers [11], and the creation of algorithms for post-quantum key distribution [12].

From the above review, it is clear that quantum threat, if it exists, is not in the near future. The question regarding how reliable and safe the tools are that modern technologies currently use remains relevant. This manuscript proposes to consider the main cryptographic primitives used in modern blockchain platforms from the point of view of their reliability at the moment.

The remaining sections of this paper are organized as follows: Section 2 provides an overview of the materials and methods. Section 3 presents the results of modeling cases with potential vulnerabilities and a discussion of a new data encryption algorithm based on the use of ECC. Section 4 presents the conclusions and recommendations.

2. Materials and Methods

2.1. Statement of the Problem

To date, there is no unified approach to determining cryptographic strength. The first concepts of cipher strength were laid down by K. Shannon in [13]. He also defined an absolutely strong cipher, the cryptographic properties of which do not allow extracting statistical information about secret keys from the intercepted cipher. It is known that only the Vernam cipher is currently considered an absolutely strong cipher. All other cryptographic algorithms are conditionally strong. Usually, the cryptographic strength of an algorithm is determined relative to how much time it will take to crack a message or restore a key, as well as the cost of the equipment required to perform the analysis. Other parameters can also be taken into account. For example, how much memory is needed to perform the analysis, how much energy must be expended, etc.? Thus, a distinction is made between conditional cryptographic strength by computation time and conditional cryptographic strength by computation cost, but additional metrics can also be used.

The purpose of this work is to systematize knowledge about cryptographic primitives in modern blockchain platforms to determine their cryptographic resistance in terms of the time spent on analysis.

To achieve this goal, it is necessary to:

• Identify the main cryptographic primitives used in modern blockchain systems, distributing them into functional groups.
• For each cryptographic primitive, provide a brief description of its operating modes and determine the purpose of its use within blockchain systems.
• Consider approaches to determining the cryptographic resistance of each of the cryptographic primitives under consideration in terms of computational costs in relation to the time of using the brute force tactic.

2.2. Object of Study

Modern cryptographic primitives can be divided into four large categories based on the number of used keys (Figure 1). The first category is keyless cryptography. These are hash functions and pseudo-random sequence (PRS) generators. The second category is single-key encryption. These are primarily symmetric encryption. These ciphers are designed to encrypt large amounts of data. Encrypted data can be stored in encrypted form for a long time. This category also includes message authentication codes (based on hash functions with secret keys) and those PRS generators that are based on a symmetric cipher. The third category is dual-key encryption, which is asymmetric cryptography and is designed to encrypt small information volumes or to create an electronic digital signature. The fourth group includes hybrid schemes that can use the principles of secret key generation based on asymmetric cryptography approaches and perform encryption using symmetric encryption algorithms.

To varying degrees, all the presented types of cryptographic primitives are involved in various blockchain system designs. Let us consider the features of each category and determine the main object of the research.

2.2.1. Keyless Cryptographic Primitives in Blockchain Technologies

Figure 1 highlights two types of keyless cryptographic primitives. Both of them are used in blockchain technologies.

The hash function h = H(M) is an irreversible, easily computable mathematical transformation H() from a message M of arbitrary length to a message of fixed length h. It is known that a cryptographically strong hash function ensures resistance to collision detection. Resistance in the weak sense means that for a given message M it is computationally difficult to find a second message M1 that has the same hash value h = H(M) = H(M1). Resistance in the strong sense means that it is computationally difficult to find two arbitrary messages M and M1 that have the same hash value h = H(M) = H(M1). Blockchain systems typically use keyless hash algorithms primarily to control the integrity of transactions and blocks, as well as sometimes to ensure the correct operation of the mechanism for building blocks into a chain (for example, in the case of the proof-of-work consensus mechanism). In addition, add-ons to hash algorithms are used. For example, the HMAC (hash message authentication code) calculation scheme is used to calculate the secret encryption key from the seed phrase or calculate keys from the master key; the Merkle tree is used to pack selected transactions into a block.

A PRN generator is an algorithm that produces a bit sequence that, at first glance, appears random. The pseudo-randomness is that sooner or later the bit sequence will begin to repeat. Resistant PRSs should have as long a period as possible so that it is difficult for an analyst to distinguish the generated sequence from a random one and also so that the analyst cannot predict the appearance of the next symbols of the generated sequence based on an analysis of the previous generated values. Various statistical tests are used to check for randomness. For example, a list of 15 basic tests is given in [14]. There are ready-made implementations of statistical tests proposed by various authors, such as NIST, DIEHARD, TEST-U01 tests, Donald Knuth tests, and others. An example of the use of NIST tests can be found in [15]; PRNs were used to assess the quality of graphic information encryption.

The 15 NIST tests together allow us to determine, based on a set of measurements, how random the sequence produced by the PRN generator is. Let us take a brief look at each test.

The frequency (monobit) test determines the ratio of zeros and ones in the entire binary sequence. The frequency test within a block determines the proportion of ones within a block of a given length. The runs test determines whether the number of rows consisting of zeros and ones of different lengths corresponds to the number in the random sequence. The test for the longest run of ones in a block determines the longest sequence of ones within a block of length m bits. The binary matrix rank test is performed to check for linear dependence of fixed-length substrings that make up the original sequence. The discrete Fourier transform (spectral) test allows us to estimate the height of the peaks of the discrete Fourier transform for the original sequence. The purpose of the test is to identify periodic properties of the input sequence, such as closely spaced repeating sections. The non-overlapping template matching test counts the number of predefined patterns found in the input sequence. The purpose of the test is to detect random or pseudo-random number generators that produce specified non-periodic patterns too frequently. The overlapping template matching test is similar to the previous test and counts the number of predefined patterns found in the input sequence. Maurer’s “Universal Statistical” test determines the number of bits between identical patterns in the input sequence. The linear complexity test is used to determine whether the input sequence is complex enough to be considered completely random. The serial test consists of counting the frequency of all possible overlaps of patterns of length m bits over the input bit sequence. The approximate entropy test counts the frequencies of all possible overlaps of patterns of length m bits over the input bit sequence. The cumulative sums test is the maximum deviation (from zero) during a random walk, determined by the cumulative sum of the given (−1, +1) digits in the sequence. The random excursions test involves counting the number of cycles that have exactly k visits during a random walk of the cumulative sum.

If all of the above tests are passed correctly, then we can expect good performance from the generator. However, in this article we propose to consider scenarios in which the quality of the generated pseudo-random sequence is compromised for some reason. Thus, it is known that a good PRN generator should use different starting parameters to generate a sequence. If the programmer uses one parameter, or even worse, the same constant, then the generator’s operation can be predicted. Since the PRN generator is an integral part of asymmetric ciphers, this in turn can lead either to the compromise of the secret key or to the substitution of the digital signature.

2.2.2. Single-Key Cryptographic Primitives in Blockchain Technologies

Symmetric ciphers are single-key cryptographic primitives. Symmetric ciphers are not directly used in classical blockchain systems. But they are widely used as additional add-ons. For example, in the core of the Bitcoin platform, in accordance with the BIP 0038 improvement standard, the AES (Advanced Encryption Standard) encryption algorithm is used as an add-on for encrypting the user’s secret key stored in the crypto wallet. Symmetric ciphers can also be used as auxiliary tools for organizing the processes of storing and processing data within the blockchain system. This is not directly related to the work of the blockchain core but can affect the strength of the information systems based on this blockchain.

When assessing the cryptographic strength of symmetric ciphers, the complexity of a brute-force key search is usually set as a standard. How vulnerable an algorithm is also depends on how much faster the analysis can be carried out, as well as what data and their volumes are required for the analysis. Since symmetric ciphers do not directly affect the work of the blockchain, approaches to assessing their strength will not be considered here. More detailed information on strength assessing symmetric ciphers can be found in numerous papers, including [16,17,18,19].

2.2.3. Two-Key Cryptographic Primitives in Blockchain Technologies

Two-key cryptographic primitives include asymmetric ciphers that use a pair of keys related by some mathematical transformation. A classic example of an asymmetric cipher is the RSA encryption algorithm. At the same time, it has not found wide application in modern blockchain systems due to a number of reasons. Firstly, modern cryptographic resistance requirements for the RSA (Rivest–Shamir–Adleman) algorithm recommend using a module size of at least 2048 bits. This means that each data signature will take up at least 256 bytes. Since the blockchain stores all information about transactions and blocks, this directly affects the size of the blockchain database. Secondly, over almost 50 years of the RSA algorithm’s existence, a large number of comments and recommendations for the implementation of the RSA algorithm have been accumulated. Failure to comply with these recommendations can significantly reduce the strength of encrypted data. The creators of blockchain platforms have found an alternative in the use of ECC. At the same time, with much smaller private key sizes, cryptographic strength is maintained, similar to the use of the RSA algorithm with the recommended private key sizes (

Table 1. Private key dimensions ratio for ECC and RSA algorithms.

Elliptic Curve	Private Key Size for ECC, Bit	Private Key Size for RSA, Bit	Key Ratio
secp160k1	160	1024	1:6
secp160r1	160	1024	1:6
secp160r2	160	1024	1:6
secp224k1	224	2048	1:9
secp224r1	224	2048	1:9
secp256k1	256	3072	1:12
secp256r1	256	3072	1:12
secp521r1	521	15,360	1:30

) [20]. The elliptic curve of the secp256k1 type has found the greatest application in blockchain platforms; it is used in the two most popular blockchain platforms: Bitcoin and Ethereum.

It should be noted that on blockchain platforms, the use of electronic signatures has acquired a new purpose, namely managing transactions to confirm the payment. When a transaction with a money transfer is created, a so-called signature script is placed in it, created using the public key of the user to whom the payment is assigned. In turn, the recipient of the transfer will be able to spend it using his private key. Thus, only the user who can present the correct private key to unlock the signature script will be able to spend the created transaction. For example, on the Bitcoin platform, transactions of the P2PKH (Pay To Public Key Hash) or P2SH (Pay To Script Hash) type are built according to this principle.

Elliptic curves of two types are used for ECC: binary elliptic curves and elliptic curves bounded by the modulus of a prime number p. In blockchain systems, ECC is used in the F_p field; so we will consider only this curve type here.

Elliptic curves in a prime field F_p are given in the Weierstrass form, i.e., in the following form:

y² = x³ + ax + b,

(1)

where a, b ∈ F_p, and 4a³ + 27b² ≠ 0.

Depending on how the parameters are specified, the following types of elliptic curves are distinguished: the Montgomery curve, the Koblitz curve, the Edwards curve, the twisted Edwards curve, the MoTE curve, and a curve with random parameters. A more detailed description of the parameters for each type of curve is given in [21,22].

Here, we will limit ourselves to considering Koblitz elliptic curve since it is used in the most famous blockchain platforms, Bitcoin and Ethereum. The Koblitz curve is specified as Equation (1). In general, elliptic curves over a field F_p are defined as a tuple:

T = (p, a, b, G, n, h_c),

where p is the large integer defining the finite field F_p, a and b are the parameters of Equation (1), G is the base point of the elliptic curve, which is defined as two coordinates (x, y), n is the prime number defining the order of the base point of G, and h_c is the cofactor of the subgroup.

For those elliptic curves from Table 1 that are formed using the Koblitz curve, the recommended parameters of the tuple T in accordance with [22] for the Part 1 and Part 2 recommendations are presented in

Table 2. Recommended parameters of elliptic curves. Part 1.

Elliptic Curve	p	a	b	hc
secp160k1	2160-232-214-212-29-28-27-23-22-1	0	7	01
secp224k1	2224-232-212-211-29-27-24-2-1	0	5	01
secp256k1	2256-232-29-28-27-26-24-1	0	7	01

and

Table 3. Recommended parameters of elliptic curves. Part 2.

Elliptic Curve	G	n
secp160k1	02 3B4C382C E37AA192 A4019E76 3036F4F5 DD4D7EBB	01 00000000 00000000 0001B8FA 16DFAB9A CA16B6B3
secp224k1	03 A1455B33 4DF099DF 30FC28A1 69A467E9 E47075A9 0F7E650E B6B7A45C	01 00000000 00000000 00000000 0001DCE8 D2EC6184 CAF0A971 769FB1F7
secp256k1	02 79BE667E F9DCBBAC 55A06295 CE870B07 029BCFDB 2DCE28D9 59F2815B 16F81798	FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF BAAEDCE6 AF48A03B BFD25E8C D0364141

, respectively.

The parameters from Table 2 and Table 3 define the parameters for the tuple T = (p, a, b, G, n, h_c), including the parameters of the elliptic curve used by Equation (1). For example, the elliptic curve secp256k1 is used for the Bitcoin and Ethereum blockchain systems. This means that in this case Equation (1) takes the form of y² = x³ + 7. All operations are performed in the field modulo p = 2¹⁶⁰-2³²-2¹⁴-2¹²-2⁹-2⁸-2⁷-2³-2²-1. The starting point of the elliptic curve is the point E = 02 79BE667E F9DCBBAC 55A06295 CE870B07 029BCFDB 2DCE28D9 59F2815B 16F81798. The first byte of point E is 02, which means that the point is specified in abbreviated form and the second coordinate of the point is even (a more detailed description is given below, including the algorithm for restoring the second coordinate). The parameter n specifies the total number of points on the elliptic curve that we can work with.

Let us consider the basic mathematical techniques used in ECC. ECC uses two basic operations: the addition of two points (Algorithm 1) and the multiplication of a point by a scalar (Algorithm 2). The multiplication of a point by a scalar is performed as repeated addition of different points or doubling of identical ones. Here, we will consider the classical method of multiplying a point by a scalar. Other algorithms offering alternative methods of multiplying a point by a scalar can be found in [23,24].

Algorithm 1. Addition of two different points of an elliptic curve

Tyte 1. Input: Elliptic curve in a prime field of the form of Equation (1). Two points of the elliptic curve are P(x1, y1) and Q(x2, y2), where P, Q ∈ Fp; P ≠ Q, x1 ≠ x2. Steps: $\lambda ={\displaystyle \frac{y_2-y_1}{x_2-x_1}}$; $x_3={\lambda }^2-x_1-x_2$; $y_3={\lambda }^2\left(x_1-x_3\right)-y_1$. Output: Point R (x3, y3) for which R = P + Q, R ∈ Fp. Tyte 2. Input: Elliptic curve in a prime field of the form of Equation (1). Two identical points of an elliptic curve are P(x1, y1) and P(x1, y1), where P ∈ Fp, y1≠ 0. Steps: $\lambda ={\displaystyle \frac{3x_1^2+a}{2y_1}}$; $x_3={\lambda }^2-2x_1$; $y_3={\lambda }^2\left(x_1-x_3\right)-y_1$. Output: Point R (x3, y3) for which R = P + P = 2P, R ∈ Fp. Tyte 3. Input: Elliptic curve in a prime field of the form of Equation (1). Two points of the elliptic curve are P(x1, y1) and Q(x2, y2), where P ≠ Q, x1 = x2. Output: Point R (x3, y3) = P + Q = ∞ (neutral element). Tyte 4. Input: Elliptic curve in a prime field of the form of Equation (1). Two points of the elliptic curve are P(x1, y1), with y1 = 0. Output: Point R (x3, y3) = 2P = ∞ (neutral element). Tyte 5. Input: Elliptic curve in a prime field of the form of Equation (1). Two points of the elliptic curve are P(x1, y1) and Q = ∞ (neutral element). Output: Point R (x3, y3) = P + Q = P + ∞ = P.

Algorithm 2. Multiplying a point on an elliptic curve by a scalar

Input: Elliptic curve in a prime field of the form of Equation (1). Elliptic curve point is P(x1, y1), where P ∈ Fp; scalar k is an integer that can be represented as a bit sequence k = (km − 1, km − 2, …, k1, k0). Steps:   1. Initialize data. Point R = (0, 0). Point S = (x1, y1).   2. For all i from 0 to m − 1    2.1 If ki = 0, then     2.1.1 If R = 0, then R = S otherwise R = R + S    2.2 S = S + S Output: Point R = kP, R ∈Fp.

Often, to save space, an elliptic curve point stores only one X coordinate. Since an elliptic curve is defined by a quadratic equation, there are always two Y coordinates for a given X. To avoid confusion, an extra byte b is placed before the X coordinate, and together they form a sequence of 33 bytes (b||X). If b = 02, the Y coordinate is even; if b = 03, the Y coordinate is odd. For the same X, the Y coordinates will always form a pair of an even and an odd number, due to the fact that operations in the field are limited to an odd number. Also, the first byte of b can be equal to 04. Usually this means that the point is stored in the expanded form with both coordinates. Algorithm 3 describes the process of obtaining the y-coordinate for an elliptic curve.

Algorithm 3. Recovering the y-coordinate for a point on an elliptic curve

Input: Elliptic curve in a simple field of the form of Equation (1). The coordinate of the point of the elliptic curve is (b||x). Steps:  1. $y=\sqrt{x^3+ax+b}$ mod p.  2. If ((b = 2) and ((y & 1) = 1)), then y = p − y. Output: Point R = (x, y).

Let us consider the application of the above operations to obtain a digital signature using the elliptic curve digital signature algorithm ECDSA (Algorithm 4).

Algorithm 4. Elliptic curve digital signature algorithm (ECDSA)

Input: Elliptic curve in a simple field of the form of Equation (1) with a tuple of parameters T = (p, a, b, G, n, hc) common to two users of the system A and B, message M, h(M) is a given hash function. Key generation: 1. User A chooses a random number dA no greater than n. dA is the private key of user A. 2. User A calculates the point QA = dAG. The point QA is the public key of user A. 3. User A sends his public key QA to user B. Signature: 1. User A chooses a random number ks no greater than n. The number ks is a session key, different each time for signing messages M. 2. User A calculates the point ksG = (x1, y1) and r = x1 mod n. 3. If r = 0, then it is necessary to return to step 1 4. User A calculates t = ks−1 mod n (using the extended Euclidean algorithm). 5. User A calculates z = h(M) and represents the result as a large integer. 6. User A calculates s = t(z + rdA) mod n. 7. If s = 0, then return to step 1 8. User A sends message M to user B and a signature in the form of a pair of values (r, s). Output: Signature = (r, s). Signature verification: 1. User B checks that the numbers r and s are in the range from 1 to n − 1. 2. User B calculates z = h(M) and represents the result as a large integer. 3. User B calculates w = s−1 mod n (using the extended Euclidean algorithm). 4. User B calculates u = zw mod n. 5. User B calculates v = rw mod n. 6. User B calculates the uG + vQA 7. If r ≠ x mod n, then the signature is incorrect. Output: Point (x, y) = uG + vQA = uG + vdAG = (u + vdA)G = (zw + rwdA)G = (z + rdA)wG = (z + rdA)s−1G = (z + rdA)s−1G = st−1s−1G = t−1G = (ks−1)−1G = ksG

It is known that the two most famous platforms, Bitcoin and Ethereum, use the same elliptic curve secp256k1 with the same parameters (Table 2 and Table 3). This means that these platforms will generate the same key pairs. This can be easily verified using any online key generator for these platforms (for example, www.rfctools.com).

2.2.4. Hybrid Cryptographic Primitives in Blockchain Technologies

Hybrid cryptographic primitives include algorithms that combine elements of both symmetric and asymmetric ciphers. As a rule, when using hybrid cryptographic primitives, schemes for generating a shared secret key based on an asymmetric cipher are used. After that, symmetric ciphers are used to encrypt the data [24]. Such algorithms are, for example, ECIES (Curve Integrated Encryption Scheme), PSEC (Provably Secure Elliptic Curve), and ACE (Advanced Cryptographic Engine). Similar to symmetric ciphers, in the field of blockchain technologies, these cryptographic primitives have an indirect application, associated rather with specific tasks of information systems that are built on blockchain platforms. To assess the cryptographic strength, it is advisable to consider these cryptographic primitives from two sides. On the one hand, it is necessary to evaluate the possibility of cryptanalysis to generate a common secret key using potential vulnerabilities of an asymmetric cipher. On the other hand, it is necessary to evaluate the possibility of determining the encryption key or opening the encrypted text based on potential vulnerabilities in a symmetric cipher.

3. Results and Discussions

3.1. Hash Functions and Their Strength When Used in Blockchain

Let us consider several cases related to the use of hash functions in the blockchain. For each case, we will define a possible attack scenario and estimate the complexity of the analysis.

Case 1.

Description of the task: Transactions are packed differently on different blockchain platforms. As a rule, a Merkle tree is used to pack transactions into a block. When calculating the hash of a block, it is not the transactions themselves that are used, but only the root of the Merkle tree. Let us consider an example of such a block in the case when a consensus mechanism is used that is not related to calculating the hash value (different from PoW (proof of work)).

Statement of the problem: Data block M consists of header information and the root of the Merkle tree RM, formed by block transactions T1, T2, T3…TN. To calculate the root of the Merkle tree, the hash function h = H(Ti) is used. It is necessary to replace one transaction in block M so that the root of the Merkle tree remains unchanged. In this case, all rules for compiling transactions and blocks must be observed.

Input: Transactions T1, T2, T3…TN. Hash function h = H(T). Merkle tree root RM.

Output: Transactions T1, T2, T3…TNew.

Solution:

Examples of constructing a Merkle tree for a different number of input transactions are shown in Figure 2. A distinctive feature of the algorithm is doubling the last hash value if the number of leaves at the processed tree level is odd. Modern blockchain platforms check for duplication of transactions in a block to avoid the CVE-2012-2459 vulnerability. From Figure 2, it is clearly seen that the simplest solution to the problem is to find a collision for the lowest level of the Merkle tree. Only in this case will all further transformations be performed identically.

In the case of an odd number of transactions, the task is reduced to replacing the last transaction TN with the transaction TNew in such a way that the relation H(TN||TN) = H(TNew||TNew) is satisfied.

In the case of an even number of transactions, the task is reduced to replacing the last transaction TN with the transaction TNew in such a way that the relation H(TN-1||TN) = H(TN-1||TNew) is satisfied.

In both cases, one of the transactions is subject to enumeration (selection). The main problem is that the new transaction TNew must be constructed according to all the rules that this blockchain system imposes on the construction of transactions. This means that in this case it is impossible to enumerate all possible binary combinations for the second part of the hashed message. In this case, several analysis techniques can be applied.

Option 1. Formation of a new transaction TNew. Calculation of the hash value H(TNew||TNew) or H(TN-1||TNew). Comparison of the obtained hash value with H(TN||TN) or H(TN-1||TN), respectively. The complexity of the analysis will depend on the length n of the generated hash sequence and will average 2^n/2 steps.

Option 2. In the case of an even number of transactions, we can try to apply the differential cryptanalysis method for the case when the difference in inputs is dT = 0|| (TN xor TNew), and the difference in outputs is dH = 0. This option may find a solution in the future, since at the moment there is no information on the application of the differential cryptanalysis method to the full-round algorithms SHA-1 and SHA-2.

Case 2.

Description of the task: For the PoW consensus, the main problem is to find a nonce value at which the block hash forms a specified number of zero bits in the most significant digits. Transactions, as in the previous case, are packed using a Merkle tree, and when calculating the hash value of a block, only the root of the Merkle tree is usually taken into account. At the same time, a change in the number and composition of transactions can affect the header information in the block.

Statement of the task: A data block M consists of header information IV, the root of the Merkle tree RM, and a nonce value. The hash function h = H(M) is used to calculate the block hash. It is necessary to replace block M with block M1 in compliance with all the rules for compiling a block (depending on the blockchain platform), such as removing or adding one or more transactions, replacing the repayment script in the transaction, etc. In this case, the hash value of the new block M1 must match the hash value of block M.

Input: Block M = (IV||RM||nonce). Hashing function h = H(T).

Output: Block M1 = (IV1||RM1||nonce1), such that h(M) = h(M1).

Solution:

This case is reduced to the problem of finding a collision. Unlike the previous case, there is no need to keep the Merkle tree root unchanged. It is enough to redefine the set of transactions in the block and the starting information of the block (IV1||RM1). After that, it is necessary to iterate over the value of nonce1 until a collision is obtained h(IV||RM||nonce) = h(IV1||RM1||nonce1). The complexity of the analysis will depend on the length n of the generated hash sequence and will average 2^n/2 steps.

Case 3.

Description of the task: In public blockchains, it is common practice to not store users’ public keys in the system in an open form. It is believed that the public key can be used to calculate the private key, despite the fact that this is a computationally complex task. For the Ethereum platform, the user’s address in the network is 20 bytes and is calculated as a hash of the public key of the ECDSA algorithm. The Keccak-256 algorithm is used as a hash function. The general scheme for generating an address for the Ethereum network is shown in Figure 3.

Problem statement: The Ethereum A_E network address is known. Determine the user’s public key.

Input: Ethereum AE network address.

Output: Public key in the form of point coordinates Q = (x, y).

Solution:

In this case, the problem is reduced to finding a preimage. The input parameters are the coordinates of the point Q = (x, y) for the ECDSA elliptic curve. Not all possible values of x in the range from 1 to 2²⁵⁶ will belong to a given elliptic curve. It is possible to determine whether a given quadratic equation is solvable for x using the Jacobi symbol. For those values of x that belong to a given elliptic curve, there will always be two values of y. In the general case, the algorithm for finding a public key will look like this (Algorithm 5).

Algorithm 5. Determining an address in the Ethereum network

For all x from 1 to 2256 − 1:   1. Determine the value of the Jacobian symbol   2. If the Jacobian symbol is not 1, then go back to step 1   3. Determine the values of y1 and y2   4. Compute h = Keccak-256(x||y1)   5. If the lower 20 bits of h are AE, then the solution is point (x||y1)   6. Compute h = Keccak-256(x||y2)   7. If the lower 20 bits of h are AE, then the solution is point (x||y2) A total of 2257 hash operations are required to compute the preimage of point Q = (x, y).

Case 4.

Description of the task: For the Bitcoin platform, the user’s address on the network is 25 bytes. The address is the Base58 encoding of the result of double hashing the public key of the ECDSA algorithm using the SHA-256 and RIPEMD-160 hashing functions. In addition, 4 integrity control bytes are added to the address, which are generated from the most significant 21 bytes of the address by double hashing using the SHA-256 algorithm. The general scheme for generating an address for the Bitcoin network is shown in Figure 4.

Problem statement: The Bitcoin network address A_B is known. Determine the user’s public key.

Input: Bitcoin network address A_B.

Output: Public key in the form of point coordinates Q = (x, y).

Solution:

In this case, the problem also comes down to finding the preimage. The input parameters are the coordinates of the point Q = (x, y) for the ECDSA elliptic curve. The first byte is always set to 0x04, which means writing the elliptic curve point in expanded form. Similar to the previous case, not all possible values of x in the range from 1 to 2²⁵⁶ will belong to the given elliptic curve. It is possible to determine whether the given quadratic equation is solvable for x using the Jacobi symbol. For those values of x that belong to the given elliptic curve, there will always be two values of y. Before searching for the public key, it is necessary to convert the given address A_B into Base256 encoding. Let the most significant 21 bytes of the address A_B be specified as MSB21AB, and the least significant 4 bytes of the address be specified as LSB4AB. Calculate the hash value of the checksum: h = SHA-256(SHA-256(MSB21AB)). Compare the least significant 4 bytes of the obtained value h with LSB4AB. If these values match, consider the address correct and start searching for the public key. In general, the algorithm for searching for the public key will look like this (Algorithm 6).

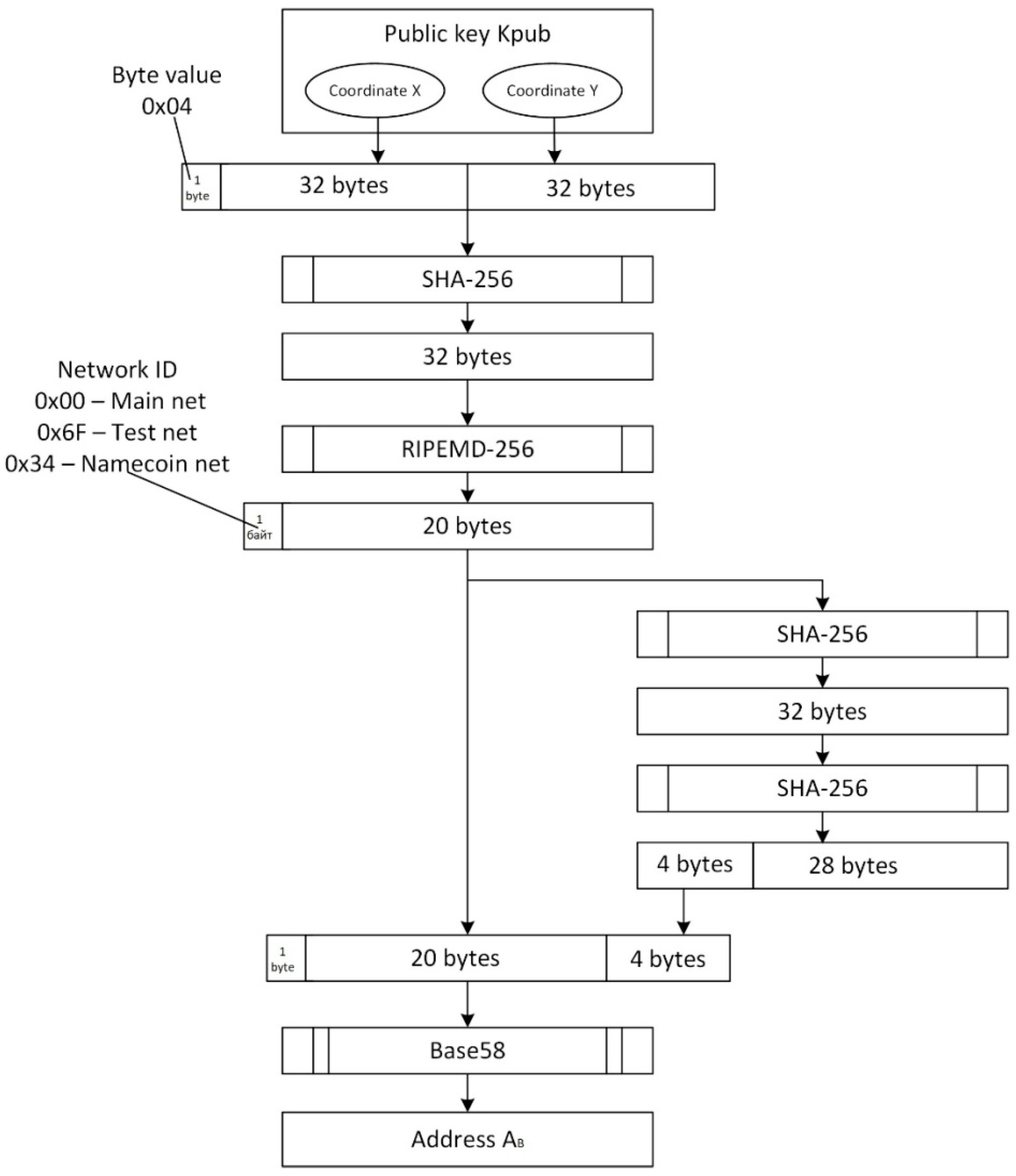
Algorithm 6. Determining an address in the Bitcoin network. Version 1

1. For all x from 1 to 2256 − 1:   1.1 Determine the Jacobian symbol value   1.2 If the Jacobian symbol is not 1, then return to step 1   1.3 Determine the values of y1 and y2   1.4 Compute h1 = SHA-256(x||y1)   1.5 Compute h2 = RIPEMD-160(h1)   1.6 If (00||h2) = MSB21AB, then the solution is point (x||y1)   1.7 If (6F||h2) = MSB21AB, then the solution is point (x||y1)   1.8 If (34||h2) = MSB21AB, then the solution is point (x||y1)   1.9 Compute h1 = SHA-256(x||y2)   1.10 Compute h2 = RIPEMD-160(h1)   1.11 If (00||h2) = MSB21AB, then the solution is point (x||y2)   1.12 If (6F||h2) = MSB21AB, then the solution is point (x||y2)   1.13 If (34||h2) = MSB21AB, then the solution is point (x||y2) In total, 2258 hash operations are required to calculate the preimage of point Q = (x, y).

An alternative search option based on the meet-in-the-middle method can be considered. In this case, it is necessary to create a database of precomputed values, which will be used for the search. The complexity of this algorithm will be added to by the need to store a large database of precomputed data.

Using Algorithm 7, a total of 3*2²⁵⁶ hash operations and about 2⁴¹⁶ comparisons against the base are required. In the worst case, the amount of memory required to store Base 1 is 2²⁶³, which corresponds to 10 PB. To store Base 2, an additional 2¹⁶⁵ bytes are required, which corresponds to about 4 PB. Based on the configuration of the world’s most powerful supercomputer as of November 2024 (top500.org), it can be seen that the problem of finding collisions and preimages is currently difficult to compute and practically unsolvable.

Algorithm 7. Determining an address in the Bitcoin network. Version 2

1. For all x from 1 to 2256 − 1:   1.1 Determine the Jacobian symbol value   1.2 If the Jacobian symbol is not 1, then return to step 1   1.3 Determine the values of y1 and y2   1.4 Calculate h1 = SHA-256(x||y1). Store the values (x||y1, h1) in Base1.   1.5 Calculate h2 = SHA-256(x||y2). Store the values (x||y2, h2) in Base1.   1.6 Calculate h3 = RIPEMD-160(x).   1.7 If (00||h3) = MSB21AB, then store the value of x in Base2.   1.8 If (6F||h3) = MSB21AB, then store the values of x in Base2.   1.9 If (34||h2) = MSB21AB, then store the values of x in Base2. 2. For all x from Base 2, compare them with the values of h1 and h2 from Base 1. If they match h1, the solution is the point (x||y1) from the corresponding entry in Base1. If they match h2, the solution is the point (x||y2) from the corresponding entry in Base1.

3.2. PRS Generators and Their Strength When Used in Blockchain

In blockchain systems, PRS generators are used to generate random numbers when developing key sequences, as well as when using electronic signature algorithms based on ECC. The strength of the blockchain system itself in relation to hacking (gaining access to managing the user’s assets) or forgery of information directly depends on how strong the used random number generator is. There are two main ways to build random number generators: hardware and software. Since this study is aimed at research in the field of blockchains, software implementations of random number generators are of particular interest. Usually, random system processes can be used as starting parameters by software random number generators, such as system time; user keyboard handwriting; user-entered data; operating system parameters; or buffer contents. It is important to apply the following rule here: a good generator should use many different sources of randomness, combine them, and change them. There are cases when, for example, using only one parameter led to a system vulnerability, despite the quality of the generator used. Thus, in 2019, a vulnerability was discovered in the password manager from Kaspersky Lab (registered under number CVE-2020-27020) due to the fact that the generator’s starting value depended only on the system time.

Case 5.

Problem description: Evaluate the quality of the implementation of the selected PRS generator. Determine the probability p with which the generator produces values k1 and k2 that are no more than d positions apart.

Problem statement: There is an implementation of the PRS generator that performs the transformation k = Gen(). Determine the probability p with which |k_i – k_j| ≤ d, where i, j = 1, …, n.

Input: Generator k = Gen(); distance d; number of considered numbers n.

Output: Probability p (|k_i − k_j| ≤ d), where i, j = 1, …, n.

Solution:

This case comes down to the problem of determining the mathematical statistics of the distribution of randomly generated numbers along the numerical axis (Algorithm 8). The more the accumulated statistics, the more accurate the result will be. In order for the values generated by the generator to be considered vulnerable, the distance d between randomly generated points must be much smaller than the dimension of the module used and available for enumeration (for example, in the range from 2³² to 2⁶⁴). In this case, the probability of forming such a difference must be at least 0.5. We will use n points in the algorithm. The greater the n, the more accurately the probability value is determined. In this case, the number of combinations considered will be ${\displaystyle \frac{n(n-1)}{2}}$.

Algorithm 8. Determining the quality of the PRS generator

1. Initialize variables k[0] = Gen(); Sum = 0; 2. For all i from 1 to n:  2.1. k[i] = Gen();  2.2. For all j from 0 to i − 1:    2.2.1 If (|k[i] − k[j]| ≤ d), then Sum = Sum + 1; 3. p = ${\displaystyle \frac{2\ast Sum}{n(n-1)}}$.

3.3. ECC and Its Strength When Used in Blockchain

Typically, ECC is used in the blockchain to form addresses and create and confirm transactions. At the same time, sometimes there may be problems when users want to save encrypted data in the blockchain. ECC is not designed to encrypt large volumes of data. The El Gamal algorithm for encrypting data for ECC is known. The disadvantage of this algorithm is the fact that the encrypted data must be a point on an elliptic curve, which is not always possible. We propose to consider our new version of using ECC to transmit encrypted data, which can be used by blockchain users to encrypt and transmit small messages (1–2 data blocks). This algorithm is not the main algorithm of the blockchain and is not included in the core of modern blockchain systems. This algorithm allows the use of the same keys that users of the system have in order to store sensitive user data in an open blockchain database in encrypted form. At the same time, we propose to consider possible vulnerabilities that may arise if this algorithm is implemented incorrectly.

The new algorithm for encrypting and decrypting data (NAEDD) is designed to transmit an encrypted message M (Algorithm 9). Message M is represented as an integer whose dimension does not exceed the length of two coordinates of any point on the elliptic curve of Equation (1). Before encryption, message M must be padded to the length of the two coordinates in message M1. The padding is conducted as follows: the difference between the length of two coordinates and the length of message M in bits is written in the most significant 9 bits. The remaining space between the most significant bits and message M is filled with the least significant bits of the SHA-512(M) value. For example, if the coordinates of a point (x, y) take 64 bytes and message M contains only 4 bytes of information, for example, 0xABCD, then the value 480 (decimal representation, which corresponds to 1E0 in hexadecimal form) must be written in the most significant 9 bits. SHA-512(ABCD) = 9B3A86C5 DDDF6C13 ACB969DB 8F54EBB9 FA50DC4F 902EFF84 3380CEBF C9CC53FF C2CC4A5F 4DDA0FAC 9E331557 8FAEBC99 9EE61609 434E10A6 C75E3D98 4EE2A426.

Then the encrypted block M1 is transformed to the form M1 = F045DDDF 6C13ACB9 69DB8F54 EBB9FA50 DC4F902E FF843380 CEBFC9CC 53FFC2CC 4A5F4DDA 0FAC9E33 15578FAE BC999EE6 1609434E 10A6C75E 3D984EE2 A426ABCD (Figure 5). Without padding performed, encryption will be vulnerable. After decryption, it is easy to restore the original value of M from M1 by discarding the number of bits that are specified in the most significant digits of the block.

Algorithm 9. New algorithm for encrypting and decrypting data

Input: Elliptic curve in a prime field of the form of Equation (1) with a tuple of parameters T = (p, a, b, G, n, hc), common to two users of the system A and B, padded message M. Key generation:   1. User A chooses a random number dA no greater than n. The number dA is the private key of user A.   2. User A calculates the point QA = dAG. The point QA is the public key of user A.   3. User A sends his public key QA to user B. Encryption:   1. User B chooses a random number ks no greater than n. The number ks is a session key, different each time for encrypting messages M.   2. User B calculates C1 = M1 ⊕ ksQA.   3. User B calculates C2 = ksG.   4. User B sends the pair of values (C1, C2) to user A. Output: Cipher = (C1, C2). Decryption:   1. User A calculates M1 = C1 ⊕dAC2.   2. Determines from the most significant 9 bits of M1 that l bits were added to the message.   3. Leaves the least significant (512 – l) bits of M1 in message M. Output: Original padded message M1 = C1 ⊕dAC2 = M ⊕ ksQA⊕dAksG = M ⊕ ksdAG⊕dAksG = M1; original message M.

In terms of cryptographic strength for the blockchain, the primary role is played by methods for finding the private key. Also relevant are scenarios for substituting signatures in messages. In the general case, it is necessary to solve the discrete logarithm problem, which is as follows. An elliptic curve with a tuple of parameters T = (p, a, b, G, n, h_c) is given. For two points P and Q, it is necessary to find such an integer d for which dP = Q. The approaches that are applied to the analysis largely depend on the parameters of the elliptic curve itself. The most effective analysis method to date is Pollard’s rho method, the execution time of which is estimated as ${\displaystyle \frac{1}{r}}\sqrt{{\displaystyle \frac{\pi n}{2}}}$, where n is the order of the elliptic curve point and r is the number of parallel processors for performing calculations [25]. The discrete logarithm problem for elliptic curves with the recommended parameters (Table 1) is currently difficult to calculate and is not applicable in practice. However, let us consider several situations where errors in implementations or incorrect use of system parameters can lead to vulnerabilities.

Case 6.

Problem description: Determine the private key of a user if his public key is known and the implementation of the key generation algorithm uses a weak PRS.

Problem statement: The key pair is generated in accordance with the ECDSA with a given tuple of parameters T = (p, a, b, G, n, h_c). The public key of user A is known as Q_A = (x, y). It is known that the implementation of the PRS generator k = Gen() generates parameters k for which p (|k_i − k_j| ≤ d) ≥ 0.5. It is required to determine the private key of user A.

Input: Generator k = Gen(); distance d; public key of user A: Q_A = (x, y).

Output: private key of user A: d_A.

Solution:

In this case, we can assume that if a new private key is formed, then with a probability of 0.5, it will be no more than d points away from the key of user A (Algorithm 10). The complexity of the algorithm will directly depend on the value of d.

Algorithm 10. Finding a private key when using a bad PRS generator

1. Generate k = Gen(). 2. Calculate point Q1 = kG; 3. If Q1 = QA, then dA = k; terminate the algorithm. 4. For all i from 1 to d:   4.1 Q1 = Q1 + G;   4.2 If Q1 = QA, then dA = k + i; terminate the algorithm. 5. If key not found, then return to step 1.

Case 7.

Problem description: Determine the private key of a user if it is known that an error has been made in the implementation of the ECDSA: a constant value of the session key k_s is used.

Problem statement: A key pair is generated in accordance with the ECDSA with a given tuple of parameters T = (p, a, b, G, n, h_c). It is known that the value k_s is the same for all messages M. Two messages M1 and M2 are known, and their corresponding signature values (r₁, s₁) and (r₂, s₂), respectively. It is required to determine the private key of user A.

Input: Messages M1 and M2 and their signatures (r₁, s₁) and (r₂, s₂), respectively.

Output: Private key of user A d_A.

Solution:

Since the value of the session key does not change, the coordinate r for points M1 and M2 will be calculated in the same way: r = r₁ = r₂ = k_sG.

For message M1, parameter s₁ is calculated as s₁ = k_s⁻¹(h(M1) + rd_A).

For message M2, parameter s₂ is calculated as s₂ = k_s⁻¹(h(M2) + rd_A).

Multiplying both equations by k_s, we get:

s₁k_s = h(M1) + rd_A

s₂k_s = h(M2) + rd_A

Then:

s₁k_s − s₂k_s = h(M1) + rd_A − h(M2) − rd_A

k_s(s₁ − s₂) = h(M1) − h(M2)

k_s = (h(M1) − h(M2))(s₁ − s₂)⁻¹

Since the values of s₁, s₂, M1, and M2 are known, we can easily determine the parameter k_s. Having found it, from the formula s₁k_s = h(M1) + rd_A we determine the value of the secret key d_A:

d_A = (s₁k_s − h(M1))r⁻¹.

Case 8.

Problem description: Replace the signature of message M1 with the signature of message M2 in the ECDSA if it is known that an error was made in the implementation of the signature algorithm: the generation of the session key k_s generates parameters k = Gen(), for which p (|k_i − k_j| ≤ d) ≥ 0.5.

Problem statement: The generation of a key pair is performed in accordance with the ECDSA. A given tuple of parameters T = (p, a, b, G, n, h_c) is used. It is known that p (|k_i − k_j| ≤ d) ≥ 0.5. The message M1 and its signature (r₁, s₁) are known. It is required to generate a signature (r₂, s₂) for message M2 on behalf of user A without knowing his secret key.

Input: Generator k = Gen(); distance d; message M1 and its signature (r₁, s₁).

Output: Signature (r₂, s₂) for message M2.

Solution:

The first part of the algorithm is similar to Algorithm 10 for Case 6. It is expected that for a new signature, the parameter k_s will be no more than d points away from the one used to sign message M1 with a probability of 0.5. The complexity of the algorithm will directly depend on the value of d. Then, using Algorithm 11, the parameter k_s of a known signature can be determined.

Algorithm 11. Finding a session key when using a bad PRS generator

1. Generate k = Gen(). 2. Calculate point Q1 = kG = (x2, y2); 3. If r1 = x2, then ks = k; terminate the algorithm. 4. For all i from 1 to d:   4.1 Q1 = Q1 + G = (xi + 2, yi + 2);   4.2 If r1 = xi + 2, then ks = k + i; terminate the algorithm. 5. If ks is not found, then return to step 1.

If Algorithm 11 is successful, the parameter k_s found for the signature of message M1 will be used to form the signature of message M2. For message M1, the signature is formed as follows:

r₁ = k_sG

s₁ = k_s⁻¹(h(M1) + rd_A)

The task is to form a signature for message M2 of the form:

r₂ = r₁ = k_sG

s₂ = k_s⁻¹(h(M2) + rd_A)

Thus, it turns out that only the value of s₂ needs to be calculated. We transform the equations for s₁ and s₂ as follows:

s₁k_s = h(M1) + rd_A

s₂k_s = h(M2) + rd_A

Then:

s₁k_s − s₂k_s = h(M1) + rd_A − h(M2) − rd_A

k_s(s₁ − s₂) = h(M1) − h(M2)

s₁ − s₂ = (h(M1) − h(M2))k_s⁻¹

s₂ = s₁ − (h(M1) − h(M2))k_s⁻¹

Since the values of s₁, M1, M2, and k_s are known, the parameter s₂ can be easily determined. The signature (r₂, s₂) is formed without using the private key of user A and will be correctly verified using the public key of user A.

Case 9.

Problem description: It is known that in the NAEDD encryption is performed without using padding. It is required to recover the encrypted message M.

Problem statement: The generation of a key pair is performed in accordance with NAEDD with a given tuple of parameters T = (p, a, b, G, n, h_c). The encrypted message (C1, C2) is known. It is required to determine the encrypted message M.

Input: Encrypted message (C1, C2).

Output: Message M.

Solution:

This case will be easy to solve if the size of the encrypted message M does not exceed the length of the y coordinate, i.e., M takes up no more than 32 bytes. In this case, message C1 will contain an unchanged x coordinate for the point k_sQ_A. To recover message M, it will be sufficient to determine the y coordinate in accordance with Algorithm 3. Then the message M will be defined as the sum modulo 2 of the y coordinate and the least significant bytes of the message C1.

Case 10.

Problem description: It is known that in the NAEDD, the padding of the message M is performed with an error. Instead of hashed data, the data is filled with fixed values, such as 0 or 1. It is required to restore the encrypted message M.

Problem statement: The generation of a key pair is performed in accordance with NAEDD with a given tuple of parameters T = (p, a, b, G, n, h_c). The encrypted message (C1, C2) is known. It is required to determine the encrypted message M.

Input: Encrypted message (C1, C2).

Output: Message M.

Solution:

This case, as well as the previous one, will be easily solved if the size of the encrypted message M does not exceed the length of the y coordinate, that is, M occupies no more than 32 bytes. In this case, message C1 will contain the x coordinate for the point k_sQ_A, which was changed by the incorrectly performed padding. To restore message M, we must first determine the value of the x coordinate. If the most significant 9 bits of the mask contain the size of the encrypted message, we will receive no more than 2⁹ = 512 variants of the x coordinate (provided that message M does not exceed 32 bytes). For each x coordinate, we can determine two possible y coordinates in accordance with Algorithm 3. Message M will be determined as the sum modulo 2 of the y coordinate and the least significant bytes of message C1. Thus, we will receive a total of 2¹⁰ = 1024 possible variants for message M, one of which will be true.

4. Conclusions

The manuscript discusses possible scenarios in which, during practical implementation, the mathematical foundations embedded in the algorithms for generating a digital signature and encrypting data using algorithms based on elliptic curves for modern blockchain systems are violated. In this case, vulnerabilities arise that can lead to a compromise of the private key or substitution of the digital signature. A total of 10 scenarios of vulnerabilities critical for blockchain systems are considered, which can arise in the event of incorrect implementation of algorithms or in the event of choosing incorrect starting parameters for the system. In particular, 10 cases of vulnerabilities for the new NAEDD algorithm are considered. For each case, rigorous calculations of the maximum computational costs are given when fulfilling the conditions of the case in question. The authors of the articles conducted numerical modeling of the algorithms under consideration to confirm each case. The purpose of this work reflects the desire of the authors to draw the attention of developers to the importance of understanding the mathematical foundations laid down by cryptography, including using the proposed cases at the stage of testing their implementations. The main results are presented in

Table 4. Main results.

Case	Description	Maximum Difficulty
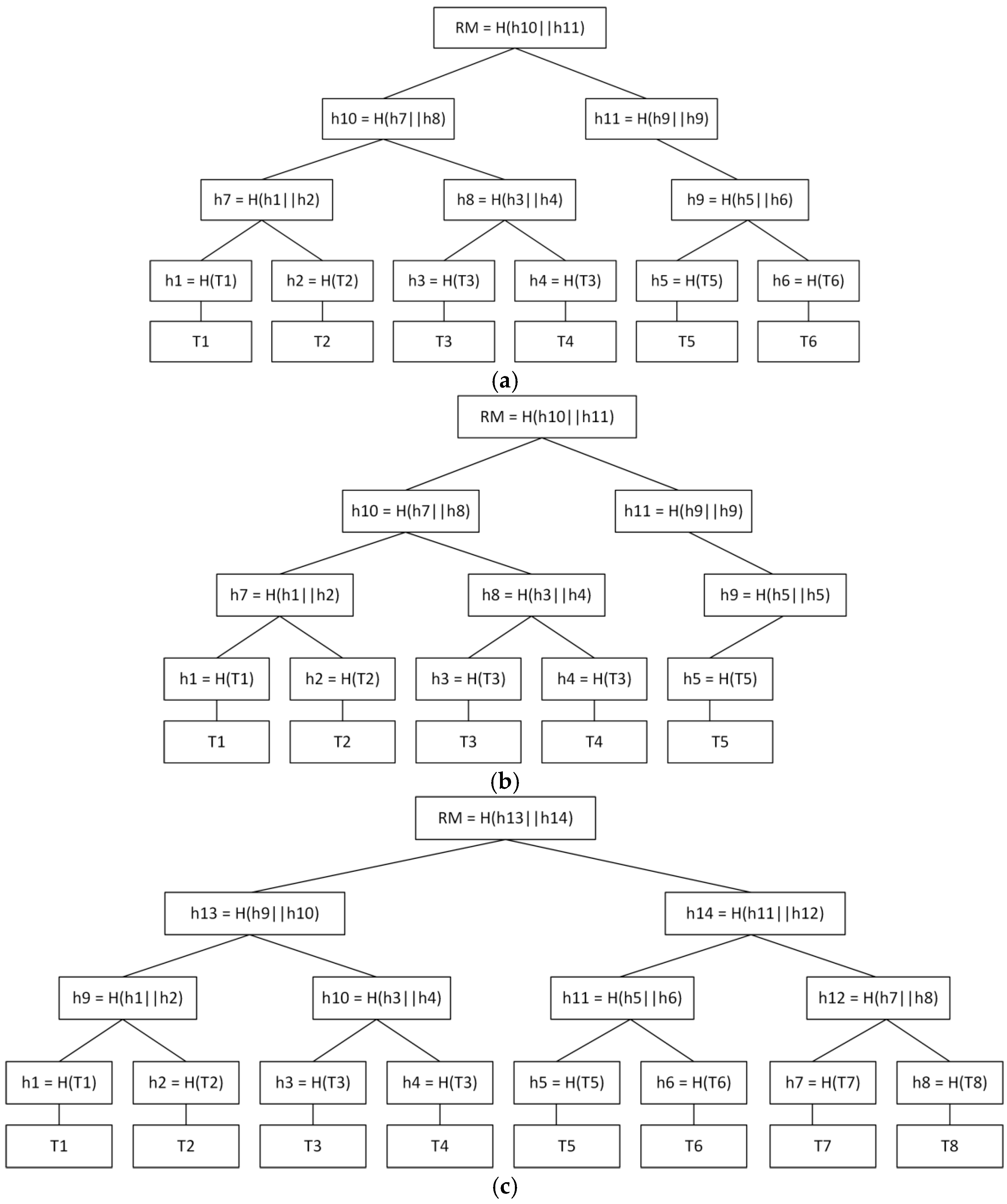
1	It is necessary to replace one transaction in block M so that the root of the Merkle tree remains unchanged	2n/2 steps, where n is the length of the generated hash sequence
2	It is necessary to replace block M with block M1 in compliance with all the rules for compiling a block (depending on the blockchain platform)	2n/2 steps, where n is the length of the generated hash sequence
3	The Ethereum AE network address is known. Determine the user’s public key	2257 hash operations are required
4	The Bitcoin network address AB is known. Determine the user’s public key	2258 hash operations are required
5	Determine the probability p with which the PRG produces values k1 and k2 that are no more than d positions apart	${\displaystyle \frac{n(n-1)}{2}}$, where n is the distance between two points
6	Determine the NAEDD private key of a user if his public key is known and the implementation of the key generation algorithm uses a weak PRS	${\displaystyle \frac{n(n-1)}{2}}$, where n is the distance between two points
7	Determine the private key of a user if it is known that an error has been made in the implementation of the ECDSA: a constant value of the session key ks is used	It has no difficulty
8	Replace the signature of message M1 with the signature of message M2 in the ECDSA if it is known that ECDSA uses a weak PRS	${\displaystyle \frac{n(n-1)}{2}}$, where n is the distance between two points
9	It is known that in the NAEDD, encryption is performed without using padding. It is required to recover the encrypted message M	It has no difficulty if the size of the encrypted message M does not exceed the length of the y coordinate
10	It is known that in the NAEDD, the padding of the message M is performed with an error. It is required to restore the encrypted message M	210

.

The obtained results are important for further development and improvement of blockchain platforms. The presented cases can be used to determine the stability of software implementations of cryptographic algorithms on the blockchain. The proposed NAEDD algorithm uses blockchain keys, which can be useful for storing in the blockchain and transmitting information in encrypted form. Future research will be aimed at practical research of the implementation of cryptographic primitives in modern blockchain platforms, such as Ethereum, Solana, Hyperledger Fabric, and others.