Benzene, an Unexpected Binding Unit in Anion–π Recognition: The Critical Role of CH/π Interactions
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
3.1. Energetic and Geometric Details of CH/π and Anion–π Complexes
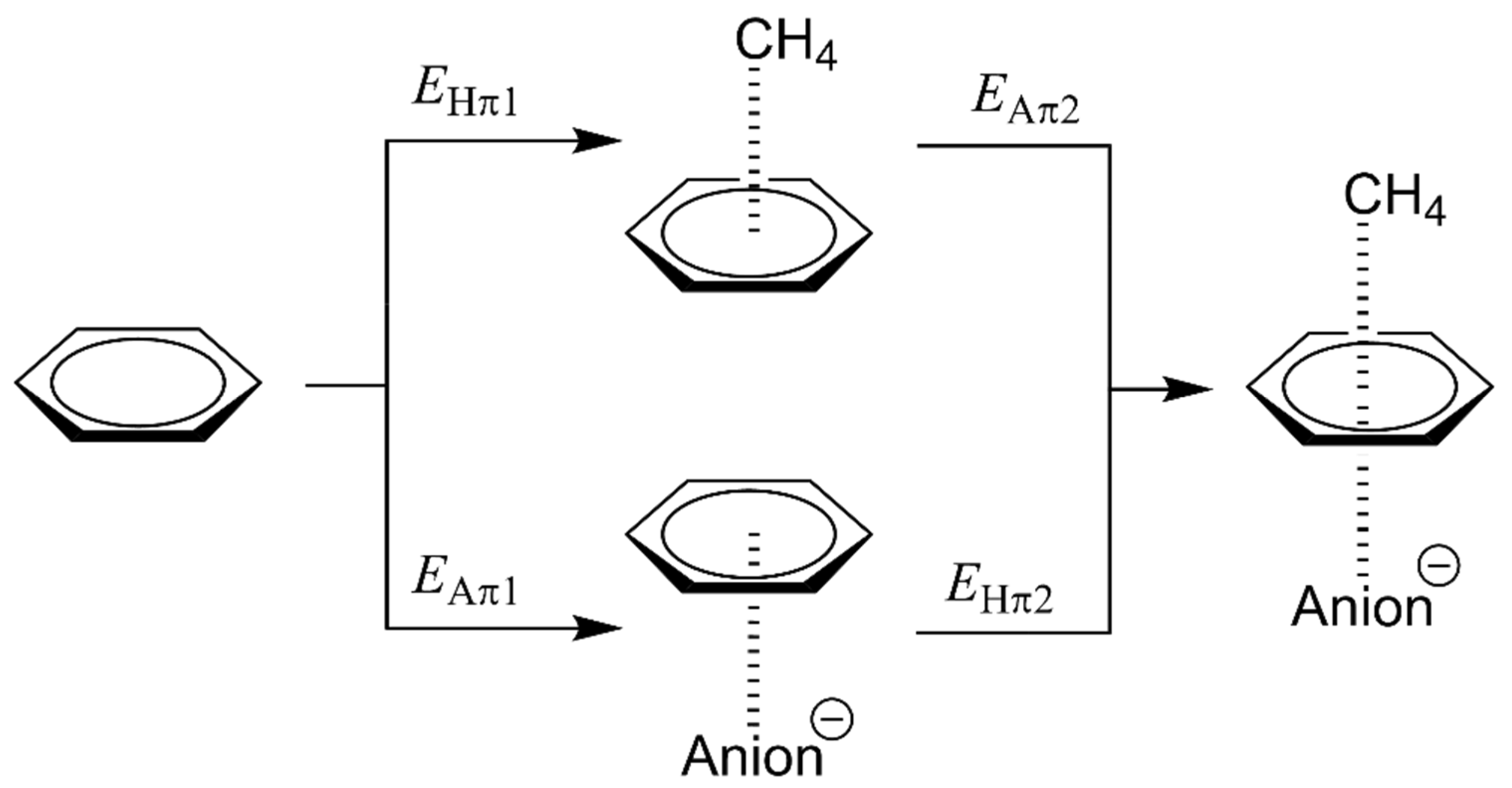
3.2. Energetic and Geometric Details of Three-Component CH/π and Anion–π Complexes
3.3. SAPT, AIM and NCI Analysis
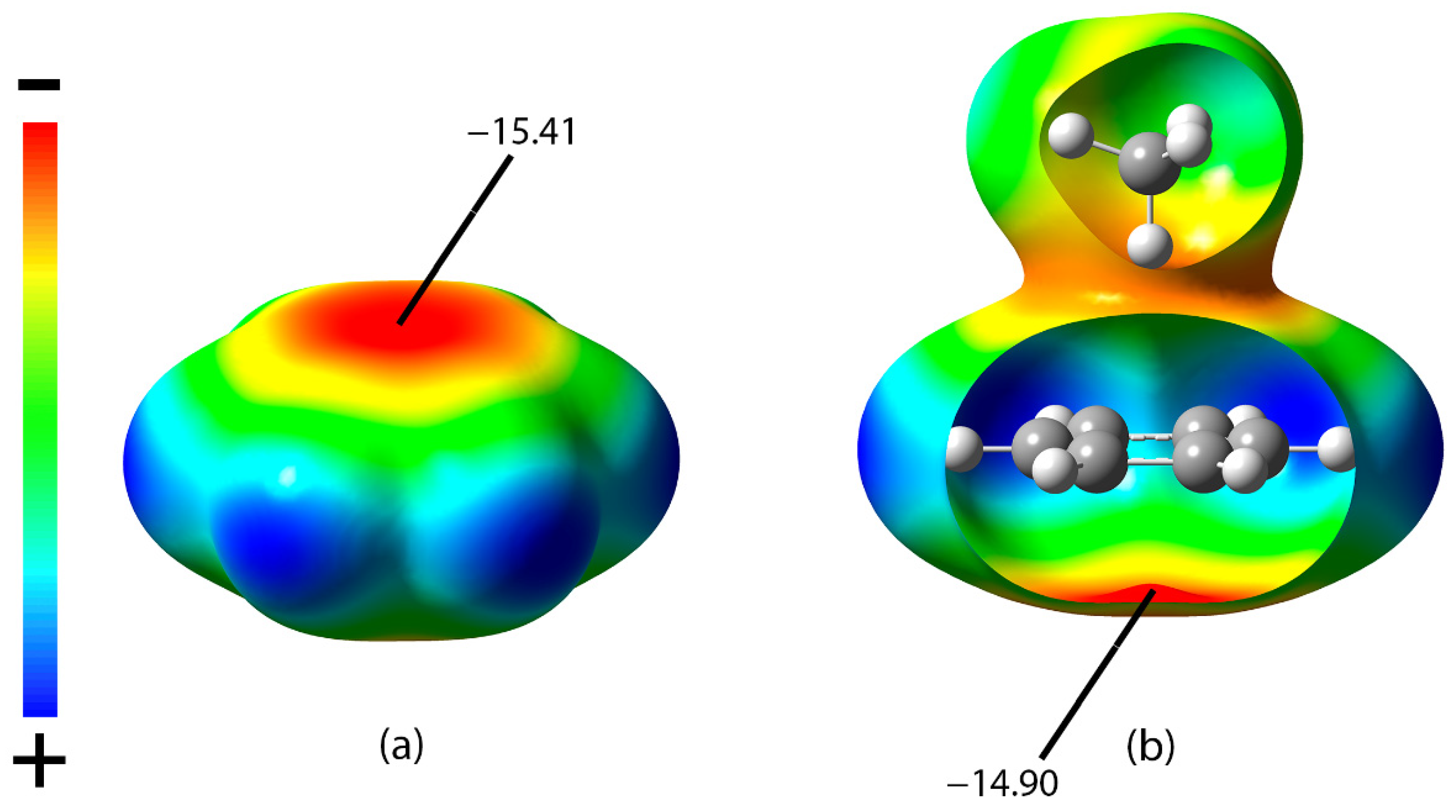
3.4. Experimental Evidences
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schneider, H.J. Binding Mechanisms in Supramolecular Complexes. Angew. Chem. Int. Ed. 2009, 48, 3924–3977. [Google Scholar] [CrossRef]
- Quiñonero, D.; Garau, C.; Rotger, C.; Frontera, A.; Ballester, P.; Costa, A.; Deyà, P.M. Anion–π Interactions: Do They Exist? Angew. Chem. Int. Ed. 2002, 41, 3389–3392. [Google Scholar] [CrossRef]
- Mascal, M.; Armstrong, A.; Bartberger, M.D. Anion−Aromatic Bonding: A Case for Anion Recognition by π-Acidic Rings. J. Am. Chem. Soc. 2002, 124, 6274–6276. [Google Scholar] [CrossRef]
- Alkorta, I.; Rozas, I.; Elguero, J. Interaction of Anions with Perfluoro Aromatic Compounds. J. Am. Chem. Soc. 2002, 124, 8593–8598. [Google Scholar] [CrossRef]
- Quiñonero, D.; Garau, C.; Frontera, A.; Ballester, P.; Costa, A.; Deyà, P.M. Counterintuitive interaction of anions with benzene derivatives. Chem. Phys. Lett. 2002, 359, 486–492. [Google Scholar] [CrossRef]
- Ballester, P. Experimental Quantification of Anion–π Interactions in Solution Using Neutral Host–Guest Model Systems. Acc. Chem. Res. 2013, 46, 874–884. [Google Scholar] [CrossRef]
- Kim, D.; Lee, E.C.; Kim, K.S.; Tarakeshwar, P. Cation−π−Anion Interaction: A Theoretical Investigation of the Role of Induction Energies. J. Phys. Chem. A 2007, 111, 7980–7986. [Google Scholar] [CrossRef]
- Kim, D.; Tarakeshwar, P.; Kim, K.S. Theoretical Investigations of Anion–π Interactions: The Role of Anions and the Nature of π Systems. J. Phys. Chem. A 2004, 108, 1250–1258. [Google Scholar] [CrossRef]
- Kim, D.Y.; Singh, N.J.; Kim, K.S. Cyameluric Acid as Anion-π Type Receptor for ClO4− and NO3−: π-Stacked and Edge-to-Face Structures. J. Chem. Theory Comput. 2008, 4, 1401–1407. [Google Scholar] [CrossRef]
- Foroutan-Nejad, C.; Badri, Z.; Marek, R. Multi-center covalency: Revisiting the nature of Anion–π interactions. Phys. Chem. Chem. Phys. 2015, 17, 30670–30679. [Google Scholar] [CrossRef]
- Novák, M.; Foroutan-Nejad, C.; Marek, R. Modulating Electron Sharing in Ion-π-Receptors via Substitution and External Electric Field: A Route toward Bond Strengthening. J. Chem. Theory Comput. 2016, 12, 3788–3795. [Google Scholar] [CrossRef] [PubMed]
- Schottel, B.L.; Chifotides, H.T.; Dunbar, K.R. Anion-π interactions. Chem. Soc. Rev. 2008, 37, 68–83. [Google Scholar] [CrossRef] [PubMed]
- Gamez, P.; Mooibroek, T.J.; Teat, S.J.; Reedijk, J. Anion Binding Involving π-Acidic Heteroaromatic Rings. Acc. Chem. Res. 2007, 40, 435–444. [Google Scholar] [CrossRef]
- Frontera, A.; Gamez, P.; Mascal, M.; Mooibroek, T.J.; Reedijk, J. Putting Anion–π Interactions into Perspective. Angew. Chem. Int. Ed. 2011, 50, 9564–9583. [Google Scholar] [CrossRef]
- Garau, C.; Frontera, A.; Quiñonero, D.; Ballester, P.; Costa, A.; Deyà, P.M. Anion-π Interactions. Recent Res. Dev. Chem. Phys. 2004, 5, 227–255. [Google Scholar] [CrossRef]
- Chifotides, H.T.; Dunbar, K.R. Anion–π Interactions in Supramolecular Architectures. Acc. Chem. Res. 2013, 46, 894–906. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.-X.; Wang, M.-X. Exploring Anion–π Interactions and Their Applications in Supramolecular Chemistry. Acc. Chem. Res. 2020, 53, 1364–1380. [Google Scholar] [CrossRef] [PubMed]
- Rather, I.A.; Wagay, S.A.; Ali, R. Emergence of anion-π interactions: The land of opportunity in supramolecular chemistry and beyond. Coord. Chem. Rev. 2020, 415, 213327. [Google Scholar] [CrossRef]
- Zhuang, S.-Y.; Cheng, Y.; Zhang, Q.; Tong, S.; Wang, M.-X. Synthesis of i-Corona[6]arenes for Selective Anion Binding: Interdependent and Synergistic Anion–π and Hydrogen-Bond Interactions. Angew. Chem. Int. Ed. 2020, 59, 23716–23723. [Google Scholar] [CrossRef]
- Gong, H.; Zhang, C.; Ogaki, T.; Inuzuka, H.; Hashizume, D.; Miyajima, D. Azacalix[3]triazines: A Substructure of Triazine-Based Graphitic Carbon Nitride Featuring Anion-π Interactions. Angew. Chem. Int. Ed. 2021, 60, 16377–16381. [Google Scholar] [CrossRef]
- Maynard, J.R.J.; Galmés, B.; Stergiou, A.D.; Symes, M.D.; Frontera, A.; Goldup, S.M. Anion–π Catalysis Enabled by the Mechanical Bond. Angew. Chem. Int. Ed. 2022, 61, e202115961. [Google Scholar] [CrossRef]
- Clements, A.; Lewis, M. Arene−Cation Interactions of Positive Quadrupole Moment Aromatics and Arene−Anion Interactions of Negative Quadrupole Moment Aromatics. J. Phys. Chem. A 2006, 110, 12705–12710. [Google Scholar] [CrossRef]
- Geronimo, I.; Singh, N.J.; Kim, K.S. Can Electron-Rich π Systems Bind Anions? J. Chem. Theory Comput. 2011, 7, 825–829. [Google Scholar] [CrossRef]
- Elgengehi, S.M.; El-Taher, S.; Ibrahim, M.A.A.; El-Kelany, K.E. Unexpected favourable noncovalent interaction between chlorine oxyanions (ClOx−; x = 1–4) and benzene: Benchmarking DFT and SAPT methods with respect to CCSD(T). Comput. Theor. Chem. 2021, 1199, 113214. [Google Scholar] [CrossRef]
- Xu, Z.; Singh, N.J.; Kim, S.K.; Spring, D.R.; Kim, K.S.; Yoon, J. Induction-Driven Stabilization of the Anion–π Interaction in Electron-Rich Aromatics as the Key to Fluoride Inclusion in Imidazolium-Cage Receptors. Chem. Eur. J. 2011, 17, 1163–1170. [Google Scholar] [CrossRef]
- Estarellas, C.; Frontera, A.; Quiñonero, D.; Deyà, P.M. Relevant Anion–π Interactions in Biological Systems: The Case of Urate Oxidase. Angew. Chem. Int. Ed. 2011, 50, 415–418. [Google Scholar] [CrossRef]
- Robertazzi, A.; Krull, F.; Knapp, E.-W.; Gamez, P. Recent advances in Anion–π interactions. CrystEngComm 2011, 13, 3293–3300. [Google Scholar] [CrossRef] [Green Version]
- Estarellas, C.; Frontera, A.; Quiñonero, D.; Deyà, P.M. Anion–π Interactions in Flavoproteins. Chem. Asian J. 2011, 6, 2316–2318. [Google Scholar] [CrossRef]
- Philip, V.; Harris, J.; Adams, R.; Nguyen, D.; Baudry, J.; Howell, E.E.; Hinde, R.J. A Survey of Aspartate−Phenylalanine and Glutamate−Phenylalanine Interactions in the Protein Data Bank: Searching for Anion–π Pairs. Biochemistry 2011, 50, 2939–2950. [Google Scholar] [CrossRef]
- Chakravarty, S.; Sheng, Z.-Z.; Iverson, B.; Moore, B. “η6”-Type Anion–π in biomolecular recognition. FEBS Lett. 2012, 586, 4180–4185. [Google Scholar] [CrossRef] [Green Version]
- Breberina, L.M.; Milčić, M.K.; Nikolić, M.R.; Stojanović, S.Đ. Contribution of Anion–π interactions to the stability of Sm/LSm proteins. JBIC J. Biol. Inorg. Chem. 2014, 20, 475–485. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Quiñonero, D.; Deyà, P.M.; Frontera, A. On the Importance of Anion–π Interactions in the Mechanism of Sulfide: Quinone Oxidoreductase. Chem. Asian J. 2013, 8, 2708–2713. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Quiñonero, D.; Deyà, P.M.; Frontera, A. Long-Range Effects in Anion–π Interactions: Their Crucial Role in the Inhibition Mechanism of Mycobacterium Tuberculosis Malate Synthase. Chem. Eur. J. 2014, 20, 6985–6990. [Google Scholar] [CrossRef]
- Jenkins, D.D.; Harris, J.B.; Howell, E.E.; Hinde, R.; Baudry, J. STAAR: Statistical analysis of aromatic rings. J. Comput. Chem. 2013, 34, 518–522. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.S.; Lawrence, E.E.K.; Billings, W.M.; Larsen, K.S.; Bécar, N.A.; Price, J.L. An Anion–π Interaction Strongly Stabilizes the β-Sheet Protein WW. ACS Chem. Biol. 2017, 12, 2535–2537. [Google Scholar] [CrossRef]
- Nishio, M. CH/π hydrogen bonds in crystals. CrystEngCommun 2004, 6, 130–158. [Google Scholar] [CrossRef]
- Takahashi, O.; Kohno, Y.; Nishio, M. Relevance of Weak Hydrogen Bonds in the Conformation of Organic Compounds and Bioconjugates: Evidence from Recent Experimental Data and High-Level ab Initio MO Calculations. Chem. Rev. 2010, 110, 6049–6076. [Google Scholar] [CrossRef]
- Salonen, L.M.; Ellermann, M.; Diederich, F. Aromatic Rings in Chemical and Biological Recognition: Energetics and Structures. Angew. Chem. Int. Ed. 2011, 50, 4808–4842. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Fujii, A. Nature and physical origin of CH/π interaction: Significant difference from conventional hydrogen bonds. Phys. Chem. Chem. Phys. 2008, 10, 2584–2594. [Google Scholar] [CrossRef]
- Nishio, M.; Umezawa, Y.; Honda, K.; Tsuboyama, S.; Suezawa, H. CH/π hydrogen bonds in organic and organometallic chemistry. CrystEngComm 2009, 11, 1757–1788. [Google Scholar] [CrossRef]
- Nishio, M.; Hirota, M. CH/π interaction: Implications in organic chemistry. Tetrahedron 1989, 45, 7201–7245. [Google Scholar] [CrossRef]
- Nishio, M.; Umezawa, Y. The CH/Hydrogen Bond: An Important Molecular Force in Controlling the Crystal Conformation of Organic Compounds and Three-Dimensional Structure of Biopolymers. Top Stereochem. 2006, 25, 255–307. [Google Scholar]
- Nishio, M.; Hirota, M.; Umezawa, Y. The CH/π Interaction: Evidence, Nature, and Consequences; Wiley-VCH: New York, NY, USA, 1998. [Google Scholar]
- Nishio, M. CH/π hydrogen bonds in organic reactions. Tetrahedron 2005, 61, 6923–6950. [Google Scholar] [CrossRef]
- Klein, E.; Ferrand, Y.; Barwell, N.P.; Davis, A.P. Solvent Effects in Carbohydrate Binding by Synthetic Receptors: Implications for the Role of Water in Natural Carbohydrate Recognition. Angew. Chem. Int. Ed. 2008, 47, 2693–2696. [Google Scholar] [CrossRef] [PubMed]
- Ferrand, Y.; Crump, M.P.; Davis, A.P. A Synthetic Lectin Analog for Biomimetic Disaccharide Recognition. Science 2007, 318, 619–622. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trembleau, L.; Rebek, J., Jr. Helical Conformation of Alkanes in a Hydrophobic Cavitand. Science 2003, 301, 1219–1220. [Google Scholar] [CrossRef]
- Hooley, R.J.; Van Anda, H.J.; Rebek, J., Jr. Extraction of Hydrophobic Species into a Water-Soluble Synthetic Receptor. J. Am. Chem. Soc. 2007, 129, 13464–13473. [Google Scholar] [CrossRef]
- Scarso, A.; Trembleau, L.; Rebek, J., Jr. Encapsulation Induces Helical Folding of Alkanes. Angew. Chem. Int. Ed. 2003, 42, 5499–5502. [Google Scholar] [CrossRef]
- Scarso, A.; Trembleau, L.; Rebek, J., Jr. Helical Folding of Alkanes in a Self-Assembled, Cylindrical Capsule. J. Am. Chem. Soc. 2004, 126, 13512–13518. [Google Scholar] [CrossRef]
- Carrillo, R.; López-Rodríguez, M.; Martín, V.S.; Martín, T. Quantification of a CH–π Interaction Responsible for Chiral Discrimination and Evaluation of Its Contribution to Enantioselectivity. Angew. Chem. Int. Ed. 2009, 48, 7803–7808. [Google Scholar] [CrossRef]
- Ballester, P.; Capó, M.; Costa, A.; Deyà, P.M.; Gomila, R.; Decken, A.; Deslongchamps, G. Dual Binding Mode of Methylmethanetriacetic Acid to Tripodal Amidopyridine Receptors. J. Org. Chem. 2002, 67, 8832–8841. [Google Scholar] [CrossRef] [PubMed]
- Frontera, A.; Garau, C.; Quiñonero, D.; Ballester, P.; Costa, A.; Deyà, P.M. Weak C−H/π Interaction Participates in the Diastereoselectivity of a Host−Guest Complex in the Presence of Six Strong Hydrogen Bonds. Org. Lett. 2003, 5, 1135–1138. [Google Scholar] [CrossRef] [PubMed]
- Shibasaki, K.; Fujii, A.; Mikami, N.; Tsuzuki, S. Magnitude and Nature of Interactions in Benzene−X (X = Ethylene and Acetylene) in the Gas Phase: Significantly Different CH/π Interaction of Acetylene as Compared with Those of Ethylene and Methane. J. Phys. Chem. A 2007, 111, 753–758. [Google Scholar] [CrossRef]
- Ringer, A.L.; Figgs, M.S.; Sinnokrot, M.O.; Sherrill, C.D. Aliphatic C−H/π Interactions: Methane−Benzene, Methane−Phenol, and Methane−Indole Complexes. J. Phys. Chem. A 2006, 110, 10822–10828. [Google Scholar] [CrossRef] [PubMed]
- Stone, A.J. Computation of charge-transfer energies by perturbation theory. Chem. Phys. Lett. 1993, 211, 101–109. [Google Scholar] [CrossRef]
- Nishio, M.; Umezawa, Y.; Fantini, J.; Weiss, M.S.; Chakrabarti, P. CH–π hydrogen bonds in biological macromolecules. Phys. Chem. Chem. Phys. 2014, 16, 12648–12683. [Google Scholar] [CrossRef] [PubMed]
- Umezawa, Y.; Nishio, M. CH/π Interactions as demonstrated in the crystal structure of guanine-nucleotide binding proteins, Src homology-2 domains and human growth hormone in complex with their specific ligands. Bioorg. Med. Chem. 1998, 6, 493–504. [Google Scholar] [CrossRef]
- Tatko, C.D.; Waters, M.L. Comparison of C−H···π and Hydrophobic Interactions in a β-Hairpin Peptide: Impact on Stability and Specificity. J. Am. Chem. Soc. 2004, 126, 2028–2034. [Google Scholar] [CrossRef]
- Umezawa, Y.; Nishio, M. CH/π interactions in the crystal structure of class I MHC antigens and their complexes with peptides. Bioorg. Med. Chem. 1998, 6, 2507–2515. [Google Scholar] [CrossRef]
- Umezawa, Y.; Nishio, M. CH/π interactions in the crystal structure of TATA,box binding protein/DNA complexes. Bioorg. Med. Chem. 2000, 8, 2643–2650. [Google Scholar] [CrossRef]
- Spiwok, V. CH/π Interactions in Carbohydrate Recognition. Molecules 2017, 22, 1038. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lucas, X.; Bauzá, A.; Frontera, A.; Quiñonero, D. A thorough Anion–π interaction study in biomolecules: On the importance of cooperativity effects. Chem. Sci. 2016, 7, 1038–1050. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Quiñonero, D.; Frontera, A.; Garau, C.; Ballester, P.; Costa, A.; Deyà, P.M. Interplay between cation–π, Anion–π and π–π interactions. Chem. Phys. Chem. 2006, 7, 2487–2491. [Google Scholar] [CrossRef] [PubMed]
- Frontera, A.; Quiñonero, D.; Costa, A.; Ballester, P.; Deyà, P.M. MP2 study of cooperative effects between cation-π, anion-π and π-π interactions. New J. Chem. 2007, 31, 556–560. [Google Scholar] [CrossRef]
- Lucas, X.; Estarellas, C.; Escudero, D.; Frontera, A.; Quiñonero, D.; Deyà, P.M. Very long-range effects: Cooperativity between Anion–π and hydrogen-bonding interactions. ChemPhysChem 2009, 10, 2256–2264. [Google Scholar] [CrossRef]
- Escudero, D.; Frontera, A.; Quiñonero, D.; Deyà, P.M. Interplay between Anion–π and hydrogen-bonding interactions. J. Comput. Chem. 2009, 30, 75–82. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Masoodi, H.R.; Khorassani, M.H.; Ghaleno, M.H. The influence of cation–π and Anion–π interactions on the strength and nature of N-H hydrogen bond. Comput. Theor. Chem. 2012, 988, 48–55. [Google Scholar] [CrossRef]
- Azizi, A.; Ebrahimi, A. The X−···benzohydrazide complexes: The interplay between anion-π and H-bond interactions. Struct. Chem. 2016, 28, 687–695. [Google Scholar] [CrossRef]
- Quiñonero, D.; Frontera, A.; Deyà, P.M. Interplay between ion–π and Ar/π Van der Waals interactions. Comput. Theor. Chem. 2012, 998, 51–56. [Google Scholar] [CrossRef]
- Estarellas, C.; Frontera, A.; Quiñonero, D.; Deyà, P.M. Theoretical study on cooperativity effects between Anion–π and halogen-bonding interactions. ChemPhysChem 2011, 12, 2742–2750. [Google Scholar] [CrossRef]
- Razmazma, H.; Ebrahimi, A. The effects of cation–π and Anion–π interactions on halogen bonds in the [N⋯X⋯N]+ complexes: A comprehensive theoretical study. J. Mol. Graph. Model. 2018, 84, 134–144. [Google Scholar] [CrossRef]
- Du, S.; Wang, B.; Zhang, J.; Zhang, C. Tuning anion-π interaction via halogen substituent effects in cyanuric acids and its derivatives. Int. J. Quantum Chem. 2015, 115, 1147–1152. [Google Scholar] [CrossRef]
- Esrafili, M.D.; Mousavian, P. The triel bond: A potential force for tuning Anion–π interactions. Mol. Phys. 2018, 116, 388–398. [Google Scholar] [CrossRef]
- Feyereisen, M.W.; Fitzgerald, G.; Komornicki, A. Use of approximate integrals in ab initio theory. An application in MP2 energy calculations. Chem. Phys. Lett. 1993, 208, 359–363. [Google Scholar] [CrossRef]
- Vahtras, O.; Almlof, J.; Feyereisen, M.W. Integral approximations for LCAO-SCF calculations. Chem. Phys. Lett. 1993, 213, 514–518. [Google Scholar] [CrossRef]
- Grimme, S. Improved second-order Møller–Plesset perturbation theory by separate scaling of parallel- and antiparallel-spin pair correlation energies. J. Chem. Phys. 2003, 118, 9095–9102. [Google Scholar] [CrossRef]
- Grimme, S.; Goerigk, L.; Fink, R.F. Spin-component-scaled electron correlation methods. WIREs Comput. Mol. Sci. 2012, 2, 886–906. [Google Scholar] [CrossRef]
- Gerenkamp, M.; Grimme, S. Spin-component scaled second-order Møller–Plesset perturbation theory for the calculation of molecular geometries and harmonic vibrational frequencies. Chem. Phys. Lett. 2004, 392, 229–235. [Google Scholar] [CrossRef]
- Quiñonero, D.; Frontera, A. Hydrogen Bond versus Halogen Bond in HXOn (X = F, Cl, Br, and I) Complexes with Lewis Bases. Inorganics 2019, 7, 9. [Google Scholar] [CrossRef] [Green Version]
- Halkier, A.; Helgaker, T.; Jørgensen, P.; Klopper, W.; Olsen, J. Basis-set convergence of the energy in molecular Hartree–Fock calculations. Chem. Phys. Lett. 1999, 302, 437–446. [Google Scholar] [CrossRef]
- Halkier, A.; Klopper, W.; Helgaker, T.; Jørgensen, P.; Taylor, P.R. Basis set convergence of the interaction energy of hydrogen-bonded complexes. J. Chem. Phys. 1999, 111, 9157–9167. [Google Scholar] [CrossRef]
- TURBOMOLE V7.0 2015, a Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, Since 2007. Available online: http://www.turbomole.com (accessed on 10 May 2022).
- Werner, H.-J.; Knowles, P.J.; Manby, F.R.; Schütz, M.; Celani, P.; Knizia, G.; Korona, T.; Lindh, R.; Mitrushenkov, A.; Rauhut, G.; et al. MOLPRO, Version 2010.1. A Package of ab Initio Programs. Stuttgart, Germany.
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Popelier, P.L.A. Atoms in Molecules: An Introduction; Prentice Hall: Harlow, UK, 2000. [Google Scholar]
- Keith, T.A. TK Gristmill Software, version 19.10.12 edn. Overland Park, KS, USA; 2019. Available online: aim.tkgristmill.com (accessed on 26 April 2022).
- Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
- Quiñonero, D. Anion Recognition by Pyrylium Cations and Thio-, Seleno- and Telluro- Analogues: A Combined Theoretical and Cambridge Structural Database Study. Molecules 2015, 20, 11632–11659. [Google Scholar] [CrossRef] [Green Version]
- Misquitta, A.J.; Podeszwa, R.; Jeziorski, B.; Szalewicz, K. Intermolecular potentials based on symmetry-adapted perturbation theory with dispersion energies from time-dependent density-functional calculations. J. Chem. Phys. 2005, 123, 214103–214114. [Google Scholar] [CrossRef]
- Hesselmann, A.; Jansen, G. The helium dimer potential from a combined density functional theory and symmetry-adapted perturbation theory approach using an exact exchange–correlation potential. Phys. Chem. Chem. Phys. 2003, 5, 5010–5014. [Google Scholar] [CrossRef]
- Moszynski, R. Symmetry-adapted perturbation theory for the calculation of Hartree-Fock interaction energies. Mol. Phys. 1996, 88, 741–758. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Weigend, F. A fully direct RI-HF algorithm: Implementation, optimised auxiliary basis sets, demonstration of accuracy and efficiency. Phys. Chem. Chem. Phys. 2002, 4, 4285–4291. [Google Scholar] [CrossRef]
- Weigend, F.; Köhn, A.; Hättig, C. Efficient use of the correlation consistent basis sets in resolution of the identity MP2 calculations. J. Chem. Phys. 2002, 116, 3175–3183. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing noncovalent interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [Green Version]
- Tsuzuki, S.; Honda, K.; Uchimaru, T.; Mikami, M.; Fujii, A. Magnitude and Directionality of the Interaction Energy of the Aliphatic CH/π Interaction: Significant Difference from Hydrogen Bond. J. Phys. Chem. A 2006, 110, 10163–10168. [Google Scholar] [CrossRef]
- Bauzá, A.; Frontera, A.; Mooibroek, T. NO3− anions can act as Lewis acid in the solid state. Nat. Commun. 2017, 8, 14522. [Google Scholar] [CrossRef] [Green Version]
- Vajdos, F.F.; Yoo, S.; Houseweart, M.; Sundquist, W.I.; Hill, C.P. Crystal structure of cyclophilin A complexed with a binding site peptide from the HIV-1 capsid protein. Protein Sci. 1997, 6, 2297–2307. [Google Scholar] [CrossRef] [Green Version]
- Ramoni, R.; Spinelli, S.; Grolli, S.; Conti, V.; Merli, E.; Cambillau, C.; Tegoni, M. Deswapping bovine odorant binding protein. Biochim. Biophys. Acta 2008, 1784, 651–657. [Google Scholar] [CrossRef]
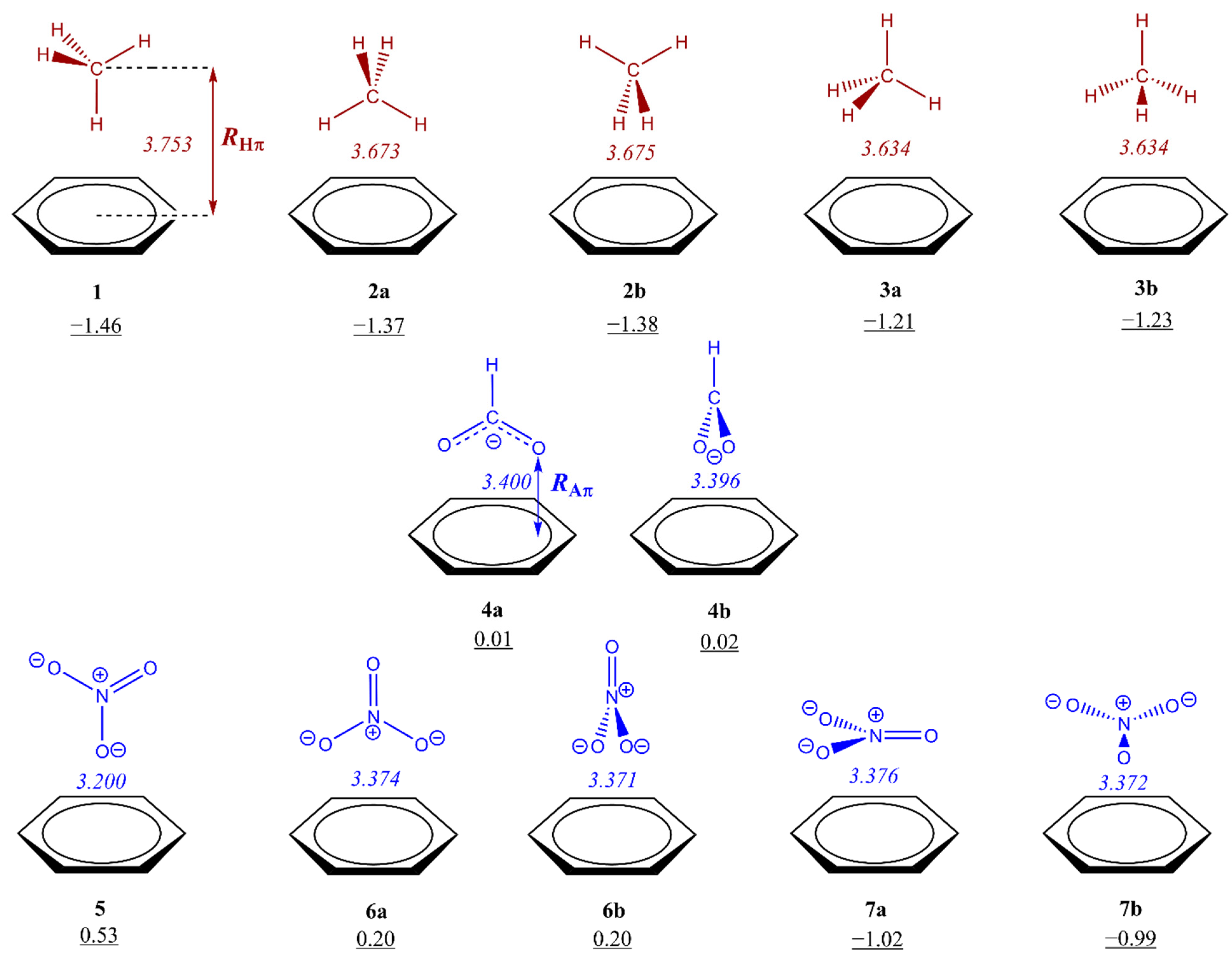
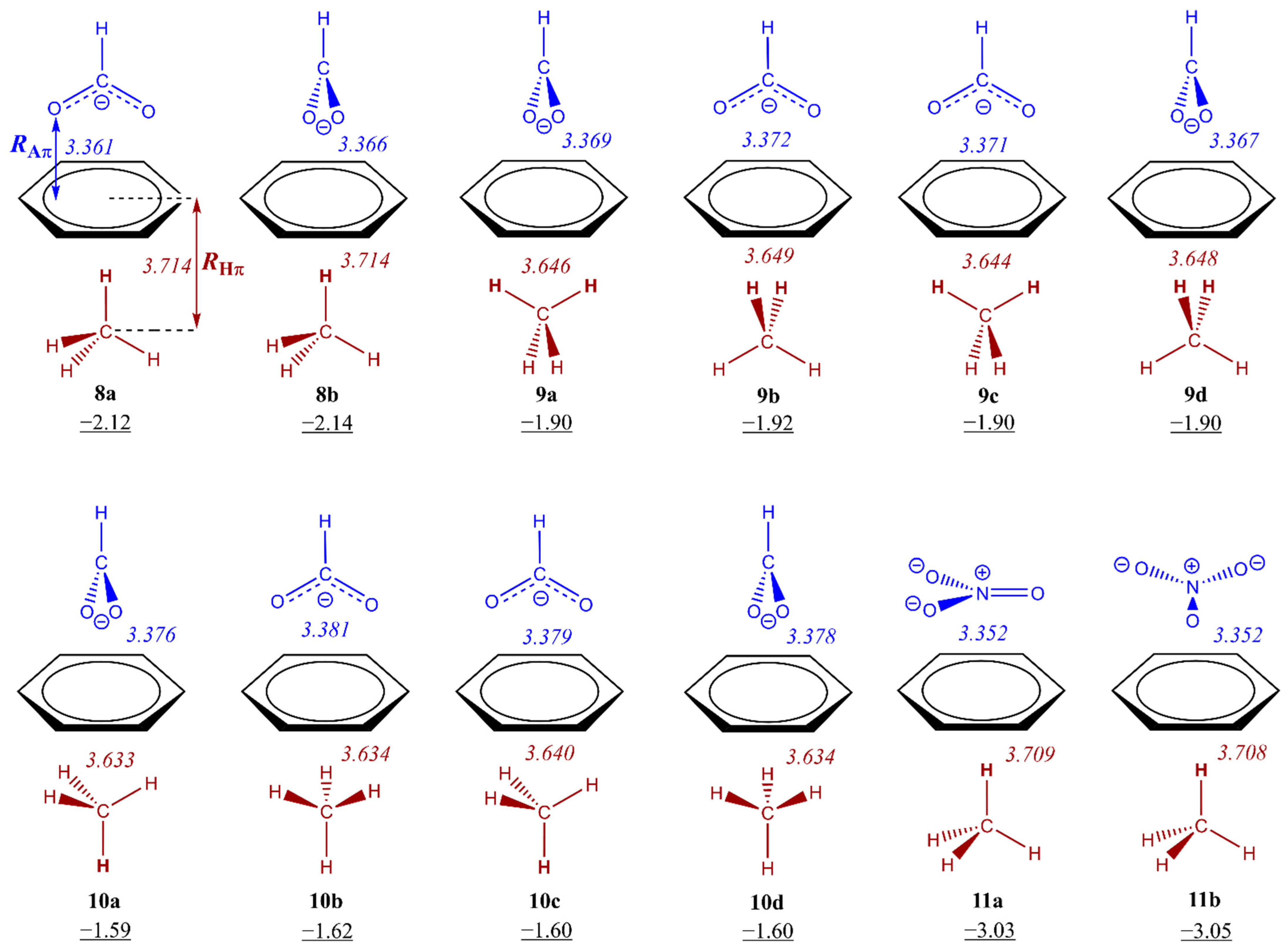


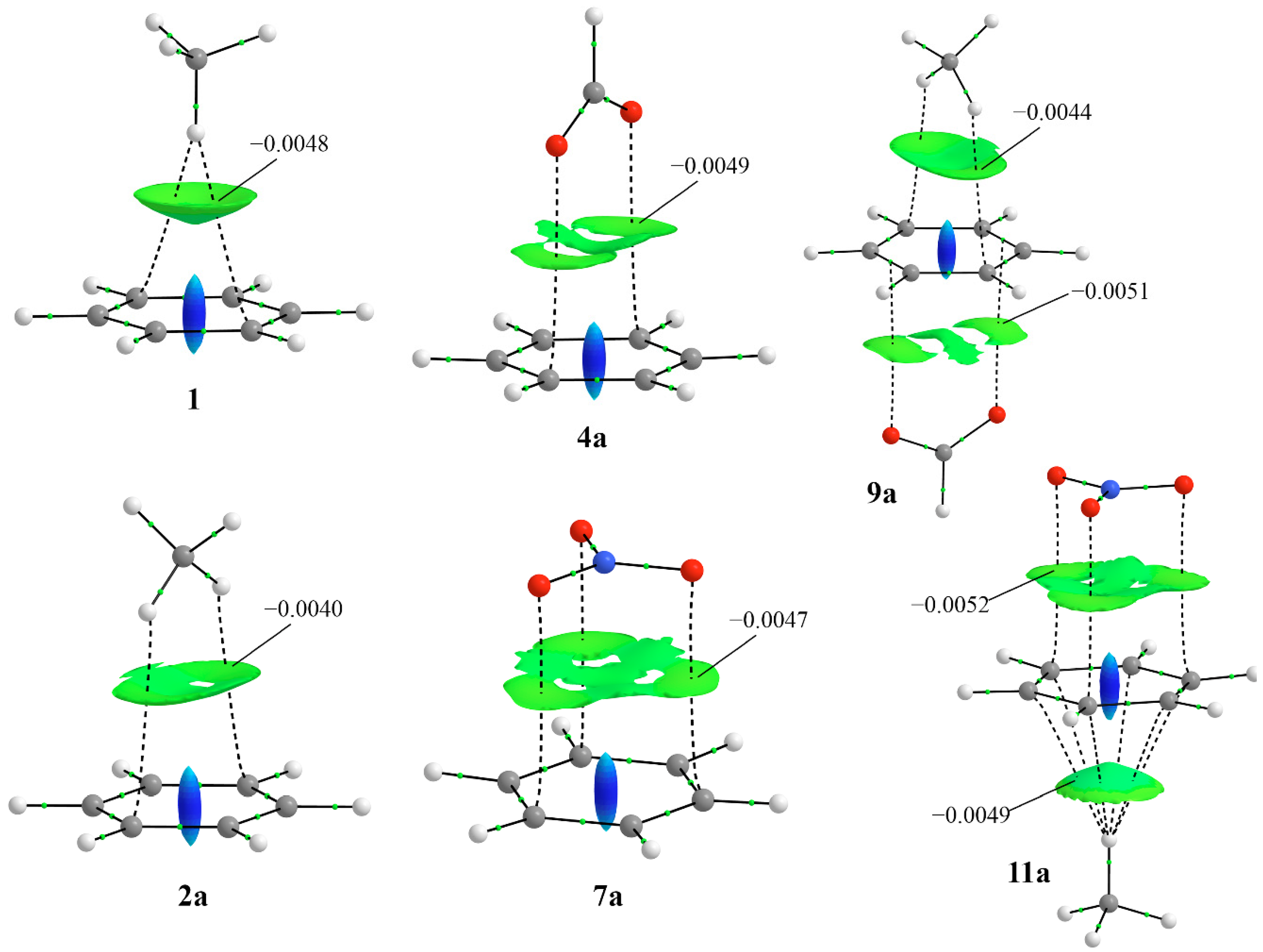
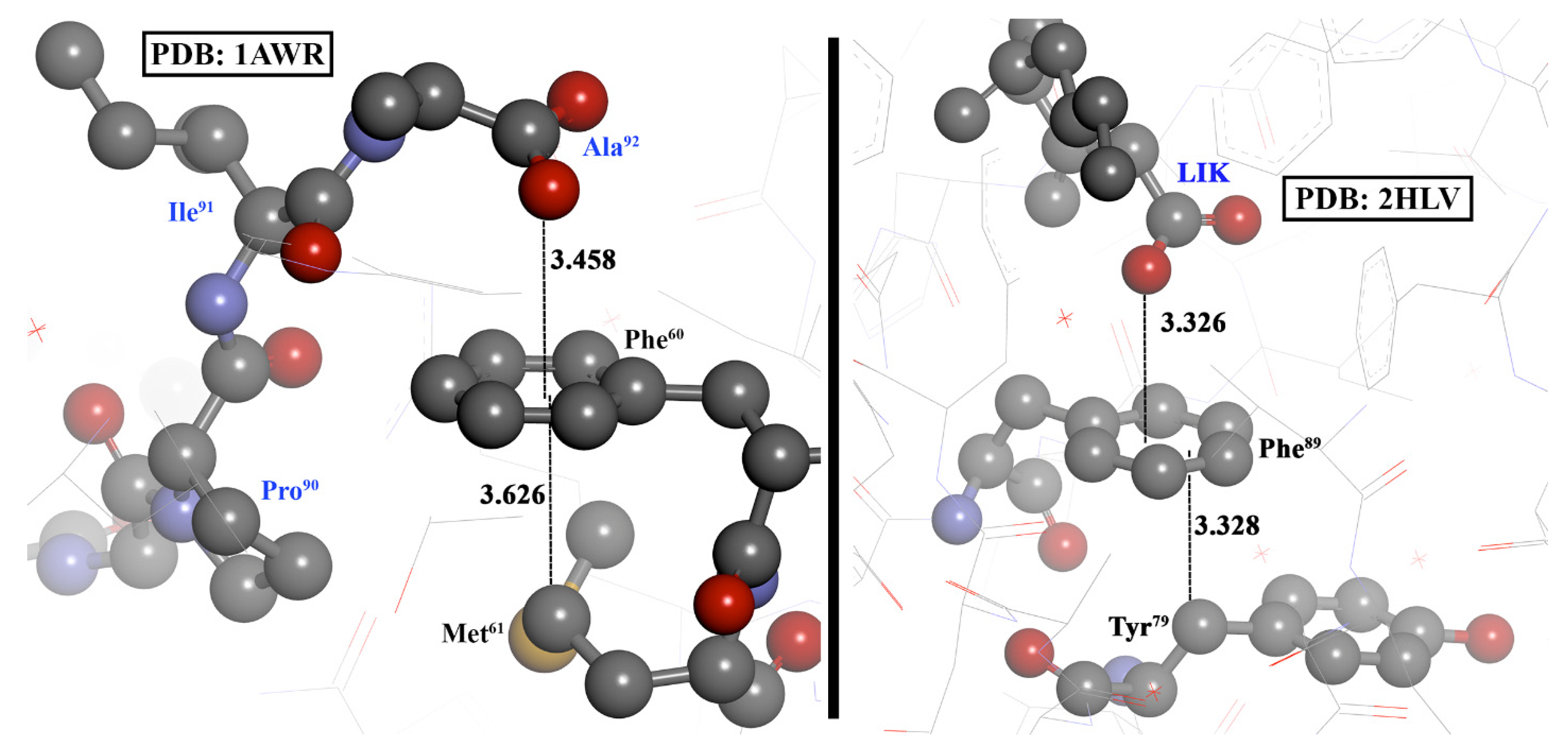
| Compound | RHπ [a] | RAπ [a] | ΔRHπ [b] | ΔRAπ [b] | E |
|---|---|---|---|---|---|
| 1 | 3.753 | - | - | - | −1.46 |
| 2a | 3.673 | - | - | - | −1.37 |
| 2b | 3.675 | - | - | - | −1.38 |
| 3a | 3.634 | - | - | - | −1.21 |
| 3b | 3.634 | - | - | - | −1.23 |
| 4a | 3.931 | 3.400 | - | - | 0.01 |
| 4b | 3.927 | 3.396 | - | - | 0.02 |
| 5 | - | 3.200 | - | - | 0.53 |
| 6a | - | 3.374 | - | - | 0.20 |
| 6b | - | 3.371 | - | - | 0.20 |
| 7a | - | 3.376 | - | - | −1.02 |
| 7b | - | 3.372 | - | - | −0.99 |
| 8a | 3.714 | 3.361 | −0.039 | −0.035 | −2.12 |
| 8b | 3.714 | 3.366 | −0.039 | −0.034 | −2.14 |
| 9a | 3.646 | 3.369 | −0.027 | −0.027 | −1.90 |
| 9b | 3.649 | 3.372 | −0.026 | −0.028 | −1.92 |
| 9c | 3.644 | 3.371 | −0.029 | −0.029 | −1.90 |
| 9d | 3.648 | 3.367 | −0.027 | −0.029 | −1.90 |
| 10a | 3.633 | 3.376 | −0.001 | −0.020 | −1.59 |
| 10b | 3.634 | 3.381 | 0.000 | −0.019 | −1.62 |
| 10c | 3.640 | 3.379 | 0.006 | −0.021 | −1.60 |
| 10d | 3.634 | 3.378 | 0.000 | −0.018 | −1.60 |
| 11a | 3.709 | 3.350 | −0.046 | −0.022 | −3.03 |
| 11b | 3.708 | 3.352 | −0.045 | −0.024 | −3.05 |
| Compound | Ecoop | %Ecoop | EAπ2 | EHπ2 | ΔEAπ | ΔEHπ |
|---|---|---|---|---|---|---|
| 8a | −0.51 | 23.9 | −0.66 | −2.14 | −0.68 | −0.68 |
| 8b | −0.51 | 23.8 | −0.67 | −2.14 | −0.68 | −0.68 |
| 9a | −0.48 | 25.3 | −0.53 | −1.91 | −0.55 | −0.55 |
| 9b | −0.48 | 25.2 | −0.54 | −1.93 | −0.55 | −0.55 |
| 9c | −0.46 | 24.1 | −0.53 | −1.91 | −0.54 | −0.54 |
| 9d | −0.46 | 24.1 | −0.52 | −1.92 | −0.54 | −0.54 |
| 10a | −0.37 | 23.4 | −0.36 | −1.61 | −0.38 | −0.40 |
| 10b | −0.37 | 23.0 | −0.39 | −1.62 | −0.40 | −0.40 |
| 10c | −0.37 | 23.2 | −0.39 | −1.60 | −0.39 | −0.39 |
| 10d | −0.37 | 23.2 | −0.38 | −1.62 | −0.40 | −0.40 |
| 11a | −0.54 | 17.9 | −1.56 | −2.03 | −0.57 | −0.57 |
| 11b | −0.54 | 17.6 | −1.58 | −2.03 | −0.56 | −0.56 |
| Compound | Eel | Eind | Edisp | Eexch | δHF | ESAPT | E | |
|---|---|---|---|---|---|---|---|---|
| 1 | −0.89 | −0.10 | −2.46 | 2.31 | −0.17 | −1.30 | −1.46 | |
| 2a | −0.68 | −0.07 | −2.45 | 2.15 | −0.15 | −1.20 | −1.37 | |
| 4b | 3.75 | −4.59 | −3.85 | 4.84 | 0.01 | 0.16 | 0.02 | |
| 9a | Hπ2 Aπ2 | −0.99 3.35 | −0.55 −4.94 | −2.77 −4.03 | 2.75 5.21 | −0.24 0.00 | −1.81 −0.40 | −1.91 −0.53 |
| 7b | 2.65 | −3.22 | −4.99 | 4.89 | −0.18 | −0.85 | −0.99 | |
| 11b | Hπ2 Aπ2 | −1.17 2.19 | −0.50 −3.20 | −2.81 −5.21 | 2.82 5.26 | −0.27 −0.21 | −1.93 −1.17 | −2.03 −1.56 |
| Compound | ρBCP × 103 | ∇2ρBCP × 102 | ρCCP × 103 | ∇2ρCCP × 102 |
|---|---|---|---|---|
| 1 | 4.64 | 1.65 | 4.14 | 1.78 |
| 2a | 3.93 | 1.24 | 2.44 | 1.07 |
| 2b | 3.88 | 1.24 | 2.43 | 1.06 |
| 3a | 2.98 | 0.97 | 2.02 | 0.89 |
| 3b | 2.94 | 0.97 | 2.01 | 0.89 |
| 4a | 4.73 | 1.46 | 2.13 | 0.86 |
| 4b | 4.69 | 1.47 | 2.14 | 0.86 |
| 5 | 3.45 | 1.35 | 2.82 | 1.40 |
| 6a | 4.61 | 1.52 | 2.11 | 0.92 |
| 6b | 4.58 | 1.52 | 2.12 | 0.92 |
| 7a | 4.61 | 1.50 | 2.27 | 1.14 |
| 7b | 4.56 | 1.50 | 2.28 | 1.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quiñonero, D.; Frontera, A. Benzene, an Unexpected Binding Unit in Anion–π Recognition: The Critical Role of CH/π Interactions. Sci 2022, 4, 32. https://doi.org/10.3390/sci4030032
Quiñonero D, Frontera A. Benzene, an Unexpected Binding Unit in Anion–π Recognition: The Critical Role of CH/π Interactions. Sci. 2022; 4(3):32. https://doi.org/10.3390/sci4030032
Chicago/Turabian StyleQuiñonero, David, and Antonio Frontera. 2022. "Benzene, an Unexpected Binding Unit in Anion–π Recognition: The Critical Role of CH/π Interactions" Sci 4, no. 3: 32. https://doi.org/10.3390/sci4030032
APA StyleQuiñonero, D., & Frontera, A. (2022). Benzene, an Unexpected Binding Unit in Anion–π Recognition: The Critical Role of CH/π Interactions. Sci, 4(3), 32. https://doi.org/10.3390/sci4030032







