Abstract
Aromaticity, a very important term in organic chemistry, has never been defined unambiguously. Various ways to describe it come from different phenomena that have been experimentally observed. The most important examples related to some theoretical concepts are presented here.
1. Introduction
Aromaticity belongs to typical terms in chemistry called by Coulson as the “primitive patterns of understanding” [1] enabling communication among researchers in chemistry and related fields as well as allowing the understanding of a large amount of chemical and physicochemical properties of chemical compounds. There are many such terms, but let us take electronegativity as an example, for which seven different physical definitions (with different units!) were already presented in 1961 [2]. However, despite this, most chemists know very well when somebody says that due to the electronegativity of an atom or substituent, some kind of change in a particular property can be expected. Aromaticity is a similar term for which there are several definitions and a great number of quantitative descriptors, sometimes called aromaticity indices. Moreover, aromaticity is one of the oldest and most important concepts in chemistry. It has long been a cornerstone of organic chemistry and now extends to inorganic and organometallic chemistry and related fields. It is also well known that aromaticity is associated with a wide range of molecular properties, such as thermodynamic stability, specific chemical reactivity, changes in molecular geometry, and magnetic susceptibility. This range of manifestations makes aromaticity difficult to define or quantify.
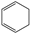
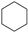
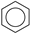
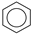
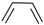
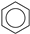
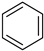
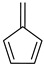
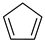
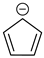
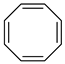
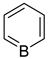
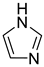
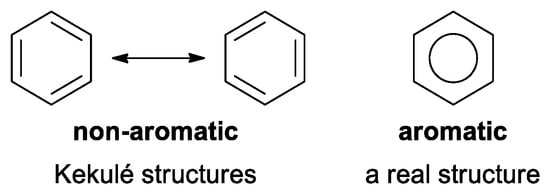
Historically, the first attempt to designate the problem of aromaticity has come from the pleasant smell of some chemical species, mostly derivatives of the benzenoid hydrocarbons. Additionally, a high degree of unsaturation and, despite this, the low reactivity of these compounds have been observed. Thus, the structure of the model aromatic compound, benzene, was a subject of extensive debate among chemists. In 1865, Kekulé proposed a cyclic planar structure of benzene with three alternating double bonds (1,3,5-cyclohexatriene) [3]. Later, an ‘oscillation’ between two possible 1,3,5-cyclohexatrienic structures and C6h symmetry was proposed. Finally, in 1929, Lonsdale proved planarity of the benzene ring by determining the structure of hexamethylbenzene using X-ray diffraction [4]. Soon after, in 1931, Erich Hückel explained the unusual stability of benzene using the molecular orbital theory calculations and proposed the famous 4n + 2 rule (n = 1, 2, etc.) [5]. Therefore, it can be said that this rule was the first strict definition of aromatic compounds. Examples of monocyclic aromatic compounds with 6 π-electrons (n = 1) are shown in Scheme 1. It should be emphasized that they are all planar.
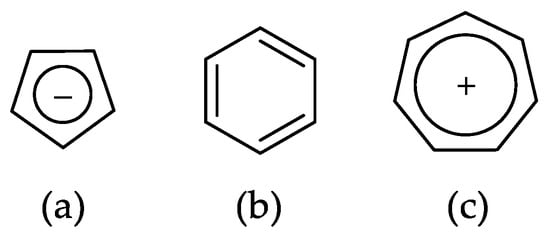
Scheme 1.
Six π-electron monocyclic hydrocarbons: cyclopentadienyl anion (a), benzene (b), and cycloheptatrienyl cation (c).
Moreover, from the beginning (two papers, in 1865 and 1866) [3,6], the term “aromatic/aromaticity” appeared in two different circumstances: as referring to molecules with a special structure (the ring) and as molecules characterized by some special properties. This type of duality has been present up to now and may sometimes lead to misunderstandings, but it is still the subject of many fruitful inspirations. In addition, the term “aromaticity” is used in organic chemistry in many cases far away from its classical understanding, for example, with various prefixes, such as homo-aromaticity [7], metal-aromaticity [8], quasi-aromaticity [9], Möbius aromaticity [10], spherical aromaticity [11], and many others [12]. Nowadays, the concept of aromaticity, originally formulated for planar hydrocarbons, has been expanded and is used to describe some properties of macrocycles (e.g., porphyrins), metal clusters, non-planar molecules (Möbius aromaticity), molecules in an excited state (Baird’s rule), and molecular cages, such as fullerenes, where the term 3-D aromaticity is used.
Despite its widespread use, the concept of aromaticity has not yet been unambiguously defined. This work deals with the classical understanding of aromaticity. Krygowski et al. [13] proposed the following (slightly modified) definition:
“Aromatic compounds are planar cyclic delocalized π-electron systems and are typified by the following ground-state properties:
- they are more stable than their olefinic analogs by energy named ‘resonance energy’,
- they have bond lengths intermediate between those for typical single and double bonds,
- a π-electron ring current induced in aromatic molecules by an external magnetic field leads to increased diamagnetic susceptibility and typical diatropic (low field) chemical shifts of exocyclic protons in 1H NMR spectra,
- aromatic compounds generally undergo substitution reactions more easily than addition.”
To make the definition clearer, let us attach the IUPAC definition of electron delocalization: [14]
“Delocalization is a redistribution of the valence-shell electron density throughout a molecular entity as compared with some localized models (individual atoms in their valence states, separated bonds, or separated fragments). Different topological modes of the electron delocalization include:
- ribbon delocalization of either π- or σ-electrons (i.e., electrons occupying respectively π- and σ-orbitals);
- surface delocalization of σ-electrons occurring through an overlap of radially oriented σ-orbitals of a cyclic molecule as is the case of cyclopropane and
- volume delocalization of σ-electrons through an overlap of σ-orbitals directed inside a molecular polyhedron.”
The above definition of aromaticity combines the various phenomena observed in molecules. Accordingly, the methods for assessing aromaticity use various measurable properties of the molecules: energetic, geometric, magnetic, and electronic (Figure 1).
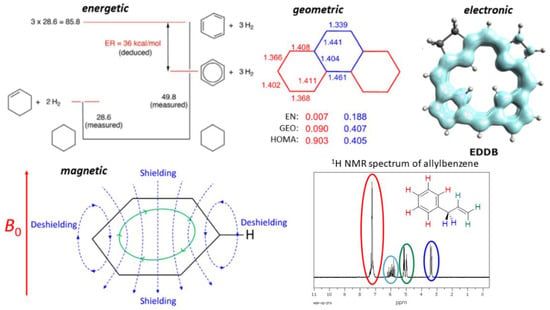
Figure 1.
Energetic, geometric, electronic, and magnetic properties of molecules used for the assessment of aromaticity. The energetic scheme used in the evaluation of benzene resonance energy reprinted from Ref. [15], Copyright (2021), with permission from Elsevier. The NMR spectrum is taken from Ref. [16].
It should be mentioned that no method for assessment of aromaticity combines all the phenomena used in its definition. As new measurement methods are introduced, more phenomena related to aromaticity are observed (see Figure 2 and Figure 3). However, in most cases, they are mainly used for the qualitative characterization of aromaticity, but they successfully and elegantly validate the possibilities of new theoretical concepts for the description of aromaticity. Additionally, for highly symmetric molecules, it has recently been shown that the experimental determination of the Raman frequency of the breather mode characterizes the aromaticity of molecules [17].
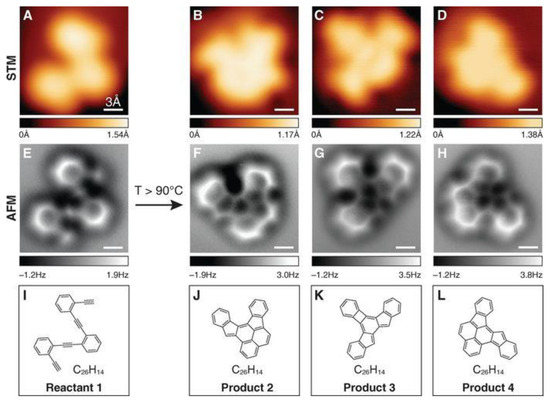
Figure 2.
Comparison of STM images, nc-AFM images, and structures for molecular reactant (1) and products (2, 3, 4). (A) STM image of 1 on Ag(100) before annealing. (B–D) STM images of individual products 2, 3, and 4 on Ag(100) after annealing at T > 90 °C. (E) The nc-AFM image of the same molecule (reactant 1) depicted in (A). (F–H) The nc-AFM images of the same molecules (products 2, 3, and 4) depicted in (B–D). (I–L) Schematic representation of the molecular structure of reactant 1 and products 2, 3, and 4. Reprinted from Ref. [18] with permission from AAAS.

Figure 3.
Hexabenzocoronene model (A) and constant height AFM measurements on Cu(111) at z = 3.7 Å (B) and 3.5 Å (C). In (C), a pseudo-3D representation is shown to highlight the local maxima. (D) Calculated electron density at a distance of 2.5 Å above the molecular plane. Note that i bonds are imaged as brighter (B) and shorter (C) compared with j bonds. Reprinted from Ref. [19] with permission from AAAS.
The STM (scanning tunneling microscopy) and AFM (atomic force microscopy) methods seem to be the most promising. They allow both the direct imagining of the covalent bond structure in a single-molecule chemical reaction (Figure 2) [18], in molecular engineering in 2D surface covalent organic frameworks [20], and the assessment of the bond order [19], thus providing insight into aromaticity. In the last case, the results of the measurements of hexabenzocoronene by noncontact atomic force microscopy (nc-AFM) are shown in Figure 3. The AFM image reveals the structure of internal bonds, and the increased electron density is manifested in the brightness of these bonds. In general, the bonds at the periphery of the planar molecule show increased brightness compared with bonds in the central region. This effect is mainly related to the delocalization of electrons in a π-conjugated system leading to increased electron density at the boundary. However, this is also due to a smaller van der Waals background and electrostatic forces. Therefore, to distinguish the bond orders, the bonds i and j in the central region of the molecule (Figure 3A) were considered. The mean values for the six corresponding bonds are 1.48(4) Å and 1.68(7) Å, respectively. Furthermore, the calculated image (part D in Figure 3) is qualitatively similar to the image obtained from the measurements.
2. Aromaticity Concepts Based on Experiments
2.1. Energy-Based Approaches
The first quantitative description of aromaticity was proposed in 1933 by Pauling and Sherman [21]. They introduced a thermodynamic concept, namely, the resonance energy (RE), that is, the energy that makes the π-delocalized compound more stable than its hypothetical olefin analog with electrons fully localized as alternating single and double bonds. In the case of benzene, RE can be estimated as the difference between the energy of benzene and the energy of 1,3,5-cyclohexatriene, that is, the Kekulé structure of benzene with localized single and double bonds (see Scheme 2 and Equation (1)).
where ΔHa0 (benzene)g denotes the heat of atomization of gaseous benzene and E is an energy of the particular bonds (double C=C, single C-C, and C-H) estimated from the heat of the atomization of ethene, ethane, and methane. Substituting data from thermochemical measurements into Equation (1) gives RE equal to 37 kcal/mol. A very similar value (36 kcal/mol) was determined experimentally by the calorimetric measurements of the heats of the hydrogenation of benzene and cyclohexene [22]. However, it should be remembered that RE includes not only the stabilization related to aromaticity but also to all π-conjugation. RE obtained from the heats of the hydrogenation of benzene and cyclohexane also includes some energetic contribution of steric strain present in the saturated cyclohexane ring.
Scheme 2.
Structures of benzene.
In more advanced approaches, RE has been replaced by more precisely defined reference systems and is called aromatic stabilization energy (ASE) (for details, see [23]). In ASE, reference systems are chosen to extract only the energy related to the aromatic character of a given molecule. To estimate ASE, isodesmic [24] or homodesmotic [25,26,27] reactions are used. Isodesmic reactions are defined as reactions, hypothetical or observed in nature, in which the substrates and products contain the same number of each bond type (CC, CH, CO, etc.). Homodesmotic reactions are a subclass of isodesmic reactions, in which additionally the number of each bond between atoms in a given hybridization state (Csp3 − Csp3, Csp3 − Csp2, Csp2 − Csp2, Csp2 = Csp2, etc.) and the number of each type of carbon atom (sp3, sp2, and sp) with zero, one, two, and three hydrogen atoms attached are preserved. For benzene, examples of isodesmic reactions are (1)–(3) in Table 1, while a homodesmotic reaction is illustrated by reactions (4)–(7). For each reaction in Table 1, several ASE values are given. They correspond to the different methods used in obtaining this energy, experimental or quantum-chemical calculations. It can be noticed that these values do not differ much. This is due to the important property of the isodesmic and homodesmotic reactions: that the errors, caused by the method used in obtaining energy, cancel out.

Table 1.
Examples of aromatic stabilization energies (ASE) for benzene obtained experimentally and calculated at B3LYP/6-311+G** (+ZPE) level [23].
Conceptually, ASE is well defined. However, a careful look at the data for benzene in Table 1 may lead to an unsettling conclusion: that the choice of the model reaction has a great influence on the ASE value. Strikingly, the obtained values range from 19 to 67 kcal/mol. This is because the transition from substrates to products in some reactions involves a significant change in conformation, hybridization, or ring stress. This contaminates the ASE value with a contribution of effects other than aromaticity. Therefore, it is important to carefully design the reaction. Rather, a homodesmotic reaction should be considered without substantial conformational differences between substrates and products (e.g., trans and cis-butadiene, reactions (4) and (5) in Table 1, respectively). The problem of the selection of reference systems is discussed in detail by Cyrański [23]. Nevertheless, if the group of considered systems is treated by the same ASE model, then the reliability of the treatment increases. It should also be mentioned that, when the RE or ASE concepts are applied to heterocyclic systems, special care should be taken as new complications arise in building proper reference systems.
It should be mentioned that many theoretical methods for obtaining ASE and RE exist, with the best known possibly being the Hückel molecular orbital theory (HMO) [35]. In combination with graph theory, HMO has also been used to define a topological resonance energy (TRE). A comprehensive article on this topic was published by Aihara [36].
2.2. Geometry-Based Approaches
The first method of determining molecular structure, X-ray diffraction, appeared in the 1920s. Since then, it is still the most important method used to study the geometry of aromatic compounds. A vast amount of structural data available inspired scientists to formulate quantitative descriptors of aromaticity based on the experimental bond lengths. Nowadays, the same descriptors are used for computationally obtained molecular geometries.
One of the easiest-to-observe properties of aromatic systems is their tendency to equalize the bond lengths (Figure 4). This can be clearly seen when comparing the bond lengths in exemplary non-aromatic and aromatic systems: butadiene, benzene, and cyclopentadiene, which is non-aromatic in the neutral form and aromatic in the anionic form, where it adopts D5h symmetry (Figure 4). Therefore, the bond lengths and their variance can be effectively used to assess the π-electron delocalization and, in the case of cyclic systems, their aromaticity.
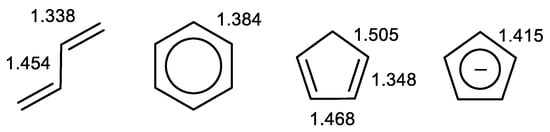
Figure 4.
Bond lengths (in Å) in butadiene (experimental data) [37], benzene (D6h symmetry, experimental data) [37], cyclopentadiene (B3LYP/6-311++G (d,p) results), and cyclopentadienyl anion (D5h, B3LYP/6-311++G (d,p) results).
The lengths of CC bonds in aromatic molecules are between the values typical for single and double bonds, as can be seen even in Figure 4. It should be noted that this was observed very early [38]. Julg and François [39] were the first to use this observation to assess aromaticity. They defined the aromaticity index Aj as a normalized function of the CC bond lengths’ variance for a given molecule, Equation (2).
where n is the number of peripheral bonds of length Ri, while Rav is the mean value of all bond lengths (in the original paper the bond length was denoted by d). The constant 225, resulting from the normalization condition, was chosen so that Equation (2) returns Aj = 0 for the Kekulé structure of benzene with bond lengths as in trans-1,3-butadiene (a model non-aromatic system).
The Julg index was a significant step forward; but, limiting it only to hydrocarbon systems was a big disadvantage. Additionally, it returns Aj = 1 for any system with all bonds of the same length, for example, cyclohexane.
Five years later (in 1972), Krygowski and Kruszewski [40] proposed replacing the mean value of all bond lengths, Rav, with a conceptual parameter called optimal bond length, Ropt. This bond length is expected to be realized in fully aromatic compounds. The new aromaticity index HOMA (abbreviation for Harmonic Oscillator Model of Aromaticity) is expressed by Equation (3):
where α is a normalization constant (chosen to give HOMA = 0 for a model non-aromatic system and HOMA = 1 for a system where all bonds are equal to Ropt), n is the number of bonds taken into summation, and Ri is the experimental or computed bond lengths of the system, whose aromaticity is calculated.
The next step and significant progress are related to the extension of the HOMA model to heterocyclic systems [41]. The formula for HOMA is given by Equation (4):
where subscript j denotes the type of the bond, i.e., CC, CN, CO, CP, CS, NN, NO, etc.
The values of the determined parameters Ropt,j and αj are collected in Table 2, along with references to the original works. More details can be found in the review by Krygowski et al. [42].

Table 2.
Optimal bond lengths, Ropt, and α values for different type of bonds used in the HOMA calculation (Equation (4)).
In the current century, the HOMA approach was modified by Raczyńska et al. [47] and named HOMED (Harmonic Oscillator Model of Electron Delocalization), then by Frizzo and Martins [48] and named HOMHED (Harmonic Oscillator Model of Heterocycle Electron Delocalization). It should be emphasized, however, that in both cases the basic idea of the HOMA index remained unchanged. Raczyńska modified the reference parameters in order to allow a consistent description of not only aromaticity but also other types of electron delocalization: π-π and n-π conjugation as well as σ-π hyperconjugation in cyclic and acyclic compounds. The new parametrization also improves the description of oxygen-containing heterocyclic systems, in which aromaticity has not been correctly described by the HOMA index. For example, HOMA for the furan molecule is surprisingly small, 0.289, whereas HOMED gives a more correct description of the aromatic character of this molecule, 0.749 [47,49].
In addition, it has recently been suggested to replace the use of bond lengths in Equation (3) by using local stretching force constants or their associated relative bond strength order (BSO) values as direct measures for the intrinsic bond strength [50,51].
A very important advantage of HOMA-like approaches is that they can be used to assess both global and local aromaticity, i.e., to characterize the whole π-electron system and particular ring(s), respectively. Moreover, they can also be applied to any planar π-electron fragment of a molecule, providing information about its local π-electron delocalization.
Figure 5 shows the structures and HOMA values of each ring for polycyclic aromatic hydrocarbons formed by fusing four benzene rings. Changes in HOMA values of individual rings depend on the topological order of the rings forming a given molecule. The smallest changes in ring aromaticity occur for tetracene, and the largest, for triphenylene. In the case of the linear system, the HOMA values observed for the central rings are greater than for the terminal rings. In other cases, however, the opposite is true. In addition, pyrene rings fused with two others have the highest HOMA value (0.952, Figure 5). Taking into account the peripheral CC bonds, the HOMA values decrease in the order obtained for tetracene, chrysene, triphenylene, and pyrene.
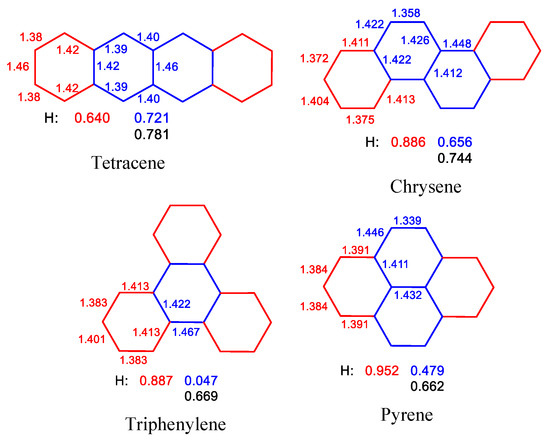
Figure 5.
Structures and HOMA values of each ring in some polycyclic aromatic hydrocarbons (bond lengths in Å). Symmetric equivalent rings are marked in the same color. HOMA value of the perimeter of molecule marked in black. Tetracene: X-ray data obtained in Ref. [52] and reevaluated in Ref. [53], chrysene: B3LYP/cc-pVTZ [51], triphenylene: B3LYP/6-31G(d) [54], and pyrene: RHF/6-31G results [55].
In kekulene (2 in Scheme 3), the HOMA values for two adjacent rings are 0.92 (ring A) and 0.65 (ring B), while for [30]annulene (outer perimeter) and [18]annulene (inner perimeter), the paths are 0.80 and 0.77, respectively (Figure 6d). The synthesis of kekulene on the Cu surface (1, after annealing, undergoes a cyclodehydrogenation reaction, Scheme 3) is confirmed by STM images. The increased electron density in fused benzene rings is manifested in the brightness of these rings (Figure 6a,b). Moreover, the orbital structure of kekulene’s highest occupied molecular orbital was determined using photoemission tomography, supported by density functional calculations. Thus, photoemission tomography can be a complementary method of assessing the role of aromatic stabilization in π-conjugated molecules.
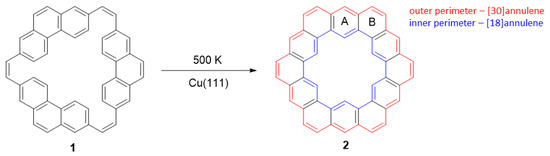
Scheme 3.
Reaction of 1 on the Cu(111) surface, leading to kekulene (2).
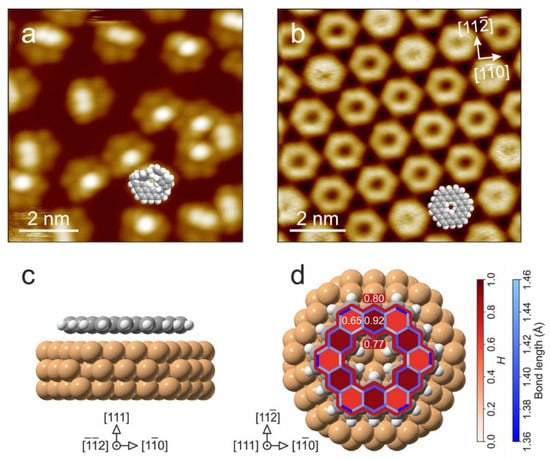
Figure 6.
Structural information from STM and DFT: STM micrographs of the (a) precursor (1) and (b) kekulene (2) on Cu(111), measured at 100 K. Space-filling molecular models are added to illustrate nonplanar and planar molecular conformations of 1 and 2, respectively. (c,d) Side and top views, respectively, of the relaxed adsorption geometry of kekulene/Cu(111) as obtained by DFT. HOMA values H and the bond lengths of adsorbed kekulene are color coded in red and blue, respectively. Reproduced from Ref. [56]; this work is licensed under the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/, accessed on 22 April 2022).
Bird [57,58,59], using the same idea as Julg and François [39], replaced the bond lengths, R, by the Gordy bond orders, N [60]; the bond between the different atoms may be the same length but may differ in the bond orders. These modifications led to the following formula for the coefficient of variation of the bond order, V (Equation (5)), and finally to the aromaticity index, IA, defined by Equation (6).
In Equation (5), Ni is the bond order of the i-th bond, Nav denotes the average bond order, and n is the number of bonds. For a fully aromatic ring, V is equal to 0, while for the Kekulé structure with alternating single and double bonds, this value depends on the type of the ring system under consideration. Therefore, in Equation (6), for a six-membered ring, Vk = 33.3 and 35 for a five-membered ring. Hence, a fully aromatic system has IA=100. As the value of the index I depends on the size of the ring, a subscript 5 or 6 has been added. Thus, I5 and I6 represent the Bird index for five- [57,61] and six-membered [58,62] rings, respectively.
Values of the abovementioned geometry-based aromaticity indices for five- and six-membered heterocycles, published since 2000, can be found in Tables 6 and 7 in the review by Krygowski et al. [42].
For macromolecular compounds, such as polymers, the most popular geometry-based approach to assess aromaticity is the bond-length alternation (BLA) index [63]. It is generally defined as the difference in bond lengths between the long and short carbon-carbon bonds in the conjugated molecule. For this purpose, the average bond lengths of consecutive bonds in a ring are also used [64]. In addition, this index can also be expressed as the averaged sum of the absolute values of the differences between the bond length and the averaged bond length. In this case, however, only bonds of the same type should be considered [65]. A very low BLA value indicates an effective aromatic structure, e.g., BLA of benzene is zero, but the same is true for cyclohexane, which is not a π-electron system.
HOMA and Bird indices can be easily calculated in the Multiwfn program, provided we have a file with molecular geometry [66].
2.3. Magnetism-Based Aromaticity Descriptors
Another important piece of information about aromaticity comes from the magnetic properties of chemical compounds. There are two main sources to consider: (1) the magnetic properties of molecules as a whole, e.g., diamagnetic susceptibility exaltation [67] and (2) the application of NMR spectral data [68].
One of the first descriptors of this type was the diamagnetic susceptibility exaltation, which was proposed as a criterion of aromaticity already in 1968 [69]. It was based on the assumption that a high diamagnetic susceptibility exaltation indicates the presence of π-electron delocalization in a molecule [70,71]. It should be stressed that magnetic susceptibility is a property of the whole molecule and can be obtained both experimentally and by quantum chemistry computations.
The proton chemical shifts of aromatic molecules are obviously related to the presence of the π-electron ring current (Figure 1). However, to some extent, they may depend significantly on the structural neighboring. The use of NMR measurements to assess aromaticity is shown in an excellent review by Mitchell [72]. Recently, NMR measurements of macrocycles containing 1H and 19F probes located at specific positions have been used to assess the aromaticity of such compounds [73]. The results are summarized in a very interesting paper about the size limits of aromaticity [74].
It is worth mentioning that the π-electron ring current, induced by an external magnetic field, can be studied and visualized using ACID (anisotropy of the magnetically induced current density tensor) [75,76] or GIMIC (gauge including magnetically induced current) [77] methods. Recently, an extended version of ACID, AACID (anisotropy of the asymmetric magnetically induced current density tensor) [78], has been developed, which, unlike ACID, takes into account the asymmetricity of the current density tensor. It has been shown that the results obtained with AACID, compared to ACID, were shown to correlate better with geometric data of aromatic compounds [78] and better reproduce the electron delocalization energies in aromatic systems, obtained using the Hückel molecular orbital theory [79].
The most commonly used magnetic aromaticity criterion, nucleus independent chemical shift (NICS), is based on the NMR chemical shift; however, it is calculated using quantum chemistry methods. NICS was introduced by Schleyer in 1996 [80]. Originally, NICS was defined as the negative value of the absolute shielding of a dummy-atom probe located at the geometric center of the ring system, that is, where the magnetic field is weakened by the ring current and the shielding effect occurs (Figure 1). Now, it is also computed at other points inside or around molecules, e.g., 1 Å above the geometric center of the ring and named NICS(1) [81,82]. It is well known that magnetic response properties are tensors [83] and that their trace can be very different for a number of reasons [84]. Therefore, Schleyer recommended NICSzz, the component of a shielding tensor corresponding to the principal axis perpendicular to the ring plane, as the preferred measure of the aromaticity of the π system [85]. The more negative the NICS value, the more aromatic the ring is, while positive values indicate anti-aromaticity. Quite recently, NICSzz values have been used to generate quantitative bond-current graphs, NICS2BC, which are a simple method for visualizing the π-electron ring currents in the molecule [86].
NICS can be calculated at different calculation levels. However, the comparison of the obtained values is reliable when, for a given series of compounds, the NICS values are calculated using the same approach, that is, the same position of the probe and the same level of theory [87]. Unlike other magnetism-based aromaticity criteria, such as magnetic susceptibility [88] or its anisotropy [89], all NICS values describe only local aromaticity, i.e., the aromaticity of a particular ring; in addition, they depend on the size of the ring. However, it has recently been shown that NICS-XY scans (NICS scans along the X and Y axes at 1.7 Å above the ring plane, see Figure 7) reveal local and global ring currents in multi-ring conjugated systems [90,91], even with B, N, O, and S heteroatoms [92].
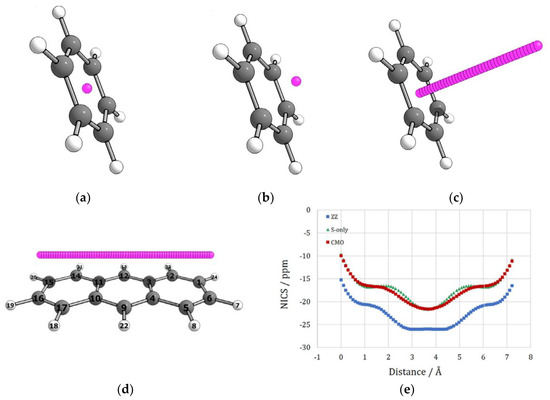
Figure 7.
Examples of NICS probe locations and scan results. Benzene: (a) NICS(0), (b) NICS(1), (c) NICS scan along the z coordinate. Anthracene: (d) NICS scan along the x–y coordinate and (e) scan results: NICS(1.7)zz (blue) and two models eliminating σ-electron contribution to shielding: NICS σ only model (green) and canonical molecular orbitals NICS (red). Adapted from Ref. [93]. Copyright (2021), with permission from Elsevier.
In 2018, Baez-Grez et al. conducted a study on the aromaticity of benzene, cyclopropane, planar cyclooctatetraene, borazine, and Al42− cluster [94]. Various approaches for obtaining NICS data were compared to the ring current data, the source of specific shielding or deshielding occurring at specific regions in space around the aromatic ring (as illustrated in Figure 1). The conclusion was that NICS(1)zz is the most adequate approach for describing aromaticity, as its values are least contaminated by sources of shielding other than magnetically induced ring currents. A similar comparison for a 20-molecule test set was performed by Stanger et al. [95]. The test set consisted of specifically designed molecules, which contained many paratropic and diatropic ring currents. Current density analyses mostly agreed with the results of the NICS-XY scans at 1 Å above the molecular surface. In most cases, these scans were able to reproduce the paratropic or diatropic (in other words, causing deshielding and shielding above the ring center, respectively) character of currents in particular rings. It was shown that the best method for obtaining each individual point in the scan is CMO-NICSπ,zz, a method in which the contribution of each canonical molecular orbital to the shielding tensor is calculated separately. This allows us to extract the contribution of the π orbitals responsible for the aromatic magnetic phenomena. Details on this and other NICS methods can be found in Ref. [93].
Calculation input files with NICS probes placed at desired locations can be automatically generated with the Aroma program written by Rahalkar [96]. The program also runs calculations automatically and outputs the results when coupled with Gaussian software. The current state of the magnetic aromaticity criteria was recently presented by Gershoni-Poranne and Stanger [93,97].
2.4. Electron Delocalization Indices
Since the aromaticity originates from the π-electron conjugation and ring currents, many methods for the estimation of aromaticity employ analysis of electron density or electronic wave function. Electron delocalization pathways can be observed experimentally or computationally using various methods. For example, they produce distinctive regions in STM images due to differences in tunneling currents (Figure 2). Similarly, a specific interaction of the AFM probe with the π-electron-rich region allows distinguishing them (Figure 2 and Figure 3). Computationally, aromatic delocalization pathways can be observed as currents induced by an external magnetic field using the ACID or GIMIC methods. Current density maps as probes for global and local aromaticity were also presented by Steiner et al. [98].The other approach, electron density of delocalized bonds (EDDB) [99,100,101,102], employs a decomposition scheme for electron density. These three computational approaches, applied to porphyrins, give a similar picture of the [18]annulene global delocalization pathway (Figure 8), while the local delocalization does not appear to be so equal.
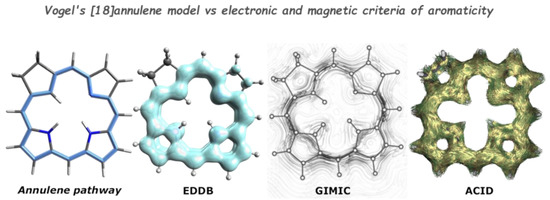
Figure 8.
EDDB, GIMIC, and ACID visualization of electron delocalization pathway in porphyrin, compared to the [18]annulene pathway proposed by Vogel to explain aromaticity in porhyrins. Source: [103].
It should be mentioned that recent advances in crystallography and quantum crystallography have made it possible to reproduce the electron density with enough resolution to utilize it in studies of aromaticity involving the electron density [104,105], for example, using the aromaticity indices described below.
The first three electronic aromaticity indices discussed below use a property called the delocalization index (DI), defined in Equation (7). It is a measure of how many electrons are delocalized between the two atomic basins defined within the QTAIM theory [106,107].
where Sij(A) and Sij(B) are the overlaps between orbitals i and j in the atomic basin of A and B, respectively.
In 2003, Matta proposed the ‘θ’ aromaticity index [108]. It is a modification of the HOMA equation, in which the bond lengths were replaced with the values of the delocalization index (Equation (8)).
where c is a constant that depends on the level of calculations (at HF/6-31G** level, c = 0.1641), n is the number of bonds, δ0 is the reference value of DI, and δi is the DI value of i-th bond. For a model aromatic system, benzene, θ = 1, while, for cyclohexane, θ = 0.
Another electronic aromaticity index based on the delocalization index is called the para-delocalization index (PDI) [109]. It is calculated as an average value of delocalization indices between all para-related atoms of the ring. Unfortunately, it can only be used to estimate the local aromaticity of six-membered rings. PDI uses a different scale of aromaticity than θ and HOMA; for example, for benzene, PDI = 0.101, whereas for the middle ring of triphenylene of non-aromatic character, HOMA = 0.047, NICS = −2.2, and PDI = 0.025.
In 2005, the Solà group proposed another electronic aromaticity index based on DI [110]. The aromatic fluctuation index, abbreviated FLU, measures the weighted divergences in DI of each bonded pair with respect to a reference aromatic system. FLU is calculated using the formula shown in Equation (9):
where the ring considered is formed by atoms in the string {A} = {A1, A2, … AN}, A0 ≡ AN and the atomic delocalization V(A) is defined by Equation (10),
while α is a function that ensures that the ratio of atomic delocalizations in Equation (9) is always greater or equal to 1,
Additionally, in planar systems, δref can be replaced with an average delocalization index δavg, calculated for π electrons. This eliminates the need for a reference system. Such a modification of FLU is called FLUπ. However, it should be remembered that values obtained using these two methods cannot be compared. Low values of FLU indicate high aromaticity; for example, FLU and FLUπ = 0 for benzene, whereas high values indicate a non-aromatic character and, for the aforementioned middle ring of triphenylene, FLU = 0.027 and FLUπ = 0.181. An important asset of FLU is that it can be used to evaluate both local and global aromaticity for a ring of any size.
The multicenter index, MCI [111], is a measure of electron delocalization between multiple atomic centers. It is a popular and versatile aromaticity index that can be used in organic and inorganic systems, for both local and global aromaticity. One drawback of the MCI is that calculation time scales exponentially with the size of a system; thus, it cannot be applied in macrocycles. Here, it is worth mentioning that an aromaticity index, which calculates the approximate MCI value, AV1245 [112], can be used in macrocyclic systems, such as porphyrins. The high value of the MCI indicates the high aromaticity of a system. The equations used in the calculation of the MCI, the comparison between PDI, FLU, and MCI, as well as the application of these indices for aromaticity analysis in interesting chemical topics can be found in a recent review by Feixas et al. [113].
PDI, FLU, FLUπ, and MCI aromaticity indices can be calculated in the Multiwfn program [66].
Recently, it was shown that the source function (SF), introduced in the 1990s by Bader and Gatti [114] and based on the electron density, can be used to measure aromaticity. The source function is a measure of contribution of electron density of a chosen AIM-defined atom or group of atoms to the electron density at a given point in space. Therefore, when the electron delocalization is present, one should expect a greater contribution from distant atoms to the electron density at, e.g., a bond critical point. It should be mentioned that SF is based solely on the electron density, which can be either calculated or obtained experimentally by X-ray diffraction of crystals [115]. A new aromaticity index based on the SF, called SFLAI [116] (source function local aromaticity index), showed consistent results with HOMA and PDI indices in describing local aromaticity of polycyclic aromatic hydrocarbons and some of their partially hydrogenated derivatives. SFLAI is normalized to yield values between 0 and 1, with the former corresponding to the nonaromatic cyclohexane and the latter to the fully aromatic reference system, benzene. It can be calculated from Equation (12):
where ΣSFΩb% is the sum of the percentage contribution to the SF of each carbon atom (its atomic basin Ω) to each bth CC bond critical point in the benzenoid ring, k is the analogous value in the reference benzene system, and c is the normalization constant.
The last index discussed here, the electron density of delocalized bonds (EDDB), comes from the decomposition of electron density (ED(r)), into layers (Figure 9). These layers correspond to core electrons and lone pairs (EDLA(r)), electrons localized at bonds (EDLB(r)), and, finally, electrons delocalized between several atomic centers (EDDB(r)). The last contribution, EDDB(r), is used to quantify aromaticity and visualize π-electron circuits in a molecule by analyzing its isosurfaces.
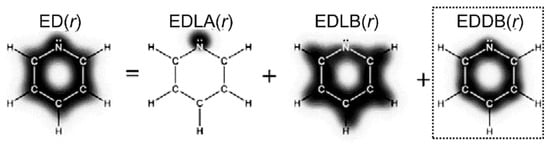
Figure 9.
Decomposition of total electron density, ED(r), into three contributions. Adapted from Ref. [117] with permission from the PCCP Owner Societies. Copyright (2017) with permission from Royal Society of Chemistry.
An important feature of EDDB(r) is that it allows evaluating both local (EDDBP(r)) and global (EDDBG(r)) aromaticity. A mathematical definition of EDDB and the theory behind it can be found in papers by Szczepanik [99,100,101,102]. From a practical point of view, it is worth mentioning that the RunEDDB program, written by Szczepanik and available online [118], allows the calculation of values of various EDDB variants, further dissection of the π and σ electron contributions to each variant, and the visualization of the π-electron circuits.
Figure 10 shows how the AFM image of a polycyclic aromatic hydrocarbon (pentacene) relates to aromaticity. In Figure 10a, the bright edges in the AFM image correspond to molecular fragments, in which electrons are highly localized at particular bonds. A separate theoretical calculation of EDDB(r) isosurfaces (Figure 10b) as well as the HOMA values from the experimental geometry (Figure 10c) indicate a lower aromatic character of the peripheral rings containing these highly localized π-bonds.
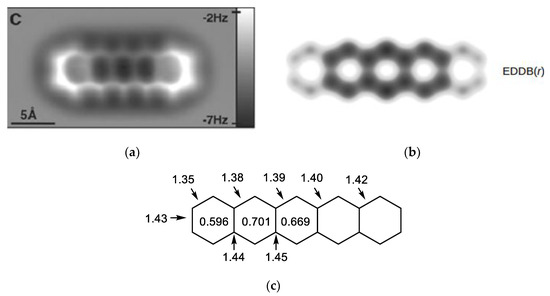
Figure 10.
This pentacene molecule: (a) AFM image, (b) isosurfaces of EDDB(r), and (c) experimental bond lengths (in Å, from Ref. [53]) along with HOMA of each ring. The AFM image is reproduced from Ref. [119] with permission from AAAS. The EDDB(r) representation is reproduced from Ref. [99] with permission from the PCCP Owner Societies. Copyright (2018) with permission from the Royal Society of Chemistry.
3. Summary
As a summary, the values of four aromaticity indices, based on the geometric, electronic, and magnetic criteria, are presented in Table 3 and Table 4. The selected systems include mono- and polycyclic molecules, all-carbon and hetero-aromatics, as well as non-aromatic and anti-aromatic systems, according to the Hückel rule (4N + 2). In all cases, the values of the individual indices correctly indicate their aromatic or non-aromatic character. However, mutual relations between the various aromaticity parameters occur only for EDDB and HOMA, as well as EDDB and FLU (the correlation coefficients, cc, are 0.932 and −0.933, respectively). Moreover, considering only aromatic systems, the EDDB and HOMA indices are even better correlated with each other (cc = 0.960); similar results were obtained for a much larger set of molecular rings [117]. Thus, HOMA and EDDB speak with the same voice. While the HOMA index can be determined from experimental data, currently, the EDDB results can be compared only with those of AFM or STM microscopy.

Table 3.
Values of aromaticity indices for several aromatic (+), anti-aromatic (−), and non-aromatic (0) monocyclic molecules: geometric (HOMA), electronic (FLU and EDDB), magnetic (NICS(1)zz).

Table 4.
Values of aromaticity indices for several polycyclic molecules.
Author Contributions
Conceptualization, H.S. and T.M.K.; investigation, H.S. and P.A.W.; writing—original draft preparation, H.S. and P.A.W.; writing—review and editing, P.A.W. and T.M.K.; visualization, P.A.W.; supervision, H.S.; project administration, H.S.; funding acquisition, H.S. and T.M.K. All authors have read and agreed to the published version of the manuscript.
Funding
H.S. and P.A.W. thank the Warsaw University of Technology for financial support. The APC was funded by MDPI.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Coulson, C.A.; McWeeny, R. Coulson’s Valence, 3rd ed.; Oxford University Press: Oxford, UK; New York, NY, USA, 1979. [Google Scholar]
- Iczkowski, R.P.; Margrave, J.L. Electronegativity. J. Am. Chem. Soc. 1961, 83, 3547–3551. [Google Scholar] [CrossRef]
- Kekule, A. Über die Constitution der aromatischen Substanzen. Bull. Soc. Chim. Fr. 1865, 3, 98–110. [Google Scholar]
- Lonsdale, K. The structure of the benzene ring in C6(CH3)6. Proc. R. Soc. A Math. Phys. Eng. Sci. 1929, 123, 494–515. [Google Scholar]
- Hückel, E. Quantentheoretische Beiträge zum Benzolproblem. Z. Physik 1931, 70, 204–286. [Google Scholar] [CrossRef]
- Erlenmayer, E. Studien über die s. g. aromatischen Säuren. Ann. Chem. Pharm. 1866, 137, 327–359. [Google Scholar]
- Childs, R.F. The Homotropylium Ion and Homo-aromaticity. Acc. Chem. Res. 1984, 17, 347–352. [Google Scholar] [CrossRef]
- Boldyrev, A.I.; Wang, L.-S. All-metal aromaticity and antiaromaticity. Chem. Rev. 2005, 105, 3716–3757. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Bankiewicz, B.; Czarnecki, Z.; Palusiak, M. Quasi-aromaticity—What does it mean? Tetrahedron 2015, 71, 4895. [Google Scholar] [CrossRef]
- Rzepa, H.S. Möbius aromaticity and delocalization. Chem. Rev. 2005, 105, 3697–3715. [Google Scholar] [CrossRef]
- Chen, Z.; King, R.B. Spherical aromaticity: Recent work in fullerenes, polyhedral boranes, and related structures. Chem. Rev. 2005, 105, 3613–3642. [Google Scholar] [CrossRef]
- Solà, M. Why Aromaticity Is a Suspicious Concept? Why? Front. Chem. 2017, 5, 22. [Google Scholar] [CrossRef] [PubMed]
- Krygowski, T.M.; Cyrański, M.K.; Czarnocki, Z.; Haefelinger, G.; Katritzky, A.R. Aromaticity: A theoretical concept of immense practical importance. Tetrahedron 2000, 56, 1783–1796. [Google Scholar] [CrossRef]
- Minkin, V.I. Glossary of Terms Used in Theoretical Organic Chemistry. Pure Appl. Chem. 1999, 71, 1919–1981. [Google Scholar] [CrossRef]
- Alonso, M.; Fernández, I. Quantifying Aromaticity According to the Energetic Criterion. In Aromaticity; Fernández, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 6; pp. 195–235. [Google Scholar]
- SDBSWeb (National Institute of Advanced Industrial Science and Technology). Available online: https://sdbs.db.aist.go.jp (accessed on 20 April 2022).
- Guo, Y.-B.; Liu, Z.-Z.; Liu, H.-X.; Zhang, F.-Y.; Yin, J.-Q. A new aromatic probe—The ring stretching vibration Raman spectroscopy frequency. Spectrochim. Acta A 2016, 164, 84–88. [Google Scholar] [CrossRef]
- De Oteyza, D.G.; Gorman, P.; Chen, Y.-C.; Wickenburg, S.; Riss, A.; Mowbray, D.J.; Etkin, G.; Pedramrazi, Z.; Tsai, H.-Z.; Rubio, A.; et al. Direct Imaging of Covalent Bond Structure in Single-Molecule Chemical Reactions. Science 2013, 340, 1434–1437. [Google Scholar] [CrossRef] [PubMed]
- Gross, L.; Mohn, F.; Moll, N.; Schuler, B.; Criado, A.; Guitián, E.; Peña, D.; Gourdon, A.; Meyer, G. Bond-Order Discrimination by Atomic Force Microscopy. Science 2012, 337, 1326–1329. [Google Scholar] [CrossRef] [PubMed]
- Pigot, C.; Dumur, F. Molecular engineering in 2D surface covalent organic frameworks: Towards next generation of molecular tectons—A mini review. Synth. Met. 2020, 260, 116265. [Google Scholar] [CrossRef]
- Pauling, L.; Sherman, J. The Nature of the Chemical Bond. VI. The Calculation from Thermochemical Data of the Energy of Resonance of Molecules Among Several Electronic Structures. J. Chem. Phys. 1933, 1, 606–617. [Google Scholar] [CrossRef]
- Kistiakowsky, G.B.; Ruhoff, J.R.; Smith, H.A.; Vaughan, W.E. Heats of Organic Reactions. IV. Hydrogenation of Some Dienes and of Benzene. J. Am. Chem. Soc. 1936, 58, 146–153. [Google Scholar] [CrossRef]
- Cyranski, M.K. Energetic Aspects of Cyclic Pi-Electron Delocalization: Evaluation of the Methods of Estimating Aromatic Stabilization Energies. Chem. Rev. 2005, 105, 3773–3811. [Google Scholar] [CrossRef]
- Hehre, W.J.; Ditchfield, R.; Radom, L.; Pople, J.A. Molecular orbital theory of the electronic structure of organic compounds. V. Molecular theory of bond separation. J. Am. Chem. Soc. 1970, 92, 4796–4801. [Google Scholar] [CrossRef]
- George, P.; Trachtman, M.; Bock, C.W.; Brett, A.M. Homodesmotic reactions for the assessment of stabilization energies in benzenoid and other conjugated cyclic hydrocarbons. J. Chem. Soc. Perkin Trans. 2 1976, 11, 1222–1227. [Google Scholar] [CrossRef]
- Pross, A.; Radom, L.; Taft, R.W. Theoretical Approach to Substituent Effects. Phenols and Phenoxide Ions. J. Org. Chem. 1980, 45, 818–826. [Google Scholar] [CrossRef]
- Wheeler, S.E. Homodesmotic reactions for thermochemistry. WIREs Comput. Mol. Sci. 2012, 2, 204–220. [Google Scholar] [CrossRef]
- George, P.; Bock, C.W.; Trachtman, M.J. The evaluation of empirical resonance energies as reaction enthalpies with particular reference to benzene. J. Chem. Educ. 1984, 61, 225. [Google Scholar] [CrossRef]
- Afeely, H.Y.; Liebman, J.F.; Stein, S.E. Neutral Thermochemical Data. In NIST Chemistry WebBook; NIST Standard Reference Database No. 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022. [Google Scholar]
- George, P. A Critique of the Resonance Energy Concept with Particular Reference to Nitrogen Heterocycles, Especially Porphyrins. Chem. Rev. 1975, 75, 85–111. [Google Scholar] [CrossRef]
- Pedley, J.B.; Naylor, R.D.; Kirby, S.P. Thermodynamical Data of Organic Compounds; Chapman and Hall: London, UK, 1986. [Google Scholar]
- Schleyer, P.v.R.; Puhlhofer, F. Recommendations for the Evaluation of Aromatic Stabilization Energies. Org. Lett. 2002, 4, 2873–2876. [Google Scholar] [CrossRef]
- Fishtik, I.; Datta, R. Aromaticity vs Stoichiometry. J. Phys. Chem. A 2003, 107, 10471–10476. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Jiao, H.; van Eikema Hommes, N.J.R.; Malkin, V.G.; Malkina, O.L. An Evaluation of the Aromaticity of Inorganic Rings: Refined Evidence from Magnetic Properties. J. Am. Chem. Soc. 1997, 119, 12669–12670. [Google Scholar] [CrossRef]
- Schrier, J. Introduction to Computational Physical Chemistry; University Science Books: Mill Valley, CA, USA, 2017. [Google Scholar]
- Aihara, J. Graph Theory of Aromatic Stabilization. BCSJ 2016, 89, 1425–1454. [Google Scholar] [CrossRef]
- Allen, F.H.; Kennard, O.; Watson, D.G.; Brammer, L.; Orpen, A.G.; Taylor, R. Tables of bond lengths determined by x-ray and neutron diffraction. Part 1. Bond lengths in organic compounds. J. Chem. Soc. Perkin Trans. 2 1987, 12, S1–S19. [Google Scholar] [CrossRef]
- Hückel, E. Theoretische Grundlagen der Organischen Chemie, 1 Band; Akademische Verlagsgesellschaft: Leipzig, Germany, 1956. [Google Scholar]
- Julg, A.; François, P. Recherches sur la geometrie de quelques hydrocarbures non-altenants—Son influence sur les energies de transition une nouvelle definition de l’aromaticite. Theor. Chim. Acta 1967, 7, 249–256. [Google Scholar] [CrossRef]
- Kruszewski, J.; Krygowski, T.M. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
- Krygowski, T.M. Crystallographic Studies of Inter- and Intra- molecular Interactions Reflected in Aromatic Character of π-electron Systems. J. Chem. Inf. Comp. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Szatylowicz, H.; Stasyuk, O.A.; Dominikowska, J.; Palusiak, M. Aromaticity from the Viewpoint of Molecular Geometry: Application to Planar Systems. Chem. Rev. 2014, 114, 6383–6422. [Google Scholar] [CrossRef] [PubMed]
- Zborowski, K.K.; Alkorta, I.; Elguero, J.; Proniewicz, L.M. HOMA parameters for the boron-boron bond: How the interpretation of the BB bond influences the aromaticity of selected hydrocarbons. Struct. Chem. 2013, 24, 543–548. [Google Scholar]
- Zborowski, K.K.; Alkorta, I.; Elguero, J.; Proniewicz, L.M. Calculation of the HOMA model parameters for the carbon-boron bond. Struct. Chem. 2012, 23, 595–600. [Google Scholar]
- Madura, I.D.; Krygowski, T.M.; Cyrański, M.K. Structural Aspects of the Aromaticity of Cyclic π-electron Systems with BN Bonds. Tetrahedron 1998, 54, 14913–14918. [Google Scholar] [CrossRef]
- Zborowski, K.K.; Proniewicz, L.M. HOMA Model Extension for the Compounds Containing the Carbon–Selenium Bond. Pol. J. Chem. 2009, 83, 477–484. [Google Scholar]
- Raczyńska, E.D.; Hallman, M.; Kolczyńska, K.; Stępniewski, T. On the Harmonic Oscillator Model of Electron Delocalization (HOMED) Index and its Application to Heteroatomic π-Electron Systems. Symmetry 2010, 2, 1485–1509. [Google Scholar] [CrossRef]
- Frizzo, C.P.; Martins, M.A.P. Aromaticity in heterocycles: New HOMA index parametrization. Struct. Chem. 2012, 23, 375–380. [Google Scholar] [CrossRef]
- Raczyńska, E. Application of the Extended HOMED (Harmonic Oscillator Model of Aromaticity) Index to Simple and Tautomeric Five-Membered Heteroaromatic Cycles with C, N, O, P, and S Atoms. Symmetry 2019, 11, 146. [Google Scholar] [CrossRef]
- Kalescky, R.; Kraka, E.; Cremer, D. Description of Aromaticity with the Help of Vibrational Spectroscopy: Anthracene and Phenanthrene. J. Phys. Chem. A 2014, 118, 223–237. [Google Scholar] [CrossRef] [PubMed]
- Setiawan, D.; Kraka, E.; Cremer, D. Quantitative Assessment of Aromaticity and Antiaromaticity Utilizing Vibrational Spectroscopy. J. Org. Chem. 2016, 81, 9669–9686. [Google Scholar] [CrossRef] [PubMed]
- Robertson, J.M.; Sinclair, V.C.; Trotter, J. The Crystal and Molecular Structure of Tetracene. Acta Cryst. 1961, 14, 697–704. [Google Scholar] [CrossRef]
- Campbell, R.B.; Robertson, J.M. The crystal structure of hexacene, and a revision of the crystallographic data for tetracene and pentacene. Acta Cryst. 1962, 15, 289–290. [Google Scholar] [CrossRef]
- Berionni, G.; Wu, J.I.-C.; Schleyer, P.v.R. Aromaticity Evaluations of Planar (6)Radialenes. Org. Lett. 2014, 16, 6116–6119. [Google Scholar] [CrossRef] [PubMed]
- Krygowski, T.M.; Cyrański, M.K.; Nakata, K.; Fujio, M.; Tsuno, Y. Separation of the Energetic and Geometric Contributions to Aromaticity. Part VI. Changes of the Aromatic Character of the Rings in Naphthalene, Anthracene, Phenanthrene and Pyrene Derivatives Induced by the Charged Substituent CH2+. Tetrahedron 1997, 53, 11383–11398. [Google Scholar] [CrossRef]
- Haags, A.; Reichmann, A.; Fan, Q.; Egger, L.; Kirschner, H.; Naumann, T.; Werner, S.; Vollgraff, T.; Sundermeyer, J.; Eschmann, L.; et al. Kekulene: On-Surface Synthesis, Orbital Structure, and Aromatic Stabilization. ACS Nano 2020, 14, 15766–15775. [Google Scholar] [CrossRef] [PubMed]
- Bird, C.W. A new aromaticity index and its application to five membered ring heterocycles. Tetrahedron 1985, 41, 1409–1414. [Google Scholar] [CrossRef]
- Bird, C.W. The application of a new aromaticity index to six-membered ring heterocycles. Tetrahedron 1986, 42, 89–92. [Google Scholar] [CrossRef]
- Bird, C.W. Hetero-aromaticity, 8, the influence of N-oxide formation on heterocyclic aromaticity. Tetrahedron 1993, 49, 8441–8448. [Google Scholar] [CrossRef]
- Gordy, W.J. A Relation between Bond Force Constants, Bond Orders, Bond Lengths, and the Electronegativities of the Bonded Atoms. J. Chem. Phys. 1947, 14, 305–310. [Google Scholar] [CrossRef]
- Bird, C.W. Heteroaromaticity. 4 The status of phosphorus and arsenic heteroatoms. Tetrahedron 1990, 46, 5697–5702. [Google Scholar] [CrossRef]
- Bird, C.W. The application of a new aromaticity index to some bicyclic heterocycles. Tetrahedron 1987, 43, 4725–4730. [Google Scholar] [CrossRef]
- Kertesz, M.; Choi, C.H.; Yang, S. Conjugated Polymers and Aromaticity. Chem. Rev. 2005, 105, 3448–3481. [Google Scholar] [CrossRef] [PubMed]
- Casademont-Reig, I.; Woller, T.; Contreras-Garcıa, J.; Alonso, M.; Torrent-Sucarrat, M.; Matito, E. New electron delocalization tools to describe the aromaticity in porphyrinoids. Phys. Chem. Chem. Phys. 2018, 20, 2787–2796. [Google Scholar] [CrossRef] [PubMed]
- Kurach, E.; Djurado, D.; Rimarcik, J.; Kornet, A.; Wlostowski, M.; Lukes, V.; Pecaut, J.; Zagorska, M.; Pron, A. Effect of substituents on redox, spectroscopic and structural properties of conjugated diaryltetrazines—A combined experimental and theoretical study. Phys. Chem. Chem. Phys. 2011, 13, 2690–2700. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Dauben, H.J.; Wilson, J.D.; Laity, J.L. Diamagnetic susceptibility exaltation in hydrocarbons. J. Am. Chem. Soc. 1969, 91, 1991–1998. [Google Scholar] [CrossRef]
- Minkin, V.I.; Glukhovtsev, M.N.; Simkin, B.Y. Aromaticity and Antiaromaticity. Electronic and Structural Aspects; Wiley: New York, NY, USA, 1994; pp. 63–103. [Google Scholar]
- Dauben, H.J.; Wilson, J.D.; Laity, J.L. Diamagnetic susceptibility exaltation as a criterion of aromaticity. J. Am. Chem. Soc. 1968, 90, 811–813. [Google Scholar] [CrossRef]
- Benson, R.C.; Flygare, W.H. Molecular Zeeman Effect of Cyclopentadiene and Isoprene and Comparison of the Magnetic Susceptibility Anisotropies. J. Am. Chem. Soc. 1970, 92, 7523–7529. [Google Scholar]
- Flygare, W.H. Magnetic interactions in molecules and an analysis of molecular electronic charge distribution from magnetic parameters. Chem. Rev. 1974, 74, 653–687. [Google Scholar] [CrossRef]
- Mitchell, R.H. Measuring Aromaticity by NMR. Chem. Rev. 2001, 101, 1301–1315. [Google Scholar] [CrossRef] [PubMed]
- Rickhaus, M.; Jirasek, M.; Tejerina, L.; Gotfredsen, H.; Peeks, M.D.; Haver, R.; Jiang, H.-W.; Claridge, T.D.W.; Anderson, H.L. Global aromaticity at the nanoscale. Nat. Chem. 2020, 12, 236–241. [Google Scholar] [CrossRef] [PubMed]
- Jirásek, M.; Anderson, H.L.; Peeks, M.D. From Macrocycles to Quantum Rings: Does Aromaticity Have a Size Limit? Acc. Chem. Res. 2021, 54, 3241–3251. [Google Scholar] [CrossRef] [PubMed]
- Herges, R.; Geuenich, D. Delocalization of Electrons in Molecules. J. Phys. Chem. A 2001, 105, 3214–3220. [Google Scholar] [CrossRef]
- Geuenich, D.; Hess, K.; Köhler, F.; Herges, R. Anisotropy of the Induced Current Density (ACID), a General Method to Quantify and Visualize Electronic Delocalization. Chem. Rev. 2005, 105, 3758–3772. [Google Scholar] [CrossRef] [PubMed]
- Fliegl, H.; Taubert, S.; Lehtonen, O.; Sundholm, D. The Gauge Including Magnetically Induced Current Method. Phys. Chem. Chem. Phys. 2011, 13, 20500. [Google Scholar] [CrossRef] [PubMed]
- Monaco, G.; Zanasi, R. AACID: Anisotropy of the Asymmetric Magnetically Induced Current Density Tensor. J. Phys. Chem. A 2018, 122, 4681–4686. [Google Scholar] [CrossRef]
- Monaco, G.; Zanasi, R. Delocalization Energy Retrieved from the Current Density Tensor. Phys. Chem. Chem. Phys. 2019, 21, 11564–11568. [Google Scholar] [CrossRef] [PubMed]
- Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Cyrański, M.K.; Krygowski, T.M.; Wisiorowski, M.; van Eikema Hommes, N.J.R.; Schleyer, P.v.R. Global and Local Aromaticity in Porphyrins: An Analysis Based on Molecular Geometriesand Nucleus-Independent Chemical Shifts. Angew. Chem. Int. Ed. 1998, 37, 177–180. [Google Scholar] [CrossRef]
- Chen, Z.; Wannere, C.S.; Carminboef, C.; Puchta, R.; Schleyer, P.v.R. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef]
- Lazzeretti, P. Ring currents. Progr. Nucl. Magn. Res. Spectr. 2000, 36, 1–88. [Google Scholar] [CrossRef]
- Lazzeretti, P. Assessment of aromaticity via molecular response properties. Phys. Chem. Chem. Phys. 2004, 6, 217–223. [Google Scholar] [CrossRef]
- Corminboeuf, C.; Heine, T.; Seifert, G.; Schleyer, P.v.R.; Weber, J. Induced magnetic fields in aromatic [n]-annulenes—Interpretation of NICS tensor components. Phys. Chem. Chem. Phys. 2004, 6, 273–276. [Google Scholar] [CrossRef]
- Paenurk, E.; Gershoni-Poranne, R. Simple and efficient visualization of aromaticity: Bond currents calculated from NICS values. Phys. Chem. Chem. Phys. 2022, 24, 8631–8644. [Google Scholar] [CrossRef]
- Gajda, L.; Kupka, T.; Broda, M.A.; Leszczyńska, M.; Ejsmont, K. Method and basis set dependence of the NICS indexes of aromaticity for benzene. Magn. Reson. Chem. 2018, 56, 265–275. [Google Scholar] [CrossRef] [PubMed]
- London, F. Théorie quantique des courants interatomiques dans les combinaisons aromatiques. J. Phys. Radium 1937, 8, 397–409. [Google Scholar] [CrossRef]
- Fowler, P.W.; Havenith, R.W.A.; Jenneskens, L.W.; Soncini, A.; Steiner, E. Survival and extinction of delocalised ring currents in clamped benzenes. Chem. Commun. 2001, 22, 2386–2387. [Google Scholar] [CrossRef] [PubMed]
- Gershoni-Poranne, R.; Stanger, A. The NICS-XY-Scan: Identification of Local and Global Ring Currents in Multi-Ring Systems. Chem. Eur. J. 2014, 20, 5673–5688. [Google Scholar] [CrossRef] [PubMed]
- Gershoni-Poranne, R. Piecing it together: An additivity scheme for aromaticity using NICS-XY scans. Chem. Eur. J. 2018, 24, 4165–4172. [Google Scholar] [CrossRef] [PubMed]
- Finkelstein, P.; Gershoni-Poranne, R. An additivity scheme for aromaticity: The heteroatom case. ChemPhysChem 2019, 20, 1508. [Google Scholar] [CrossRef]
- Gershoni-Poranne, R.; Stanger, A. NICS—Nucleus-Independent Chemical Shift. In Aromaticity; Fernández, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 4; pp. 99–154. [Google Scholar]
- Báez-Grez, R.; Ruiz, L.; Pino-Rios, R.; Tiznado, W. Which NICS Method Is Most Consistent with Ring Current Analysis? Assessment in Simple Monocycles. RSC Adv. 2018, 8, 13446–13453. [Google Scholar] [CrossRef]
- Stanger, A.; Monaco, G.; Zanasi, R. NICS- XY -Scan Predictions of Local, Semi-Global, and Global Ring Currents in Annulated Pentalene and S-Indacene Cores Compared to First-Principles Current Density Maps. ChemPhysChem 2020, 21, 65–82. [Google Scholar] [CrossRef]
- Amnon Stanger, the Aroma Package. Available online: https://chemistry.technion.ac.il/en/team/amnon-stanger/ (accessed on 20 April 2022).
- Gershoni-Poranne, R.; Stanger, A. Magnetic criteria of aromaticity. Chem. Soc. Rev. 2015, 44, 6597–6615. [Google Scholar] [CrossRef]
- Steiner, E.; Fowler, P.W.; Soncini, A.; Jenneskens, L.W. Current-Density Maps as Probes of Aromaticity: Global and Clar π Ring Currents in Totally Resonant Polycyclic Aromatic Hydrocarbons. Faraday Discuss. 2007, 135, 309–323. [Google Scholar] [CrossRef]
- Szczepanik, D.W.; Solà, M.; Krygowski, T.M.; Szatylowicz, H.; Andrzejak, M.; Pawełek, B.; Dominikowska, J.; Kukułka, M.; Dyduch, K. Aromaticity of Acenes: The Model of Migrating π-Circuits. Phys. Chem. Chem. Phys. 2018, 20, 13430–13436. [Google Scholar] [CrossRef]
- Szczepanik, D.W.; Żak, E.; Dyduch, K.; Mrozek, J. Electron Delocalization Index Based on Bond Order Orbitals. Chem. Phys. Lett. 2014, 593, 154–159. [Google Scholar] [CrossRef]
- Szczepanik, D.W.; Andrzejak, M.; Dyduch, K.; Żak, E.; Makowski, M.; Mazur, G.; Mrozek, J. A Uniform Approach to the Description of Multicenter Bonding. Phys. Chem. Chem. Phys. 2014, 16, 20514–20523. [Google Scholar] [CrossRef] [PubMed]
- Szczepanik, D.W.; Solà, M. The Electron Density of Delocalized Bonds (EDDBs) as a Measure of Local and Global Aromaticity. In Aromaticity; Fernández, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 8; pp. 259–284. [Google Scholar]
- Homepage: D.W. Szczepanik—EDDB. Available online: http://www.eddb.pl/runeddb/gallery/ (accessed on 20 April 2022).
- Casati, N.; Kleppe, A.; Jephcoat, A.P.; Macchi, P. Putting Pressure on Aromaticity along with in Situ Experimental Electron Density of a Molecular Crystal. Nat. Commun. 2016, 7, 10901. [Google Scholar] [CrossRef] [PubMed]
- Genoni, A.; Macchi, P. Quantum Crystallography in the Last Decade: Developments and Outlooks. Crystals 2020, 10, 473. [Google Scholar] [CrossRef]
- Bader, R.F.W. A Quantum Theory of Molecular Structure and Its Applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; The International Series of Monographs on Chemistry; Clarendon Press: Oxford, UK; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Matta, C.F.; Hernández-Trujillo, J. Bonding in Polycyclic Aromatic Hydrocarbons in Terms of the Electron Density and of Electron Delocalization. J. Phys. Chem. A 2003, 107, 7496–7504. [Google Scholar] [CrossRef]
- Poater, J.; Fradera, X.; Duran, M.; Solà, M. The Delocalization Index as an Electronic Aromaticity Criterion: Application to a Series of Planar Polycyclic Aromatic Hydrocarbons. Chem. Eur. J. 2003, 9, 400–406. [Google Scholar] [CrossRef]
- Matito, E.; Duran, M.; Solà, M. The Aromatic Fluctuation Index (FLU): A New Aromaticity Index Based on Electron Delocalization. J. Chem. Phys. 2005, 122, 014109. [Google Scholar] [CrossRef]
- Bultinck, P.; Ponec, R.; van Damme, S. Multicenter Bond Indices as a New Measure of Aromaticity in Polycyclic Aromatic Hydrocarbons. J. Phys. Org. Chem. 2005, 18, 706–718. [Google Scholar] [CrossRef]
- Matito, E. An Electronic Aromaticity Index for Large Rings. Phys. Chem. Chem. Phys. 2016, 18, 11839–11846. [Google Scholar] [CrossRef]
- Feixas, F.; Matito, E.; Poater, J.; Solà, M. Quantifying aromaticity with electron delocalisation measures. Chem. Soc. Rev. 2015, 44, 6434–6451. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Gatti, C. A Green’s Function for the Density. Chem. Phys. Lett. 1998, 287, 233–238. [Google Scholar] [CrossRef]
- Gatti, C.; Saleh, G.; Lo Presti, L. Source Function Applied to Experimental Densities Reveals Subtle Electron-Delocalization Effects and Appraises Their Transferability Properties in Crystals. Acta Crystallogr. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 180–193. [Google Scholar] [CrossRef] [PubMed]
- Monza, E.; Gatti, C.; Lo Presti, L.; Ortoleva, E. Revealing Electron Delocalization through the Source Function. J. Phys. Chem. A 2011, 115, 12864–12878. [Google Scholar] [CrossRef]
- Szczepanik, D.W.; Andrzejak, M.; Dominikowska, J.; Pawełek, B.; Krygowski, T.M.; Szatylowicz, H.; Solà, M. The Electron Density of Delocalized Bonds (EDDB) Applied for Quantifying Aromaticity. Phys. Chem. Chem. Phys. 2017, 19, 28970–28981. [Google Scholar] [CrossRef] [PubMed]
- Szczepanik, D.W. RunEDDB, Version 26-Jun-2021. Available online: http://www.eddb.pl/runeddb/ (accessed on 20 April 2022).
- Gross, L.; Mohn, F.; Moll, N.; Liljeroth, P.; Meyer, G. The Chemical Structure of a Molecule Resolved by Atomic Force Microscopy. Science 2009, 325, 1110–1114. [Google Scholar] [CrossRef]
- Casademont-Reig, I.; Ramos-Cordoba, E.; Torrent-Sucarrat, M.; Matito, E. Aromaticity Descriptors Based on Electron Delocalization. In Aromaticity; Fernández, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 7; pp. 235–259. [Google Scholar]
- Curutchet, C.; Poater, J.; Sola, M.; Elguero, J. Analysis of the effects of n-substituents on some aspects of the aromaticity of imidazoles and pyrazoles. J. Phys. Chem. A 2011, 115, 8571–8577. [Google Scholar] [CrossRef] [PubMed]
- Stanger, A. Reexamination of NICS π,zz: Height Dependence, Off-Center Values, and Integration. J. Phys. Chem. A 2019, 123, 3922–3927. [Google Scholar] [CrossRef]
- Alonso, M.; Miranda, C.; Martin, N.; Herradon, B. Chemical applications of neural networks: Aromaticity of pyrimidine derivatives. Phys. Chem. Chem. Phys. 2011, 13, 20564–20574. [Google Scholar] [CrossRef]
- Wieczorkiewicz, P.A.; Szatylowicz, H.; Krygowski, T.M. Energetic and Geometric Characteristics of Substituents, Part 3: The Case of NO2 and NH2 Groups in Their Mono-Substituted Derivatives of Six-Membered Heterocycles. Symmetry 2022, 14, 145. [Google Scholar] [CrossRef]
- Matito, E.; Salvador, P.; Duran, M.; Solà, M. Aromaticity Measures from Fuzzy-Atom Bond Orders (FBO). The Aromatic Fluctuation (FLU) and the Para-Delocalization (PDI) Indexes. J. Phys. Chem. A 2006, 110, 5108–5113. [Google Scholar] [CrossRef]
- Szatylowicz, H.; Wieczorkiewicz, P.A.; Krygowski, T.M. Molecular Geometry as a Source of Electronic Structure of π-Electron Systems and Their Physicochemical Properties. In Aromaticity; Fernández, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 3; pp. 71–99. [Google Scholar]
- Szatylowicz, H.; Stasyuk, O.A.; Solà, M.; Krygowski, T.M. Aromaticity of Nucleic Acid Bases. WIREs Comput. Mol. Sci. 2021, 11, e1509. [Google Scholar] [CrossRef]
- Jezuita, A.; Szatylowicz, H.; Marek, P.H.; Krygowski, T.M. Aromaticity of the Most Stable Adenine and Purine Tautomers in Terms of Hückel’s 4N+2 Principle. Tetrahedron 2019, 75, 130474. [Google Scholar] [CrossRef]
- Mohajeri, A.; Shahamirian, M. Pi-electron delocalization in aza derivatives of naphthalene and indole. Comput. Theor. Chem. 2011, 976, 19–29. [Google Scholar] [CrossRef]
- Rakhi, R.; Suresh, C.H. A DFT study on dihydropyrazine annulated linear polyacenes: Aromaticity, stability and HOMO–LUMO energy modulation. Phys. Chem. Chem. Phys. 2016, 18, 24631–24641. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).