Abstract
In recent years, innovative progress in information and communication technology (ICT) has introduced new sources for traffic data collection and analysis. On-board sensors like GPS-GPRS boxes, generally installed for insurance purposes, communicate information from circulating vehicles to data centers. Geographic location, date and time, vehicles’ speed and direction, are systematically transmitted and stored as Historical Car Data (HCD) from probe vehicles in the traffic stream. These databases provide a good opportunity to analyze the vehicles’ motion both in the temporal and spatial domains. The aim of this study is to pay attention to the reliability of this kind of data gathering. Since instrumented vehicles account for a small percentage of the entire vehicle fleet, it is important to understand if they can be considered as a sample representative of the whole population. The paper presents a comparison of speed data obtained from HCD with the ones recorded by inductive-loop detectors and microwave radar sensors; the performed analysis required the definition of specific methodologies and procedures. The obtained results show a high correspondence between the two sets of data. Therefore, HCD can be proposed for the detailed monitoring of, and studies on, the operating conditions of mobility along road networks.
1. Introduction
Operating speeds are one of the crucial aspects for the management, monitoring and analysis of a road network; therefore, their assessment is an interesting and constantly evolving research topic [1,2]. In order to define traffic operating conditions based on actual speed data, different traffic measurement devices have been used over the years, which can be divided into two groups: static and dynamic ones.
Among the static devices, there are traditional traffic detectors, such as manual counting, as well as more advanced ones such as road detection stations, automatic traffic counters, video cameras, radar and laser guns, and point-based sensors, like microwave radars and acoustic sensors [3,4,5,6,7,8,9,10]. These methods have the valuable ability to sample the entire traffic flow, but at the same time show the impossibility of being able to guarantee a full coverage of the road network as it would require a significant economic investment. To overcome this limitation, innovative methods of collecting speed data have been tested through the use of vehicles equipped with GPS devices, capable of recording and sending travel information to operation centers with a high sampling rate [11,12,13,14,15,16]. This new data source allows researchers to observe real driver behavior and develop detailed models of operating speeds.
In contrast to punctual and isolated measurements, continuous speed data are useful for creating and studying actual driver speed profiles, in relation to the behavior adopted in different territorial contexts [17,18].
Recent innovative progress in the field of information and communication technologies (ICT) have further expanded and improved the connection between road users and the mobile network, simplifying the acquisition and exchange of a large amount of georeferenced data [19]. Specifically, the increasing use of mobile digital devices equipped with GPS, such as smartphones, tablets and black boxes mounted on vehicles for insurance purposes, generates a large and complex set of data, which are known as Big Data. It is therefore essential to define new tools and new methods able to store, manage and process them, through the definition of data-mining models [20,21,22,23,24].
The wide-scale collection of georeferenced data from road vehicles, known as Floating Car Data (FCD) if processed in real time or Historical Car Data (HCD) if collected and analyzed in different periods, represents one of the traffic monitoring tools today. It is a very effective and low-cost instrument for the study and evaluation of road traffic conditions. Its increasing use in road mobility analyses is due to the simplicity of the data acquisition method, as each vehicle anonymously sends data relating to the geolocation, speed, direction and date and travel time to a processing center. In particular, the FCD/HCD represent an alternative solution to measuring speeds, travel times and performances of the mobility system along a single road or the road network.
Since the vehicles which transmit data are free to move anywhere on the road network, they may be considered as floating probes in the traffic flow. Several studies have shown the potential of such data to deepen aspects such as drivers’ travel route prediction, proper perception by road users of the traffic signals, traffic conditions’ estimation and consistency evaluation between drivers’ behavior and theoretical design speeds in the various road elements [13,15,22,25,26,27,28].
Although probe vehicle data provide a large amount of information and represent an excellent technology to analyze the traffic conditions and to manage road mobility, they have the disadvantage of achieving a relatively low penetration rate. In fact, various studies state that vehicles equipped with GPS account for around 2–5% of the entire vehicle fleet [15,22,29,30], although in last few years this percentage has rapidly increased.
In order to conduct correct analyses of operating speeds, it is necessary to ensure that the data from the probe vehicles is adequately representative of the entire fleet, in terms of the number and type of vehicles. In recent years, several studies have tried to verify the reliability of these data samples, relying mainly on examining the accuracy of the FCD/HCD travel times and speeds’ estimation by comparing them with data recorded by point-based sensors; the assessments were carried out with regard to different categories of infrastructures and vehicles [31,32].
One of the earliest studies investigated the benefits and limitations of FCD technology by analyzing a particular case study that compared data obtained from a taxi-FCD fleet with data from license plate recognition (LPR). Travel times’ evaluation indicated that the taxi-FCD system could provide good information about travel times, but it was not sufficient for direct, sole application, due to the limited data available and the high variation in data coverage. However, it became a valuable tool for integrating the data collected by local sensors [33].
Subsequently, for the Beijing highways, which showed a high penetration rate of FCD, a regression analysis was performed between the data detected by the Remote Traffic Microwave Sensors (RTMS) and the speeds of the FCD, obtaining a high correlation between the two data samples with R2 equal to 0.97 [34].
Other studies have then assessed the speed quality of the dynamic surveys, comparing the measurements of the probe vehicles with the measurements of speed by the radar sensors. Good results were generally obtained, and in one case a regression analysis had showed a non-linear relationship with a correlation coefficient of 0.82 [35], while in another study it was observed that radar sensors tended to measure slower speeds than loop detectors during periods of free flow conditions [36]. In the latter case, it was found that radar measurements are generally good, but several aspects have been identified to consider before their implementation. Among these aspects, which can influence the quality of the measurements, are: lag, different data biases during the two phases of free and congested traffic, vulnerability to rainfall and sensitivity to the device mounting angle. On the other hand, FCD are certainly an important data source as they guarantee a higher spatial coverage and lower costs than the detectors installed. However, the accuracy and representativeness of the FCD sample is closely related to the number of probe vehicles and the quality of GPS geolocation and data transmission. Consequently, data from multiple sources are often managed and analyzed, i.e., static and floating sensors, because when used together they are capable of improving the knowledge of traffic status and of reducing the uncertainty of individual sources [14,37].
In this paper, in accordance with the scientific literature, the reliability of the HCD sample has been evaluated by directly comparing its information with the data recorded by inductive ring detectors and microwave radar sensors, in terms of speed distribution. The obtained results show a high correlation between the two data sources. A good representativeness of this type of speed data is demonstrated, despite the relatively low penetration rate of FCD.
2. Data and Methods
The analysis of the operating speed is an important topic to study in order to improve the knowledge of the operating conditions of a road network, as it allows the observation of the relationships between road users’ actual behavior and the characteristics of the infrastructure. Especially in road safety analyses, the operating speed is used to observe how it can be correlated with the frequency and severity of accidents along a route [38,39].
Generally, according to scientific literature, the operating speed is assumed to be the 85th percentile of the distribution of the actual speeds practiced by users [40,41]. Therefore, it is necessary that the data source adopted is as reliable as possible, in order to obtain operating speed profiles that effectively represent the actual trend. In the past, most operational speed models were based on speed data collected on specific road sections, through static acquisition methods, able to provide data only in the temporal domain. Subsequently, attempts were made to overcome this limitation by introducing and experimenting with innovative methods, in particular by collecting speed data from vehicles equipped with GPS systems. This new methodology allowed the researchers to observe the actual behavior of drivers and to develop more effective operating speed models, so providing a more accurate representation of the real phenomenon [42,43,44,45,46,47,48,49]. It has to be noted that the data from the point-based sensors refer only to the road sections in which they are installed, providing information only in the temporal domain. The probe vehicles, on the other hand, allow the observation of the data in the temporal and spatial domains, providing information on mobility for the entire route. Despite the advantages related to this new method of data collection, the reliability of speed data obtained from “floating cars” needs to be verified, due to the notable lack of instrumented vehicles when compared to the entire fleet.
In order to investigate this aspect, in this research the performed analyses were focused on identifying a correspondence between the HCD obtained from a sample of instrumented vehicles and the data returned by one of the classic traffic detection methods. In particular, it was decided to carry out a comparison of the HCD with the data collected by the Automatic Statistical Traffic Detection System of the Italian national road network manager, ANAS SpA. The Traffic Observatory is a structure that the company mainly uses to provide traffic data and information to users; all the sensors send their data to a central Platform for Monitoring and Analysis—called PANAMA—and the reliability of the acquired data is ensured by a series of control procedures [50].
In particular, the study analyzed the data that came from the measurement sections placed along the two-lane rural roads of the Veneto Region, managed by the ANAS Company, as shown in Figure 1:

Figure 1.
Location of the measuring sections along the state roads of the Veneto Region, reported in the legend.
A detailed traffic survey was available for each control unit. Among the different information, the variables employed for the analysis are shown in Table 1. In detail, Time Reference is the date and time of the data acquisition, Lane represents the lane on which the vehicle was traveling, Direction indicates the direction of travel, Speed (km/h) is the value of the speed recorded by the control unit and Vehicle Class is a code assigned to identify the different types of vehicles (i.e., 1–9 classes).

Table 1.
Example of Control unit traffic survey.
The sample of Historical Car Data, on the other hand, was acquired from a commercial operator who has GPS data coming anonymously from over four million black boxes mounted on passenger cars and heavy vehicles, in addition to those generated by 1.5 million Apps downloaded to customers’ smartphones [51].
The actual speeds’ extraction from Big Data did not take place in real time, but the HCD were used; these data were subsequently processed by means of a relational database management software with which it is possible to store and manage large amounts of data. Table 2 shows the most important information that can be extracted from the dataset for the proposed study: Identification code; Longitude (in WGS 84 coordinates); Latitude (in WGS 84 coordinates); Direction is the vehicle’s travel direction expressed as azimuth angle; Speed; Date and Time of the signal emission; Signal Quality; Vehicle ID is a code assigned by the collection center to each individual vehicle during its travel; Vehicle Type.

Table 2.
Example of Historical Car Data information.
The two data sources (point-based sensors and HCD) have provided information relating to a three months’ period, respectively, August 2018, February 2019 and May 2019, and located within the Veneto Region. Specifically, for the time period and the location analyzed, the HCD data sample amounts to almost one billion items of data, as shown in the following scheme (Table 3).

Table 3.
HCD sample within the Veneto Region in the three analyzed months.
A study of the statistical reliability of the data detected by the measurement sections was preliminarily performed. At first, the traffic flows recorded by the control units were divided into the two main travel directions, characterized by the lane (1 or 2)-direction (ascendant and descendant) combination, equal to “1A” and “2D”. Subsequently, the overtaking situations were identified by the combinations “1D” and “2A”.
The raw data show a trend similar to the Gaussian distribution, as it is generally recognized in the literature [52]. As can be seen from Figure 2, the average value is located near the center of the distribution and the trend is mainly symmetrical to it. Furthermore, most of the surveys are located around the mean value, specifically it is noted that 75% of the speed values are in the range (μ − σ, μ + σ), in terms of mean square deviations, and that 95% of the speed values are in the range (μ − 2σ, μ + 2σ).
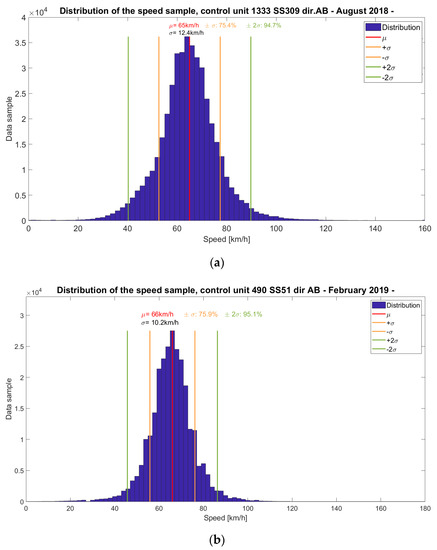
Figure 2.
Control units’ speed samples’ distributions: (a) Control unit 1333, AB direction, August 2018; (b) Control unit 490, AB direction, February 2019.
These trends confirm that the experimental data can be represented by a statistical model, whose parameters can be known and are shown, as an example, in Figure 2. Indeed, the trend is in agreement with the classical statistical modeling of traffic flows; the data sample does not present anomalies due to local or special phenomena. From the observation of the reliability and representativeness of this sample, it is possible to use them for more advanced studies, such as the one addressed in this study.
The HCD data sample contains all the data sent from the instrumented vehicles within the Veneto Region; therefore, data filtering operations were performed, in order to continue with their reliability research. The study started with the geometric reconstruction of the road alignments, using an automated, economical and rapid method capable of identifying the elements of existing road layouts through the georeferenced vertices of the road graph [53]. Once the horizontal alignment of the road layouts were known, a map-matching procedure was performed, by which the geographic coordinates of the vehicles were matched to the graph of each road [54,55,56,57,58,59,60].
The map matching was carried out using a programming code, with which the raw HCD near the examined road are preliminarily identified and subsequently projected onto the curvilinear abscissa. However, since the GPS signal on board the vehicles could be affected by intrinsic or accidental errors, the position accuracy could be low; the area of investigation was expanded to avoid eliminating from the analysis those vehicles that had a slightly inaccurate location compared to their actual position. At the end of the map-matching procedure, the point speed data extracted from the HCD were divided into the two main travel directions.
The two analyzed data samples differed in the domain in which they were defined. The point-based sensors provided a very detailed traffic survey in the temporal domain, at the forced and constant sections where they were installed. Instead, the HCD allowed the observation of a tiny sample of the vehicle fleet along the entire road network, providing data in both the temporal and spatial domains. For this reason, to carry out a direct comparison between the two data samples, the proposed analysis method involved a preliminary restriction of the spatial domain of the HCD, taking into consideration the only data was located 10 m forward and 10 m behind the control unit. The reason for this spatial interval is to consider the possibility that the vehicle recorded by the control unit may have emitted the signal not exactly in correspondence with the measurement section, but a few meters before or after it. The HCD sample is constituted of temporal-spatial information whose sampling frequency is 1 Hz. This high sampling rate is sufficient to consider the HCD located just 10 m forward and 10 m behind the control unit. If the frequency was lower the spatial interval would be much bigger, with the risk of contributing to a less accurate analysis, because of the speeds changing along the explored road stretch.
After the first filtering operation on the HCD sample, it was possible to evaluate a representative rate of the GPS data around each analyzed control unit. The evaluation was performed as a ratio of the HCD, located near the control unit, and the vehicles recorded by the control unit itself. Table 4 lists the values of the relationship between the probe vehicles and the entire vehicle flow passing through the sections where the point-based sensors are located, which are about 1–2‰, with an average value of 1.4‰.

Table 4.
Values of the representativeness rate of the HCD sample evaluated for each control unit.
A study of the statistical parameters of the GPS data set has been performed through a preliminary histogram representation of the HCD speeds, as shown in Figure 3. The speed data suggest again a shape similar to the one of a Gaussian distribution, even if the two diagrams show some irregularities due to the low amount of data in some speed classes. However, it has to be noticed that the statistical parameters of the distributions of both sensors and HCD are comparable. Therefore, it can be stated that a small sample of data (the HCD) can represent the behavior of the entire traffic flow.
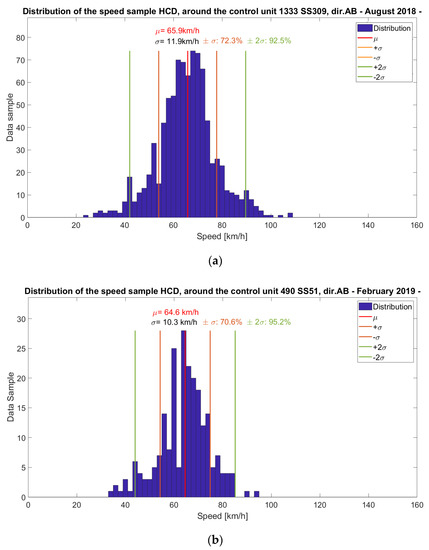
Figure 3.
HCD speed samples’ distributions: (a) close to the control unit 1333, AB direction, August 2018; (b) close to the control unit 490, AB direction, February 2019.
Finally, in order to complete the overall evaluation of the reliability of the HCD and their correspondence with the data recorded by the control units, it has been necessary to extend the analysis of the two samples also in the temporal domain. The second filtering operation of the HCD sample identified the data from the probe vehicles in the same time frame defined by the traffic measurement stations. A methodology was therefore defined that made it possible to directly compare the speed data extracted from the two different sources, evaluating their coherence and correspondence through a linear regression. The reliability of the obtained result can thus be interpreted by means of the coefficient of determination R2, which measures the weak or strong linear relationship between the two variables compared, assuming a value between 0 and 1.
3. Results
The reliability evaluation of the HCD has been performed by direct comparison with the traffic data recorded by a set of point-based sensors placed in the investigated road network. Due to the big difference between the two datasets, as the HCD sample provides space-time information while the control units only record data in the time domain, it has been necessary to properly filter the HCD.
Firstly, the HCD close to the measurement stations have been identified and selected; then, as shown in Figure 4, the speed data extracted from the two different sources have been overlapped in the same graph as a function of time. In Figure 4, the representation of the Gaussian distributions of the two different data samples is flanked (on the right side) by the speed-time graph (on the left side).
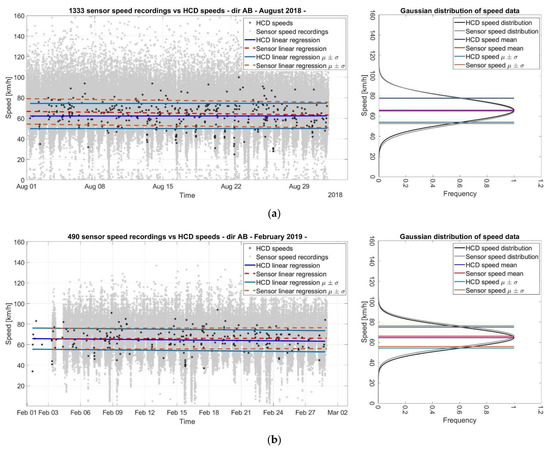
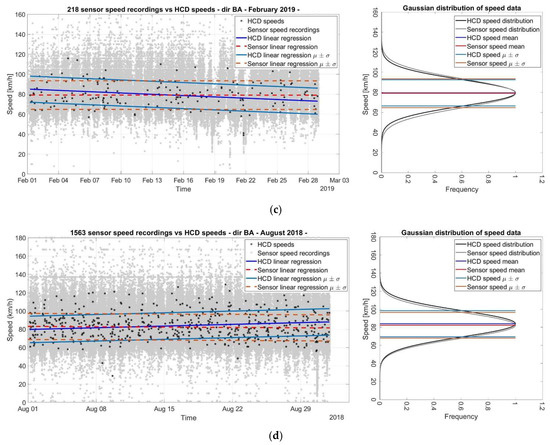
Figure 4.
Control units vs. HCD speed samples and linear regressions as a function of time: (a) Control unit 1333, AB direction, August 2018; (b) Control unit 490, AB direction, February 2019; (c) Control unit 218, BA direction, February 2019; (d) Control unit 1563, BA direction, August 2018.
From the graphs in Figure 4, the following observations can be deduced:
- Observing the Gaussian distributions, an overlap of the two trends can be noticed, and it demonstrates how the two samples can be considered statistically coincident, as their main parameters are almost equal;
- The mean and the standard deviations linear regression lines of the two data samples in the speed-time diagrams approximate the mean and standard deviations of the Gaussian distributions displayed in the diagrams on the right;
- The point cloud of the control units’ data completely encloses the HCD values. As has been said before, the probe vehicles account for a small percentage of the vehicle fleet, which is, instead, completely detected by the fixed sensors;
- Fluctuations in the graphs, especially their peaks and troughs, are similar between the HCD and the point-based-sensor point cloud; therefore, a matching between the qualitative trends of the data samples can be observed;
- The linear regressions on the data show almost constant values as the lines are slightly inclined, with angular coefficients close to zero and intercept equal to the average speed;
- There is a minimal difference between the average speed values, evaluated, respectively, from the two data samples, which generally assumes a value of around 3 km/h. These minor differences are probably caused by systematic errors, linked to sensor calibration defects or to errors caused by the relative angle between the signals emitted and received by the radar sensors and the vehicles’ driving direction. The point-based sensors are in fact located on the sides of the carriageway and are not in line with the lanes;
- The two linear regression lines have been moved vertically on and under by a value equal to the corresponding standard deviation. In this way, it can be observed that the data dispersion is almost coincident between the two samples and that the only difference is due to the systematic error;
- Most of the HCD fall into the range defined by the ± σ linear regression parallel, thus demonstrating the strong reliability of the sample, which is located around the average speed values.
The two tables in Appendix A (Table A1 and Table A2) show the results from all the measurement sections that were analyzed. The results indicate the values of the angular coefficient m, the intercept q of the regression lines, the average speed μ referred to each monitored month and the standard deviation σ of the speeds for both the data recorded by the control units and for the HCD.
A second data filtering has been performed on the HCD to identify the information emitted by the probe vehicles in a time interval coincident with the measurements made by the point-based sensors. The results have been plotted and are shown in Figure 5: the graphs show the HCD speeds on the x-axis and the speeds recorded by the control units on the y-axis.
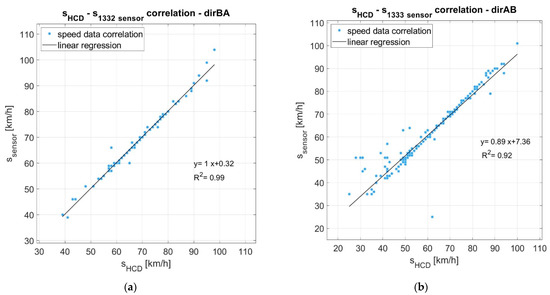
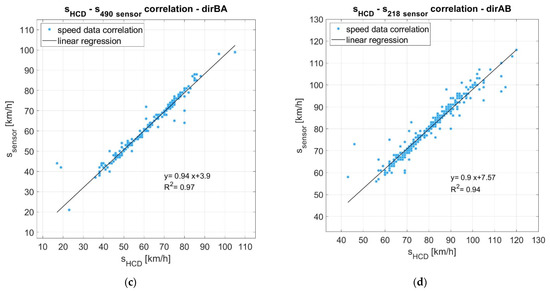
Figure 5.
HCD and sensors’ speeds’ samples correlation: (a) Control unit 1332, BA direction; (b) Control unit 1333, AB direction; (c) Control unit 490, BA direction; (d) Control unit 218, BA direction.
As shown in Figure 5, the reliability assessment was performed considering the linear regression between the speed data from the two different data sources, and the following observations are carried out:
- The very good correspondence between the data is proved by the points’ arrangement and concentration along the diagram bisector: speed data acquired by the HCD has been also recorded by the control units, with minimal deviations;
- A regression line facilitates the graph readability: it immediately shows how much the dispersion of the recorded data approaches or deviates from the bisector, by means of its angular coefficient value;
- Therefore, the data correspondence is also readable through the coefficient of determination R2, which is almost always close to 1;
- Minor deviations come from outlier points within the sample, generally related to very low speed values of the HCD. Probably these anomalies are related to vehicles, close to the control unit, performing maneuvers outside the carriageway. This is an intrinsic limit due to the characteristics of the GPS systems;
- The problem observed in the previous point cannot be completely ignored, but paying attention to the central zone of the graph, it is always found that most of the points are near the bisector, and it corresponds to the most plausible speeds assumed along the examined roads.
The two diagrams shown in Figure 6 summarize the results obtained, shown as a cumulative curve, with which it is possible to observe the percentage of cases with a specific value of R2. The percentage distribution of the results shows that almost 80% of the analyzed comparisons return an R2 greater than 0.8, demonstrating the reliability of the HCD sample and its application for more advanced monitoring studies.
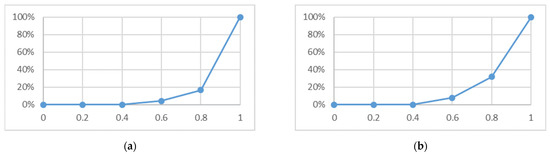
Figure 6.
Cumulative percentage diagram of the obtained values of the coefficients of determination R2: (a) Percentage distribution of the coefficients of determination R2 for the whole sample of analyzed data, evaluated for the driving direction AB; (b) Percentage distribution of the obtained values of the coefficients of determination R2 for the whole sample of analyzed data, evaluated for the driving direction BA.
The two tables (Table A3 and Table A4) presented in Appendix A, one per each driving direction, are presented to summarize the angular coefficient m, the intercept q of the regression lines, and the coefficient of determination values obtained for all the measurement sections.
4. Discussion
The proposed original method for evaluating the reliability of a sample of HCD obtains good results, by comparing speed values from probe vehicles and measurement stations. However, as can be seen in Table A3 and Table A4, not all the results show a good correspondence between the two samples of data, since the angular coefficient m and the coefficient of determination R2 in some cases are far from value 1. However, these results are acceptable considering the hypotheses and the aims of this study. First, it should be noted that the research carried out does not attempt to establish an instantaneous comparison in time and space between the GPS data and the traffic measurements performed by the control units, but a correspondence of data both in statistical terms and in terms of actual vehicular speeds. Therefore, thanks to the study, a reliable and representative data source of the driving population can be identified in the small sample of HCD, even if a very high match is not achieved in all cases.
The high sampling rate of GPS data has allowed us to carry out an accurate analysis through the different filtering phases. The most important filtering operation was to consider in the analysis only the HCD emitted 10 m forward and 10 m behind the control unit. When HCD have been recorded in mountainous environments, technical problems related to both poor satellite coverage and quality of GPS signal were found. The probe vehicles, in fact, send little or incorrect information in that territory. Another reason to explain anomalous information can be related to the location of some measurement sections along the infrastructure, for example near tunnels. The presence of the tunnel determines a GPS signal loss, resulting in low data quality; consequently, this kind of data could be not representative and have been excluded from the analysis. Observing Figure 5, the presence of outliers affects the final outcome of the analysis, which results in R2 values not close to 1. By examining the proposed calculation method, it can be said that outliers may have been generated by different causes. It is likely that some vehicles had a lower-than-average emission frequency, and so did not register in the defined spatial and temporal interval around the control unit. As a result, the data recorded by the control unit did not find the corresponding vehicle in the filtered sample of the HCD. In relation to the frequency, it may happen that a given GPS signal is emitted inside the analyzed interval, but towards the beginning of it: in this case the driver could change the driving speed in the meantime, so that the control unit may have detected the same vehicle but at a different speed. Moreover, by investigating geographical maps, in cases where the examined road section presents another parallel road close to it, it is possible that the geolocalized data does not belong to the studied road, due to errors related to the GPS detection system. In general, although sometimes less valid results in terms of determination coefficient have been found, in most cases the reliability of the HCD sample should be considered acceptable. In Figure 5, ignoring the outliers, it is notable that there is a concentration of the speed data along the bisector, especially in the speed range between 50–80 km/h, which represents indeed the range of operating speeds on the examined roads. Therefore, the point cloud thus distributed shows that the data obtained from probe vehicles are actually reliable and can be considered representative of the entire vehicle fleet, except for some individual cases that relate to the availability or quality of HCD.
5. Conclusions
This paper presents a reliability study of Historical Car Data (HCD), evaluating their correlation in terms of actual vehicular speeds with the data recorded by sensors installed along existing roads. The sample of the analyzed data revealed that it is possible to obtain information from them to describe operational variables of the entire vehicular flow, in terms of speed profile and the typical behavior of user drivers.
The main objective of this study is to understand the reliability of this kind of data, with the aim of validating them, so the data can be used for all analyses that are needed in road safety studies and road network management. Regardless of the different traffic conditions across different time periods of the day, a daily analysis of the data has not been developed because that was not a specific aim of the study. Another limitation of the study is that, considering that the environmental and traffic conditions are different between rural and urban roads, the research wanted to observe the operational parameters of traffic flow only under the unconstrained conditions that are typical of rural roads. Therefore, the results of the study allow general conclusions to be obtained about the reliability of HCD which are valid only for this kind of context.
The achieved results show a high HCD reliability and representativeness of the traffic flow, achieving R2 > 0.9 in most cases. The statistical comparison of the GPS data with a typically recognized source, such as that of the control units, allows the opportunity to be extended to utilize HCD samples for safety and management assessments on road networks, despite the fact that, to date, the instrumented vehicles account for a small percentage of the entire vehicle fleet.
The sample of the control units captures a great proportion of all the traffic flow, with the exception of those vehicles which, for example, decide to enter or exit from the surveyed road, right before the sensor location; therefore, it represents a large sample, that it might almost represent the entire population. In contrast, the HCD sample is very small, and, on average, accounts for 1.4‰ of the traffic surveyed by the sensor; however, focusing on their statistical distributions and related variables, they have lot of similarities to each other. As a result, both the control units and HCD can be used to represent key features of the whole population, like traffic flow characteristics and operating conditions. In particular, the control units provide complete information about traffic stream and its sensitivity to certain variables, such as environmental conditions, differences between hours of night and day or the presence of heavy vehicles in the traffic flow. The HCD, instead, are useful to make data available about both the single driver’s behavior and the vehicular path and speed along the entire route. In other words, the control units are especially useful for data about traffic patterns, while GPS data are suitable to perform a monitoring of the vehicular motion along the entire infrastructure. This conclusion agrees with the literature, where HCD have been proposed to study drivers’ travel route prediction, the proper perception by road users of the traffic signals, traffic conditions’ estimation and consistency evaluation between drivers’ behavior and theoretical design speeds in the various road elements.
More generally, the results obtained from this research support the thesis that Big Data, and specifically HCD, can be adopted as an essential data source to carry out important analyses on the operational conditions of road traffic. Furthermore, by exploiting the large amount of information associated with each type of data, it is possible to extend the survey by identifying many factors that influence the traffic conditions, even if the evaluation analyses require specific methodologies and procedures.
In particular, the Historical Car Data allows the extraction of continuous operating speed profiles along infrastructures and networks, because of the data’s geolocation along the entire road layout and the high sampling rate. It should be noted that this data source allows the main limits associated with the traditional methods of traffic surveys to be overcome, with which the information is related only to the sections in which the sensors are installed.
In light of the statistical reliability and trustworthiness of the HCD sample, the authors want to extend the research to implementing innovative mobility analysis processes, thanks to the quantitative and qualitative advantages offered by the HCD. In this way, a detailed and continuous monitoring of the actual operating conditions of road traffic can be performed.
Author Contributions
Conceptualization, G.C. and G.D.S.; methodology, G.D.S.; software, P.P.; validation, G.C., G.D.S. and P.P.; formal analysis, G.C.; investigation, P.P.; resources, G.C.; data curation, P.P.; writing—original draft preparation, P.P.; writing—review and editing, G.C. and G.D.S.; visualization, P.P.; supervision, G.C.; project administration, G.D.S.; funding acquisition, G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to confidentiality issues and respect for privacy.
Acknowledgments
We thank the national public company ANAS for making its Traffic Observatory information available and for the technical support.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
HCD and sensors angular coefficients m, and intercepts q of the regression lines, average speeds μ, and the standard deviations σ referred to each monitored month in Dir AB.
Table A1.
HCD and sensors angular coefficients m, and intercepts q of the regression lines, average speeds μ, and the standard deviations σ referred to each monitored month in Dir AB.
| Historical Car Data | Sensor Recordings | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sensor ID | Road Name | Month | m | q | μ | σ | m | q | Μ | σ |
| (-) | (km/h) | (km/h) | (km/h) | (-) | (km/h) | (km/h) | (km/h) | |||
| 197 | SS12 | August 2018 | 0.21 | 59.29 | 62.11 | 13.75 | −0.09 | 64.81 | 63.37 | 11.3 |
| February 2019 | −0.15 | 75.15 | 73.08 | 13.8 | 0.03 | 65.81 | 66.32 | 12.11 | ||
| May 2019 | −0.04 | 72.7 | 72.07 | 12.26 | 0.01 | 65.69 | 65.88 | 12.42 | ||
| 208 | SS13 | August 2018 | 0.02 | 67.53 | 67.8 | 10.22 | −0.04 | 70.36 | 69.77 | 10.69 |
| February 2019 | 0 | 65.8 | 65.77 | 9.53 | 0.02 | 67.96 | 68.29 | 9.99 | ||
| May 2019 | −0.01 | 66.02 | 65.86 | 9.52 | 0.03 | 67.52 | 68.03 | 11.01 | ||
| 209 | SS13 | August 2018 | 0.21 | 57.08 | 60.03 | 10.82 | −0.03 | 61.92 | 61.45 | 12.17 |
| February 2019 | 0.02 | 56.48 | 56.73 | 10.92 | 0.02 | 58.27 | 58.57 | 11.52 | ||
| May 2019 | −0.12 | 61.92 | 60.25 | 11.02 | 0 | 58.48 | 58.53 | 11.63 | ||
| 920,074 | SS13 | August 2018 | 0.23 | 65.21 | 68.47 | 12.32 | −0.03 | 73.09 | 72.63 | 12.46 |
| February 2019 | 0.03 | 66.78 | 67.21 | 11 | 0.03 | 68.97 | 69.39 | 11.21 | ||
| May 2019 | 0.17 | 64.72 | 67.18 | 12.58 | 0 | 70.03 | 70.01 | 11.78 | ||
| 218 | SS14 | August 2018 | −0.14 | 82.31 | 80.35 | 11.1 | 0.02 | 77.95 | 78.32 | 13.56 |
| February 2019 | 0.07 | 76.77 | 77.77 | 12.32 | −0.03 | 78.98 | 78.48 | 13.75 | ||
| May 2019 | 0.03 | 77.77 | 78.12 | 10.67 | −0.03 | 77.39 | 76.93 | 14.56 | ||
| 219 | SS14 | August 2018 | −0.11 | 74.11 | 72.52 | 11.21 | 0.07 | 74.1 | 75.06 | 12.47 |
| February 2019 | −0.22 | 72.13 | 68.75 | 14.55 | −0.03 | 73.64 | 73.14 | 13.24 | ||
| May 2019 | 0.07 | 71.28 | 72.31 | 11.67 | −0.08 | 74.95 | 73.64 | 12.16 | ||
| 3191 | SS14 | August 2018 | −0.13 | 74.72 | 72.73 | 10.96 | 0.06 | 73.65 | 74.58 | 10.72 |
| February 2019 | −0.04 | 78.89 | 78.26 | 10.71 | 0.01 | 80.61 | 80.71 | 12.23 | ||
| May 2019 | −0.12 | 79.16 | 77.32 | 11.11 | 0 | 77.98 | 77.99 | 11.6 | ||
| 481 | SS50 | August 2018 | 0.2 | 68.25 | 71.24 | 11.52 | −0.02 | 64.85 | 64.61 | 10.59 |
| February 2019 | −0.15 | 74.1 | 72.13 | 11.22 | 0.22 | 59.2 | 63.23 | 10.73 | ||
| May 2019 | 0.26 | 68.56 | 72.43 | 11.96 | −0.08 | 65.54 | 64.34 | 10.32 | ||
| 482 | SS50 | August 2018 | 0.22 | 77.26 | 80.53 | 11.34 | −0.39 | 76.22 | 71.16 | 19.38 |
| February 2019 | −0.21 | 87.01 | 84.08 | 15.44 | 0.14 | 77.68 | 77.8 | 19.61 | ||
| May 2019 | 0.12 | 79.62 | 81.07 | 10.05 | −1.07 | 71.39 | 55.14 | 29.78 | ||
| 2404 | SS50 | May 2019 | −0.12 | 71.26 | 69.21 | 10.13 | −0.12 | 83.44 | 81.93 | 13.38 |
| 487 | SS51 | August 2018 | −0.46 | 64.88 | 60.6 | 12.4 | −0.06 | 61.14 | 60.28 | 13.62 |
| February 2019 | −0.15 | 67.59 | 66.23 | 12.7 | 0.05 | 65.27 | 66.01 | 12.54 | ||
| May 2019 | −0.48 | 78.11 | 71.4 | 14.59 | −0.03 | 65.78 | 65.25 | 13.35 | ||
| 489 | SS51 | August 2018 | 0.01 | 65.45 | 65.63 | 8.15 | −0.03 | 67.49 | 67.09 | 12.53 |
| February 2019 | 0.11 | 63.31 | 64.82 | 10.65 | 0.07 | 67.3 | 68.37 | 12.55 | ||
| May 2019 | 0.13 | 61.94 | 63.86 | 10.52 | −0.04 | 68.65 | 68.08 | 12.53 | ||
| 490 | SS51 | August 2018 | 0.25 | 51.39 | 54.8 | 16.66 | 0.15 | 56.58 | 58.84 | 14.89 |
| February 2019 | −0.09 | 65.89 | 64.59 | 10.29 | 0.02 | 65.69 | 66.02 | 10.15 | ||
| May 2019 | −0.04 | 66.92 | 66.29 | 10.92 | −0.07 | 68.38 | 67.2 | 10.15 | ||
| 491 | SS51 | August 2018 | 0.09 | 43.35 | 44.66 | 5.2 | −0.03 | 41.93 | 41.46 | 5.67 |
| February 2019 | 0.06 | 45.26 | 46.19 | 6.8 | 0.16 | 40.4 | 42.8 | 6.49 | ||
| May 2019 | −0.09 | 48.34 | 47.3 | 5.86 | −0.04 | 44.84 | 44.2 | 6.54 | ||
| 492 | SS51 | August 2018 | 0.13 | 66.24 | 68.23 | 10.92 | −0.01 | 61.23 | 61.07 | 11.93 |
| February 2019 | −0.11 | 71.66 | 70.16 | 10.55 | 0.46 | 59.81 | 62.93 | 10.02 | ||
| 10,040 | SS51 | August 2018 | −1.76 | 72.99 | 50 | 30.13 | 0.02 | 84.03 | 84.28 | 13.8 |
| February 2019 | 3.54 | 20.84 | 61.2 | 30.88 | 0.42 | 81.94 | 87.67 | 18.58 | ||
| May 2019 | 0 | 79 | 79 | 0 | −0.02 | 93.22 | 93.04 | 15.08 | ||
| 920,075 | SS51 | August 2018 | 0.14 | 49.5 | 51.58 | 6.04 | 0.01 | 54.36 | 54.54 | 9.36 |
| 494 | SS51-bis | August 2018 | 0.07 | 54.65 | 55.55 | 7.08 | 0.01 | 50.82 | 50.91 | 7.31 |
| February 2019 | 0.07 | 54.94 | 56.02 | 8.17 | 0.34 | 46.93 | 53.19 | 8.14 | ||
| May 2019 | −0.17 | 58.87 | 56.16 | 6.36 | −0.01 | 54.01 | 53.85 | 8.08 | ||
| 498 | SS52 | August 2018 | 6.42 | 17.96 | 51 | 23.45 | −0.08 | 72.59 | 71.44 | 15.58 |
| February 2019 | \ | \ | \ | \ | \ | \ | \ | \ | ||
| May 2019 | \ | \ | \ | \ | \ | \ | \ | \ | ||
| 499 | SS52 | August 2018 | −0.04 | 51.57 | 51.06 | 5.44 | 0.04 | 52.43 | 52.99 | 9.15 |
| February 2019 | 0.14 | 50.49 | 52.32 | 8.14 | 0.66 | 43.03 | 54.49 | 11.04 | ||
| May 2019 | 0 | 49 | 49 | 0 | 0.01 | 57.01 | 57.17 | 11.27 | ||
| 3193 | SS52 | August 2018 | 0 | 59.36 | 59.4 | 8.62 | −0.01 | 55.2 | 55.01 | 9.49 |
| February 2019 | −0.07 | 65.9 | 65 | 9.73 | 0.27 | 57.41 | 61.36 | 10.58 | ||
| May 2019 | −0.21 | 71.76 | 68.97 | 9.29 | −0.08 | 65.07 | 63.81 | 11.27 | ||
| 920,076 | SS52 | August 2018 | 0 | 37 | 37 | 3 | 0.07 | 38.62 | 39.72 | 10.05 |
| February 2019 | 0.5 | 42 | 43.5 | 2.12 | 0.13 | 40.78 | 43.29 | 9.69 | ||
| May 2019 | 86,400.03 | 35 | 36 | 1.41 | 0.11 | 42.34 | 44.19 | 10.92 | ||
| 503 | SS53 | August 2018 | 0.02 | 63.57 | 63.83 | 14.03 | 0.19 | 65.1 | 68.09 | 11.9 |
| February 2019 | 0.05 | 65.22 | 65.97 | 8.18 | 0.01 | 69.22 | 69.35 | 9.05 | ||
| May 2019 | −0.07 | 65.74 | 64.73 | 8.79 | −0.05 | 68.54 | 67.7 | 9.62 | ||
| 1332 | SS309 | August 2018 | 0.36 | 64.9 | 70.7 | 12.68 | −0.02 | 73.77 | 73.45 | 12.39 |
| 1333 | SS309 | August 2018 | 0.01 | 62.22 | 62.31 | 12.27 | −0.11 | 66.75 | 65.01 | 12.37 |
| 1563 | SS434 | August 2018 | −0.19 | 94.47 | 91.47 | 16.48 | −0.05 | 96.73 | 95.98 | 14.6 |
| 1703 | SS516 | August 2018 | 0.02 | 69.08 | 69.36 | 10.11 | −0.1 | 74.45 | 72.89 | 15.94 |
| February 2019 | −0.15 | 74.76 | 72.57 | 11.08 | −0.05 | 77.02 | 76.69 | 14.44 | ||
| May 2019 | −0.05 | 72.52 | 71.93 | 11.66 | 0.08 | 74.54 | 75.78 | 13.88 | ||

Table A2.
HCD and sensors angular coefficients m, and intercepts q of the regression lines, average speeds μ, and the standard deviations σ referred to each monitored month in Dir BA.
Table A2.
HCD and sensors angular coefficients m, and intercepts q of the regression lines, average speeds μ, and the standard deviations σ referred to each monitored month in Dir BA.
| Historical Car Data | Sensor Recordings | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sensor ID | Road Name | Month | m | q | μ | σ | m | q | μ | σ |
| (-) | (km/h) | (km/h) | (km/h) | (-) | (km/h) | (km/h) | (km/h) | |||
| 197 | SS12 | August 2018 | −0.45 | 76.14 | 69.15 | 12.08 | 0.11 | 64.29 | 65.88 | 13.59 |
| February 2019 | −0.42 | 81.27 | 75.55 | 15.48 | 0.06 | 70.81 | 71.54 | 14.44 | ||
| May 2019 | −0.72 | 83.66 | 73.14 | 14.46 | 0.01 | 69.97 | 70.06 | 14.19 | ||
| 208 | SS13 | August 2018 | −0.1 | 69.09 | 67.5 | 9.92 | −0.02 | 64.75 | 64.37 | 9.92 |
| February 2019 | 0.05 | 65.82 | 66.54 | 8.72 | 0.02 | 62.42 | 62.76 | 9.29 | ||
| May 2019 | 0 | 67.44 | 67.48 | 9.71 | 0.01 | 62.66 | 62.81 | 9.39 | ||
| 209 | SS13 | August 2018 | 0.14 | 56.83 | 59.11 | 10.52 | −0.07 | 64.5 | 63.4 | 12.46 |
| February 2019 | 0.13 | 55.77 | 57.58 | 9.82 | 0.02 | 60.01 | 60.26 | 11.69 | ||
| May 2019 | 0.21 | 54.55 | 57.57 | 10.74 | 0.03 | 60.9 | 61.3 | 11.27 | ||
| 920,074 | SS13 | August 2018 | 0.04 | 66.74 | 67.44 | 7.69 | −0.02 | 69.29 | 69 | 12.03 |
| February 2019 | 0.15 | 65.22 | 67.45 | 9.91 | −0.01 | 66.57 | 66.48 | 11.37 | ||
| May 2019 | 0.13 | 65.63 | 67.52 | 9.96 | 0 | 67.06 | 67.02 | 11.9 | ||
| 218 | SS14 | August 2018 | −0.14 | 83.57 | 81.39 | 12.9 | 0.02 | 79.51 | 79.78 | 13.53 |
| February 2019 | −0.43 | 85.02 | 79.49 | 13.04 | 0 | 79.16 | 79.09 | 14.34 | ||
| May 2019 | −0.17 | 79.21 | 76.77 | 12.26 | 0.04 | 77.87 | 78.45 | 13.8 | ||
| 219 | SS14 | August 2018 | −0.14 | 74.08 | 71.9 | 10.59 | −0.02 | 62.52 | 62.2 | 20.04 |
| February 2019 | 0.04 | 70.23 | 70.78 | 9.39 | 0.14 | 56.08 | 58.42 | 26.71 | ||
| May 2019 | −0.16 | 72.88 | 70.61 | 10.98 | −0.13 | 67.82 | 65.72 | 21.32 | ||
| 3191 | SS14 | August 2018 | 0 | 70.67 | 70.62 | 9.94 | −0.01 | 70.3 | 70.2 | 12.19 |
| February 2019 | −0.01 | 76.89 | 76.74 | 10.53 | 0 | 75.66 | 75.7 | 13.23 | ||
| May 2019 | 0.02 | 74.73 | 75 | 9.97 | 0.03 | 73.77 | 74.2 | 12.43 | ||
| 481 | SS50 | August 2018 | 0.03 | 71.2 | 71.74 | 11.73 | 0 | 77.29 | 77.3 | 13.07 |
| February 2019 | 0 | 70.85 | 70.82 | 12.42 | 0.22 | 73.28 | 77.21 | 13.12 | ||
| May 2019 | 0.01 | 71.83 | 71.98 | 11.63 | −0.05 | 78.43 | 77.7 | 12.87 | ||
| 482 | SS50 | August 2018 | 0.15 | 73.37 | 75.67 | 11.85 | 0.05 | 75.79 | 76.56 | 12.03 |
| February 2019 | 0 | 76.5 | 76.54 | 13.69 | 0.2 | 74.85 | 78.43 | 13.44 | ||
| May 2019 | −0.05 | 79.63 | 78.95 | 16.12 | −0.03 | 78.7 | 78.26 | 12.69 | ||
| 2404 | SS50 | May 2019 | 0.58 | 67.27 | 75.6 | 18.87 | −0.11 | 83.08 | 81.79 | 13.69 |
| 487 | SS51 | August 2018 | 0.48 | 51.91 | 57.85 | 11.21 | 0.05 | 60.49 | 61.29 | 14.39 |
| February 2019 | −0.28 | 71.91 | 67.58 | 13.23 | 0.03 | 68.09 | 68.55 | 14.59 | ||
| May 2019 | −0.04 | 60.44 | 60.03 | 11.88 | −0.11 | 69.87 | 68.21 | 15.79 | ||
| 489 | SS51 | August 2018 | 0.15 | 62.82 | 65.13 | 8.9 | −0.03 | 66.01 | 65.55 | 11.89 |
| February 2019 | −0.03 | 69.08 | 68.68 | 13.92 | 0.09 | 63.63 | 64.9 | 11.74 | ||
| May 2019 | −0.12 | 69.61 | 67.75 | 12.97 | −0.04 | 65.95 | 65.26 | 11.92 | ||
| 490 | SS51 | August 2018 | −0.03 | 58.92 | 58.45 | 8.76 | −0.01 | 58.96 | 58.75 | 9.98 |
| February 2019 | 0.12 | 59.76 | 61.6 | 9.98 | −0.03 | 62.51 | 62.13 | 11.1 | ||
| May 2019 | 0.09 | 65.02 | 66.37 | 9.65 | −0.07 | 65.68 | 64.54 | 10.88 | ||
| 491 | SS51 | August 2018 | −0.03 | 44.59 | 44.08 | 4.43 | 0 | 50.79 | 50.84 | 6.9 |
| February 2019 | −0.08 | 46.55 | 45.38 | 5.58 | 0.21 | 49.62 | 52.71 | 7.51 | ||
| May 2019 | −0.18 | 49.05 | 46.6 | 5.8 | −0.05 | 55.3 | 54.44 | 7.9 | ||
| 492 | SS51 | August 2018 | −0.05 | 62.69 | 62 | 9.9 | 0 | 72.14 | 72.16 | 12.09 |
| February 2019 | −0.09 | 67.26 | 66.02 | 9.42 | 0.49 | 70.7 | 73.81 | 11.19 | ||
| 10,040 | SS51 | August 2018 | 0.52 | 55.08 | 63.59 | 22.03 | −0.07 | 73.13 | 72.13 | 13.43 |
| February 2019 | 0.65 | 59.92 | 69.72 | 21.84 | 0.06 | 73.26 | 74.16 | 19.28 | ||
| May 2019 | −0.17 | 78.04 | 75.9 | 13.15 | −0.2 | 82.02 | 78.98 | 14.42 | ||
| 920,075 | SS51 | August 2018 | 0.1 | 51.73 | 53.29 | 6.86 | −0.03 | 55.1 | 54.66 | 8.89 |
| 494 | SS51-bis | August 2018 | 0.05 | 57.18 | 57.96 | 7.35 | 0.02 | 60.87 | 61.14 | 9.38 |
| February 2019 | −0.01 | 60.49 | 60.4 | 6.47 | 0.35 | 58.28 | 64.53 | 10.49 | ||
| May 2019 | −0.14 | 64.64 | 62.89 | 6.9 | −0.01 | 65.91 | 65.75 | 10.64 | ||
| 498 | SS52 | August 2018 | 0.14 | 60.25 | 62.26 | 8.31 | −0.06 | 71.43 | 70.6 | 13.13 |
| February 2019 | −0.39 | 72.58 | 67.18 | 12.02 | 0.33 | 72.97 | 77.79 | 14.3 | ||
| May 2019 | 0.02 | 70.1 | 70.44 | 7.05 | −0.04 | 82.31 | 81.84 | 13.98 | ||
| 499 | SS52 | August 2018 | 0.11 | 53.28 | 54.88 | 7.81 | 0 | 53.84 | 53.91 | 8.35 |
| February 2019 | 0.41 | 49.32 | 54.53 | 9.58 | 0.85 | 40.79 | 55.6 | 11.28 | ||
| May 2019 | −0.33 | 61.16 | 56.29 | 6.34 | −0.01 | 60.58 | 60.49 | 10.66 | ||
| 3193 | SS52 | August 2018 | −0.1 | 56.44 | 54.96 | 8.7 | 0.02 | 62.19 | 62.39 | 9.42 |
| February 2019 | 0.02 | 60.74 | 60.96 | 8.85 | 0.3 | 62.94 | 67.3 | 10.48 | ||
| May 2019 | 0 | 64.7 | 64.67 | 10.14 | −0.05 | 69.79 | 68.95 | 11.15 | ||
| 920,076 | SS52 | August 2018 | 0.03 | 41.98 | 42.36 | 6.07 | 0.02 | 43.09 | 43.38 | 12.28 |
| February 2019 | 0 | 51 | 51 | 0 | 0.2 | 41.66 | 45.62 | 11.03 | ||
| May 2019 | 0.39 | 37.15 | 38.5 | 5.74 | 0.09 | 45.49 | 46.94 | 12.13 | ||
| 503 | SS53 | August 2018 | −0.05 | 65.06 | 64.24 | 9.93 | 0.22 | 61.48 | 64.89 | 10.49 |
| February 2019 | −0.03 | 64.95 | 64.51 | 7.31 | 0.01 | 65.52 | 65.69 | 8.27 | ||
| May 2019 | −0.02 | 64.99 | 64.65 | 8.17 | −0.03 | 65.07 | 64.67 | 8.66 | ||
| 1332 | SS309 | August 2018 | 0 | 68 | 67.92 | 10.56 | 0 | 71.84 | 71.83 | 12.67 |
| 1333 | SS309 | August 2018 | 0.25 | 58.07 | 62.08 | 12.88 | −0.14 | 68.29 | 66.14 | 14.67 |
| 1563 | SS434 | August 2018 | 0.27 | 79.77 | 83.91 | 14.5 | −0.05 | 83.05 | 82.23 | 14.25 |
| 1703 | SS516 | August 2018 | 0.04 | 67.67 | 68.2 | 18.54 | −0.18 | 75.78 | 73.08 | 14.13 |
| February 2019 | −0.16 | 76.76 | 74.41 | 12.11 | −0.14 | 77.69 | 76.64 | 13.86 | ||
| May 2019 | 0.19 | 71.6 | 74.27 | 14.31 | 0.02 | 75.02 | 75.27 | 13.44 | ||

Table A3.
Comparison between HCD and sensors speeds through angular coefficients m, and intercepts q of the regression lines, and coefficient of determination R2 in Dir AB.
Table A3.
Comparison between HCD and sensors speeds through angular coefficients m, and intercepts q of the regression lines, and coefficient of determination R2 in Dir AB.
| Sensor ID | Road Name | m | q | R2 |
|---|---|---|---|---|
| 197 | SS12 | 0.63 | 24.89 | 0.69 |
| 208 | SS13 | 0.89 | 7.07 | 0.89 |
| 209 | SS13 | 0.86 | 8.66 | 0.91 |
| 920,074 | SS13 | 0.86 | 10.36 | 0.88 |
| 218 | SS14 | 0.90 | 7.57 | 0.94 |
| 219 | SS14 | 0.79 | 15.87 | 0.85 |
| 3191 | SS14 | 0.87 | 10.07 | 0.90 |
| 481 | SS50 | 0.82 | 12.16 | 0.87 |
| 2404 | SS50 | 0.83 | 12.34 | 0.93 |
| 487 | SS51 | 0.64 | 22.40 | 0.70 |
| 489 | SS51 | 0.84 | 11.03 | 0.80 |
| 490 | SS51 | 0.83 | 11.04 | 0.87 |
| 491 | SS51 | 0.85 | 6.45 | 0.83 |
| 492 | SS51 | 0.65 | 24.39 | 0.64 |
| 10,040 | SS51 | 0.51 | 41.10 | 0.52 |
| 920,075 | SS51 | 0.85 | 8.14 | 0.84 |
| 494 | SS51-bis | 0.94 | 3.00 | 0.96 |
| 499 | SS52 | 0.88 | 5.60 | 0.81 |
| 3193 | SS52 | 0.90 | 6.27 | 0.88 |
| 503 | SS53 | 0.84 | 10.88 | 0.90 |
| 1332 | SS309 | 0.85 | 11.00 | 0.94 |
| 1333 | SS309 | 0.89 | 7.36 | 0.92 |
| 1563 | SS434 | 0.91 | 8.65 | 0.96 |
| 1703 | SS516 | 0.94 | 4.55 | 0.93 |

Table A4.
Comparison between HCD and sensors speeds through angular coefficients m, and intercepts q of the regression lines, and coefficient of determination R2 in Dir BA.
Table A4.
Comparison between HCD and sensors speeds through angular coefficients m, and intercepts q of the regression lines, and coefficient of determination R2 in Dir BA.
| Sensor ID | Road Name | m | q | R2 |
|---|---|---|---|---|
| 197 | SS12 | 0.71 | 20.90 | 0.81 |
| 208 | SS13 | 0.90 | 6.42 | 0.94 |
| 209 | SS13 | 0.91 | 5.81 | 0.96 |
| 920,074 | SS13 | 0.91 | 6.71 | 0.92 |
| 218 | SS14 | 0.93 | 5.59 | 0.93 |
| 3191 | SS14 | 0.75 | 19.18 | 0.59 |
| 481 | SS50 | 0.89 | 8.83 | 0.91 |
| 482 | SS50 | 0.82 | 13.76 | 0.81 |
| 2404 | SS50 | 0.81 | 15.78 | 0.70 |
| 487 | SS51 | 0.84 | 10.87 | 0.74 |
| 489 | SS51 | 0.81 | 12.45 | 0.91 |
| 490 | SS51 | 0.94 | 3.90 | 0.97 |
| 491 | SS51 | 0.70 | 14.67 | 0.63 |
| 492 | SS51 | 0.60 | 27.33 | 0.57 |
| 10,040 | SS51 | 0.75 | 18.69 | 0.78 |
| 920,075 | SS51 | 0.84 | 9.43 | 0.79 |
| 494 | SS51-bis | 0.95 | 3.26 | 0.95 |
| 498 | SS52 | 0.89 | 8.19 | 0.88 |
| 499 | SS52 | 0.69 | 16.57 | 0.70 |
| 3193 | SS52 | 0.85 | 9.44 | 0.89 |
| 503 | SS53 | 0.84 | 10.08 | 0.91 |
| 1332 | SS309 | 1.00 | 0.32 | 0.99 |
| 1333 | SS309 | 0.95 | 3.26 | 0.95 |
| 1563 | SS434 | 0.95 | 4.33 | 0.98 |
| 1703 | SS516 | 0.77 | 17.03 | 0.84 |
References
- Esposito, T.; Mauro, R.; Russo, F.; Dell’Acqua, G. Operating speed prediction models for sustainable road safety management. In International Conference on Sustainable Design and Construction (ICSDC) 2011; ASCE: Reston, VA, USA, 2012; pp. 712–721. [Google Scholar] [CrossRef]
- Misaghi, P.; Hassan, Y. Modeling operating speed and speed differential on two-lane rural roads. J. Transp. Eng. 2005, 131, 408–418. [Google Scholar] [CrossRef]
- De Luca, M.; Lamberti, R.; Dell’Acqua, G. Freeway Free Flow Speed: A Case Study in Italy. Procedia-Soc. Behav. Sci. 2012, 54, 628–636. [Google Scholar] [CrossRef]
- Dell’Acqua, G. European Speed Environment Model for Highway Design-Consistency. Mod. Appl. Sci. 2012, 6, 1–10. [Google Scholar] [CrossRef]
- Hashim, I.H. Analysis of speed characteristics for rural two-lane roads: A field study from Minoufiya Governorate, Egypt. Ain Shams Eng. J. 2011, 2, 43–52. [Google Scholar] [CrossRef]
- Lobo, A.; Rodrigues, C.; Couto, A. Free-Flow Speed Model Based on Portuguese Roadway Design Features for Two-Lane Highways. Transp. Res. Rec. J. Transp. Res. Board 2013, 2348, 12–18. [Google Scholar] [CrossRef]
- Ottesen, J.L.; Krammes, R.A. Speed-Profile Model for a Design-Consistency Evaluation Procedure in the United States. Transp. Res. Rec. J. Transp. Res. Board 2000, 1701, 76–85. [Google Scholar] [CrossRef]
- Bassani, M.; Cirillo, C.; Molinari, S.; Tremblay, J.-M. Random Effect Models to Predict Operating Speed Distribution on Rural Two-Lane Highways. J. Transp. Eng. 2016, 142, 04016019. [Google Scholar] [CrossRef]
- Cantisani, G.; Del Serrone, G.; Di Biagio, G. Calibration and validation of and results from a micro-simulation model to explore drivers’ actual use of acceleration lanes. Simul. Model. Pract. Theory 2018, 89, 82–99. [Google Scholar] [CrossRef]
- Cantisani, G. Results of Micro-Simulation Model for Exploring Drivers’ Behavior on Acceleration Lanes. Eur. Transp. Eur. 2020, 77, 1–10. [Google Scholar] [CrossRef]
- Eboli, L.; Guido, G.; Mazzulla, G.; Pungillo, G. Experimental Relationships between operating speeds of successive road design elements in two-lane rural highways. Transport 2015, 32, 138–145. [Google Scholar] [CrossRef]
- Castro, M. Automated GIS-Based System for Speed Estimation. J. Comput. Civ. Eng. 2008, 22, 325–331. [Google Scholar] [CrossRef]
- Astarita, V.; Giofrè, V.P.; Guido, G.; Vitale, A. A review of traffic signal control methods and experiments based on Floating Car Data (FCD). Procedia Comput. Sci. 2020, 175, 745–751. [Google Scholar] [CrossRef]
- Gitahi, J.; Hahn, M.; Storz, M.; Bernhard, C.; Feldges, M.; Nordentoft, R. Multi-sensor traffic data fusion for congestion detection and tracking. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B1-2, 173–180. [Google Scholar] [CrossRef]
- Ajmar, A.; Arco, E.; Boccardo, P.; Perez, F. Floating car data (FCD) for mobility applications. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W13, 1517–1523. [Google Scholar] [CrossRef]
- Ma, W.; Qian, S. High-Resolution Traffic Sensing with Probe Autonomous Vehicles: A data-driven approach. Sensors 2021, 21, 464. [Google Scholar] [CrossRef]
- Del Serrone, G. Analisi Di Floating Car Data (FCD). 2020. Available online: http://hdl.handle.net/11573/1365640 (accessed on 13 January 2022).
- Talebpour, A.; Mahmassani, H.S. Influence of connected and autonomous vehicles on traffic flow stability and throughput. Transp. Res. Part C Emerg. Technol. 2016, 71, 143–163. [Google Scholar] [CrossRef]
- Verma, D.; Varghese, V.; Jana, A. Applicability of Big Data for transportation planning and management. In Advances in Urban Planning in Developing Nations; Routledge: England, UK, 2021; pp. 99–110. [Google Scholar]
- Joe Grengs, L.K.; Wang, X. Using GPS Data to Understand Driving Behavior. J. Urban Technol. 2008, 15, 33–53. [Google Scholar] [CrossRef]
- Leduc, G. Road Traffic Data: Collection Methods and Applications. EUR Number Tech. 2008, 47967, 55. Available online: http://ftp.jrc.es/EURdoc/EURdoc/JRC47967.TN.pdf (accessed on 15 December 2021).
- Fusco, G.; Colombaroni, C.; Isaenko, N. Short-term speed predictions exploiting big data on large urban road networks. Transp. Res. Part C Emerg. Technol. 2016, 73, 183–201. [Google Scholar] [CrossRef]
- Valenti, G.; Liberto, C.; Mastroianni, P. L’importanza dei big data sulla mobilità urbana. Energ. Ambiente Innov. 2016, 42–47. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, X.; Wu, G.-Q.; Ding, W. Data mining with big data. IEEE Trans. Knowl. Data Eng. 2013, 26, 97–107. [Google Scholar] [CrossRef]
- Dabbas, H.; Fourati, W.; Friedrich, B. Using Floating Car Data in Route Choice Modelling-Field Study. Transp. Res. Procedia 2021, 52, 700–707. [Google Scholar] [CrossRef]
- Andersen, C.S.; Reinau, K.H.; Agerholm, N. The Relationship between Road Characteristics and Speed Collected from Floating Car Data. J. Traffic Transp. Eng. 2016, 4, 1–10. [Google Scholar] [CrossRef][Green Version]
- Colombaroni, C.; Fusco, G.; Isaenko, N. Analysis of Road Safety Speed from Floating Car Data. Transp. Res. Procedia 2020, 45, 898–905. [Google Scholar] [CrossRef]
- Seo, T.; Kusakabe, T. Probe Vehicle-based Traffic Flow Estimation Method without Fundamental Diagram. Transp. Res. Procedia 2015, 9, 149–163. [Google Scholar] [CrossRef][Green Version]
- Wagner, P. How many Floating Car Data (FCD) are needed for Traffic Management? In Proceedings of the 4th International Symposium Networks for Mobility, Stuttgart, Germany, 25 September 2008; pp. 1–29. Available online: http://elib.dlr.de/60552/1/FOVUS-FCD4VM.pdf (accessed on 8 January 2022).
- Fourati, W.; Dabbas, H.; Friedrich, B. Estimation of Penetration Rates of Floating Car Data at Signalized Intersections. Transp. Res. Procedia 2021, 52, 228–235. [Google Scholar] [CrossRef]
- Chase, R.T.; Williams, B.M.; Rouphail, N.M.; Kim, S. Comparative Evaluation of Reported Speeds from Corresponding Fixed-Point and Probe-Based Detection Systems. Transp. Res. Rec. J. Transp. Res. Board 2012, 2308, 110–119. [Google Scholar] [CrossRef]
- Karlsson, T. An Observational Study of the Characteristics of Taxi Floating Car Data Compared to Radar Sensor Data. No. 2012:051. 2012. Available online: http://www.nada.kth.se/utbildning/grukth/exjobb/rapportlistor/2012/rapporter12/karlsson_tony_12051.pdf (accessed on 27 December 2021).
- Brockfeld, E.; Lorkowski, S.; Mieth, P.; Wagner, P. Benefits and Limits of Recent Floating Car Data Technology—An Evaluation Study. In Proceedings of the 11th WCTR Conference, Berkeley, CA, USA, 24 June 2007; pp. 24–28. Available online: http://elib.dlr.de/49618/1/Brockfeld_WCTR2007.pdf (accessed on 3 January 2022).
- Zhao, N.; Yu, L.; Zhao, H.; Guo, J.; Wen, H. Analysis of traffic flow characteristics on ring expressways in Beijing: Using floating car data and remote traffic microwave sensor data. Transp. Res. Rec. 2009, 2124, 178–185. [Google Scholar] [CrossRef]
- Altintasi, O.; Tuydes-Yaman, H.; Tuncay, K. Quality of floating car data (FCD) as a surrogate measure for urban arterial speed. Can. J. Civ. Eng. 2019, 46, 1187–1198. [Google Scholar] [CrossRef]
- Kim, S.; Coifman, B. Assessing the Performance of SpeedInfo Radar Traffic Sensors. J. Intell. Transp. Syst. 2016, 21, 179–189. [Google Scholar] [CrossRef]
- Croce, A.; Musolino, G.; Rindone, C.; Vitetta, A. Estimation of Travel Demand Models with Limited Information: Floating Car Data for Parameters’ Calibration. Sustainability 2021, 13, 8838. [Google Scholar] [CrossRef]
- Hossain, F.; Medina, J.C. Effects of Operating Speed and Traffic Flow on Severe and Fatal Crashes using the U.S. Road Assessment Program Methodology and Field Data Verification. Transp. Res. Rec. J. Transp. Res. Board 2020, 2674, 30–41. [Google Scholar] [CrossRef]
- Park, E.S.; Fitzpatrick, K.; Das, S.; Avelar, R. Exploration of the relationship among roadway characteristics, operating speed, and crashes for city streets using path analysis. Accid. Anal. Prev. 2020, 150, 105896. [Google Scholar] [CrossRef]
- Transportation Officials. A Policy on Geometric Design of Highways and Streets; AASHTO: Washington, DC, USA, 2011. [Google Scholar]
- Tottadi, K.K.; Mehar, A. Operating speed: Review and recommendations for future research. Innov. Infrastruct. Solut. 2021, 7, 67. [Google Scholar] [CrossRef]
- Cafiso, S.; Di Graziano, A.; La Cava, G. Actual Driving Data Analysis for Design Consistency Evaluation. Transp. Res. Rec. J. Transp. Res. Board 2005, 1912, 19–30. [Google Scholar] [CrossRef]
- Cafiso, S.; Cerni, G. New Approach to Defining Continuous Speed Profile Models for Two-Lane Rural Roads. Transp. Res. Rec. J. Transp. Res. Board 2012, 2309, 157–167. [Google Scholar] [CrossRef]
- Fabrizi, V.; Ragona, R. A pattern matching approach to speed forecasting of traffic networks. Eur. Transp. Res. Rev. 2014, 6, 333–342. [Google Scholar] [CrossRef][Green Version]
- Silva, A.B.; Almeida, R.; Vasconcelos, L. A speed model for curves of two-lane rural highways based on continuous speed data. In Transport Infrastructure and Systems, Proceedings of the AIIT International Congress on Transport Infrastructure and Systems; TIS: Rome, Italy; CRC Press: Boca Raton, FL, USA, 2017; pp. 177–183. [Google Scholar]
- Javier, F.; Torregrosa, C. New Geometric Design Consistency Model Based on. Accid. Anal. Prev. 2013, 61, 33–42. [Google Scholar]
- Zuriaga, A.M.P.; García, A.G.; Torregrosa, F.J.C.; D’Attoma, P. Modeling Operating Speed and Deceleration on Two-Lane Rural Roads with Global Positioning System Data. Transp. Res. Rec. J. Transp. Res. Board 2010, 2171, 11–20. [Google Scholar] [CrossRef]
- Hashim, I.H.; Abdel-Wahed, T.A.; Moustafa, Y. Toward an operating speed profile model for rural two-lane roads in Egypt. J. Traffic Transp. Eng. 2016, 3, 82–88. [Google Scholar] [CrossRef]
- Cvitanić, D.; Maljković, B. Operating speed models of two-lane rural state roads developed on continuous speed data. Teh. Vjesn.-Tech. Gaz. 2017, 24, 1915–1921. [Google Scholar] [CrossRef]
- Osservatorio-Del-Traffico @ www.stradeanas.it. Available online: https://www.stradeanas.it/it/le-strade/osservatorio-del-traffico (accessed on 12 January 2022).
- Index @ Www.Infoblu.It. Available online: https://www.infoblu.it/?page_id=29 (accessed on 29 November 2021).
- Jabari, S.E.; Liu, H. A stochastic model of traffic flow: Gaussian approximation and estimation. Transp. Res. Part B Methodol. 2013, 47, 15–41. [Google Scholar] [CrossRef]
- Cantisani, G.; Del Serrone, G. Procedure for the Identification of Existing Roads Alignment from Georeferenced Points Database. Infrastructures 2021, 6, 2. [Google Scholar] [CrossRef]
- Cho, W.; Choi, E. A GPS Trajectory Map-Matching Mechanism with DTG Big Data on the HBase System. ACM Int. Conf. Proceed. Ser. 2015, 22–23, 22–29. [Google Scholar] [CrossRef]
- Mclaughlin, S.B.; Hankey, J.M. Matching GPS Records to Digital Map Data: Algorithm Overview and Application. NSTSCE; 15-UT-033. 2015. Available online: https://vtechworks.lib.vt.edu/handle/10919/51585 (accessed on 12 January 2022).
- Chen, F.; Shen, M.; Tang, Y. Local Path Searching Based Map Matching Algorithm for Floating Car Data. Procedia Environ. Sci. 2011, 10, 576–582. [Google Scholar] [CrossRef]
- Miwa, T.; Kiuchi, D.; Yamamoto, T.; Morikawa, T. Development of map matching algorithm for low frequency probe data. Transp. Res. Part C Emerg. Technol. 2012, 22, 132–145. [Google Scholar] [CrossRef]
- Quddus, M.; Ochieng, W.Y.; Noland, R. Current map-matching algorithms for transport applications: State-of-the art and future research directions. Transp. Res. Part C Emerg. Technol. 2007, 15, 312–328. [Google Scholar] [CrossRef]
- Xi, L.; Liu, Q.; Li, M.; Liu, Z. Map Matching Algorithm and Its Application. In Proceedings of the Intelligent Systems and Knowledge Engineering (ISKE2007), Chengdu, China, 15–16 October 2007. [Google Scholar] [CrossRef]
- Chen, B.Y.; Yuan, H.; Li, Q.; Lam, W.H.K.; Shaw, S.-L.; Yan, K. Map-matching algorithm for large-scale low-frequency floating car data. Int. J. Geogr. Inf. Sci. 2013, 28, 22–38. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).