Are Scientific Models of Life Testable? A Lesson from Simpson’s Paradox

Abstract

We address the need for a model by considering two competing theories regarding the origin of life: (i) the Metabolism First theory, and (ii) the RNA World theory. We discuss two interrelated points, namely: (i) Models are valuable tools for understanding both the processes and intricacies of origin-of-life issues, and (ii) Insights from models also help us to evaluate the core objection to origin-of-life theories, called “the inefficiency objection”, which is commonly raised by proponents of both the Metabolism First theory and the RNA World theory against each other. We use Simpson’s Paradox (SP) as a tool for challenging this objection. We will use models in various senses, ranging from taking them as representations of reality to treating them as theories/accounts that provide heuristics for probing reality. In this paper, we will frequently use models and theories interchangeably. Additionally, we investigate Conway’s Game of Life and contrast it with our SP-based approach to emergence-of-life issues. Finally, we discuss some of the consequences of our view. A scientific model is testable in three senses: (i) a logical sense, (ii) a nomological sense, and (iii) a current technological sense. The SP-based model is testable in the first two senses but it is not feasible to test it using current technology.

1. Overview

Philosophy of science is replete with case studies describing both how scientists use models and how philosophers have interpreted the application of these models [1,2,3]. We will use models in various senses, ranging from taking them as representations of reality to treating them as theories/accounts that provide heuristics for probing reality [4]. In this paper, we will frequently use models and theories interchangeably. We begin with John Conway’s influential Game of Life, that sidesteps empirical issues concerning theories of life (Section 1). After a brief historical note on the theories of life [5], we broach two current competing theories of the origin of life, known as the Metabolism First Theory (MFT), and the RNA World Theory (RWT) (Section 2). We discuss the core objection to origin-of-life theories, called “the inefficiency objection”, which is commonly used by proponents of both MFT and RWT against each other. The inefficiency objection states that the chemical reactions proposed by these competing theories are too inefficient and not specific enough to explain the emergence of early life (Section 3). We will propose models that exploit dynamical cases of SP [6,7,8,9] to assess the inefficiency objection and conclude that the inefficiency objection is untenable (Section 4). SP involves the reversal of the direction of a comparison or the cessation of an association when data from multiple groups are combined to form one body of data. Applications of the paradox will show that even though the reactions in question could be inefficient locally (i.e., in subpopulations), they could be efficient globally (i.e., in the overall population). This, in turn, suggests that the emergence of life is chemically plausible, despite the objections of competing theorists. Here, we compare Conway’s mathematical modelling of life with SP-based modelling (Section 4). Finally, we revisit the question: “is the SP-based model of life testable?” (Section 5).

2. Conway’s Game of Life

The Cambridge mathematician John Conway sidesteps issues regarding empirical methods of testing a scientific theory [10]. He instead proposes a mathematical model called “the game of life” to investigate how complex life (in a certain sense) could emerge from some simple rules [11]. This is a zero-sum game and its evolution is determined by its initial state without requiring further input [12]. By interacting with the game of life, given certain initial configurations, one can observe how the game evolves with patterns. The universe of the game of life Conway lays out is a two-dimensional orthogonal square of cells, each of which has two possible states, i.e., dead or alive, where the square extends infinitely in all directions. However, to see how the game evolves into certain complex structures, the former must follow some rules: (i) A live cell with two or three live neighbors survives; (ii) A dead cell with exactly three live neighbors becomes a live cell; (iii) A cell dies or remains dead in the case where a live cell has zero or one neighbor, i.e., the game causes it to die from loneliness; and (iv) If a live cell has more than three neighbors, then it dies from overpopulation.

There are three points worth mentioning about Conway’s game. First, the appeal of this mathematical model is that the local rules are clear and simple, while its global behavior could be complex. Second, to the question “Could life emerge?” Conway answers that it is inescapable, at least with some constraints on how the game should be played. If the square array of cells is totally empty, nothing will emerge. In contrast, if every cell is occupied, then all of them will be eliminated in the next generation due to overcrowding. In addition, there would be numerous other initial configurations, resulting in no self-replicability. However, these are all special cases where life will not emerge. Unless we interfere with life considerably, it could emerge at some time, somewhere in that infinite plane of every conceivable finite pattern [13]. Third, although growth is often associated with the definition of life [14], Conway realized that we need something more to characterize life, and he found patterns which were alive in the game to be a characteristic of what we perceive as life.

One could, however, raise concerns about Conway’s mathematical modelling of life. All possible configurations in play are the results of some initial conditions, and follow deterministically therefrom. Consequently, they are error-free, self-replicating, and almost perfect copies at each stage of their evolution. It also overlooks the open-ended system of how nature evolves through minor point-mutations and tweaks via the process of natural selection [15,16]. There are at least two ways in which empirical theories of life and Conway’s game of life differ. First, the former concerns the open-ended system of nature where the studied mechanism and the system in which we intervene are uncertain in terms of what they might reveal. Several auxiliary assumptions that could play significant roles in the mechanism have not yet been properly grasped. Second, unlike Conway’s model, nature has more than two dimensions, further complicating the understanding of nature.

3. Two Competing Empirical Theories about the Origin of Life

Serious scientific experimentation on the origin of life can be traced to the first organic synthesis of urea by Friedrich Wohler in 1828. Wohler showed that it is possible to produce molecules formed by biological processes in a test tube [17]. This production of an organic molecule from inorganic compounds is arguably the first step on the road to the origin of life. Darwin speculated in 1871 (in a letter to Joseph Hooker) that life might have originated in a “warm little pond”, in the presence of water, ammonia and phosphates, light, heat and electricity, etc. However, the first testable theories were put forward by AI Oparin and JBS Haldane during the early 1920s, suggesting that life formed within vesicles in a primordial soup [18,19].

There are presently over a dozen hypotheses trying to address the question of the origin of life [20]. We focus on two, namely, the Metabolism First Theory (MFT) [21,22] and the RNA World Theory (RWT) [23]. One way to frame the debate between these two hypotheses is in terms of which factor, i.e., “energy” or “heredity”, is the central theme behind the emergence of life. The MFT upholds energy as the central driving force for life’s emergence, whereas the RWT champions heredity. According to the MFT, the development of the first living system must have involved a sequence of chemical transformations achieving increasing levels of chemical complexity—including pathways, cycles and hypercycles—compared to its available starting materials. Within this framework, one possible starting point for the sequence to become living entities is considered to be polymers of amino acids, namely, peptides. MFT suggests that the chemistry leading to life could have occurred in a relatively stable environment containing some catalytic activities that would have expedited the production of other important and relevant bio-molecules. Many proponents of MFT believe minerals served several critical functions during this process [24,25]. These functions include catalysis, protection, support, and selection. Minerals could have acted as a surface for the assemblage of chemical systems, and protected these systems from dispersal and destruction. The surfaces of these minerals could have also acted as platforms upon which molecules could accumulate and interact with each other. In addition, it is conjectured that minerals might have acted as selective agents, thereby affording a framework for certain biologically useful molecules such as the amino acid, leucine, which breaks down within a few minutes in 2000 °C pressurized water, but may persist for days when pyrrhotite, an iron-sulfur mineral commonly found at submarine volcanic vents, is added to the mix [26]. In short, proponents of MFT contend that life originated through metabolic processes, and not via heredity.

Now consider the RNA World Theory (RWT). In the 1960s, Francis Crick and several other biochemists suggested that the ancestral molecule which triggered the journey towards the origin of life was neither DNA nor proteins, but perhaps RNA or other chemical informational molecules such as peptide nucleotides (PNA), threose nucleic acid (TNA), glycerol-derived nucleic-acid (GNA) and/or pyranosyl-RNA [27,28]. In addition, the reasons that the chemical informational molecule is now probably thought to have been RNA is that it would be able to both carry out catalytic activity (i.e., to act as a ribozyme) and act as a chemical informational code carrying molecule (e.g., mRNA, tRNA, retroviral RNA—flu, HIV), as well as being able to carry out self-replication. Good examples of this are (i) nicotinamide adenine dinucleotide (NAD, a dimer), which can act as co-enzyme and can self-replicate [29,30,31,32,33,34], and (ii) Spiegelman’s monster [35,36,37]. Leslie Orgel [38], one of the supporters of this view, wrote: “[t]here were a few reasons why we favored RNA over DNA as the originator of the genetic system, even though DNA is now the main repository of hereditary information. One consideration was that the ribonucleotides in RNA are more readily synthesized than are the deoxyribonucleotides in DNA. Moreover, it was easy to envision ways that DNA could evolve from RNA and then, being more stable, take over RNA’s role as the guardian of heredity.”

Difficulties appraising theories about the emergence of life are exacerbated due to its being an intractable problem. We cannot time-travel to observe the unfolding of life. However, fortunately, there is a long tradition in science where intractable problems are sometimes transformed into manageable ones [39,40] and theories in astrobiology are no exception [41]. The apparent intractability of MFT and RWT can be overcome to some extent by constructing models in labs to conceptualize the conditions leading to the emergence of life. Schoonen et al. [42] showed that iron and nickel sulfides could have served as a template, catalyst, and energy source for the possible production of biological molecules, thus supporting the MFT theory. As for the RWT, Altman and Cech independently showed that RNA, unlike DNA, can perform some of the enzymatic functions needed for replication [43,44,45]. As pointed out earlier, in principle, RNA molecules could store genetic information and act as catalysts and consequently, they could make proteins which are unnecessary for simpler life forms [46,47]. Experimental data suggests that RNA-based life could possibly have existed before protein-catalyzed life emerged.

4. The Inefficiency Objection to the Two Origin-of-Life Theories

Proponents of each theory criticize one another for failing to provide a satisfactory account of the emergence of life on early Earth. One of the fundamental objections they advance against one another is what has been called “the inefficiency objection”. The objection states that the reactions proposed by each of the competing theories are too inefficient and not specific enough to explain life’s emergence.

Orgel, a proponent of the RWT, examined various metabolic pathways to determine whether such pathways could have existed under the conditions present on early Earth. He agrees with MFT proponents that it is logically possible to think that some metabolic cycles could have evolved which then “kick-started” early life. However, Orgel insists that scientists are solely concerned with “chemical plausibility.” He wrote: “It must be recognized that assessment of the feasibility of any particular proposed prebiotic cycle must depend on arguments about chemical plausibility, rather than on a decision about logical possibility” [48].

One of the metabolic cycles which is important to MFT is the reverse tricarboxylic acid cycle (rTCA). This process is used by some organisms to synthesize reduced carbon compounds using CO₂ from the atmosphere. This type of reaction is an alternative to the Calvin cycle observed in plants. Wächtershäuser [49] has suggested that this cycle is a possible candidate for the production of reduced carbon in a prebiotic setting. Orgel used this cycle to investigate whether it is chemically plausible to demonstrate that life could have emerged from such metabolic cycles. While the TCA takes complex carbon molecules in the form of sugars and oxidizes them to CO₂ and water, the rTCA fixes CO₂ and water to make useable carbon compounds, typically sugar (C₆H₁₂O₆). Orgel states that each metabolic cycle, including the rTCA, “must be evaluated in terms of the efficiencies and specificities”. He concludes that early reactions were not efficient, and the existence of side reactions would disrupt the rTCA. These side reactions would siphon off carbon captured in earlier steps of the rTCA cycle, reducing the efficiency of the total cycle.

Robert Shapiro, an MFT theorist, questions the RWT. In a series of articles spanning more than twenty years, he argues that RNA, a versatile class of molecules, is a “highly implausible start for life”, [and although] “no physical law need be broken for spontaneous RNA formation to happen, …the chances against it are… immense,” [50]. To appreciate Shapiro’s arguments against the RWT and some of the subsequent comments by his opponents, we discuss some of the components of the RWT beginning with precursors to nucleic acids.

According to RWT critics, RNA nucleotides are difficult to synthesize and are very easily destroyed when synthesized under laboratory conditions [27]. One of the examples Shapiro considers is the autocatalytic formose reactions [51] for the prebiotic synthesis of ribose. Ribose is a 5C ring D-sugar which along with alternating phosphate groups forms a phosphodiester bond linkage in order to make the necessary backbone observed in polyribonucleotides. The synthesis of ribose, as one such component of the RNA world hypothesis, is a necessary integral step during the prebiotic production of RNA. However, Shapiro wrote, “[the] evidence that is currently available does not support the availability of ribose on the prebiotic Earth, except perhaps for brief periods of time and in low concentrations as part of a complex mixture, as well as being under conditions unsuitable for nucleotide synthesis.” He argues that although the Urey-Miller experiment yielded amino acids, it failed to provide nucleotides, the building blocks of RNA. He states that the reactions yielding RNA precursors are too “inefficient” and produce these precursors in very low amounts. Recent work has, however, shown that borate minerals are able to stabilize ribose in early Earth conditions against the inevitable Browning reactions which transform sugars into largely nonfunctional polymeric mixtures of nonessential molecules for the emergence of life [52]. However, Shapiro’s principal argument that reactions for RNA precursors are inefficient could still be salvaged. Although borate minerals are able to stabilize ribose, Ricardo and his co-authors’ paper showed that the rate of the formation of ribose as a natural outcome of the chemical polymerization of formaldehyde remained inefficient compared to the rate of the nonribose molecules produced in an 8:2 ratio of nonribose to ribose. Therefore, ribose synthesis is still likely to be too inefficient to produce the large concentrations necessary for RNA precursors.

Two inter-related points deserve mention, since they are shared by both Orgel and Shapiro, despite their opposition to each other’s theories. First, both agree that it is logically possible for the reactions cited by their opposing group to occur on early Earth. The fact that organic molecule X is logically possible means that it does not violate rules of logic or pure mathematics. However, the point of the disagreement between the two theorists is not about the logical possibility of those reactions taking place on early Earth. On the contrary, it concerns the chemical plausibility of those reactions on early Earth. The fact that organic molecule Y is chemically possible means that Y does not violate the laws of physicochemistry. Neither Orgel nor Shapiro hold the view that these reactions violate laws of physicochemistry, but each argue that the reactions cited by the other are chemically improbable. Both think that since these reactions are improbable, they are therefore chemically implausible. The second and final point, on which, surprisingly, both agree, concerns what we have called the inefficiency objection. If we read the objection raised by both adherents against each other, then we find that they both argue that the early Earth reactions invoked by the other are too inefficient and not specific enough to explain the emergence of life.

5. Two Types of Simpson’s Paradox and a Response to the Inefficiency Objection

Simpson’s Paradox (SP) is defined as the reversal of the direction of a comparison or the cessation of an association when data from multiple groups are combined to form a single whole. This is called the static version of the paradox (

Table 1. “CV” includes two categorical variables, “F” for “females” and “M” for “males”. “A” and “R” represent “the number of accepted/rejected” for two departments, D1, and D2. This is a formulation of the paradox in which the association in the subpopulations is reversed in the combined population. Although the acceptance rates for females are higher than for males in each department, in the combined population, the rates are reversed.

Simpson’s Paradox (Static Version)
CV	D1		D2		Acceptance Rates		Overall Acceptance Rates
	A	R	A	R	D1	D2
F	180	20	100	200	90%	33%	56%
M	480	120	10	90	80%	10%	70%

). Here is a familiar example of the static version:

This is a static version because it involves a static, one-time cross-section of a dataset without constant updates in light of the impact of new data. However, there is another version of the Paradox called the dynamic version, which was recently described by Chuang [53]. In molecular dynamic cases of SP, the reversal, over a period, of the direction of a major molecular product evolving as a whole was observed when minor molecular products were pooled together from their subreactions. We will be exploiting the theme behind the dynamic version of the Paradox to contend the untenability of the inefficiency objection. First, we will provide an example to illustrate both how a dynamic case of the Paradox works, and why Orgel’s objection is not necessarily true. Then, we will apply the same treatment to Shapiro’s objection. Since the molecular dynamical case involves a change in growth-rate, we first define the notion of growth rate (G) as in Equation (1):

$$G=\left(\frac{T_j-T_i}{T_i}\right)\times 100$$

(1)

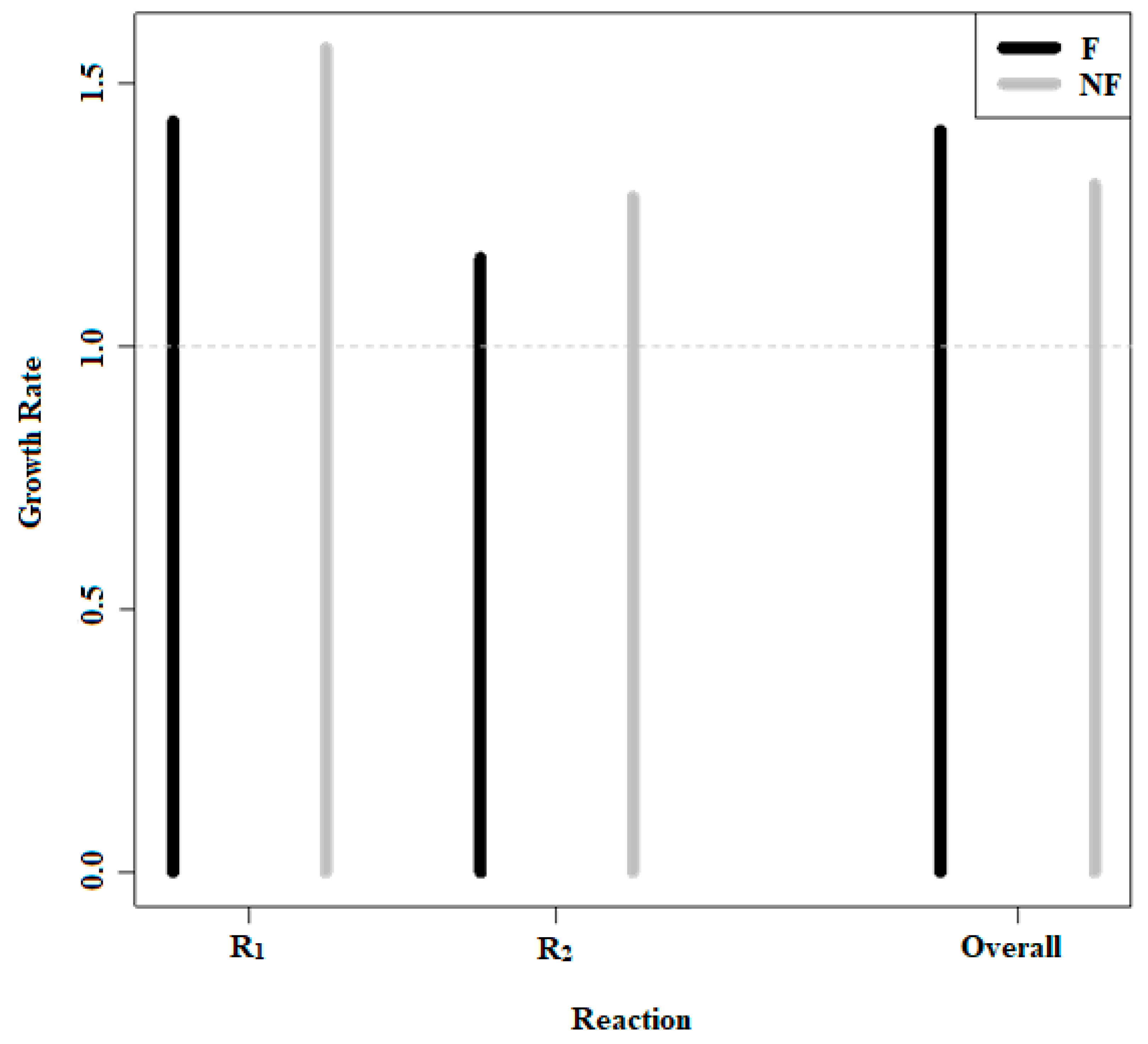
where T_j is the number of molecules at a later time and T_i represents the number at an earlier time. One example of the dynamic case of the Paradox is represented by

Table 2. “CV” represents two categorical variables, “F” (acetyl-CoA) and “NF” (nonfunctional molecules). “R₁” and “R₂” represent different individual reaction groups and T₁ and T₂ represent two time points where a count is made. Although the growth rates for nonfunctional molecules are higher than acetyl-CoA in each reaction group, the relationship is reversed in the combined population.

Simpson’s Paradox (Dynamic Version)
CV	R1		R2		Growth Rates		Overall Growth Rates
	T1	T2	T1	T2	R1	R2
F	1000	1430	100	117	1.43	1.17	1.41
NF	100	157	1000	1285	1.57	1.285	1.31

, with growth rates between 1.17 and 1.57, depending on the groups being compared. Here, we observe the growth rate change of, for example, acetyl-CoA in subreactions over a period of time. In the rTCA cycle, the functional molecules are represented by acetyl-CoA, the product of the 8 steps of the rTCA cycle gaining two carbon atoms in the acetyl functional group via reduction of CO₂. Nonfunctional molecules are created every time an entire cycle is not completed. An inefficient reaction results in a loss of the carbon captured earlier in the rTCA. For this example, we have made three assumptions following Orgel [48]: (i) each reaction within the rTCA is 90% efficient; (ii) Acetyl-CoA is stable enough in its environment in that it does not undergo any appreciable loss; and (iii) the supply of CO₂ is not limiting. According to Orgel’s example, a 90% efficiency per reaction should not produce an adequate supply of acetyl-CoA, because after eight reactions of 90% efficiency, the efficiency of the total cycle of acetyl-CoA is less than 45%, meaning that the cycle produces only nonfunctional molecules more than half of the time. This presumably led Orgel to conclude that a noncatalyzed rTCA is chemically implausible.

Consider Table 2 below:

In R1, we began with 1100 molecules in total; 1000F and 100NF respectively. In R₁, NF grew at a rate of n × 1.57 from its original number n over time T_jto T_j+1 whereas F grew at a rate of n × 1.43 over the same period. In R₂, we began with 1100 molecules altogether; 100F and 1000NF. NF grew at a rate of n × 1.285, whereas F grew at a rate of n × 1.17. We see that although acetyl-CoA is a minor product within each subpopulation, the overall growth rate for F is 1.41, which is greater than the NF growth rate of 1.31 for the global population. This possible scenario casts doubt on the inefficiency objection raised by Orgel against the MFT. Table 2 is visually represented by Figure 1.

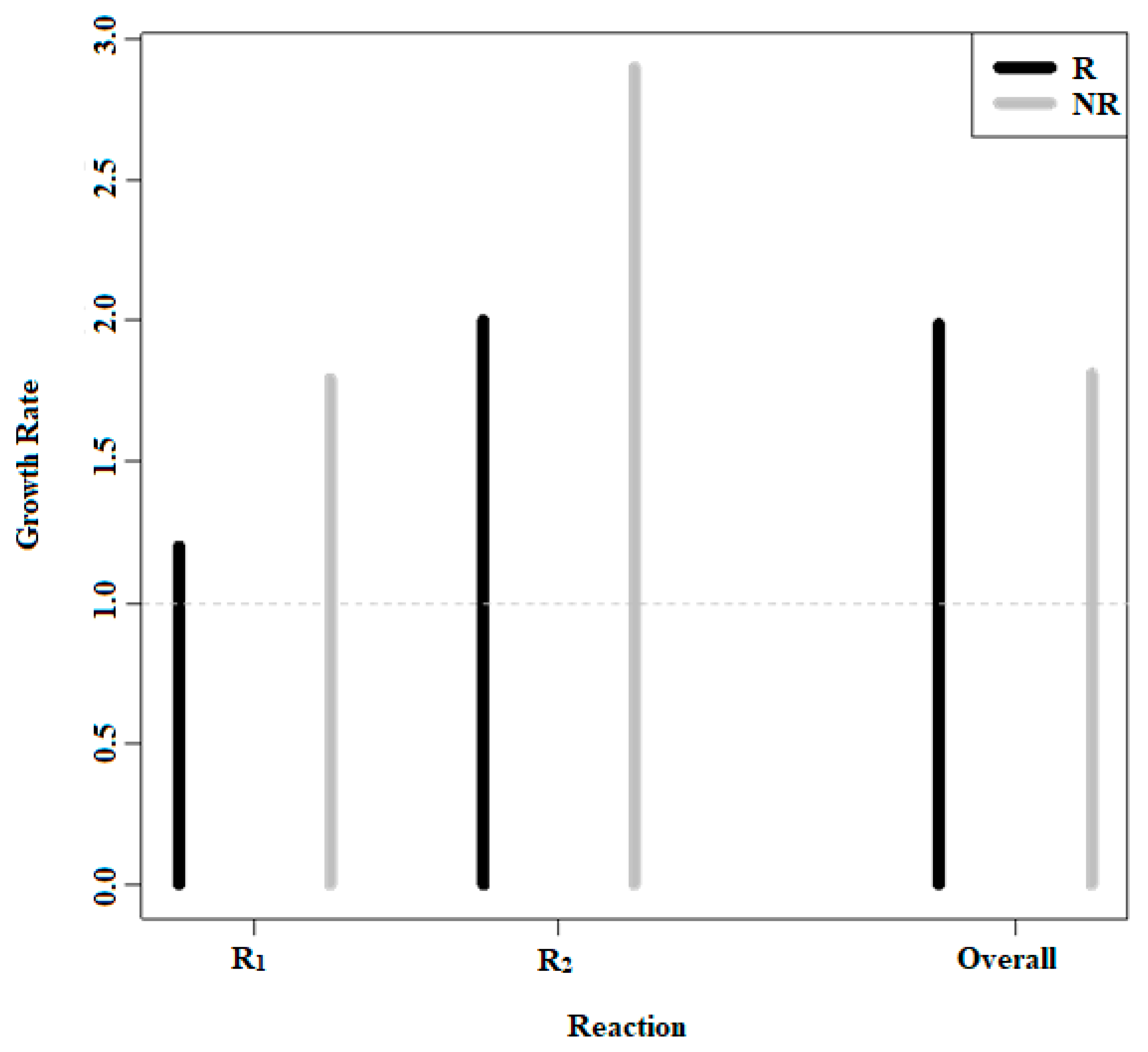
Shapiro raised a similar objection involving the inefficiency of RNA production for the RWT. He argued that ribose reactions are inefficient, since they cannot generate an adequate amount of the RNA precursors required for the production of polymerized RNA. Three assumptions are made for this example of Simpson’s paradox, as follows: (i) the ratios of percentage yields of each reaction are as reported in Ricardo, et al. [52]. So, the conditions that produce these yields must be present. While the ratios of these yields must stay fixed to those reported reaction times, reaction rates can vary (such as might happen if the reaction temperature changes during the experiment); (ii) ribose is stable enough not to undergo appreciable loss; and (iii) The supply of precursors must not be limiting. Based on these assumptions, we have produced

Table 3. “CV” represents two categorical variables, “R” (ribose) and “NR” (nonribose; see Figure 1. and “R₂” represent different individual reaction groups and T₁ and T₂ represent two time points where a count is made. Although the growth rates for nonribose products are higher than ribose in each reaction group, the relationship is reversed in the combined population.

Simpson’s Paradox (Dynamic Version)
CV	R1		R2		Growth Rates		Overall Growth Rates
	T1	T2	T1	T2	R1	R2
R	10	12	1000	2000	1.2	2	1.99
NR	1000	1795	10	29	1.795	2.9	1.81

:

We show that although functional molecules (ribose) grow less rapidly than nonribose products, the ribose can still emerge as the major product globally against the nonfunctional molecules. This indicates that the production of functional molecules from prebiotic precursors can be far more chemically plausible globally than indicated by the detractors of each theory (RWT and MFT). If a reaction can be globally efficient as shown by SP, then the inefficiency objection to origin-of-life theories is untenable, and thus, the emergence of life on early Earth seems more probable. In Table 3, while the ratio of the growth rates (about 1.2:1.8 as in [52]) remains the same in subreactions, the overall growth rates display another example of SP. Figure 2 visually represents Table 3.

The lesson from Simpson’s paradox is that life could emerge from the accumulation of minor products of subreactions. These products become major products globally, and thus contribute to the emergence of life. The use of dynamic versions of the paradox does not just show that it is logically possible for functional molecules to emerge as a major product globally; it also shows that it is chemically plausible for functional molecules to emerge as a major product globally, since this emergence is not improbable.

Readers may wonder how the SP-based model is meaningfully distinct from Conway’s modelling of the game of life, since both Conway’s mathematical model and the SP-based model are deductive in nature. In the case of Conway’s model, if the four rules of the game of life are obeyed, then the unfolding of future configurations of the game are already in-built in those rules (see Section 2) Likewise, in three tables of SP, once those numbers are provided in subpopulation, the combined population table with exact numbers and portions follow automatically. Also, both models are dynamic in nature. In Conway’s game of life, whether there will be a next generation depends on the previous states of the neighbors, and whether it will stabilize or continue forever depends on its preceding state. The dynamic version of SP might be similar. Life may appear or disappear depending on its previous changing states and the conditions required for producing the paradox. However, there are differences between them. The conditions for the Conway model are few and simple, whereas those which must be satisfied for the emergence of SP, if not complex, could be numerous. Unlike Conway’s model, where there are few rules to follow, in the case of SP, there are various ways R1 and R2 in tables II and III that could be satisfied (for example, in those two tables, we get two ratios leading to reversals, but other ratios in R1 and R2 would also be able to produce reversals characteristic of SP-based models). One fundamental way they are different is that the SP-based model is devised to address the inefficiency objection. Conway’s model is not meant to tackle the objection. Additionally, none of the terms in the SP-based model is given a biological interpretation (e.g., “life,” “survival,” etc.) as are in the case of the game of life.

6. Testability of Scientific Models of Life

One feature that distinguishes scientific theories from nonscientific ones is that the former must be testable, at least in principle [54]. Consequently, whether the SP-based model is testable is an important question. Following Sober [55], we distinguish testability in three senses, viz.: (i) is it logically possible to test the model? (ii) is it nomologically possible to test the model in principle? and (iii) is a test feasible for the model, given current technology? As mentioned before, a model is logically possible if it does not violate the laws of mathematics, physics, chemistry, and biology. If a test is feasible for a model given current technology, then the model is testable at the present time. Obviously, the SP model is testable in the first sense, because it is logically consistent.

Is the model testable in the second sense? Work by Russell et al. has more direct implications for addressing this question. The hydrothermal vents and methane seeps on the ocean floor were once thought to be geological and biological oddities; however, their features are now emerging as important attributes in ocean ecosystems. Through their process of methane consumption, the lifeforms surviving at these vents are able to help prevent potentially catastrophic greenhouse effects. Russell and his co-authors state that compartments, in the form of tiny bubbles formed at hydrothermal vents, could act as membranes that sequester some molecules while allowing others to pass through [21]. Similar compartments have been used to show enzyme free polynucleotide replication [56]. We mention the idea of prebiotic hydrothermal compartments to explain a scenario in which SP can be validated. In this scenario, each compartment acts as an individual subreaction chamber, producing molecules in yields similar to those reported by other investigators [24,25]. However, in this scenario, these compartments release the products of their reaction, either via destruction of the compartment or through leaky walls. This ultimately creates a global population of molecules. Thus, hydrothermal vents provide conditions under which a plausible scenario for the Simpson’s paradox could affect chemical yields. Thus, the SP-based model is, at least in principle, nomologically testable.

Is the model testable in the third sense? That is, is it feasible to propose a test for the SP-based model given our current technology? When we consulted a biochemist regarding how to devise an experiment to test it, we received the answer that it is not yet technologically feasible to do so. The rationale remains unclear to us as to why. So, whether the model is testable given current technology remains a consideration for further investigation.