Atmospheric Temperature and CO2: Hen-Or-Egg Causality?
Abstract
Πότερον ἡ ὄρνις πρότερον ἢ τὸ ᾠὸν ἐγένετο (Which of the two came first, the hen or the egg?).
Πλούταρχος, Hθικά, Συμποσιακὰ Β, Πρόβλημα Γ (Plutarch, Moralia, Quaestiones convivales, B, Question III).
1. Introduction
2. Temperature and Carbon Dioxide—From Arrhenius and Palaeo-Proxies to Instrumental Data
Conversations with my friend and colleague Professor Högbom together with the discussions above referred to, led me to make a preliminary estimate of the probable effect of a variation of the atmospheric carbonic acid [meaning CO2] on the temperature of the earth. As this estimation led to the belief that one might in this way probably find an explanation for temperature variations of 5–10 °C, I worked out the calculation more in detail and lay it now before the public and the critics.
- Indeed, CO2 plays a substantial role as a greenhouse gas. However, modern estimates of the contribution of CO2 to the greenhouse effect differ largely from Arrhenius’s results, attributing 19% of the long-wave radiation absorption to CO2 against 75% of water vapour and clouds (Schmidt et al. [15]), or a ratio of 1:4.
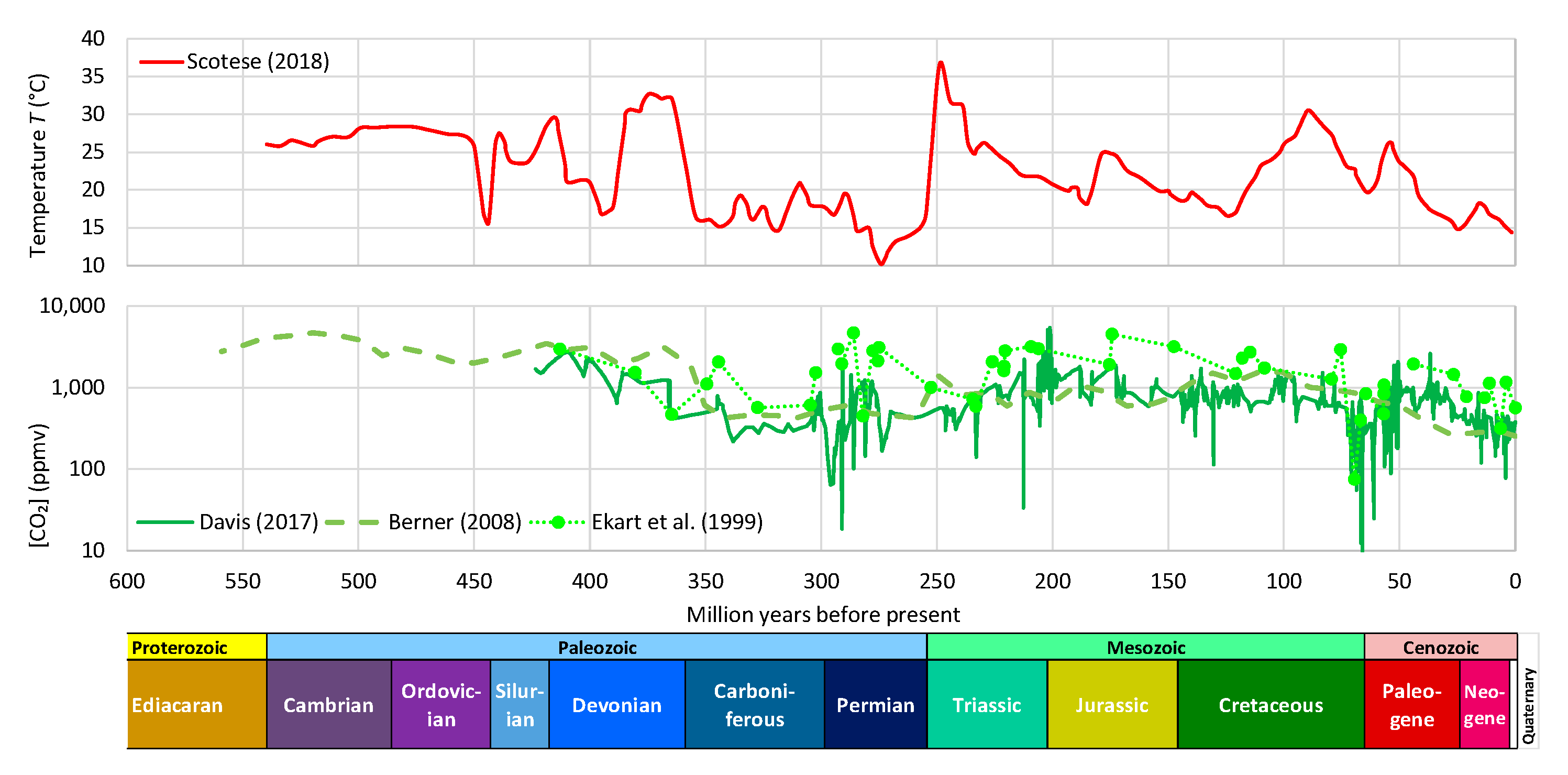
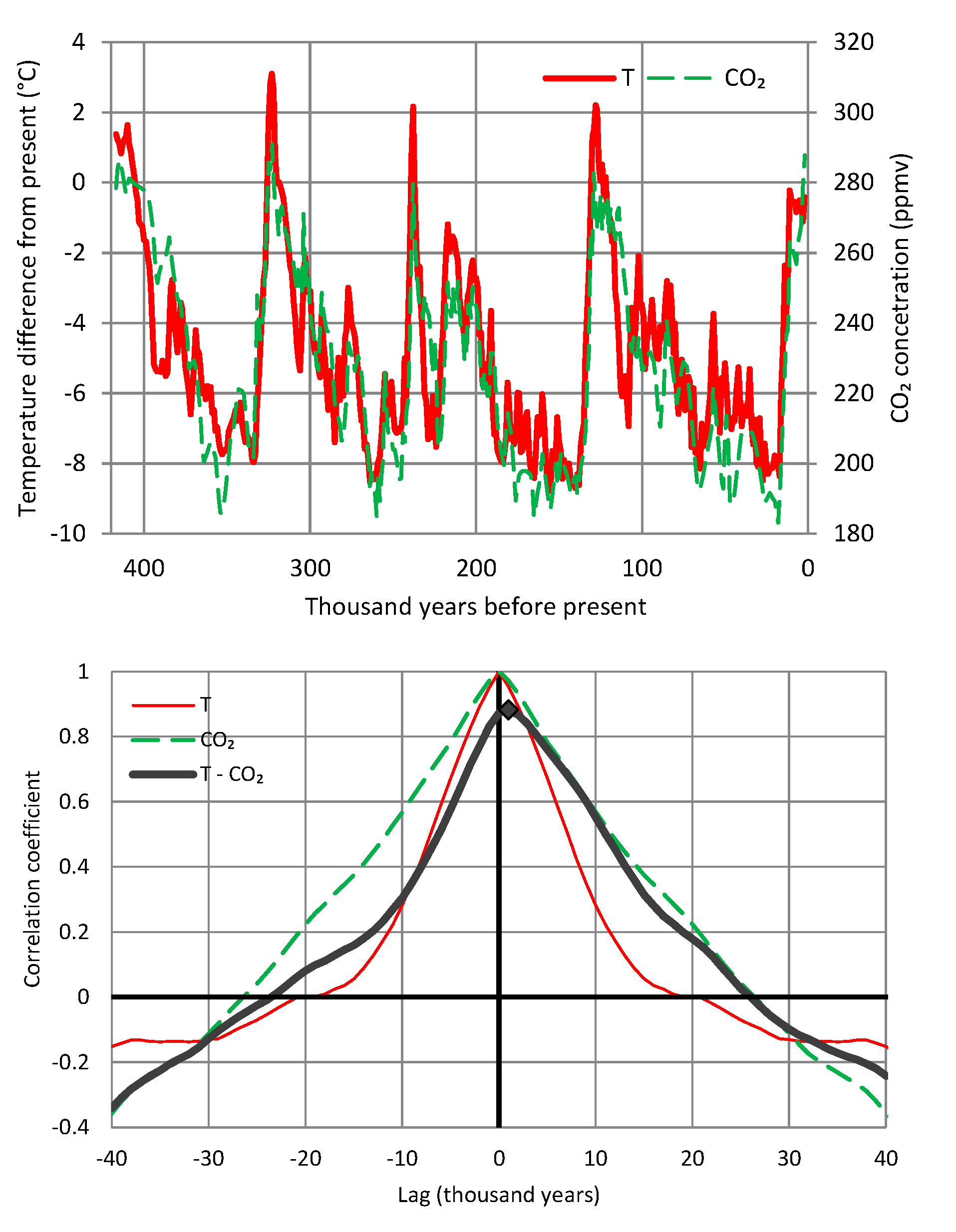
- During the Phanerozoic Eon, Earth’s temperature varied by even more than 5–10 °C, which was postulated by Arrhenius—see Figure 3. Even though the link of temperature and CO2 is beyond doubt, this is not clear in Figure 3, where it is seen that the CO2 concentration has varied by about two orders of magnitude and does not always synchronize with the temperature variation. Other factors may become more important at such huge time scales. Thus, an alternative hypothesis of the galactic cosmic ray flux as a climate driver via solar wind modulation has been suggested [16,17], which has triggered discussion or dispute [14,18,19,20,21,22,23]. The T–CO2 relationship becomes more legible and rather indisputable in proxy data of the Quaternary (see Figure 4). It has been demonstrated in a persuasive manner by Roe [24] that in the Quaternary, it is the effect of Milanković cycles (variations in eccentricity, axial tilt, and precession of Earth’s orbit), rather than of atmospheric CO2 concentration, that explains the glaciation process. Specifically (quoting Roe [24]),variations in atmospheric CO2 appear to lag the rate of change of global ice volume. This implies only a secondary role for CO2—variations in which produce a weaker radiative forcing than the orbitally-induced changes in summertime insolation—in driving changes in global ice volume.
show that properly specified tests of Ganger [sic] causality validate the consensus that human activity is partially responsible for the observed rise in global temperature and that this rise in temperature also has an effect on the global carbon cycle.
study unambiguously shows one-way causality between the total Greenhouse Gases and GMTA [global mean surface temperature anomalies]. Specifically, it is confirmed that the former, especially CO2, are the main causal drivers of the recent warming.
- The short-term effects deserve to be studied, as well as the long-term ones.
- The modern instrumental records are short themselves and only allow the short-term effects to be studied.
- For the long-term effects, the palaeo-proxies provide better indications, as already discussed above.
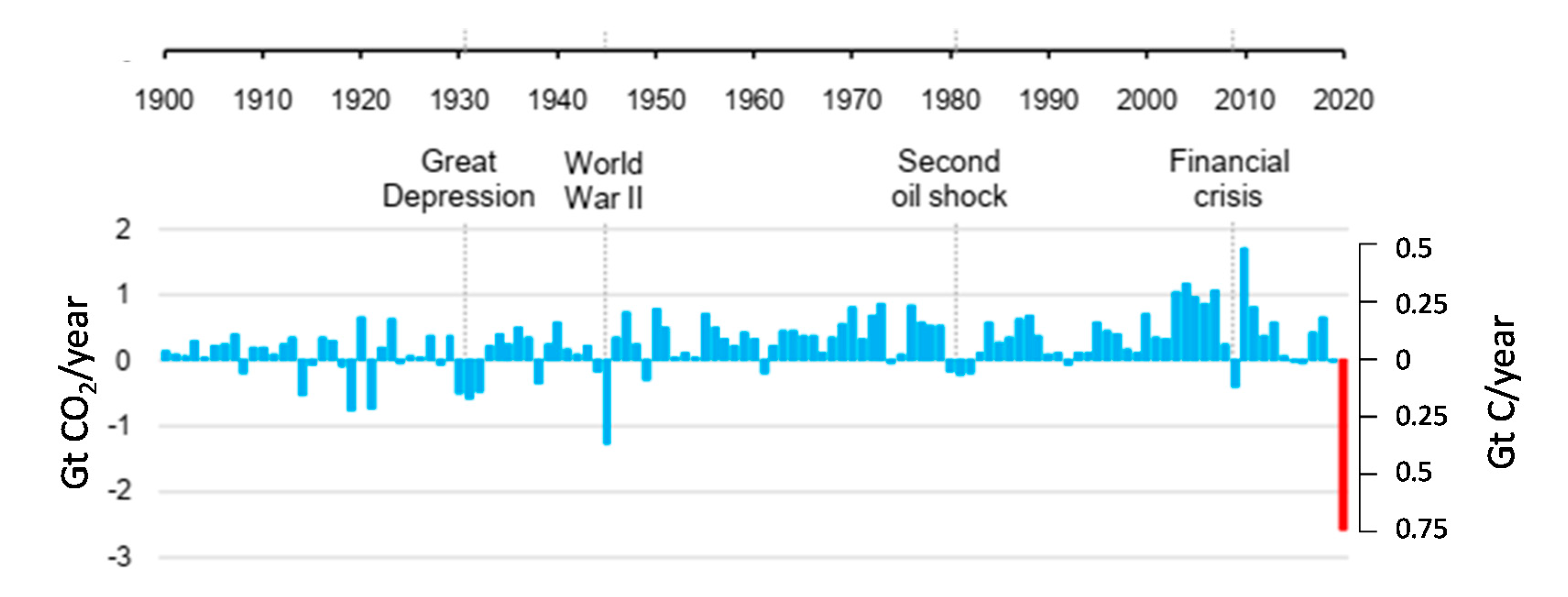
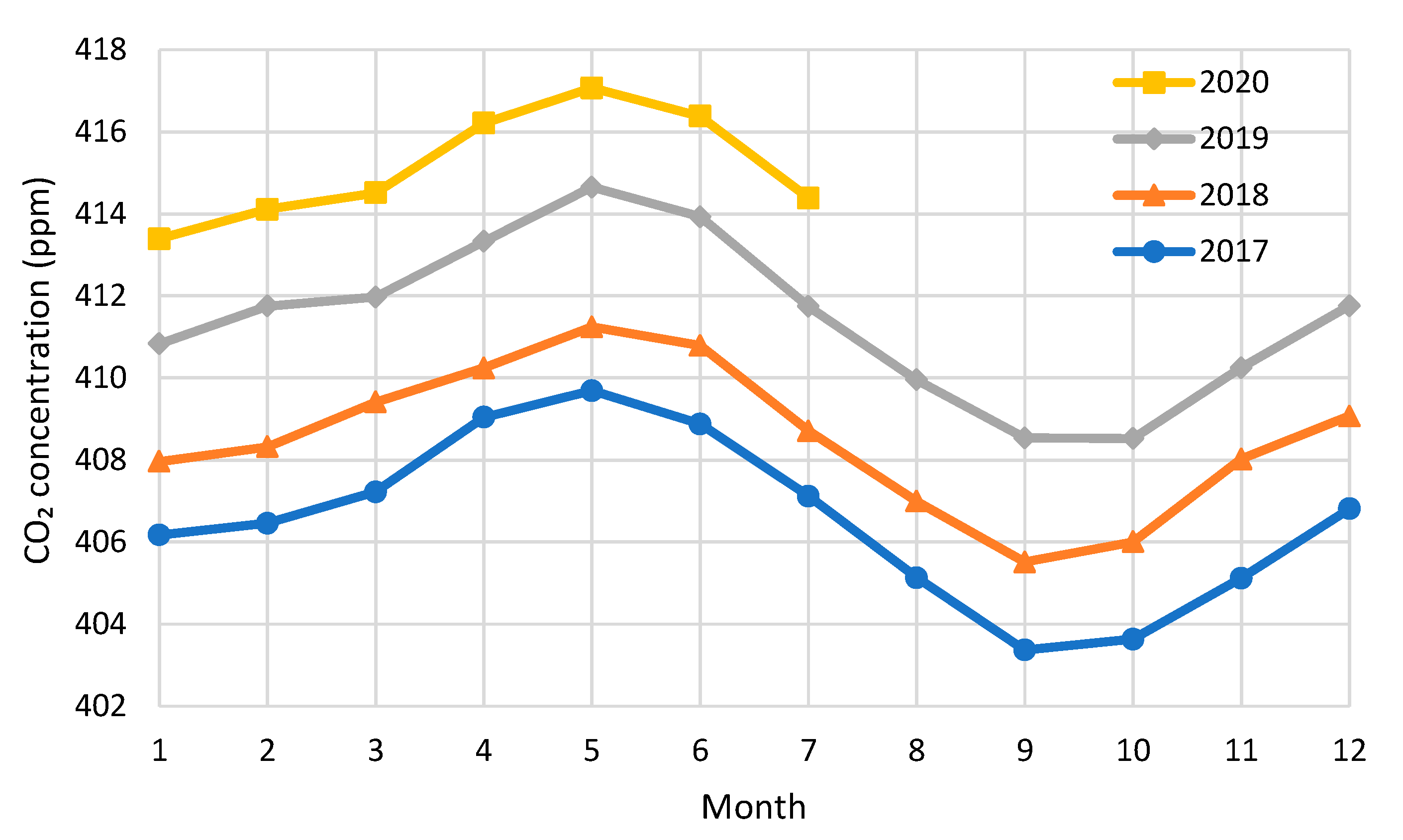
3. Data
4. Methods
4.1. Stochastic Framework
- A time reversible process is also stationary (Lawrance [53]).
- If a scalar process is Gaussian (i.e., all its finite dimensional distributions are multivariate normal) then it is reversible (Weiss [54]). The consequences are (a) a directional process cannot be Gaussian; (b) a discrete-time ARMA process (and a continuous-time Markov process) is reversible if and only if it is Gaussian.
- However, a vector (multivariate) process can be Gaussian and irreversible at the same time. A multivariate Gaussian linear process is reversible if and only if its autocovariance matrices are all symmetric (Tong and Zhang [55]).
- If η1 = 0, then there is no dominant direction.
- If , then the dominant direction is .
- If , then the dominant direction is .
4.2. Complications in Seeking Causality
when discussing the interpretation of a correlation coefficient or a regression, most textbooks warn that an observed relationship does not allow one to say anything about causation between the variables.
Determining true causality requires not only the establishment of a relationship between two variables, but also the far more difficult task of determining a direction of causality.
Results from Granger causality analyses neither establish nor require causality. Granger causality results do not reveal causal interactions, although they can provide evidence in support of a hypothesis about causal interactions.
coupled chaotic dynamical systems violate the first principle of Granger causality that the cause precedes the effect.[68]
4.3. Additional Clarifications of Our Approach
- To make our assertions and, in particular, to use the “hen-or-egg” metaphor, we do not rely on merely statistical arguments. If we did that, based on our results presented in the next section, we would conclude that only the causality direction T → [CO2] exists. However, one may perform a thought experiment of instantly adding a big quantity of CO2 to the atmosphere. Would the temperature not increase? We believe it would, as CO2 is known to be a greenhouse gas. The causation in the opposite direction is also valid, as will be discussed in Section 6, “Physical Interpretation”. Therefore, we assert that both causality directions exist, and we are looking for the dominant one under the current climate conditions (those manifest in the datasets we use) instead of trying to make assertions of an exclusive causality direction.
- While we occasionally use statistical tests (namely, the Granger test, Equations (14) and (15)), we opt to use, as the central point of our analyses, Equation (13) (and the conditions below it) because it is more intuitive and robust, fully reflects the basic causality axiom of time precedence, and is more straightforward, transparent (free of algorithmic manipulations), and easily reproducible (without the need for specialized software).
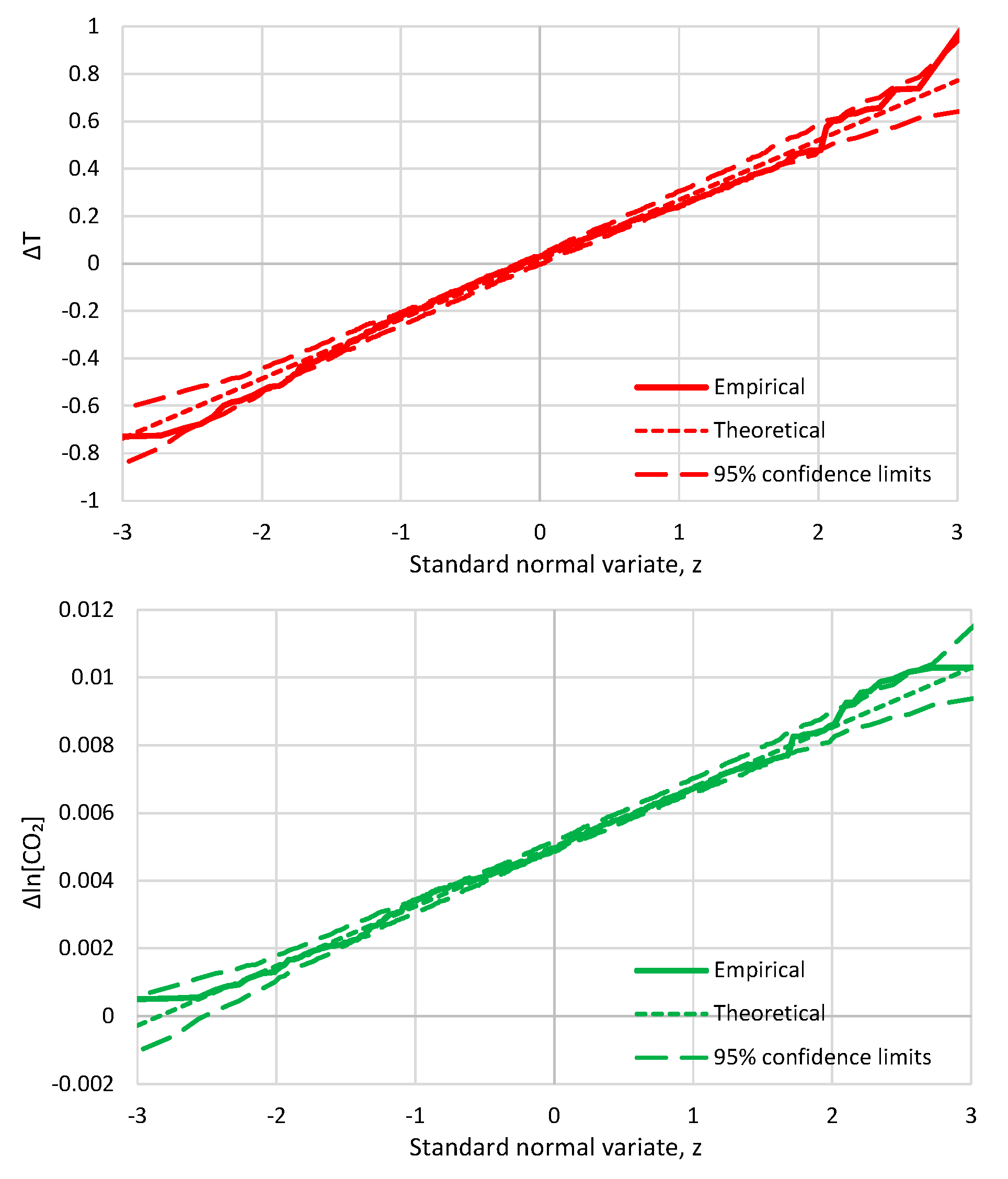
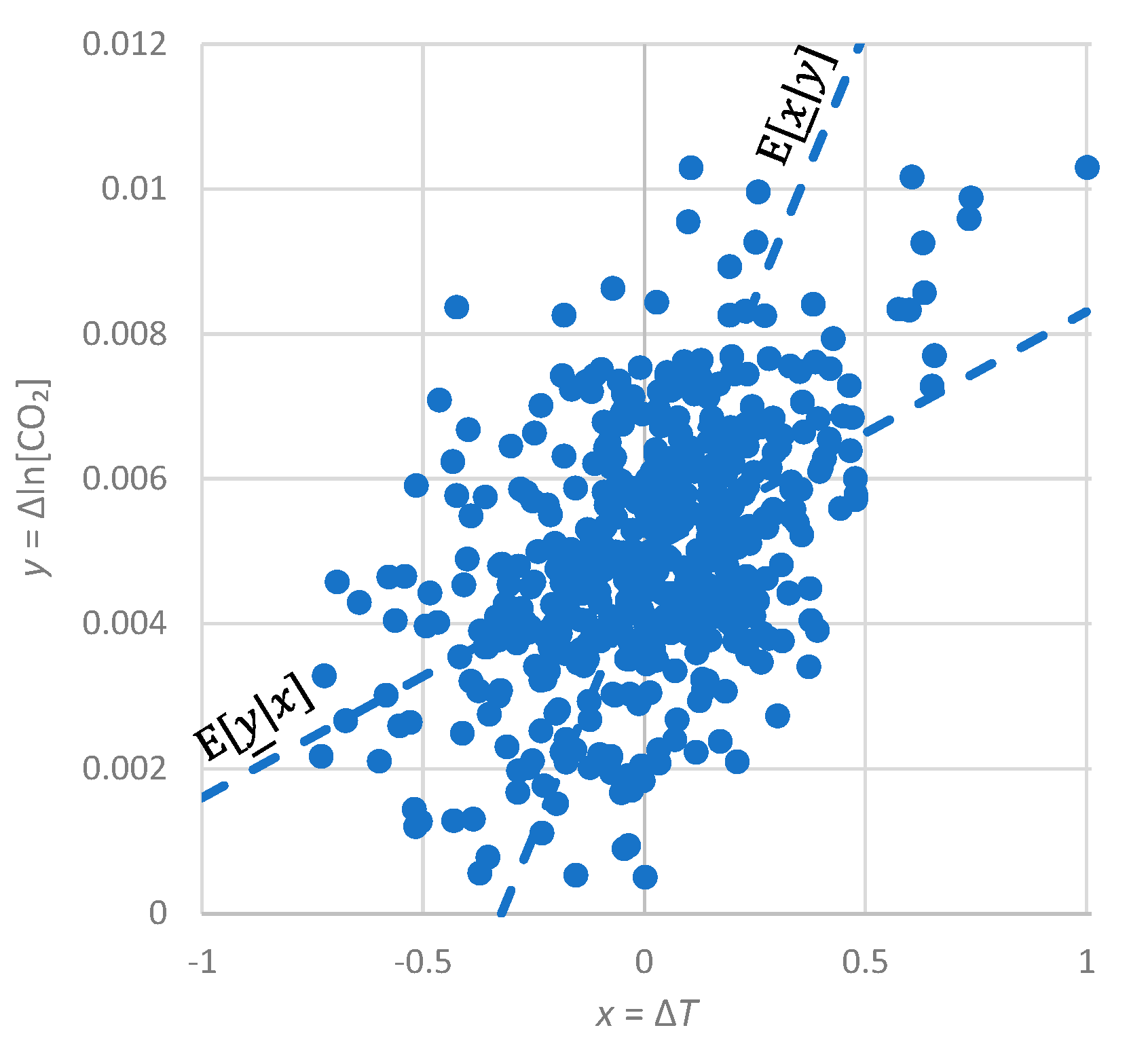
- For simplicity, we do not use any statistic other than correlation here. We stress that the system we are examining is indeed classified as Gaussian and, thus, it is totally unnecessary to examine any statistic in addition to correlation. The evidence of Gaussianity is provided by Figure A1 and Figure A2 in Appendix A.5, in terms of marginal distributions of the processes examined and in terms of their relationship. In particular, Figure A2 suggests a typical linear relationship for the bivariate process. We note that the linearity here is not a simplifying assumption or a coincidence as there are theoretical reasons implying it, which are related to the principle of maximum entropy [67,69].
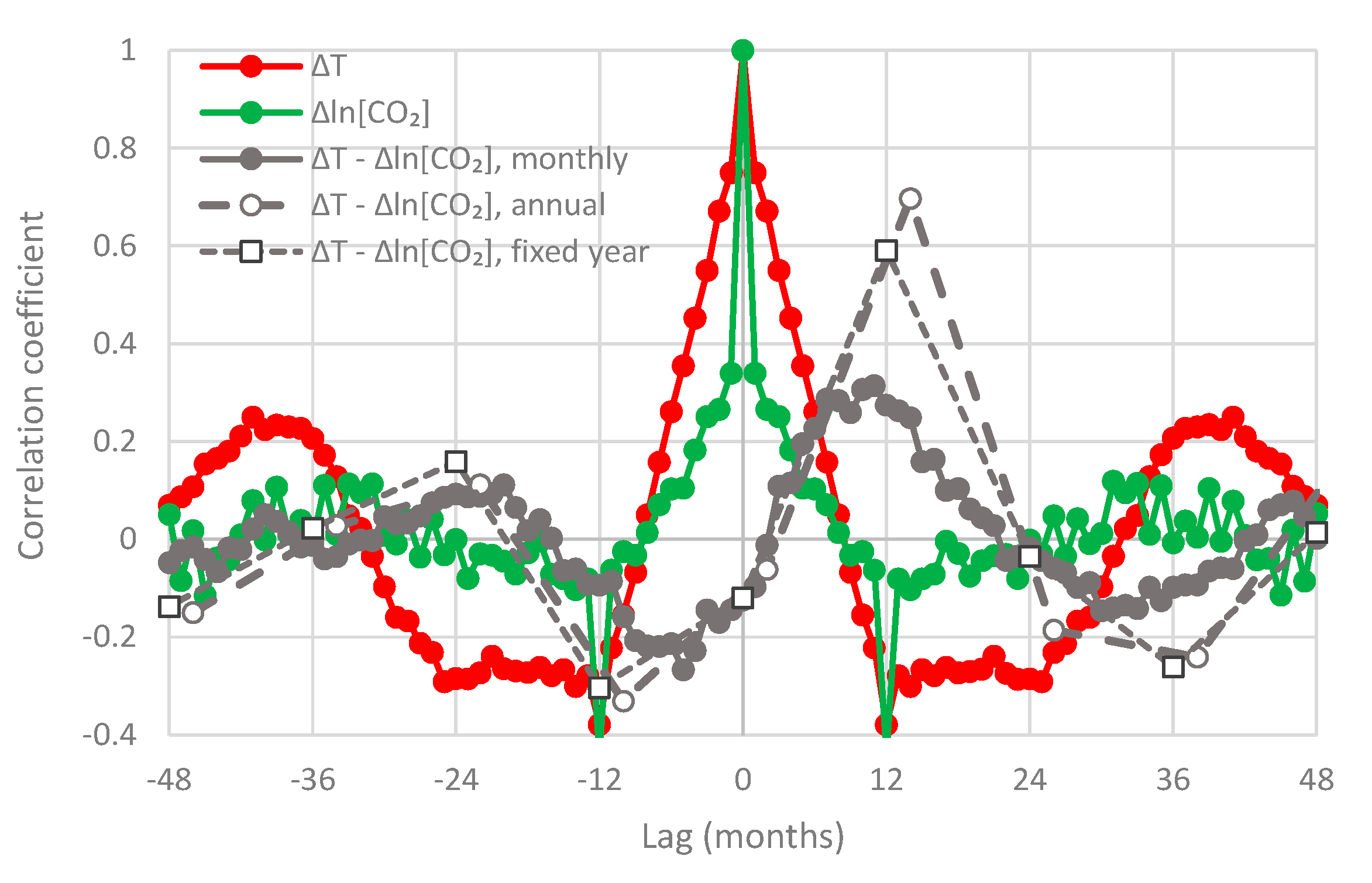
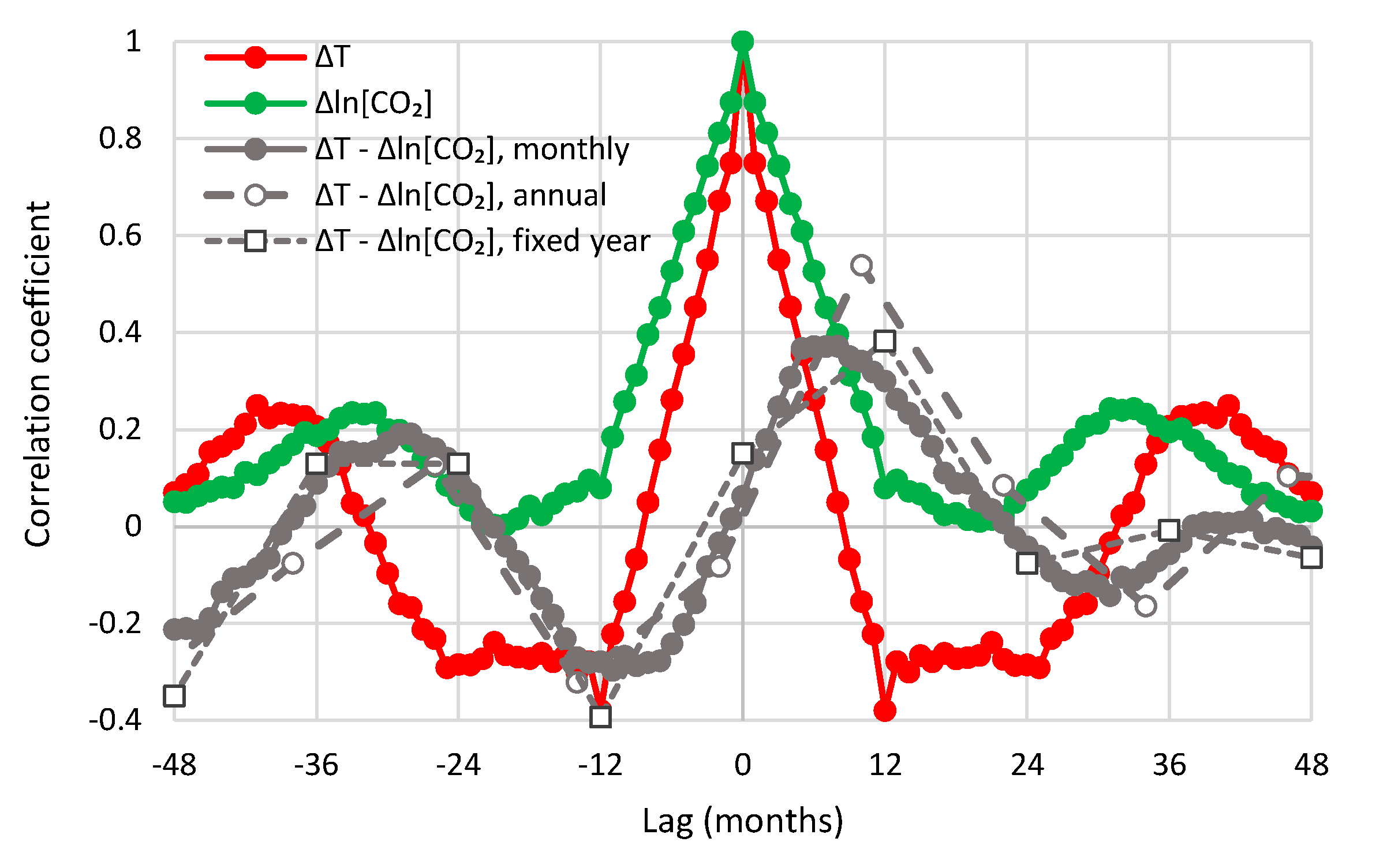
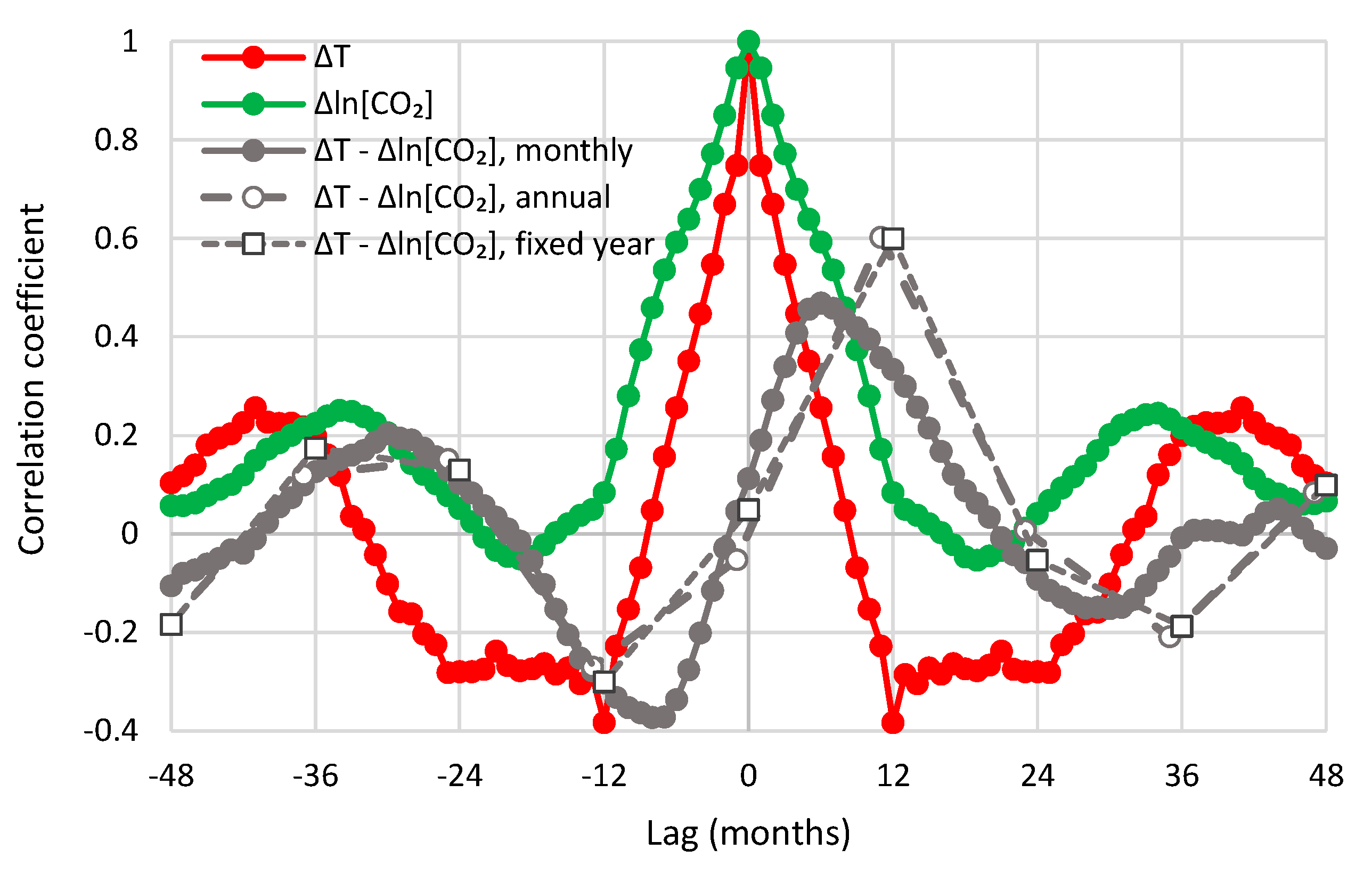
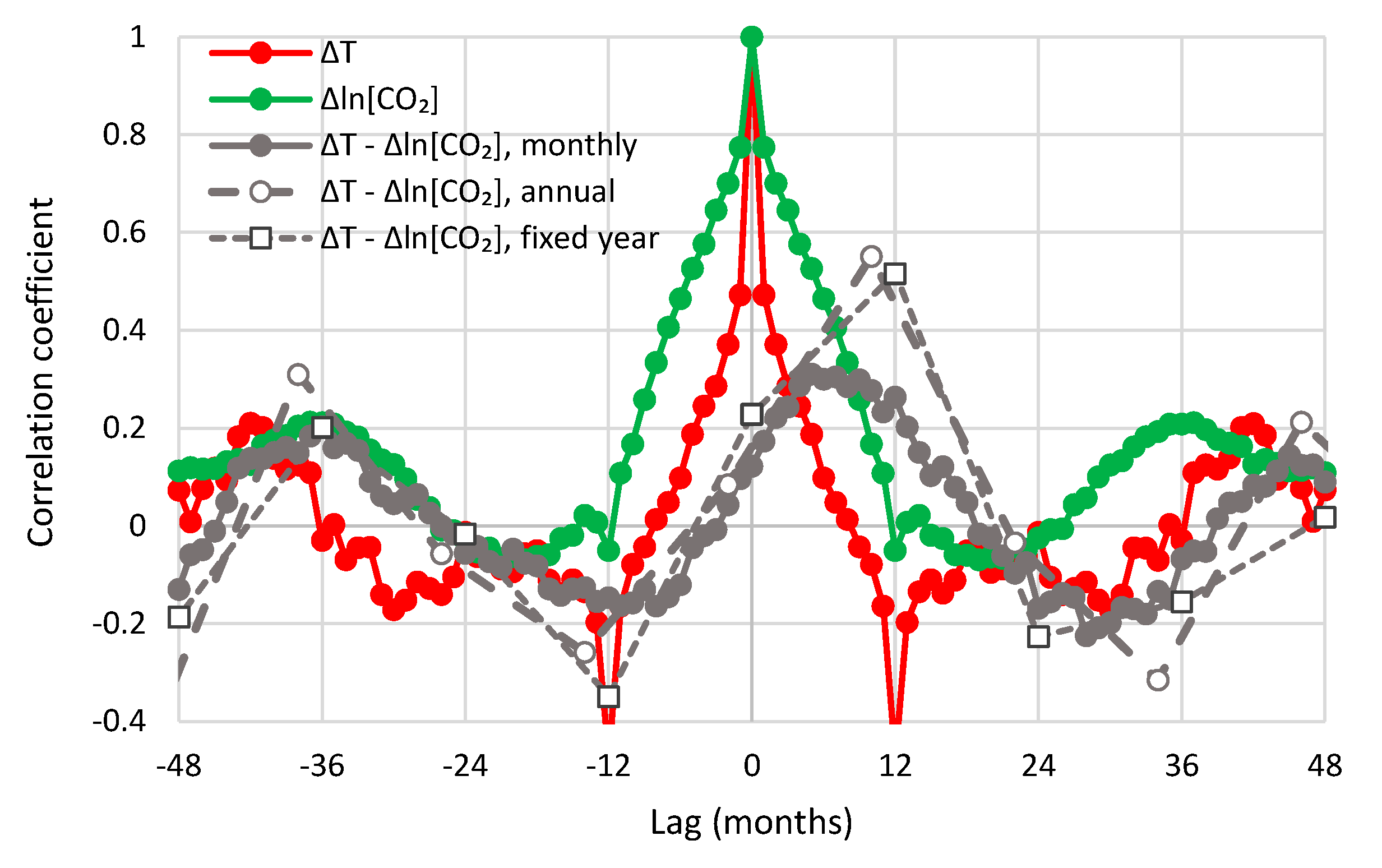
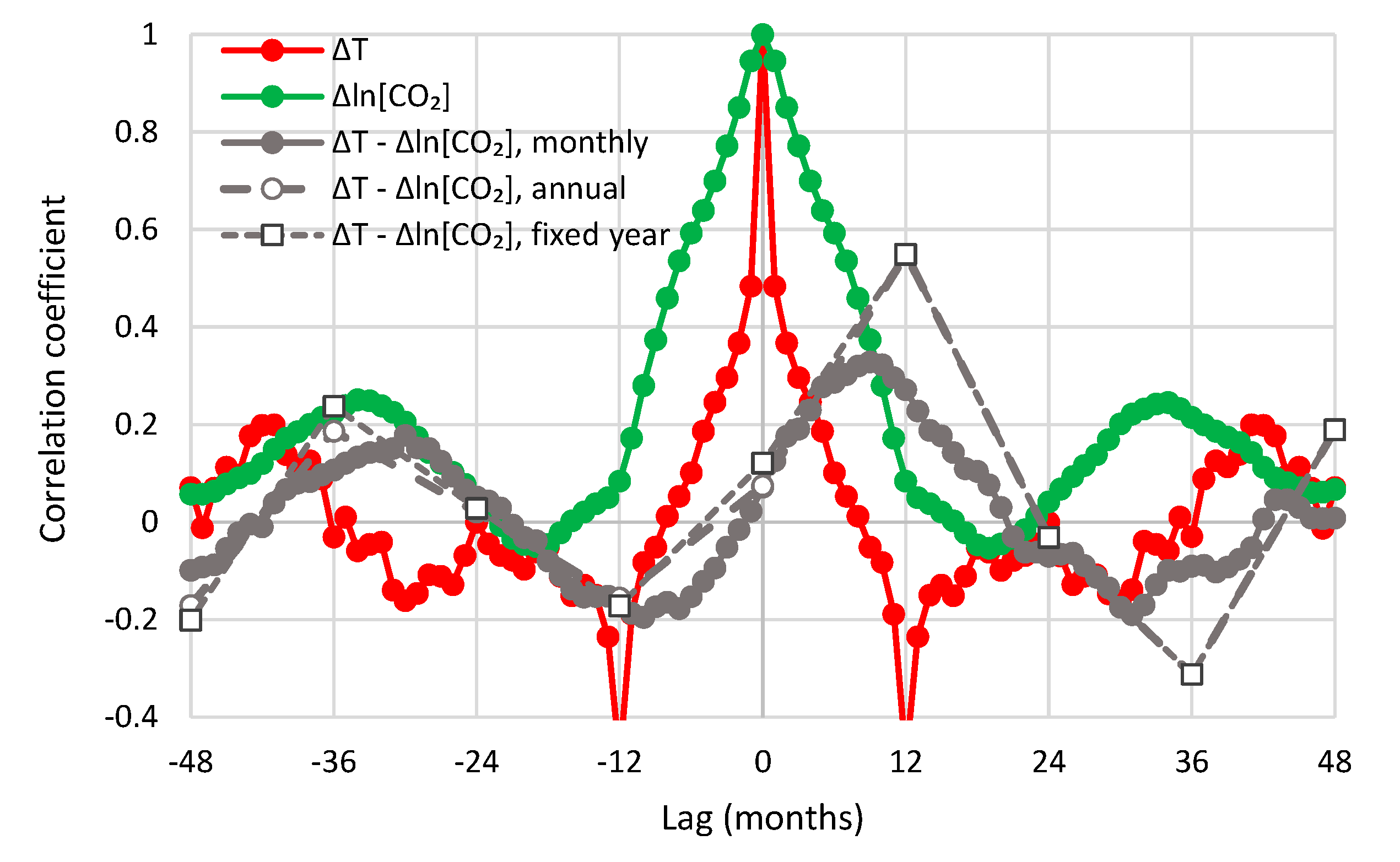
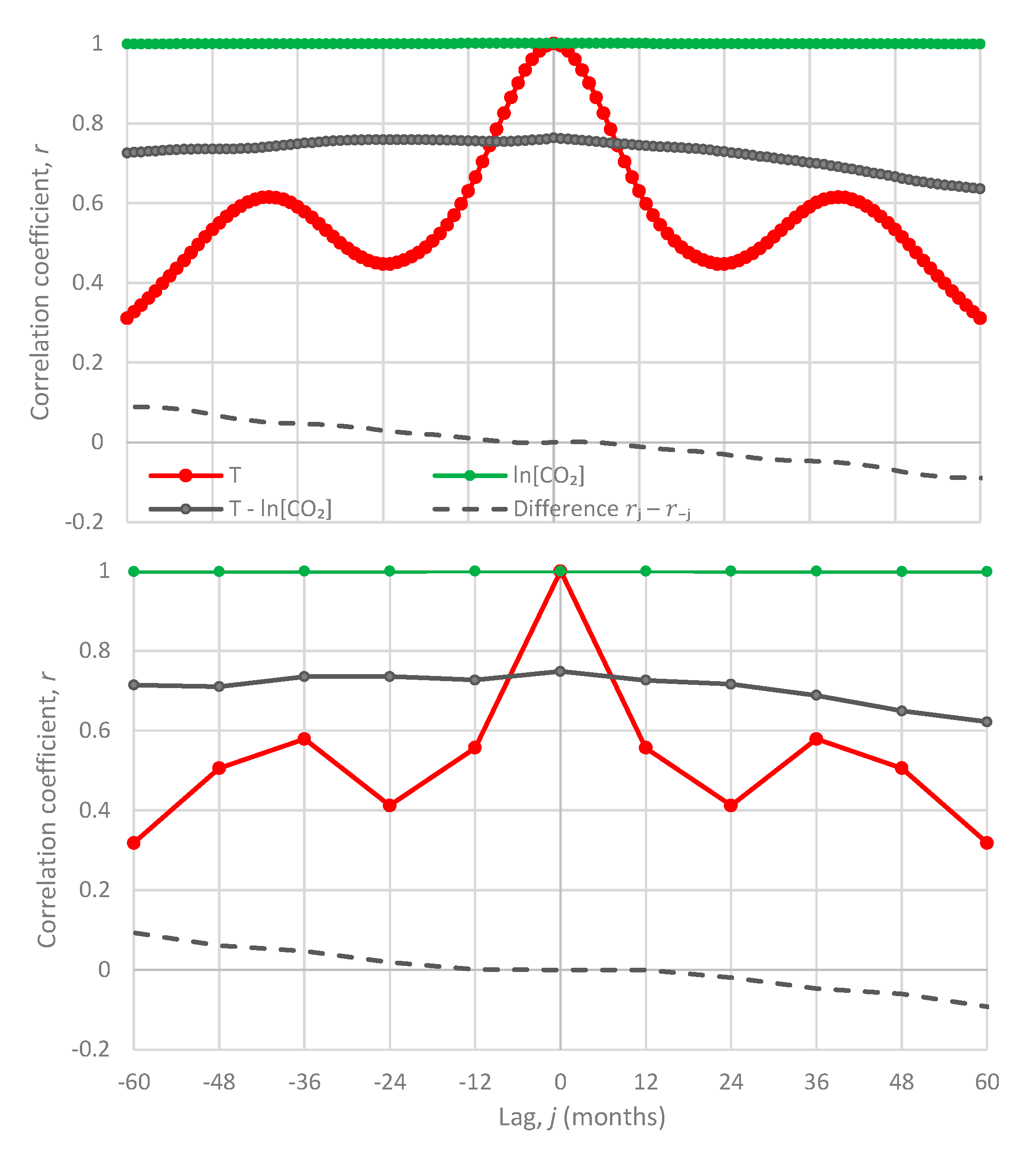
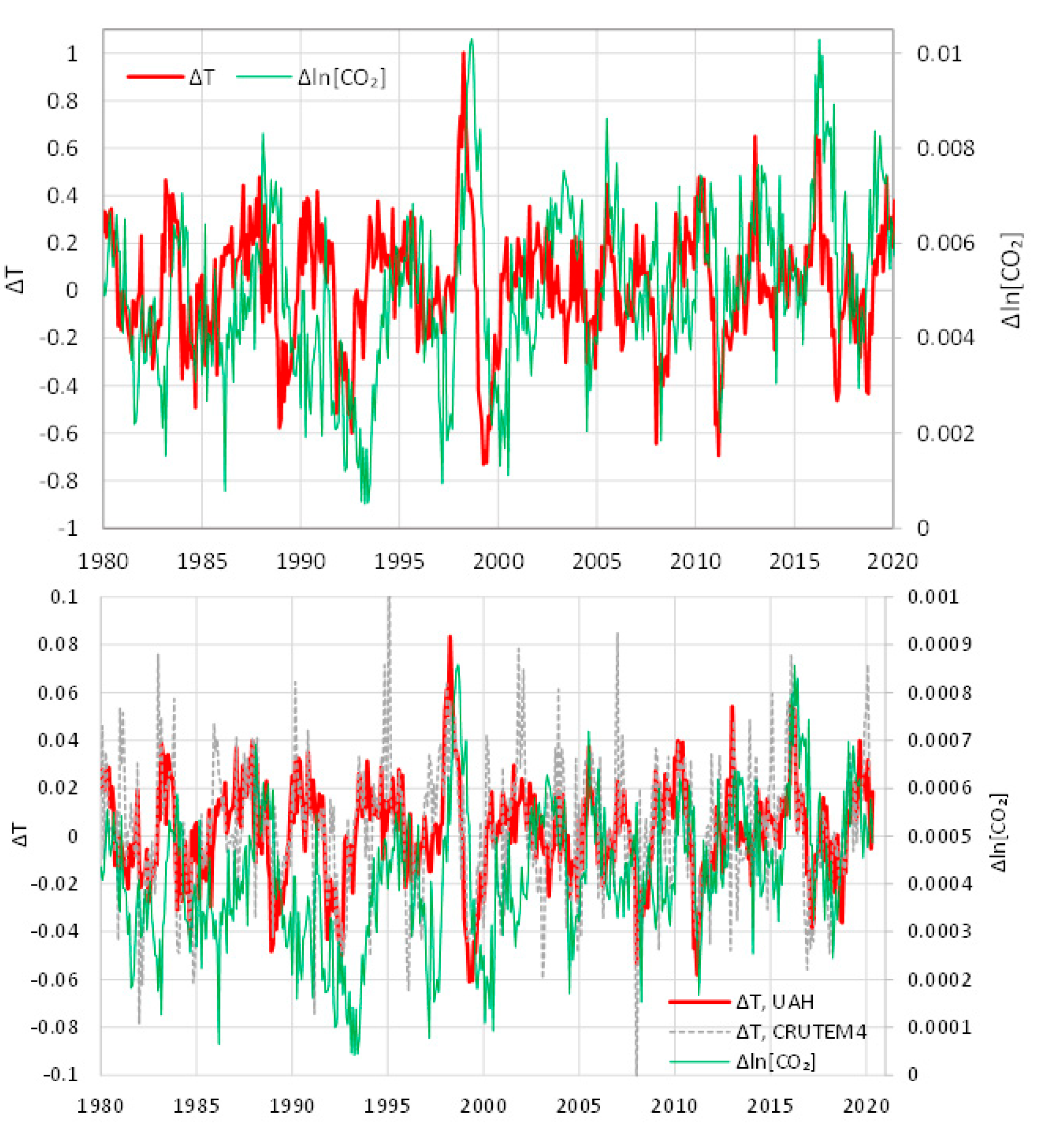
- All in all, we adhere to simplicity and transparency and, in this respect, we illustrate our results graphically, so they are easily understandable, intuitive, and persuasive. Indeed, our findings are easily verifiable even from simple synchronous plots of time series, yet we also include plots of autocorrelations and lagged cross-correlation, which are also most informative in terms of time directionality.
5. Results
5.1. Original Time Series
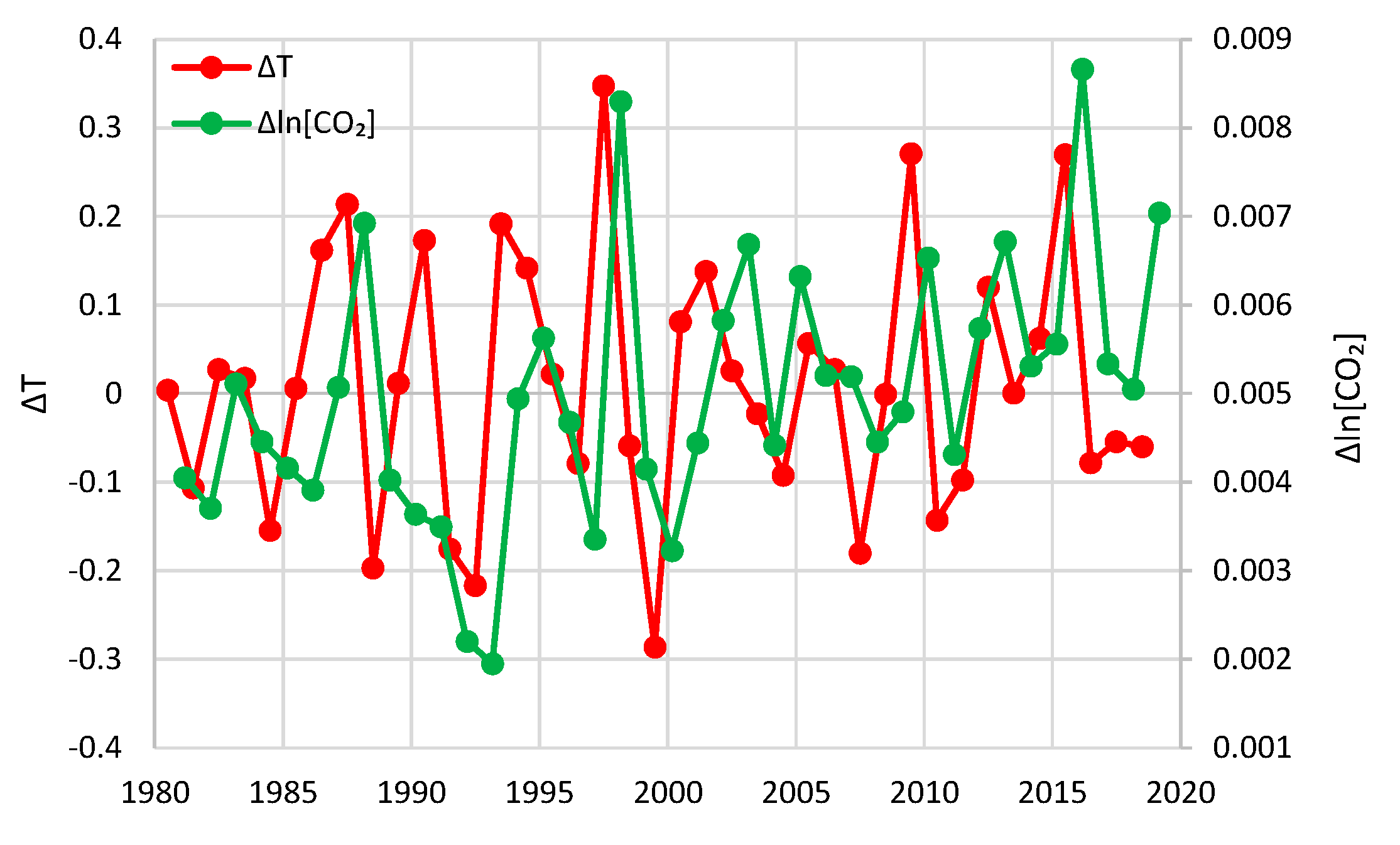
5.2. Differenced Time Series
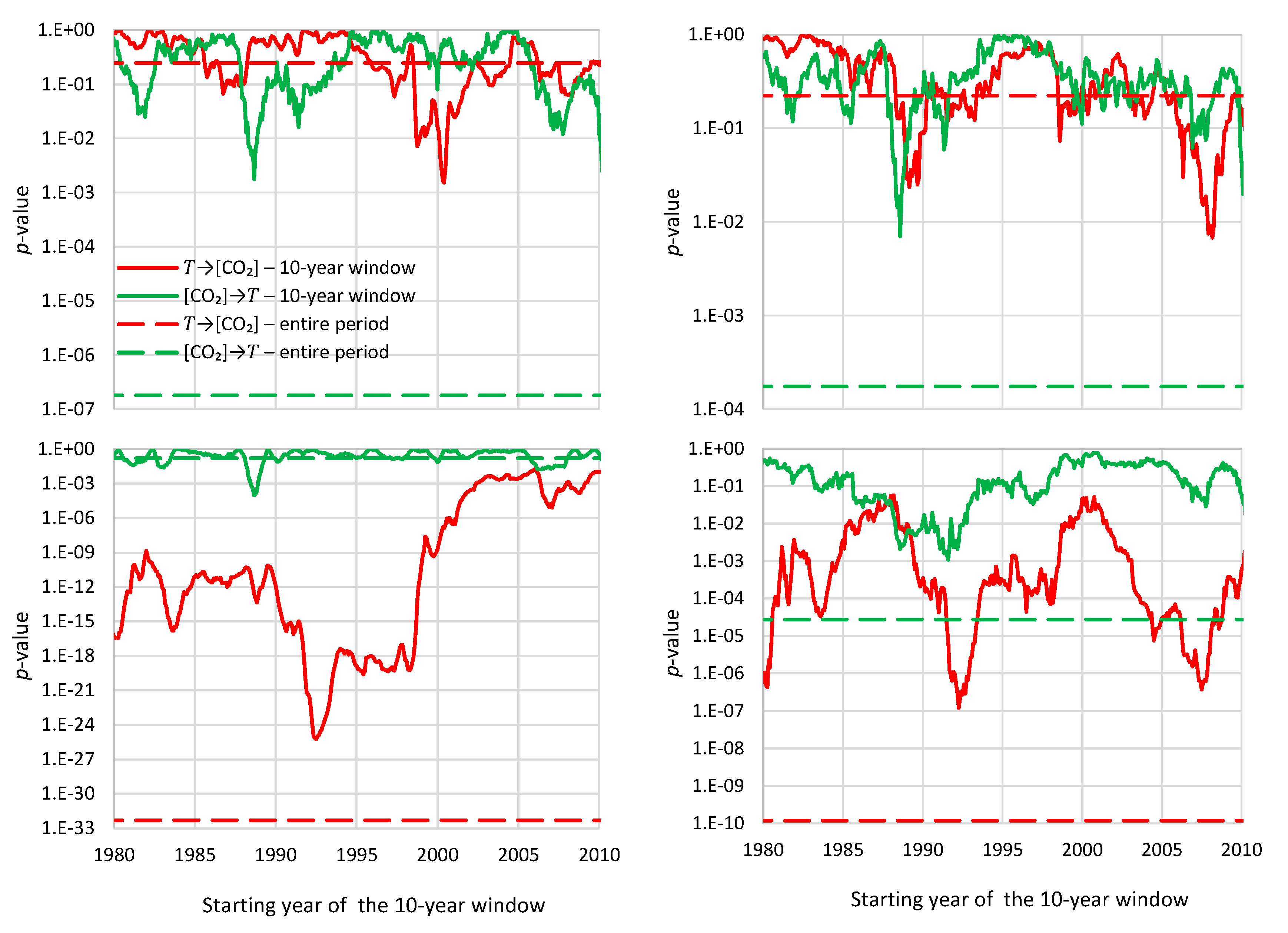
- For the monthly scale and the causality direction [CO2] → T, the null hypothesis is not rejected at all usual significance levels for lag η = 1 and is rejected for significance level 1% for η = 2–8, with minimum attained p-value 1.8 × 10−4 for η = 6.
- For the monthly scale and the causality direction T → [CO2], the null hypothesis is rejected at all usual significance levels for all lags η, with minimum attained p-value 2.1 × 10−8 for η = 7.
- For the monthly scale, the attained p-values in the direction T → [CO2] are always smaller than in direction [CO2] → T by about 4 to 5 orders of magnitude, thus clearly supporting T → [CO2] as dominant direction.
- For the annual scale with fixed year specification and the causality direction [CO2] → T, the null hypothesis is not rejected at all usual significance levels for any lag η, thus indicating that this causality direction does not exist.
- For the annual scale with fixed year specification and the causality direction T → [CO2], the null hypothesis is not rejected at significance level 1% for all lags η = 1–6, with minimum attained p-value 5% for lag η = 2, thus supporting this causality direction at this significance level.
- For the annual scale with fixed year specification, the attained p-values in the direction T → [CO2] are always smaller than in direction [CO2] → T, again clearly supporting T → [CO2] as the dominant direction.
6. Physical Interpretation
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
Appendix A
Appendix A.1. On Early Non-Systematic Measurements of CO2
Appendix A.2. Some Notes on the Averaged Differenced Process
Appendix A.3. Some Notes on Time Directionality of Causal Systems
Appendix A.4. Some Notes on the Alternative Procedures on Causality
Our thoughts and enquiries are, therefore, every moment, employed about this relation: Yet so imperfect are the ideas which we form concerning it, that it is impossible to give any just definition of cause, except what is drawn from something extraneous and foreign to it.
The probabilityof the event occurring in the real world, with f present, is referred to as factual, whileis referred to as counterfactual. Both terms will become clear in the light of what immediately follows. The so-called fraction of attributable risk (FAR) is then defined asThe FAR is interpreted as the fraction of the likelihood of an event that is attributable to the external forcing.
- x = 1: being hot above a threshold;
- y = 1: wearing clothes with weight below a threshold;
- z = 1: sweat quantity above a threshold;
- Cold, heavy clothes:
- Cold, light clothes:
- Hot, heavy clothes:
- Hot, light clothes:
| x | y | z = 0 | z = 1 |
|---|---|---|---|
| 0 | 0 | 0.38 | 0.095 |
| 0 | 1 | 0.0225 | 0.0025 |
| 1 | 0 | 0.00125 | 0.02375 |
| 1 | 1 | 0.095 | 0.38 |
| 0.49875 | 0.50125 |
Appendix A.5. Additional Graphical Depictions
References
- Πλούταρχος, Συμποσιακά Β’ (Plutarch, Quaestiones Convivales B)—Βικιθήκη. Available online: https://el.wikisource.org/wiki/Συμποσιακά_Β’ (accessed on 15 October 2020).
- Plutarchus-Quaestiones Convivales (612c–748d). Available online: http://www.poesialatina.it/_ns/Greek/html/map-en.html (accessed on 15 October 2020).
- IEA (International Energy Agency). Global Energy Review 2020; IEA: Paris, French, 2020; Available online: https://www.iea.org/reports/global-energy-review-2020 (accessed on 1 July 2020).
- Le Quéré, C.; Jackson, R.B.; Jones, M.W.; Smith, A.J.; Abernethy, S.; Andrew, R.M.; De-Gol, A.J.; Willis, D.R.; Shan, Y.; Canadell, J.G.; et al. Temporary reduction in daily global CO2 emissions during the COVID-19 forced confinement. Nat. Clim. Chang. 2020, 10, 647–653. [Google Scholar] [CrossRef]
- Global Carbon Atlas. Available online: http://www.globalcarbonatlas.org/en/CO2-emissions (accessed on 1 July 2020).
- Our World in Data. Available online: https://ourworldindata.org/grapher/annual-co-emissions-by-region (accessed on 1 July 2020).
- Peters, G.P.; Marland, G.; Le Quéré, C.; Boden, T.; Canadell, J.G.; Raupach, M.R. Rapid growth in CO2 emissions after the 2008–2009 global financial crisis. Nat. Clim. Chang. 2012, 2, 2–4. [Google Scholar] [CrossRef]
- Arrhenius, S. On the influence of carbonic acid in the air upon the temperature of the ground. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1896, 41, 237–276. [Google Scholar] [CrossRef]
- De Marchi, L. Le Cause dell’Era Glaciale; Premiato dal R. Instituto Lombardo: Pavia, Italy, 1895. [Google Scholar]
- Tyndall, J. Heat a Mode of Motion, 2nd ed.; Longmans: London, UK, 1865; Available online: https://archive.org/details/heatamodemotion05tyndgoog/ (accessed on 1 September 2020).
- Foote, E. Circumstances affecting the heat of the sun’s rays. Am. J. Sci. Arts 1856, 22, 382–383. [Google Scholar]
- Jackson, R. Eunice Foote, John Tyndall and a question of priority. Notes Rec. 2020, 74, 105–118. [Google Scholar] [CrossRef]
- Ortiz, J.D.; Jackson, R. Understanding Eunice Foote’s 1856 experiments: Heat absorption by atmospheric gases. Notes Rec. 2020. [Google Scholar] [CrossRef]
- Connolly, R. Review of “Atmospheric temperature and CO2: Hen-or-egg causality?” (Version 1). Sci 2020. Available online: https://www.mdpi.com/2413-4155/2/4/77/review_report (accessed on 9 October 2020).
- Schmidt, G.A.; Ruedy, R.A.; Miller, R.L.; Lacis, A.A. Attribution of the present-day total greenhouse effect. J. Geophys. Res. 2010, 115, D20106. [Google Scholar] [CrossRef]
- Shaviv, N.J.; Veizer, J. Celestial driver of Phanerozoic climate? Geol. Soc. Am. Today 2003, 13, 4–10. [Google Scholar] [CrossRef]
- Shaviv, N.J. On climate response to changes in the cosmic ray flux and radiative budget. J. Geophys. Res. Space Phys. 2005, 110, A08105. [Google Scholar] [CrossRef]
- Rahmstorf, S.; Archer, D.; Ebel, D.S.; Eugster, O.; Jouzel, J.; Maraun, D.; Neu, U.; Schmidt, G.A.; Sever-Inghaus, J.; Weaver, A.J.; et al. Cosmic rays, carbon dioxide, and climate. Eos 2004, 85, 38–41. [Google Scholar] [CrossRef]
- Shaviv, N.J.; Veizer, J. Comment on Cosmic rays, carbon dioxide, and climate. Eos 2004, 85, 510. [Google Scholar] [CrossRef]
- Rahmstorf, S.; Archer, D.; Ebel, D.S.; Eugster, O.; Jouzel, J.; Maraun, D.; Neu, U.; Schmidt, G.A.; Sever-Inghaus, J.; Weaver, A.J.; et al. Reply to Comment [by Shaviv and Veizer]. Eos 2004, 85, 511. [Google Scholar] [CrossRef]
- Royer, D.L.; Berner, R.A.; Montañez, I.P.; Tabor, N.J.; Beerling, D.J. CO2 as a primary driver of phanerozoic climate. Geol. Soc. Am. Today 2004, 14, 4–10. [Google Scholar] [CrossRef]
- Shaviv, N.J.; Veizer, J. Comment on “CO2 as a primary driver of Phanerozoic climate” by Royer et al. Geol. Soc. Am. Today 2004, 14, 18. [Google Scholar]
- Royer, D.L.; Berner, R.A.; Montañez, I.P.; Tabor, N.J.; Beerling, D.J. Reply to Comment on “CO2 as a primary driver of Phanerozoic climate” by Royer et al. Geol. Soc. Am. Today 2004, 14, 18. [Google Scholar]
- Roe, G. In defense of Milankovitch. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Jouzel, J.; Lorius, C.; Petit, J.R.; Genthon, C.; Barkov, N.I.; Kotlyakov, V.M.; Petrov, V.M. Vostok ice core: A continuous isotope temperature record over the last climatic cycle (160,000 years). Nature 1987, 329, 403–408. [Google Scholar] [CrossRef]
- Petit, J.R.; Jouzel, J.; Raynaud, D.; Barkov, N.I.; Barnola, J.-M.; Basile, I.; Bender, M.; Chappellaz, J.; Davis, M.; Delayque, G.; et al. Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature 1999, 399, 429–436. [Google Scholar] [CrossRef]
- Caillon, N.; Severinghaus, J.P.; Jouzel, J.; Barnola, J.M.; Kang, J.; Lipenkov, V.Y. Timing of atmospheric CO2 and Antarctic temperature changes across Termination III. Science 2003, 299, 1728–1731. [Google Scholar] [CrossRef]
- Soon, W. Implications of the secondary role of carbon dioxide and methane forcing in climate change: Past, present, and future. Phys. Geogr. 2007, 28, 97–125. [Google Scholar] [CrossRef]
- Pedro, J.B.; Rasmussen, S.O.; van Ommen, T.D. Tightened constraints on the time-lag between Antarctic temperature and CO2 during the last deglaciation. Clim. Past 2012, 8, 1213–1221. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Time’s arrow in stochastic characterization and simulation of atmospheric and hydrological processes. Hydrol. Sci. J. 2019, 64, 1013–1037. [Google Scholar] [CrossRef]
- Beeman, J.C.; Gest, L.; Parrenin, F.; Raynaud, D.; Fudge, T.J.; Buizert, C.; Brook, E.J. Antarctic temperature and CO2: Near-synchrony yet variable phasing during the last deglaciation. Clim. Past 2019, 15, 913–926. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, S.; Jin, Z. Breakpoint lead-lag analysis of the last deglacial climate change and atmospheric CO2 concentration on global and hemispheric scales. Quat. Int. 2018, 490, 50–59. [Google Scholar] [CrossRef]
- Scotese, C.R. Phanerozoic Temperatures: Tropical Mean Annual Temperature (TMAT), Polar Mean Annual Temperature (PMAT), and Global Mean Annual Temperature (GMAT) for the last 540 Million Years. In Proceedings of the Earth’s Temperature History Research Workshop, Smithsonian National Museum of Natural History, Washington, DC, USA, 30–31 March 2018; Available online: https://www.researchgate.net/publication/324017003 (accessed on 8 September 2020).
- Grossman, E.L. Oxygen isotope stratigraphy. In The Geological Time Scale; Gradstein, F.M., Ogg, J.G., Schmitz, M.D., Ogg, G.M., Eds.; Elsevier: Amsterdam, The Netherlands, 2012; pp. 181–206. [Google Scholar]
- Veizer, J.; Prokoph, A. Temperatures and oxygen isotopic composition of Phanerozoic oceans. Earth Sci. Rev. 2015, 146, 92–104. [Google Scholar] [CrossRef]
- Boucot, A.J.; Xu, C.; Scotese, C.; Morley, R.J. Phanerozoic Paleoclimate: An Atlas of Lithologic Indications of Climate; SEPM Concepts Sedimentol. Paleontol. No 11; SEPM Publication Editors: Tulsa, OK, USA, 2013; p. 30. ISBN 978-1-56576-282-4. [Google Scholar]
- Davis, W.J. The relationship between atmospheric carbon dioxide concentration and global temperature for the last 425 million years. Climate 2017, 5, 76. [Google Scholar] [CrossRef]
- Berner, R.A. Addendum to “Inclusion of the weathering of volcanic rocks in the GEOCARBSULF model” (R. A. Berner, 2006, v. 306, p. 295–302). Am. J. Sci. 2008, 308, 100–103. [Google Scholar] [CrossRef]
- Ekart, D.D.; Cerling, T.E.; Montanez, I.P.; Tabor, N.J. A 400 million year carbon isotope record of pedogenic carbonate: Implications for paleoatmospheric carbon dioxide. Am. J. Sci. 1999, 299, 805–827. [Google Scholar] [CrossRef]
- International Commission on Stratigraphy. Available online: https://stratigraphy.org/chart (accessed on 1 September 2020).
- Kodra, E.; Chatterjee, S.; Ganguly, A.R. Exploring Granger causality between global average observed time series of carbon dioxide and temperature. Theor. Appl. Climatol. 2011, 104, 325–335. [Google Scholar] [CrossRef]
- Stern, D.I.; Kaufmann, R.K. Anthropogenic and natural causes of climate change. Clim. Chang. 2014, 122, 257–269. [Google Scholar] [CrossRef]
- Stips, A.; Macias, D.; Coughlan, C.; Garcia-Gorriz, E.; Liang, X.S. On the causal structure between CO2 and global temperature. Sci. Rep. 2016, 6, 21691. [Google Scholar] [CrossRef]
- Liang, X.S. Information flow and causality as rigorous notions ab initio. Phys. Rev. E 2016, 94, 052201. [Google Scholar] [CrossRef] [PubMed]
- Humlum, O.; Stordahl, K.; Solheim, J.E. The phase relation between atmospheric carbon dioxide and global temperature. Glob. Planet. Chang. 2013, 100, 51–69. [Google Scholar] [CrossRef]
- Richardson, M. Comment on “The phase relation between atmospheric carbon dioxide and global temperature” by Humlum, Stordahl and Solheim. Glob. Planet. Chang. 2013, 107, 226–228. [Google Scholar] [CrossRef]
- Spencer, R.W.; Christy, J.R. Precise monitoring of global temperature trends from satellites. Science 1990, 247, 1558–1562. [Google Scholar] [CrossRef] [PubMed]
- Christy, J.R.; Norris, W.B.; Spencer, R.W.; Hnilo, J.J. Tropospheric temperature change since 1979 from tropical radiosonde and satellite measurements. J. Geophys. Res. 2007, 112, D06102. [Google Scholar] [CrossRef]
- Jones, P.D.; Lister, D.H.; Osborn, T.J.; Harpham, C.; Salmon, M.; Morice, C.P. Hemispheric and large-scale land surface air temperature variations: An extensive revision and an update to 2010. J. Geophys. Res. 2012, 117, D05127. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Revisiting global hydrological cycle: Is it intensifying? Hydrol. Earth Syst. Sci. 2020. [Google Scholar] [CrossRef]
- Keeling, C.D.; Bacastow, R.B.; Bainbridge, A.E.; Ekdahl, C.A.; Guenther, P.R.; Waterman, L.S. Atmospheric carbon dioxide variations at Mauna Loa observatory, Hawaii. Tellus 1976, 28, 538–551. [Google Scholar]
- Global Monitoring Laboratory—Carbon Cycle Greenhouse Gases. Available online: https://www.esrl.noaa.gov/gmd/ccgg/about/global_means.html (accessed on 1 September 2020).
- Lawrance, A.J. Directionality and reversibility in time series. Int. Stat. Rev. 1991, 59, 67–79. [Google Scholar] [CrossRef]
- Weiss, G. Time-reversibility of linear stochastic processes. J. Appl. Probab. 1975, 12, 831–836. [Google Scholar] [CrossRef]
- Tong, H.; Zhang, Z. On time-reversibility of multivariate linear processes. Stat. Sin. 2005, 15, 495–504. [Google Scholar]
- Koutsoyiannis, D. Generic and parsimonious stochastic modelling for hydrology and beyond. Hydrol. Sci. J. 2016, 61, 225–244. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Wienersche spiralen und einige andere interessante Kurven im Hilbertschen Raum. Dokl. Akad. Nauk SSSR 1940, 26, 115–118. [Google Scholar]
- Hurst, H.E. Long term storage capacities of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 776–808. [Google Scholar]
- Heller, M. Time, causality, and the quantum theory. Rev. Metaphys. 1983, 37, 408–409. [Google Scholar]
- Kline, A.D. Are there cases of simultaneous causation? PSA Proc. Bienn. Meet. Philos. Sci. Assoc. 1980, 1980, 292–301, Philosophy of Science Association. [Google Scholar] [CrossRef]
- Suppes, P. A Probabilistic Theory of Causality; North-Holland Publishing: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Granger, C.W. Testing for causality: A personal viewpoint. J. Econ. Dyn. Control 1980, 2, 329–352. [Google Scholar] [CrossRef]
- Granger, C.; Newbold, P. Forecasting Economic Time Series; Academic Press: San Diego, CA, USA, 1986. [Google Scholar]
- Gujarati, D.N.; Porter, D.C. Basic Econometrics, 5th ed.; McGraw Hill: Boston, MA, USA, 2009. [Google Scholar]
- McGraw, M.C.; Barnes, E.A. Memory matters: A case for Granger causality in climate variability studies. J. Clim. 2018, 31, 3289–3300. [Google Scholar] [CrossRef]
- Cohen, M.X. Analyzing Neural Time Series Data: Theory and Practice; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Papoulis, A. Probability, Random Variables and Stochastic Processes, 3rd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Paluš, M.; Krakovská, A.; Jakubík, J.; Chvosteková, M. Causality, dynamical systems and the arrow of time. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 75307. [Google Scholar] [CrossRef] [PubMed]
- Koutsoyiannis, D.; Yao, H.; Georgakakos, A. Medium-range flow prediction for the Nile: A comparison of stochastic and deterministic methods. Hydrol. Sci. J. 2008, 53, 142–164. [Google Scholar] [CrossRef]
- Zaiontz, C. Real Statistics Using Excel. Available online: http://www.realstatistics.com/ (accessed on 1 September 2020).
- Zaiontz, C. Real Statistics Examples Workbooks. Available online: http://www.real-statistics.com/free-download/real-statistics-examples-workbook/ (accessed on 1 September 2020).
- Kundzewicz, Z.W.; Pińskwar, I.; Koutsoyiannis, D. Variability of global mean annual temperature is significantly influenced by the rhythm of ocean-atmosphere oscillations. Sci. Total Environ. 2020, 747, 141256. [Google Scholar] [CrossRef]
- Masters, T.; Benestad, R. Comment on “The phase relation between atmospheric carbon dioxide and global temperature”. Glob. Planet. Chang. 2013, 106, 141–142. [Google Scholar] [CrossRef]
- Bond-Lamberty, B.; Thomson, A. Temperature-associated increases in the global soil respiration record. Nature 2010, 464, 579–582. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. Available online: http://www.climatechange2013.org/report/ (accessed on 14 February 2020).
- Raich, J.W.; Schlesinger, W.H. The global carbon dioxide flux in soil respiration and its relationship to vegetation and climate. Tellus B Chem. Phys. Meteorol. 1992, 44, 81–99. [Google Scholar] [CrossRef]
- Makita, N.; Kosugi, Y.; Sakabe, A.; Kanazawa, A.; Ohkubo, S.; Tani, M. Seasonal and diurnal patterns of soil respiration in an evergreen coniferous forest: Evidence from six years of observation with automatic chambers. PLoS ONE 2018, 13, e0192622. [Google Scholar] [CrossRef]
- ÓhAiseadha, C.; Quinn, G.; Connolly, R.; Connolly, M.; Soon, W. Energy and Climate Policy—An Evaluation of Global Climate Change Expenditure 2011–2018. Energies 2020, 13, 4839. [Google Scholar] [CrossRef]
- Pomeroy, R.; Bowlus, F.D. Progress report on sulfide control research. Sew. Work. J. 1946, 18, 597–640. [Google Scholar]
- Green, C.; Byrne, K.A. Biomass: Impact on carbon cycle and greenhouse gas emissions. In Encyclopedia of Energy; Cleveland, C.J., Ed.; Elsevier: Amsterdam, The Netherlands, 2004; pp. 223–236. [Google Scholar] [CrossRef]
- Weiss, R. Carbon dioxide in water and seawater: The solubility of a non-ideal gas. Mar. Chem. 1974, 2, 203–215. [Google Scholar] [CrossRef]
- Zhu, Z.; Piao, S.; Myneni, R.B.; Huang, M.; Zeng, Z.; Canadell, J.G.; Ciais, P.; Sitch, S.; Friedlingstein, P.; Arneth, A.; et al. Greening of the earth and its drivers. Nat. Clim. Chang. 2016, 6, 791–795. [Google Scholar] [CrossRef]
- Chen, C.; Park, T.; Wang, X.; Piao, S.; Xu, B.; Chaturvedi, R.K.; Fuchs, R.; Brovkin, V.; Ciais, P.; Fensholt, R.; et al. China and India lead in greening of the world through land-use management. Nat. Sustain. 2019, 2, 122–129. [Google Scholar] [CrossRef] [PubMed]
- Connolly, R.; Connolly, M.; Carter, R.M.; Soon, W. How Much Human-Caused Global Warming Should We Expect with Business-As-Usual (BAU) Climate Policies? A Semi-Empirical Assessment. Energies 2020, 13, 1365. [Google Scholar] [CrossRef]
- Aryal, Y. Review of Atmospheric Temperature and CO2: Hen-or-Egg Causality? (Version 1). Sci 2020. Available online: https://www.mdpi.com/2413-4155/2/4/77/review_report (accessed on 25 September 2020).
- Alexandris, S. Review of Atmospheric Temperature and CO2: Hen-or-Egg Causality? (Version 1). Sci 2020. Available online: https://www.mdpi.com/2413-4155/2/4/77/review_report (accessed on 26 September 2020).
- Beck, E.-G. 180 Years of atmospheric CO2 gas analysis by chemical methods. Energy Environ. 2007, 18, 259–282. [Google Scholar] [CrossRef]
- Letts, E.A.; Blake, R.F. The carbonic anhydride of the atmosphere. Proc. R. Soc. Dublin 1900, 9, 107–270. [Google Scholar]
- Stepanova, N.A. A Selective Annotated Bibliography of Carbon Dioxide in the Atmosphere. Meteorol. Abstr. 1952, 3, 137–170. [Google Scholar]
- Keeling, R.F. Comment on “180 Years of Atmospheric CO2 Gas Analysis by Chemical Methods” by Ernst-Georg Beck. Energy Environ. 2007, 18, 637–639. [Google Scholar]
- Meijer, H.A.J. Comment on “180 Years of Atmospheric CO2 Gas Analysis by Chemical Methods” by Ernst-Georg Beck. Energy Environ. 2007, 18, 635–636. [Google Scholar]
- Hannart, A.; Pearl, J.; Otto, F.E.L.; Naveau, P.; Ghil, M. Causal counterfactual theory for the attribution of weather and climate-related events. Bull. Am. Meteorol. Soc. 2016, 97, 99–110. [Google Scholar] [CrossRef]
- Verbitsky, M.Y.; Mann, M.E.; Steinman, B.A.; Volobuev, D.M. Detecting causality signal in instrumental measurements and climate model simulations: Global warming case study. Geosci. Model Dev. 2019, 12, 4053–4060. [Google Scholar] [CrossRef]
- Hume, D. An Enquiry Concerning Human Understanding; Oxford World’s Classics; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Koutsoyiannis, D.; Efstratiadis, A.; Mamassis, N.; Christofides, A. On the credibility of climate predictions. Hydrol. Sci. J. 2008, 53, 671–684. [Google Scholar] [CrossRef]
- Anagnostopoulos, G.G.; Koutsoyiannis, D.; Christofides, A.; Efstratiadis, A.; Mamassis, N. A comparison of local and aggregated climate model outputs with observed data. Hydrol. Sci. J. 2010, 55, 1094–1110. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Stakhiv, E.Z. Are climate models “ready for prime time” in water resources management applications, or is more research needed? Hydrol. Sci. J. 2010, 55, 1085–1089. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Christofides, A.; Efstratiadis, A.; Anagnostopoulos, G.G.; Mamassis, N. Scientific dialogue on climate: Is it giving black eyes or opening closed eyes? Reply to “A black eye for the Hydrological Sciences Journal” by D. Huard. Hydrol. Sci. J. 2011, 56, 1334–1339. [Google Scholar] [CrossRef]
- Tsaknias, D.; Bouziotas, D.; Koutsoyiannis, D. Statistical comparison of observed temperature and rainfall extremes with climate model outputs in the Mediterranean region. ResearchGate 2016. [Google Scholar] [CrossRef]
- Tyralis, H.; Koutsoyiannis, D. On the prediction of persistent processes using the output of deterministic models. Hydrol. Sci. J. 2017, 62, 2083–2102. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. On the quest for chaotic attractors in hydrological processes. Hydrol. Sci. J. 2006, 51, 1065–1091. [Google Scholar] [CrossRef]
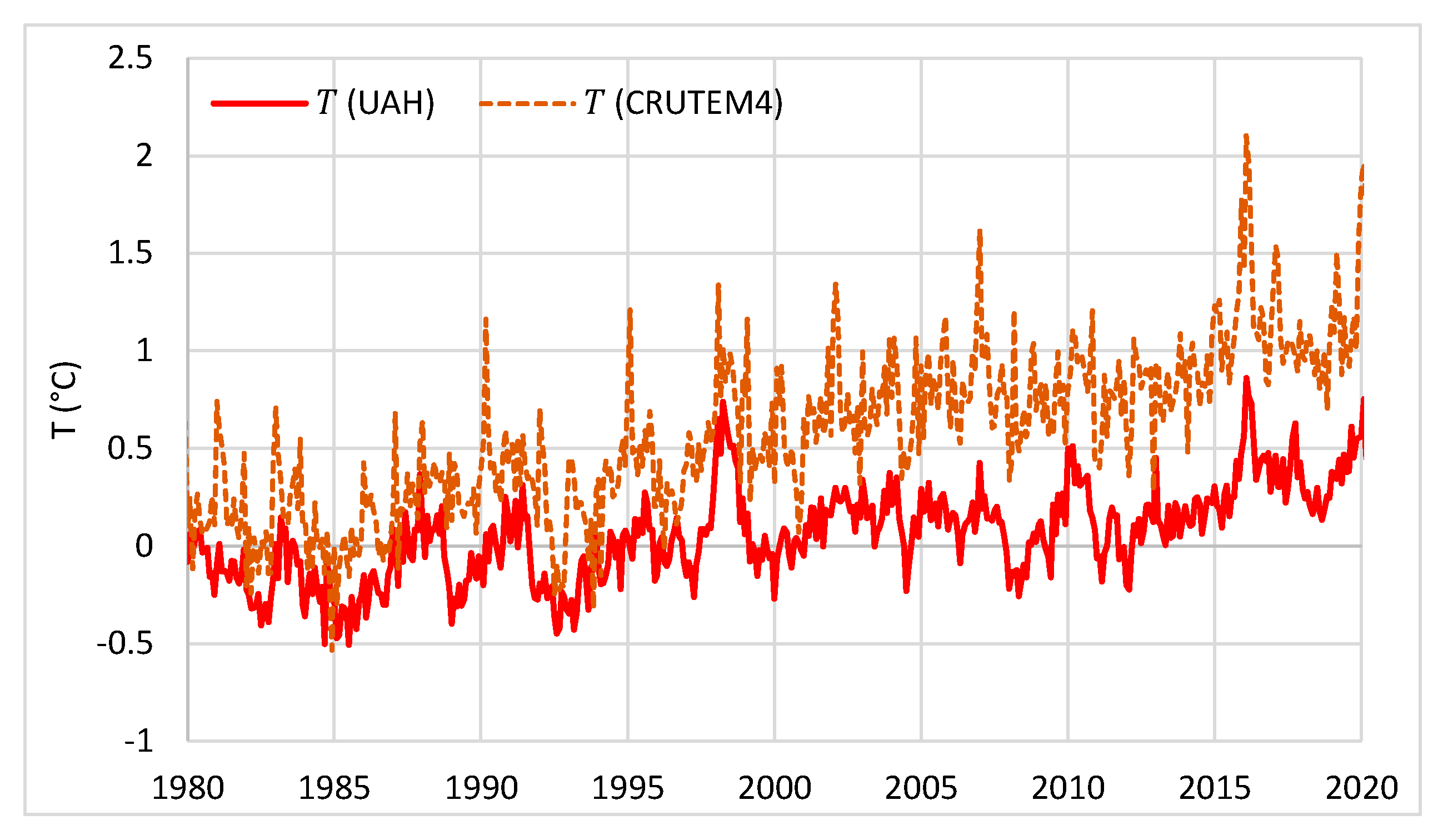
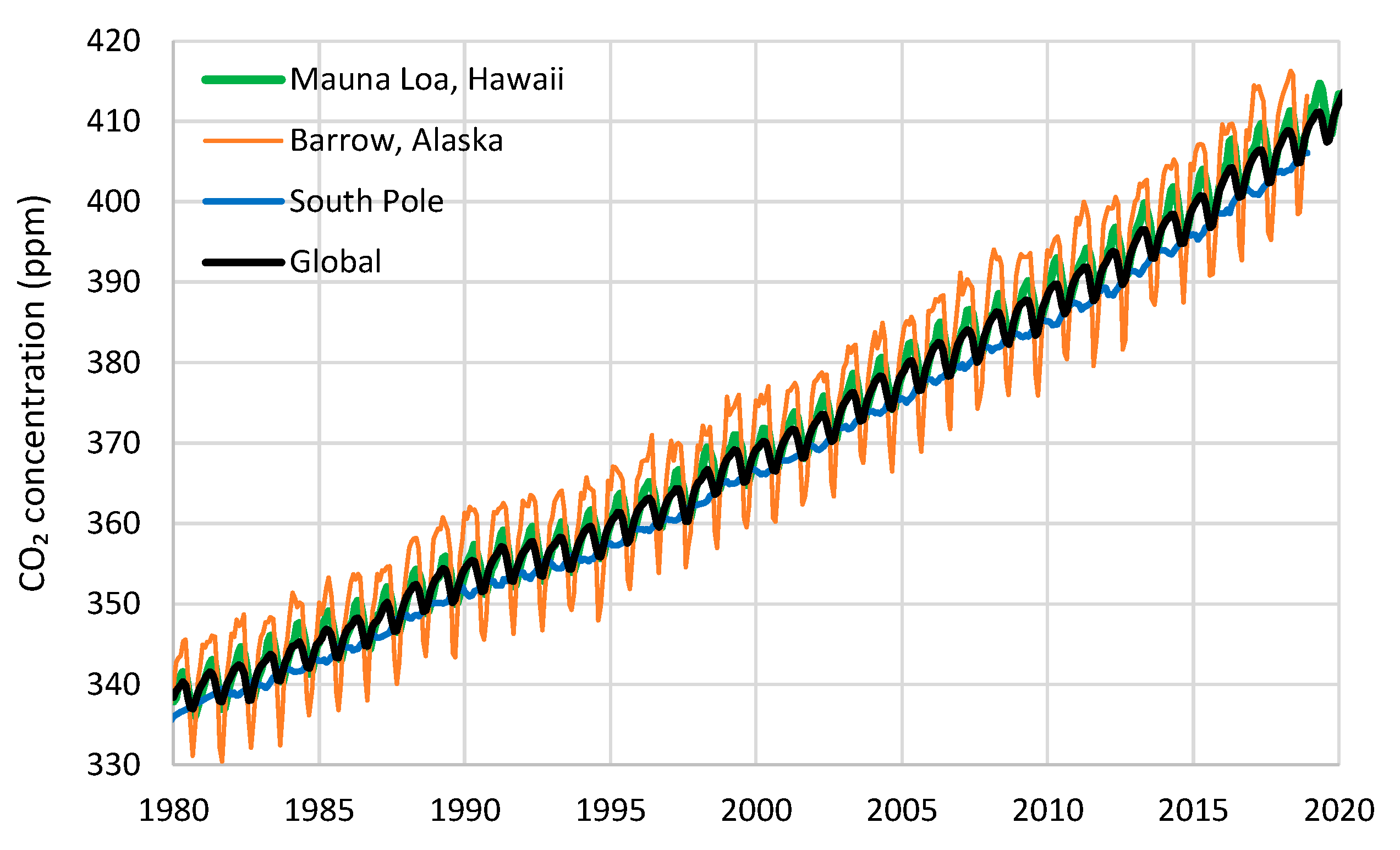
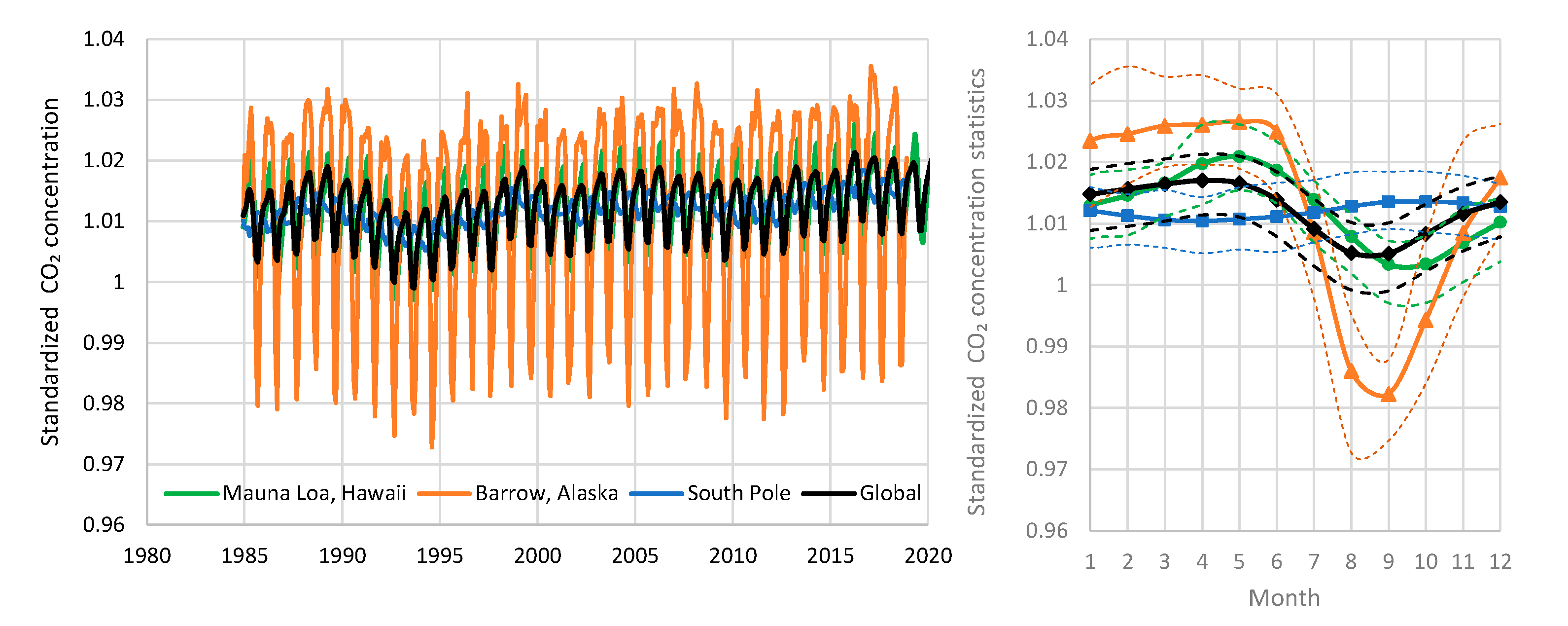
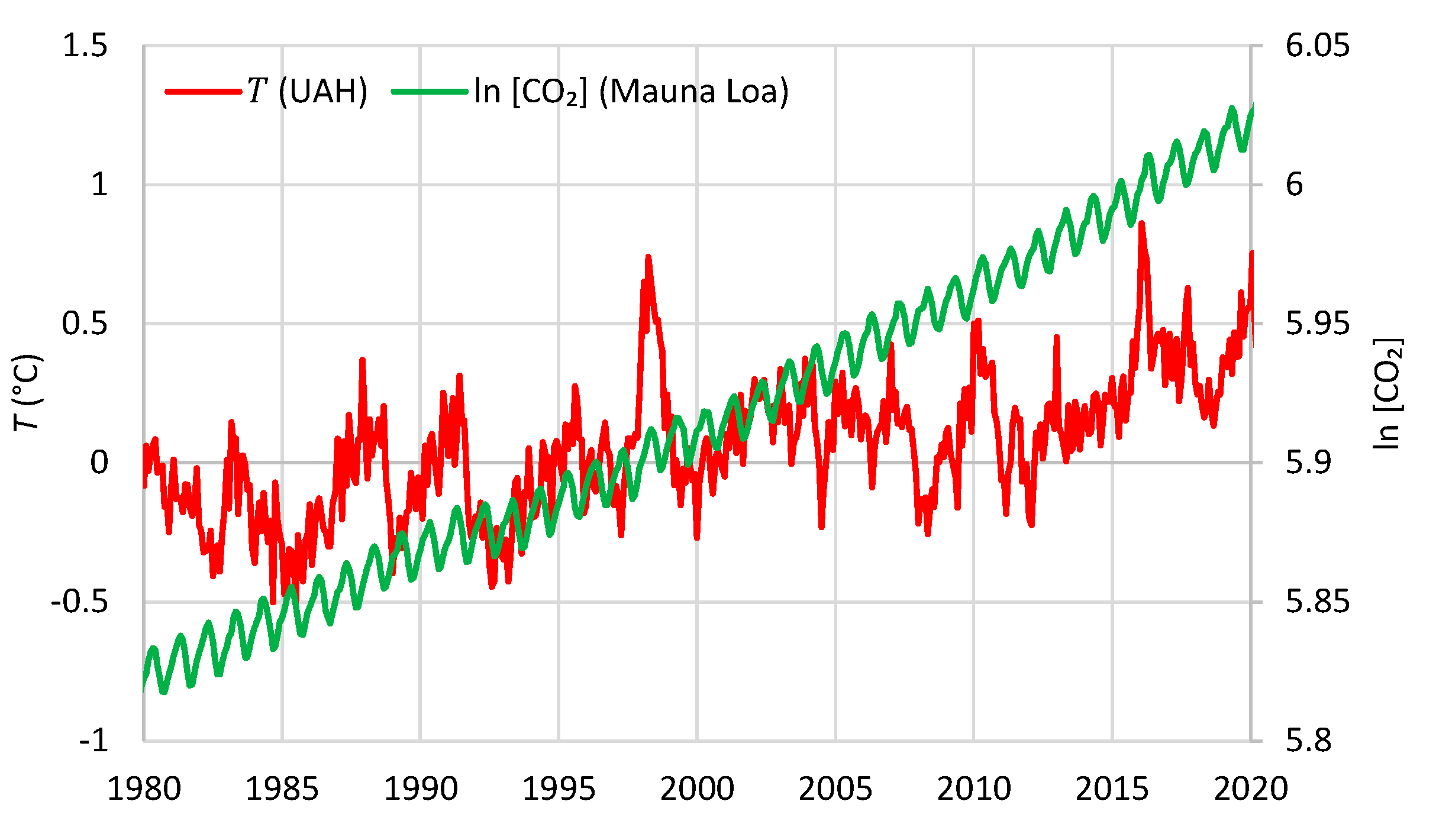
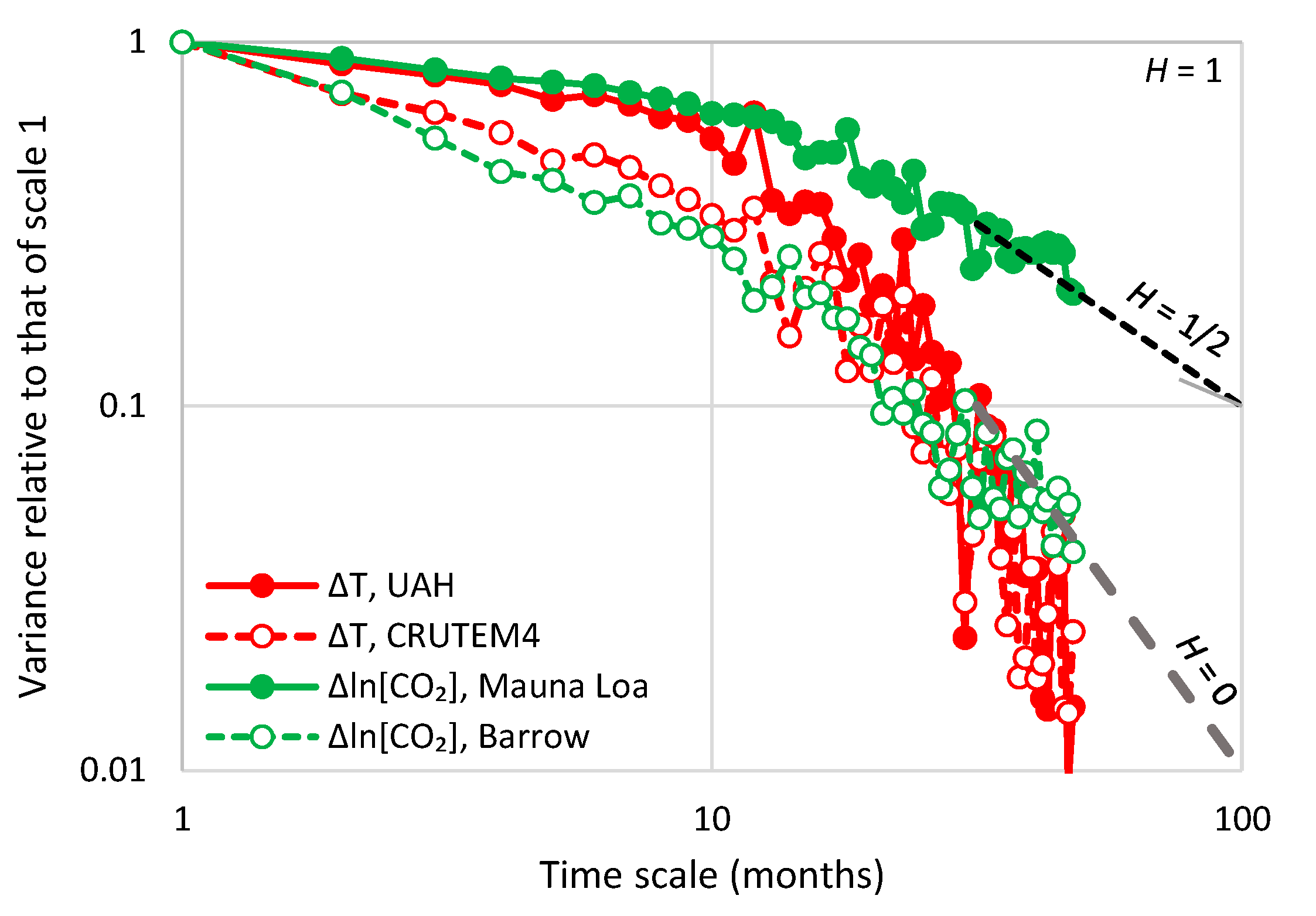
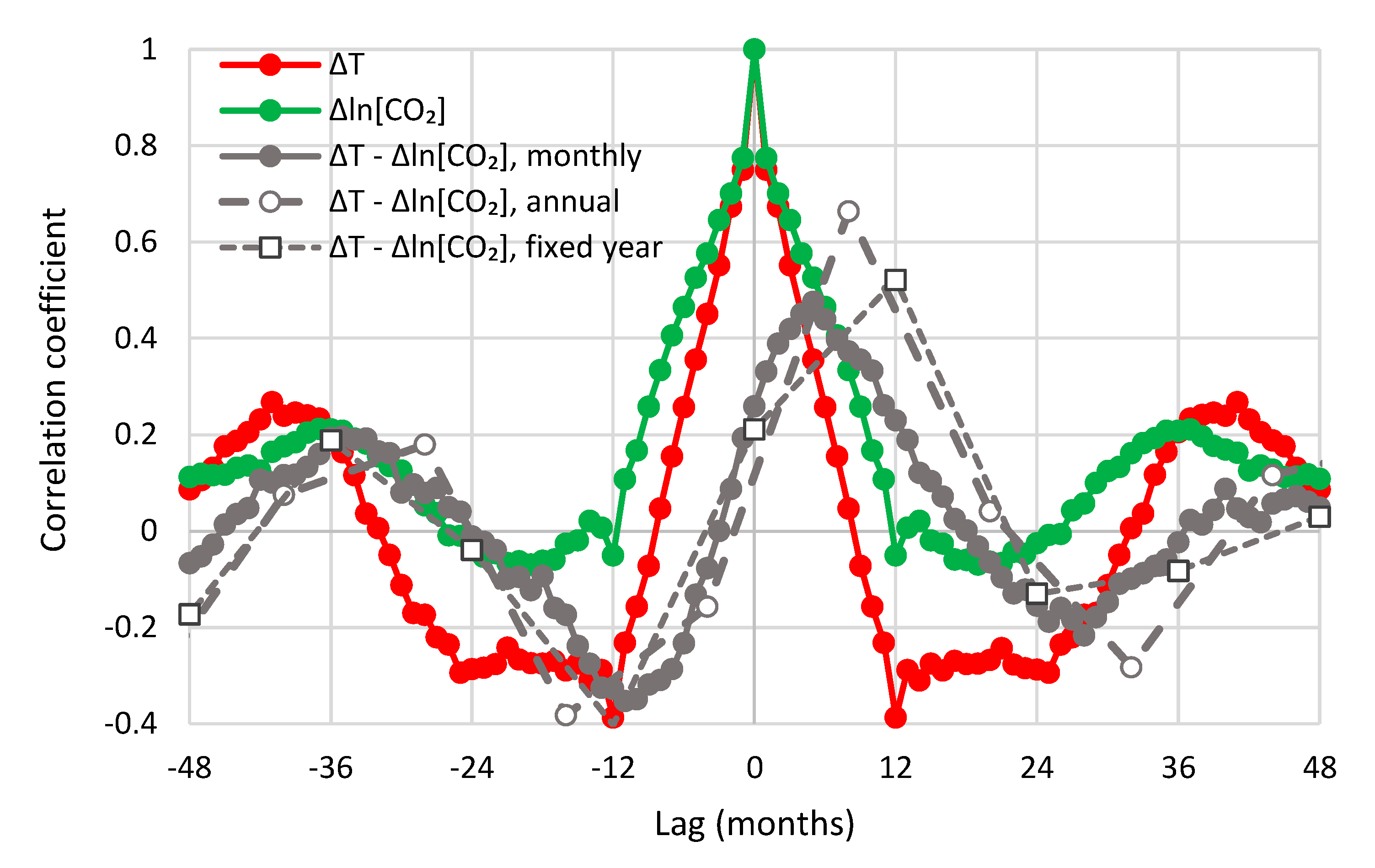
| Temperature—CO2 Series | Monthly Time Series | Annual Time Series—Sliding Annual Window | Annual Time Series—Fixed Annual Window | |||
|---|---|---|---|---|---|---|
| MCCC | Lag | MCCC | Lag | MCCC | Lag | |
| UAH—Mauna Loa | 0.47 | 5 | 0.66 | 8 | 0.52 | 12 |
| UAH—Barrow | 0.31 | 11 | 0.70 | 14 | 0.59 | 12 |
| UAH—South Pole | 0.37 | 6 | 0.54 | 10 | 0.38 | 12 |
| UAH—Global | 0.47 | 6 | 0.60 | 11 | 0.60 | 12 |
| CRUTEM4—Mauna Loa | 0.31 | 5 | 0.55 | 10 | 0.52 | 12 |
| CRUTEM4—Global | 0.33 | 9 | 0.55 | 12 | 0.55 | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koutsoyiannis, D.; Kundzewicz, Z.W. Atmospheric Temperature and CO2: Hen-Or-Egg Causality? Sci 2020, 2, 83. https://doi.org/10.3390/sci2040083
Koutsoyiannis D, Kundzewicz ZW. Atmospheric Temperature and CO2: Hen-Or-Egg Causality? Sci. 2020; 2(4):83. https://doi.org/10.3390/sci2040083
Chicago/Turabian StyleKoutsoyiannis, Demetris, and Zbigniew W. Kundzewicz. 2020. "Atmospheric Temperature and CO2: Hen-Or-Egg Causality?" Sci 2, no. 4: 83. https://doi.org/10.3390/sci2040083
APA StyleKoutsoyiannis, D., & Kundzewicz, Z. W. (2020). Atmospheric Temperature and CO2: Hen-Or-Egg Causality? Sci, 2(4), 83. https://doi.org/10.3390/sci2040083