Quantum Calcium-Ion Interactions with EEG
Abstract
:1. Introduction
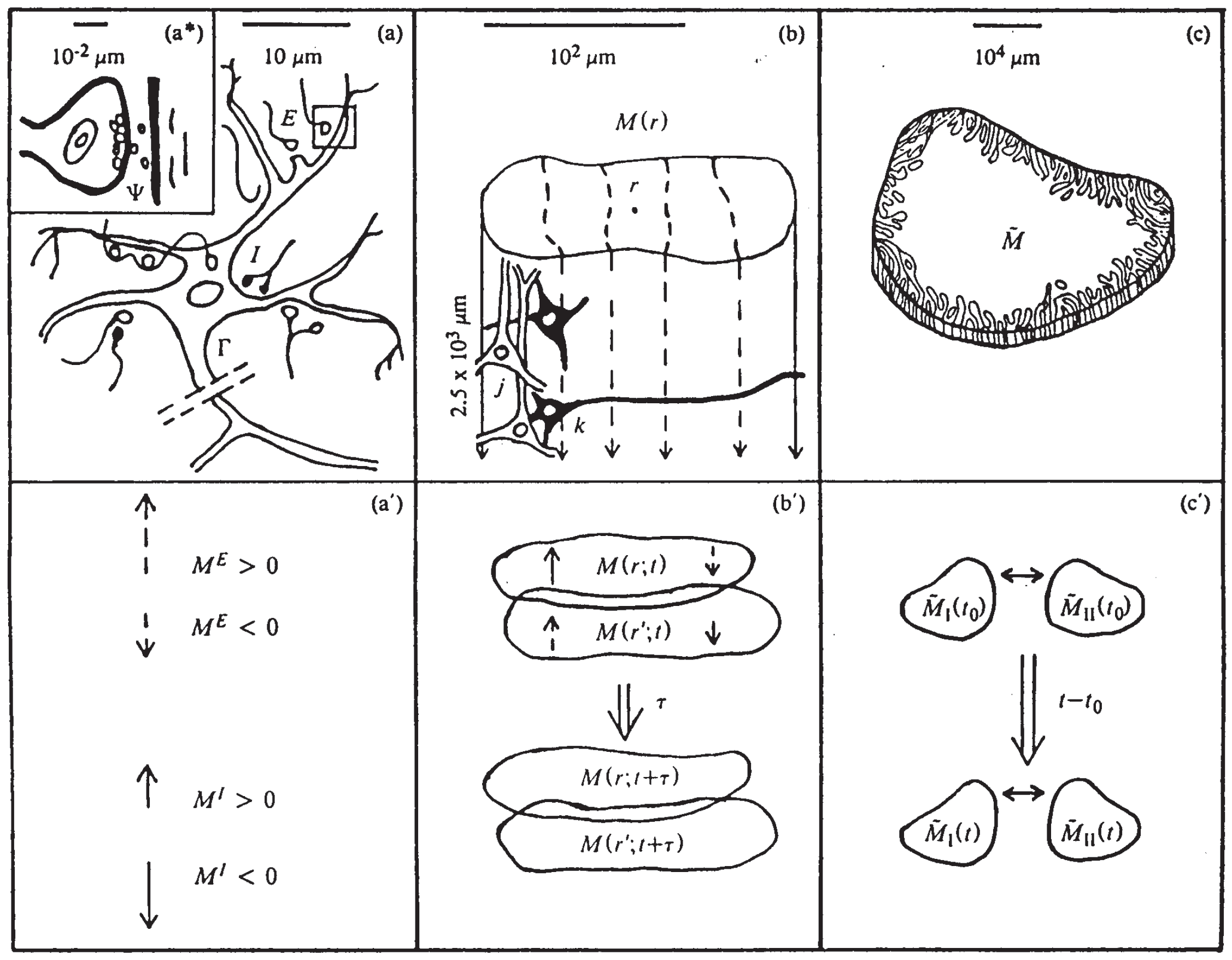
2. Statistical Mechanics of Neocortical Interactions (SMNI)
2.1. Synaptic Interactions
2.2. Neuronal Interactions
2.3. Columnar Interactions
2.4. SMNI Parameters From Experiments
2.5. Previous Applications
2.5.1. Verification of basic SMNI Hypothesis
2.5.2. SMNI Calculations of Short-Term Memory (STM)
2.5.3. Three Basic SMNI Models
- (a)
- case EC, dominant excitation subsequent firings
- (b)
- case IC, inhibitory subsequent firings
- (c)
- case BC, balanced between EC and IC
2.6. Comparing EEG Testing Data with Training Data
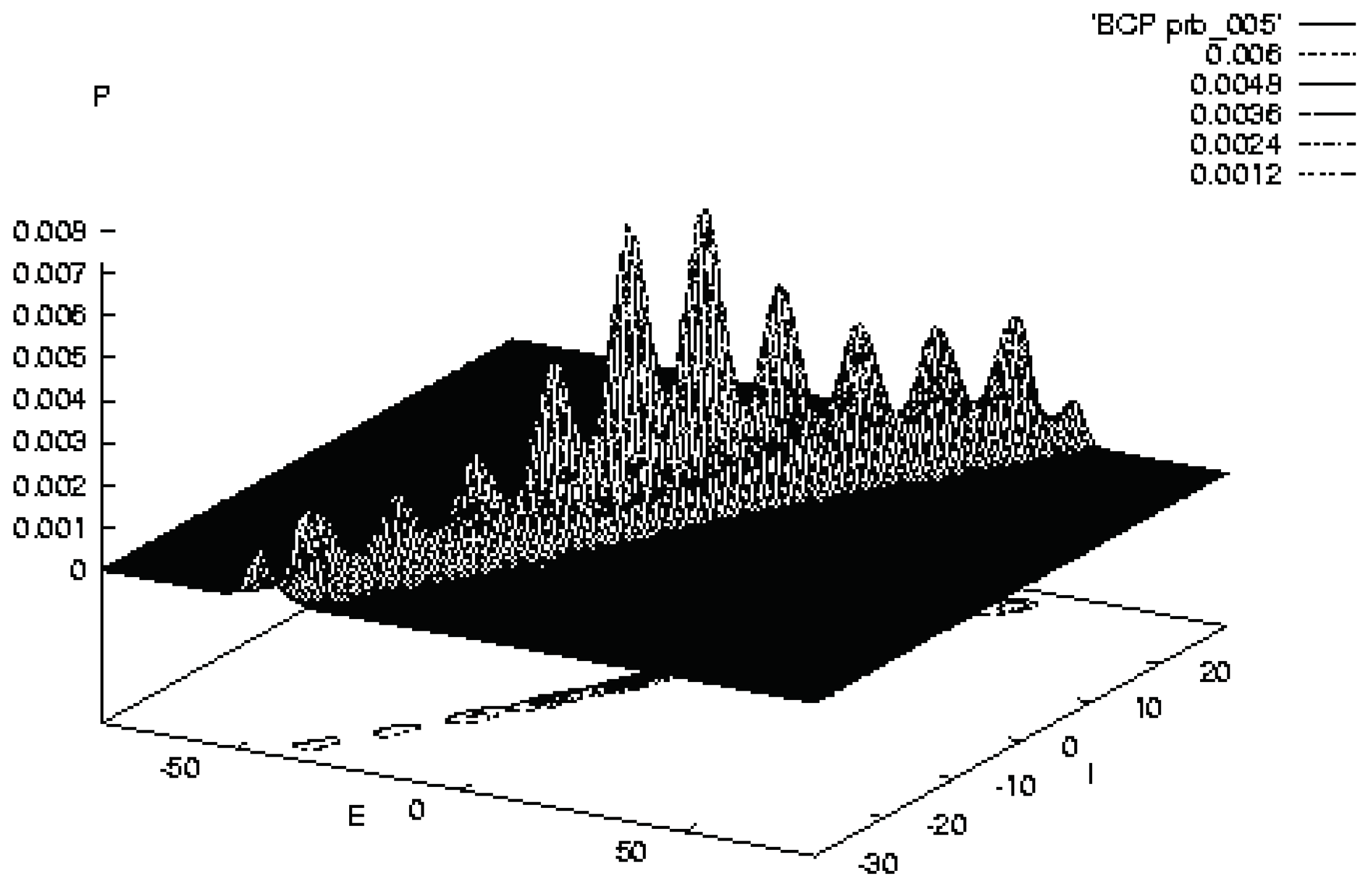
2.7. STM PATHINT Calculations
2.7.1. PATHINT STM
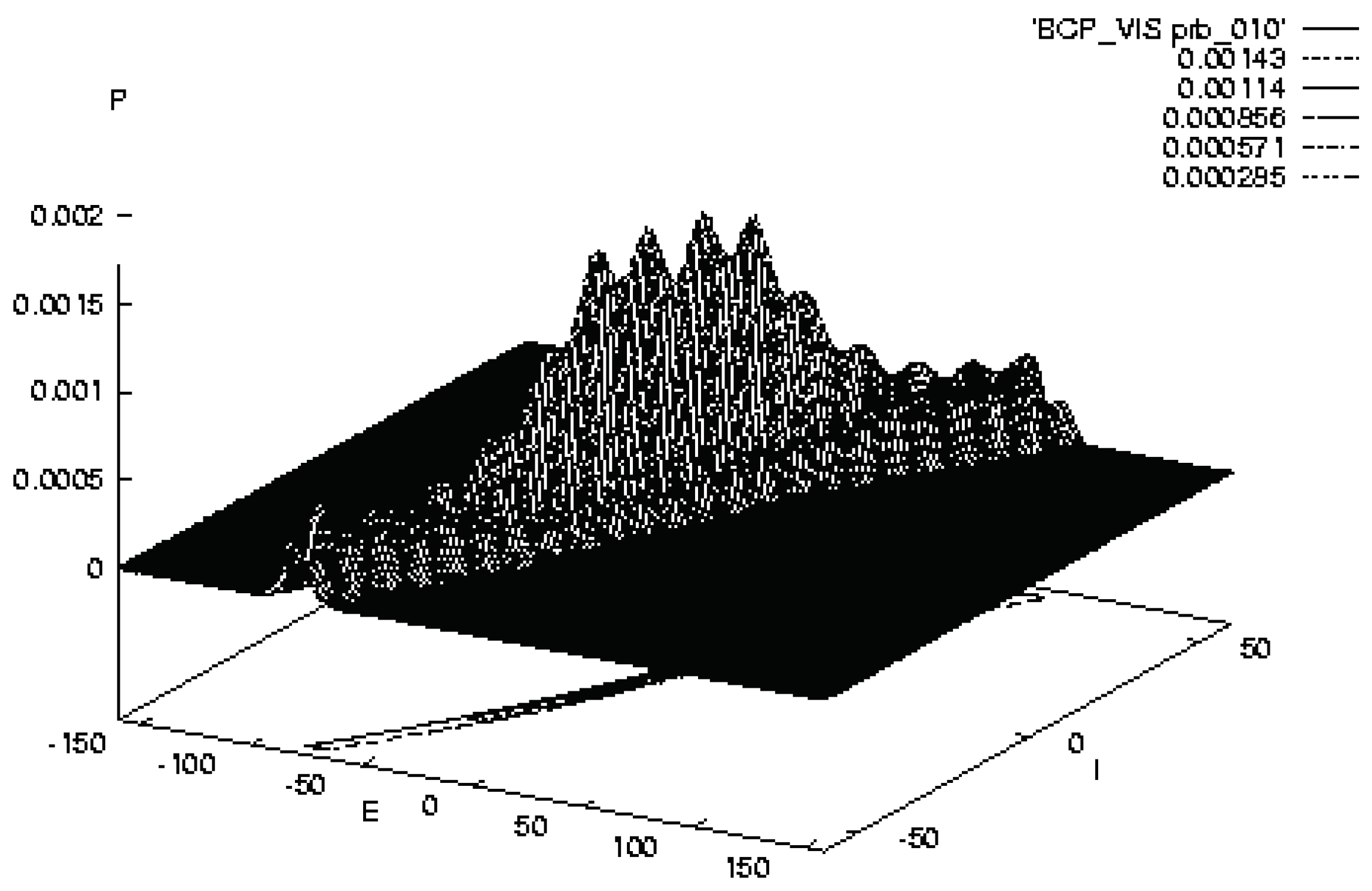
2.7.2. PATHINT STM Visual
2.8. Tripartite Synaptic Interactions
2.8.1. Canonical Momentum
2.8.2. Vector Potential of Wire
2.8.3. Effects of Vector Potential on Momenta
2.8.4. Reasonable Estimates
2.9. Model of Models (MOM)
Ideas by Statistical Mechanics
3. Adaptive Simulated Annealing (ASA) Algorithm
3.1. Importance Sampling
3.2. Outline of ASA Algorithm
3.3. ASA Applications
4. Path-Integral Algorithms PATHINT and qPATHINT
4.1. Path Integral in Stratonovich (Midpoint) Representation
4.2. Path Integral in Ito (Prepoint) Representation
4.3. Path-Integral Riemannian Geometry
4.4. Three Approaches Are Mathematically Equivalent
- (a)
- Fokker-Planck/Chapman-Kolmogorov partial-differential equations
- (b)
- Langevin coupled stochastic-differential equations
- (c)
- Lagrangian or Hamiltonian path-integrals
4.4.1. Stochastic Differential Equation (SDE)
4.4.2. Partial Differential Equation (PDE)
4.5. PATHINT Applications
4.6. PATHINT/qPATHINT Code
4.6.1. Shocks
4.6.2. PATHINT/qPATHINT Histograms
4.6.3. Meshes For [q]PATHINT
4.7. Lessons Learned From SMFM and SMNI
Calculations At Each Node At Each Time Slice
- PATHINT using the Classical SMNI Lagrangian
- qPATHINT using the Quantum wave-packet Lagrangian
- Sync in time during P300 attentional tasks.
- Time/phase relations between classical and quantum systems may be important.
- ASA-fit synchronized classical-quantum PATHINT-qPATHINT model to EEG data.
- is determined experimentally from EEG, and includes all synaptic background effects.
5. Results Including Quantum Scales
5.1. SMNI + Wave-Packet
5.2. Supercomputer Resources
5.3. Results Using
5.4. Quantum Zeno Effects
Survival of Wave Packet
6. Quantum Applications
6.1. Nano-Robotic Applications
6.2. Free Will
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Ingber, L. Towards a unified brain theory. J. Soc. Biol. Struct. 1981, 4, 211–224. [Google Scholar] [CrossRef]
- Ingber, L. Statistical mechanics of neocortical interactions. I. Basic formulation. Phys. D 1982, 5, 83–107. [Google Scholar] [CrossRef]
- Ingber, L. Statistical mechanics of neocortical interactions. Dynamics of synaptic modification. Phys. Rev. A 1983, 28, 395–416. [Google Scholar] [CrossRef]
- Ingber, L. Statistical mechanics of neocortical interactions. Derivation of short-term-memory capacity. Phys. Rev. A 1984, 29, 3346–3358. [Google Scholar] [CrossRef]
- Ingber, L. Statistical mechanics of neocortical interactions: Stability and duration of the 7+−2 rule of short-term-memory capacity. Phys. Rev. A 1985, 31, 1183–1186. [Google Scholar] [CrossRef]
- Ingber, L. Statistical mechanics of neocortical interactions: Path-integral evolution of short-term memory. Phys. Rev. E 1994, 49, 4652–4664. [Google Scholar] [CrossRef]
- Ingber, L. Columnar EEG magnetic influences on molecular development of short-term memory. In Short-Term Memory: New Research; Kalivas, G., Petralia, S., Eds.; Nova: Hauppauge, NY, USA, 2012; pp. 37–72. [Google Scholar]
- Ericsson, K.; Chase, W. Exceptional memory. Am. Sci. 1982, 70, 607–615. [Google Scholar]
- Zhang, G.; Simon, H. STM capacity for Chinese words and idioms: Chunking and acoustical loop hypotheses. Mem. Cognit. 1985, 13, 193–201. [Google Scholar] [CrossRef] [PubMed]
- Hick, W. On the rate of gains of information. Q. J. Exp. Psychol. 1952, 34, 1–33. [Google Scholar] [CrossRef]
- Ingber, L. Statistical mechanics of neocortical interactions: Reaction time correlates of the g factor. Psycholoquy 1999, 10. Article Number 35. [Google Scholar]
- Jensen, A. Individual differences in the Hick paradigm. In Speed of Information-Processing and Intelligence; Vernon, P., Ed.; Ablex: Norwood, NJ, USA, 1987; pp. 101–175. [Google Scholar]
- Ingber, L. Statistical mechanics of neocortical interactions: Applications of canonical momenta indicators to electroencephalography. Phys. Rev. E 1997, 55, 4578–4593. [Google Scholar] [CrossRef]
- Ingber, L. EEG Database; UCI Machine Learning Repository: Irvine, CA, USA, 1997. [Google Scholar]
- Ingber, L. Statistical mechanics of multiple scales of neocortical interactions. In Neocortical Dynamics and Human EEG Rhythms; Nunez, P., Ed.; Oxford University Press: New York, NY, USA, 1995; pp. 628–681. ISBN 0-19-505728-7. [Google Scholar]
- Asher, J. Brain’s Code for Visual Working Memory Deciphered in Monkeys NIH-Funded Study; Technical Report NIH Press Release; NIH, Bethesda: Rockville, MD, USA, 2012. [Google Scholar]
- Salazar, R.; Dotson, N.; Bressler, S.; Gray, C. Content-specific fronto-parietal synchronization during visual working memory. Science 2012, 338, 1097–1100. [Google Scholar] [CrossRef]
- Ingber, L. Statistical mechanics of neocortical interactions: Constraints on 40 Hz models of short-term memory. Phys. Rev. E 1995, 52, 4561–4563. [Google Scholar] [CrossRef]
- Ingber, L. Computational algorithms derived from multiple scales of neocortical processing. In Pointing at Boundaries: Integrating Computation and Cognition on Biological Grounds; Pereira, A., Jr., Massad, E., Bobbitt, N., Eds.; Springer: New York, NY, USA, 2011; pp. 1–13. [Google Scholar]
- Ingber, L. Influence of macrocolumnar EEG on Ca waves. Curr. Prog. J. 2012, 1, 4–8. [Google Scholar] [CrossRef]
- Ingber, L. Calculating consciousness correlates at multiple scales of neocortical interactions. In Horizons in Neuroscience Research; Costa, A., Villalba, E., Eds.; Nova: Hauppauge, NY, USA, 2015; pp. 153–186. ISBN 978-1-63482-632-7. [Google Scholar]
- Ingber, L. Statistical mechanics of neocortical interactions: Large-scale EEG influences on molecular processes. J. Theor. Biol. 2016, 395, 144–152. [Google Scholar] [CrossRef]
- Ingber, L. Evolution of regenerative Ca-ion wave-packet in neuronal-firing fields: Quantum path-integral with serial shocks. Int. J. Innov. Res. Inf. Secur. 2017, 4, 14–22. [Google Scholar] [CrossRef]
- Ingber, L. Quantum Path-Integral qPATHINT Algorithm. Open Cybern. Syst. J. 2017, 11, 119–133. [Google Scholar] [CrossRef]
- Ingber, L.; Pappalepore, M.; Stesiak, R. Electroencephalographic field influence on calcium momentum waves. J. Theor. Biol. 2014, 343, 138–153. [Google Scholar] [CrossRef]
- Nunez, P.; Srinivasan, R.; Ingber, L. Theoretical and experimental electrophysiology in human neocortex: Multiscale correlates of conscious experience. In Multiscale Analysis and Nonlinear Dynamics: From Genes to the Brain; Pesenson, M., Ed.; Wiley: New York, NY, USA, 2013; pp. 149–178. [Google Scholar] [CrossRef]
- Ingber, L. Towards clinical applications of statistical mechanics of neocortical interactions. Innov. Technol. Biol. Med. 1985, 6, 753–758. [Google Scholar]
- Ingber, L. Statistical mechanics of neocortical interactions. EEG dispersion relations. IEEE Trans. Biomed. Eng. 1985, 32, 91–94. [Google Scholar] [CrossRef] [PubMed]
- Briggs, F.; Mangun, G.; Usrey, W. Attention enhances synaptic efficacy and the signal-to-noise ratio in neural circuits. Nature 2013, 499, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Mountcastle, V.; Andersen, R.; Motter, B. The influence of attentive fixation upon the excitability of the light-sensitive neurons of the posterior parietal cortex. J. Neurosci. 1981, 1, 1218–1235. [Google Scholar] [CrossRef] [PubMed]
- Citi, L.; Poli, R.; Cinel, C. Documenting, modelling and exploiting P300 amplitude changes due to variable target delays in Donchin’s speller. J. Neural Eng. 2010, 7, 1–21. [Google Scholar] [CrossRef]
- Goldberger, A.; Amaral, L.; Glass, L.; Hausdorff, J.; Ivanov, P.; Mark, R.; Mietus, J.; Moody, G.; Peng, C.K.; Stanley, H. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef]
- Ingber, L.; Nunez, P. Statistical mechanics of neocortical interactions: High resolution path-integral calculation of short-term memory. Phys. Rev. E 1995, 51, 5074–5083. [Google Scholar] [CrossRef]
- Agulhon, C.; Petravicz, J.; McMullen, A.; Sweger, E.; Minton, S.; Taves, S.; Casper, K.; Fiacco, T.; McCarthy, K. What is the role of astrocyte calcium in neurophysiology? Neuron 2008, 59, 932–946. [Google Scholar] [CrossRef] [PubMed]
- Araque, A.; Navarrete, M. Glial cells in neuronal network function. Phil. Trans. R. Soc. B-Boil. Sci. 2010, 365, 2375–2381. [Google Scholar] [CrossRef]
- Banaclocha, M.; Bookkon, I.; Banaclocha, H. Long-term memory in brain magnetite. Med. Hypotheses 2010, 74, 254–257. [Google Scholar] [CrossRef]
- Bellinger, S. Modeling calcium wave oscillations in astrocytes. Neurocomputing 2005, 65, 843–850. [Google Scholar] [CrossRef]
- Innocenti, B.; Parpura, V.; Haydon, P. Imaging extracellular waves of glutamate during calcium signaling in cultured astrocytes. J. Neurosci. 2000, 20, 1800–1808. [Google Scholar] [CrossRef]
- Pereira, A.; Furlan, F.A. On the role of synchrony for neuron-astrocyte interactions and perceptual conscious processing. J. Biol. Phys. 2009, 35, 465–480. [Google Scholar] [CrossRef]
- Reyes, R.; Parpura, V. The trinity of Ca2+ sources for the exocytotic glutamate release from astrocytes. Neurochem. Int. 2009, 55, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Scemes, E.; Giaume, C. Astrocyte calcium waves: What they are and what they do. Glia 2006, 54, 716–725. [Google Scholar] [CrossRef]
- Volterra, A.; Liaudet, N.; Savtchouk, I. Astrocyte Ca2+ signalling: An unexpected complexity. Nat. Rev. Neurosci. 2014, 15, 327–335. [Google Scholar] [CrossRef] [PubMed]
- Ross, W. Understanding calcium waves and sparks in central neurons. Nat. Rev. Neurosci. 2012, 13, 157–168. [Google Scholar] [CrossRef] [PubMed]
- Majhi, S.; Ghosh, D. Alternating chimeras in networks of ephaptically coupled bursting neurons. Chaos 2018, 28. [Google Scholar] [CrossRef]
- Murakami, S.; Okada, Y. Contributions of principal neocortical neurons to magnetoencephalography and electroencephalography signals. J. Physiol. 2006, 575, 925–936. [Google Scholar] [CrossRef]
- Nunez, P.; Srinivasan, R. Electric Fields of the Brain: The Neurophysics of EEG, 2nd ed.; Oxford University Press: London, UK, 2006. [Google Scholar]
- Ingber, L. Ideas by Statistical Mechanics (ISM); Technical Report Report 2006:ISM, Lester Ingber Research; Ashland: Covington, OR, USA, 2006. [Google Scholar]
- Ingber, L. Ideas by Statistical Mechanics (ISM). J. Integr. Syst. Des. Process Sci. 2007, 11, 31–54. [Google Scholar] [CrossRef]
- Ingber, L. AI and Ideas by Statistical Mechanics (ISM). In Encyclopedia of Artificial Intelligence; Rabunal, J., Dorado, J., Pazos, A., Eds.; Information Science Reference: New York, NY, USA, 2008; pp. 58–64. ISBN 978-1-59904-849-9. [Google Scholar]
- Ingber, L. Very fast simulated re-annealing. Math. Comput. Model. 1989, 12, 967–973. [Google Scholar] [CrossRef]
- Ingber, L. Adaptive Simulated Annealing (ASA); Technical Report Global optimization C-code; Caltech Alumni Association: Pasadena, CA, USA, 1993. [Google Scholar]
- Ingber, L. Adaptive Simulated Annealing. In Stochastic Global Optimization and Its Applications with Fuzzy Adaptive Simulated Annealing; Oliveira, H.A., Petraglia, A., Ingber, L., Machado, M., Petraglia, M., Eds.; Springer: New York, NY, USA, 2012; pp. 33–61. [Google Scholar]
- Ingber, L. Simulated annealing: Practice versus theory. Math. Comput. Model. 1993, 18, 29–57. [Google Scholar] [CrossRef]
- Atiya, A.; Parlos, A.; Ingber, L. A reinforcement learning method based on adaptive simulated annealing. In Proceedings International Midwest Symposium on Circuits and Systems (MWCAS), December 2003; IEEE CAS: Cairo, Egypt, 2003. [Google Scholar]
- Ingber, L.; Srinivasan, R.; Nunez, P. Path-integral evolution of chaos embedded in noise: Duffing neocortical analog. Math. Comput. Model. 1996, 23, 43–53. [Google Scholar] [CrossRef]
- Ingber, L. Statistical mechanics of combat and extensions. In Toward a Science of Command, Control, and Communications; Jones, C., Ed.; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 1993; pp. 117–149. ISBN 1-56347-068-3. [Google Scholar]
- Ingber, L. Data mining and knowledge discovery via statistical mechanics in nonlinear stochastic systems. Math. Comput. Model. 1998, 27, 9–31. [Google Scholar] [CrossRef]
- Ingber, L. Statistical mechanical aids to calculating term structure models. Phys. Rev. A 1990, 42, 7057–7064. [Google Scholar] [CrossRef]
- Ingber, L. Canonical momenta indicators of financial markets and neocortical EEG. In Progress in Neural Information Processing, Proceedings of the 1996 International Conference on Neural Information Processing (ICONIP’96), Hong Kong, 24–27 September 1996; Amari, S.I., Xu, L., King, I., Leung, K.S., Eds.; Springer: New York, NY, USA, 1996; pp. 777–784. [Google Scholar]
- Ingber, L. High-resolution path-integral development of financial options. Phys. A 2000, 283, 529–558. [Google Scholar] [CrossRef]
- Ingber, L. Trading in Risk Dimensions (TRD); Technical Report Report 2005:TRD, Lester Ingber Research; Ashland: Covington, OR, USA, 2005. [Google Scholar]
- Ingber, L.; Chen, C.; Mondescu, R.; Muzzall, D.; Renedo, M. Probability tree algorithm for general diffusion processes. Phys. Rev. E 2001, 64, 056702–056707. [Google Scholar] [CrossRef]
- Ingber, L.; Mondescu, R. Automated internet trading based on optimized physics models of markets. In Intelligent Internet-Based Information Processing Systems; Howlett, R., Ichalkaranje, N., Jain, L., Tonfoni, G., Eds.; World Scientific: Singapore, 2003; pp. 305–356. [Google Scholar]
- Ingber, L. Statistical mechanics of neocortical interactions: A scaling paradigm applied to electroencephalography. Phys. Rev. A 1991, 44, 4017–4060. [Google Scholar] [CrossRef]
- Ingber, L. Generic mesoscopic neural networks based on statistical mechanics of neocortical interactions. Phys. Rev. A 1992, 45, R2183–R2186. [Google Scholar] [CrossRef]
- Ingber, L. Statistical mechanics of neocortical interactions: Multiple scales of EEG. In Frontier Science in EEG: Continuous Waveform Analysis (Electroencephal. clin. Neurophysiol. Suppl. 45); Dasheiff, R., Vincent, D., Eds.; Elsevier: Amsterdam, The Netherlands, 1996; pp. 79–112. ISBN 0-444-82429-4. [Google Scholar]
- Ingber, L. Statistical mechanics of neocortical interactions: Training and testing canonical momenta indicators of EEG. Math. Comput. Model. 1998, 27, 33–64. [Google Scholar] [CrossRef]
- Ingber, L. Statistical Mechanics of Neocortical Interactions: Portfolio of Physiological Indicators; Technical Report Report 2006:PPI, Lester Ingber Research; Ashland: Covington, OR, USA, 2006. [Google Scholar]
- Ingber, L. Statistical mechanics of neocortical interactions: Portfolio of physiological indicators. Open Cybern. Syst. J. 2009, 3, 13–26. [Google Scholar] [CrossRef]
- Ingber, L. Statistical mechanics of neocortical interactions: Nonlinear columnar electroencephalography. NeuroQuantology J. 2009, 7, 500–529. [Google Scholar]
- Ingber, L. Electroencephalographic (EEG) Influence on Ca2+ Waves: Lecture Plates; Technical Report Report 2013:LEFI, Lester Ingber Research; Ashland: Covington, OR, USA, 2013. [Google Scholar]
- Ingber, L.; Nunez, P. Neocortical Dynamics at Multiple Scales: EEG Standing Waves, Statistical Mechanics, and Physical Analogs. Math. Biosci. 2010, 229, 160–173. [Google Scholar] [CrossRef] [PubMed]
- Ingber, L. Adaptive simulated annealing (ASA): Lessons learned. Control Cybern. 1996, 25, 33–54. [Google Scholar]
- Ingber, L.; Rosen, B. Genetic algorithms and very fast simulated reannealing: A comparison. Math. Comput. Model. 1992, 16, 87–100. [Google Scholar] [CrossRef]
- Langouche, F.; Roekaerts, D.; Tirapegui, E. Discretization problems of functional integrals in phase space. Phys. Rev. D 1979, 20, 419–432. [Google Scholar] [CrossRef]
- Langouche, F.; Roekaerts, D.; Tirapegui, E. Functional Integration and Semiclassical Expansions; Reidel: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Schulman, L. Techniques and Applications of Path Integration; J. Wiley Sons: New York, NY, USA, 1981. [Google Scholar]
- Ingber, L.; Fujio, H.; Wehner, M. Mathematical comparison of combat computer models to exercise data. Math. Comput. Model. 1991, 15, 65–90. [Google Scholar] [CrossRef]
- Ingber, L. Path-integral quantum PATHTREE and PATHINT algorithms. Int. J. Innov. Res. Inf. Secur. 2016, 3, 1–15. [Google Scholar] [CrossRef]
- Ingber, L. Options on quantum money: Quantum path-integral with serial shocks. Int. J. Innov. Res. Inf. Secur. 2017, 4, 7–13. [Google Scholar] [CrossRef]
- Ingber, L.; Wilson, J. Statistical mechanics of financial markets: Exponential modifications to Black-Scholes. Math. Comput. Model. 2000, 31, 167–192. [Google Scholar] [CrossRef]
- Ingber, L. Path-integral evolution of multivariate systems with moderate noise. Phys. Rev. E 1995, 51, 1616–1619. [Google Scholar] [CrossRef]
- Ingber, L.; Wilson, J. Volatility of volatility of financial markets. Math. Comput. Model. 1999, 29, 39–57. [Google Scholar] [CrossRef]
- Wehner, M.; Wolfer, W. Numerical evaluation of path-integral solutions to Fokker-Planck equations. I. Phys. Rev. A 1983, 27, 2663–2670. [Google Scholar] [CrossRef]
- Wehner, M.; Wolfer, W. Numerical evaluation of path-integral solutions to Fokker-Planck equations. II. Restricted stochastic processes. Phys. Rev. A 1983, 28, 3003–3011. [Google Scholar] [CrossRef]
- Wehner, M.; Wolfer, W. Numerical evaluation of path integral solutions to Fokker-Planck equations. III. Time and functionally dependent coefficients. Phys. Rev. A 1987, 35, 1795–1801. [Google Scholar] [CrossRef]
- Schulten, K. Quantum Mechanics; Technical Report PHYS480 Lecture Notes, Chapter 2. Available online: http://www.ks.uiuc.edu/Services/Class/PHYS480/ (accessed on 29 November 2018).
- Burgarth, D.; Facchi, P.; Nakazato, H.; Pascazio, S.; Yuasa, K. Quantum Zeno Dynamics from General Quantum Operations. arXiv, 2018; arXiv:1809.09570. [Google Scholar]
- Facchi, P.; Lidar, D.; Pascazio, S. Unification of dynamical decoupling and the quantum Zeno effect. Phys. Rev. A 2004, 69, 1–6. [Google Scholar] [CrossRef]
- Facchi, P.; Pascazio, S. Quantum Zeno dynamics: Mathematical and physical aspects. J. Phys. A 2008, 41, 1–45. [Google Scholar] [CrossRef]
- Giacosa, G.; Pagliara, G. Quantum Zeno effect by general measurements. Phys. Rev. A 2014, 052107, 1–5. [Google Scholar]
- Kozlowski, W.; Caballero-Benitez, S.; Mekhov, I. Non-Hermitian Dynamics in the Quantum Zeno Limit. arXiv, 2018; arXiv:1510.04857. [Google Scholar] [CrossRef]
- Muller, M.; Gherardini, S.; Caruso, F. Quantum Zeno Dynamics through Stochastic Protocols. arXiv, 2018; arXiv:1607.08871v1. [Google Scholar] [CrossRef]
- Patil, Y.; Chakram, S.; Vengalattore, M. Measurement-induced localization of an ultracold lattice gas. Phys. Rev. Lett. 2015, 115, 1–5. [Google Scholar] [CrossRef]
- Wu, S.; Wang, L.; Yi, X. Time-dependent decoherence-free subspace. J. Phys. A 2012, 405305, 1–11. [Google Scholar] [CrossRef]
- Zhang, P.; Ai, Q.; Li, Y.; Xu, D.; Sun, C. Dynamics of quantum Zeno and anti-Zeno effects in an open system. Sci. China Phys. Mech. Astron. 2014, 57, 194–207. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Mechanics; Technical Report Lecture Notes; Caltech: Pasadena, CA, USA, 2015. [Google Scholar]
- Hagan, S.; Hameroff, S.; Tuszynski, J. Quantum computation in brain microtubules: Decoherence and biological feasibility. Phys. Rev. E 2002, 65, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Hameroff, S.; Penrose, R. Consciousness in the universe: A review of the ‘Orch OR’ theory. Phys. Life Rev. 2013, 403, 1–40. [Google Scholar] [CrossRef]
- McKemmish, L.; Reimers, J.; McKenzie, R.; Mark, A.; Hush, N. Penrose-Hameroff orchestrated objective-reduction proposal for human consciousness is not biologically feasible. Phys. Rev. E 2009, 80, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Conway, J.; Kochen, S. The free will theorem. Found. Phys. 2006, 36, 1441–1473. [Google Scholar] [CrossRef]
- Conway, J.; Kochen, S. The strong free will theorem. Notices Am. Math. Soc. 2009, 56, 226–232. [Google Scholar]
| Sub | TR0 | TE0 | TRA | TEA | sTR0 | sTE0 | sTRA | sTEA |
|---|---|---|---|---|---|---|---|---|
| s01 | 85.75 | 121.23 | 84.76 | 121.47 | 120.48 | 86.59 | 119.23 | 87.06 |
| s02 | 70.80 | 51.21 | 68.63 | 56.51 | 51.10 | 70.79 | 49.36 | 74.53 |
| s03 | 61.37 | 79.81 | 59.83 | 78.79 | 79.20 | 61.50 | 75.22 | 79.17 |
| s04 | 52.25 | 64.20 | 50.09 | 66.99 | 63.55 | 52.83 | 63.27 | 64.60 |
| s05 | 67.28 | 72.04 | 66.53 | 72.78 | 71.38 | 67.83 | 69.60 | 68.13 |
| s06 | 84.57 | 69.72 | 80.22 | 64.13 | 69.09 | 84.67 | 61.74 | 114.21 |
| s07 | 68.66 | 78.65 | 68.28 | 86.13 | 78.48 | 68.73 | 75.57 | 69.58 |
| s08 | 46.58 | 43.81 | 44.24 | 49.38 | 43.28 | 47.27 | 42.89 | 63.09 |
| s09 | 47.22 | 24.88 | 46.90 | 25.77 | 24.68 | 47.49 | 24.32 | 49.94 |
| s10 | 53.18 | 33.33 | 53.33 | 36.97 | 33.14 | 53.85 | 30.32 | 55.78 |
| s11 | 43.98 | 51.10 | 43.29 | 52.76 | 50.95 | 44.47 | 50.25 | 45.85 |
| s12 | 45.78 | 45.14 | 44.38 | 46.08 | 44.92 | 46.00 | 44.45 | 46.56 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ingber, L. Quantum Calcium-Ion Interactions with EEG. Sci 2019, 1, 20. https://doi.org/10.3390/sci1010020
Ingber L. Quantum Calcium-Ion Interactions with EEG. Sci. 2019; 1(1):20. https://doi.org/10.3390/sci1010020
Chicago/Turabian StyleIngber, Lester. 2019. "Quantum Calcium-Ion Interactions with EEG" Sci 1, no. 1: 20. https://doi.org/10.3390/sci1010020
APA StyleIngber, L. (2019). Quantum Calcium-Ion Interactions with EEG. Sci, 1(1), 20. https://doi.org/10.3390/sci1010020





