Abstract
By way of studying the difference of the proton and neutron distributions in isotopes, isotones and isobars, we used the results of theoretical calculations obtained from the scattering of protons and electrons on nuclei. To calculate the differential cross section of proton scattering, an expression was obtained for the distorted-wave formfactor of the nucleus, which, using the mathematical method proposed by us, is expressed through the plane-wave Born formfactor. In addition, using the data for elastic scattering of electrons on nuclei, the average characteristic parameters of , , , , nuclei were determined. In this work, for calculating the differential cross section of the elastic scattering of electrons on spherical nuclei, the Fermi function was chosen as a trial function of the proton density distribution. In the calculations, the pole method was used to solve the Born integral of the target nucleus formfactor. Based on an analysis of the calculations of the differential cross section of the elastic scattering of electrons and the calculations of the differential cross section of the scattering of protons on the same nuclei, the main patterns of behavior of the general characteristics of nuclei, such as the root mean square radius (RMS), diffuseness, and the isotopic and isotonic shifts of parameters, were determined. For the nucleus, the radial dependence of the nucleon density distribution on the center of the nucleus, as well as the ratio of proton to neutron densities, have been studied. Changes in the distribution of densities of protons and neutrons with the addition of two neutrons to nucleus as well as changes in the distributions of densities of protons and neutrons when two neutrons are replaced by protons in isobars have been studied. The results of changes in the distribution of densities of protons and neutrons were justified on the basis of the shell model of the nucleus, using characteristic parameters determined for these nuclei from elastic electron scattering. A joint analysis of experimental work on the elastic scattering of electrons and protons on spherical nuclei leads to the conclusion that the distribution patterns of protons and neutrons differ from each other. In particular, this follows from calculations of the RMS of proton, neutron and nucleon distributions.
1. Introduction
In the last decade, issues of the quark phase in stars have become widely discussed. All of these problems form a new direction of research, one which has now begun to be called quark nuclear physics. The theory of nuclear reactions is also of great practical importance when bombarding a solid body with protons with energies in the megaelectronvolt range.
In the modern development of nuclear physics, several new directions can be traced. One of these is associated with the growing role of theoretical and experimental studies of nuclear reactions at high energies. In the past, the most important questions of the nucleus were quite clearly “separated” from the mechanism of nuclear reactions, which played an auxiliary role in the study of the nucleus. Currently, nuclear spectroscopy goes beyond the traditional framework of weakly excited bound states of nuclei and covers regions of high excitation energies, in which the concept of individual states of a system gradually loses its meaning due to the fact that the resonances of the compound system increasingly overlap with each other. At the same time, questions of the structure of the nucleus and the mechanism of reactions are increasingly intertwined. Another trend is associated with the accumulation of experimental information, improving its quality and increasing its complexity. In order to discover a new phenomenon, it is necessary to carry out a quantitative analysis of processes already known to us, which significantly increases the requirements for modern theory. In this regard, it is necessary to have a theory of nuclear reactions that can give a fairly complete quantitative description of the process in a wide range of energies of incident particles and reaction products.
Currently, the study of the spatial structures of atomic nuclei by the method of scattering electrons and protons on nuclei is widely used in both experimental and theoretical studies. The fact is that protons and neutrons located on the inner shells of atomic nuclei have a fairly high energy and come together so that their internal structure begins to be affected. Physicists associate the difference in the behavior of nucleons in the nucleus and in the free state with changes in their internal structure due to interaction [1]. Understanding how the quark–gluon structure of a nucleon bound in an atomic nucleus is modified by surrounding nucleons is an important problem in nuclear physics. Typically, the nuclei of atoms are represented as balls of neutrons and protons huddled together, which are evenly distributed throughout the volume. However, this idea is not entirely correct for neutron-rich nuclei, in which the number of neutrons significantly exceeds the number of protons. This situation is especially typical for heavy nuclei, in which an excess of neutrons leads to the neutrons and protons becoming differently associated with the nucleus. As a result, in some nuclei, an excess of neutrons appears on the surface of the nucleus; these can be considered as a thin “skin” that holds nuclear matter within the nucleus.
It is quite difficult to experimentally measure the thickness of the surface neutron layer [2]. The distribution of protons in the nucleus is easy to determine: the protons are charged, which means that other charged particles with less energy will obey the laws of the Coulomb interaction when they fly past. This means that, from the pattern of their scattering, it is possible to determine exactly how the protons are located in the nucleus. Neutrons, in turn, are neutral particles, which means they cannot be “seen” directly in experiments on the scattering of charged particles by a nucleus. As a result, neutron distributions of nuclei are measured using a wide variety of techniques: from work with antiproton atoms to experiments on measuring the pion production cross section during the interaction of electrons with nuclei [3]. However, such diversity also leads to a wide range of results, which often contradict each other. At the same time, accurate measurements of the neutron density distribution [4] in nuclei are extremely important for physicists. Firstly, the neutron skin affects the fundamental properties of the nuclei themselves—their shape, at least, depends on its size. However, another factor is also important: nuclear matter obeys its equation of state, and it is from measurements of the thickness of the surface neutron layer that one of its parameters can be obtained—symmetry energy. The value of this parameter will determine exactly how nuclear systems with a large difference between neutron and proton densities will behave [5]. Such systems include neutron stars: at a first approximation, they do not differ from ordinary nuclei, but with a large number of neutrons and protons they will obey the same equation of state.
2. Materials and Methods
Simple and accurate analytical expressions for the scattering amplitudes of the corresponding processes reveal important information from experimental data. Therefore, we need to obtain a general strict expression for the amplitude of scattering of high-energy nucleons on nuclei. In studies of the interaction of nucleons with nuclei, high energies are those energies of relative motion of a nucleon and a nucleus at which the wavelength corresponding to their relative motion would be significantly less than the radius of the nucleus. This condition is satisfied for nucleons with energies of several hundred MeV. Therefore, the motion of a nucleon can be considered semiclassical. This means that we can talk about the “place” where a nucleon hits the nucleus, about the “trajectory” of its movement inside the nucleus, etc. The idea of the motion of a nucleon in a nucleus along a trajectory allows one to calculate the change in the phase of the incident wave along each possible path and consider the total change in phase as a geometric sum of such changes, which also allows one to calculate the scattering cross section. For this purpose, we write the general expression for the differential cross section of nucleon scattering on nuclei in the following form:
Here, is the scattering amplitude of the nucleon; is the wave number of an incident particle in the initial state with energy and , is the wave number of an incident particle in the final state with energy ; is a target nucleus spin projection; and is a recoil nucleus spin projection nucleus, which is different from zero in the case of inelastic scattering. The amplitude of nucleon–nuclear scattering in the distorted wave method can be written as follows [6]:
where is a nuclear state wave function and is the reduced mass of an incident nucleon. In this case, we will write the wave function of the relative motion of the incident and scattered nucleons, as a result of solving the Schrödinger equation, in the following three-dimensional form:
where the distorting term in the phase, in contrast to Glauber’s theory, depends on the potential of the nucleus, which in turn is a function of the distribution of nucleons in the nucleus and is expressed through the following integral functions:
When choosing the nuclear potential, we use the advantage of proton scattering on nuclei of intermediate energies, in which during the time of the fast proton’s flight through the nucleus, the change in the positions of nucleons in the nucleus can be neglected. In this case, scattering occurs mainly forward—at small angles. As a consequence of the short-range nature of the nucleon–nucleon interaction, the scattering of a nucleon on a nucleus can be written as a sequence of single scatterings. Taking this into account, we represent the nuclear potential as the integral of the components of the interactions of the incident particle with individual nucleons of the scattering nucleus, as follows:
As the binding energy of the nucleons of the nucleus is small compared with the energy of the incident proton, the effects of nucleon binding can be neglected and, therefore, the nucleon–nucleon interaction potential can be expressed in terms of the scattering amplitudes on free nucleons, which are determined from the solution of the Schrödinger equation, as follows:
The wave function of the incident nucleon as a solution to the Schrödinger equation has the following form:
Taking into account (7) in (6) for the amplitude of nucleon–nucleon scattering we obtain the following expression:
where is the momentum of transfer of incident particle to target nucleon. Taking into account the Fourier transform for the nuclear potential we obtain the following:
Here, the amplitude of the free nucleon–nucleon interaction is selected in the following parametric form [7,8]:
Thus, we obtain the following expression for the scattering amplitude:
After integrating (11) over and then over we express the differential cross section through the nucleus form factor, as follows:
where the nucleus form factor, taking into account the phase distortion, takes the following form:
After applying the mathematical method, we proposed the distorted-wave form factor of the nucleus, expressed in terms of the plane-wave form factor, which is simplified into the following form:
where represents the momentum transfer to the target nucleus.
To study the differential cross section of elastic scattering of protons on nuclei, we use the expression we obtained earlier in previous works, as follows:
where the Mott cross section is the cross section for scattering of protons on a point nucleus.
In Formula (13) the distorting term in the phase of the incident nucleon is a function of the nucleon distribution density in the nucleus. Therefore, we decided to determine how the proton and neutron distributions in nuclei separately affect the behavior of incident and scattered particles. In this case, the proton distribution density in nuclei is determined from the elastic scattering of electrons on nuclei. For this purpose, we used the expression for the differential cross section of elastic scattering of electrons on nuclei obtained in our previous work [8]. The form factor of the nucleus in expression (15), obtained from the elastic scattering of electrons on nuclei in the distorted-wave approximation, is expressed through the plane-wave Born form factor, as follows:
here, , which, as stated above, is the momentum of electron transfer to the target nucleus (clearly, are the momenta of the electron before and after scattering).
It is known that fast protons have approximately the same sensitivity to protons and neutrons of the nucleus. This means that from the data on proton scattering on nuclei, it is possible to extract information on the isoscalar density, i.e., on the sum of the distributions of neutron and proton densities, as follows:
In calculations, we choose the distribution of nucleon density in nuclei in the form of a Fermi function, as follows:
here is radius of half-recession of nucleon density in nuclei.
Unlike incident protons, scattered electrons are more sensitive to the distribution of protons on the surfaces of nuclei, which makes it possible to choose the radial density of proton distribution in the form of a three-parameter Fermi function, as follows:
where is equilibrium proton density at the center of the nucleus and is a free parameter. Thus, determining the parameters of the nucleon density distribution from proton scattering on nuclei, and the proton distribution from electron scattering, we use expression (1) to determine the neutron density distribution function, as follows:
here is equilibrium neutron density at the center of the nucleus.
As noted above, our goal is based on an analysis of calculations of the differential cross section for the elastic scattering of electrons [8,9,10,11], and calculations of the differential cross section for proton scattering [12,13,14,15,16] on the same nuclei determine the main patterns of behavior of the general characteristics of nuclei, such as RMS, diffuseness, and isotopic and isotonic shifts of parameters.
The study of the RMS and its changes upon the addition of nucleons is one of the central topics of recent years in nuclear physics. If the charge radius characterizes the nucleus as a whole, then the change in the RMS with the addition of protons and neutrons is associated both with the structure of atomic nuclei and with the nature of the effective forces.
In addition, in isotones, changes in the RMS of charge density distributions can be determined by the scattering of electrons, as they are more sensitive to the distributions of protons in nuclei.
Structural changes in the nuclei of isotopes and isotones are mainly associated with the filling of nuclear shells, and these changes occur mainly on the surface of the nuclei. Therefore, the purpose of such studies is mainly to identify patterns in changes in the distribution of both protons and neutrons when filling shells.
In order to study and determine the difference in the radial distributions of charge densities in isotones in different approximations for the scattering of electrons on nuclei, numerous works have been carried out [17,18]. From the analysis of the results obtained, we can come to the conclusion that there is a clear correlation between changes in the parameters of the charge density distribution (CDD) and charge RMS with the shell-model structure of the studied nuclei. From the point of view of the independent single-particle model, the manifestation of a difference in the charge densities of isotonic pairs is a consequence of the addition of one proton, which leads to a change in the structure of the nucleus and the Coulomb field.
However, it should be noted that the determined average characteristic parameters, i.e., the thickness of the surface layer of nuclei, the RMS distribution of protons and neutrons, etc., cannot unambiguously reveal where and how additional protons or neutrons are “placed”. More specifically, it is necessary to determine during the transition between pairs of isotopes and isotones.
3. Results
The characteristic nuclear parameters obtained from a joint analysis of cross sections for elastic scattering of electrons and protons on the same nuclei make it possible to more reliably determine the difference in the distributions of isotopes and isotones [19]. A comparison of changes in these parameters, in particular the radius of the half-recession of nucleon density in nuclei (c), surface layer thickness () and the RMS of proton, neutron and nucleon distributions in isotopes, isotones and isobars (, ), are given in Table 1.

Table 1.
Changing the parameters of proton, neutron and nucleon distributions in isotopes, isotones and isobars.
Figure 1 for the nucleus shows the radial dependence of the nucleon density distribution on the center of the nucleus, as well as the ratio of proton to neutron densities.
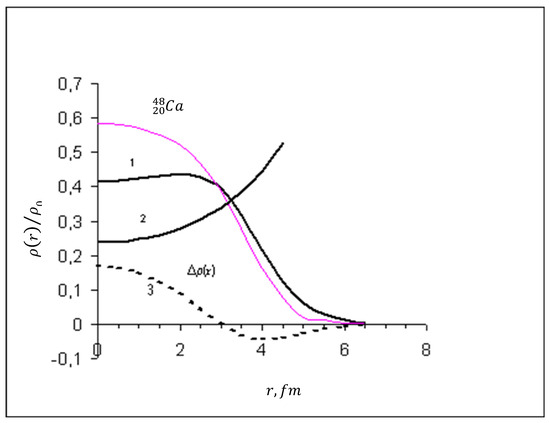
Figure 1.
Curve 1—radial dependence of nucleon density for Curve 2—ratio of proton to neutron densities; and Curve 3—the difference in the distributions of neutron and proton densities, i.e., . The experimental curve is shown in pink [20].
As can be seen from this figure, the ratio of proton to neutron density slowly increases starting from the central part of the nucleus. At a distance of about 3 fm, the difference in distributions, one might say, disappears and becomes less than the ratio , i.e., there is a relative depletion in neutrons, while, on the contrary, at the periphery of the nucleus there is an enrichment in neutrons.
During the transition from the nucleus to the nucleus, there is a significant increase in the thickness of the surface layer (Δt > 0) of the nucleon distribution. If we pay attention to the change in the RMS for these isotopes, we note that their proton radii are practically the same. In the nucleus, the change in the neutron radius becomes noticeable. Changes in these parameters can also be explained on the basis of the shell model of the nucleus using the example of the isotopes and . The small increase in the RMS of the proton distribution upon going from to can be explained by the fact that the added two neutrons occupy the subshell and close it. The angular momentum of the subshell of this new isotope is less than the angular momentum of the filled proton subshell Therefore, these neutrons push protons towards the surface of the nucleus and increase the RMS of the proton distribution and the thickness of the surface layer of the nucleus.
During the transition from the nucleus to its isotope two neutrons are added, taking up space in the new subshell , whose orbital momentum is less than that of the last proton (), constraining protons towards the surface of the nucleus. As can be seen from Figure 2, during the transition in these isotopes closer to the center of the nucleus the proton density decreases, and towards the periphery of the nucleus it increases sharply.
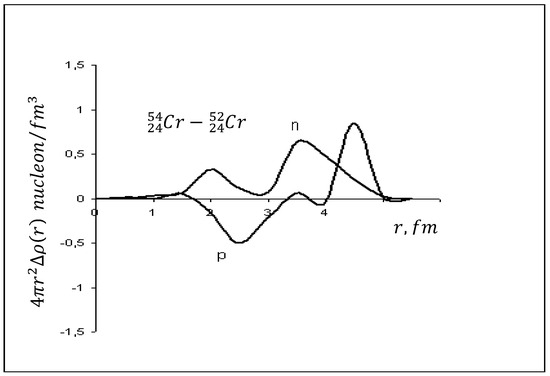
Figure 2.
Changes in the distribution of densities of protons and neutrons with the addition of two neutrons to the nucleus .
Now, we observe the change in the characteristic parameters of isotones. Changes in the distributions of the densities of protons and neutrons with the addition of two protons to the nucleus, as a result of which its isotone is obtained, are shown in Figure 3. These changes are interpreted on the basis of the shell nuclear model as follows; the added two protons, occupying places in the unfilled subshell , shift the filled neutron subshell towards the surface of the nucleus. Therefore, in places where the number of protons increases, there is a noticeable decrease in neutrons.
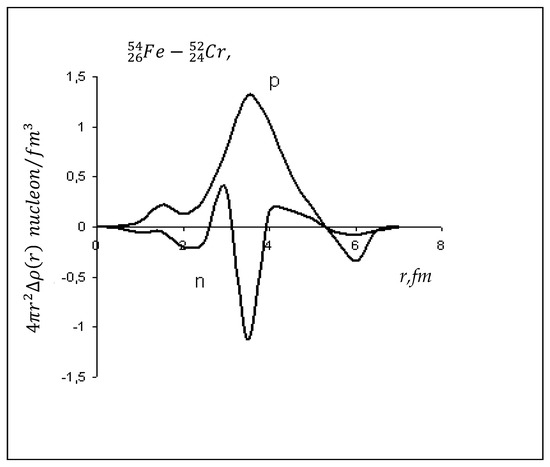
Figure 3.
Changes in proton and neutron density distributions with the addition of two protons to the nucleus .
Finally, as shown in Figure 4, during the transition in the isobars, the added protons occupy places in the unfilled subshell and, at the same time, due to the replaced neutrons located in subshell in the chromium core, the neutron density at the periphery decreases sharply.
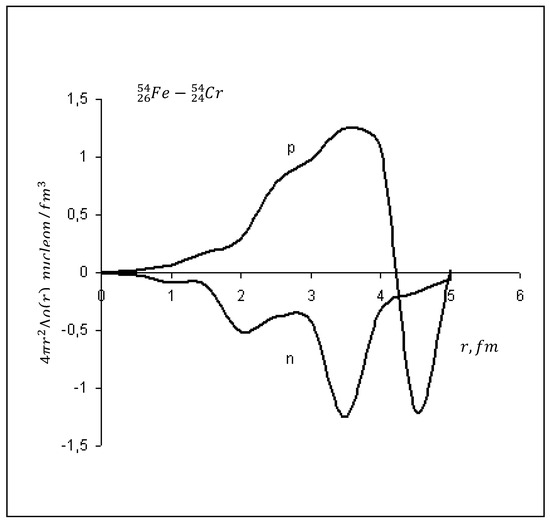
Figure 4.
Changes in the distributions of densities of protons and neutrons when two neutrons are replaced by protons in isobars .
The results in changes in the distribution of densities of protons and neutrons were justified on the basis of the shell model of the nucleus using the characteristic parameters determined for these nuclei from elastic electron scattering and are shown in Table 2.

Table 2.
Characteristic parameters of nuclei obtained from the elastic scattering of electrons and protons.
Thus, a joint analysis of experimental work on the elastic scattering of electrons and protons on spherical nuclei leads to a conclusion regarding the RMS of proton, neutron and nucleon distributions, one which is calculated using the following expressions, obtained from the above:
for the above nuclei, which are located within the limits, as follows:
In this case, for the half-recession radius of the nucleon density we have . These results have a very narrow range of uncertainties and are in good agreement with the results of numerous studies obtained by different methods.
4. Discussion
As can be seen from these figures, in nuclei in which a pair of protons or a pair of neutrons is added to an overfilled shell, the thickness of the surface layer increases, and, when the shell (or subshell) is closed by protons or neutrons, the thickness of the surface layer decreases in comparison with nuclei with an unfilled shell. This change in nuclear parameters with the addition of neutrons and protons is well explained by the application of the theory of nuclear matter to the effects of openness of the shell—the interaction of nucleons inside the subshell, the polarization of the core, and the pairing of nucleons added to the subshell.
In the independent particle model, this pattern in changes in the RMS distribution of protons and neutrons in nuclei is explained by the fact that, in heavy nuclei, the existence of a neutron excess leads to unequal average potentials acting on neutrons and protons.
This effect, which characterizes more subtle features of the structure of the nucleus, leads to the appearance of a potential part of the symmetry energy.
5. Conclusions
Based on our research, we can conclude the following: the RMS of matter distribution increases ; the densities of neutron and proton distributions are different inside the nucleus; the difference in the RMS distributions of matter in isotopes increases as the number of neutrons increases; for medium-sized nuclei, the RMS of the proton distribution is 0.3–0.5 fm greater than the neutron one, though the neutron distribution has a greater extent than the proton one; and that the change in the thickness of the surface layer of nucleons does not practically change with an increase in the mass number of nuclei, though this is significant only when a certain shell is closed, which leads to a decrease in the thickness of the surface layer of proton (neutron) distributions.
Author Contributions
Conceptualization, M.M.; methodology, M.M. and M.A.; software, M.A.; validation, M.M.; formal analysis, M.M.; investigation, M.A.; resources, M.A.; writing—original draft, M.A.; writing—review and editing, M.M.; visualization, M.A.; supervision, M.M.; project administration, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original data presented in the study are openly available in [Research Gate] at [DOI]: 1. https://doi.org/10.29083/HJ.44.01.2021; 2. https://doi.org/10.9734/bpi/cppsr/v3/6419C; 3. https://doi.org/10.1134/1.1842293; 4. https://www.osti.gov/etdeweb/biblio/7310209 (accessed on 1 August 1975); 5. https://doi.org/10.1103/PhysRevC.77.024302; 6. https://doi.org/10.1103/PhysRevC.44.2328.
Acknowledgments
The authors received no external support because of the theoretical nature of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RMS | root mean square |
References
- Mirabutalibov, M.; Aliyeva, M. Study of nuclear exotics by high-energy electrons scattering. Eur. Phys. J. Plus 2023, 138, 672. [Google Scholar]
- Mirabutalibov, M.; Aliyeva, M. Study of the structure of atomics by the method of electron scattering in the distorted-wave approximation. Turk. Comput. Theor. Chem. 2025, 9, 38–44. [Google Scholar]
- Adhikari, D.; Albataineh, H.; Androic, D.; Aniol, K.; Armstrong, D.S.; Averett, T.; Gayoso, C.A.; Barcus, S.; Bellini, V.; Beminiwattha, S.; et al. Accurate Determination of the Neutron Skin Thickness of 208Pb through Parity-Violation in Electron Scattering. Phys. Rev. Lett. 2021, 126, 172502. [Google Scholar] [CrossRef] [PubMed]
- National Academies of Sciences, Engineering, and Medicine; Division on Engineering and Physical Sciences; Board on Physics and Astronomy; Committee on U.S.-Based Electron-Ion Collider Science Assessment. An Assessment of U.S.-Based Electron-Ion Collider Science; National Academies Press: Washington, DC, USA, 2018. [Google Scholar] [CrossRef]
- Chen, J. Nuclear Data Sheets for A = 48. Nucl. Data Sheets 2022, 179, 1–382. [Google Scholar] [CrossRef]
- Casten, R.F.; Sherrill, B.M. The study of exotic nuclei. Prog. Part. Nucl. Phys. 2000, 45, S171–S233. [Google Scholar] [CrossRef]
- Mirabutalibov, M.M. Analytic distorted-wave approximation for nucleons quasi-elastic scattering calculations. Hadron. J. 2021, 44, 1–17. [Google Scholar] [CrossRef]
- Mirabutalibov, M.M. Nonrelativistic description of nucleon-nucleus scattering. Nucl. Phys. Russ. 2004, 67, 2171–2177. [Google Scholar] [CrossRef]
- Javadov, A.V.; Mirabutalybov, M.M.; Sadykhov, A.R. Elastic electron scattering and fine structure of the nuclear charge density distribution . Izv. Acad. Sci. Ser. Phys. 1975, 39, 1761–1768. [Google Scholar]
- Javadov, A.V.; Mirabutalibov, M.M.; Tveretsky, A.P. Elastic scattering of electrons and distribution of nucleon density in the nucleus. Izv. Acad. Sci. Ser. Phys. 1978, 42, 1875–1882. [Google Scholar]
- Javadov, A.V.; Mirabutalibov, M.M. Scattering of electrons by nuclei and variations in charge density distribution. Izv. Acad. Sci. Ser. Phys. 1978, 42, 1869–1873. [Google Scholar]
- Javadov, A.V.; Mirabutalibov, M.M. Elastic scattering of high-energy electrons on spherical nuclei. Izv. Acad. Sci. Ser. Phys. 1976, 40, 2156–2162. [Google Scholar]
- Mirabutalibov, M.M. Excitation of giant resonances in nuclei by inelastic scattering of protons. Izv. V. Russ. 2010, 59–73. Available online: https://www.osti.gov/etdeweb/biblio/22242664 (accessed on 15 July 2010).
- Javadov, A.V.; Mirabutalibov, M.M. Elastic scattering of electrons on isotopes and isotones. Izv. Acad. Sci. Ser. Phys. 1980, 44, 1910–1915. [Google Scholar]
- Mirteimour, M.M. Mina Aliyeva Distorted—Wave Approximation Theory for Electron Scattering from Atomic. Curr. Perspect. Phys. Sci. Res. 2023, 3. [Google Scholar] [CrossRef]
- Bertozzi, W.; Friar, J.; Heisenberg, J.; Negele, J.W. Contributions of neutrons to elastic electron scattering from nuclei. Phys. Lett. 1972, B41, 408–412. [Google Scholar] [CrossRef]
- Chrien, R.E. Quasi-free nucleon scattering on isotopes 16O. Phys. Rev. C 1986, 2, 1012–1022. [Google Scholar]
- OECD; NEA. Fission Gas Behaviour in Water Reactor Fuels: Seminar Proceedings, Cadarache, France, 26–29 September 2000; Nuclear Science; OECD Publishing: Paris, France, 2000. [Google Scholar] [CrossRef]
- Kverev, M.V. Elastic scattering of electrons on nuclei and charge radius of a proton in nuclear matter. Nucl. Phys. Russ. 1987, 45, 1212–1220. [Google Scholar]
- Gulkarov, I.S.; Nigam, B.P. Charge densities of isotopes and occupation numbers of shell states and. Nucl. Phys. Russ. 1997, 60, 995–1012. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).