Relationship between Internal Stress Distribution and Microstructure in a Suspension-Sprayed Thermal Barrier Coating with a Columnar Structure
Abstract
1. Introduction
2. Experimental Procedures
2.1. Materials and Specimen Preparation
2.2. Hybrid X-ray Deflection Analysis to Measure the Internal Stress in SPS-TBC
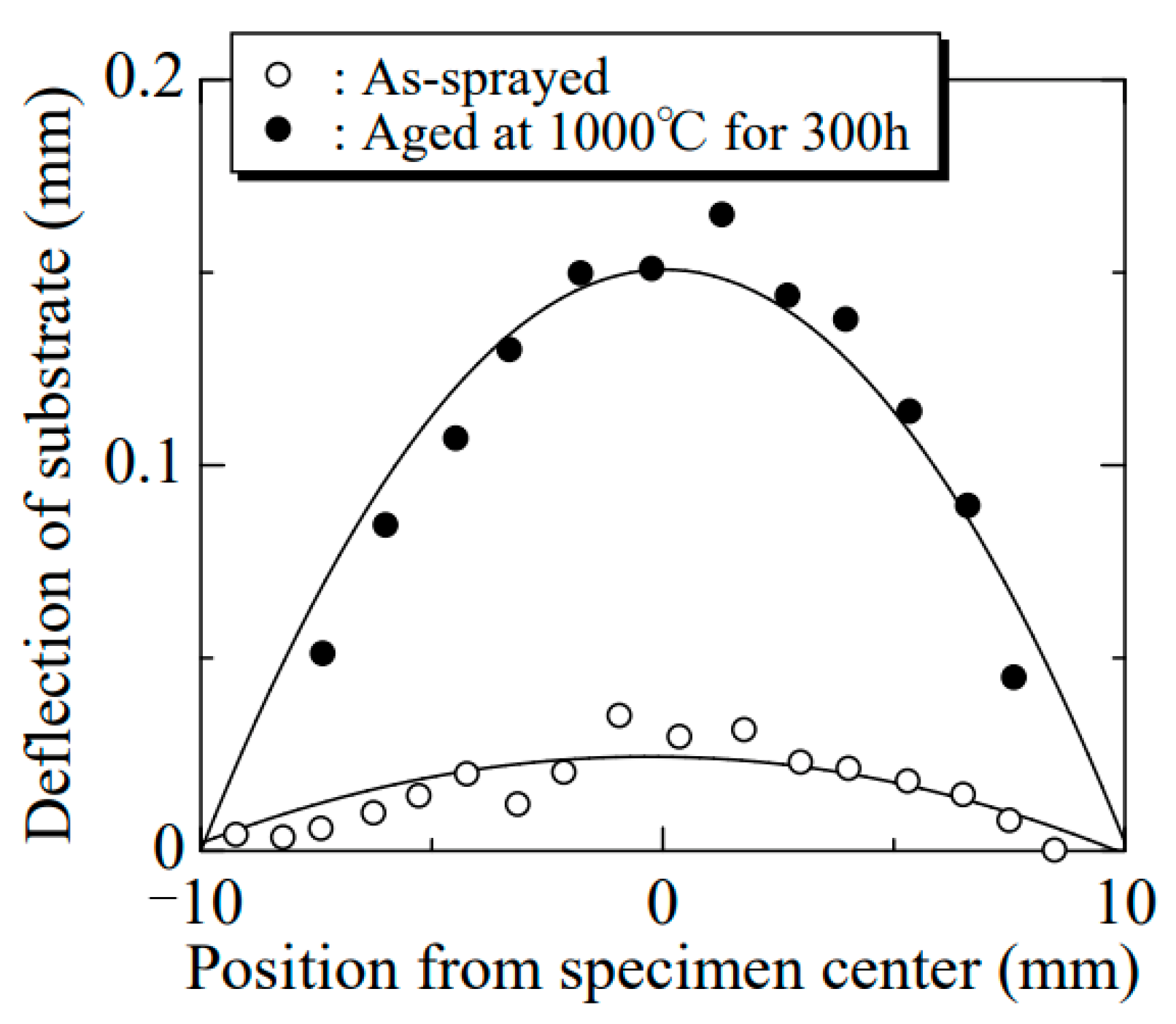
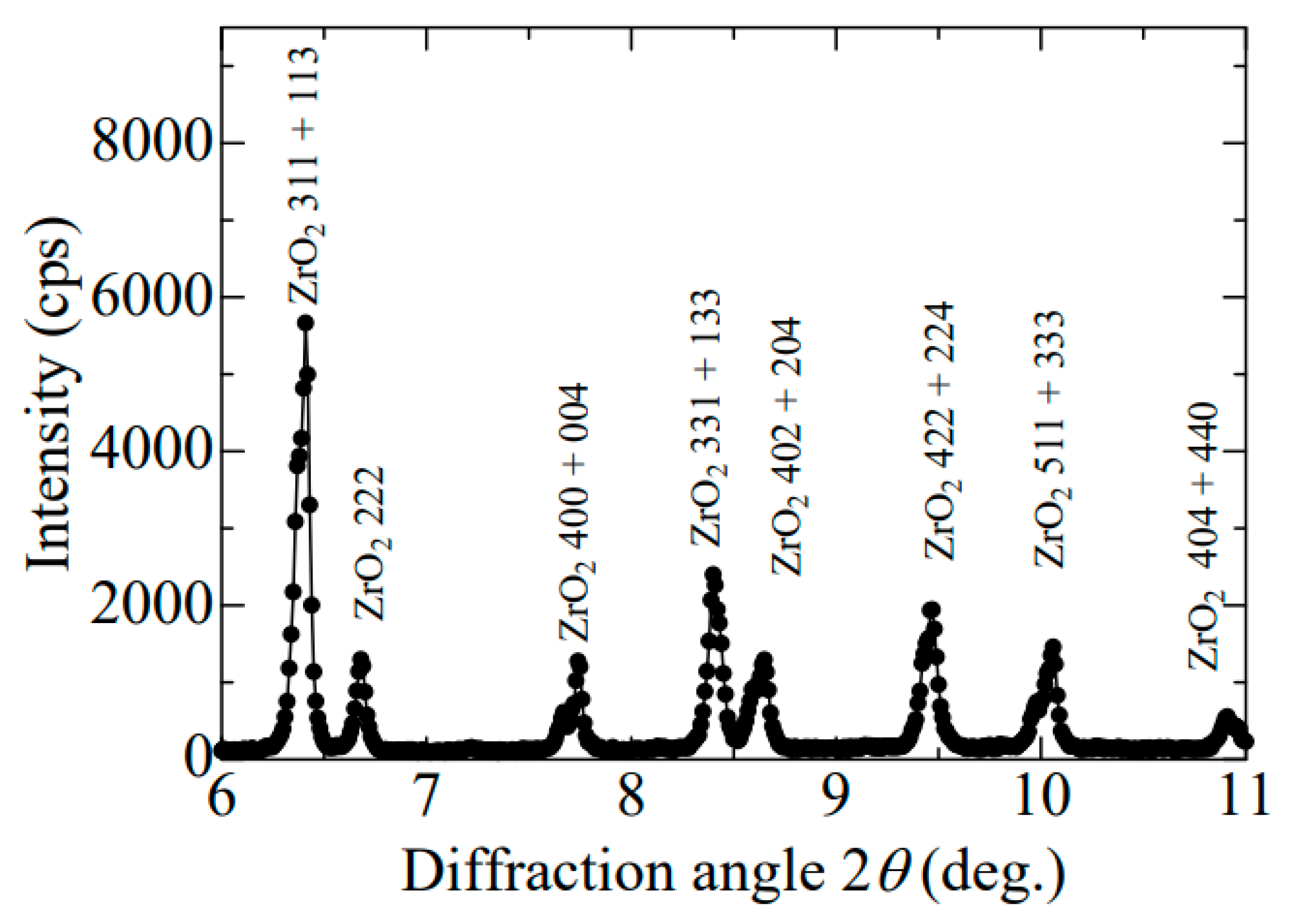
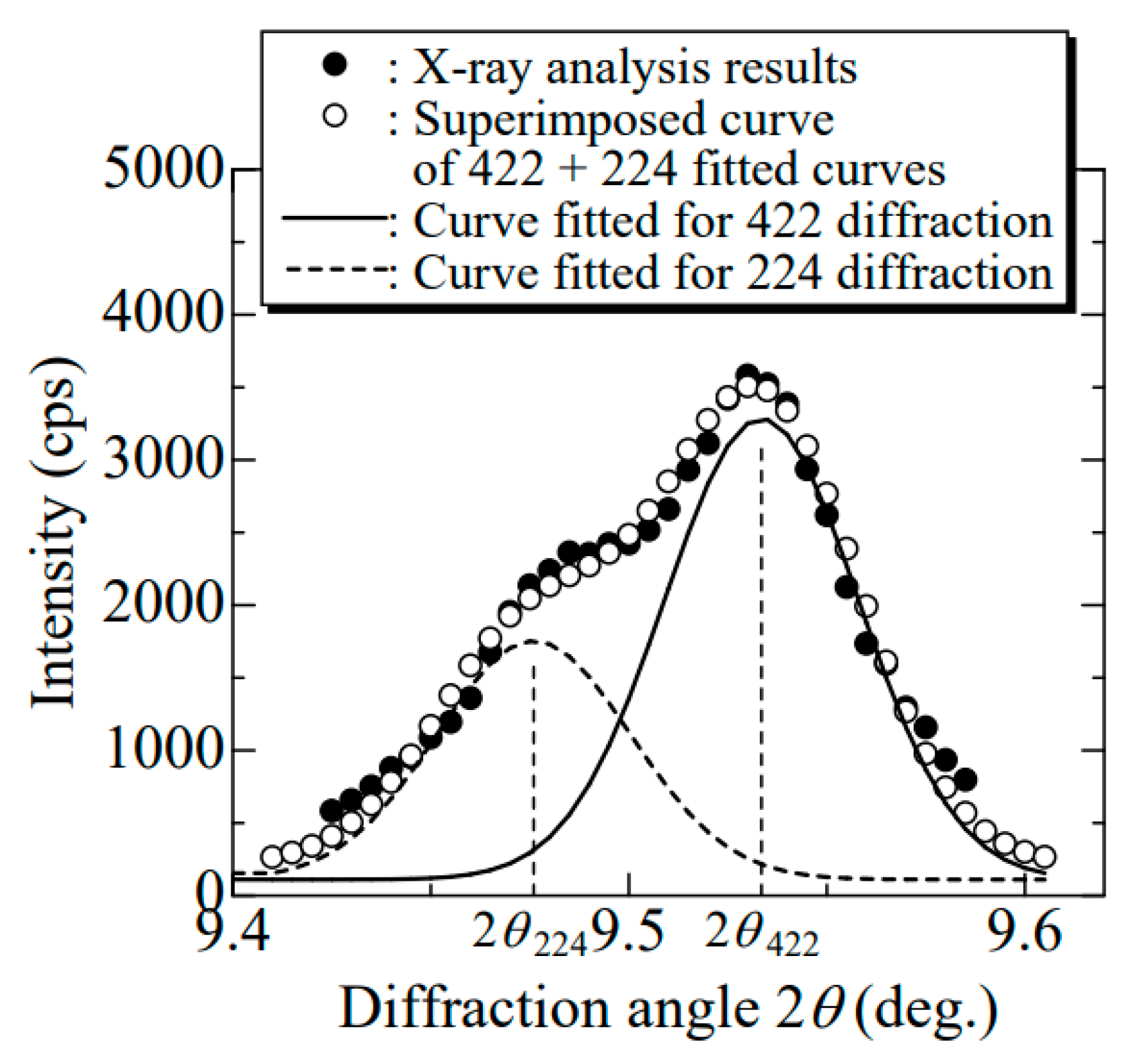
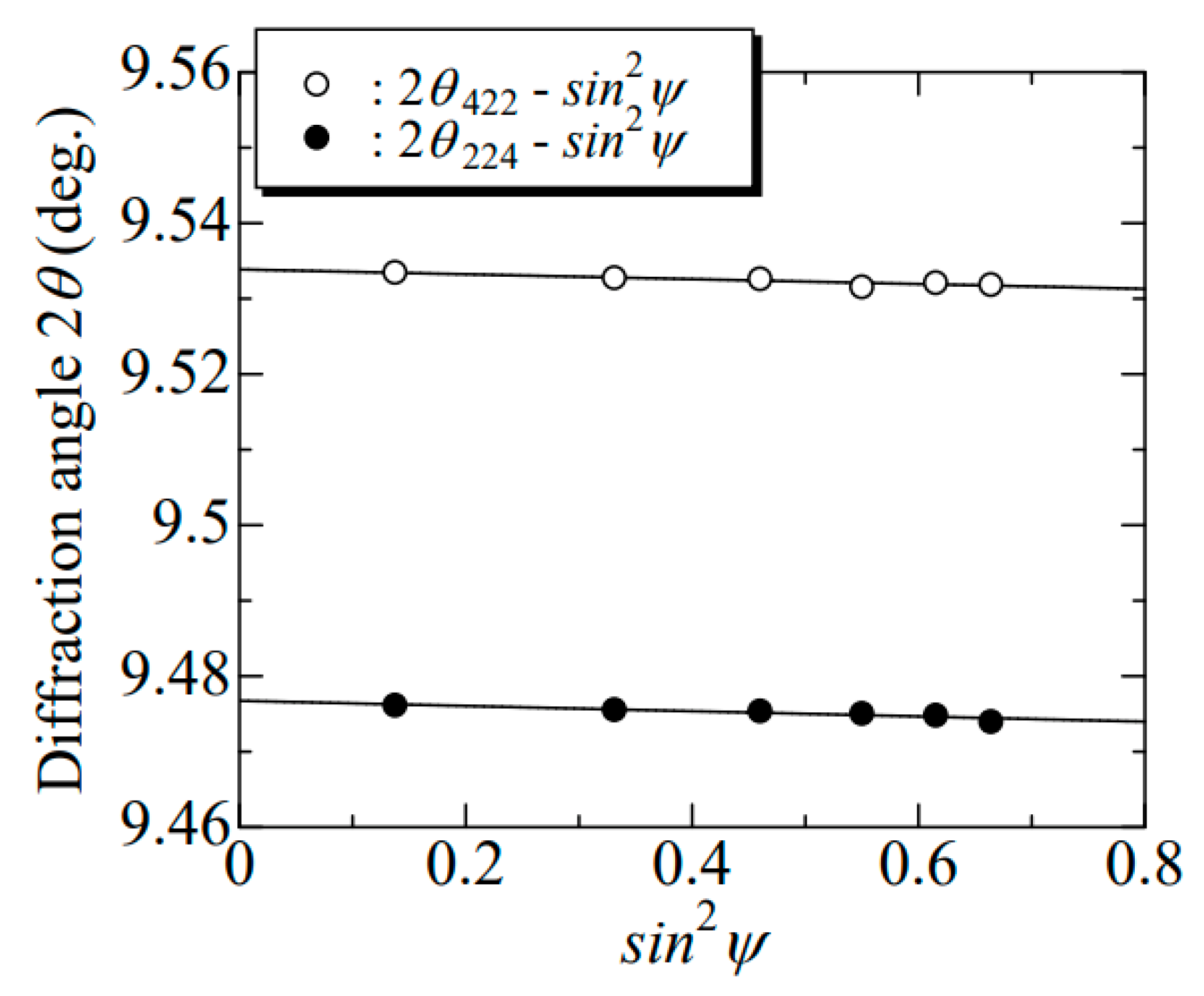
3. Results and Discussion
4. Summary Remarks
- (1)
- In the top coat of the SPS-TBC, the internal stress was almost in the in-plane stress state, and the out-of-plane stress component was practically equal to zero;
- (2)
- The in-plane internal stress in the top coat decreased by decreasing the column diameter. The thin column microstructure of the SPS-TBC had superior strain tolerance;
- (3)
- In measuring internal stress using high-energy synchrotron X-rays, periodic stress decrements were observed in the internal stress distribution because internal stress was released at the porous layer.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Padture, N.P.; Gell, M.; Jordan, E.H. Thermal barrier coatings for gas-turbine engine applications. Science 2002, 296, 280–284. [Google Scholar] [CrossRef]
- Vaßen, R.; Kaßner, H.; Stuke, A.; Hauler, F.; Hathiramani, D.; Stöver, D. Advanced thermal spray technologies for applications in energy systems. Surf. Coat. Technol. 2008, 202, 4432–4437. [Google Scholar] [CrossRef]
- Bakan, E.; Vasßen, R. Ceramic top coats of plasma-sprayed thermal barrier coatings: Materials, Processes, and Properties. J. Therm. Spray Technol. 2017, 26, 992–1010. [Google Scholar]
- Li, G.-R.; Yang, G.-J.; Chen, X.-F.; Li, C.-X.; Li, C.-J. Strain/sintering co-induced multiscale structural changes in plasma-sprayed thermal barrier coatings. Ceram. Int. 2018, 44, 14408–14416. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Schmidt, A.; Scholz, A. The determination of delamination resistance in thermal barrier coating system by four-point bending tests. Surf. Coat. Technol. 2006, 201, 744–754. [Google Scholar] [CrossRef]
- Trunova, O.; Beck, T.; Herzog, R.; Steinbrech, R.W.; Singheiser, L. Damage mechanisms and lifetime behavior of plasma sprayed thermal barrier coating systems for gas turbines—Part I: Experiments. Surf. Coat. Technol. 2008, 202, 5027–5032. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Yoshida, T.; Fukanuma, H.; Ohno, N. Thermal Cycle Damage and Residual Adhesion Strength in a Thermal Barrier Coating. J. Soc. Mater. Sci. Jpn. 2009, 58, 168–174. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Kinebchi, T.; Fukanuma, H.; Ohno, N. Influence of the spray process parameters and the thermal exposure on the mechanical properties of the free-standing air-plasma sprayed thermal barrier coating. J. Jpn. Therm. Spray Soc. 2007, 44, 88–95. [Google Scholar]
- Yamazaki, Y. Correlation between the mechanical properties and splat microstructures of an air plasma sprayed thermal barrier coatings. J. Solid Mech. Mater. Eng. 2008, 2, 1275–1286. [Google Scholar] [CrossRef]
- Okazaki, M.; Yamagishi, S.; Yamazaki, Y.; Ogawa, K.; Waki, H.; Arai, M. Adhesion Strength of Ceramic Top Coat in Thermal Barrier Coatings Subjected to Thermal Cycles: -Effects of Thermal Cycle Testing Method and Environment. Int. J. Fatigue 2013, 53, 33–39. [Google Scholar] [CrossRef]
- Arikawa, H.; Kojima, Y. Heat Resistant Coatings for Gas Turbine Materials. J. Surf. Finish. Soc. Jpn. 2001, 52, 11–15. [Google Scholar]
- Matsumoto, K.; Kawagishi, K.; Harada, H. Development of Thermal Barrier Coating Technology. Mater. Jpn. 2013, 52, 469–474. [Google Scholar] [CrossRef]
- Watanabe, K.; Takahashi, T. Development of Gas Turbine Based on Energy Planning of Japan and Issues on GTCC Contributing to Stability of Electric Power System. J. Gas Turbine Soc. Jpn. 2019, 47, 2–7. [Google Scholar]
- Schlegel, N.; Ebert, S.; Mauer, G.; Vaßen, R. Columnar-structured Mg-Al-spinel thermal barrier coatings (TBCs) by suspension plasma spraying (SPS). J. Therm. Spray Technol. 2015, 24, 144–151. [Google Scholar] [CrossRef]
- Schlegel, N.; Sebold, D.; Sohn, Y.; Mauer, G.; Vaßen, R. Cycling performance of a columnar-structured complex perovskite in a temperature gradient test. J. Therm. Spray Technol. 2015, 24, 1205–1212. [Google Scholar]
- Ganvir, A.; Curry, N.; Björklund, S.; Markocsan, N.; Nylén, P. Characterization of microstructure and thermal properties of YSZ Coatings obtained by axial suspension plasma spraying (ASPS). J. Therm. Spray Technol. 2015, 24, 1195–1204. [Google Scholar] [CrossRef]
- Guignard, A.; Maur, G.; Vaßen, R.; Stöver, D. Deposition and characteristics of submicronmeter-structured thermal barrier coatings by suspension plasma spraying. J. Therm. Spray Technol. 2012, 21, 416–424. [Google Scholar] [CrossRef]
- Ganvir, A.; Curry, N.; Markocsan, N.; Nylén, P.; Joshi, S.; Vilemova, M.; Pala, Z. Influence of microstructure on thermal properties of axial suspension plasma-sprayed YSZ thermal barrier coatings. J. Therm. Spray Technol. 2016, 25, 202–212. [Google Scholar] [CrossRef]
- Curry, N.; VanEvery, K.; Snyder, T.; Markocsan, N. Thermal Conductivity Analysis and Lifetime Testing of Suspension Plasma-Sprayed Thermal Barrier Coatings. Coatings 2014, 4, 630–650. [Google Scholar]
- Xu, P.; Meng, G.; Liu, G.; Cpyle, T.; Pershin, L.; Mostaghimi, J. Columnar-structured thermal barrier coatings deposited via the water-based suspension plasma spray process. J. Phys. D Appl. Phys. 2022, 55, 204001. [Google Scholar] [CrossRef]
- Curry, N.; Tang, Z.; Markocsan, N.; Nylén, P. Influence of bond coat surface roughness on the structure of axial suspension plasma spray thermal barrier coatings—Thermal and lifetime performance. Surf. Coat. Technol. 2015, 268, 15–23. [Google Scholar] [CrossRef]
- Curry, N.; Mahade, S.; Venkat, A.; Joshi, S. Erosion performance of suspension plasma spray thermal barrier coatings—A comparison with state of art coatings. Surf. Coat. Technol. 2022, 437, 12811. [Google Scholar] [CrossRef]
- Ma, X.; Ruggiero, P. Practical aspects of suspension plasma spray for thermal barrier coatings on potential gas turbine components. J. Therm. Spray Technol. 2018, 27, 591–602. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Shinomiya, K.; Hamaguchi, T.; Habu, Y.; Takagi, K. Effect of the microstructure of suspension plasma-sprayed thermal barrier coatings on their thermal cycling damage. Surf. Coat. Technol. 2023, 456, 129269. [Google Scholar] [CrossRef]
- Wu, R.T.; Osawa, M.; Yokokawa, T.; Kawagishi, K.; Harada, H. Degradation Mechanisms of an Advanced Jet Engine Service-Retired TBC Component. J. Solid Mech. Mater. Eng. 2010, 4, 119–130. [Google Scholar] [CrossRef]
- Ito, A.; Kobayashi, D. Degradation evaluation of 1300 °C-class 1st-stage gas turbine blades after long-term service. In Proceedings of the International Gas Turbine Congress 2015, Tokyo, Japan, 15–20 November 2015; pp. 614–619. [Google Scholar]
- Matejicek, J.; Sampath, S. Intrinsic residual stresses in single splats produced by thermal spray processes. Acta Mater. 2001, 49, 1993–1999. [Google Scholar] [CrossRef]
- Chun, L.; Zhang, X.; Chen, Y.; Carr, J.; Jacques, S.; Behnsen, J.; Michiel, M.; Xiao, P.; Cernik, R. Understanding the residual stress distribution through the thickness of atmosphere plasma sprayed (APS) thermal barrier coatings (TBCs) by high energy synchrotron XRD; digital image correlation (DIC) and image based modelling. Acta Mater. 2017, 132, 1–12. [Google Scholar]
- Suzuki, K.; Shobu, T.; Wada, K.; Matsubara, H.; Kawamura, M. Microstructure and Residual Stress of EB-PVD TBCs Grown under Substrate Rotation. J. Soc. Mater. Sci. Jpn. 2008, 57, 674–680. [Google Scholar] [CrossRef]
- Suzuki, K.; Matsumoto, K.; Kubo, T.; Machiya, S.; Tanaka, K.; Akiniwa, Y. Analysis on Residual Stress in Electron Beam-Physical Vapor Deposited Thermal Barrier Coating using Hard Synchrotron X-rays. Trans. Jpn. Soc. Mech. Eng. Ser. A 2005, 71, 1523–1529. [Google Scholar] [CrossRef]
- Suzuki, K.; Kawamura, M.; Shobu, T.; Kubo, T.; Tanaka, K.; Akiniwa, Y. Residual stress and deformation characteristics of thermal barrier coatings on curved substrate. J. Soc. Mater. Sci. Jpn. 2006, 55, 634–640. [Google Scholar] [CrossRef]
- Knipe, L.; Manero, A.; Siddiqui, S.; Meid, C.; Wischek, J.; Okasinski, J.; Almer, J.; Karlsson, A.M.; Bartsch, M.; Raghavan, S. Strain response of thermal barrier coatings captured under extreme engine environments through synchrotron X-ray diffraction. Nat. Commun. 2014, 5, 4559. [Google Scholar] [CrossRef]
- Zhou, D.; Guillon, O.; Vassen, R. Development of YSZ thermal barrier coatings using axial suspension plasma spraying. Coatings 2017, 7, 120. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Shinomiya, K.; Okumura, T.; Suzuki, K.; Shobu, T.; Nakamura, Y. Internal stress distribution in suspension plasma sprayed thermal barrier coating subjected to in-plane tensile loading. J. Jpn. Therm. Spray Soc. 2023, 60. In press. [Google Scholar]
- Suzuki, K.; Tanaka, K. Applications on High-Energy X-Rays to Stress Measurements of Thermal Barrier Coatings. Textures Microstruct. 2003, 35, 207–217. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Morikawa, M.; Hamaguchi, T.; Habu, Y.; Ohide, Y.; Takagi, K. Relationship between the mechanical properties and structure of a suspension plasma-sprayed thermal barrier coating with columnar microstructure. Surf. Coat. Technol. 2022, 439, 128430. [Google Scholar] [CrossRef]





| Bond Coat | Top Coat | |
|---|---|---|
| Spray method | HVOF | SPS |
| Spray material | CoNiCrAlY | Ethanol-based YSZ suspension (solid-phase content in suspension was 25 wt.%) |
| Spray torch | JP-5000 | 100HE |
| Plasma gas | N/A | Ar + N2 + H2 (flow rate:199 SLPM) |
| Plasma power | N/A | 105 kW |
| Beamline | BL02B1 |
| Wave length | 0.01736 nm (71.4 KeV) |
| Size of slit (V × H) | 0.2 mm × 1.0 mm |
| Analysis method | Constant penetration depth method (Side-inclination configuration) |
| Crystal | ZrO2 |
| Diffraction plane | (422) + (224) |
| 9.4992° | |
| Stress constant [28] | −11,492 MPa/deg |
| 0–0.7 |
| Analysis method | cos α |
| Characteristic X-ray | Cr-Kα |
| Tube voltage | 30 V |
| Tube current | 1.2 mA |
| Crystal | ZrO2 |
| Diffraction plane | 111 |
| 15.2578° | |
| Stress constant | −193,160 MPa/deg |
| Young’s modulus [36] | 107 GPa |
| 0–0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamazaki, Y.; Shinomiya, K.; Okumura, T.; Suzuki, K.; Shobu, T.; Nakamura, Y. Relationship between Internal Stress Distribution and Microstructure in a Suspension-Sprayed Thermal Barrier Coating with a Columnar Structure. Quantum Beam Sci. 2023, 7, 14. https://doi.org/10.3390/qubs7020014
Yamazaki Y, Shinomiya K, Okumura T, Suzuki K, Shobu T, Nakamura Y. Relationship between Internal Stress Distribution and Microstructure in a Suspension-Sprayed Thermal Barrier Coating with a Columnar Structure. Quantum Beam Science. 2023; 7(2):14. https://doi.org/10.3390/qubs7020014
Chicago/Turabian StyleYamazaki, Yasuhiro, Keisuke Shinomiya, Tadaharu Okumura, Kenji Suzuki, Takahisa Shobu, and Yuiga Nakamura. 2023. "Relationship between Internal Stress Distribution and Microstructure in a Suspension-Sprayed Thermal Barrier Coating with a Columnar Structure" Quantum Beam Science 7, no. 2: 14. https://doi.org/10.3390/qubs7020014
APA StyleYamazaki, Y., Shinomiya, K., Okumura, T., Suzuki, K., Shobu, T., & Nakamura, Y. (2023). Relationship between Internal Stress Distribution and Microstructure in a Suspension-Sprayed Thermal Barrier Coating with a Columnar Structure. Quantum Beam Science, 7(2), 14. https://doi.org/10.3390/qubs7020014







