In Situ Observation for Deformation-Induced Martensite Transformation (DIMT) during Tensile Deformation of 304 Stainless Steel Using Neutron Diffraction. PART I: Mechanical Response

Abstract

304 stainless steel is one of the most common stainless steels due to its excellent corrosion resistance and mechanical properties. Typically, a good balance between ductility and strength derives from deformation-induced martensite transformation (DIMT), but this mechanism has not been fully explained. In this study, we conducted in situ neutron diffraction measurements during the tensile deformation of commercial 304 stainless steel (at room temperature) by means of a Time-Of-Flight type neutron diffractometer, iMATERIA (BL20), at J-PARC MLF (Japan Proton Accelerator Research Complex, Materials and Life Science Experimental Facility), Japan. The fractions of α′-(BCC) and ε-(HCP) martensite were quantitatively determined by Rietveld-texture analysis, as well as the anisotropic microstrains. The strain hardening behavior corresponded well to the microstrain development in the austenite phase. Hence, the authors concluded that the existence of martensite was not a direct cause of hardening, because the dominant austenite phase strengthened to equivalent values as in the martensite phase. Moreover, the transformation-induced plasticity (TRIP) mechanism in austenitic steels is different from that of low-alloy bainitic TRIP steels.

1. Introduction

Austenitic stainless steels are widely used in industries because they have both superior corrosion resistance and mechanical properties. The most commonly used grade is JIS-SUS304 (equivalent to AISI 304), which contains mainly 18 mass% Cr, 8 mass% Ni, and less than 0.08 mass% C. In this steel, the FCC austenite (γ phase) is a metastable phase at room temperature. The more stable BCC martensite (α′ phase) is obtained by deformation-induced martensite transformation (DIMT) when the steel is plastically deformed. It is well known that DIMT leads to a high-strain hardening rate, resulting in a very large elongation until the tensile stress is achieved [1,2]. To address the role of DIMT in detail, many studies have been conducted using DIMT in 304 stainless steel, but the involved mechanism has not been fully addressed to date. This may be due to the reasons explained as follows:

HCP ε martensite may (or may not) be formed in Cr-Ni steels by DIMT. The existence of ε martensite in 18Cr-8Ni steel was first confirmed in the 1950s. However, Nishiyama showed that the occurrence of ε martensite is strongly affected by chemical composition, microstructure, and temperature [3]. Such factors also affect the route of DIMT, i.e., whether it will proceed as γ→ε→α′ or the simultaneous γ→α′ and γ→ε transformations occur [4,5].

In addition, the quantitative detection of HCP martensite is difficult compared to the detection of α′ (BCC) martensite. The amount of α′ martensite can be determined accurately by saturated magnetization measurements [5]. In the case of nonmagnetic ε martensite, microscopy and diffraction measurements are used, but the results frequently have large uncertainties because of statistic reliability and sharp textures analysis, respectively.

Grosse et al. and Kalkhof et al. attempted to use the fraction of α′ martensite as an indicator of accumulated plastic strain by low-cycle fatigue for AISI 321 (18Cr-10Ni) steel [6,7]. They found a linear relationship between the martensite fraction and the number of cycles. However, the slope of the linear fitting regression strongly depended on the initial state. The existence of ε martensite was not mentioned in those studies. However, Tiamiyu et al. confirmed ε martensite by XRD and EBSD after the compressive deformation of AISI 321 [8], although it disappeared with increasing strain. They also pointed out that the developments of α′ and ε martensite are dependent on the initial grain size.

The authors recently reported that the neutron-diffraction-based Rietveld texture analysis (NDRTA) can be a powerful tool for the quantitative detection of both ε and α′ martensite in 18Cr-8Ni steels [5]. In this study, the authors applied this technique for in situ observation during the tensile deformation of a 304 stainless steel sheet sample.

This study consists of two successive papers. In part I, we report the relationship between the fraction of martensite phases and the corresponding mechanical behavior. In addition, the line profile analysis, as part of the NDRTA, was assessed to discuss the role of dislocation hardening. In part II, the mechanism of DIMT will be discussed from the texture point of view.

2. Materials and Methods

2.1. Materials

A commercial SUS304 stainless steel sheet with a thickness of 2 mm was evaluated. The chemical composition is presented in

Table 1. Chemical composition of the tested steel (mass%).

Element	C	Si	Mn	P	S	Ni	Cr	Cu	N	Fe
	0.042	0.52	0.92	0.030	0.002	8.08	18.26	0.22	0.052	Balance

. Figure 1a shows the initial grain structure of SUS304 that was observed by electron backscattered diffraction (EBSD), using a Hitachi SU-5000 electron microscope equipped with EDAX OIM system. It was observed that the sample had a fully recrystallized grain structure with annealing twins. The average grain size was 19 μm. No secondary phase was confirmed by EBSD, nor by neutron diffraction. A weak rolling texture was confirmed, but the maximum pole density on any pole figure was less than 2.

A tensile coupon (Figure 1b) was prepared by spark cutting of the SUS304 sheet. The basic design of the coupon was Type 14B, as defined in JIS Z 2201. However, to fix the coupon with minimum volume of the anvils, additional wings, 40 mm in width, were added to both ends. Loading was achieved by hooking these wings to the protrusions of anvils, as shown in Figure 1c. The deformation tests were conducted at room temperature (300 K).

2.2. In Situ Neutron Diffraction Experiments

The Time-Of-Flight (TOF) neutron diffractometer, iMATERIA, at Japan Proton Accelerator Research Complex in Materials and Life Science Experimental Facility (J-PARC MLF, Tokai, Japan) was used in this study [9]. As shown in Figure 2, iMATERIA has numerous detectors surrounding the incident neutron beam. The detectors were divided into small areas called observation points (OPs) and categorized into 7 bank groups. Each bank group consisted of OPs having almost the same 2θ angles. For example, 2θ angles for the OPs of Bank 31 were approximately 31°.

The deformation-testing machine was installed in the sample chamber of iMATERIA, which enabled uniaxial deformation along Y_D. The testing machine was set inclined so that the components of the machine did not obstruct the diffraction beam paths to the OPs. However, the tensile coupon was set so that the ND was parallel to X_D, the incident beam direction.

The deformation test was conducted with a constant crosshead speed of 0.03 mm/min without stopping the deformation. The neutron scattering data at every OP was constantly acquired during the test. The acquired neutron diffraction data was divided into an 1800 s acquisition time increment, which corresponded to a true strain increment of approximately 0.02–0.025. Note that the test was interrupted before breaking point due to limitations of the testing machine at that time.

2.3. Analysis

The neutron diffraction data was analyzed using MAUD software (version 2.9.3), based on the method called Rietveld texture analysis (RTA) [9,10,11,12,13]. The analysis comprises the simultaneous and interactive refinement of textures and diffraction patterns fitting, which can quantitatively determine the phase fractions of γ austenite and α′ or ε martensite. The result of the texture analysis is reported in a separate paper.

Herein, the macroscopic stress correction was conducted. The “moment pole stress” model was applied for the γ austenite and α′ martensite phases, to fit the peak shifts due to the external stress. This model calculates the bulk elastic modulus from the single crystalline stiffness, considering the texture of the sample. In this study, we used the weighted Hill’s model to connect the bulk and single crystalline elastic modulus. As it is well known, the original Hill’s (or Voigt–Reuss–Hill) model calculates the bulk elastic compliance as an arithmetic mean of the Voigt and Reuss values. On the one hand, the weighted Hill’s model calculates the weighted average of them [14]. The weight is called “Voigt–Reuss ratio” in MAUD, which can be refined as one of the parameters in RTA.

The elastic stiffness values used in this study were: C₁₁ = 209 GPa, C₁₂ = 133 GPa, and C₄₄ = 121 GPa for the γ phase [15], and C₁₁ = 230 GPa, C₁₂ = 135 GPa, and C₄₄ = 117 GPa for the α′ phase [16]. For the ε phase, it was not possible to apply the same method since the corresponding elastic stiffness values were not available. The “real” lattice parameters for this phase were also difficult to determine, because the ε phase appeared during loading with relatively strong texture. Hence, the isotropic elastic model was applied for the ε phase.

To evaluate the line broadening of the diffraction peak, we applied the “Popa rules” [17] model to the MAUD software [12]. This is actually equivalent to the line broadening treatment on the modified Williamson–Hall method suggested by Ungár et al. [18]. For a better understanding of this model, we will describe its basic theory.

The simplest model for the line profile analysis was proposed by Williamson and Hall [19], which is

$$\Delta K=\langle \epsilon \rangle K+A/D$$

(1)

where K = 2sinθ/λ, $\Delta K$ is the peak breath, D is the crystallite size, $\langle \epsilon \rangle$ is the root-square-mean microstrain, and A is a constant that can vary depending on how the peak breaths are evaluated. However, due to the anisotropic features of the crystal and dislocation, a perfect linear relationship between K and ΔK was merely observed. Hence, an advanced treatment was suggested as the modified Williamson–Hall (mWH) method [18,20], expressed as follows:

$$\Delta K=\mathrm{O}{\left(K\sqrt{C}\right)}^2+\mathsf{\phi }K\sqrt{C}+1/D.$$

(2)

The notable feature in the above equation was the introduction of the contrast factor, C. The first squared term, $\mathrm{O}{\left(K\sqrt{C}\right)}^2,$ is negligibly small. C is defined as follows:

$$C=C_{h00}\frac{1}{{\left(h^2+k^2+l^2\right)}^2}\left\{\left(h^4+k^4+l^4\right)+\left(2-q\right)\left(h^2{k}^2+k^2{l}^2+l^2{h}^2\right)\right\},$$

(3)

where C_h00 is a constant and q is the factor related to the ratio of screw and edge dislocations. In Equation (2), φ can be found as the slope when plotting $\Delta K$ against $K\sqrt{C}$.

On the other hand, Popa proposed a similar model to fit the anisotropic line broadening in the Rietveld analysis [17]. This model suggests the variation of $\langle \epsilon \rangle$ in Equation (1) depending on hkl. For a cubic crystal, the following derives:

$$\langle {\epsilon }_{hkl}^2\rangle =\frac{1}{{\left(h^2+k^2+l^2\right)}^2}\left\{e_0^2\left(h^4+k^4+l^4\right)+2\frac{e_1}{\left|e_1\right|}{e}_1^2\left(h^2{k}^2+k^2{l}^2+l^2{h}^2\right)\right\},\langle {\epsilon }_{hkl}\rangle =\sqrt{\langle {\epsilon }_{hkl}^2\rangle },$$

(4)

where coefficients e₀ and e₁ are refined parameters in the Rietveld analysis. Note that Equation (4) was slightly modified from Popa’s original equation in order to be implemented in MAUD software. Since Equations (3) and (4) are essentially identical, it follows

$${\mathsf{\phi }}^2{C}_{h00}=e_0^2,{\mathsf{\phi }}^2{C}_{h00}\left(2-q\right)=\frac{e_1}{\left|e_1\right|}{e}_1^2.$$

(5)

Even if not calculated in this study, Equation (5) may enable to determine the quantitative ratio of screw and edge dislocations by RTA. Herein, the development of $\langle {\epsilon }_{100}\rangle$, $\langle {\epsilon }_{110}\rangle$, and $\langle {\epsilon }_{111}\rangle$ was separately determined.

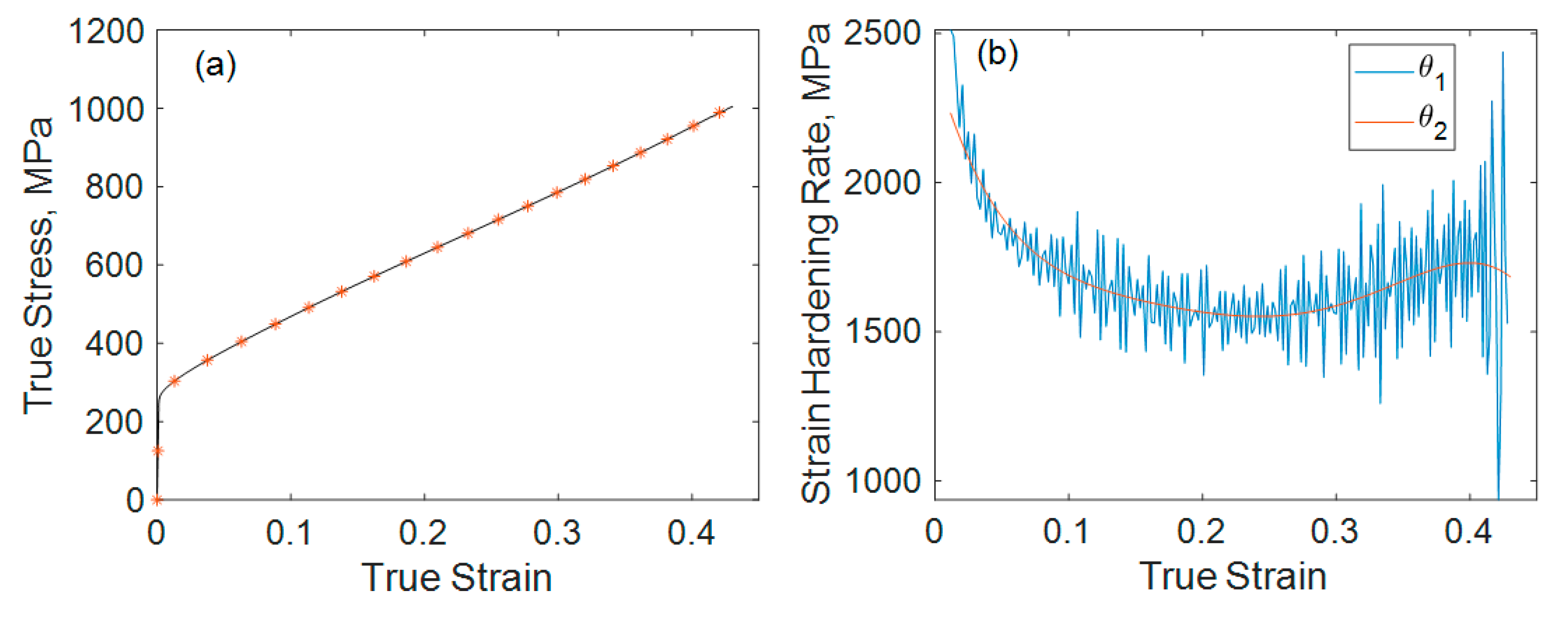
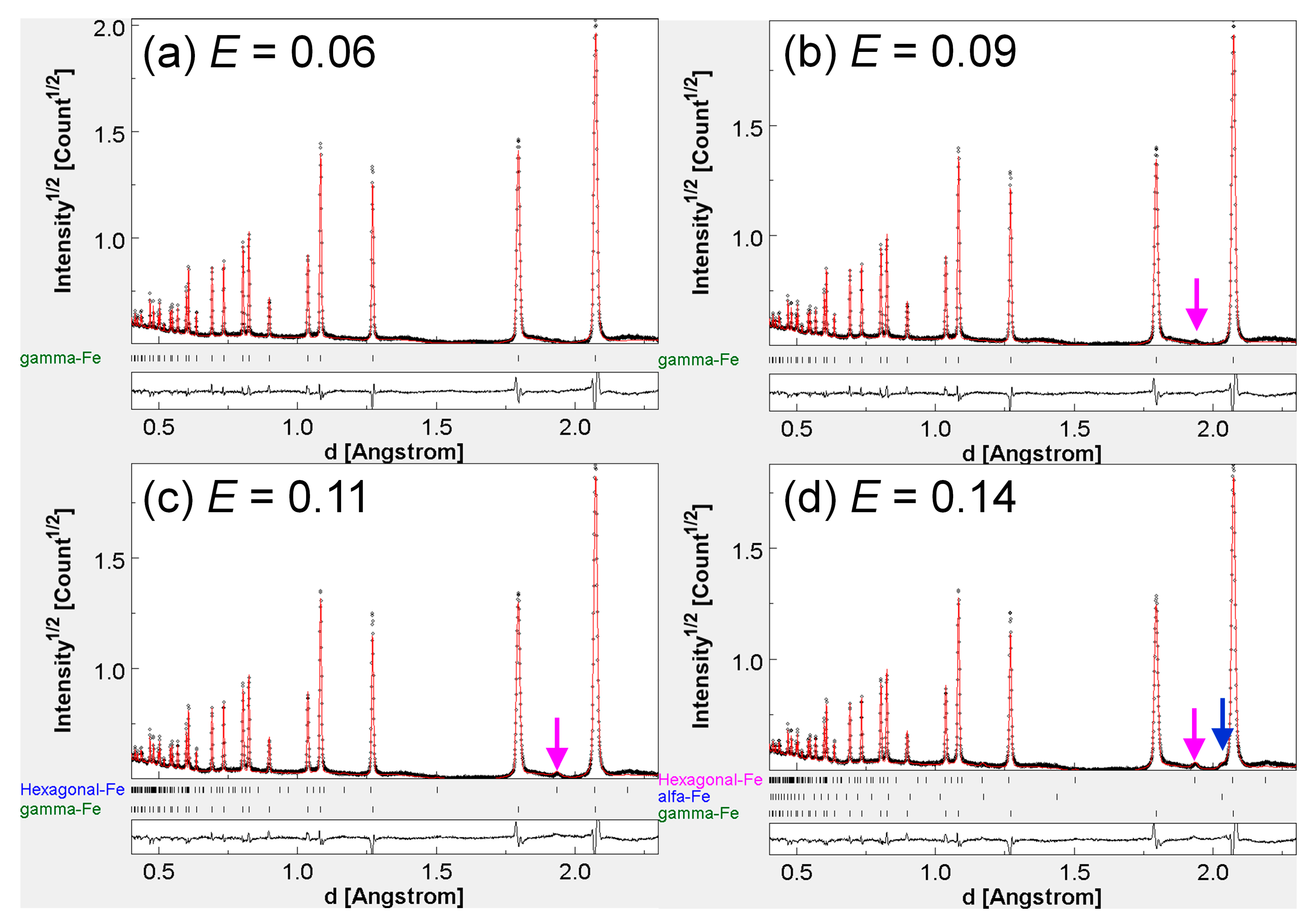
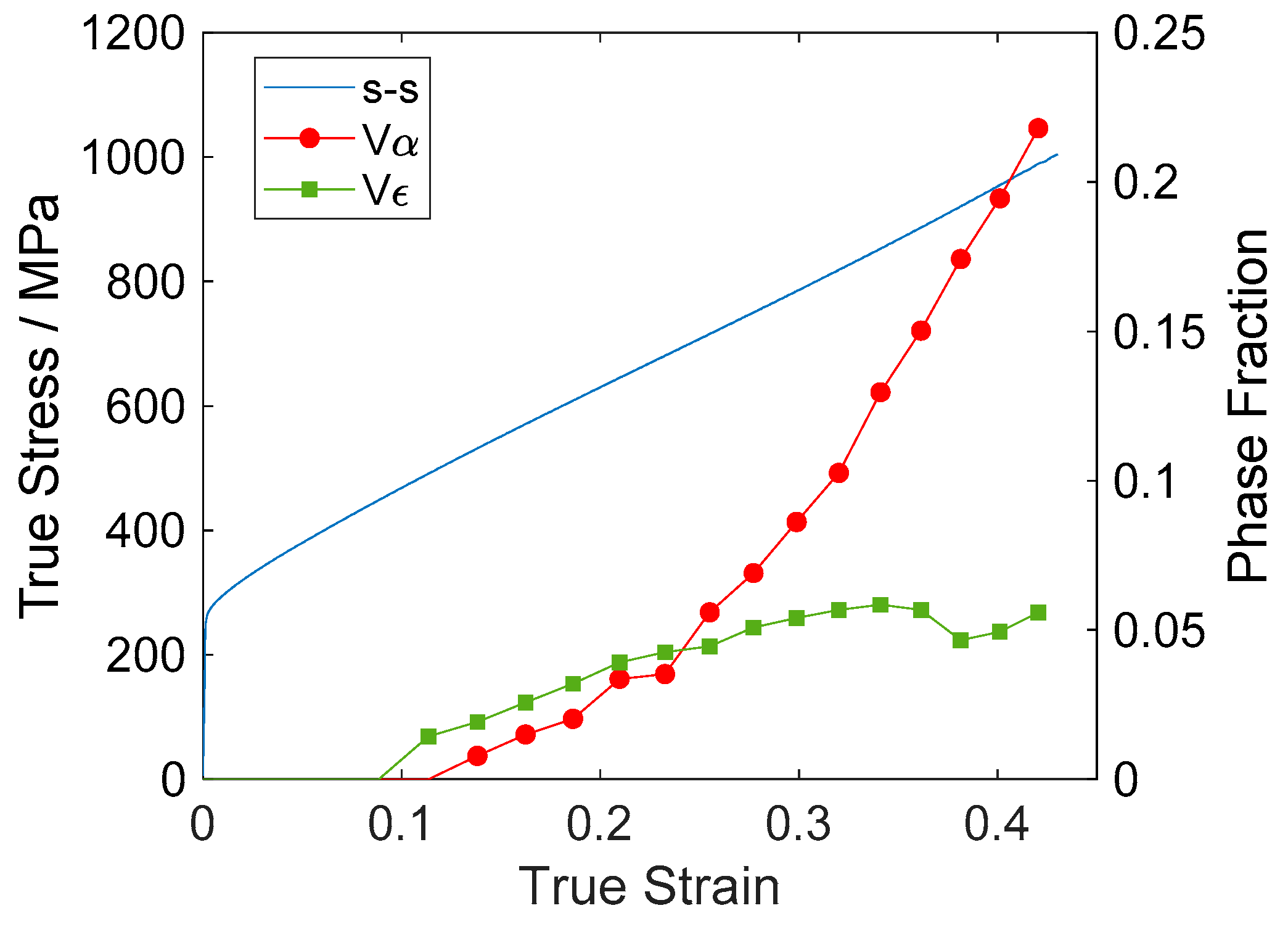
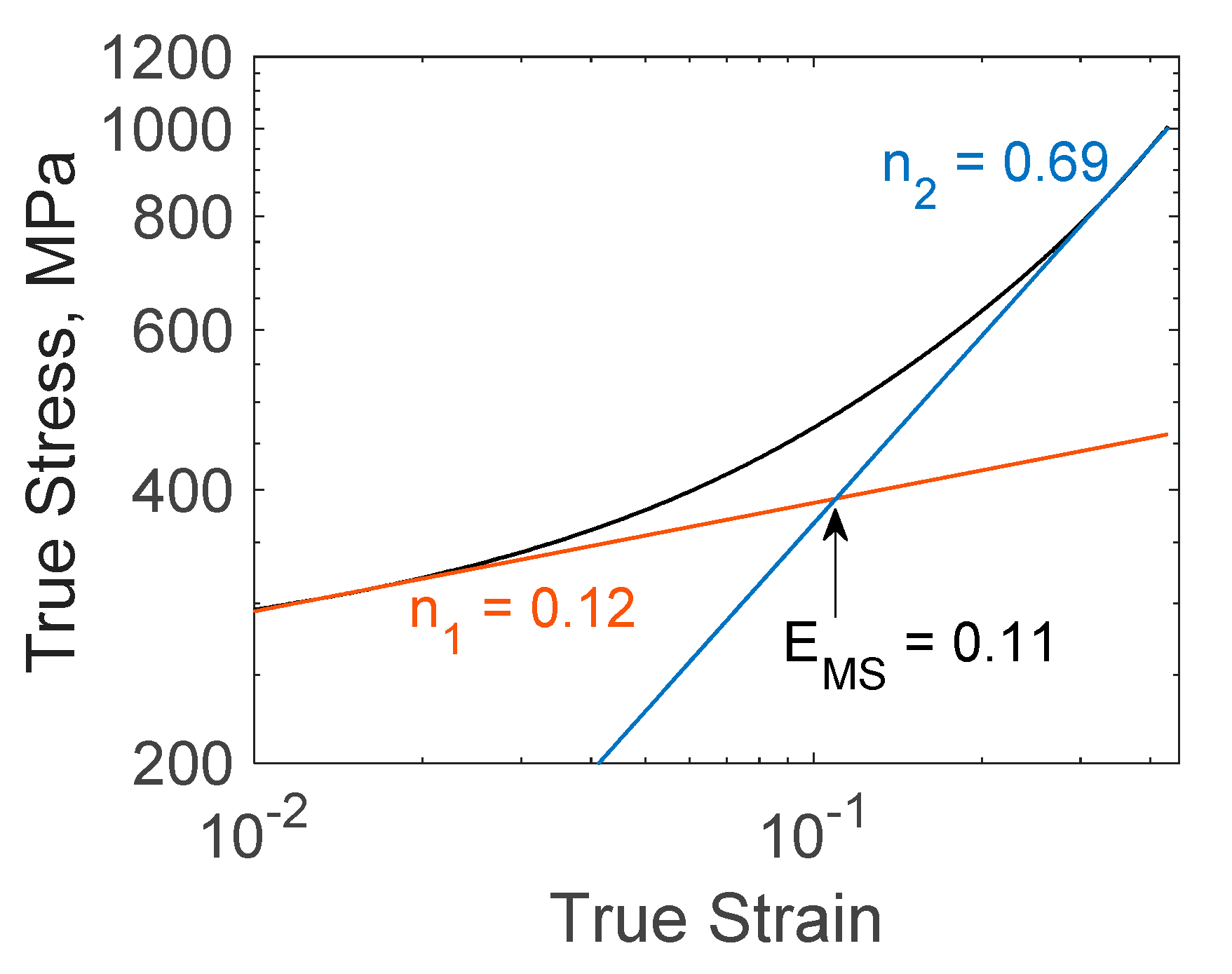
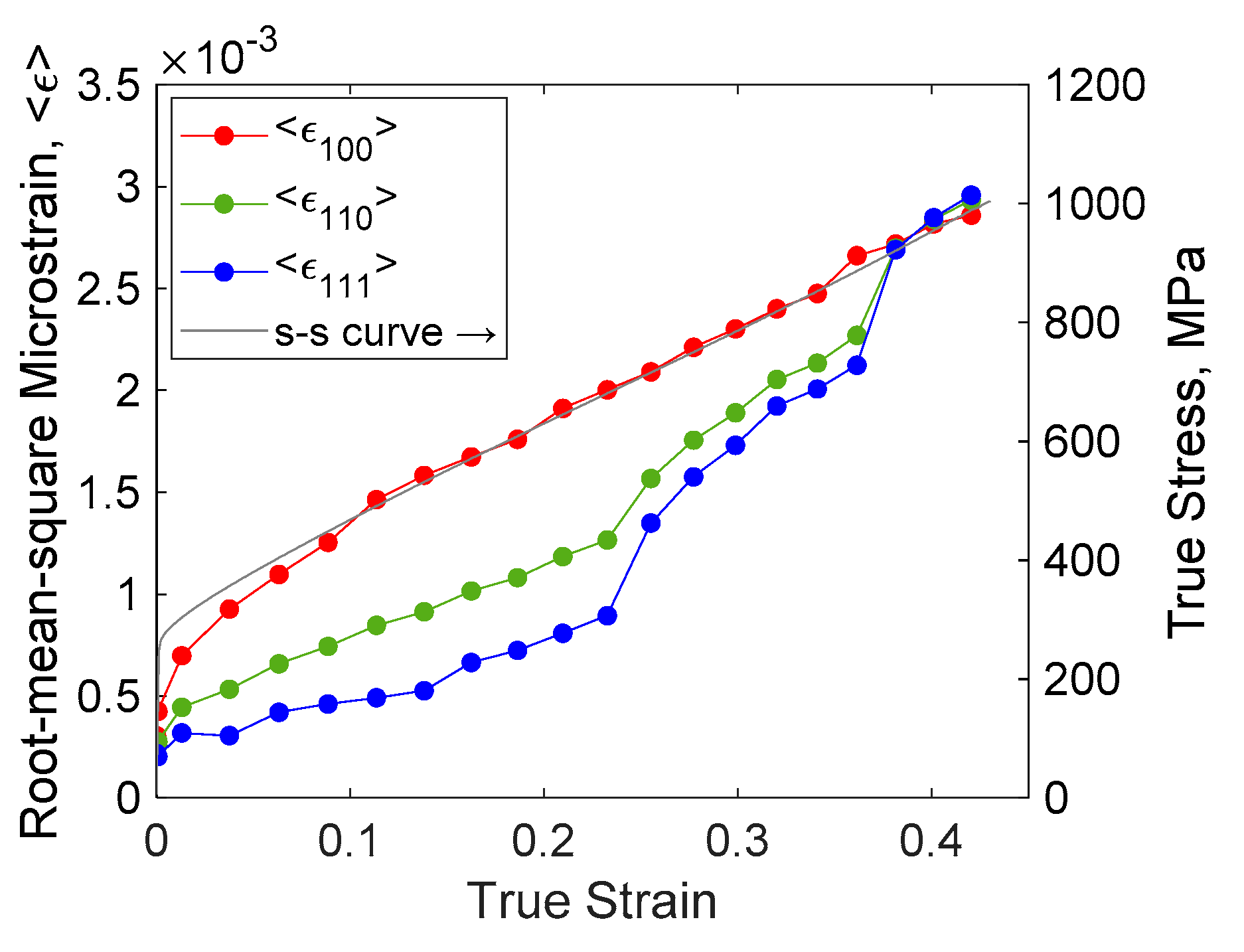
3. Results

From the true stress–true strain curve (Figure 3a), a stable, mostly, monotonic strain hardening was observed, as frequently reported in the literature [1]. The strain hardening rate (θ) was calculated as θ = dσ/dΕ, as shown in Figure 3b. In this study, Ε represents the macroscopic true strain to distinguish it from the microstrain $(\langle \epsilon \rangle )$, and the ε (HCP) martensite. We calculated θ = dσ/dΕ in the following two ways: (1) a simple calculation from stress and strain increments, Δσ and ΔΕ, observed during a certain period (θ₁) and (2) analytical derivation of the fitting curve for σ(Ε) using a 6th-order polynomial function (θ₂). The latter gives a smooth curve, which has its minimum at a true strain of 0.24.

Figure 4 shows the diffraction patterns around the onset point of DIMT. First, 110ε peaks appeared at E = 0.09. However, the peak was too small to conduct quantitative fitting. At E = 0.11, the fitting for ε was possible, and we calculated a 1.4 vol% fraction, which was the lowest limit of detection in the current analysis. Hence, a small amount of ε-martensite might be formed at an earlier stage of deformation. In contrast, the onset of α′ martensite formation at E = 0.14 was a little more evident; in this case, due to the high crystal symmetry of α′ martensite, the lowest detection limit was 0.7 vol%.

Figure 5 illustrates the increase in the volume fractions of α′ and ε martensite, Vα and Vε, with increasing strain. Note that the analyzed phase fractions might have larger errors than the analytically determined standard uncertainties, which were quite small. In both the qualitative (experimentally observed) and the quantitative (computer-based) analyses, the minor phase detection corresponds to distinguishing the diffraction peak from background fluctuation. When a background pattern has a large fluctuation, small diffraction peaks are difficult to be found. Even if the diffraction peaks are high enough to be observed, the background uncertainty directly relates to the uncertainty of the estimated diffraction intensity; i.e., the phase fraction. Hence, the authors estimate the error or uncertainty of the phase fraction analysis to be almost equal to the lowest detection limit, which was around 1–2%.

4. Discussion

4.1. Analysis of Stress–Strain Curve

Miura et al. suggested a method to determine the strain Ε_MS at which DIMT may start, when fitting the true stress–true strain curve [21]. Considering that their deformation test was conducted at 77 K, the sigmoidal, two-step hardening behavior was evident. Hence, they fitted the low strain (without DIMT) and high strain (with DIMT) regions using the well-known relationship, σ = KΕⁿ. The coefficient n for each of the two regions was n₁ and n₂, respectively. This approach was adopted to analyze our results, as shown in Figure 6. Since the current deformation test was conducted at room temperature, the transition from σ = K₁Εⁿ¹ to σ = K₂Εⁿ² was unclear. However, the cross point of the two fitting curves was Ε_MS = 0.11. This is in good agreement with the strain value where the ε and α′ martensite first appear on the neutron diffraction pattern (Figure 5). Hence, the approach seemed to be valid to describe the stress–strain behavior with DIMT. However, this does not correspond to the point of the acceleration of the strain hardening, E = 0.24, shown in Figure 3b. This is rather related to the strain where the n₂ curve starts fitting exactly the experimental stress–strain curve.

4.2. Dislocation Hardening

Since the fitting using σ = KΕⁿ was a phenomenological approach, the microscopic hardening mechanism should be discussed from a different approach. In this section, the degree of dislocation hardening is considered. Dislocation hardening is often modeled using the Bailey–Hirsch equation, $\Delta {\mathsf{\sigma }}_{disl}=M\alpha \mu b\sqrt{\rho }$, where α is a constant, M is the Taylor factor, μ is the shear modulus, b is the length of Burgers vector, and ρ is the dislocation density. As previously stated, $\langle \epsilon \rangle$ (or $\mathsf{\phi }$ in the mWH description) is proportional to $\sqrt{\rho }$, so $\Delta {\mathsf{\sigma }}_{disl}\propto \langle \epsilon \rangle$. In Figure 7, the development curves of $\langle {\epsilon }_{100}\rangle$, $\langle {\epsilon }_{110}\rangle$, and $\langle {\epsilon }_{111}\rangle$ for austenite as a function of true strain are shown. It is known that austenitic stainless steel has a large elastic anisotropy [15]. Hence, it is accepted that the softest direction <100> exhibits a large scatter of lattice plane displacement (i.e., microstrain); <111> is the hardest and <110> is an intermediate direction.

As indicated by Equation (3) and Equation (5), $\langle {\epsilon }_{100}\rangle$ is a function of $e_0=\phi \sqrt{C_{h00}}$ that is not affected by $e_1$. Hence, we can observe that $\langle {\epsilon }_{100}\rangle \propto \phi \propto \sqrt{\rho }$. The good correspondence between $\langle {\epsilon }_{100}\rangle$ and the true stress–true strain curve in Figure 7 indicates that the hardening behavior can be described by dislocation hardening in austenite.

Therefore, the strengthening by DIMT was not due to the existence of plastically hard martensite particles, but due to the enhancement of dislocation hardening. In other words, austenite was as strong as deformation-induced martensite, at any stage of deformation. In contrast, for the so-called low-alloy TRIP steels, martensite formed by DIMT is much stronger than the preexisting phases, and in fact, the one causing strain hardening [22]. The mechanisms of the TRIP effects in the two kinds of steels should be considered separately.

At the true strain of approximately 0.24, the increases of $\langle {\epsilon }_{110}\rangle$ and $\langle {\epsilon }_{111}\rangle$ were accelerated. A true strain of 0.24 was the point where the strain-hardening rate started to increase, as shown in Figure 3b. In addition, this was approximately the start point where the n₂ curve in Figure 6 fitted the s–s curve as well. The increase for α′ martensite was also accelerated around E = 0.24.

The acceleration effect was observed for $\langle {\epsilon }_{110}\rangle$ and $\langle {\epsilon }_{111}\rangle$, but not for $\langle {\epsilon }_{100}\rangle$. This was due to the increase of the coefficient e₁ in Equation (4). According to Equation (5), this corresponds to the decrease in q; i.e., an increase in the ratio of edge dislocations to the screw ones. Although further microstructural studies are needed, this may explain why the dislocation hardening was not exhausted even at large strains. Since the edge dislocation cannot experience cross slipping, this has less opportunity for recovery compared to that of screw dislocations.

4.3. Chemical Stability of Austenite

The stability of austenite against DIMT is frequently expressed by the factor Md₃₀. The most used equation to calculate Md₃₀ was suggested by Nohara et al. [23]. Using the composition presented in Table 1, Md₃₀ resulted to be 277 K. Masumura et al. recently revised this equation and suggested an alternative equation, when separating the roles of C and N [24]. According to their equation, the calculated Md₃₀ was 303 K. Since their equation did not include the effect of Cu, we considered it by applying the coefficient suggested by Nohara et al. Then we obtained 297 K. As seen in Figure 5, at a true strain of 0.31, volume fractions of α′ and ε martensite were 6.9% and 5.1%, respectively. Therefore, Md₃₀, the temperature where 50% volume fraction of α′ is achieved at a true strain of 0.3, should be much lower than the test temperature, 300 K. Hence, the evaluated case happened to be away from the Masumura’s equation. As pointed out by them, the validity of the combining effects of all the variables into a simple equation must be carefully revised.

The study addressed the 18Cr-8Ni steels containing only C or N. The effect of adding N was coupled with the effect of adding C. However, they also reported that N- and C-added 18Cr-8Ni steels led to different morphologies of martensite [4,24]. According to these studies, C-added steels showed a γ→ε→α′ DIMT route, but the N-added steel exhibited γ→α′. Hence, when the steel contains both C and N, the analysis would be more complex. Additionally, Masumura et al. omitted the effect of the average grain size on Md₃₀. Tiamiyu et al. reported that the grain size seems to be a factor to determine if γ→ε→α′ DIMT occurs and the fraction of α′ martensite that may be obtained at a certain strain [8].

Although Nohara’s equation resulted in a more feasible value, Md₃₀ = 277 K, there is no scientific reason to conclude this is more valid. Since the current sample has a similar composition to that used by Nohara et al., their phenomenological equation led to a suitable prediction. To obtain a better prediction for DIMT in austenitic steels, further studies will be necessary on the conditions and the mechanism of the γ→ε→α′ type DIMT.

5. Conclusions

In situ Time-Of-Flight type neutron diffraction during the tensile test of 304 stainless steel (18Cr-8Ni) was conducted to observe the deformation-induced martensite transformation (DIMT). As the strain increased, the ε (HCP) martensite first appeared followed by α′ martensite formation at the true strain of 0.11. This strain corresponded to the transition of the strain hardening state without DIMT to the state with DIMT. However, the transient region corresponded to a true strain approximately in the range of 0.02–0.2. A clear acceleration of strain hardening was confirmed, at a true strain of 0.24; this also leaded to accelerate the increase in α′ martensite fraction. Together, the increase of microstrain along <111> and <110> accelerated. The mechanical behavior of this metastable austenitic steel was mainly governed by dislocation structure in the austenite phase. The deformation-induced martensite may play a specific role in the development of dislocation structure in austenite, rather than supporting large stress as the hard particles in the tested steels.