1. Introduction
For more than a decade, medium and high manganese steels have been the focus of innovative steel development due to its light weight, high strength, outstanding formability and energy absorption ability. It has been widely accepted that, due to its low-stacking fault energy, twinning is an effective means of deformation in high manganese austenitic steel, called twinning-induced plasticity (TWIP) steel. This has been supported by transmission electron microscopy and electron backscatter diffraction (EBSD), wherein it has been demonstrated that the volume fraction of twins increases concomitantly with plastic deformation [
1]. Specifically, one variant of the {111} <112> twin system is activated within grains at the early stages of plastic deformation, followed by the nucleation of twins that are different variants of the {111} <112> twin system between the boundaries of the first set of twins, leading to a ladder-like structure [
2]. Recent work by Barbier et al. [
3] employed texture component analysis to explore the fraction of dislocation slip and deformation twinning during plastic deformation. However, the combination of various conventional surface microstructure analysis methods are limited in their provision of bulk information, particularly in terms of the evolving dislocation density, bulk texture, local strain, stacking faults and deformation mechanisms that operate in the total volume of a tested material.
When low-stacking fault materials are deformed, the possible deformation mechanisms (e.g., dislocation slip, mechanical twinning and phase transformation) closely interact and compete with one another [
4,
5,
6]. The potential of each mechanism is determined by the stacking fault energy (SFE), which is controlled by the chemical composition of the material [
7]. The twinning effect is activated at a low SFE (between 12 and 35 mJ /m
2) [
8], which is inherent in these materials. As deformation proceeds, twins nucleate and grow in the core of large grains and move to the next strong obstacle, such as grain boundaries or twin boundaries. Subsequently, twins become thicker, more closely spaced and longer as the applied stress increases, and it is believed that dislocation movement interacts with—and is hindered and obstructed by—mechanical twinning [
6]. Consequently, higher stress is needed for new twins to form [
9], which generates a rise in the work hardening rate, thereby enhancing the strength and increasing ductility [
2].
Despite the well-received theory of twinning-induced plasticity in low-stacking fault materials, particularly during tensile deformation, the activity of twinning is actually suppressed in compression. As one of the main potential applications for TWIP steel is within the automobile industry, automobile manufacturers require not only a material that can maintain its mechanical properties under quasi-static loading conditions, but also under dynamic loading conditions. The question as to how TWIP steel responds to dynamic loading during a collision has become a key issue in design and material optimization. In addition to microstructure features, such as grain size, defect density and phase morphology, which determine the mechanical and physical properties of most metallic materials, grain orientation distribution (texture) is also an important consideration and may well have a definitive influence on the application of TWIP steels in the automotive industry.
Texture is a collective term for non-uniform distributions of crystallographic orientations in polycrystalline aggregates. In metallic materials processing, texture ‘components’ and ‘fibres’ are often used to represent the simplified orientation distribution. Texture components are a superposition of a small number of single crystals, with some spread (which may be quantified by Gaussian processes). Others can be idealized as fibres in orientation space, in which a single angle can be used to specify an orientation within the fibre. Through Euler angles, a certain crystallographic plane,
hkl, and direction,
uvw, can be transformed to align with sample coordinates. For face-centred-cubic (
fcc) materials, the brass component has the {110} plane parallel to the deformation plane (N) and the <112> direction parallel to the deformation direction (L), which is noted as {110} <112>. Other typical texture components, like Goss ({110} <100>), cube ({001} <100>), and copper ({112} <111>), are usually used to demonstrate the texture types after plastic deformation. In addition, these typical texture components provide information of deformation mechanisms for materials that contain different stacking fault energy, alloy elements and/or deform at different temperature and strain rates. The influence of strain rate on texture has been extensively investigated by other researchers [
10,
11]. It is well accepted that at low strain rate or at the early stage of plastic deformation, initial texture is significantly reduced, while at higher strain rates plastic deformation texture components develop and the grains elongate along the loading direction. Moreover, grain boundary sliding and shear bands are accepted as deformation mechanisms during high strain rate deformation [
12]. For microstructural evolution during high strain rate deformation, three stages for obtaining an ultra-fine grain size structure may be described: (i) Elongated cells and subgrains form, generating an increase in misorientations between neighbouring grains, and thus breakup of elongated grains into smaller units occurs; (ii) these subgrains are then rotated by grain boundary rotation; and, finally, (iii) an equiaxed structure forms. Although these previous studies have supplied information of materials’ microstructure, including texture evolution during high strain rate deformation, only a few studies have focused on
fcc-structured materials with low-stacking fault energy, which may introduce martensitic phase transformation and mechanical twinning under extreme loading conditions.
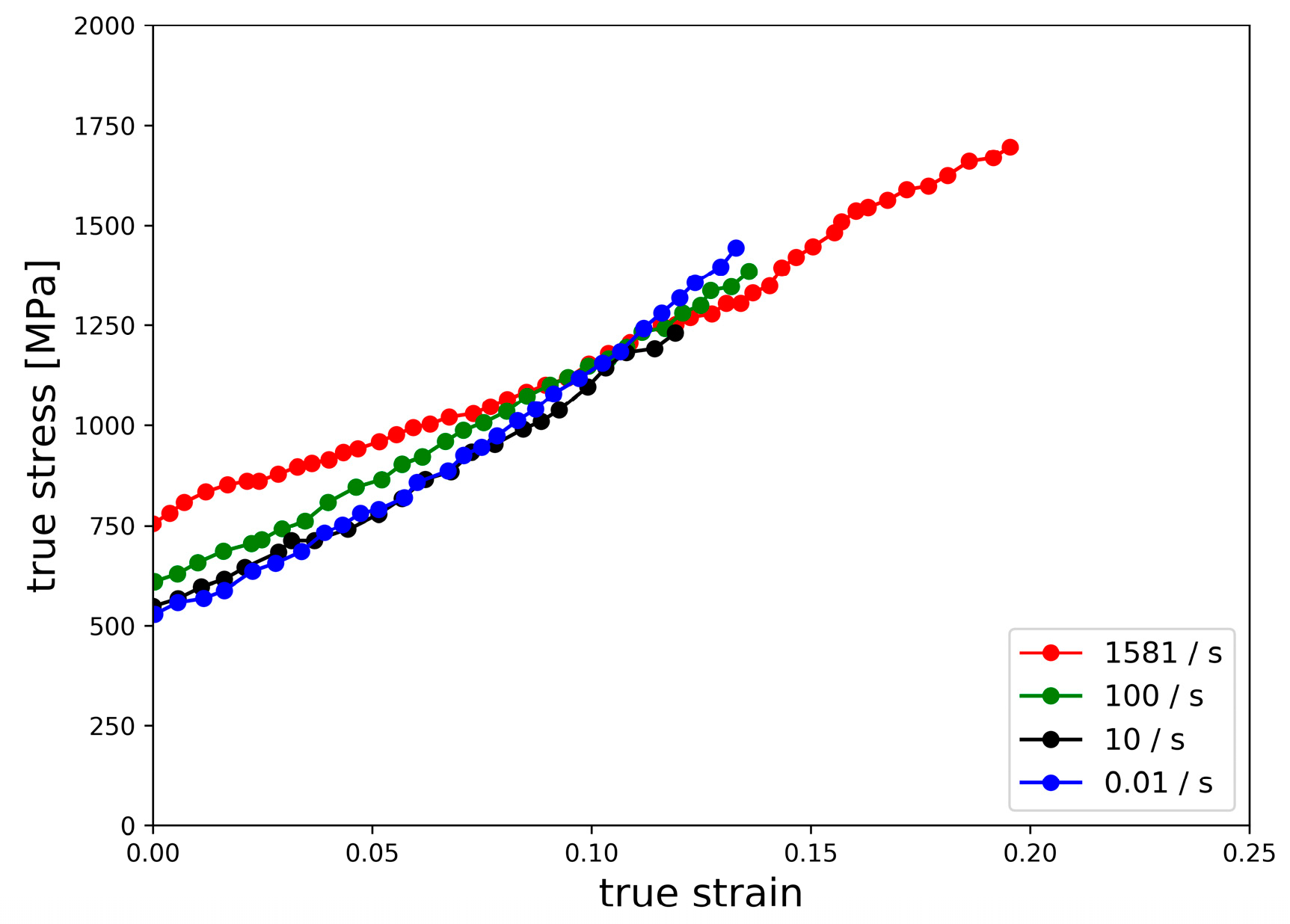
In a similar manner to strain-induced martensitic transformation (SIMT), the formation of twinning is also diffusionless. It is speculated that twinning activity should be irrelevant to deformation rate at room temperature. However, with a higher strain rate, improved ductility may be observed in comparison to the same materials deformed under a lower straining rate. In this context, the deformation mechanisms of TWIP steel (Fe-18Mn-0.6C-1.5Al), compressed with various strain rates ranging from 0.01/s to 1581/s, were investigated using microstructural analysis and texture component analysis.
2. Materials and Methods
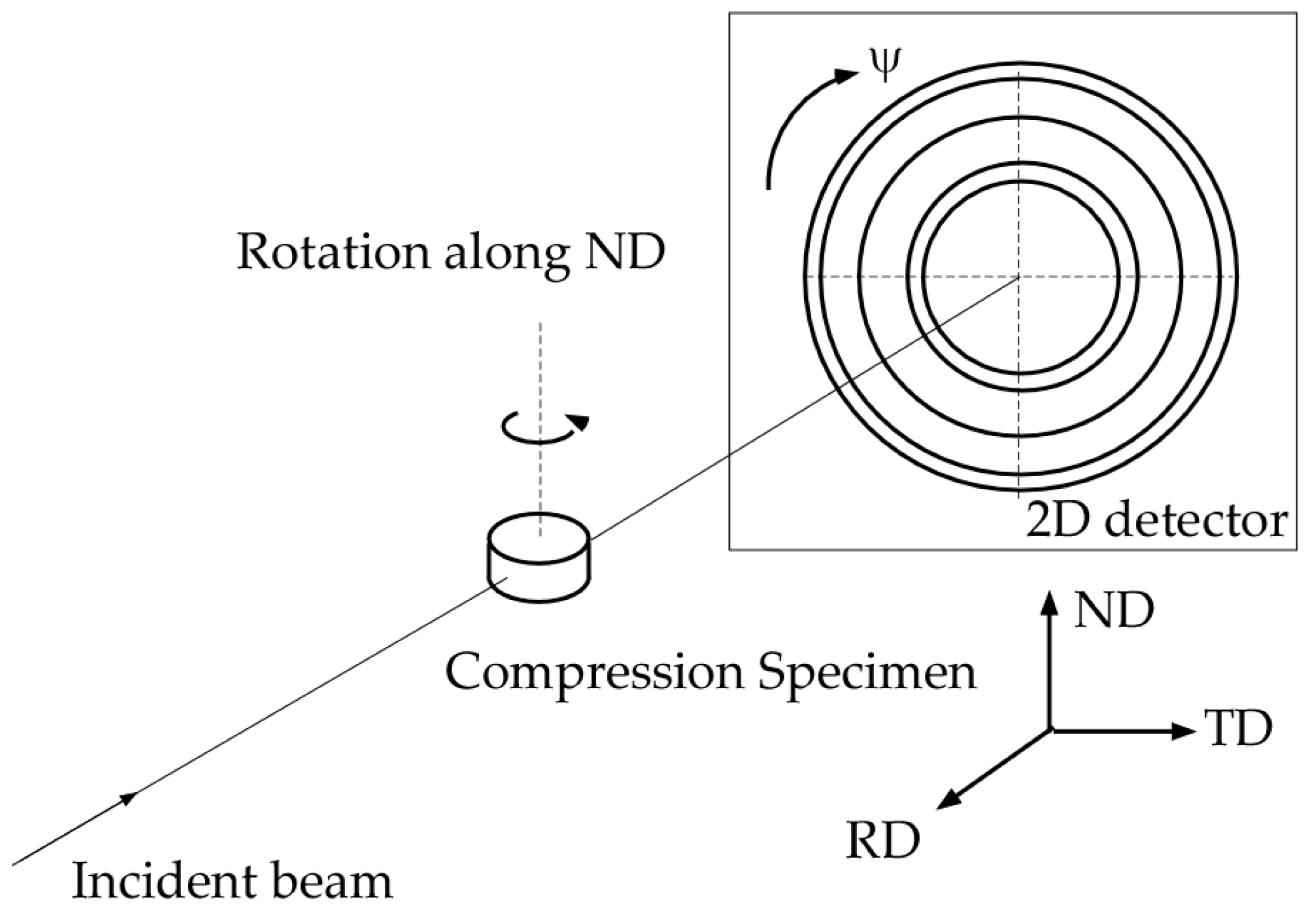
Cylindrical specimens 5 mm in diameter and 2.5 mm in thickness were extracted from a rolled plate for compression tests, further texture measurement and microstructural analyses. Four specimens were compressed at different strain rates. One specimen was compressed using a split-Hopkinson pressure bar (SHPB) test at a strain rate of 1581/s to a total strain of ~20%; three other specimens were compressed using a Gleeble 3500 thermo-mechanical simulator at strain rates of 0.01/s, 10/s and 100/s to a total strain of ~15%. All specimens were compressed along the normal direction (ND) of the steel sheet via both SHPB and Gleeble 3500 instruments.
The texture measurements were conducted by high-energy X-ray diffraction [
13] at the beamline ID15B of the European Synchrotron Radiation Facility (ESRF). The size of the incident X-ray beam was 0.3 × 0.3 mm at an X-ray energy of 89.70 keV. A two-dimensional detector was used for collecting the Debye–Scherrer diffraction data. Details of the experimental setup and the raw materials are identical to those of Reference [
14]. As shown in
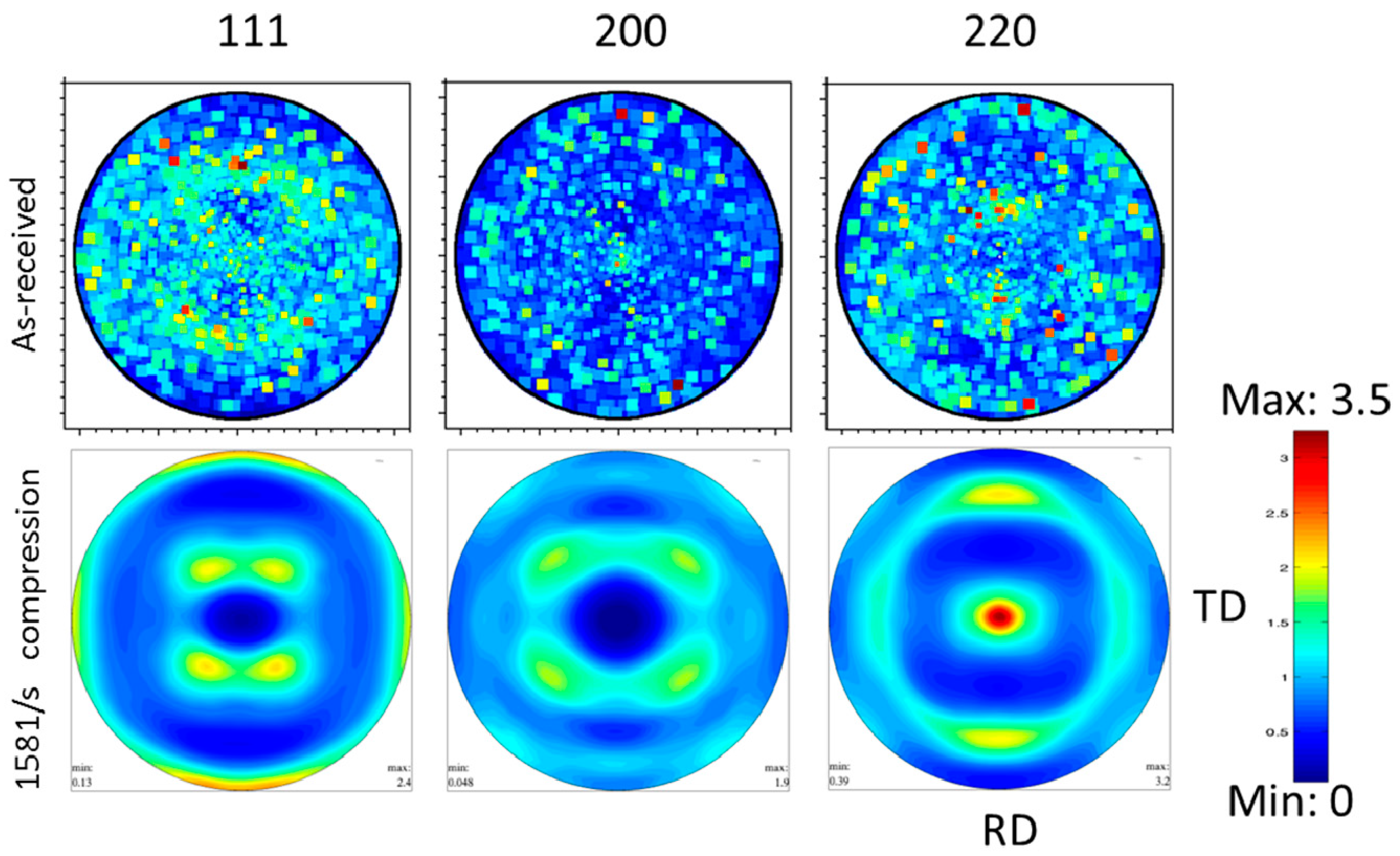
Figure 1, the incident beam was aligned perpendicular to the plane composed by the rolling direction (RD) and transverse direction (TD), in accordance with the rolled plate. The specimen was then rotated around its axial axis from 0° to 360° with steps of 2.5°. Pole figures for reflections 111, 200, 220 and 311 were calculated from radically integral intensity distributions along the azimuthal angel ψ. An Mtex/Matlab program [
15] was employed to calculate the orientation distribution function (ODF) and the selected section of the ODF was plotted accordingly.
After deformation and texture measurements by synchrotron radiation X-ray diffraction, all specimens were mechanically ground and polished in accordance with standard procedures for steels and etched with 2.5% Nital. Microstructural characterization was conducted using a Leica DMR optical microscope and a JEOL JSM-6490 scanning electron microscope (SEM).
4. Discussion
Before further discussions, it is worth clarifying the terms low, medium and high strain rate deformation conditions. As is described in Reference [
17], at strain rates of the order 10
−6 to 10
−5/s, the creep behaviour of the material is the primary consideration and creep laws are used to describe the mechanical behaviour. At higher rates, e.g., in the range of 0.0001/s to 0.01/s, a uniaxial test or a quasi-static stress–strain curve obtained from a constant strain rate test is used to describe the material behaviour. In this region, the mechanical response of the material may change, and alternate testing techniques may have to be used. The range of strain rates from 0.1/s to 100/s is generally referred to as an intermediate or medium strain rate regime. Within this regime, strain rate effects become a consideration in most materials, although the magnitude of such effects may be quite small. Strain rates of 1000/s or more are generally treated as high strain rate responses. It is within the high strain rate range that inertia and wave propagation effects become important in interpreting experimental data. At these high rates of strain, care must be taken to distinguish between average and local values of stress, which may be the result of one or more high-intensity stress waves propagating through the material.
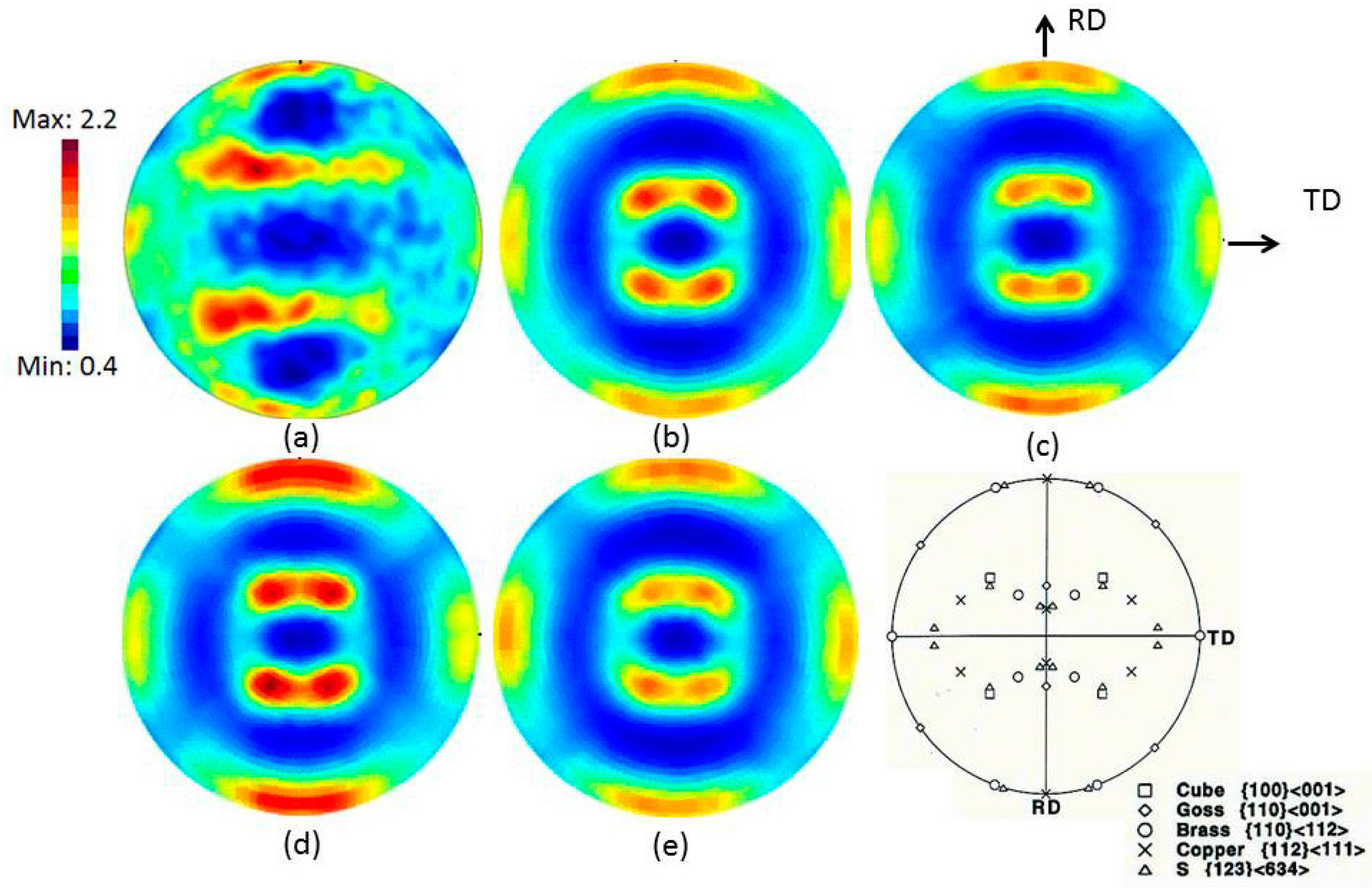
When researchers have correlated texture and microscopy results with the compressive deformation mechanisms of TWIP steel, they have reported that different deformation mechanisms are activated to accommodate the speed of external loading. Jia et al. [
12] reported that for materials with low to medium stacking fault energy, shear bands play an important role during high strain rate plastic deformation. This conclusion was based on the observation of shear bands in 304L stainless steel specimens, which were compressed to ~54% strain at a high strain rate of 10000/s by SHPB testing. No shear band structure was observed in the deformed TWIP steel specimens in the current work, hence, it is inappropriate to include shear bands as a third deformation mechanism. As such, only the two deformation mechanisms of mechanical twinning and dislocation slip were considered. Furthermore, Jia et al. [
12] found that the texture intensity difference in SHPB-deformed specimen and “quasi-static” deformed specimen was attributed to the roll of shear bands. However, there were no observations of shear band structures, nor significant texture intensity differences found between the SHPB deformed specimen and the quasi-static deformed specimens in the current study. As previously detailed, only dislocation slip and mechanical twinning were considered here as deformation mechanisms of TWIP steel. Meng et al. [
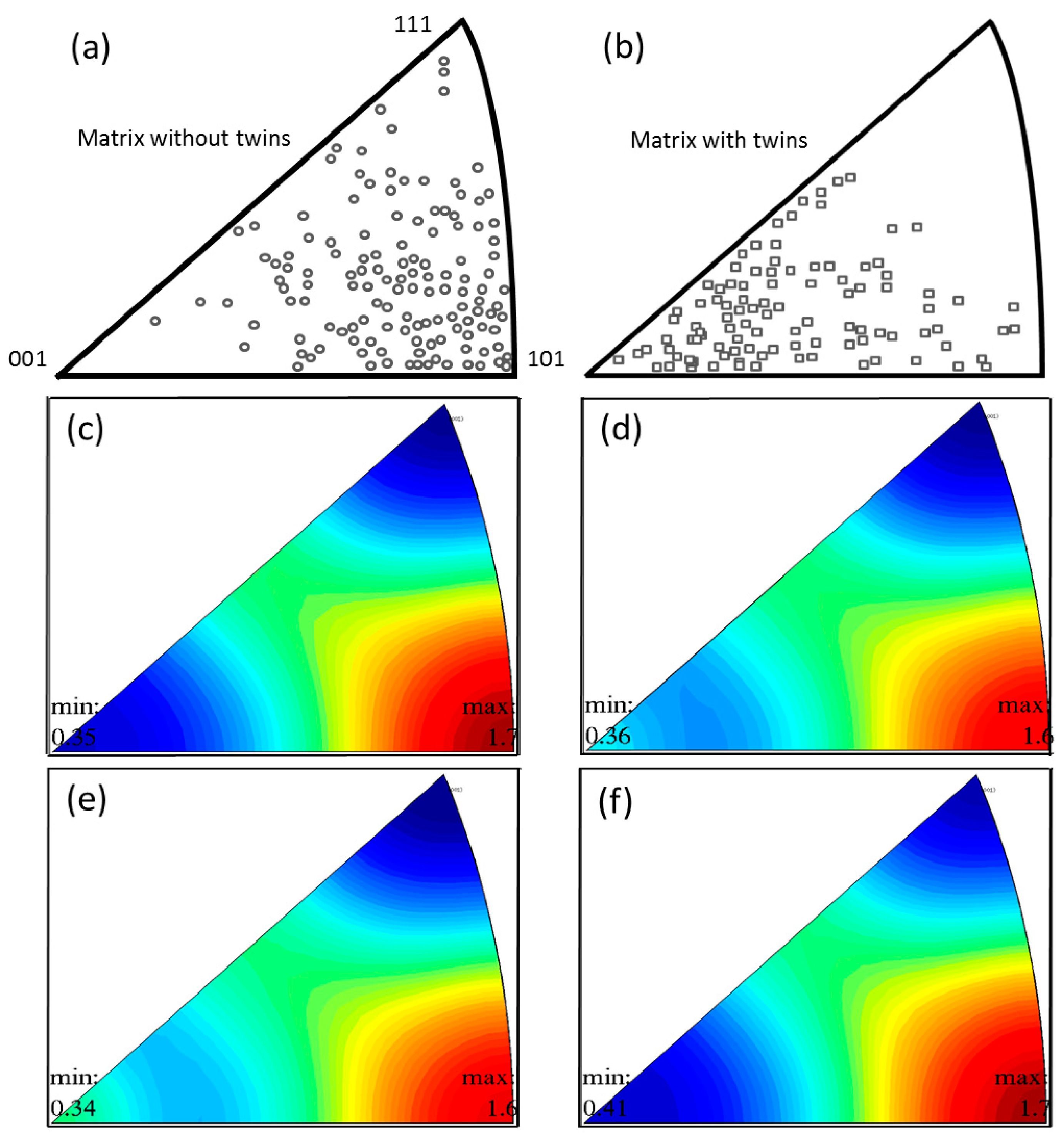
18] reported the grain orientation distribution of TWIP steels after various levels of final compressive strain. In Meng’s study, with detailed mapping using electron backscatter diffraction, grains with and without twin structure were extracted from full scan mapping. As shown in
Figure 7a,b, twinning mainly occurred in the <001>-oriented grains, rather than the <101>-oriented grains. In comparison, <101>-oriented grains tended to slip as the preferred deformation mechanism. In addition, there was reasonable overlap between the <001> and <111> orientation, which could be explained by grain rotation (i.e., <001> to <101> due to slip). For similar levels of final compressive strain but different strain rates, and using the same method, we found that all the compression samples showed high intensity for <101>-oriented grains along the loading direction. However, more <001>-oriented grains were found in 100/s and 10/s compressed samples (
Figure 7d,e), indicating a higher level of twinning.
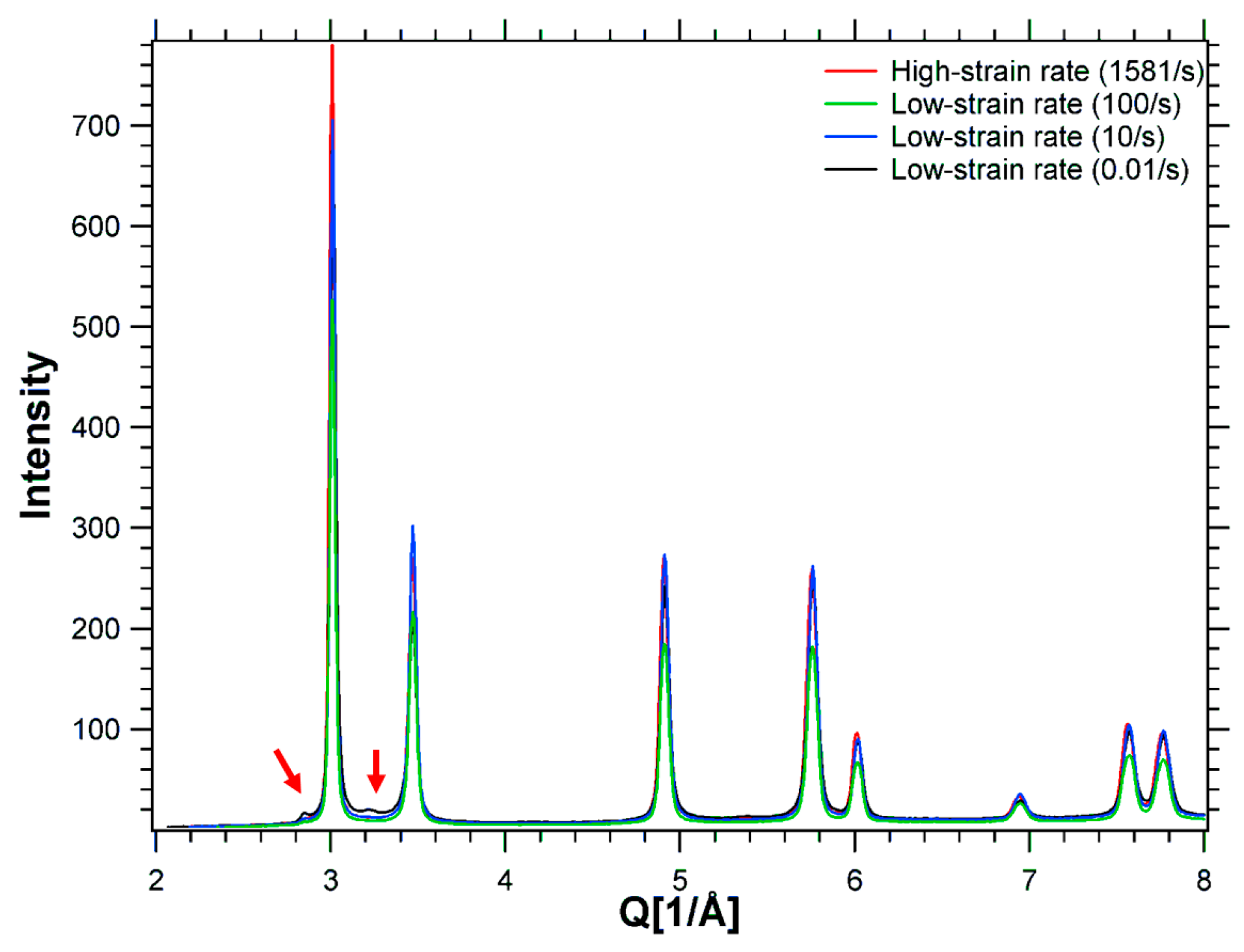
Diffraction profiles were also used to demonstrate the microstructural changes in the specimens deformed at different strain rates. In
Figure 8, the diffraction intensities for each specimen are plotted against the scattering vector, Q. As can be seen in the figure, no displacements in the diffraction peak positions were observed. Interestingly, extra peaks, as indicated by arrows in
Figure 8, revealed the evolution of a different phase in the specimen deformed at a strain rate of 0.01/s—a phase which possessed a crystallographic structure other than the
fcc austenite phase. With preliminary refinement, these extra peaks were found to belong to the
hcp structured martensite or ABABAB structured stacking faults; however, the fraction of this new phase was very small. Additionally, the integrated peak width of different reflections—shown in
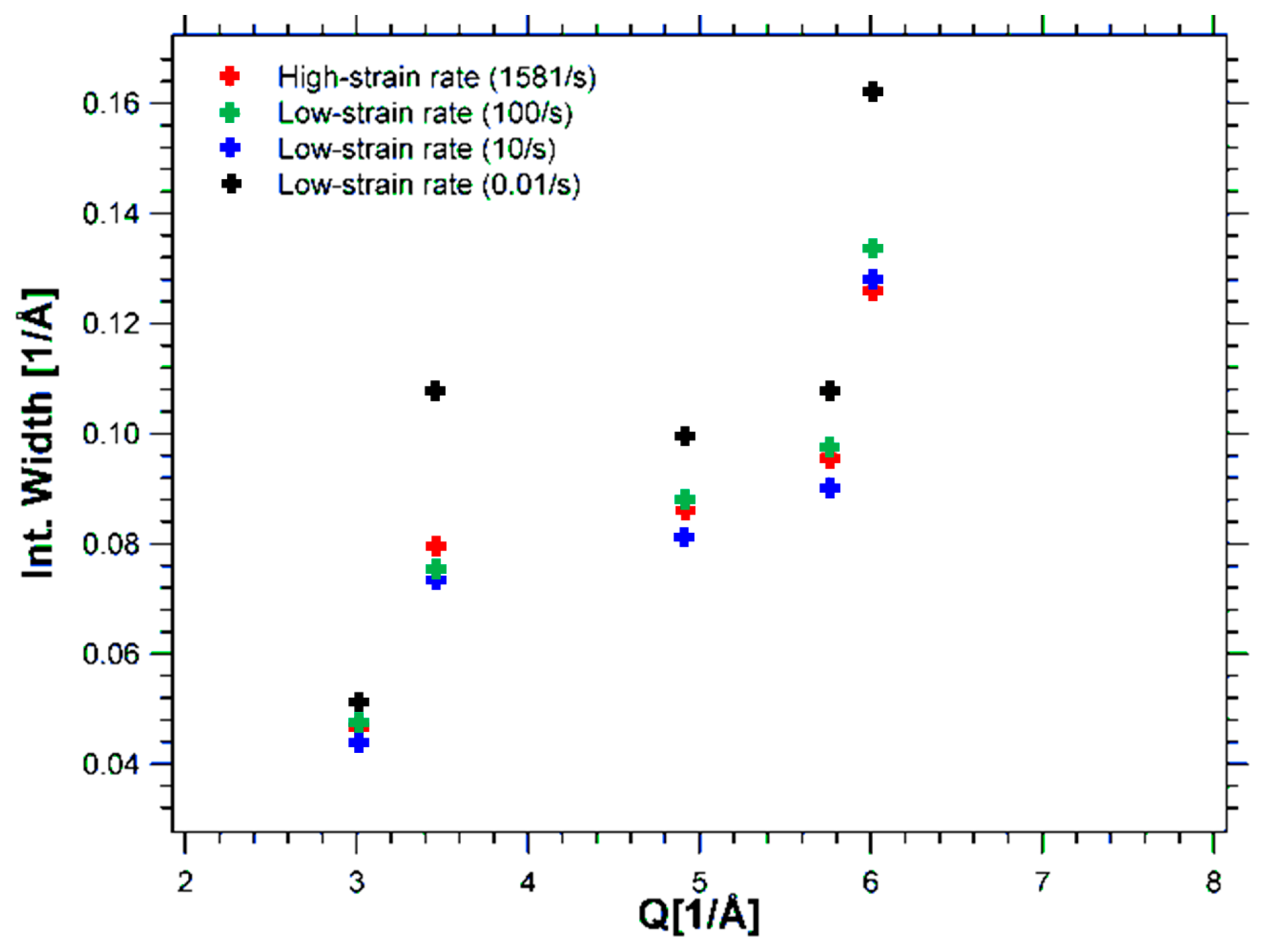
Figure 9—indicated that the specimen deformed at the lowest strain rate (0.01/s) obtained the broadest peak width. Diffraction peak broadening, as Estrin et al. [
19] described, indicates small crystallites, grains or subgrains, and/or the presence of micro-stresses. In the test with the lowest strain rate (0.01/s), the broad peak width can mainly be attributed to finer grain size, the contents of dislocations and the subgrain structure introduced by dislocation movement, which are all due to slip. In
Figure 9, the typical high width value of the austenite 200 peak (i.e., the second peak) may be observed, which has previously been reported by Ungár et al. [
20] to be particularly broadened by the anisotropy of crystallographic slip on {111}, a/2<110>. This observation further emphasises the role of dislocation gliding in plastic deformation at our lowest strain rate of 0.01/s. As twinning has a larger role at elevated deformation rates, fewer dislocations accumulate due to slip, leading to a smaller broadening.