Inertial Methodology for the Monitoring of Structures in Motion Caused by Seismic Vibrations
Abstract
1. Introduction
- Continuous monitoring and measurement of structure displacement caused by seismic vibration.
- An inertial system is implemented to perform SHM under seismic vibrations and provide information to perform a non-destructive evaluation.
- Correction algorithm ZVOB: ZVOB is a robust technique that evaluates whether a body is still in motion or in a steady-state phase.
- Drift reduction: error caused by drift due to the accelerometer is attenuated to increase the precision of measurements.
- Frequency analysis of a structure to measure the displacement when it is excited by seismic vibrations.
2. Inertial Sensor Computations
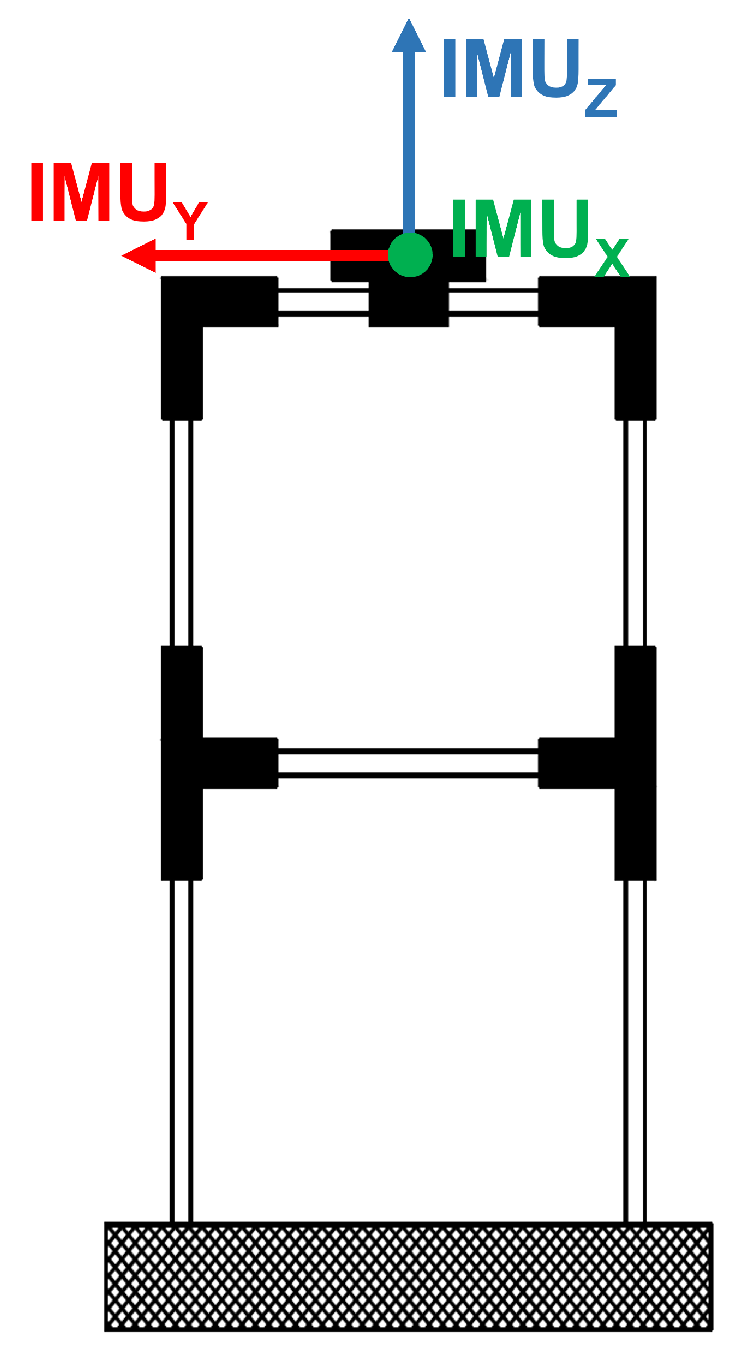
2.1. Local Level Reference Frame
2.2. Velocity and Position
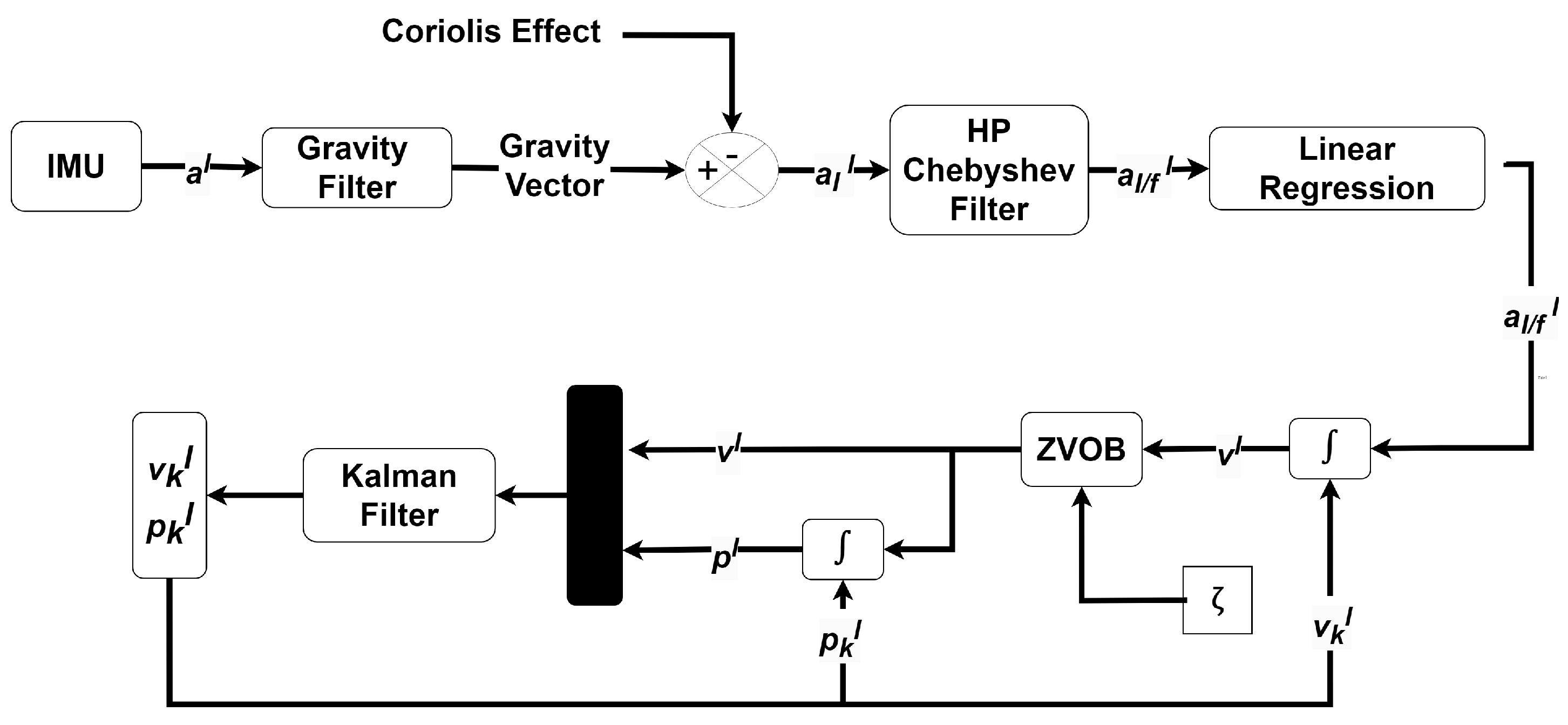
3. Signal Conditioning
3.1. Kalman Filter
3.2. Gravity Filter
3.3. Chebyshev Filter
3.4. Zero Velocity Observation Update (ZVOB)
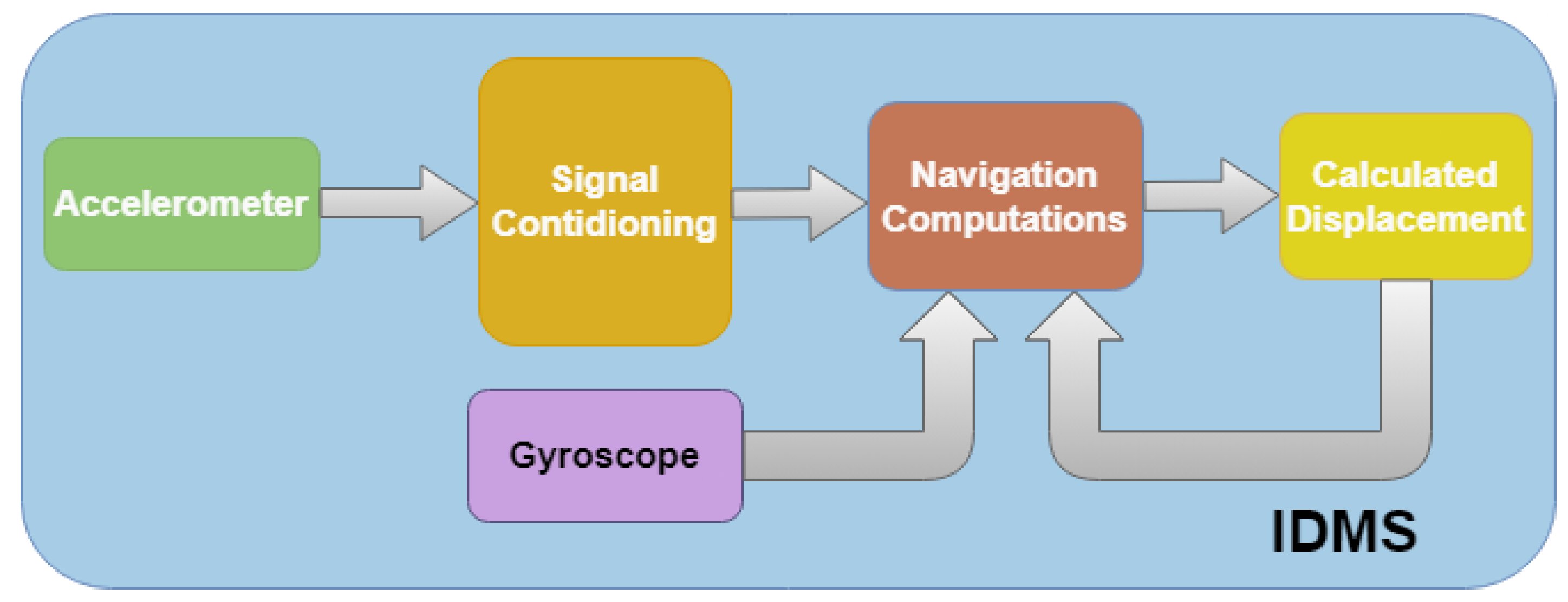
4. Inertial Displacement Monitoring System (IDMS) Methodology
5. Experimentation
- 6.25 Hz movement in x-axis.
- 6.94 Hz movement in x-axis.
- 7.81 Hz movement in x-axis.
- 8.92 Hz movement in x-axis.
6. Results
6.1. Signal Analysis
6.2. Displacement Measurements
7. Discussion of the Results
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, C.; Mousavi, A.A.; Masri, S.F.; Gholipour, G.; Yan, K.; Li, X. Vibration feature extraction using signal processing techniques for structural health monitoring: A review. Mech. Syst. Signal Process. 2022, 177, 109175. [Google Scholar] [CrossRef]
- Deng, Z.; Huang, M.; Wan, N.; Zhang, J. The Current Development of Structural Health Monitoring for Bridges: A Review. Buildings 2023, 13, 1360. [Google Scholar] [CrossRef]
- Dang, H.V.; Tran-Ngoc, H.; Nguyen, T.V.; Bui-Tien, T.; De Roeck, G.; Nguyen, H.X. Data-Driven Structural Health Monitoring Using Feature Fusion and Hybrid Deep Learning. IEEE Trans. Autom. Sci. Eng. 2021, 18, 2087–2103. [Google Scholar] [CrossRef]
- Shao, Y.; Li, L.; Li, J.; An, S.; Hao, H. Computer vision based target-free 3D vibration displacement measurement of structures. Eng. Struct. 2021, 246, 113040. [Google Scholar] [CrossRef]
- Dong, C.Z.; Bas, S.; Catbas, F.N. Investigation of vibration serviceability of a footbridge using computer vision-based methods. Eng. Struct. 2020, 224, 111224. [Google Scholar] [CrossRef]
- Zinno, R.; Haghshenas, S.S.; Guido, G.; VItale, A. Artificial Intelligence and Structural Health Monitoring of Bridges: A Review of the State-of-the-Art. IEEE Access 2022, 10, 88058–88078. [Google Scholar] [CrossRef]
- Luan, L.; Zheng, J.; Wang, M.L.; Yang, Y.; Rizzo, P.; Sun, H. Extracting full-field subpixel structural displacements from videos via deep learning. J. Sound Vib. 2021, 505, 116142. [Google Scholar] [CrossRef]
- Boscato, G.; Fragonara, L.Z.; Cecchi, A.; Reccia, E.; Baraldi, D. Structural Health Monitoring through Vibration-Based Approaches. Shock Vib. 2019, 2019, 2380616. [Google Scholar] [CrossRef]
- Moradi, M.; Broer, A.; Chiachío, J.; Benedictus, R.; Loutas, T.H.; Zarouchas, D. Intelligent health indicator construction for prognostics of composite structures utilizing a semi-supervised deep neural network and SHM data. Eng. Appl. Artif. Intell. 2023, 117, 105502. [Google Scholar] [CrossRef]
- Torzoni, M.; Manzoni, A.; Mariani, S. A Deep Neural Network, Multi-fidelity Surrogate Model Approach for Bayesian Model Updating in SHM. In European Workshop on Structural Health Monitoring; Rizzo, P., Milazzo, A., Eds.; Springer: Cham, Switzerland, 2023; pp. 1076–1086. [Google Scholar]
- Lopez-Higuera, J.M.; Rodriguez Cobo, L.; Quintela Incera, A.; Cobo, A. Fiber Optic Sensors in Structural Health Monitoring. J. Light. Technol. 2011, 29, 587–608. [Google Scholar] [CrossRef]
- Carani, L.B.; Martin, T.D.; Eze, V.O.; Okoli, O.I. Impact sensing and localization in composites structures with embedded mechanoluminescence-perovskite sensors. Sens. Actuators A Phys. 2022, 346, 113843. [Google Scholar] [CrossRef]
- Rao, A.S.; Radanovic, M.; Liu, Y.; Hu, S.; Fang, Y.; Khoshelham, K.; Palaniswami, M.; Ngo, T. Real-time monitoring of construction sites: Sensors, methods, and applications. Autom. Constr. 2022, 136, 104099. [Google Scholar] [CrossRef]
- Jeon, J.Y.; Miao, Y.; Park, G.; Flynn, E. Compressive laser scanning with full steady state wavefield for structural damage detection. Mech. Syst. Signal Process. 2022, 169, 108626. [Google Scholar] [CrossRef]
- Choi, Y.; Abbas, S.H.; Lee, J.R. Aircraft integrated structural health monitoring using lasers, piezoelectricity, and fiber optics. Measurement 2018, 125, 294–302. [Google Scholar] [CrossRef]
- Real-Moreno, O.; Rodríguez-Quiñonez, J.C.; Sergiyenko, O.; Flores-Fuentes, W.; Castro-Toscano, M.J.; Miranda-Vega, J.E.; Mercorelli, P.; Valdez-Rodríguez, J.A.; Trujillo-Hernández, G.; Sanchez-Castro, J.J. A Quadrant Approach of Camera Calibration Method for Depth Estimation Using a Stereo Vision System. In Proceedings of the IECON 2022—48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Identification of structural stiffness and excitation forces in time domain using noncontact vision-based displacement measurement. J. Sound Vib. 2017, 406, 15–28. [Google Scholar] [CrossRef]
- Trujillo-Hernández, G.; Rodríguez-Quiñonez, J.C.; Flores-Fuentes, W.; Sergiyenko, O.; Ontiveros-Reyes, E.; Real-Moreno, O.; Hernández-Balbuena, D.; Murrieta-Rico, F.N.; Rascón, R. Development of an integrated podometry system for mechanical load measurement and visual inspection. Measurement 2022, 203, 111866. [Google Scholar] [CrossRef]
- Veluthedath Shajihan, S.A.; Chow, R.; Mechitov, K.; Fu, Y.; Hoang, T.; Spencer, B.F. Development of Synchronized High-Sensitivity Wireless Accelerometer for Structural Health Monitoring. Sensors 2020, 20, 4169. [Google Scholar] [CrossRef] [PubMed]
- Shih, J.Y.; Weston, P.; Entezami, M.; Roberts, C.; O’Callaghan, M. Experiences Using MEMS Accelerometers on Railway Bearers at Switches and Crossings to Obtain Displacement—Awkward Situations. Infrastructures 2024, 9, 91. [Google Scholar] [CrossRef]
- Hassani, S.; Dackermann, U.; Mousavi, M.; Li, J. A systematic review of data fusion techniques for optimized structural health monitoring. Inf. Fusion 2024, 103, 102136. [Google Scholar] [CrossRef]
- Qu, X.; Ding, X.; Xu, Y.L.; Yu, W. Real-time outlier detection in integrated GNSS and accelerometer structural health monitoring systems based on a robust multi-rate Kalman filter. J. Geod. 2023, 97, 38. [Google Scholar] [CrossRef]
- Castro-Toscano, M.; Rodríguez-Quiñonez, J.; Hernández-Balbuena, D.; Rivas-Lopez, M.; Sergiyenko, O.; Flores-Fuentes, W. Obtención de Trayectorias Empleando el Marco Strapdown INS/KF: Propuesta Metodológica. Rev. Iberoam. Autom. Inform. Ind. 2018, 15, 391–403. [Google Scholar] [CrossRef]
- Rodríguez-Quiñonez, J.C. Intelligent Automatic Object Tracking Method by Integration of Laser Scanner System and INS. Program. Comput. Softw. 2020, 46, 619–625. [Google Scholar] [CrossRef]
- Castro-Toscano, M.J.; Valdez-Rodríguez, J.A.; Rodríguez-Quiñonez, J.C.; Flores-Fuentes, W.; Sergiyenko, O.; Trujillo-Hernandez, G.; Real-Moreno, O. Determination of Trajectories Using IKZ/CF Inertial Navigation: Methodological Proposal/CF Inertial Navigation: Methodological Proposal. Heliyon 2023, 9, e13863. [Google Scholar] [CrossRef] [PubMed]
- Sokolov, S.; Pogorelov, V.; Shatalov, A. Solving the Autonomous Initial Navigation Task for Strapdown Inertial Navigation System on the Perturbed Basis Using Rodriguez—Hamilton Parameters. Russ. Aeronaut. 2019, 62, 42–51. [Google Scholar] [CrossRef]
- Bose, A.; Bhat, K.; Kurian, T. Fundamentals of Navigation and Inertial Sensors; Eastern Economy Edition; PHI Learning: Delhi, India, 2014. [Google Scholar]
- Valdez-Rodríguez, J.A.; Rodríguez-Quiñonez, J.C.; Flores-Fuentes, W.; Ramírez-Hernández, L.R.; Trujillo-Hernández, G.; Real-Moreno, O.; Castro-Toscano, M.J.; Miranda-Vega, J.E.; Mercorelli, P. Visual-Inertial Navigation Systems and Technologies. In Optoelectronic Devices in Robotic Systems; Sergiyenko, O., Ed.; Springer International Publishing: Cham, Switzerland, 2022; pp. 137–166. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, W.; Xiong, J. Specific force integration algorithm with high accuracy for strapdown inertial navigation system. Aerosp. Sci. Technol. 2015, 42, 25–30. [Google Scholar] [CrossRef]
- Acar, C.; Shkel, A. Introduction; MEMS Vibratory Gyroscopes: Structural Approaches to Improve Robustness. In MEMS Vibratory Gyroscopes: Structural Approaches to Improve Robustness; Springer US: Boston, MA, USA, 2009; pp. 1–14. [Google Scholar] [CrossRef]
- Klančar, G.; Zdešar, A.; Blažič, S.; Škrjanc, I. Chapter 5—Sensors Used in Mobile Systems. In Wheeled Mobile Robotics; Klančar, G., Zdešar, A., Blažič, S., Škrjanc, I., Eds.; Butterworth-Heinemann: Oxford, UK, 2017; pp. 207–288. [Google Scholar] [CrossRef]
- Kumari, N.; Kulkarni, R.; Ahmed, M.R.; Kumar, N. Use of Kalman Filter and Its Variants in State Estimation: A Review. In Artificial Intelligence for a Sustainable Industry 4.0; Awasthi, S., Travieso-González, C.M., Sanyal, G., Kumar Singh, D., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 213–230. [Google Scholar] [CrossRef]
- Quan, W.; Gong, X.; Fang, J.; Li, J. INS/GNSS Integrated Navigation Method. In INS/CNS/GNSS Integrated Navigation Technology; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2015; pp. 185–235. [Google Scholar] [CrossRef]
- Wang, Y.; Shkel, A.M. Adaptive Threshold for Zero-Velocity Detector in ZUPT-Aided Pedestrian Inertial Navigation. IEEE Sens. Lett. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Tong, X.; Su, Y.; Li, Z.; Si, C.; Han, G.; Ning, J.; Yang, F. A Double-Step Unscented Kalman Filter and HMM-Based Zero-Velocity Update for Pedestrian Dead Reckoning Using MEMS Sensors. IEEE Trans. Ind. Electron. 2020, 67, 581–591. [Google Scholar] [CrossRef]
- Benzerrouk, H.; Nebylov, A.V. Robust IMU/UWB integration for indoor pedestrian navigation. In Proceedings of the 2018 25th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), Saint Petersburg, Russia, 28–30 May 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Suresh, R.P.; Sridhar, V.; Pramod, J.; Talasila, V. Zero Velocity Potential Update (ZUPT) as a Correction Technique. In Proceedings of the 2018 3rd International Conference On Internet of Things: Smart Innovation and Usages (IoT-SIU), Bhimtal, India, 23–24 February 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Schwardt, M.; Pilger, C.; Gaebler, P.; Hupe, P.; Ceranna, L. Natural and Anthropogenic Sources of Seismic, Hydroacoustic, and Infrasonic Waves: Waveforms and Spectral Characteristics (and Their Applicability for Sensor Calibration). Surv. Geophys. 2022, 43, 1265–1361. [Google Scholar] [CrossRef] [PubMed]
- Aydan, Ö. Earthquake Science and Engineering; CRC Press: London, UK, 2022. [Google Scholar]
- Towhata, I. Geotechnical Earthquake Engineering; Springer Series in Geomechanics and Geoengineering; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Chen, Y.; Li, H.; Hou, L.; Bu, X. Feature extraction using dominant frequency bands and time-frequency image analysis for chatter detection in milling. Precis. Eng. 2019, 56, 235–245. [Google Scholar] [CrossRef]
- Shi, Y.; Mahr, F.; von Wagner, U.; Uhlmann, E. Chatter frequencies of micromilling processes: Influencing factors and online detection via piezoactuators. Int. J. Mach. Tools Manuf. 2012, 56, 10–16. [Google Scholar] [CrossRef]
- Shao, Y.; Li, L.; Li, J.; An, S.; Hao, H. Target-free 3D tiny structural vibration measurement based on deep learning and motion magnification. J. Sound Vib. 2022, 538, 117244. [Google Scholar] [CrossRef]
- Garcia-Sanchez, D.; Fernandez-Navamuel, A.; Sánchez, D.Z.; Alvear, D.; Pardo, D. Bearing assessment tool for longitudinal bridge performance. J. Civ. Struct. Health Monit. 2020, 10, 1023–1036. [Google Scholar] [CrossRef]
- Wei, K.; Yuan, F.; Shao, X.; Chen, Z.; Wu, G.; He, X. High-speed multi-camera 3D DIC measurement of the deformation of cassette structure with large shaking table. Mech. Syst. Signal Process. 2022, 177, 109273. [Google Scholar] [CrossRef]
- Castro-Toscano, M.J.; Rodríguez-Quiñonez, J.C.; Sergiyenko, O.; Flores-Fuentes, W.; Ramirez-Hernandez, L.R.; Hernández-Balbuena, D.; Lindner, L.; Rascón, R. Novel sensing approaches for structural deformation monitoring and 3D measurements. IEEE Sens. J. 2020, 21, 11318–11328. [Google Scholar] [CrossRef]




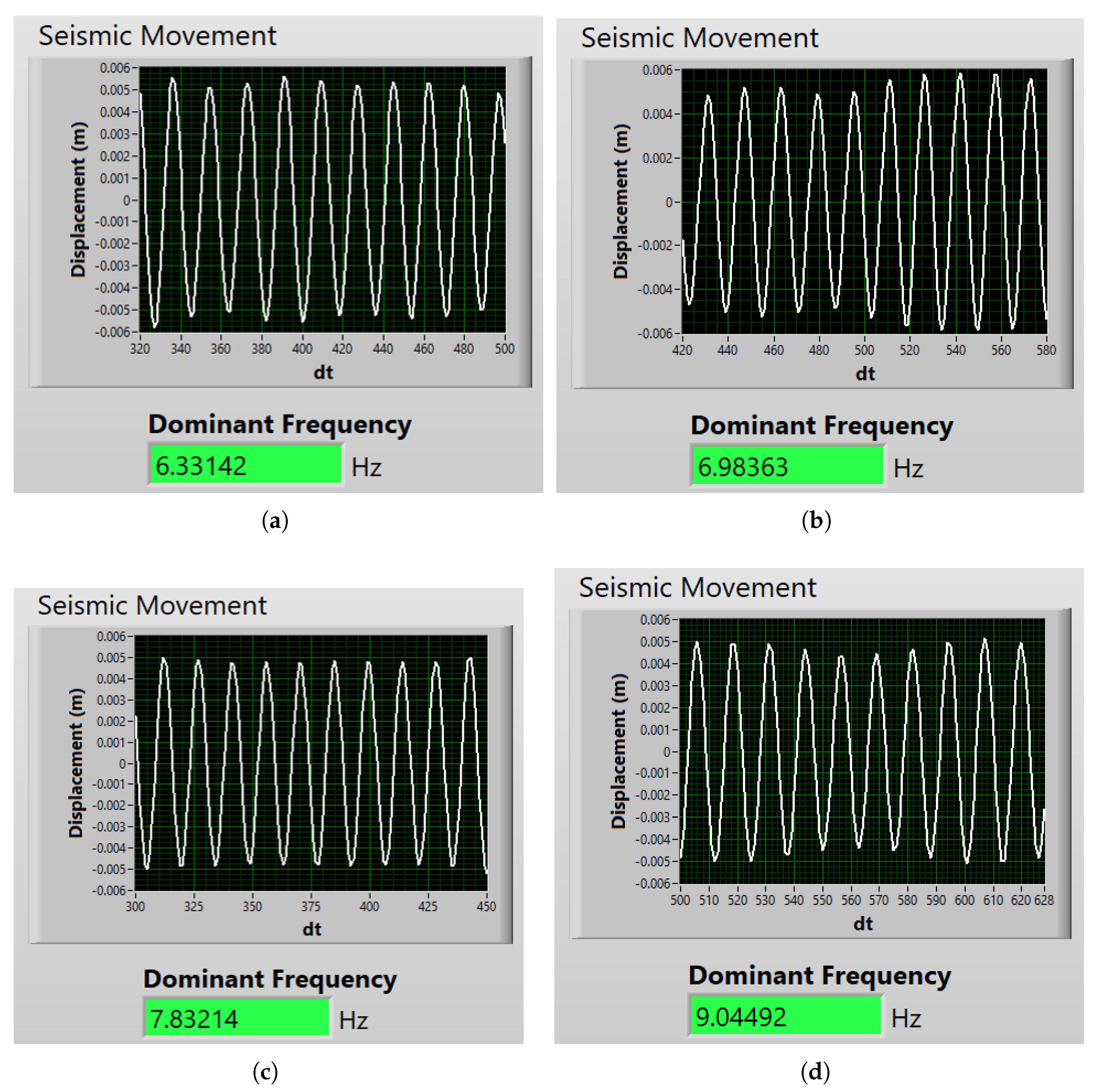
| Experiment Frequency (Hz) | System Frequency (Hz) | Relative Percentage Error |
|---|---|---|
| 6.25 | 6.2546 | 1.33% |
| 6.94 | 6.9527 | 1.74% |
| 7.81 | 7.88367 | 0.49% |
| 8.92 | 8.9375 | 1.004% |
| Overall | 1.14% | |
| RMSE | 0.088 |
| Experiment Frequency (Hz) | Structure Displacement (mm) | System Measured Displacement (mm) | Relative Percentage Error |
|---|---|---|---|
| 6.25 | 11.6000 | 11.8851 | 2.0132% |
| 6.94 | 11.3000 | 11.6923 | 2.6201% |
| 7.81 | 10.9000 | 11.6555 | 6.1587% |
| 8.92 | 10.4000 | 10.4712 | 0.5712% |
| RMSE | 0.4092 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Quiñonez, J.C.; Valdez-Rodríguez, J.A.; Castro-Toscano, M.J.; Flores-Fuentes, W.; Sergiyenko, O. Inertial Methodology for the Monitoring of Structures in Motion Caused by Seismic Vibrations. Infrastructures 2024, 9, 116. https://doi.org/10.3390/infrastructures9070116
Rodríguez-Quiñonez JC, Valdez-Rodríguez JA, Castro-Toscano MJ, Flores-Fuentes W, Sergiyenko O. Inertial Methodology for the Monitoring of Structures in Motion Caused by Seismic Vibrations. Infrastructures. 2024; 9(7):116. https://doi.org/10.3390/infrastructures9070116
Chicago/Turabian StyleRodríguez-Quiñonez, Julio C., Jorge Alejandro Valdez-Rodríguez, Moises J. Castro-Toscano, Wendy Flores-Fuentes, and Oleg Sergiyenko. 2024. "Inertial Methodology for the Monitoring of Structures in Motion Caused by Seismic Vibrations" Infrastructures 9, no. 7: 116. https://doi.org/10.3390/infrastructures9070116
APA StyleRodríguez-Quiñonez, J. C., Valdez-Rodríguez, J. A., Castro-Toscano, M. J., Flores-Fuentes, W., & Sergiyenko, O. (2024). Inertial Methodology for the Monitoring of Structures in Motion Caused by Seismic Vibrations. Infrastructures, 9(7), 116. https://doi.org/10.3390/infrastructures9070116










