The Influence of Soil Deformability on the Seismic Response of 3D Mixed R/C–Steel Buildings
Abstract
1. Introduction
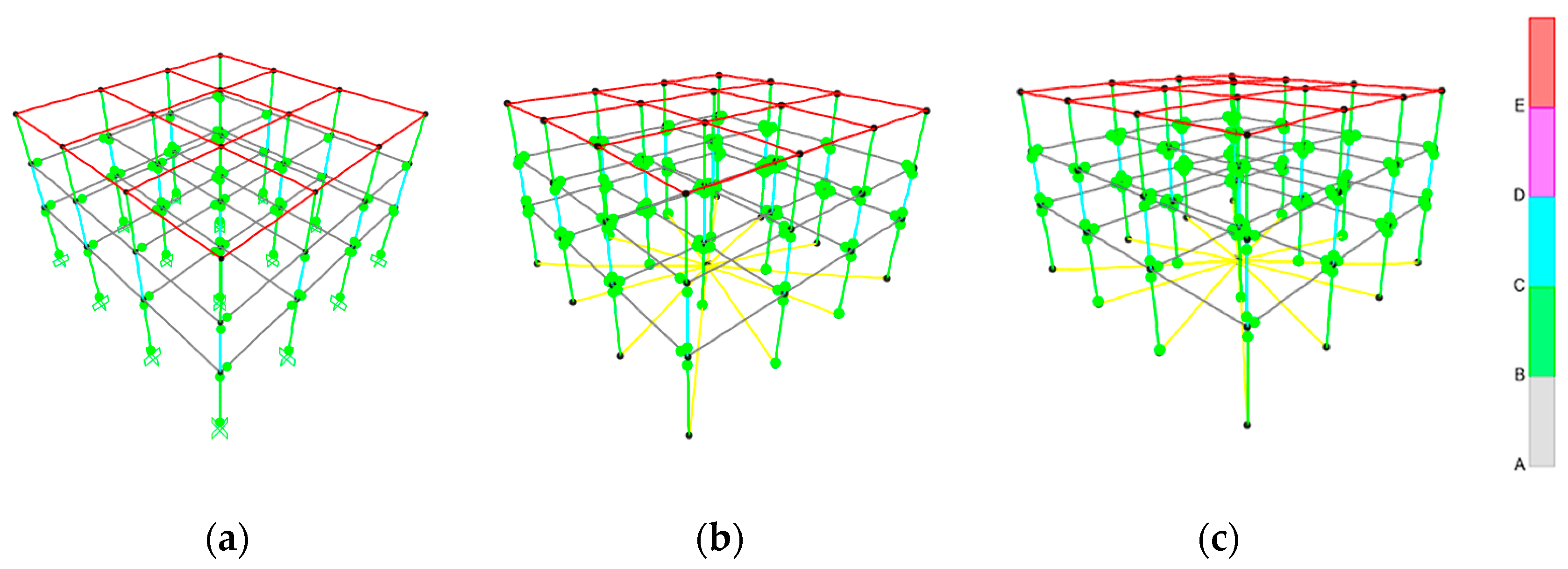
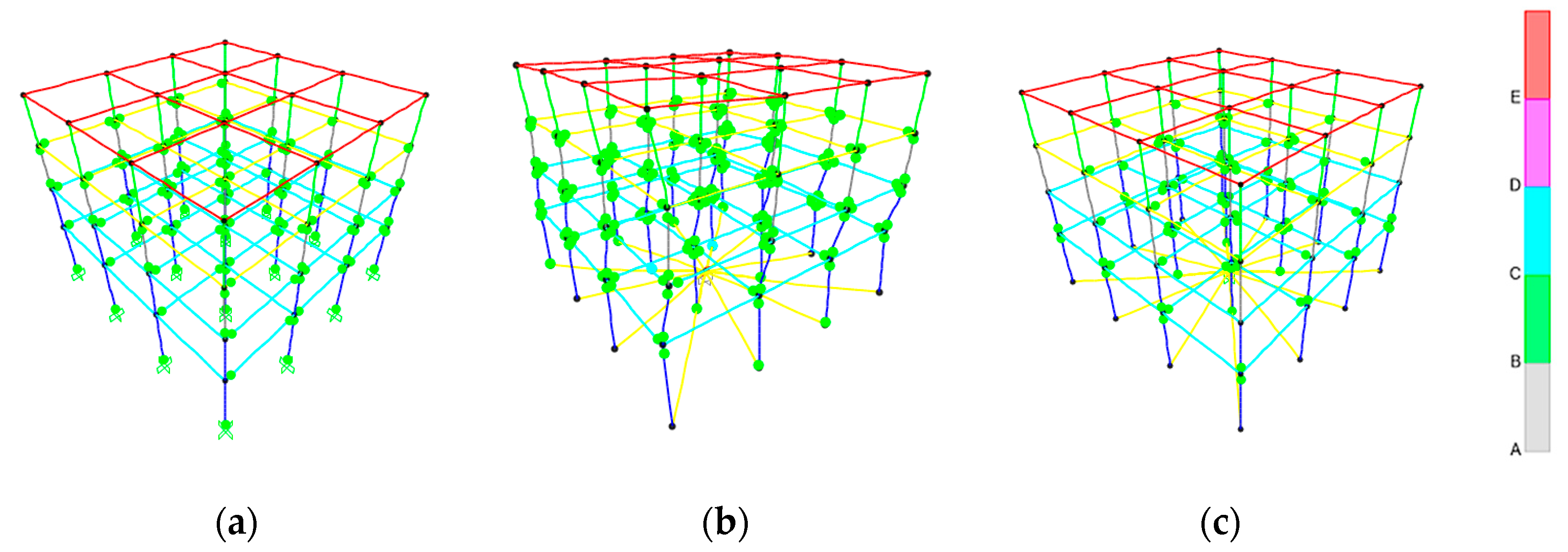
2. Description of Case Models and NLTH Analysis
3. Results and Discussion
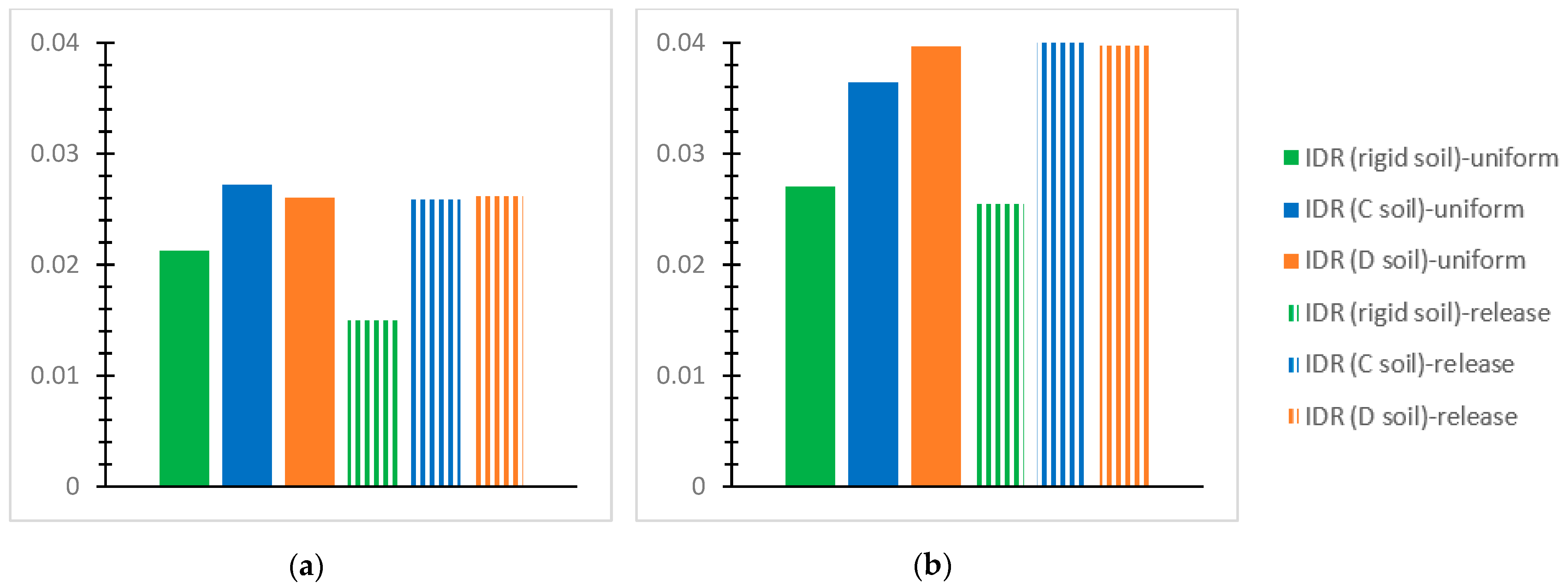
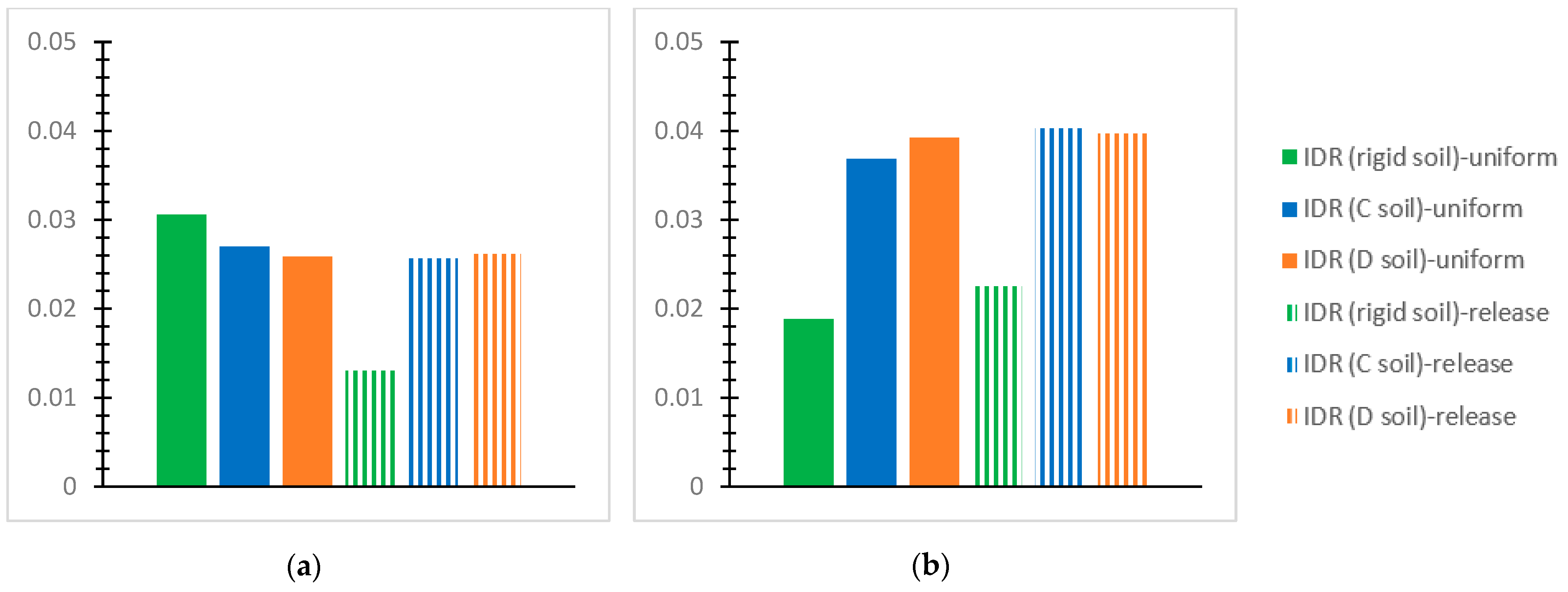
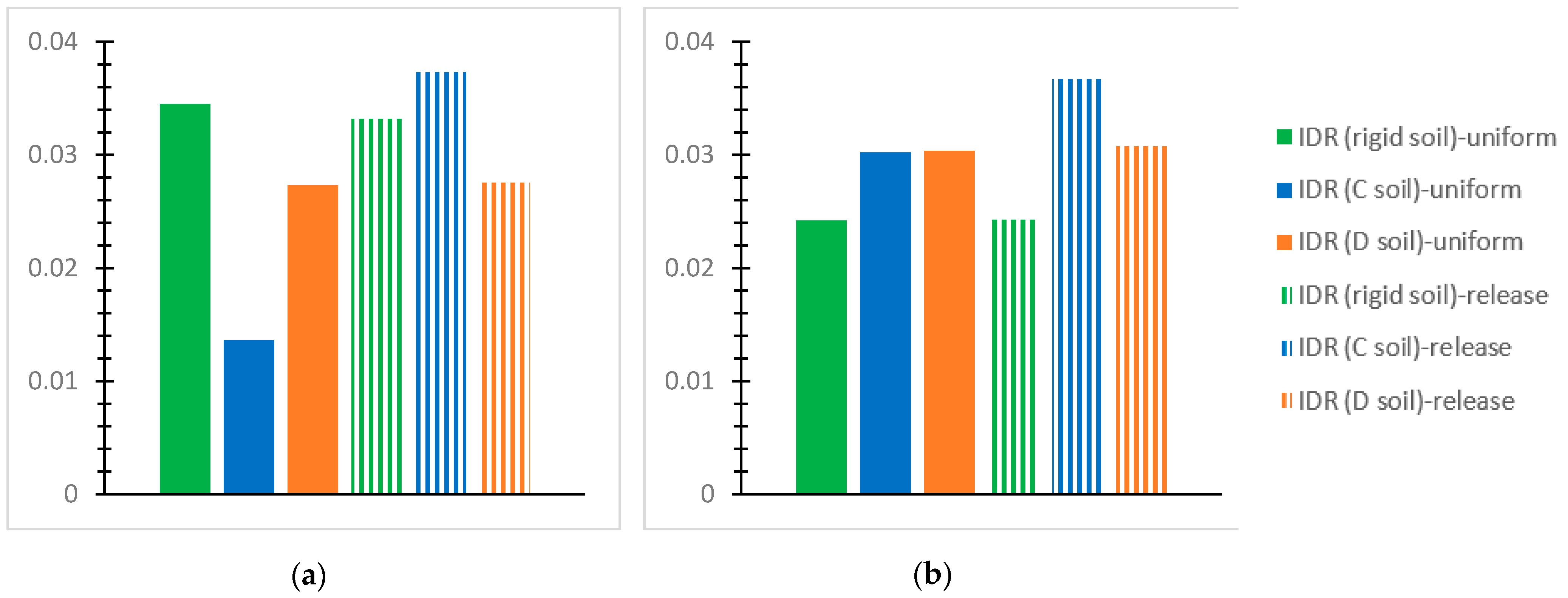
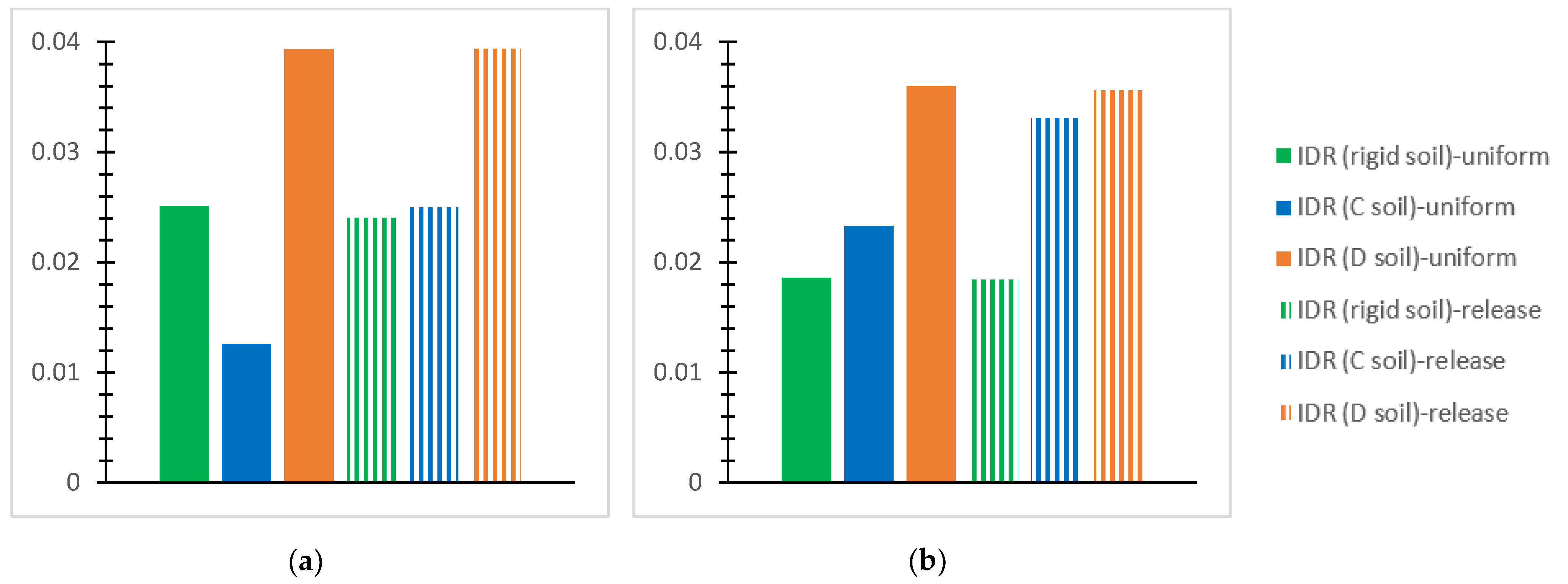
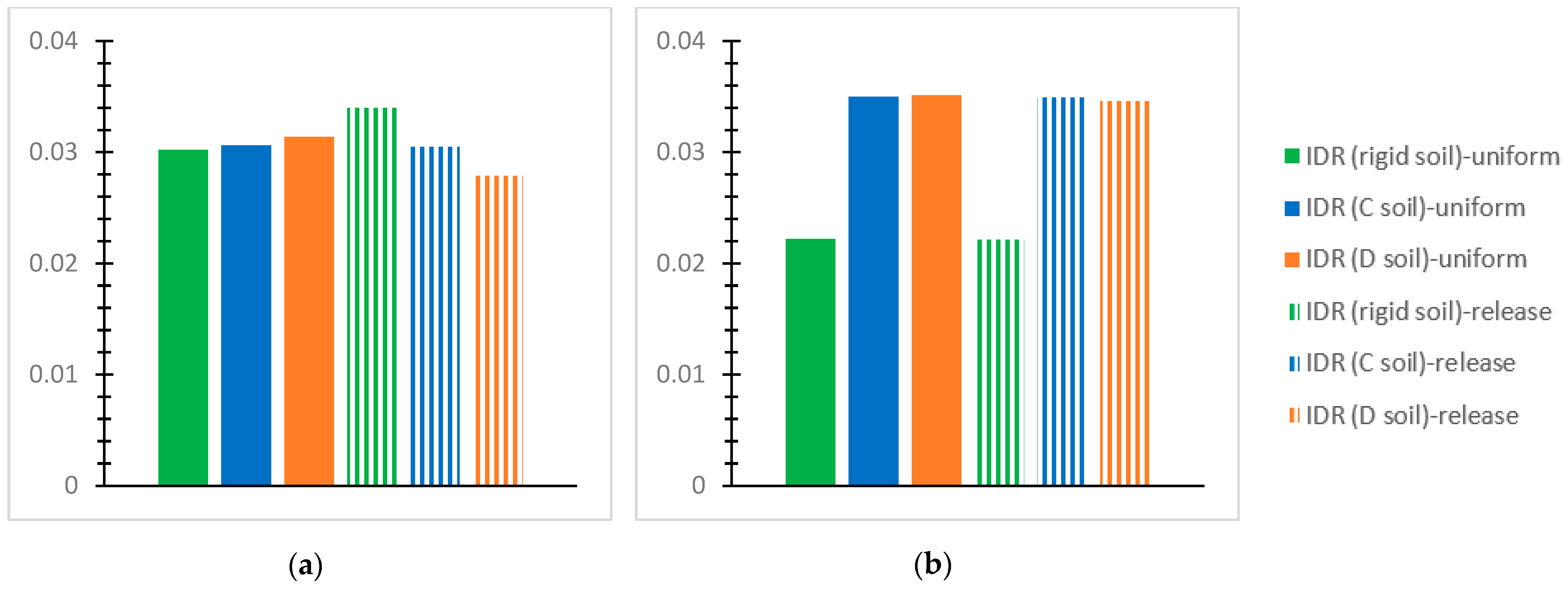
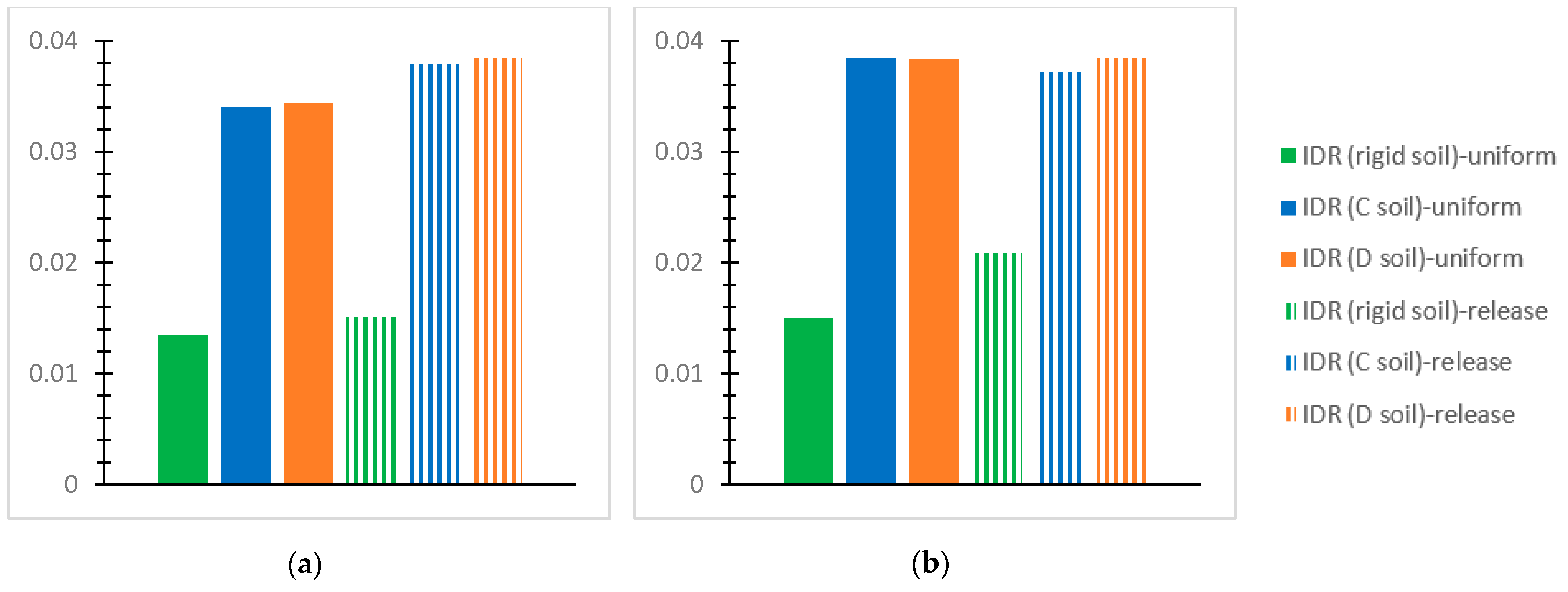
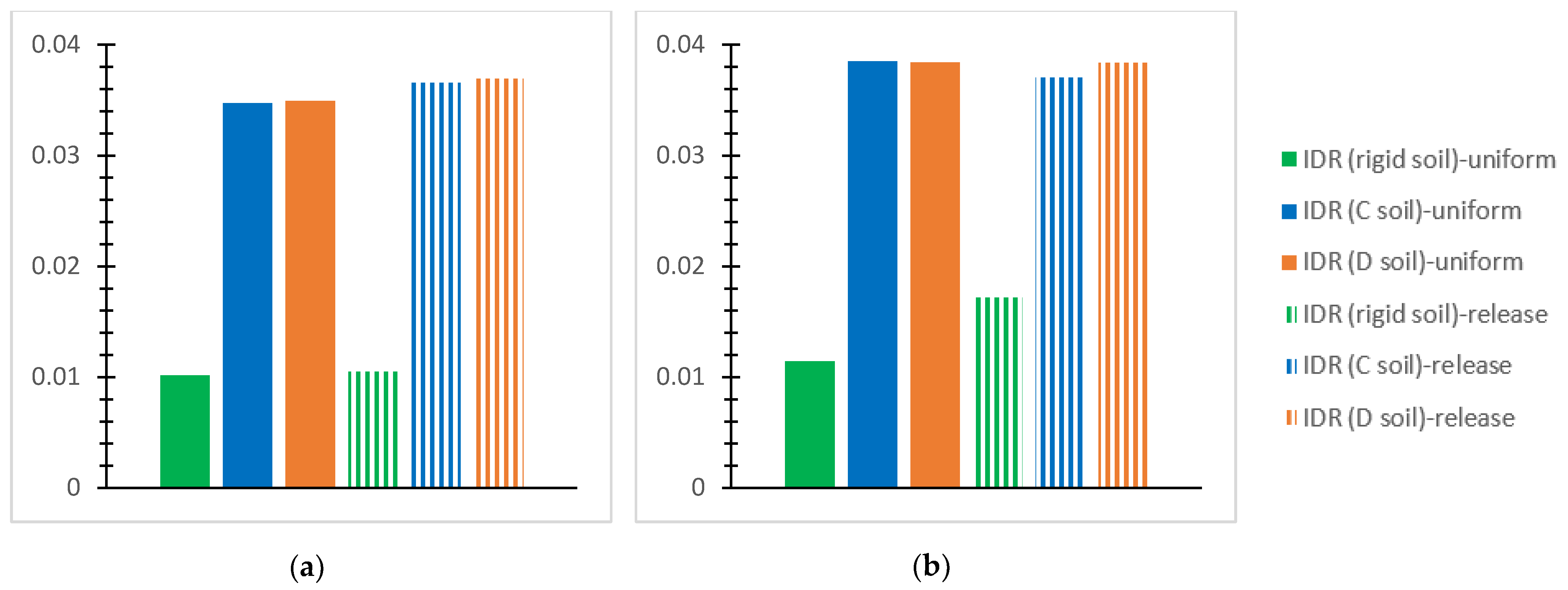
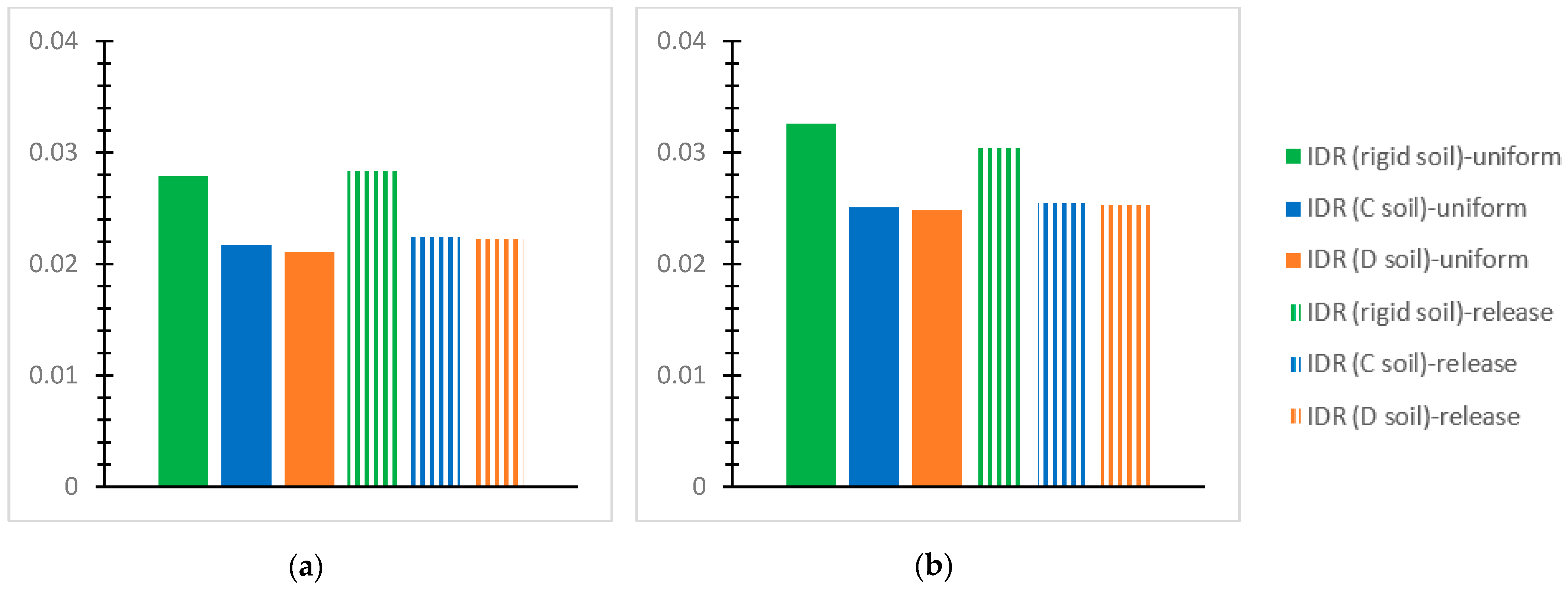
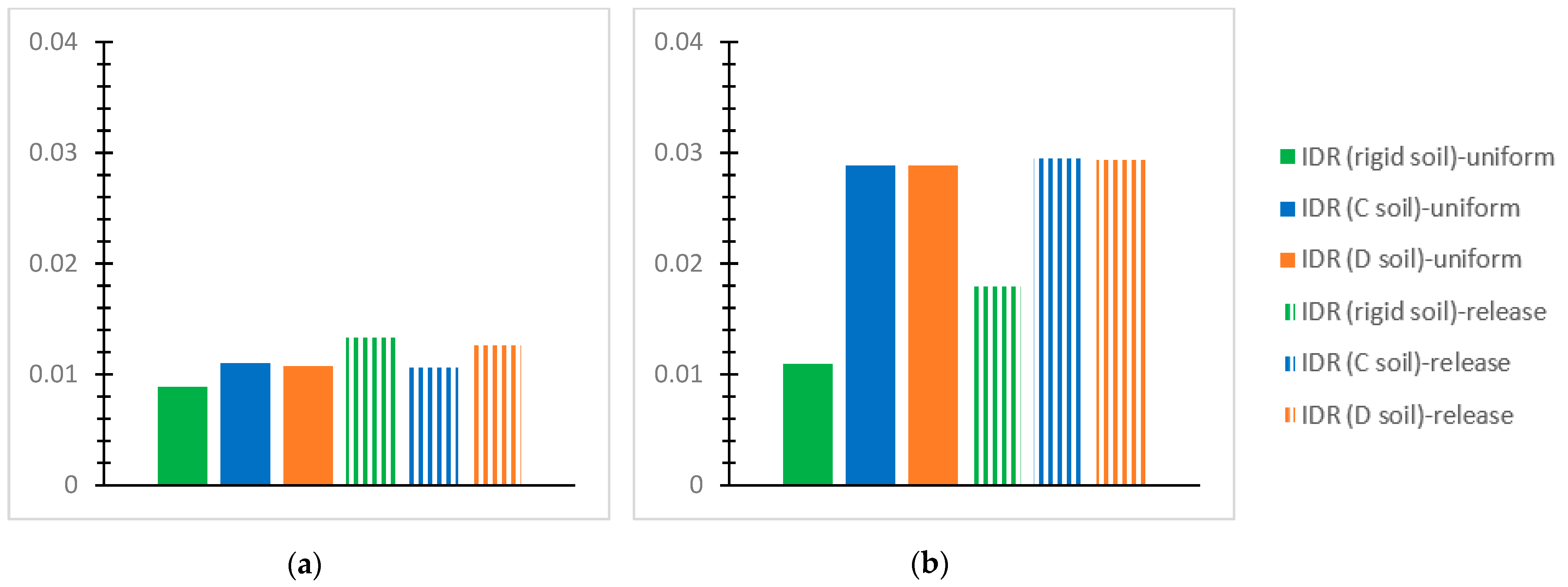
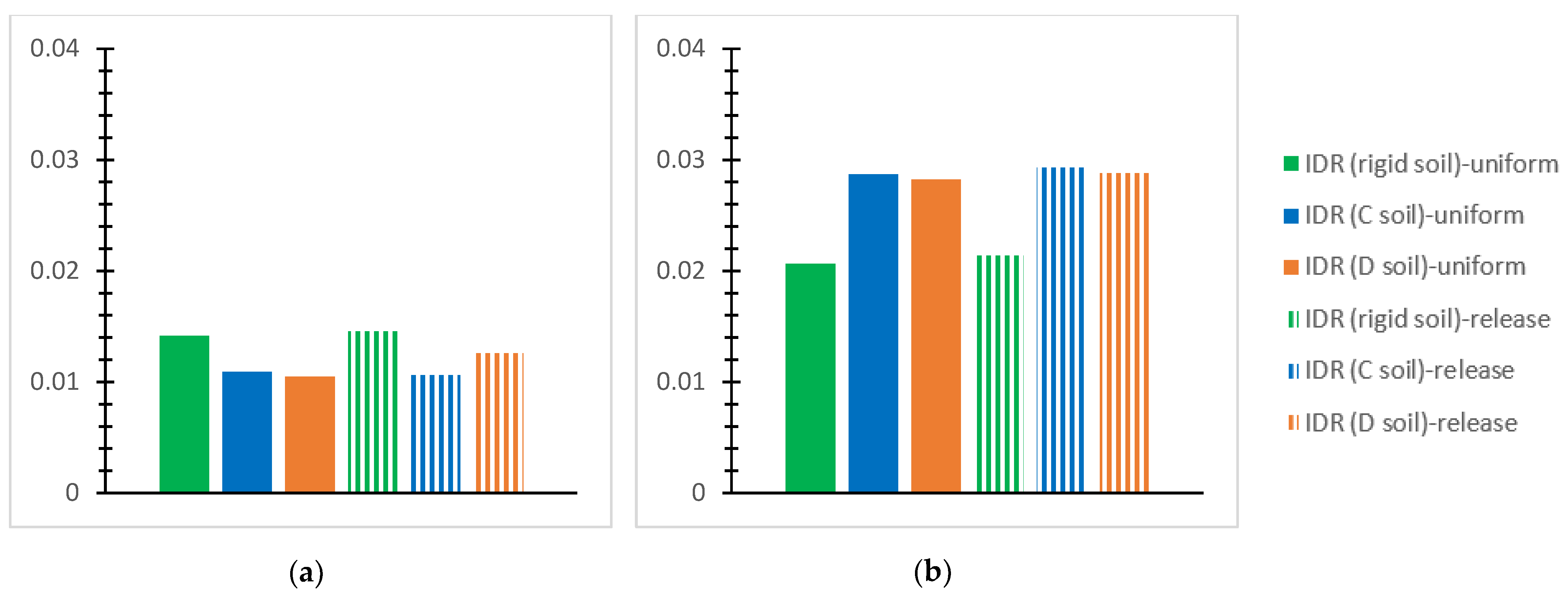
- For the inflexible soil assumption and the SSI via the C and D soil grades for the performed NLTH analyses of each mixed building at each story, the greatest value of the “interstory drift ratio (IDR)” [56] is plotted for the two interconnection forms with the notations “uniform” or “release”, as mentioned previously. The IDR values at the horizontal global axes, X and Y, are discussed concerning the effective limits for concrete frames [56] as follows: 1% in terms of the “Immediate Occupancy (IO) performance level” [56]; 2% in terms of the “Life Safety” (LS) performance level” [56]; and 4% in terms of the “Collapse Prevention (CP)” [56] level. The respective limit “IDR” [56] values for steel frames are 0.7% regarding the “IO” level [56], 2.5% referring to the “LS” level [56], and 5% regarding the “CP” level [56].
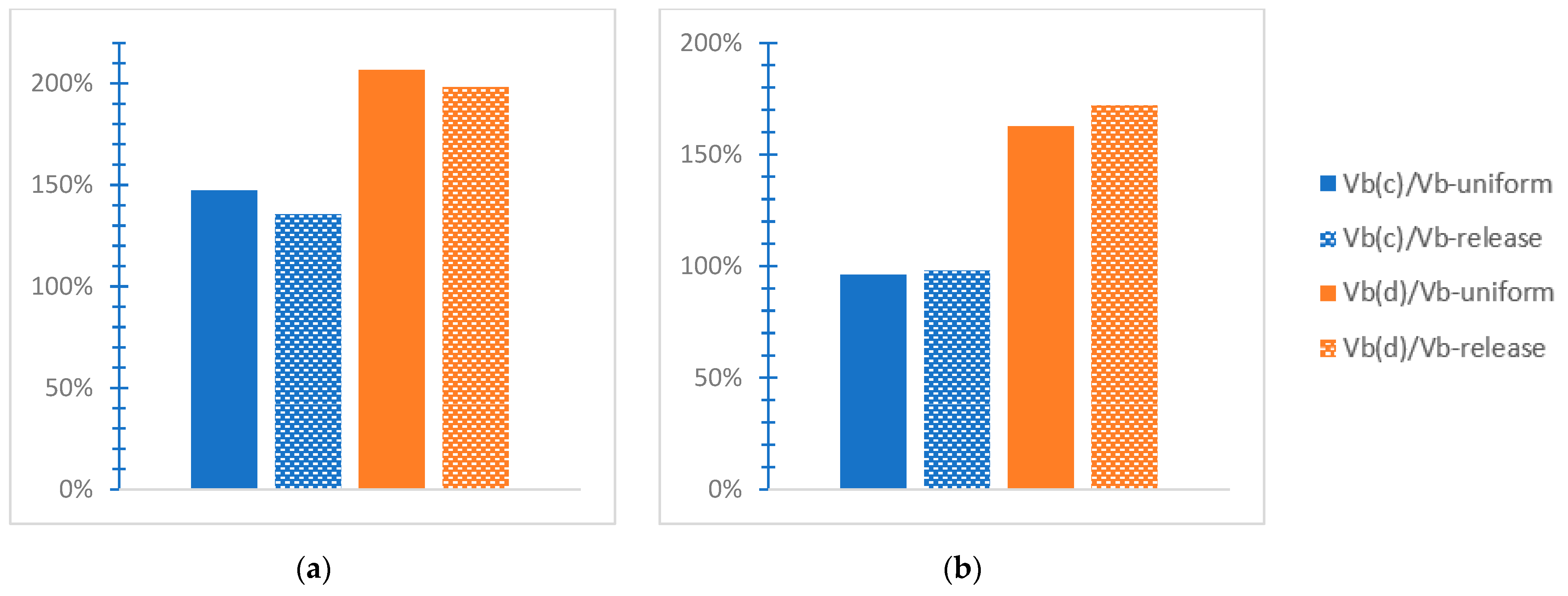
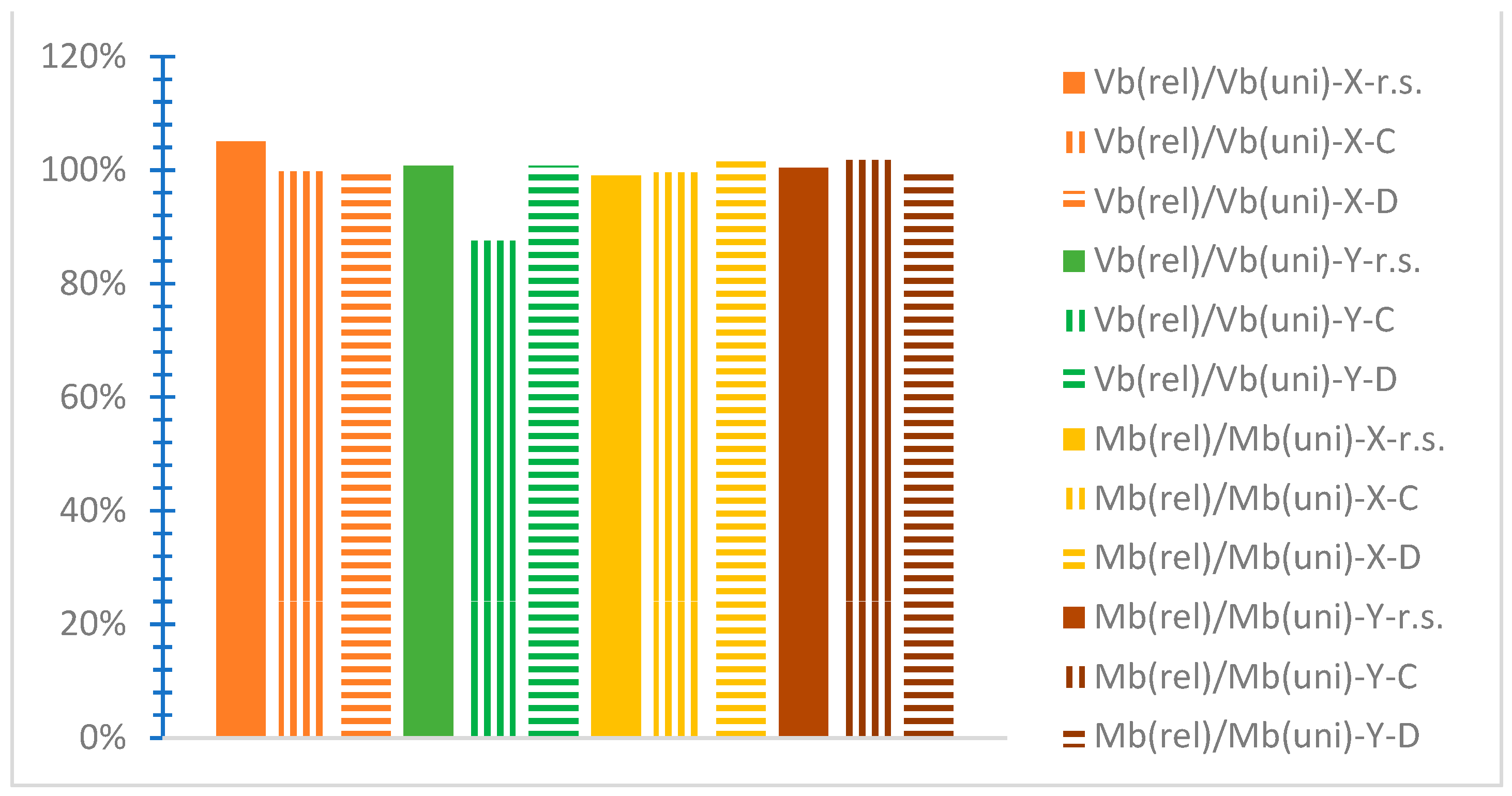
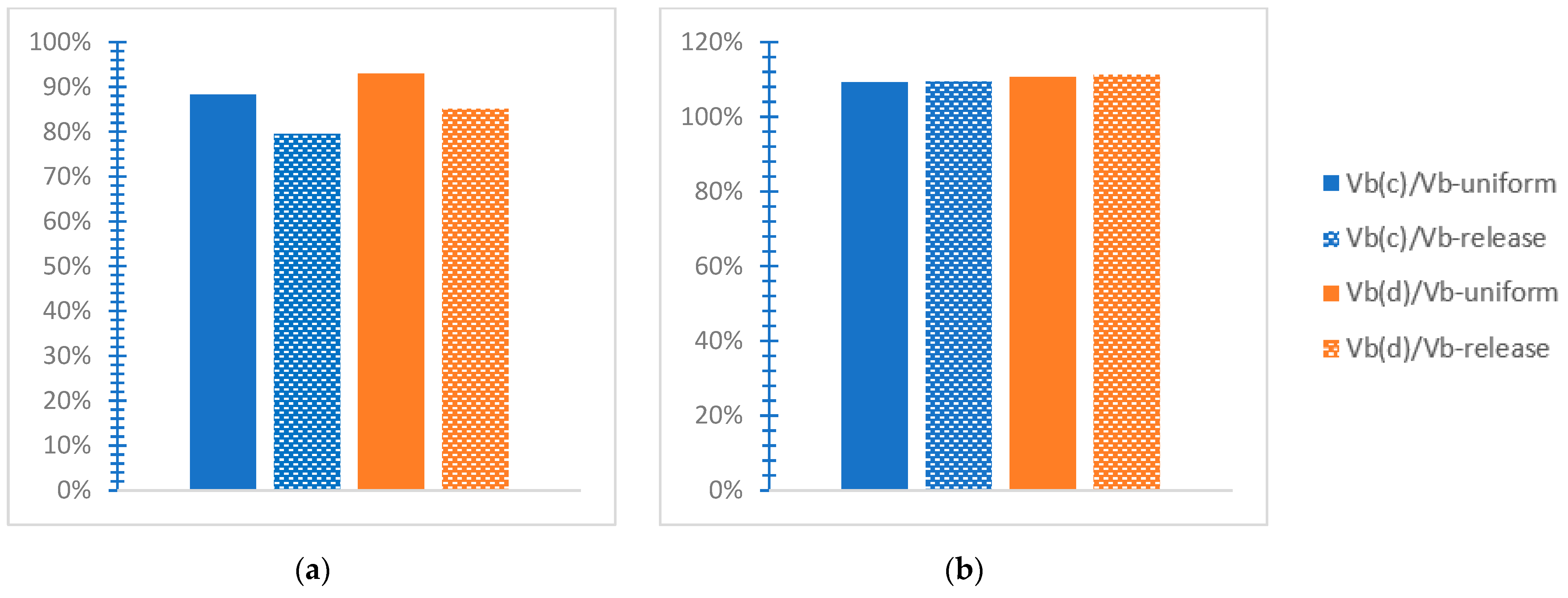
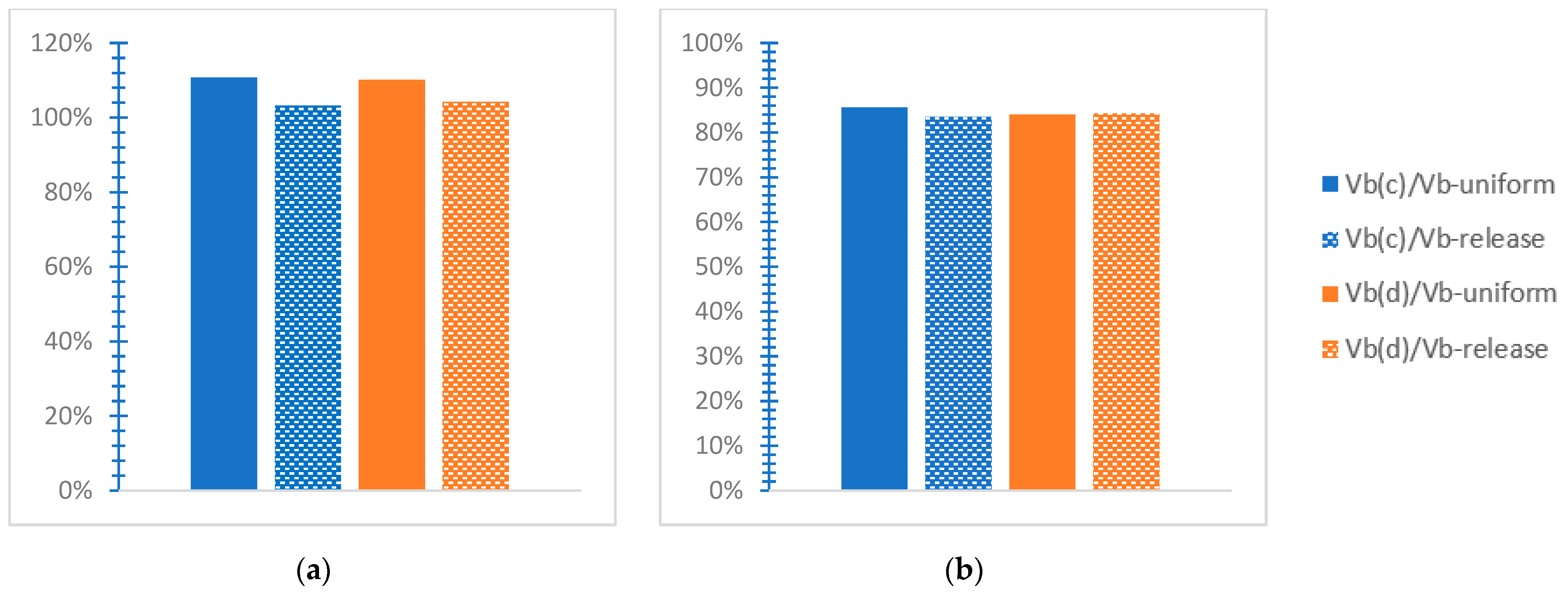
- “Vb(c)/Vb” refers to a proportion of the “greatest absolute value of the base shear” [38] for the SSI by soil C “Vb(c)” to the respective value for the inflexible soil “Vb”, with the notation “uniform” or “release”, as previously stated. Considering the SSI via soil D, this ratio is represented as “Vb(d)/Vb” along the two horizontal global axes.
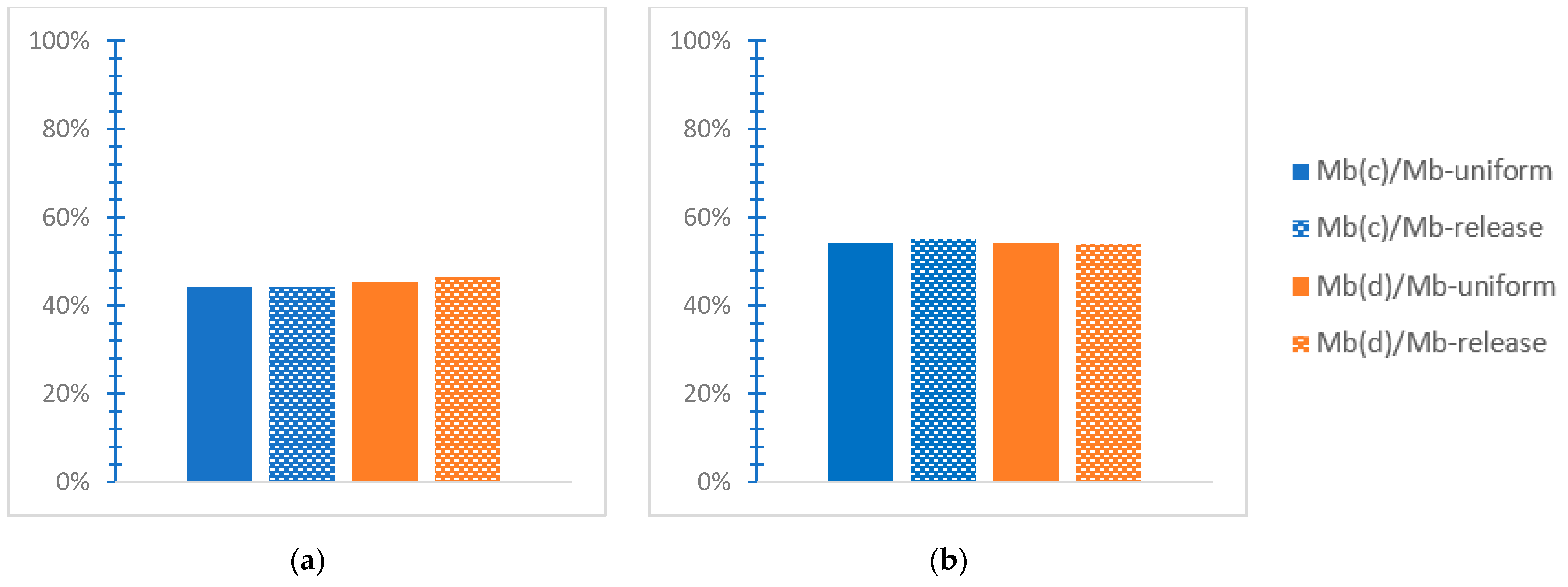
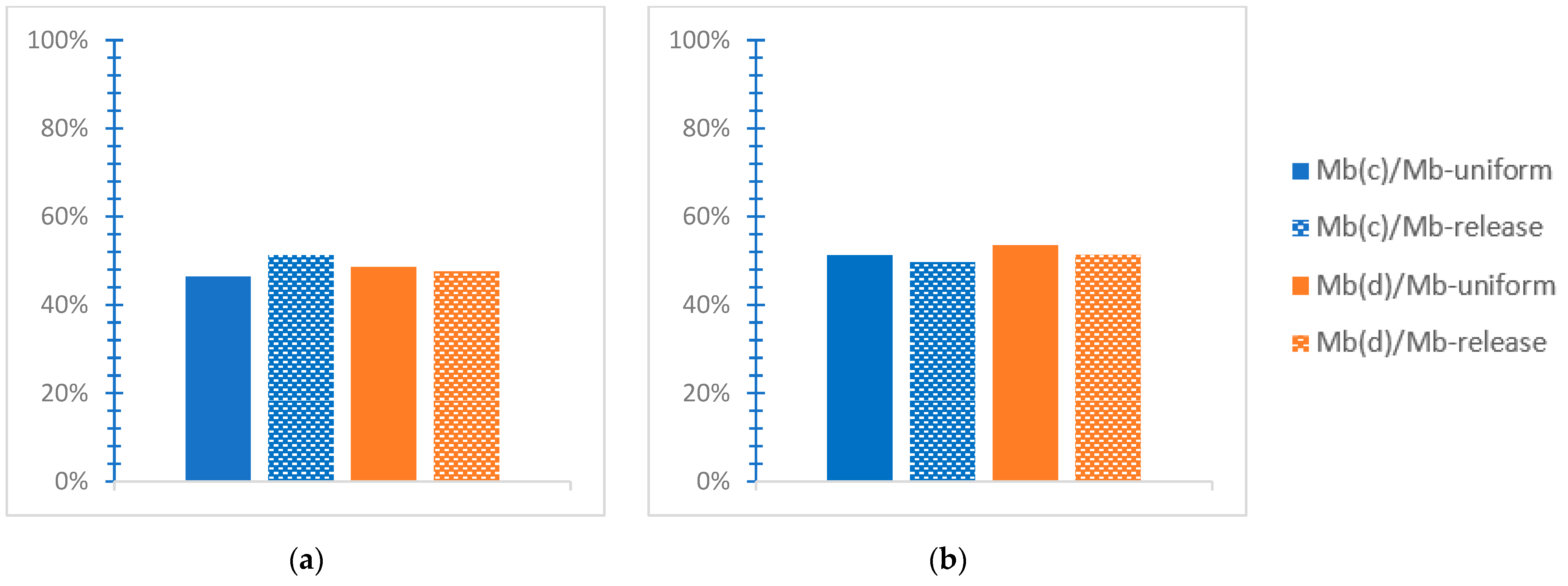
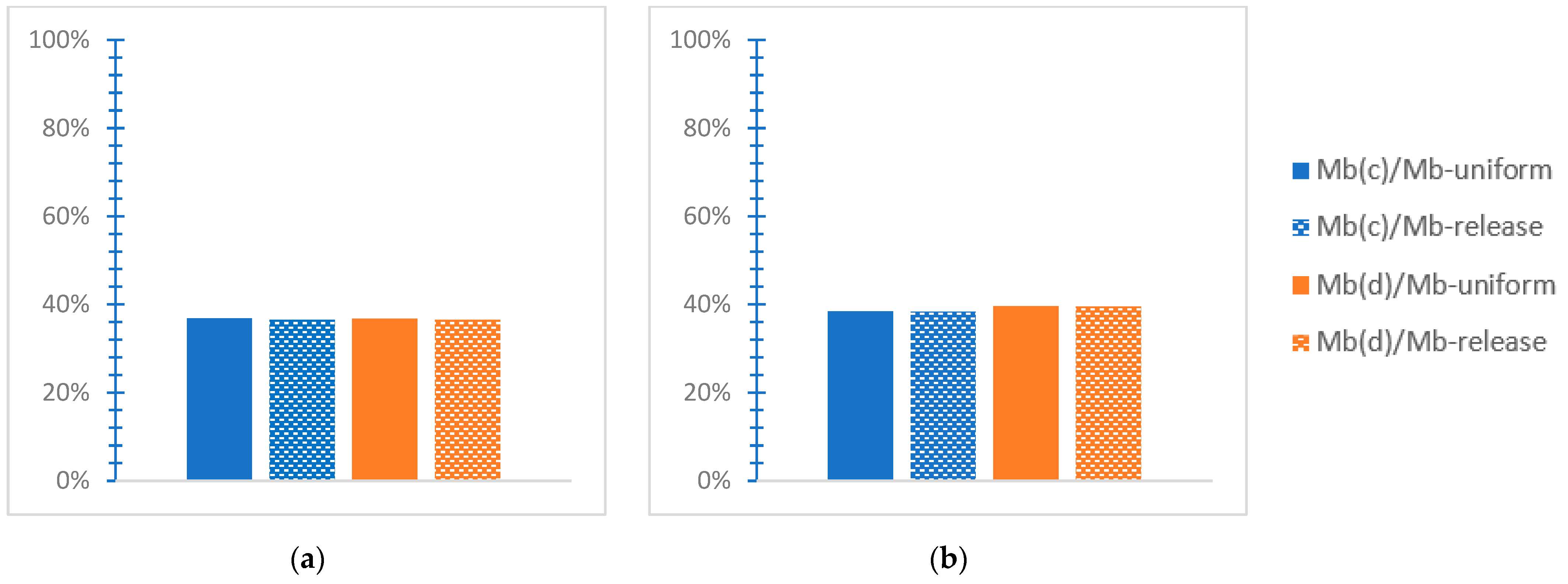
- “Mb(c)/Mb” is an analogous ratio considering the base moment for soil C, and Mb(d)/Mb refers to soil D.
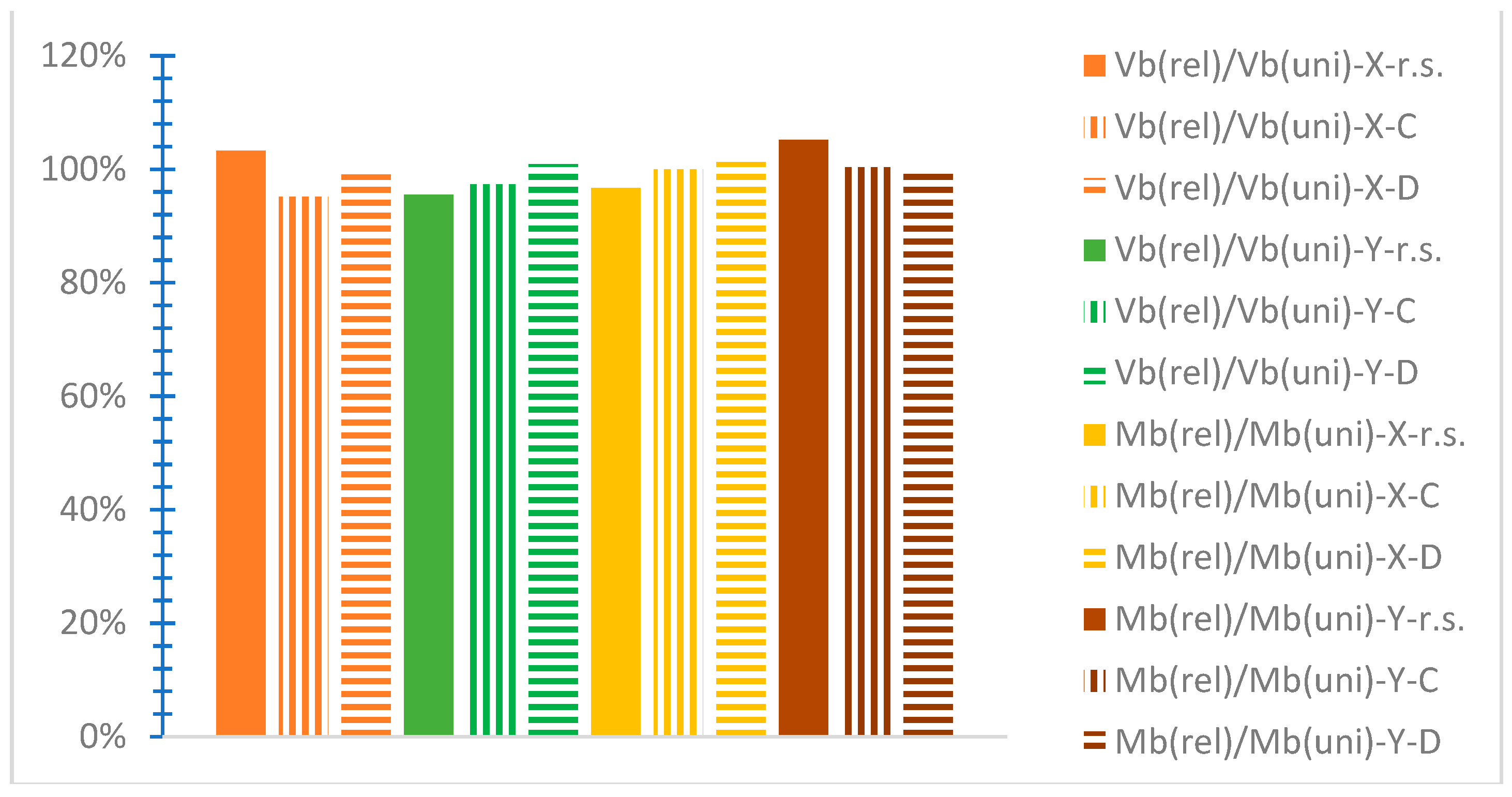
- “Vb(rel)/Vb(uni)” stands for the proportion of the greatest “absolute base shear value” [38] of the NLTH analyses for each mixed building for the “release” connection type divided by the corresponding value for the “uniform” connection type at both horizontal global axes, considering either the rigid soil “r.s.” or the SSI by the C soil type “C”, or the SSI via the D soil type “D”. Respectively, the “Mb(rel)/Mb(uni)” ratio refers to base moment ratio, with the same notations, “r.s.”, “C”, or “D”.
3.1. Comments on the Two-Story Mixed Model (RC1-ST1)
3.2. Comments on the Three-Story Mixed Model (RC2-ST1)
3.3. Comments on the Four-Story Mixed Model (RC3-ST1)
3.4. Comments on the Five-Story Mixed Model (RC3-ST2)
3.5. Comments on the Six-Story Mixed Model (RC4-ST2)
4. Conclusions
- The first story is heavily stressed by soil deformability, as compared with the rigid soil assumption, showing IDR values close to the applicable “CP” limit. Indicatively, the IDR may be greater by even 61~74% for deformable soil in comparison with the corresponding one for rigid soil.
- Considering soil deformability, the steel story shows increased IDR values, even close to 4%, which is the CP limit, as compared with the r/c part where the corresponding IDR may be less by 32%. The IDR increase in the steel story is more intense for the SSI than for the rigid base and even more obvious for the release connection type than the uniform one. In contrast, for the rigid soil assumption, the greatest IDR of the steel story tends to be smaller than that for the first r/c story by 50~65%.
- The SSI consideration may cause significant construction deformations, much higher than code restrictions, indicating building failure, while the latter is rather unusual for the rigid soil assumption.
- The SSI for soil type D tends to result in greater deformations than for soil type C when both are compared with the fixed base assumption.
- The soil’s deformability results in increased values of the base shear ratio but in smaller values of the base moment ratio. This means that deformable soil burdens the mixed building considering the base shear while favoring the structural response considering the base moment, comparatively with the rigid soil consideration.
- The release interconnection of the steel and r/c parts tends to affect the base shear by resulting in slightly smaller values and increasing the observed values of the base moment separately, considering the SSI, against the consideration of the rigid soil.
- The hinges at element ends tend to be burdened more by the SSI than by the rigid soil.
- Generally, the release interconnection of the steel component on the reinforced concrete one tends to increase the IDR values more accounting for the SSI than for the inflexible soil assumption. In the meantime, increased values of IDR are generally noticed for the inflexible soil and uniform connection, as compared with the other examined cases.
- The seismic response plots show some cases where a detrimental SSI effect is noticed on the behavior of the mixed model, while in other cases, an advantageous SSI is obvious, indicating an ambiguous SSI effect on the structural response. This means that the design analysis should be performed not only for the usual rigid soil assumption but also considering deformable soil to ensure the boundary conditions are examined and the extreme response parameters are recognized, leading to a safer mixed building conception.
Funding
Data Availability Statement
Conflicts of Interest
References
- EN 1992-1-1 Eurocode 2 (EC2); Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- EN 1993-1-1 Eurocode 3 (EC3); Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2009.
- EN 1998-5 Eurocode 8 (EC8); Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings, Part 3: Strengthening and Repair of Buildings, Part 5: Foundations, Retaining Structures and Geotechnical Aspects. Part 6: Towers, Masts and Chimneys. European Committee for Standardization: Brussels, Belgium, 2004.
- Maley, T.J.; Sullivann, T.J.; Pampanin, S. Issues with the seismic design of mixed MRF Systems. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisboa, Portugal, 24–28 September 2012. [Google Scholar]
- Villaverde, R. Seismic design of secondary structures: State of the art. J. Struct. Eng. 1997, 123, 1011–1019. [Google Scholar] [CrossRef]
- Askouni, P.K.; Papagiannopoulos, G.A. Seismic Behavior of a Class of Mixed Reinforced Concrete-Steel Buildings Subjected to Near-Fault Motions. Infrastructures 2021, 6, 172. [Google Scholar] [CrossRef]
- Askouni, P.K.; Papagiannopoulos, G.A. The Non-Linear Behavior of Mixed Reinforced Concrete–Steel Frames under Strong Earthquakes. Eng. Proc. 2023, 53, 15. [Google Scholar] [CrossRef]
- Askouni, P.K.; Papagiannopoulos, G.A. The Seismic Response of Mixed Reinforced Concrete–Steel Buildings Under Near-Fault Earthquakes. In Proceedings of the COMPDYN 2023, 9th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Athens, Greece, 12–14 June 2023. [Google Scholar] [CrossRef]
- Askouni, P.K. Τhe Behavior of Hybrid Reinforced Concrete-Steel Buildings under Sequential Ground Excitations. Computation 2023, 11, 102. [Google Scholar] [CrossRef]
- Pnevmatikos, N.; Blachowski, B.; Papavasileiou, G. Damage detection of mixed concrete/steel frame subjected to earthquake excitation. In Proceedings of the 7th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2019), Crete, Greece, 24–26 June 2019. [Google Scholar]
- Kaveh, A.; Ardebili, S.R. Optimal design of mixed structures under time-history loading using metaheuristic algorithm. Period. Polytech. Civ. Eng. 2023, 67, 57–64. [Google Scholar] [CrossRef]
- Bahri, F.; Bahri, F.; Moeini, M.E. Numerical investigation of a novel concrete-to-steel column splice in mixed structures in height. Structures 2023, 58, 105526. [Google Scholar] [CrossRef]
- Kiani, A.; Yang, T.Y.; Kheyroddin, A.; Kafi, M.A.; Naderpour, H. March. Quantification of seismic performance factors of mixed concrete/steel buildings using the FEMA P695 methodology. Structures 2024, 61, 106144. [Google Scholar] [CrossRef]
- Fanaie, N.; Shamlou, S.O. Response modification factor of mixed structures. Steel Compos. Struct. 2015, 19, 1449–1466. [Google Scholar] [CrossRef]
- Farghaly, A.A. Parametric study on equivalent damping ratio of different composite structural building systems. Steel Compos. Struct. 2013, 14, 349–365. [Google Scholar] [CrossRef]
- Huang, W.; Qian, J.; Zhou, Z.; Fu, Q. An approach to equivalent damping ratio of vertically mixed structures based on response error minimization. Soil Dyn. Earthq. Eng. 2015, 72, 119–128. [Google Scholar] [CrossRef]
- Sivandi-Pour, A.; Gerami, M.; Kheyroddin, A. Determination of modal damping ratios for non-classically damped rehabilitated steel structures. Iran. J. Sci. Technol. Trans. Civ. Eng. 2015, 39, 81. [Google Scholar]
- Sivandi-Pour, A.; Gerami, M.; Kheyroddin, A. Uniform damping ratio for non-classically damped hybrid steel concrete structures. Int. J. Civ. Eng. 2016, 14, 1–11. [Google Scholar] [CrossRef]
- Sivandi-Pour, A.; Gerami, M.; Khodayarnezhad, D. Equivalent modal damping ratios for non-classically damped hybrid steel concrete buildings with transitional storey. Struct. Eng. Mech. 2014, 50, 383–401. [Google Scholar]
- Papagiannopoulos, G.A. On the modal damping ratios of mixed reinforced concrete–steel buildings. Soil Dyn. Earthq. Eng. 2024, 178, 108481. [Google Scholar] [CrossRef]
- Mylonakis, G.; Syngros, C.; Gazetas, G.; Tazoh, T. The role of soil in the collapse of 18 piers of Hanshin Expressway in the Kobe earthquake. Earthq. Eng. Struct. Dyn. 2006, 35, 547–575. [Google Scholar] [CrossRef]
- Mylonakis, G.; Gazetas, G. Seismic soil-structure interaction: Beneficial or detrimental? J. Earthq. Eng. 2000, 4, 277–301. [Google Scholar] [CrossRef]
- Jahami, A.; Halawi, J.; Temsah, Y.; Jaber, L. Assessment of Soil–Structure Interaction Effects on the Beirut Port Silos Due to the 4 August 2020 Explosion: A Coupled Eulerian–Lagrangian Approach. Infrastructures 2023, 8, 147. [Google Scholar] [CrossRef]
- Yanik, A.; Ulus, Y. Soil–Structure Interaction Consideration for Base Isolated Structures under Earthquake Excitation. Buildings 2023, 13, 915. [Google Scholar] [CrossRef]
- Azhir, P.; Asgari Marnani, J.; Panji, M.; Rohanimanesh, M.S. A Coupled Finite-Boundary Element Method for Efficient Dynamic Structure-Soil-Structure Interaction Modeling. Math. Comput. Appl. 2024, 29, 24. [Google Scholar] [CrossRef]
- Karabalis, D.L.; Beskos, D.E. Dynamic response of 3-D flexible foundations by time domain BEM and FEM. Int. J. Soil Dyn. Earthq. Eng. 1985, 4, 91–101. [Google Scholar] [CrossRef]
- Karabalis, D.L. Non-singular time domain BEM with applications to 3D inertial soil–structure interaction. Soil Dyn. Earthq. Eng. 2004, 24, 281–293. [Google Scholar] [CrossRef]
- Riaz, M.R.; Motoyama, H.; Hori, M. Review of Soil-Structure Interaction Based on Continuum Mechanics Theory and Use of High Performance Computing. Geosciences 2021, 11, 72. [Google Scholar] [CrossRef]
- Pantelidis, L.; Gravanis, E. Elastic Settlement Analysis of Rigid Rectangular Footings on Sands and Clays. Geosciences 2020, 10, 491. [Google Scholar] [CrossRef]
- Anand, V.; Kumar, S.R. Seismic soil-structure interaction: A state-of-the-art review. Structures 2018, 16, 317–326. [Google Scholar] [CrossRef]
- Barnaure, M.; Manoli, D. Unfavourable seismic behaviour of reinforced concrete structures due to soil structure interaction. IOP Conf. Ser. Earth Environ. Sci. 2019, 362, 12119. [Google Scholar] [CrossRef]
- Krishnan, R.; Sivakumar, V.L. The Effect of Soil-Structure Interaction (SSI) on Structural Stability and Sustainability of RC Structures. Civ. Environ. Eng. Rep. 2024, 34, 116–136. [Google Scholar] [CrossRef]
- Mata, R.; Nuñez, E.; Hernández, M.; Correa, C.; Bustamante, G. Seismic Performance of RC Moment Frame Buildings Considering SSI Effects: A Case Study of the New Venezuelan Seismic Code. Buildings 2023, 13, 1694. [Google Scholar] [CrossRef]
- Wang, J.; Xie, Y.; Guo, T.; Du, Z. Predicting the Influence of Soil–Structure Interaction on Seismic Responses of Reinforced Concrete Frame Buildings Using Convolutional Neural Network. Buildings 2023, 13, 564. [Google Scholar] [CrossRef]
- Oz, I.; Senel, S.M.; Palanci, M.; Kalkan, A. Effect of soil-structure interaction on the seismic response of existing low and mid-rise RC buildings. Appl. Sci. 2020, 10, 8357. [Google Scholar] [CrossRef]
- Kamal, M.; Inel, M. Correlation between Ground Motion Parameters and Displacement Demands of Mid-Rise RC Buildings on Soft Soils Considering Soil-Structure-Interaction. Buildings 2021, 11, 125. [Google Scholar] [CrossRef]
- Askouni, P.K.; Karabalis, D.L. The Modification of the Estimated Seismic Behaviour of R/C Low-Rise Buildings Due to SSI. Buildings 2022, 12, 975. [Google Scholar] [CrossRef]
- Askouni, P.K.; Karabalis, D.L. SSI influence on the seismic response of asymmetrical small, low-rise R/C buildings. Structures 2021, 32, 1355–1373. [Google Scholar] [CrossRef]
- Askouni, P.K.; Karabalis, D.L. SSI effects on the redistribution of seismic forces in one-storey R/C buildings. Earthq. Struct. 2021, 20, 261–278. [Google Scholar] [CrossRef]
- Askouni, P.K.; Karabalis, D.L.; Beskos, D.E. SSI effects on r/c one-storey buildings under seismic loadings. In Proceedings of the EURODYN 2020, XI—International Conference on Structural Dynamics, Athens, Greece, 23–26 November 2020. [Google Scholar] [CrossRef]
- Askouni, P.K.; Karabalis, D.L. The Alteration of the Seismic Behaviour of Asymmetrical Low-Rise R/C Buildings due to Soil-Structure Interaction. In Proceedings of the 13th International Congress on Mechanics HSTAM2022, Patras, Greece, 24–27 August 2022. [Google Scholar]
- Askouni, P.K.; Karabalis, D.L. The redistribution of seismic forces in low-rise R/C buildings due to Soil-Structure Interaction. In Proceedings of the 10th GRACM International Congress on Computational Mechanics, Athens, Greece, 5–7 July 2021. [Google Scholar]
- Mekki, M.; Elachachi, S.M.; Breysse, D.; Zoutat, M. Seismic behavior of RC structures including soil-structure interaction and soil variability effects. Eng. Struct. 2016, 126, 15–26. [Google Scholar] [CrossRef]
- Tahghighi, H.; Mohammadi, A. Numerical evaluation of soil–structure interaction effects on the seismic performance and vulnerability of reinforced concrete buildings. Int. J. Geomech. 2020, 20, 04020072. [Google Scholar] [CrossRef]
- Altunişik, A.C.; Kalkan, E. Earthquake incidence angle influence on seismic performance of reinforced concrete buildings. Sigma J. Eng. Nat. Sci. 2017, 35, 609–631. [Google Scholar]
- Athanatopoulou, A.M. Critical orientation of three correlated seismic components. Eng. Struct. 2005, 27, 301–312. [Google Scholar] [CrossRef]
- Altunişik, A.C.; Kalkan, E. Influence of earthquake angle on seismic performance of concrete highway bridges. Građevinar 2023, 75, 1013–1024. [Google Scholar] [CrossRef]
- Tehrani, P.; Ghanbari, R. Investigating different methods for application of earthquake records in seismic evaluation of irregular RC bridges considering incident angles. Structures 2021, 32, 1717–1733. [Google Scholar] [CrossRef]
- EN 1991-1-1 Eurocode 1 (EC1); Actions on Structures—Part 1-1: General Actions, Densities, Self-Weight, Imposed Loads for Buildings. European Committee for Standardization: Brussels, Belgium, 2001.
- EN 1997-1 Eurocode 7 (EC7); Geotechnical Design—Part 1: General Rules. European Committee for Standardization: Brussels, Belgium, 2003.
- Mulliken, J.S.; Karabalis, D.L. Discrete model for dynamic through-the-soil coupling of 3-d foundations and structures. Earthq. Eng. Struct. Dyn. 1998, 27, 687–710. [Google Scholar]
- SAP 2000; Version 22.2.0; Static and Dynamic Finite Element Analysis of Structures; Computers and Structures (CSI): Berkeley, CA, USA, 2020.
- Center for Engineering Strong Motion Data. Available online: www.strongmotioncenter.org (accessed on 3 May 2021).
- SeismoSpect. Software for Signal Processing for Ground Motion Records: Version 2023; Seismosoft. Available online: https://seismosoft.com/products/seismospect/ (accessed on 1 April 2024).
- ASCE 41-17; Seismic Evaluation and Retrofit of Existing Buildings. American Society of Civil Engineers (ASCE): Reston, VA, USA, 2017.
- FEMA-356; Prestandard and Commentary for the Seismic Rehabilitation of Buildings. Federal Emergency Management Agency: Washington, DC, USA, 2000.
- Penelis, G.G.; Kappos, A.J. Earthquake-Resistant Concrete Structures, 1st ed.; CRC Press: London, UK, 1997. [Google Scholar] [CrossRef]
- Fardis, M.N. Seismic Design, Assessment and Retrofitting of Concrete Buildings: Based on EN-Eurocode 8, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Papagiannopoulos, G.A.; Hatzigeorgiou, G.D.; Beskos, D.E. Seismic Design Methods for Steel Building Structures, 1st ed.; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Darshini, B. Comparison of seismic behaviour of composite and rcc columns in multistoried commercial building—A review. Int. Res. J. Eng. Technol. 2020, 7, 731–735. [Google Scholar]
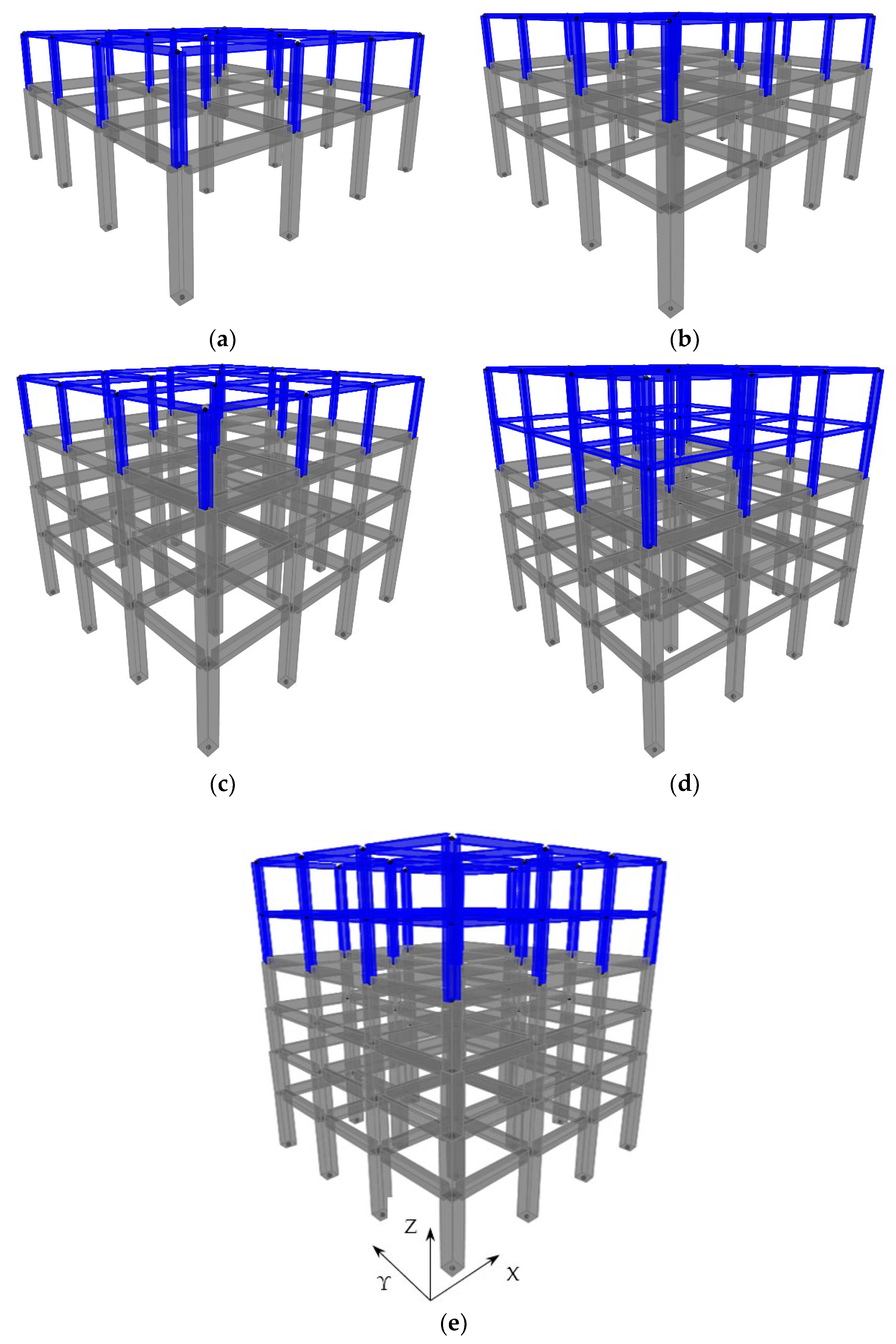











| RC1-ST1 model | Columns | Beams | |||||
|---|---|---|---|---|---|---|---|
| story | material | Cross-section (m2) | Axial reinforcement | Vertical reinforcement | Cross-section (m2) | Axial reinforcement | Vertical reinforcement |
| 1 | r/c | 0.50 × 0.50 | 8Φ22 | Φ8/10 | 0.25 × 0.60 | 8Φ18 | Φ8/10 |
| 2 | steel | HEA360 | IPE270 | ||||
| RC2-ST1 model | Columns | Beams | |||||
| Story | material | Cross-section (m2) | Axial reinforcement | Vertical reinforcement | Cross-section (m2) | Axial reinforcement | Vertical reinforcement |
| 1 | r / c | 0.55 × 0.55 | 16Φ20 | Φ8/10 | 0.25 × 0.60 | 8Φ20, 8Φ10 | Φ8/10 |
| 2 | r/c | 0.50 × 0.50 | 8Φ20, 8Φ10 | Φ8/10 | 0.25 × 0.60 | 8Φ18 | Φ8/10 |
| 3 | steel | HEA360 | IPE270 | ||||
| RC3-ST1 model | Columns | Beams | |||||
| Story | material | Cross-section (m2) | Axial reinforcement | Vertical reinforcement | Cross-section (m2) | Axial reinforcement | Vertical reinforcement |
| 1 | r/c | 0.60 × 0.60 | 16Φ20 | Φ8/10 | 0.25 × 0.70 | 8Φ20, 8Φ10 | Φ8/10 |
| 2 | r/c | 0.60 × 0.60 | 8Φ20, 8Φ16 | Φ8/10 | 0.25 × 0.70 | 8Φ20, 8Φ10 | Φ8/10 |
| 3 | r/c | 0.50 × 0.50 | 8Φ20, 8Φ10 | Φ8/10 | 0.25 × 0.60 | 8Φ18 | Φ8/10 |
| 4 | steel | HEA360 | IPE270 | ||||
| RC3-ST2 model | Columns | Beams | |||||
| Story | material | Cross-section (m2) | Axial reinforcement | Vertical reinforcement | Cross- section (m2) | Axial reinforcement | Vertical reinforcement |
| 1 | r/c | 0.70 × 0.70 | 8Φ22, 16Φ20 | Φ8/10 | 0.25 × 0.70 | 8Φ20, 8Φ16 | Φ8/10 |
| 2 | r/c | 0.70 × 0.70 | 16Φ20 | Φ8/10 | 0.25 × 0.70 | 2Φ20, 3Φ10 | Φ8/10 |
| 3 | r/c | 0.70 × 0.70 | 8Φ20, 8Φ10 | Φ8/10 | 0.25 × 0.60 | 8Φ18 | Φ8/10 |
| 4 | steel | HEΒ500 | IPE360 | ||||
| 5 | steel | HEΒ500 | IPE300 | ||||
| RC4-ST2 model | Columns | Beams | |||||
| story | material | Cross- section (m2) | Axial reinforcement | Vertical reinforcement | Cross-section (m2) | Axial reinforcement | Vertical reinforcement |
| 1 | r/c | 0.70 × 0.70 | 32Φ20 | Φ8/10 | 0.25 × 0.70 | 8Φ20, 8Φ10 | Φ8/10 |
| 2 | r/c | 0.70 × 0.70 | 16Φ20 | Φ8/10 | 0.25 × 0.70 | 8Φ18 | Φ8/10 |
| 3 | r/c | 0.70 × 0.70 | 16Φ20 | Φ8/10 | 0.25 × 0.70 | 8Φ18 | Φ8/10 |
| 4 | r/c | 0.70 × 0.70 | 16Φ20 | Φ8/10 | 0.25 × 0.70 | 8Φ18 | Φ8/10 |
| 5 | steel | HEA500 | IPE400 | ||||
| 6 | steel | HEA500 | IPE440 | ||||
| Direction | Mass Ratio β | Equivalent Radius ro | Virtual Soil Mass mv | Static Stiffness K | Damping C |
|---|---|---|---|---|---|
| Vertical | |||||
| Horizontal | |||||
| Rocking | |||||
| Torsion |
| Mixed Building | First Eigenperiod (sec) | |||||
|---|---|---|---|---|---|---|
| Rigid Soil | Soil C | Soil D | ||||
| Uniform | Release | Uniform | Release | Uniform | Release | |
| RC1-ST1 | 0.399 | 0.429 | 0.775 | 0.777 | 0.782 | 0.784 |
| RC2-ST1 | 0.506 | 0.522 | 0.910 | 0.911 | 0.919 | 0.920 |
| RC3-ST1 | 0.559 | 0.571 | 1.040 | 1.040 | 1.051 | 1.052 |
| RC3-ST2 | 0.581 | 0.601 | 1.135 | 1.135 | 1.148 | 1.148 |
| RC4-ST2 | 0.498 | 0.509 | 1.076 | 1.117 | 1.090 | 1.131 |
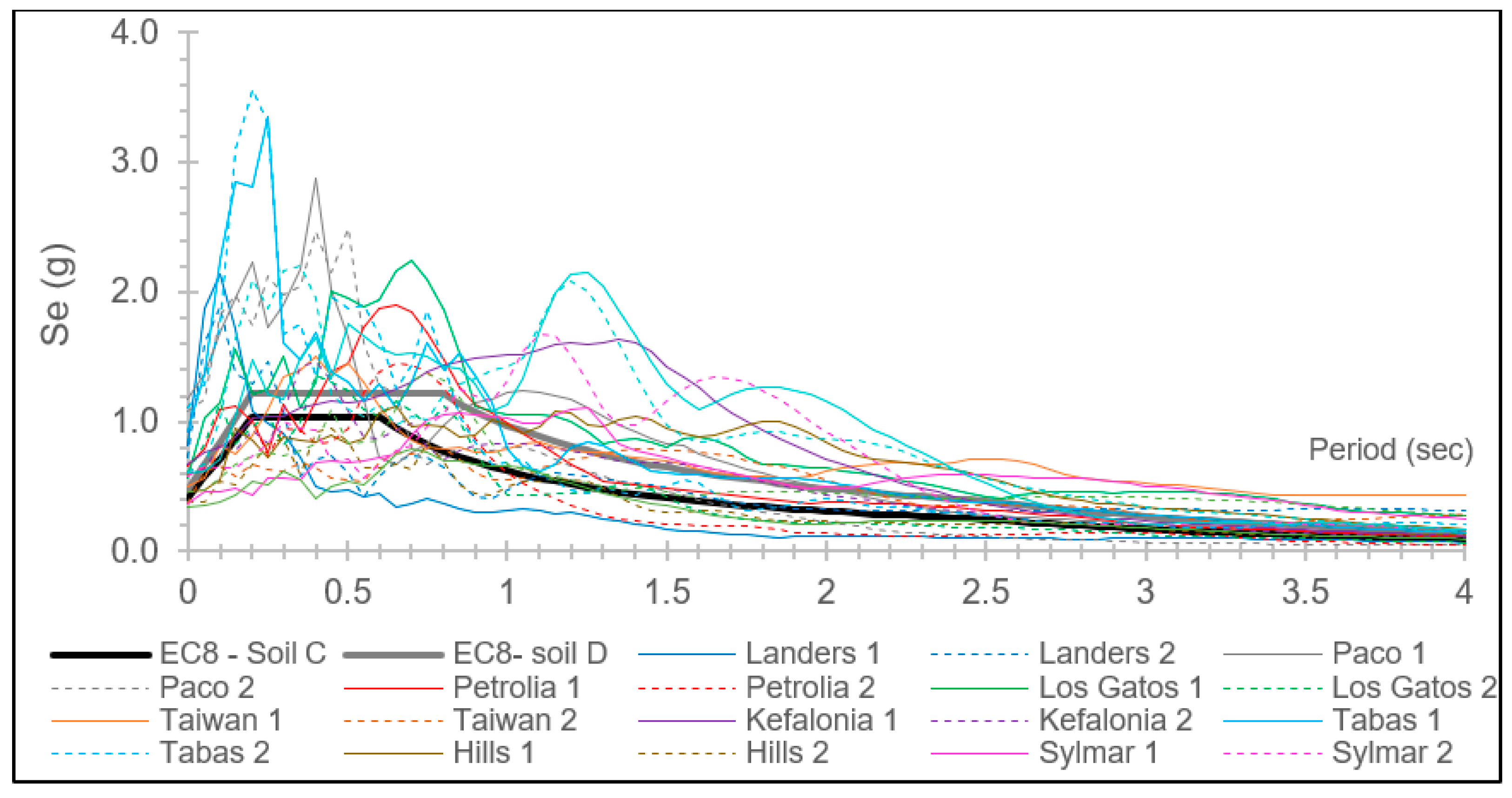
| Earthquake and Location | Year | Earthquake Recording Station | Plot Name | Duration (sec) | Mw | PGA (g) |
|---|---|---|---|---|---|---|
| San Fernando (USA) | 1971 | Pacoima Dam | Paco | 20.48 | 6.6 | 1.17/1.08 |
| Tabas (Iran) | 1978 | Tabas | Tabas | 63.48 | 7.1 | 0.93/1.10 |
| Imperial Valley (USA) | 1979 | El Centro Array 6 | Array | 36.90 | 6.5 | 0.34/0.46 |
| Superstition Hills (USA) | 1987 | Parachute Test Site | Hills | 22.40 | 6.5 | 0.45/0.38 |
| Loma Prieta (USA) | 1989 | Los Gatos | Los Gatos | 25.05 | 7.0 | 0.56/0.61 |
| Cape Mendocino (USA) | 1992 | Petrolia | Petrolia | 60.00 | 6.9 | 0.66/0.59 |
| Landers (USA) | 1992 | Lucerne Valley | Landers | 48.05 | 7.3 | 0.81/0.73 |
| Northridge (USA) | 1994 | Sylmar Converter St. | Sylmar | 28.48 | 6.7 | 0.37/0.58 |
| Kobe (Japan) | 1995 | Takatori | Kobe | 41.15 | 6.9 | 0.61/0.62 |
| Chi-Chi (Taiwan) | 1999 | TCU 052 | Taiwan | 90.01 | 7.6 | 0.50/0.36 |
| Kefalonia (Greece) | 2014 | Lixouri | Lixouri | 67.74 | 6.1 | 0.67/0.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Askouni, P.K. The Influence of Soil Deformability on the Seismic Response of 3D Mixed R/C–Steel Buildings. Infrastructures 2024, 9, 80. https://doi.org/10.3390/infrastructures9050080
Askouni PK. The Influence of Soil Deformability on the Seismic Response of 3D Mixed R/C–Steel Buildings. Infrastructures. 2024; 9(5):80. https://doi.org/10.3390/infrastructures9050080
Chicago/Turabian StyleAskouni, Paraskevi K. 2024. "The Influence of Soil Deformability on the Seismic Response of 3D Mixed R/C–Steel Buildings" Infrastructures 9, no. 5: 80. https://doi.org/10.3390/infrastructures9050080
APA StyleAskouni, P. K. (2024). The Influence of Soil Deformability on the Seismic Response of 3D Mixed R/C–Steel Buildings. Infrastructures, 9(5), 80. https://doi.org/10.3390/infrastructures9050080






