Abstract
This study intended to measure the efficiency of different strengthening techniques to advance the flexural characteristics of reinforced concrete (RC) beams using glass fiber-reinforced polymer (GFRP) laminates, including externally bonded reinforcement (EBR), externally bonded reinforcement on grooves (EBROG), externally bonded reinforcement in grooves (EBRIG), and the near-surface mounted (NSM) system. A new NSM technique was also established using an anchorage rebar. Then, the effect of the NSM method with and without externally strengthening GFRP laminates was studied. Twelve RC beams (150 × 200 × 1500 mm) were manufactured and examined under a bending system. One specimen was designated as the control with no GFRP laminate. To perform the NSM method, both steel and GFRP rebars were used. In the experiments, capability, as well as the deformation and ductileness of specimens, were evaluated, and a comparison was made between the experimental consequences and existing standards. Finally, a new regression was generated to predict the final resistance of RC beams bound with various retrofitting techniques. The findings exhibited that the NSM technique, besides preserving the strengthening materials, could enhance the load-bearing capacity and ductileness of RC beams up to 42.3% more than the EBR, EBROG, and EBRIG performances.
1. Introduction
Fiber-reinforced polymer (FRP) composites have become a more dependable material in the last twenty years for civil engineering applications such as building new structures and renovating ageing infrastructure. In addition to offering significant resistance against fatigue loading, shock, and corrosion, GFRP composites also enhance a structure’s ability to absorb energy over the long term [,,,,,,,]. Many research attempts have been conducted employing materials including steel, concrete, and GFRP jacketing to restore and retrofit both minor and major damage as well as restore the capacity and ductileness of damaged RC elements [,,,,,,,]. The most popular way for reinforcing RC beams is the EBR technique. The early debonding of sheets from the concrete surface prevents this technology from achieving the full tensile strength of GFRP laminates [,,,,,]. Mostofinejad and Mahmoudabadi designed the grooving technique to delay or smoothly stop the debonding of GFRP laminates. This procedure was named the EBROG technique []. In another study, Mostofinejad and Shameli developed an enhanced grooving technique by inserting the GFRP laminates of the EBROG technique into grooves. This method was named the EBRIG method, and it allows a greater interaction zone between the GFRP and the concrete surface compared to the EBROG procedure. The contact between the FRP and concrete increases in the EBRIG process by creating longitudinal grooves and applying the FRP laminates to the surfaces. Consequently, in comparison to alternative strengthening techniques, noticeably larger failure loads may be achieved. According to their results, the bending was improved by 140% when the EBRIG method was used in comparison with the EBROG technique without longitudinal grooves [].
Mukhtar [] modified the shear test for the bond–slip properties of EBR-FRP–concrete interfaces while considering the effects of various aggregates. It was found that the use of steel slag aggregates delayed debonding among the FRP laminates and concrete, and it improved the bending strength and ductility of RC beams as well. Mostofinejad and Moghaddas [] assessed the bond performances among the concrete surface and FRP laminates under both the EBR and EBROG techniques, considering the category of longitudinal rebars (steel and GFRP). Thus, 12 RC beams were used and examined. The results showed that EBROG, compared with EBR, led to rises in the resistance and deformation of RC beams, avoiding a debonding mechanism. In another investigation, Moshiri et al. [] measured the bond performance between the pre-stressed carbon fiber reinforced polymer (CFRP) concrete surface for EBR and EBROG. According to the results, CFRP prestressing substantially improved the bond–slip performance among the CFRP laminates and concrete, particularly when the EBROG method was utilized.
Arabzadeh and Karimizadeh [] measured the consequence of EBR- and EBROG-CFRP on improving RC deep beams with an opening. They determined the advantage of the EBROG technique, as well as the effectiveness of the persuaded alignment of strengthening laminates, in improving the resistance and deformation of RC beams. Mostofinejad and Shameli [] explored the behaviors of EBROG techniques using multilayer FRP laminates to increase the flexural characteristics of RC beams. The outcomes showed that, in comparison to the control beam, the EBROG approach produces larger failure loads in RC beams reinforced with multi-FRP laminates. Later, Mostofinejad and Shameli [] assessed the effect of the EBRIG process in interrupting the debonding of FRP laminates in RC beams. Thirty-two RC beams (120 × 140 × 1000 mm) were manufactured, strengthened with various FRP layers, and evaluated in terms of their performance. They presented that the EBRIG and EBROG methods were carried out for one FRP layer; however, EBRIG and EBROG allowed for higher failure loads and deformation, relative to those of the multiple-layer EBROG-FRP technique. Recently, Sena-Cruz et al. [] projected a novel technique called “mechanically fastened and externally bonded reinforcement” (MF-EBR). This method merges the MF-FRP technique with the external adhesion in the EBR technique. The MF-EBR method enhances the flexural strength and ductility of RC beams, compared with conventional EBR, EBROG, and EBRIG, even though the EBR, EBROG, and EBRIG methods delay, or in some cases even eradicate, the debonding phenomenon. To overcome these weaknesses, numerous works have been performed and shown that one of the most effective techniques is the NSM process. The NSM approach is a more efficient way of delaying the debonding performance than the EBR technique [,,,,,,].
In their study on the flexural performance of RC beams reinforced with the NSM-CFRP technology, Deng et al. [] investigated the effects of the concrete type, prestress ratio, and bond length on bending, deformation, and crack propagation. The results showed that the resistance of RC beams strengthened with NSM-CFRP was substantially larger than that of the simple sample. In addition, the strengthened specimens exhibited greater first-cracking, yielding, and maximum loads as the bond length and pre-stress level amplified up to a serious ratio. In another research, the effectiveness of the NSM-FRP strengthening technique on the bending responses of T-shaped concrete beams was assessed by Zhang et al. []. Their findings indicated that using FRP bars in the NSM approach significantly improved the stiffness and ductility of RC beams. Additionally, Barris et al. [] looked into the flexural properties of CFRP-reinforced concrete beams strengthened using the NSM technique. They found that the NSM technique is an effective method for improving the bending of RC beams internally reinforced with GFRP bars, despite the high degrees of deformability of GFRP. Later, Al-Abdwais and Al-Mahaidi [] evaluated the characteristics of RC beams strengthened with NSM-CFRP rebars. Their experiments illustrated a substantial and high increase in bending, attaining nearly the same consequences achieved from epoxy adhesives. In another study, Al-Obaidi et al. [] investigated the bending strengthening of RC beams with NSM-CFRP bars using mechanical interlocking. On the other hand, various studies have been conducted on numerical models to examine collapse phenomena in structural concrete beams with different fracture approaches. In this regard, Rimkus et al. [] measured the performance of RC beams with the use of uncertainty theory. The experimental results from testing RC beams in their investigation confirmed the uncertainty of a crack width model. The impacts of the bond, fracture energy, and mesh size of finite elements are included in the parametric analysis of the numerical model. The fracture mechanic-based smeared crack model was found to be capable of accurately predicting the maximum crack width, according to the model uncertainty analysis. In another investigation, De Maio et al. [] utilized a combined ALE-cohesive fracture technique for an arbitrary crack growth examination. Their new model substantially eliminates the well-known mesh dependency concerns of the typical discrete fracture techniques and permits multiple crack starts and propagation without necessitating mesh-updated processes. A reasonable comparison with tests and numerical studies of mixed-mode fracture in concrete specimens demonstrated the efficacy and dependability of the suggested model in forecasting arbitrary crack propagation.
The first portion of this research intended to measure the bond performance of NSM-CFRP bars considering different bar diameters. In the second section, RC beams were strengthened using the previously described NSM-CFRP strengthening technique. According to the literature, an RC beam with a lower steel rebar ratio benefits more from strengthening; improvements ranged from 35% to 70% for a 0.7% rebar ratio and from 60% to 130% for a 0.4% rebar ratio. Figure 1 summarizes the advantages and disadvantages of different strengthening techniques that have been discussed in this section.
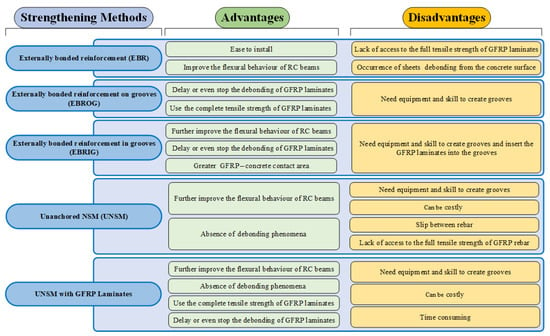
Figure 1.
Advantages and disadvantages of strengthening methods.
2. Research Significance
The impact of EBR, EBROG, and ENRIG on the performance of RC beams has been the subject of several investigations [,,,]. The literature indicates that strengthening RC beams with FRP laminates plays an effective role in improving their flexural response [,,,,,,,,,,,,,]. In 2010, Mostofinejad and Mahmoudabadi [] discovered that piercing the stress transfer area between concrete and the FRP sheet inside the concrete substrate, creating longitudinal grooves created on the surfaces of the beams, as opposed to traditional surface preparation, significantly increase the beams’ final resistance. In another investigation in 2013, it was demonstrated by Mostofinejad and Shameli [] that the EBRIG approach and the NSM method are comparable. On the other hand, an FRP sheet is directly bonded to both the surfaces outside and within the grooves on the tension face of the beam in the EBRIG approach, whereas the FRP bars or strips are fully attached inside the grooves in the NSM process. However, numerous studies have examined how various strengthening techniques affect the flexural behavior of reinforced concrete beams, but there is no study about the unanchored NSM method; moreover, to date, the simultaneous use of both GFRP rebar and laminates has been not studied. Therefore, in the current evaluation, the impacts of various GFRP-strengthening methods were studied and compared. In addition, a new strengthening NSM method was introduced that uses an anchorage rebar. Then, the effect of the NSM method with and without externally strengthening GFRP laminates was studied. Finally, the consequences were compared with existing standard necessities, and a novel model was developed to predict the ultimate load-bearing capacity of RC beams strengthened with various retrofitting techniques. Figure 2 shows the overall impression of the experimental program followed in the current evaluation.
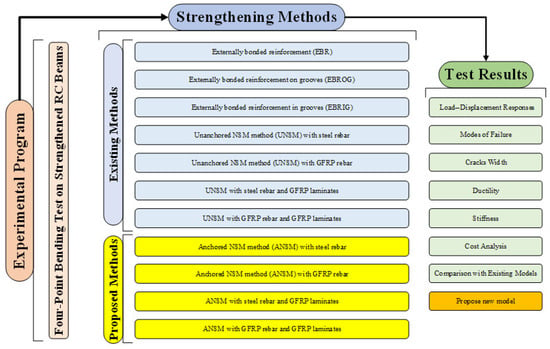
Figure 2.
General overview of the current study program.
3. Specimens’ Characteristics
3.1. Geometric Dimensions and Boundary Condition
In this study, 12,150 × 200 × 1500 mm specimens were manufactured. To reinforce the beams, 20 mm and 10 mm diameter rebars were employed as longitudinal tensile and compressive reinforcement, respectively. The geometric characteristics and rebar setup are presented in Figure 3. The plan of the bars was equal in all the specimens, and the compressive and tensile bar areas were 157 mm2 and 628 mm2, correspondingly. In addition, 8 mm rebars with 100 mm spacing were employed as stirrup bars. One specimen without GFRP fabric was selected as a control. Moreover, the 25 mm concrete cover thickness was considered constant for all specimens. The EBR, EBROG, and EBRIG methods were used to strengthen one specimen each. Consequently, for each UNSM and ANSM method, two specimens were used, reinforced by GFRP and steel rebars using the NSM method. The characteristics of the generated beams are listed in Table 1. In addition, S and G after the strengthening name indicate the type of rebar used in the groove. For instance, ANSM-S indicates a specimen strengthened using the anchorage NSM technique when a steel rebar was also put into the groove.
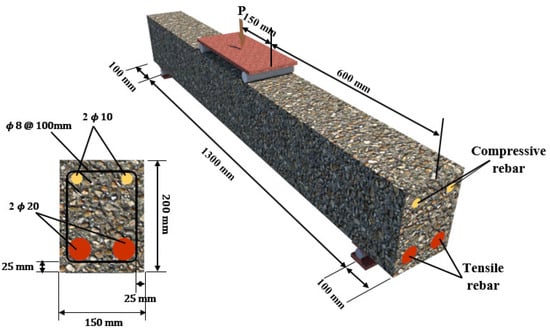
Figure 3.
Geometry of the specimens and rebar setup.

Table 1.
Characteristics of the specimens.
Figure 4 illustrates the four-point bending configuration that was used to test the specimens 28 days after curing. A 500 kN load cell applied force on the specimens at a 5 mm/min rate. The load was delivered at two points that were 300 mm apart. The specimens were supported by two round supports located at 100 mm from the two ends of the samples. The test was performed under displacement control conditions and stopped at complete failure, where the beam lost its resistance completely and the strength declined abruptly. In addition, two LVDTs with an accuracy of 0.001 mm were installed at the mid-span under the specimens to measure the deflection [].

Figure 4.
Test setup.
3.2. Concrete
In this study, Ordinary Portland Cement (OPC) with bulk density, normal consistency, and initial and final setting times of 1390.31 kg/m3, 29%, 143 min and 314 min, respectively, was employed to make concrete mixes. The concrete mixture composition used in this study is given in Table 2. To measure the compressive resistance of concrete in each concrete mix, three 150 × 150 × 150 mm cube samples were cast and evaluated under a hydraulic jack at 28 days of curing age []. The specimens’ compressive strength was determined by averaging the values of three samples (Table 3).

Table 2.
Concrete mix design (kg/m3).

Table 3.
Compressive resistance of beams (MPa).
3.3. GFRP Laminates
To strengthen the beams, a unidirectional GFRP fabric with a 100 mm width and 0.36 mm thickness was used as 100 m/roll, with the model of SikaWrap430G utilized. This laminates are produced by Sika Corporation in New Jersey, USA. The properties of the fabrics used are presented in Table 4, as per the manufacturer’s directory. GFRP laminates were fastened on the beams’ surfaces using S&P-55 HP resin produced by impson Strong-Tie in Switzerland with a weight ratio of 0.5:1. The resin’s characteristics are provided in Table 5 [,].

Table 4.
Mechanical characteristics of used polymer fiber laminate 1.

Table 5.
Properties of epoxy resin 1.
3.4. Steel Rebars
Rebars with diameters of 20 mm, 10 mm, and 8 mm were employed as tensile, compressive, and transverse reinforcements, correspondingly. Steel bars were tested using a direct tension setup according to ASTM A615 [], and their mechanical properties are provided in Table 6.

Table 6.
Rebars test results.
3.5. GFRP Rebars
Furthermore, GFRP rebars were used to reinforce beams for the external strengthening method, not in the original beam, under the GFRP laminate using the NSM technique. GFRP rebars were tested using a direct tensile setup as per ASTM D7957 []. Therefore, the elastic modulus and the ultimate resistance were obtained as 38.7 GPa and 657 MPa, respectively.
4. Strengthening Procedure
In this experimental program, the beams were characterized into six sets, in addition to that of the control sample, based on the strengthening techniques, as described below.
4.1. Externally Bonded Reinforcement (EBR)
Following the specimens’ curing process, the GFRP laminates were installed by completing the surface preparation process for the beams’ tensile surface. For surface preparation, a grinder with a dedicated concrete rubbing disk was utilized. The beam surface was completely free of concrete paste, providing a suitable surface for the setting up of GFRP laminates. Using an air jet, the beams’ surface was thoroughly cleaned of any contaminants and dust following the removal of the concrete paste. At that time, the pores in the specimens’ surface were repaired using resin as needed to reduce the pores on the surface. Then, the GFRP laminates were installed on the specimens’ surfaces using the wet layup process. The impregnated GFRP laminates were placed on the beams after the glue had been applied to the surface. Then, after the resin hardened, a 0.5 mm thickness resin was applied on the first layer of GFRP laminates, and then a second layer was applied. A roller tube was employed to remove the air, and two weeks were needed for the glue to set before loading. This strengthening method was performed according to previous studies, as shown in Figure 5 [,,].
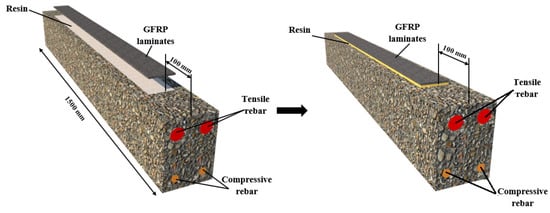
Figure 5.
Strengthening with GFRP-EBR.
4.2. Externally Bonded Reinforcement on Grooves (EBROG)
In the EBR process, the detachment of the laminates typically happens within a thin mortar-rich layer of the beam substrate. In the EBROG technique, two parallel grooves with a width, depth, and length of 8 mm, 10 mm, and 1300 mm, correspondingly, were created on the specimen’s surface from the tension face using a diamond blade. These groove dimensions were considered according to previous investigations on the EBROG method []. Then, the grooves were entirely prepared using an air jet and water jet to eliminate all possible dust particles. Thus, the groove was filled with resin. Then, one layer of GFRP laminate was mounted on the occupied grooves’ surfaces. After the resin hardened, a 0.5 mm thickness resin was applied on the first layer of GFRP laminates, and then a second layer was applied, as seen in Figure 6. Because the binding stresses are transferred to deeper concrete layers at the interface between the GFRP laminates and beam surface, the presence of grooves increases the bonding resistance [,].
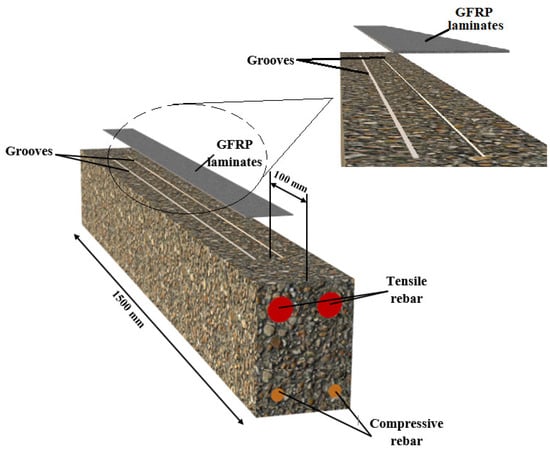
Figure 6.
Strengthening with GFRP-EBROG.
4.3. Externally Bonded Reinforcement in Grooves (EBRIG)
This method is the same as the EBROG procedure, and the only difference is the type of GFRP laminate installation. In this technique, two longitudinal notches were created on the specimens’ surfaces and were prepared just as in the EBROG process. The notches’ surfaces were enclosed with epoxy resin. Next, GFRP laminates were immediately affixed to the beam’s tension face’s external and internal groove surfaces as well as their interior surfaces. Again, the resin was administered on the surface to cover the GFRP laminate sheets in the grooves and on the specimen’s tensile surface with a very thin layer of 0.5 mm thick epoxy resin. This method was performed similarly to previous investigations [], and it is illustrated in Figure 7.
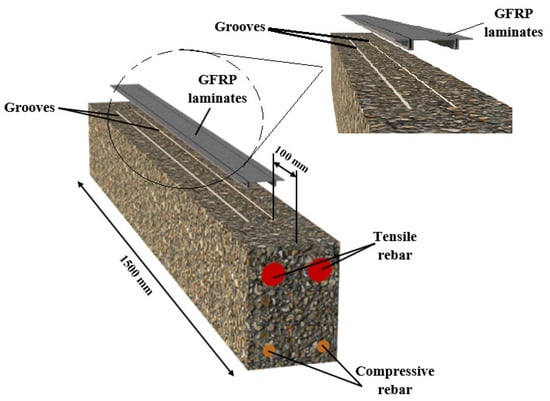
Figure 7.
Strengthening with GFRP-EBRIG.
4.4. Unanchored NSM Method (UNSM)
In this technique, one groove with a width, depth, and length of 8 mm, 30 mm, and 1300 mm, correspondingly, was created in the middle of the tension side of the beams, as shown in Figure 8. The groove was prepared using an air jet and water jet before the epoxy resin was applied to fill 2/3 of the groove depth. Then, an 8 mm steel or GFRP rebar was placed into the groove, and the groove was then entirely filled with epoxy resin. The reason for not filling the groove completely with resin is to prepare a suitable empty space to place the rebar so that the resin does not protrude from the groove after placing the rebar in it. This strengthening method in terms of groove dimensions and GFRP laminate installation was performed according to previous investigations [].
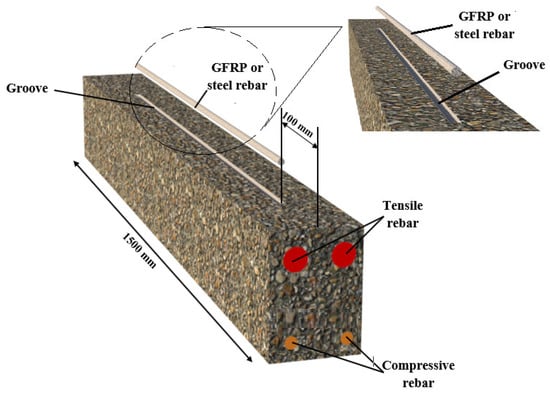
Figure 8.
Strengthening with GFRP-UNSM.
4.5. Anchored NSM Method (ANSM)
A primary shortcoming of the UNSM approach is the impossibility of achieving the full load-bearing capacity of the GFRP rebar due to slipping at a high load. Therefore, in this study, a new NSM method was introduced by providing an anchorage at both ends of the rebar. This method is the same as the UNSM technique, but the only difference is the anchorage provided by welding a smaller, perpendicular rebar at each end of the main rebar. Therefore, one I-shape groove is created on the tension side of the beams, as illustrated in Figure 9. After creating and cleaning it utilizing an air jet, 2/3 of the groove was filled with resin. Then, an 8 mm steel or GFRP I-shape rebar was inserted into the groove, and the groove was entirely filled with epoxy resin.
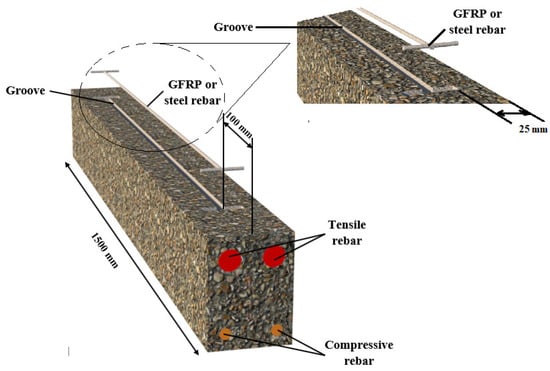
Figure 9.
Strengthening with GFRP-ANSM.
4.6. UNSM and ANSM with GFRP Laminates
UNSM and ANSM with GFRP laminates are the same as G-UNSM and G-ANSM, respectively, considering that after the groove was filled 2/3 using resin, the 8 mm rebar was inserted into the groove. Thus, the rest of the resin was employed to totally fill the groove, and after that, one layer of GFRP laminates was mounted on the filled grooves’ surfaces. After the resin hardened, a 0.5 mm thick layer of resin was applied on the first layers of the GFRP laminates, and then a second layer was applied. These methods are presented in Figure 10. The main reason for using both a mounted rebar and GFRP laminates was to obtain the highest resistance of RC beams. It should be noted that the UNSM technique with GFRP laminates have been researched by a few studies; however, none have measured the simultaneous influence of the ANSM technique with GFRP laminates, which is another novelty of this study.
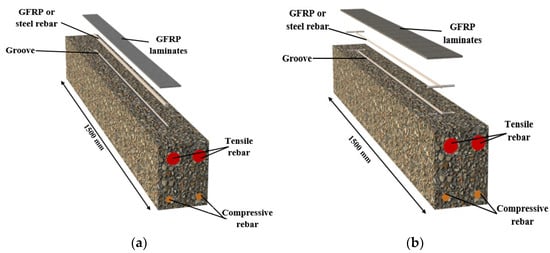
Figure 10.
Simultaneous influence of both external strengthening rebar and GFRP laminates: (a) UNSM method with GFRP laminates and (b) ANSM method with GFRP laminates.
5. Results and Discussion
5.1. Load–Displacement Behavior
In the present investigation, 12 RC beams strengthened with various techniques were manufactured and tested. The load–displacement behavior of the beams’ mid-spans, as well as the final resistance, crack propagation, and ductility ratio, were assessed. Figure 11 provides the load–displacement curves of the beams.
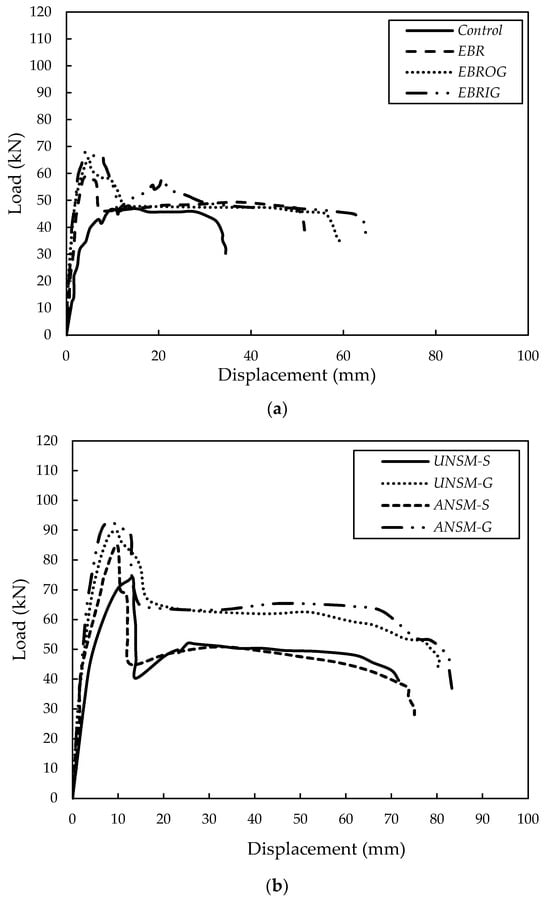
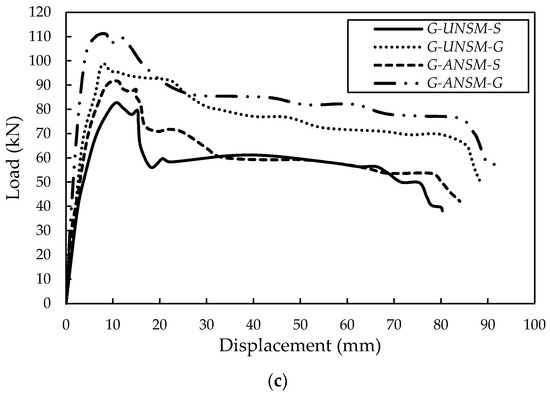
Figure 11.
Load–displacement behavior of beams strengthened with various techniques (a) specimens strengthened with GFRP laminates, (b) specimens strengthened with additional rebars and (c) Specimens strengthened with both additional rebar and GFRP laminates.
The maximum bending capacity and deformation significantly increased with the use of GFRP laminates; however, there was a minor change between the final load-bearing capacity of EBROG-GFRP and the specimen strengthened with EBRIG-GFRP laminates, while the final mid-span deflection was observed when the EBRIG-GFRP technique was used (Figure 11a). The reduction in the early step of the load–displacement of EBR- and EBROG-GFRP-strengthened specimens after concrete cracking in the tension and also steel yielding can be seen in the curves. In addition, an inferior reduction was observed in the load–displacement curves of the beams through increasing the load in EBR- and EBROG-GFRP-strengthened beams, compared to the control sample after steel yielding. This is because of the exterior GFRP laminates’ enhanced load-bearing capability and higher specimen ultimate load. Moreover, FRP failure occurred after the steel yield failure mode decreased the middle deformation and, thus, decreased the enclosed areas through the load–displacement relationship of the beams. The same observation was testified by earlier investigations that authorize the finding in this research about the load–displacement behaviors of EBR- and EBROG-GFRP-strengthened beams [,]. However, when the EBROG approach was used instead of the EBR method, the areas under the load–displacement curve of GFRP-retrofitted beams were larger, showing a more ductile behavior of the specimens reinforced using the EBROG methodology. The findings unequivocally demonstrate that the grooving approach has a major role in enhancing the energy absorption and deformability of beams reinforced through EBROG.
Moreover, inserting GFRP laminates into grooves in the EBRIG method increased the initial load–displacement behavior of the specimen and also increased the strength and deformation due to the increased level of adhesion between the GFRP laminates and the specimen’s concrete surface. Additionally, regarding Figure 11b, the use of the UNSM and ANSM methods led to extensive improvements in both the extreme displacement and load capacity of the beams, relative to the control specimen, particularly when an anchorage was provided at the ends of the longitudinal rebars (ANSM). This may have been caused by a reduction in the slip between the rebar inserted in the groove and the concrete caused through the use of the anchorage. Moreover, the improvement effects of the UNSM and ANSM methods increased when a GFRP rebar was also used, in comparison with beams reinforced with steel rebars, due to the higher strength of GFRP rebars. In the first step of loading, formerly cracking, the strengthened beams followed a linear elastic behavior form with a higher initial slope in comparison with the EBR, EBROG, and EBRIG techniques. Then, in following from cracking to steel yielding by increasing the load, the deflection amplified had a larger rate, particularly when an anchorage was designed at the end of the rebar (I-shape rebar). During this step, the GFRP rebar controls the crack width until failure. The same performance was reported by Mostofinejad and Shameli [].
Moreover, the higher strength of the GFRP rebar in comparison with the steel rebar, aside from the epoxy cracking, increased the deformation of the beam. To end, the specimen failed due to the yielding of the tension steel reinforcement after concrete–epoxy interface failure, especially in the ANSM beam []. Conversely, providing longitudinal rebar under the GFRP laminates played an effective role in enhancing the bending characteristics of beams in terms of displacement, stiffness (the early slope of the load–displacement curve), and flexural strength. Still, this effect became more obvious when using GFRP rebars instead of steel, under the GFRP laminates, particularly when a GFRP rebar was used. After reaching the maximum point, the load capacity in every specimen—aside from G-UNSM-G and G-ANSM-G—was abruptly reduced, but when GFRP rebar was used, the load resistance progressively dropped.
To accurately assess how various strengthening techniques affect the flexural performance of RC beams, Figure 12 presents the final load capacities and displacement values.
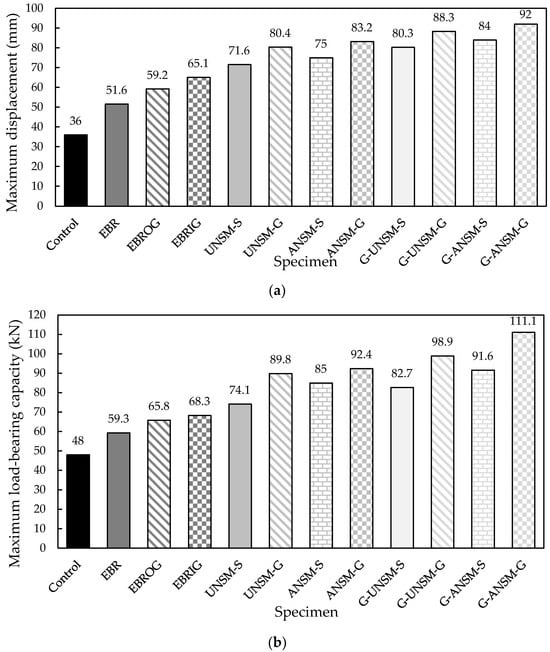
Figure 12.
Impacts of various strengthening methods on the bending characteristics of RC beams: (a) final displacement and (b) final load resistance.
Regarding Figure 12a, strengthening RC beams with different techniques significantly improved their final displacement. The figure shows that the ultimate deformation of RC beams was enhanced by 49.5%, 71.6%, and 88.7% when the EBR, EBROG, and EBRIG methods were employed, correspondingly. In addition, when a longitudinal GFRP rebar was used under the GFRP laminates, without and with an anchorage (G-UNSM-G and G-ANSM-G), the flexural displacement improved, respectively, by 156% and 168%, relative to the control specimen. Additionally, 23.5%, 37%, and 42.3% improvements were observed in the maximum load resistance when the beams were strengthened using the EBR, EBROG, and EBRIG techniques, respectively (Figure 12b). In comparison, strengthening RC beams with the G-UNSM-G and G-ANSM-G methods enhanced the maximum flexural strength by 106% and 131%, respectively, relative to the control beam without GFRP laminates.
5.2. Modes of Failure
Figure 13 shows the beams after failure with various strengthening techniques under a static pour-point flexural load. The performance of the control specimen under loading was typically bending, and the beam failed because of concrete crushing after the steel yielding. Furthermore, in this figure, crack propagation is shown. GFRP debonding occurred in the EBR-GFRP technique, and laminates were detached from the surface of the beam. As a result, fractures started at the end of the FRP reinforcement and moved horizontally until they reached the internal shear stirrups. This caused the concrete cover to become intertwined. Additionally, a failure in the major part of the GFRP, the debonding of another part, and the full failure of GFRP materials were detected in EBROG- and EBRIG-GFRP, which shows the peak use of GFRP laminate strength by providing a perfect linking among the FRP sheet and beam surface, while also avoiding debonding. Therefore, as mentioned by Mostofinejad and Moghaddas [], in EBROG- and EBRIG-GFRP-strengthened specimens, failure occurs through the devastation of the concrete after steel yield arises. Given that the GFRP laminates are properly connected to one another until failure, avoiding early debonding and concrete devastating once steel reinforcement yielding arises, it is evident that this manner of flexural failure is ductile and desirable. This failure mechanism may be linked to a high likelihood of achieving a larger strain in the beam’s compression concrete (in comparison to the code’s final strain assumption of 0.003), which could be followed by a rise in the strain of the GFRP laminates in comparison to the approximation provided by the ACI 440-2R [] requirements employed for the designs of the beams. Generally, the grooving technique (EBROG and EBRIG) prevented early separation, GFRP failure, and the concrete-crushing mechanism. Conversely, the failure modes of the UNSM and ANSM methods, with and without additional GFRP laminates on the surface of the inserted rebar, were the failure of the rebar (either steel or GFRP) and GFRP laminates.
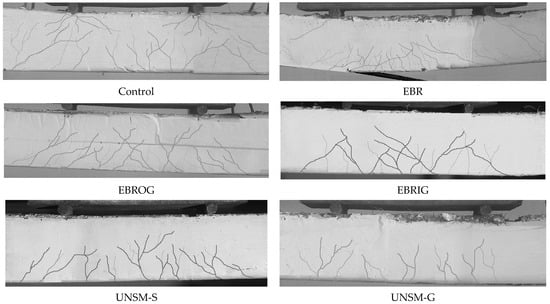
Figure 13.
Modes of failure and crack propagation mid-span.
In these specimens, the rebar failed due to bar failure extending, which caused epoxy splitting and concrete cover detachment. This demonstrates the application of a massive, reinforced rebar made of GFRP or steel. As a result, a bending fracture that began under the point load position caused the failure of these specimens, UNSM-S, UNSM-G, ANSM-S, and ANSM-G. The fracture spread to the NSM bars as the load increased. This crack was stopped from spreading transversally through the epoxy paste by the NSM bar and the epoxy paste, which also caused the crack’s breadth to decrease. Ultimately, the longitudinal propagation of the fracture led to the breakdown of the concrete–epoxy contact. The same failure observations were testified by earlier investigations that authorize the accurateness of this research []. The failure modes of specimens, as well as crack widths and flexural moments, are provided in Table 7. It should be mentioned that a CK-102 digital crack width gauge meter with an accuracy of 0.01 mm was used to measure the widths of the cracks. By increasing the load, cracking arose for the first time over the specimens’ length. The widths of all cracks that occurred for the first time were measured and recorded. Subsequently, as the weight rose, the first cracks widened and spread farther. Therefore, the width of that crack amplified, and the beam failure was considered an initial crack width.

Table 7.
Crack widths and modes of failure of the specimens.
According to Table 7, it was seen that the initial cracking moment of EBR-, EBROG- and EBIRG-GFRP specimens increased by 71.8%, 90.1%, and 97.9%, respectively, compared to the control beam, while initial crack widths decreased considerably by 31.3%, 40.6%, and 46.8%, respectively. The adhesive interface resistance between the concrete surface and the laminates may be linked to the reduction in the first crack width. This would increase the tensile resistance at the bottom section of the beam where tensile stresses are experienced. The same observation was found in previous investigations []. The maximum increase at the moment and reduction in the initial crack width were observed when GFRP laminates and rebars were used simultaneously. Therefore, the increases in the maximum moments for G-UNSM-S, G-UNSM-G, G-ANSM-S, and G-ANSM-G, relative to the control specimens, were about 139.6%, 186%, 165.4%, and 205.6%, respectively. In addition, the table shows that for the G-UNSM-S, G-UNSM-G, G-ANSM-S and G-ANSM-G specimens, the initial crack widths decreased by 75%, 84.3%, 81.2%, and 90.6%, respectively. In addition, in specimens strengthened with the NSM technique, particularly G-ANSM-S and G-ANSM-G, a flexural crack that began underneath the point load site is what caused the cracking. The fracture spread to the NSM bars as the load increased. This crack was stopped from spreading transversally through the epoxy paste by the NSM bar and the epoxy paste, which also caused the cracks’ breadth to decrease.
5.3. Ductility
A suitable metric to forecast flexural behavior in RC beams is their ductility ratio. The ductility ratio was developed by Cohn and Bartlett [,,]. As shown in Figure 14 and Equation (1), this ratio may be projected as the ratio between the displacement at 85% of the maximum load on the post-peak region of the curve and the displacement at the beam’s first yield:
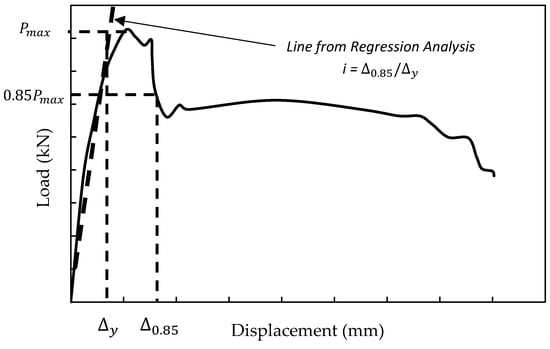
Figure 14.
Description of the ductility ratio.
Figure 15 shows the ductility ratios of the specimens. A reduction in ductility indicates a sudden failure of the RC beams, while an increase indicates that the RC beam will fail with some deformation, which functions as a warning to residents. Regarding Figure 15, the GFRP-EBR technique decreased the ductility by about 35%, and it increased slightly when EBROG or EBRIG were used. The main goal for the drop in ductility of specimens strengthened with the EBR-GFRP technique could be related to the debonding phenomena in which the load-bearing capacity of the beam increased and suddenly decreased due to debonding []. On the other hand, due to the removal of the debonding phenomena in the EBROG- and EBRIG-GFRP techniques, ductility improved. Additionally, when the UNSM or ANSM methods were performed using steel rebars, the ductility significantly declined by about 56.2% and 37.5%, respectively, relative to the control beam, while the use of GFRP rebars in the UNSM and ANSM strengthening methods slightly enhanced ductility by 5% and 50%, respectively. Conversely, the maximum improvement in ductility was observed when GFRP rebars and laminates were used simultaneously (G-UNSM-G and G-ANSM-G). Therefore, strengthening RC beams with G-UNSM-G and G-ANSM-G led to improvements in this index by 80% and 115%, respectively. According to the results, the use of GFRP laminates enhanced the flexural performance of RC beams; furthermore, the RC beams’ bending resistance and ductility were significantly increased through the concurrent usage of GFRP rebars and laminates.
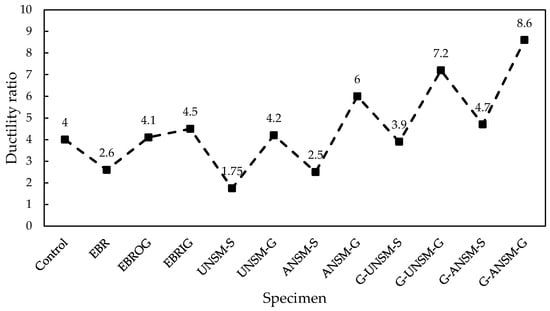
Figure 15.
Influence of various strengthening techniques on ductility ratios of beams.
5.4. Stiffness
In this section, the impact of different strengthening techniques on the stiffness of specimens is assessed. Stiffness is defined as the initial slope of the load–displacement curve of RC beams. The findings are presented in Figure 16.
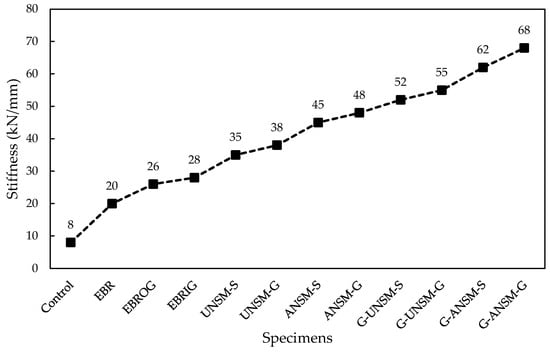
Figure 16.
Influence of the various strengthening techniques on the stiffness of the beams.
The figure shows that all strengthening techniques increased the stiffness of the beams, and creating grooves had a significant influence on improving their stiffness due to the amplified adhesion among the GFRP laminates and the beam surface. Therefore, the stiffness of the beams increased by 150%, 225% and 250% when EBR, EBROG, and EBRIG methods were employed, respectively. Moreover, using the NSM method meaningfully enhanced the stiffness of the RC beams. Thus, the stiffness of an RC beam was enhanced by 337.5% and 462.5% when a beam was strengthened using UNSM-S and ANSM-S, respectively. Additionally, the use of GFRP rebars played an active role in increasing the stiffness of beams. Therefore, using UNSM-G and ANSM-G amplified the stiffness of the RC beams by roughly 375% and 500%, respectively. The maximum enhancement in the stiffness of an RC beam was identified when rebars and laminates were used simultaneously, particularly for GFRP rebars. Therefore, the stiffness of an RC beam was increased by 750% when it was strengthened using G-ANSM-G.
5.5. Comparison with Existing Standards
5.5.1. ACI440.2R 17
The ACI440.2R-17 [] standard defines the next formula for the GFRP laminate debonding strain performed for the external strengthening of the RC beams:
where n, , and indicate the number of used laminates, the elastic modulus, and GFRP laminate thickness, correspondingly. Additionally, denotes the compressive strength of the concrete, and is the GFRP laminates’ failure strain. Therefore, the final moment of the strengthened RC beam can be considered using the following equation []:
In Equation (3), is the nominal bending resistance. Additionally, , , and denote the tensile rebar cross-sectional area, compression rebar cross-sectional area, and GFRP laminate area, respectively. and denote the tensile and compression rebars stress; c denotes the distance from the final compression fibers to the neutral axis; d denotes the distance from the final compression fiber to the centroid of tensile rebars; and d’ denotes the distance from the extreme compression fiber to the centroid of compression rebars. Additionally, , and indicate the effective depth of the GFRP laminates, the reduction bending factor generated through GFRP (equal to 0.85), and the depth of the rectangular stress block to the depth of the neutral axis ratio, respectively. Moreover, can be determined using the following formula:
This standard also defines a design process for structural members strengthened using the NSM procedure [,]. Then, the maximum strain in the external strengthening rebar in the NSM technique is defined as follows:
5.5.2. CNR-DT 200 R1/2013
The Italian standard, CNR-DT 200 R1/2013 [], presents a proper formula for the design of EBR-GFRP-strengthened RC beams []. According to this standard, the strain in the GFRP laminates should be limited to :
where is an environmental factor (1 in this research), and is a material safety factor (1 in this research). Also, indicates the failure strain of the GFRP laminates. In addition, is the debonding strain of the GFRP laminates and can be computed using the formula that follows []:
where is a safety factor (considered 1.0 in this study), FC indicates the confidence factor (considered 1.0 in this study), is a corrective factor, and is considered 1.0 according to CNR-DT 200 R1/2013 [] for a four-point bending load. Moreover, and indicate the compressive and tensile strengths of concrete, correspondingly. In addition, is a geometrical corrective factor that could be defined as
where and b denote the widths of the GFRP laminate and beam section, respectively.
5.5.3. Said and Wu
Said and Wu [] presented a new formula for forecasting the debonding failure mode of GFRP laminates. Here, the maximum of the GFRP laminate strain at debonding () can be determined as follows:
The maximum debonding capacity can be determined using the following formula:
where , , and denote the longitudinal steel rebar’s yield stress, the distance between the tensile forces of the steel rebars, and the force of the compression portion of the section including the distance between the centroid of the tensile rebar and the centroid of the GFRP laminates, respectively. may be expected to equal 0.9, increased by the effective depth.
5.5.4. Lu et al.
Lu et al. [] proposed a formula for measuring the GFRP laminate debonding strain, as seen below:
where
indicates the distance from the section to the end of the GFRP laminates, and denotes the tensile resistance of the concrete [].
5.5.5. Teng et al.
Teng et al. [] generated a novel formula considering the influences of the compressive resistance of concrete, width ratio , and GFRP axial stiffness on the debonding failure []. The formula is as follows:
where
indicates the distance from the GFRP cutoff to the adjacent performed load [].
5.5.6. Deng et al.
Deng et al. [] developed a new model to predict the load-bearing capacity of RC beams strengthened with the NSM method. Their main expectations are summarized below:
- (1)
- During loading, the strengthened specimens comply with the assumption of a plane section.
- (2)
- The tensile resistance of concrete is neglected after cracking.
- (3)
- The stress–strain curves of interior rebars can be shortened to a perfect elastic-plasticity behavior. In addition, the external strengthening rebar in the groove has a linear elastic stress–strain performance up to failure. is the maximum tensile strain of steel rebars, .
- (4)
- The compression behavior of concrete is defined below:where is the compressive stress of concrete conforming to a given strain ; is the cylinder compressive resistance of concrete; is the compressive strain of concrete; is the compressive strain of concrete at the maximum stress value and equals 0.002; and is the maximum strain of compression concrete and equals 0.003. The balanced condition for strengthened beams using the NSM technique is reached when the concrete in compression achieves a final strain of 0.003 and the tensile strain in the external strengthening rebar reaches its ultimate tensile resistance []. The tensile steel rebars had already attained their maximum resistance at this time. The distribution of strain and stress throughout cross-section depth in the balanced condition is depicted in Figure 17. The following is an expression of the equation:where
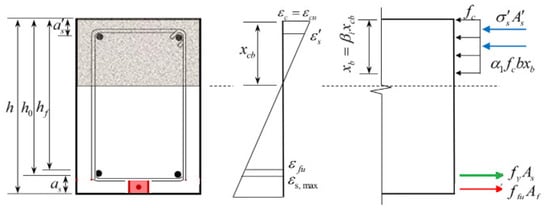 Figure 17. Strain and stress distributions over the cross-section under the balanced state.
Figure 17. Strain and stress distributions over the cross-section under the balanced state.
The area of external rebar (steel or GFRP) can be determined as
where indicates the real depth of the neutral axis; , the depth of the equivalent rectangular compression stress block; and , , and , the areas of the internal tensile, compressive rebars, and external strengthening rebar (steel or GFR), respectively. Additionally, b and are the cross-section width and the distance from the center of the external strengthening rebar to the beam. Also, is the proportion of the concrete resistance to the corresponding stress in the compression stress block, , and is the proportion of the depth of the compression stress block to the fiber depth of the neutral axis, where . In addition, , , , , and are the stress and final stress of the external strengthening rebar (either steel or GFRP), the yield resistance of the internal tensile rebar, the yield resistance of the compressive rebars, and the elastic modulus of the external strengthening rebar, correspondingly. is the maximum strain of the compression concrete, where . and are the strain and final strain of the external strengthening rebar (either steel or GFRP), respectively [].
As per Deng et al. [], the nature of tension failure indicates that external reinforcing bar failure will occur before compressive concrete crushing. Figure 18 displays the stress and strain distributions over the cross-section depth if the external strengthening rebar fails. Tension failure may be classified into two scenarios based on the final compressive strain of the concrete. Then, the concrete’s compressive strain falls short of the final amount possible, . Therefore, according to ACI 318-19, the equivalent rectangular stress cannot be used to compute the compressive stress of concrete []. The following equations can be expressed using Wang’s suggested formula from [].
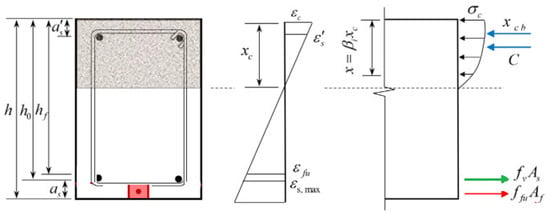
Figure 18.
Strain and stress over the cross-section when the external strengthening rebar (steel or GFRP) fails.
Situation 1:
Situation 2:
Here, is the compressive force of concrete; , the real depth of the neutral axis; , the distance from the centroid of the concrete compressive force to the compressive region; , the concrete compressive strain; and , the concrete compressive strain correspondence to the maximum stress [].
According to the strain compatibility and the equilibrium equations, the next formulas can be expressed [] as follows:
Therefore, the maximum moment of the RC beam strengthened using NSM techniques under tension failure can be obtained using Equations (26) to (32), as in the following formula:
where and denote the elastic moduli of internal compressive rebar strain, and , the external strengthening rebar (either steel or GFRP).
According to Deng et al.’s [] study, under compression failure, the beams strengthened using the NSM technique fail because of concrete being devastated in the compression region earlier than the external strengthening rebar failure when or . Therefore, the compression failure mode could be divided into two scenarios based on tensile rebar failure. Figure 19 shows the stress and strain distributions over the strengthened beam under compression failure [].
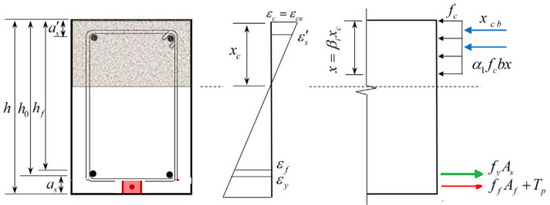
Figure 19.
Strain and stress distributions over beams caused by compression failure.
It follows that the matching load was probably transmitted to the exterior reinforcing rebar. The following is an expression for this equation []:
where indicates the load conforming to the external strengthening rebar (either steel or GFRP), and indicates the effective stress in the external strengthening rebar when prestressing stress exists (therefore, this part should be neglected when there is no prestressing load). is the tensile resistance of concrete, and is the active area of the external strengthening rebar. Thus, in using the compatibility of strain equilibrium equations, the following formulas can be established [].
Situation 3:
Situation 4:
where
The formulas of and , in this case, are the same as those in cases 3 and 4. Therefore, the final moments of the beams strengthened using the NSM technique under compression failure can be determined using the following formula []:
Therefore, based on the results obtained by Deng et al. [], compressive failure occurs in RC beams strengthened using the NSM technique when prestressing occurs.
The results from the comparison between the discussed existing models and experimental results are presented in Figure 20. Additionally, the errors are presented in Table 8. The success of the analytical models in predicting the experimental data is displayed in Figure 20, where a 45° trend indicates complete agreement between the guessed formulae and the actual results. Additionally, trends above and below the 45° reference line denote the overestimated and underestimated performance of models, respectively. Regarding Figure 17, the models proposed by ACI 440.2R-17 [] and Said and Wu [] underestimated the load resistance of RC beams strengthened with EBR properly, while the prediction model of CNR-DT 200 R1/2013 [] accurately estimated the maximum flexural strength of EBR- and EBROG-GFRP-strengthened RC beams. Conversely, the equations of ACI 440.2R-17 [], Said and Wu [], and CNR-DT 200 R1/2013 [] were unable to precisely forecast the load resistance of beams strengthened with the NSM technique, particularly for the new strengthening techniques proposed in this study: ANSM-S, ANSM-G, G-ANSM-S, and G-ANSM-G. In addition, there was good agreement among the experimental findings of the EBRIG-GFRP-strengthened RC beam and those of Said and Wu’s [] model. Additionally, the prediction model of Lu et al. [] is very conservative for EBR- and EBROG-GFRP-strengthened beams. Moreover, the model of Teng et al. [] was not highly accurate role in predicting the load resistance of retrofitted beams with various strengthening methods, especially when the NSM method was used with the anchorage I-shape rebar. In addition, the formula of Deng et al. [] revealed an excellent agreement with the experimental results of conventional NSM-strengthened RC beams without anchorage and additional GFRP laminates, UNSM-S and UNSM-G, and can be used as a proper tool. According to Table 8, errors of 5.3%, 4.5%, 15.1%, and 3.3% were obtained when the models of ACI 440.2R-17 [], CNR-DT 200 R1/2013 [], Said and Wu [], and Lu et al. [] were employed to forecast the bending load resistance of the EBR-GFRP-strengthened beams. In addition, the models proposed by Said and Wu [] and Lu et al. [] properly predicted the flexural strength of EBRIG- and EBROG-GFRP-strengthened RC beams with errors of 5.3% and 5.1%, respectively. The equation of Deng et al. [] revealed low errors of 7.0% and 3.2% when expecting the maximum bending moment of conventional NSM-strengthened beams with steel and GFRP rebars, respectively (UNSM-S and UNSM-G).
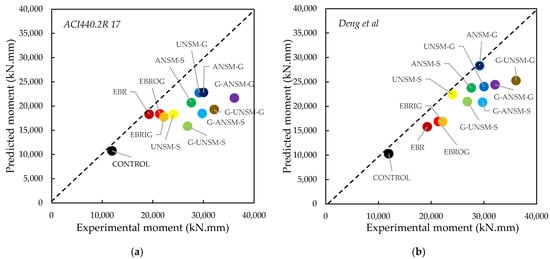
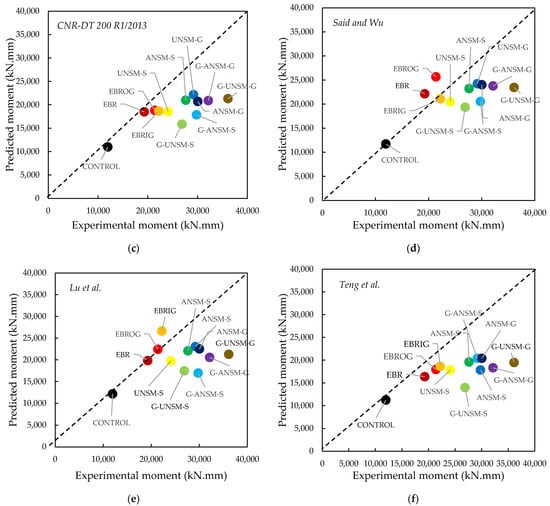
Figure 20.
Experimental load resistance versus forecast formulas for EBR-strengthened specimens. (a) ACI440.2R 17 [], (b) Deng et al, [] (c) CNR-DT 200 R1/2013 [], (d) Said and Wu [], (e) Lu et al. [] and (f) Teng et al. [].

Table 8.
Comparison between the experimental and numerical findings.
5.6. Proposed New Model
According to the results presented above, some of the existing models are appropriate for predicting the load resistance of beams strengthened with EBR, EBROG, EBRIG and conventional NSM techniques without rebar anchorage. Therefore, there is no proper formula that should be used anticipate the maximum resistance of NSM-strengthened beams with an anchorage, particularly when GFRP laminates are involved as well. So, a novel formula is generated in this section to forecast the load resistance of beams strengthened with various retrofitting techniques. For this aim, a combination of the models proposed by Said and Wu [] and Deng et al. [] that considers modification factors was taken into account. To obtain the modification factors, nonlinear regression was used with the minimum error between the experimental and numerical results. Then, the maximum debonding capacity can be presented using the following formula:
where ξ and ζ are the modification factors considering the influence of anchorage and simultaneous external GFRP laminate installation, respectively. Therefore, it is recommended to consider 1.1 and 1.0 for the external strengthening rebar with and without anchorage. In addition, it is recommended to consider 1.12 and 1.0 when using strengthening beams with and without GFRP laminates in addition to the external NSM-strengthening rebar, respectively. All variables used in Equation (42) were defined in the previous section. A comparison between the experimental findings and results of Equation (42) is illustrated in Figure 21. In addition, the error for each specimen is presented in Figure 22. These findings indicate that, for different strengthening procedures, there is a high degree of agreement between the experimental data and that of the suggested model in this work. However, it is advised that further studies assess the correctness of the new model proposed in this study and consider more specimen characteristics and size effects using more experimental results.
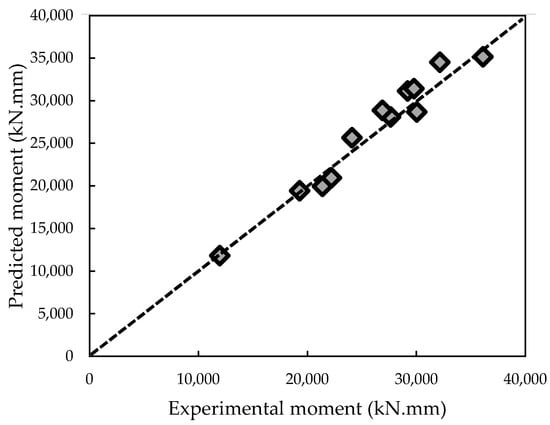
Figure 21.
Comparison with experimental results and those obtained using Equation (42).
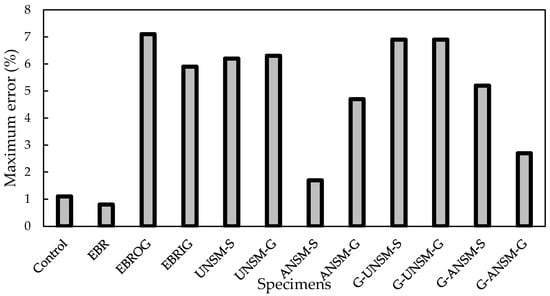
Figure 22.
Existing errors between experimental and numerical results for beams tested in this research.
5.7. Cost Examination
In this study, a cost analysis was performed to identify the economic conditions of each strengthening technique. The costs are in USD based on the average prices available in the U.S. The prices of used materials and their units are presented in Table 9. Additionally, all costs for used materials and workers to produce each specimen are shown in Table 10. As per Table 10, there is no great difference between the total costs of different strengthening methods relative to the control specimen cost. The final costs of EBR, EBROG, and EBRIG were greater than that of the control beam by about 2% (USD 9), 3% (USD 10), and 3% (USD 10), respectively. Conversely, the highest costs were obtained for G-ANSM-G, G-UNSM-G, and ANSM-G, which were 9.7% (USD 34.42), 8% (USD 28.67) and 7.2% (USD 25.86), respectively. Therefore, for laboratory tests, there is no significant difference between the cost of testing various strengthening options. However, for a large project, the total cost might be high.

Table 9.
Units and prices of the materials.

Table 10.
Cost analysis and total price of each specimen (USD).
6. Conclusions
The current research intended to assess the impact of various strengthening techniques to enhance the bending behavior of RC beams with GFRP fabrics, including EBR, EBROG, EBRIG, and NSM techniques. A new strengthening NSM method was also introduced using an anchorage rebar. Then, a new formula was generated to predict the final load resistance of RC beams strengthened with various retrofitting techniques. The results collected allowed us to draw the following conclusions:
- In terms of cost, there is no high difference between the total costs of various strengthening methods, and a maximum difference of USD 35 (9.7% relative to the control sample) was obtained when both GFRP laminates and GFRP rebar with two ends anchorage were used (G-ANSM-G). Therefore, the novel strengthening method of G-ANSM-G is recommended, since using both GFRP rebar and laminates led to the best flexural performance for the RC beam.
- However, the use of EBR, EBIRG, and EBROG meaningfully increased the load-carrying capacity and deformation of the RC beams; these responses were further enhanced when rebar was provided under the GFRP laminates, particularly if it was composed of GFRP. Among these, the newly proposed strengthening methods with the use of an anchorage I-shape rebar, ANSM-S, ANSM-G, G-ANSM-S, and G-ANSM-G showed the highest improvements in the bending resistance and deformation of RC beams, particularly when both the I-shape anchorage GFRP rebar and GFRP laminates were used.
- Debonding phenomena were observed in the EBR technique, which prevented the GFRP laminates from reaching the highest tensile strength; however, creating grooves led to an increase in the GFRP laminates’ engaged capacity. Therefore, with the use of EBROG and EBRIG, the crack widths decreased, and the initial cracking moments increased. In addition, the minimum crack width was observed when new G-ANSM-S and G-ANSM-G methods were used.
- Using novel techniques, not only was the debonding phenomenon eliminated, but also more GFRP strength was used to provide an anchorage that led to the best bending behavior of the RC beams in terms of initial crack width and cracking moment.
- The ductility of the RC beams decreased with the use of EBR, while using EBROG and EBRIG slightly improved ductility. Performing UNSM and ANSM using steel rebars decreased ductility, while using GFRP rebars improved it. Conversely, the highest ductility was observed when GFRP rebars and laminates were used simultaneously (G-UNSM-G and G-ANSM-G).
- The existing standards are unable to predict either the ultimate or initial cracking moments of RC beams strengthened with various GFRP laminate strengthening techniques, especially when the UNSM and ANSM techniques were used with and without GFRP rebars and laminates. However, the model proposed in the current examination with a high agreement with experimental findings can be utilized as a reliable tool to estimate the bending resistance of RC beams strengthened with various retrofitting practices.
It should be mentioned that the size effect is a vital parameter, but it was not analyzed in this study. In addition, prestressing may be a useful technique for enhancing the bending resistance and ductility of the strengthened specimens. Therefore, assessing the size effect while considering the influence of prestressing is recommended for future studies. In addition, this study presented the effects of various strengthening techniques that could be utilized for numerical verification and validation to assess the effect of more variables on the performances of strengthened concrete beams. Therefore, numerical analyses for further investigations are highly recommended. On the other hand, the mentioned techniques could be utilized for concrete girder bridges with different cross-sections, which need more examination.
Author Contributions
A.K.P. and M.K. (Mehrdad Karamiand) contributed to the conceptualization and formal analysis and writing, reviewing, and editing the original draft. M.K. (Moses Karakouzian) contributed to the conceptualization and supervision and writing, reviewing, and editing the original draft. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Some or all data, models, or codes that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Acronyms and Symbols:
| ANSM | Anchored NSM method |
| Tensile rebar cross-sectional area | |
| Compression rebar cross-sectional area | |
| FRP laminate area | |
| Active area of the external strengthening rebar | |
| Width of the GFRP laminates | |
| b | Width of beam section |
| c | Distance from final compression fibers to the neutral axis |
| FC | Confidence factor |
| CFRP | Carbon fiber-reinforced polymer |
| d | Distance from final compression fiber to the centroid of tensile rebars |
| d’ | Distance from the extreme compression fiber to the centroid of compression rebars |
| EBR | Externally bonded reinforcement |
| EBROG | Externally bonded reinforcement on grooves |
| EBRIG | Externally bonded reinforcement in grooves |
| Elastic moduli | |
| FRP | Fiber-reinforced polymer |
| Stress of the external strengthening rebar | |
| Final stress of the external strengthening rebar | |
| GFRP | Glass fiber-reinforced polymer |
| i | Ductility index |
| MF-EBR | Mechanically fastened and externally bonded reinforcement |
| Nominal bending resistance | |
| n | Number of used laminates |
| NSM | Near-surface mounted |
| OPC | Ordinary Portland cement |
| RC | Reinforced concrete |
| GFRP laminates thickness | |
| Load conforming to the external strengthening rebar | |
| UNSM | Unanchored NSM method |
| Distance among the tensile force of the steel rebars | |
| 85% of the maximum load on the post-peak region of the curve | |
| Displacement at the beam’s first yield | |
| Compressive strength of the concrete | |
| Tensile rebars stress | |
| Compression rebar stress | |
| GFRP laminates’ failure strain | |
| Effective depth of the GFRP laminates | |
| Reduction bending factor generated by GFRP | |
| Depth of the rectangular stress block to the depth of the neutral axis ratio | |
| Strain in the GFRP laminates | |
| Environmental factor | |
| Material safety factor | |
| Failure strain of the GFRP laminates | |
| Debonding strain of the GFRP laminates | |
| Safety factor | |
| Corrective factor | |
| Geometrical corrective factor | |
| Maximum of the GFRP laminates strain at debonding | |
| Force of the compression portion of the section including the distance between centroid of the tensile rebar and the centroid of the GFRP laminates | |
| Distance from the section to the end of the GFRP laminates | |
| Distance from the GFRP cutoff to the adjacent performed load | |
| Maximum tensile strain of steel rebars | |
| Compressive strain of concrete | |
| Compressive strain of concrete at the maximum stress | |
| Maximum strain of compression concrete | |
| Real depth of the neutral axis | |
| Depth of the equivalent rectangular compression stress block | |
| Proportion of the concrete resistance to the corresponding stress in the compression stress block | |
| Compressive force of concrete | |
| Effective stress in the external strengthening rebar when prestressing stress exists | |
| Tensile resistance of concrete | |
| ξ | Modification factors considering the influence of anchorage |
| ζ | Modification factors considering simultaneous external GFRP laminate installation |
References
- Yang, D.Y.; Frangopol, D.M.; Teng, J.G. Probabilistic life-cycle optimization of durability-enhancing maintenance actions: Application to FRP strengthening planning. Eng. Struct. 2019, 188, 340–349. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, X.; Wu, Z. Life cycle cost analysis of FRP cables for long-span cable-supported bridges. Structures 2020, 25, 24–34. [Google Scholar] [CrossRef]
- Pour, A.K.; Edalati, M. Retrofitting of the corroded reinforced concrete columns with CFRP and GFRP fabrics under different corrosion levels. Eng. Struct. 2021, 228, 111523. [Google Scholar]
- Pour, A.K.; Ghalehnvoi, M.; Gencel, O. Torsional behaviour of rectangular high-performance fibre-reinforced concrete beams. Structures 2022, 35, 511–519. [Google Scholar]
- Farokhpour, A.; Ghalehnovi, M.; Karimipour, M. The behavior of concrete beams reinforced with polymer reinforcement and hybrid fibers. In Proceedings of the 10th National Conference of Concrete, Tehran, Iran, 7 October 2018. [Google Scholar]
- Pour, A.K. Experimental and numerical evaluation of steel fibres RC patterns influence on the seismic behaviour of the exterior concrete beam-column connections. Eng. Struct. 2022, 263, 114358. [Google Scholar] [CrossRef]
- Pour, A.K.; Farsangi, E.N. Health monitoring of recycled aggregates reinforced concrete beams retrofitted by concrete jacket using piezoelectric transducers. In Data-Centric Structural Health Monitoring; De Gruyte: Berlin, Germany, 2023. [Google Scholar]
- Kashi, A.; Ramezanianpour, A.A.; Moodi, F. Durability evaluation of retrofitted corroded reinforced concrete columns with FRP sheets in marine environmental conditions. Constr. Build. Mater. 2017, 151, 520–533. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, X.; Wang, X.; Sui, L.; Huang, X.; Guo, M. Seismic performance of large rupture strain FRP retrofitted RC columns with corroded steel reinforcement. Eng. Struct. 2020, 216, 110744. [Google Scholar] [CrossRef]
- Al-Nimry, H.; Soman, A. On the slenderness and FRP confinement of eccentrically-loaded circular RC columns. Eng. Struct. 2018, 164, 92–108. [Google Scholar] [CrossRef]
- Spadea, G.; Bencardino, F.; Swamy, R.N. Structural behaviour of composite RC beams with externally bonded CFRP. J. Compos. Constr. 1998, 2, 132–137. [Google Scholar] [CrossRef]
- Pimanmas, A.; Pornpongsaroj, P. Peeling behaviour of reinforced concrete beams strengthened with CFRP plates under various end restraint conditions. Mag. Concr. Res. 2004, 56, 73–81. [Google Scholar] [CrossRef]
- Toutanji, H.; Zhao, L.Z.; Zhang, Y. Flexural behavior of reinforced concrete beams externally strengthened with CFRP sheets bonded with an inorganic matrix. Eng. Struct. 2006, 28, 557–566. [Google Scholar] [CrossRef]
- Galecki, G.; Marez, N.; Nanni, A.; Myers, J. Limitations to the use of waterjets in concrete substrate preparation. In Proceedings of the 2001 WJTA American Waterjet Conference, Minneapolis, MN, USA, 18–21 August 2001. [Google Scholar]
- Rezaiee-Pajand, M.; Pour, A.K. Three stress-based triangular elements. Eng. Comput. 2019, 36, 1325–1345. [Google Scholar] [CrossRef]
- Pour, A.K.; Shirkhani, A.; Zeng, J.-J.; Zhuge, Y.; Farsangi, E.N. Experimental investigation of GFRP-RC beams with Polypropylene fibers and waste granite recycled aggregate. Structures 2023, 50, 1021–1034. [Google Scholar] [CrossRef]
- Pour, A.K.; Shirkhani, A.; Farsangi, E.N. Influence of Fiber Type on the Performance of Reinforced Concrete Beams Made of Waste Aggregates: Experimental, Numerical and Cost Analyses. Pract. Period. Struct. Des. Constr. 2023, 28, 04023007. [Google Scholar] [CrossRef]
- Pour, A.K.; Shirkhani, A.; Hamzehkolaei, N.S.; Zhuge, Y.; Farsangi, E.N. Performance evaluation of composite concrete-flled steel tube columns by steel fbers and different cross-section shapes: Experimental and numerical investigations. J. Constr. Steel Res. 2023, 200, 107656. [Google Scholar] [CrossRef]
- Pour, A.K.; Shirkhani, A.; Kirgiz, M.S.; Farsangi, E.N. Experimental investigation of GFRP-reinforced concrete columns made with waste aggregates under concentric and eccentric loads. Struct. Concr. 2022, 24, 1670–1688. [Google Scholar] [CrossRef]
- Farokhpour, A.; Ghalehnovi, M.; Pour, A.K. Structural Performances of Concrete Beams with Hybrid, Fiber-Reinforced Polymer-Steel Reinforcements. In Proceedings of the 7th National and 3th International Conference in Civil Engineering, Fredericton, NB, Canada, 13–16 June 2018. [Google Scholar]
- Chaboki, H.R.; Ghalehnovi, M.; Pour, A.K. Investigation of shear behavior of concrete beams made of recycled aggregate. Archit. Urban Manag. 2018. [Google Scholar]
- Pour, A.K.; Chaboki, H.R.; Ghalehnovi, M. Investigation of flexural behavior of concrete beams made of recycled aggregate. Concr. Res. Q. J. 2019, 10, 45–68. [Google Scholar]
- Mostofinejad, D.; Mahmoudabadi, E. Grooving as an alternative method of surface preparation to postpone debonding of FRP laminates in concrete beams. J. Compos. Constr. 2010, 6, 804–811. [Google Scholar] [CrossRef]
- Ghaleh, R.Z.; Mostofinejad, D. Behaviour of EBRIG CFRP sheet-concrete joint: Comparative assess-ment with EBR and EBROG methods. Constr. Build. Mater. 2002, 346, 128374. [Google Scholar] [CrossRef]
- Mukhtar, F.M. Customized shear test for bond-slip characterization of EBR FRP-concrete system: Influence of substrate aggregate type. Compos. Part B Eng. 2019, 163, 606–621. [Google Scholar] [CrossRef]
- Mostofinejada, D.; Shamelia, S.M.; Hosseini, A. EBROG and EBRIG methods for strengthening of RC beams by FRP sheets. Eur. J. Environ. Civ. Eng. 2014, 18, 652–668. [Google Scholar] [CrossRef]
- Moshiri, N.; Czaderski, C.; Mostofinejad, D.; Motavalli, M. Bond resistance of prestressed CFRP strips attached to concrete by using EBR and EBROG strengthening methods. Constr. Build. Mater. 2021, 266, 121209. [Google Scholar] [CrossRef]
- Arabzadeh, A.; Karimizadeh, H. Experimental study of RC deep beams with opening and FRP composites installed by means of EBR and EBROG methods. Constr. Build. Mater. 2019, 208, 780–791. [Google Scholar] [CrossRef]
- Mostofinejad, D.; Shameli, M. Performance of EBROG method under multilayer FRP sheets for flexural strengthening of concrete beams. Procedia Eng. 2011, 14, 3176–3182. [Google Scholar] [CrossRef]
- Mostofinejad, D.; Shameli, S.D. Externally bonded reinforcement in grooves (EBRIG) technique to postpone debonding of FRP sheets in strengthened concrete beams. Constr. Build. Mater. 2013, 38, 751–758. [Google Scholar] [CrossRef]
- Sena-Cruz, J.M.; Barros, J.A.O.; Coelho, M.R.F.; Silva, L.F.F.T. Efficiency of different techniques in the flexural strengthening of RC beams under monotonic and fatigue loading. Constr. Build. Mater. 2012, 29, 175–182. [Google Scholar] [CrossRef]
- El-Hacha, R.; Rizkalla, S. Near-surface-mounted fibre reinforced polymer reinforcement for flexural strengthening of concrete structures. ACI Struct. 2004, 101, 717–726. [Google Scholar]
- Ceroni, F. Experimental performances of RC beams strengthened with FRP materials. Constr. Build. Mater. 2010, 95, 1547–1559. [Google Scholar] [CrossRef]
- Nordin, H.; Taljsten, B. Concrete beams strengthened with prestressed NSM CFRP. J. Compos. Constr. 2006, 10, 60–68. [Google Scholar] [CrossRef]
- Jalali, M.; Sharbatdar, M.K.; Fei-Chen, J.; Alaee, F.J. Shear strengthening of RC beams using innovative manually made NSM FRP bars. Constr. Build. Mater. J. 2011, 36, 990–1000. [Google Scholar] [CrossRef]
- Chaboki, H.R.; Ghalehnovi, M.; Karimi, A. Study of the Flexural behaviour of recycled aggregate concrete beams. J. Concr. Res. 2019, 12, 45–60. [Google Scholar]
- Pour, A.K.; Farsangi, E.N. Experimental evaluation of concrete having Fly Ash and recycled asphalt aggregates for infrastructure constructions. J. Appl. Sci. Eng. 2024, 7, 159. [Google Scholar]
- Karimi, A.; Mohebbi Najm Abad, J.; Fasihihour, N. Predicting the load-carrying capacity of GFRP-reinforced concrete columns using ANN and evolutionary strategy. Compos. Struct. 2021, 275, 114470. [Google Scholar]
- Deng, Y.; Li, Z.; Zhang, H.; Corigliano, A.; Angus, C.C.; Lam, A.C.C.; Hansapinyo, C.; Yan, Z. Experimental and analytical investigation on flexural behaviour of RC beams strengthened with NSM CFRP prestressed concrete prisms. Compos. Struct. 2021, 257, 113385. [Google Scholar] [CrossRef]
- Zhang, Y.; Elsayed, M.; Zhang, L.V.; Nehdi, M.L. Flexural behaviour of reinforced concrete T-section beams strengthened by NSM FRP bars. Eng. Struct. 2021, 233, 111922. [Google Scholar] [CrossRef]
- Barris, C.; Sala, P.; Gómez, J.; Torres, L. Flexural behaviour of FRP reinforced concrete beams strengthened with NSM CFRP strips. Compos. Struct. 2020, 241, 112059. [Google Scholar] [CrossRef]
- Al-Abdwais, A.H.; Al-Mahaidi, R.S. Performance of reinforced concrete beams strengthened with NSM CFRP composites for flexure using cement-based adhesives. Structures 2020, 27, 1446–1457. [Google Scholar] [CrossRef]
- Al-Obaidi, S.; Saeed, Y.M.; Rad, F.N. Flexural strengthening of reinforced concrete beams with NSM-CFRP bars using mechanical interlocking. J. Build. Eng. 2020, 31, 101422. [Google Scholar] [CrossRef]
- Rimkusa, A.; Cervenkab, V.; Gribniaka, V.; Cervenka, J. Uncertainty of the smeared crack model applied to RC beams. Eng. Fract. Mech. 2020, 233, 107088. [Google Scholar] [CrossRef]
- De Maio, U.; Greco, F.; Lonetti, P.; Pranno, A. A combined ALE-cohesive fracture approach for the arbitrary crack growth analysis. Eng. Fract. Mech. 2024, 301, 109996. [Google Scholar] [CrossRef]
- Soleimani Borujerdi, A.; Mostofinejad, D.; Hwang, H.J. Cyclic loading test for shear-deficient reinforced concrete exterior beam-column joints with high-strength bars. Eng. Struct. 2021, 237, 112140. [Google Scholar] [CrossRef]
- BS EN 12390-33; Testing Hardened Concrete: Compressive Strength of Test Specimens. British Standards Institution: London, UK, 2009.
- Ospina Cadavid, M.; Al-Khudairi, O.; Hadavini, H.; Liaghat, G. Experimental studies of stiffness degradation and dissipated energy in glass fibre reinforced polymer composite under fatigue loading. Polym. Polym. Compos. 2017, 25, 435–446. [Google Scholar]
- Jadee, K.J.; Othman, A.R. Analysis of stress mitigation through defence hole system in GFRP composite bolted joint. Am. J. Mech. Eng. 2015, 3, 126–134. [Google Scholar]
- ASTM A615/A615M-20; Standard Specification for Deformed and Plain Carbon Steel Bars for Concrete Reinforcement. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM D7957/D7957M-17; Standard Specification for Solid Round Glass Fibre Reinforced Polymer Bars for Concrete Reinforcement. ASTM International: West Conshohocken, PA, USA, 2017.
- Toutanji, H.; Ortiz, G. The effect of surface preparation on the bond interface between FRP sheets and concrete members. Compos. Struct. 2001, 53, 457–462. [Google Scholar] [CrossRef]
- Barros, J.A.; Dias, S.J.; Lima, J.L. Efficacy of CFRP-based techniques for the flexural and shear strengthening of concrete beams. Cem. Concr. Compos. 2007, 29, 203–217. [Google Scholar] [CrossRef]
- Maalej, M.; Leong, K.S. Effect of beam size and FRP thickness on interfacial shear stress concentration and failure mode of FRP-strengthened beams. Compos. Sci. Technol. 2005, 65, 1148–1158. [Google Scholar] [CrossRef]
- Mostofinejad, D.; Moghaddas, A. Bond efficiency of EBR and EBROG methods in different flexural failure mechanisms of FRP strengthened RC beams. Constr. Build. Mater. 2014, 54, 605–614. [Google Scholar] [CrossRef]
- Mostofinejad, D.; Akhlaghi, A. Experimental investigation of the efficacy of EBROG method in seismic rehabilitation of deficient reinforced concrete beam-column joints using CFRP sheets. J. Compos. Constr. 2016, 21, 04016116. [Google Scholar] [CrossRef]
- Sharaky, I.A.; Torres, L.; Comas, J.; Barris, C. Flexural response of reinforced concrete (RC) beams strengthened with near-surface mounted (NSM) fibre reinforced polymer (FRP) bars. Compos. Struct. 2014, 109, 8–22. [Google Scholar] [CrossRef]
- ACI 440.2R-17; Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures. Report by ACI Committee 440. American Concrete Institute: Michigan, MI, USA, 2017.
- Karayannis, C.G.; Kosmidou, P.M.K.; Chalioris, C.E. Reinforced concrete beams with carbon-fibre-reinforced polymer bars—Experimental study. Fibers 2018, 6, 99. [Google Scholar] [CrossRef]
- Cohn, M.Z.; Bartlett, M. Computer-simulated flexural test of the partially pre-stressed concrete section. J. Struct. Div. 1982, 5, 2747–2765. [Google Scholar] [CrossRef]
- Pour, A.K.; Esfahani, M.R. The Effect of Steel Fibers on Flexural Cracking of Fiber in Reinforced Concrete Beams with Lap-spliced Bars. Ferdowsi Univ. J. Civ. Eng. 2017, 31, 1–18. [Google Scholar]
- Pour, A.K.; Ghalehnovi, M. New model for the lap-splice length of tensile reinforcement in concrete elements. J. Struct. Eng. 2021, 147, 12. [Google Scholar]
- Antino, T.D.; Pisani, M.A. Evaluation of the effectiveness of current guidelines in determining the strength of RC beams retrofitted by means of NSM reinforcement. Compos. Struct. 2017, 167, 166–177. [Google Scholar] [CrossRef]
- CNR-DT 200 R1/2013; Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Existing Structures. National Research, Council: Rome, Italy, 2013.
- Said, H.; Wu, Z. Evaluating and proposing models of predicting IC debonding failure. J. Compos. Constr. 2008, 12, 284–299. [Google Scholar] [CrossRef]
- Lu, X.Z.; Teng, J.G.; Ye, L.P.; Jiang, J.J. Intermediate crack debonding in FRP-strengthened RC beams: FE analysis and strength model. J. Compos. Constr. 2007, 11, 161–174. [Google Scholar] [CrossRef]
- Teng, J.G.; Smith, S.T.; Yao, J.; Chen, J.F. Intermediate crack-induced debonding in RC beams and slabs. Constr. Build. Mater. 2003, 17, 447–462. [Google Scholar] [CrossRef]
- ACI 318–319; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Michigan, MI, USA, 2016; Report 624.
- Wang, W.W. Technology and Application of FRP Reinforced Concrete Structures; China Construction Industry Press: Beijing, China, 2007. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).