Numerical Modeling and Performance Evaluation of Carbon Fiber-Reinforced Polymer-Strengthened Concrete Culverts against Water-Induced Corrosion
Abstract
1. Introduction
2. Materials and Methods
2.1. Geometric Description of Model
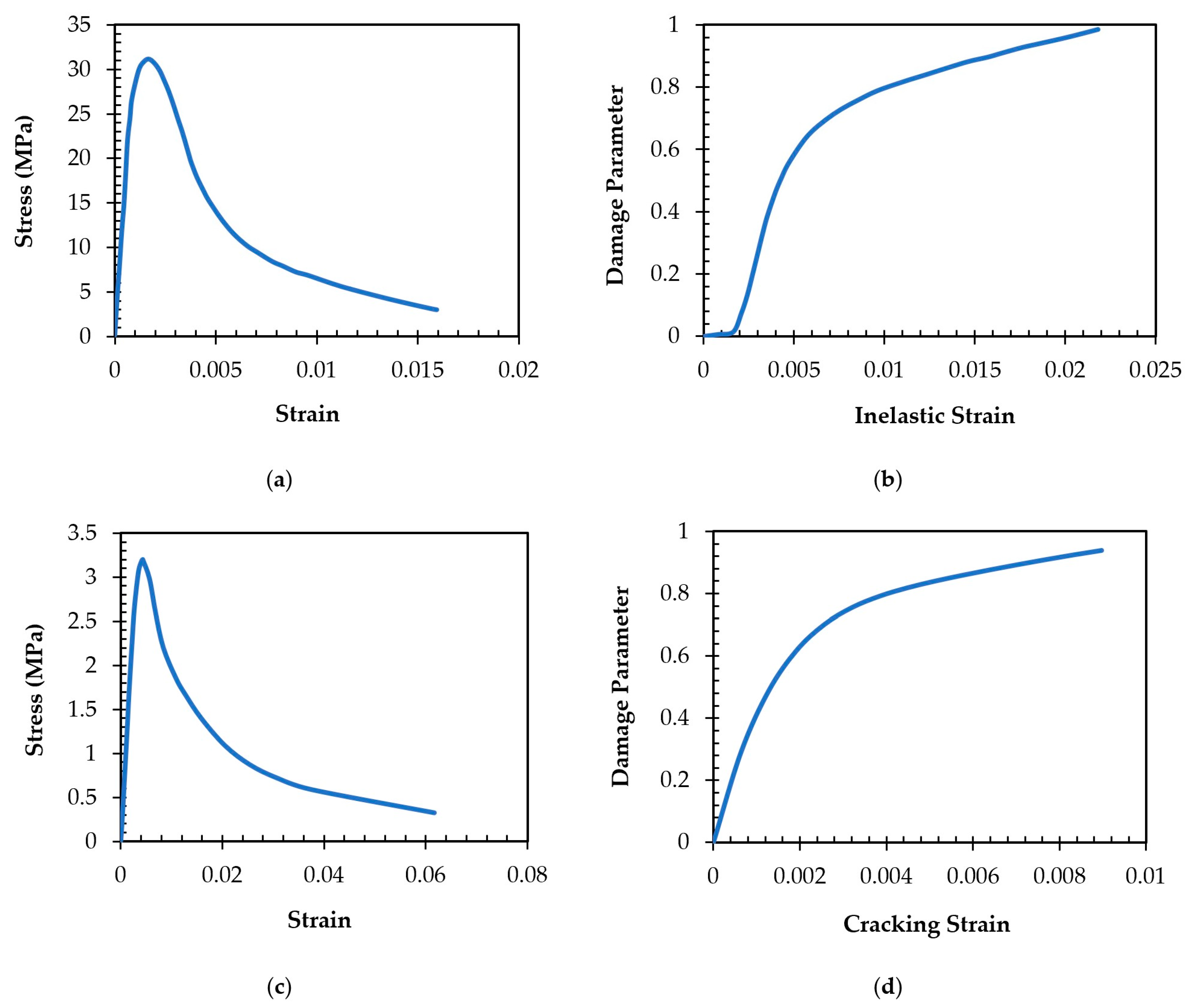
2.2. Constitutive Modeling of Concrete and Steel
2.3. Modeling of Corrosion
2.4. Constitutive Modeling of CFRP
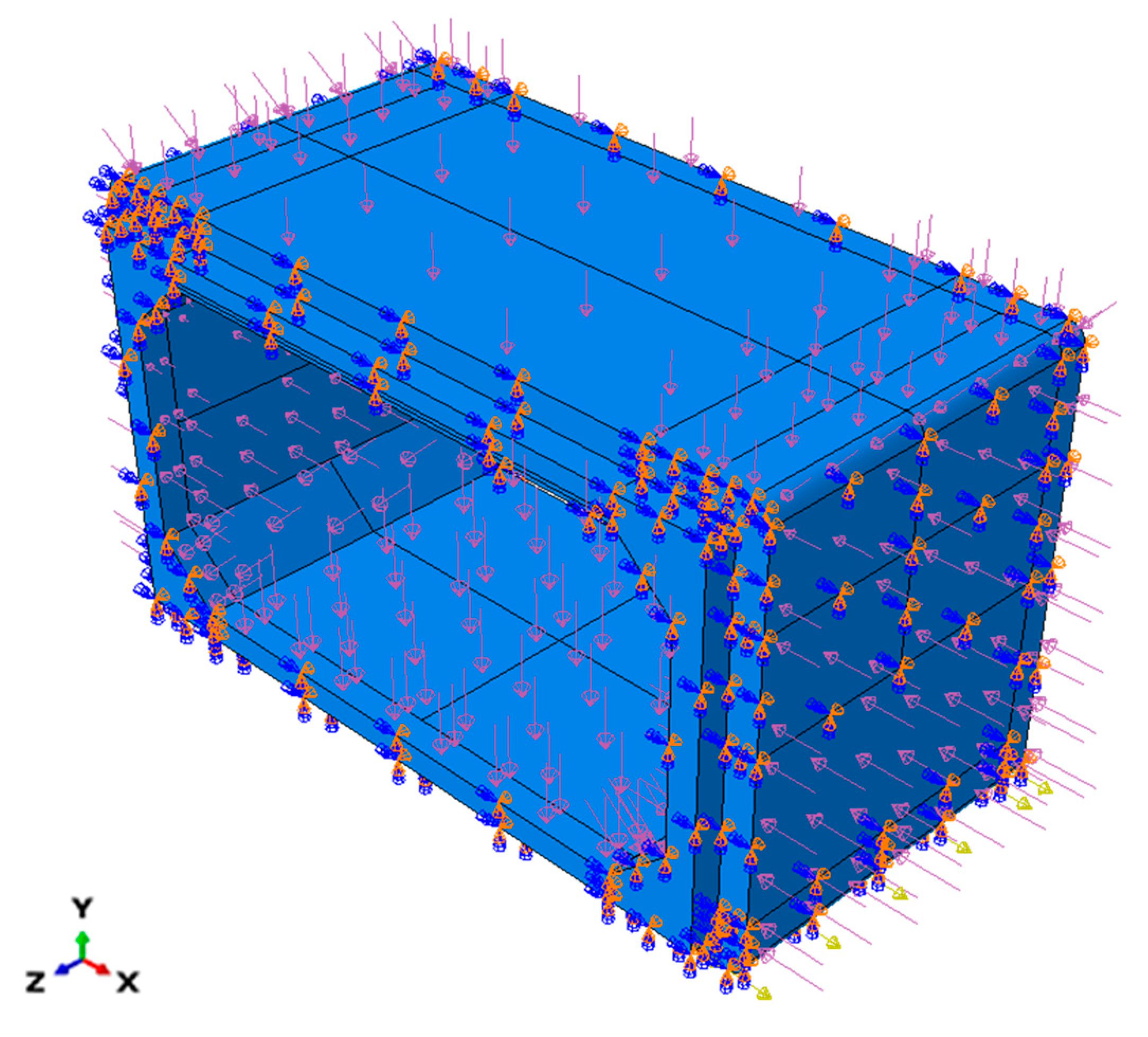
2.5. Boundary Conditions, Interactions, and Loading
2.6. Validation of Model and Mesh Sensitivity Analysis
3. Results and Discussion
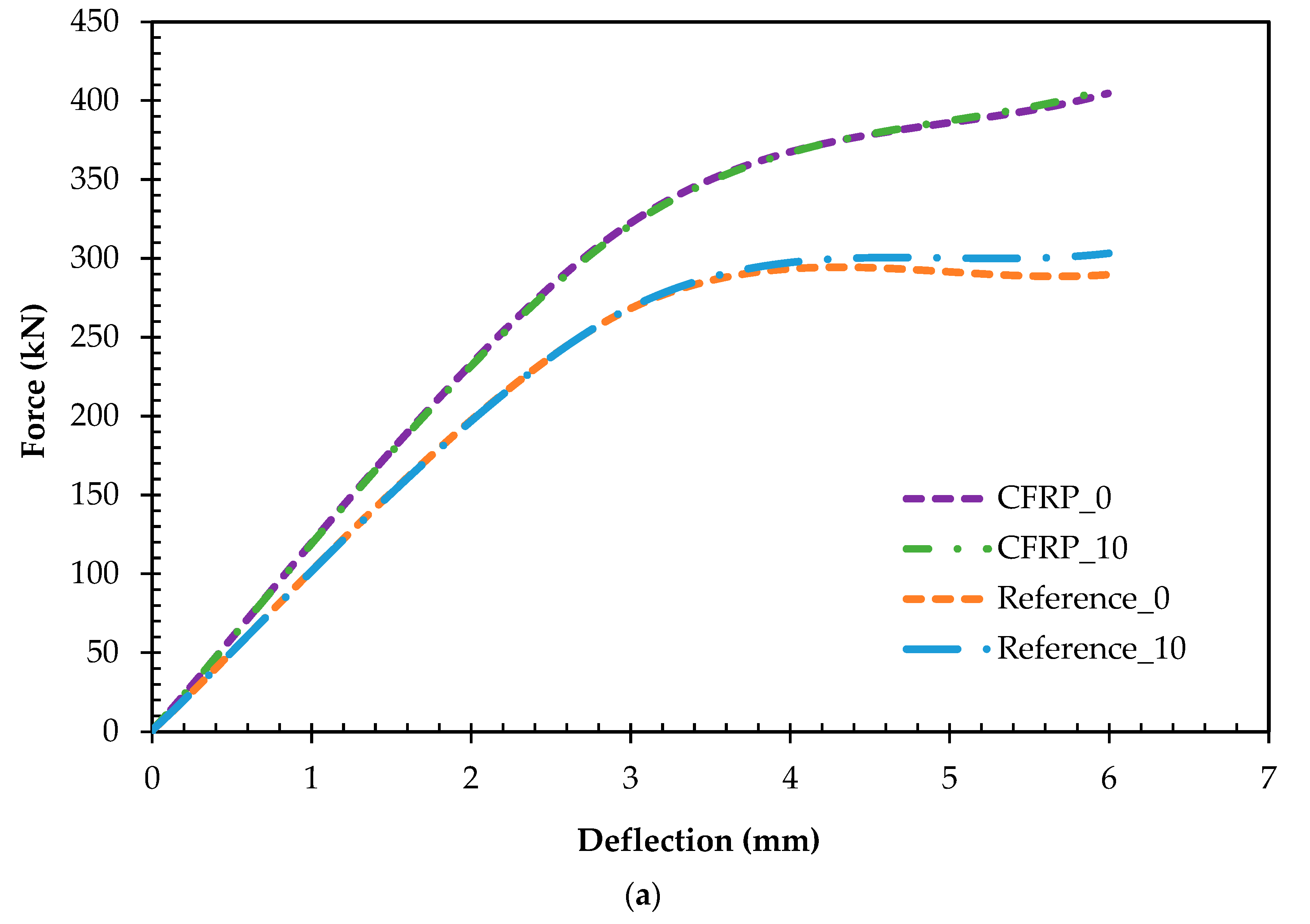
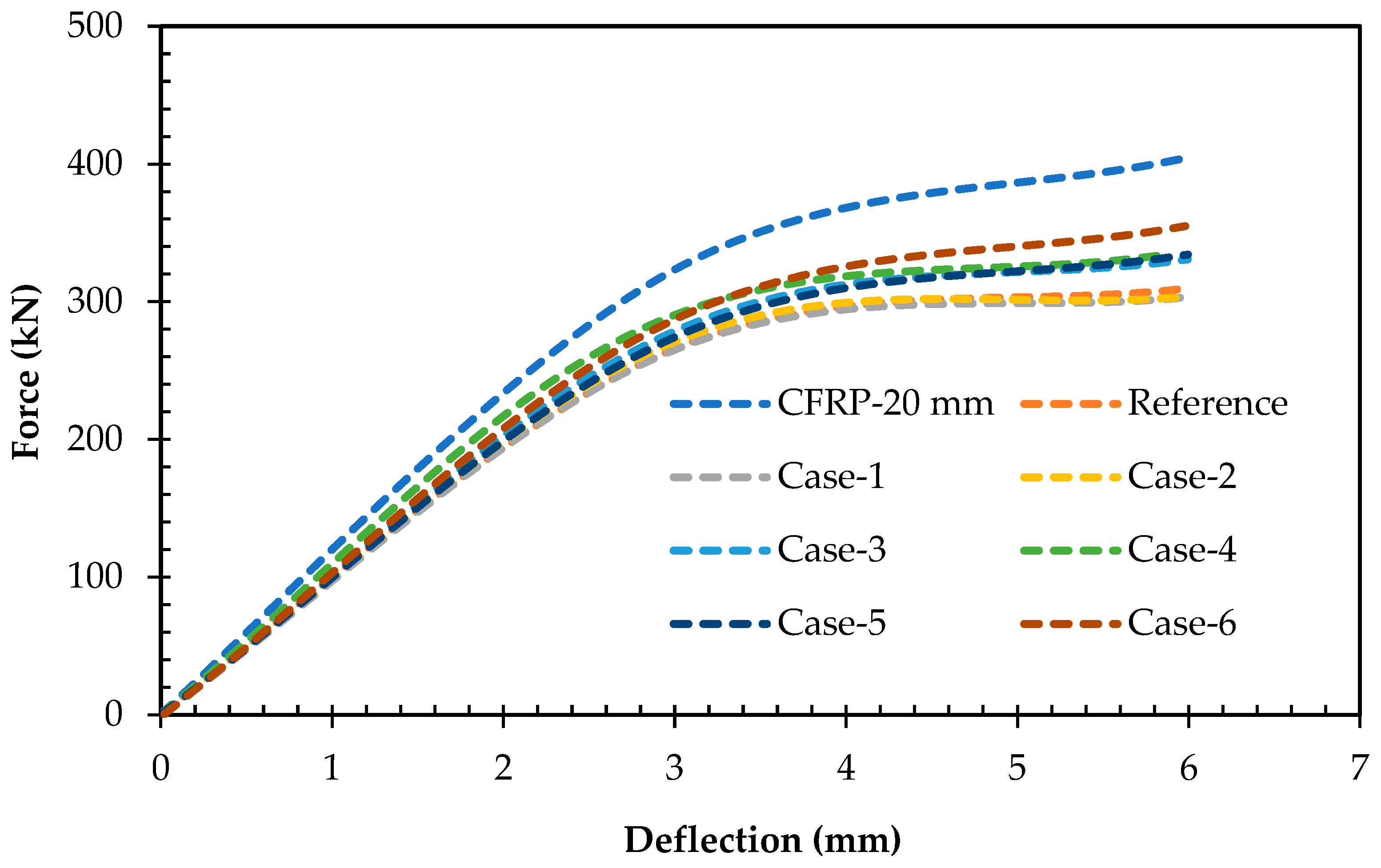
3.1. Comparison of CFRP-Strengthened and Reference Model
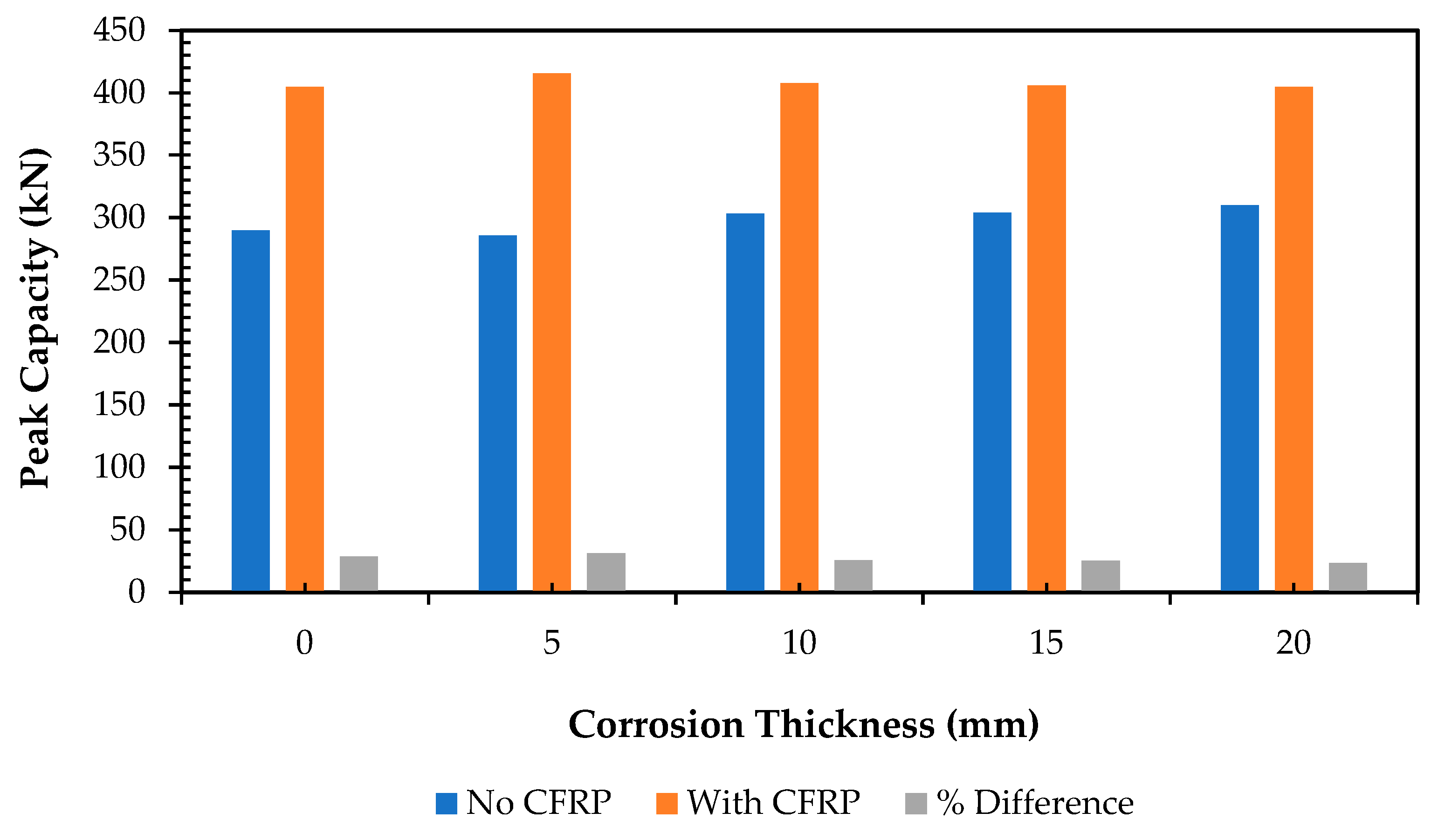
3.2. Parametric Study of Using CFRP Stirrups
4. Conclusions
- This research revealed the effectiveness of CFRP sheets in mitigating the effects of corrosion, resulting in a noticeable increase in the structural capacity of box culverts. CFRP is a promising solution for the improvement of the service life and strength of corroded box culverts.
- CFRP strengthening depicted its potential to mitigate the effects of corrosion and enhance the overall performance, with a remarkable 25% increase in the structural capacity of corroded box culverts compared to those without CFRP strengthening.
- Utilizing a full CFRP sheet emerged as a crucial factor for the efficient design and repair of deteriorated culvert boxes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Smart, P.; Herbertson, J.G. Drainage Design; Blackie: Glasgow, UK, 1992; p. 299. [Google Scholar]
- McGrath, T.; Moore, I.; Selig, E.; Webb, M.C.; Taleb, B. Recommended Specifications for Large-Span Culverts; NCHRP Report; Transportation Research Board National Research Council 2101 Constitution Avenue: Washington, DC, USA, 2002. [Google Scholar]
- AASHTO. AASHTO LRFD Bridge Design Specifications, 9th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2020; pp. 3–33. [Google Scholar]
- Mackie, K.; Stojadinovic, B. Seismic Demands for Performance-Based Design of Bridges; PEER Report 2003-16; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2003. [Google Scholar]
- Miyazaki, Y. Fundamental Study on Seismic Behavior of Hinge Types of Precast Arch Culverts in Culvert Longitudinal Direction. 2019. Available online: https://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/242475/2/dkogk04553.pdf (accessed on 24 August 2023).
- Bian, X.; Tang, X.; Shen, W.; Ling, D.; Chen, Y. An Experimental Study on a Culvert Buried in Granular Soil Subjected to Vehicle Loads. Adv. Struct. Eng. 2012, 15, 1031–1040. [Google Scholar] [CrossRef]
- Gong, Y.; Ma, Y.; Tan, G.; Bi, H.; Pang, Y.; Ma, C. Experimental Study and Numerical Simulation on Failure Process of Reinforced Concrete Box Culvert. Adv. Civ. Eng. 2020, 2020, 5423706. [Google Scholar] [CrossRef]
- Tang, Y.; Bao, Y.; Zheng, Z.; Zhang, J.; Cai, Y. Performance Assessment of Deteriorating Reinforced Concrete Drainage Culverts: A Case Study. Eng. Fail. Anal. 2022, 131, 105845. [Google Scholar] [CrossRef]
- Ali, A.M. Manual RC Box Culvert Analysis and Designing. Int. J. Innov. Sci. Res. Technol. 2020, 5, 91–115. [Google Scholar] [CrossRef]
- Moradi, M.; Valipour, H.; Foster, S. Reserve of Strength in Inverted U-Shaped RC Culverts: Effect of Backfill on Ultimate Load Capacity and Fatigue Life. J. Bridge Eng. 2015, 21, 04015051. [Google Scholar] [CrossRef]
- Maximos, H.; Erdogmus, E.; Tadros, M.K. Fatigue evaluation for reinforced concrete box culverts. ACI Struct. J. 2010, 107, 13–20. Available online: https://experts.nebraska.edu/en/publications/fatigue-evaluation-for-reinforced-concrete-box-culverts (accessed on 24 August 2023).
- Garg, A.K.; Abolmaali, A.; Fernandez, R. Experimental Investigation of Shear Capacity of Precast Reinforced Concrete Box Culverts. J. Bridg. Eng. 2007, 12, 511–517. [Google Scholar] [CrossRef]
- Gebremedhn, Z.; Qiao, G.; Li, J. Finite Element Modeling and Analysis of Precast Reinforced Concrete U-Shaped Box Culvert Using ABAQUS. Am. J. Civ. Eng. 2018, 6, 162. [Google Scholar] [CrossRef][Green Version]
- Haghani, R.; Yang, J.; Gutierrez, M.; Eamon, C.D.; Volz, J. Fiber Reinforced Polymer Culvert Bridges—A Feasibility Study from Structural and LCC Points of View. Infrastructures 2021, 6, 128. [Google Scholar] [CrossRef]
- Hassanli, R.; Youssf, O.; Manalo, A.; Najafgholipour, M.A.; Elchalakani, M.; Castillo, E.d.R.; Lutze, D. An Experimental Study of the Behavior of GFRP-Reinforced Precast Concrete Culverts. J. Compos. Constr. 2022, 26, 04022043. [Google Scholar] [CrossRef]
- Vijayan, D.S.; Sivasuriyan, A.; Devarajan, P.; Stefańska, A.; Wodzyński, Ł.; Koda, E. Carbon Fibre-Reinforced Polymer (CFRP) Composites in Civil Engineering Application—A Comprehensive Review. Buildings 2023, 13, 1509. [Google Scholar] [CrossRef]
- Bakkour, F.; Tuhta, S.; Günday, F. Determination of Modal Parameters of Reinforced Concrete Box Culvert Retrofitted with GFRP Using Finite Element Method. Int. J. Innov. Eng. Res. Technol. 2022, 9, 1–9. [Google Scholar] [CrossRef]
- Sabdono, P.; Sukamta. Reinforcement on existing concrete that has been reinforced with CFRP. Int. Conf. Educ. Soc. Sci. Technol. (ICESST) 2022, 1, 108–121. [Google Scholar] [CrossRef]
- Chen, B.-G.; Zheng, J.-J.; Han, J. Experimental Study and Numerical Simulation on Concrete Box Culverts in Trenches. J. Perform. Constr. Facil. 2010, 24, 223–234. [Google Scholar] [CrossRef]
- Acharya, R.; Han, J.; Brennan, J.J.; Parsons, R.L.; Khatri, D.K. Structural Response of a Low-Fill Box Culvert under Static and Traffic Loading. J. Perform. Constr. Facil. 2016, 30, 04014184. [Google Scholar] [CrossRef]
- Awwad, E.; Mabsout, M.; Sadek, S.; Tarhini, K. Finite Element Analysis of Concrete Box Culverts. In Proceedings of the 8th International Conference on Computing in Civil and Building Engineering, Stanford, CA, USA, 14–16 August 2000; Volume 279, pp. 1051–1053. [Google Scholar] [CrossRef]
- Shuhong, W.; Jierula, A.; Wang, P.; Liu, W.; Jie, R. Simulation of force performance of precast rectangular box culvert and its potential failure mode. J. Northeastern Univ. (Nat. Sci.) 2018, 2, 260–265. [Google Scholar]
- Uddin, Z.; Waqas, H.A.; Husnain, M.; Ibrahim, M.; Naveed, M.; Zaib, H. Design Optimization of Precast Reinforced Box Culvert with the Application of Finite Element Modeling and Analysis. In Proceedings of the 1st International Conference on Advances in Civil & Environmental Engineering, University of Engineering & Technology, Taxila, Pakistan, 22–23 February 2022. [Google Scholar]
- Ozturk, B. Seismic behavior of two monumental buildings in historical Cappadocia region of Turkey. Bull. Earthq. Eng. 2017, 15, 3103–3123. [Google Scholar] [CrossRef]
- Moon, J.S.; Kim, D.Y.; Ko, M.S.; Kim, C. Performance of Reinforced Concrete Beams Strengthened by Bidirectional Carbon-Fiber-Reinforced Polymers Based on Numerical Models. Polymers 2023, 15, 1012. [Google Scholar] [CrossRef] [PubMed]
- Mahmoud, M.H.; Afefy, H.M.; Kassem, N.M.; Fawzy, T.M. Strengthening of defected beam–column joints using CFRP. J. Adv. Res. 2013, 5, 67–77. [Google Scholar] [CrossRef] [PubMed]
- Joyklad, P.; Waqas, H.A.; Hafeez, A.; Ali, N.; Ejaz, A.; Hussain, Q.; Khan, K.; Sangthongtong, A.; Saingam, P. Experimental Investigations of Cement Clay Interlocking Brick Masonry Structures Strengthened with CFRP and Cement-Sand Mortar. Infrastructures 2023, 8, 59. [Google Scholar] [CrossRef]
- Tanarslan, H. Behavior of RC beams strengthened with inclined CFRP strips. J. Reinf. Plast. Compos. 2010, 29, 3275–3286. [Google Scholar] [CrossRef]
- Singh, J.P.; Kumar, A.; Kumar, A. Application of CFRP in Concrete Culvert Bridges. Lect. Notes Civ. Eng. 2022, 221, 527–537. [Google Scholar] [CrossRef]
- ASTM C1577; Standard Specification for Precast Reinforced Concrete Box Sections for Culverts, Storm Drains, and Sewers Designed According to AASHTO LRFD. ASTM International: West Conshohocken, PA, USA, 2005; p. 17.
- Smith, M. ABAQUS/Standard UProvidence,. User’s Manual, Version 6.9; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2009. [Google Scholar]
- Xiao, Y.; Chen, Z.; Zhou, J.; Leng, Y.; Xia, R. Concrete plastic-damage factor for finite element analysis: Concept, simulation, and experiment. Adv. Mech. Eng. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Ferretti, E. Experimental procedure for verifying strain-softening in concrete. Int. J. Fract. 2004, 126, L27–L34. [Google Scholar] [CrossRef]
- Najafgholipour, M.; Dehghan, S.; Dooshabi, A.; Niroomandi, A. Finite element analysis of reinforced concrete beam-column connections with governing joint shear failure mode. Lat. Am. J. Solids Struct. 2017, 14, 1200–1225. [Google Scholar] [CrossRef]
- Khan, A.; Ullah, A.; Tariq, M.; Waqas, H.A.; Khan, A.; Khan, J.S. Response of shear critical RC beam under transverse impact using improved linear complementarity. Structures 2023, 54, 1520–1540. [Google Scholar] [CrossRef]
- Zhao, K.; Wei, Y.; Yan, S.; Chen, S.; Dong, F. Experimental and analytical investigations on flexural behavior of bamboo beams strengthened with steel bars. Adv. Struct. Eng. 2021, 24, 3338–3356. [Google Scholar] [CrossRef]
- Iqbal, M.; Rai, S.; Sadique, M.; Bhargava, P. Numerical simulation of aircraft crash on nuclear containment structure. Nucl. Eng. Des. 2012, 243, 321–335. [Google Scholar] [CrossRef]
- Senthil, K.; Rupali, S.; Kaur, N. The Performance of Monolithic Reinforced Concrete Structure Includes Slab, Beam and Column against Blast Load. J. Mater. Eng. Struct. 2018, 5, 137–151. [Google Scholar]
- Senthil, K.; Rupali, S.; Satyanarayanan, K.S. Experiments on ductile and non-ductile reinforced concrete frames under static and cyclic loading. J. Coupled Syst. Multiscale Dyn. 2017, 5, 38–50. [Google Scholar] [CrossRef]
- Wen, Q.-Q.; Chen, M.-C. Study on the nonlinear performance degradation of reinforced concrete beam under chloride ion corrosion. Eng. Fail. Anal. 2021, 124, 105310. [Google Scholar] [CrossRef]
- Sastry, Y.S.; Budarapu, P.R.; Krishna, Y.; Devaraj, S. Studies on ballistic impact of the composite panels. Theor. Appl. Fract. Mech. 2014, 72, 2–12. [Google Scholar] [CrossRef]
- Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X. Simulating low-velocity impact induced delamination in composites by a quasistatic load model with surface-based cohesive contact. Compos. Struct. 2015, 125, 51–57. [Google Scholar] [CrossRef]
- Shin, D.; Kim, H.; Lee, J. Numerical analysis of the damage behavior of an aluminum/CFRP hybrid beam under three point bending. Compos. Part B Eng. 2013, 56, 397–407. [Google Scholar] [CrossRef]
- Waqas, H.A.; Husnain, A.; Ubaid, H.; Khan, A.P.; Shah, M.; Ilyas, M.; Waseem, M. Assessment of In-fluence of Reinforcement Detailing on Blast Resistance of Reinforced Concrete Beam-column Connections. J. Mater. Eng. Struct. « JMES » 2023, 10, 357–375. Available online: https://revue.ummto.dz/index.php/JMES/article/view/3339 (accessed on 26 August 2023).
- Kalfat, R.; Al-Mahaidi, R. Numerical and Experimental Validation of FRP Patch Anchors Used to Improve the Performance of FRP Laminates Bonded to Concrete. J. Compos. Constr. 2014, 18. [Google Scholar] [CrossRef]
- ASTM C1433; Standard Specifications for Precast Reinforced Concrete Box Sections for Culverts, Storm Drains, and Sewers. ASTM International: West Conshohocken, PA, USA, 2004; p. 25.
- Al-Ameedee, H.S.; Al-Khafaji, H.M. Improving the flexural behavior of RC beams strengthening by near-surface mounting. J. Mech. Behav. Mater. 2022, 31, 701–709. [Google Scholar] [CrossRef]







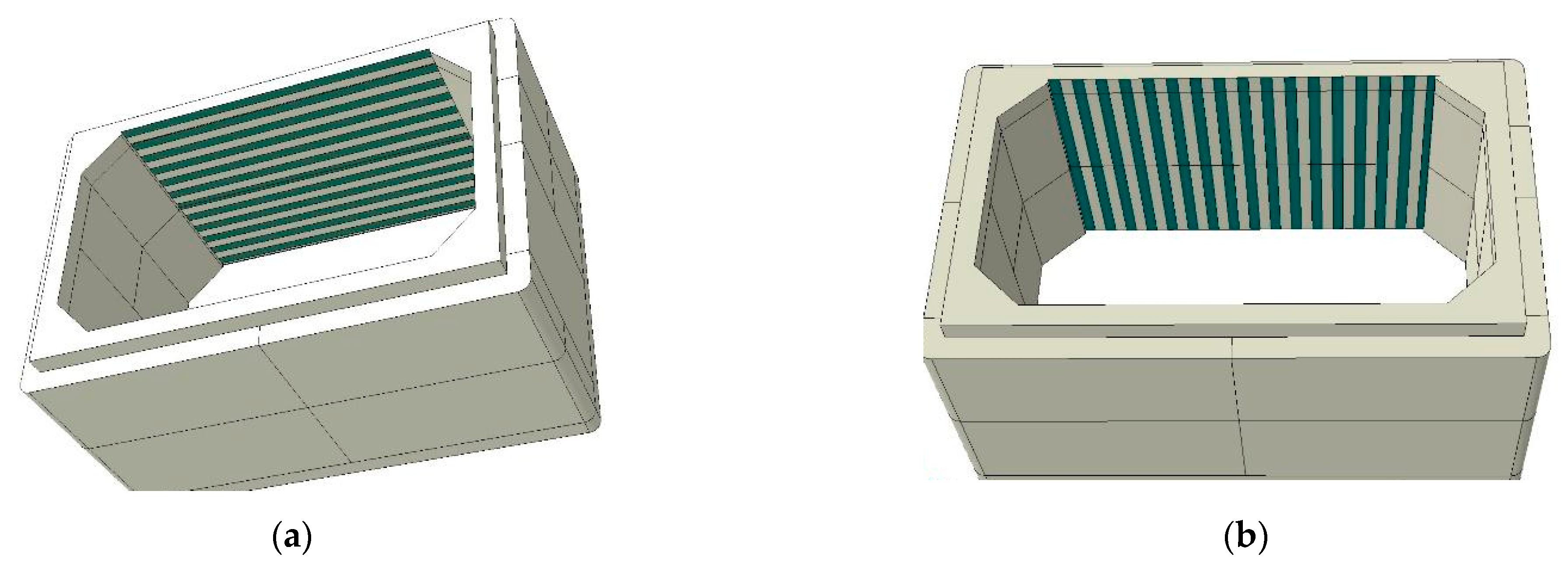
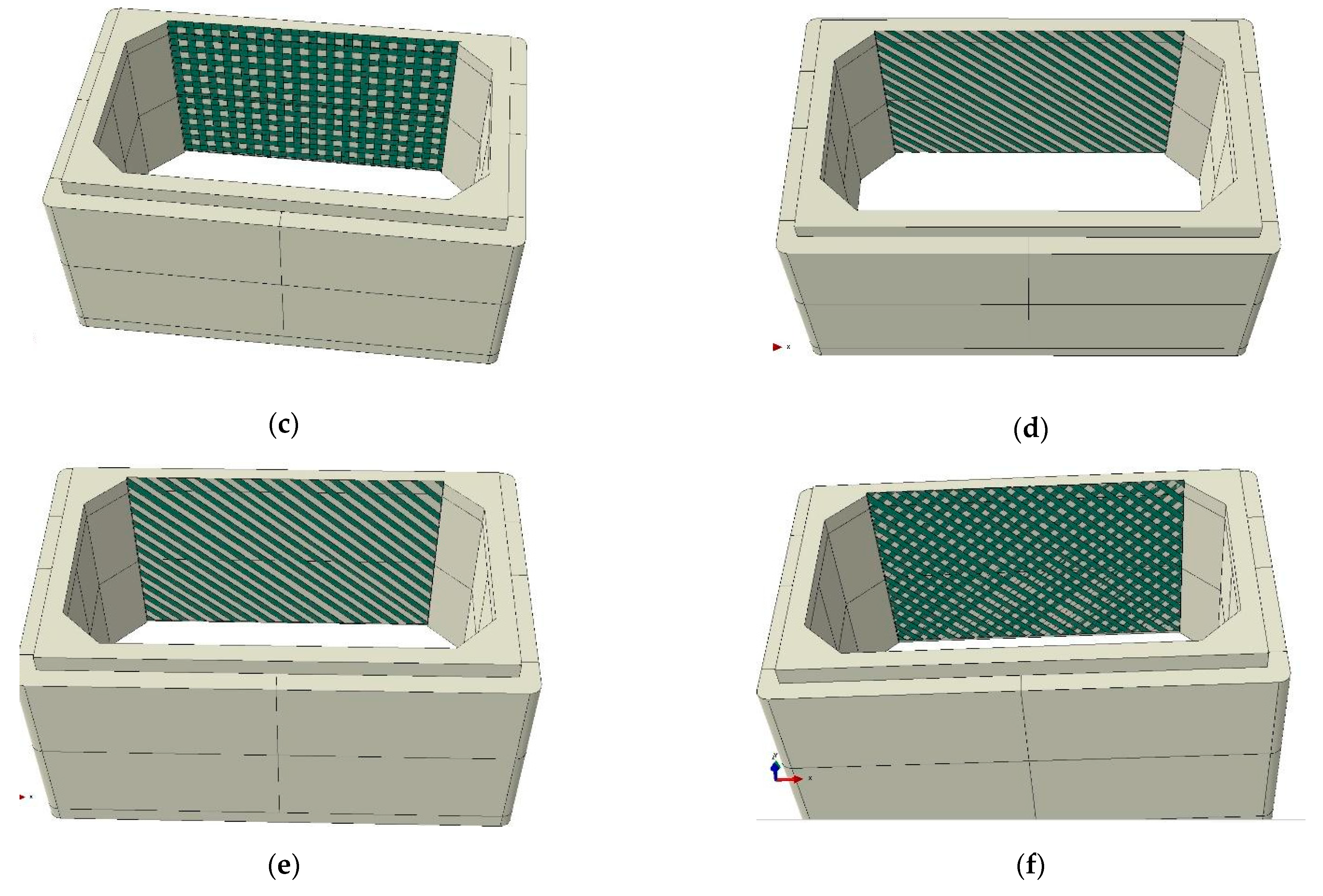
| Material | Density (kg/m3) | Young’s Modulus (MPa) | Compressive Strength (MPa) | Post-Yielding Young’s Modulus (MPa) | Tensile Strength (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| Concrete | 2400 | 32,500 | 26.8 | - | 2.4 | 0.2 |
| Reinforced steel | 7850 | 200,000 | 450 | 20,000 | 450 | 0.3 |
| Parameter | Value |
|---|---|
| Ψ | 40° |
| E | 0.1 |
| 1.16 | |
| K | 0.66 |
| μ | 0.001 |
| Density (t/mm3) | E1 (MPa) | E2 (MPa) | u12 | G12 (MPa) | G13 (MPa) | G23 (MPa) |
|---|---|---|---|---|---|---|
| 1.56 × 10−9 | 130,000 | 8000 | 0.28 | 4500 | 4500 | 3600 |
| Longitudinal Tensile Strength (MPa) | Longitudinal Compressive Strength (MPa) | Transverse Tensile Strength (MPa) | Transverse Compressive Strength (MPa) | Longitudinal Shear Strength (MPa) | Transverse Shear Strength (MPa) |
|---|---|---|---|---|---|
| 2200 | 2200 | 61 | 130 | 85 | 40 |
| Longitudinal Tensile Fraction Energy (mJ/mm2) | Longitudinal Compressive Fraction Energy (mJ/mm2) | Transverse Tensile Fraction Energy (mJ/mm2) | Transverse Compressive Fraction Energy (mJ/mm2) |
|---|---|---|---|
| 70 | 70 | 0.25 | 0.25 |
| Mesh Size (mm) | Displacement (mm) | Force (t) | |
|---|---|---|---|
| Concrete | Steel | ||
| 20 | 20 | 4.5 | 23.9 |
| 50 | 50 | 4.5 | 24.0 |
| 100 | 100 | 3.45 | 27 |
| 200 | 200 | 5 | 35 |
| Chosen mesh size | For both steel and concrete, a mesh size of 100 mm was utilized | Percentage error in numerical analysis results | 10 |
| Corrosion Damage (mm) | Ultimate Capacity, Pu (kN) | Percentage Difference | |
|---|---|---|---|
| Reference | CFRP | ||
| 0 | 289.66 | 404.64 | 28.42 |
| 5 | 285.53 | 415.67 | 31.31 |
| 10 | 303.22 | 407.61 | 25.61 |
| 15 | 303.71 | 405.72 | 25.14 |
| 20 | 309.86 | 404.78 | 23.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waqas, H.A.; Bahrami, A.; Amin, F.; Sahil, M.; Saud Khan, M. Numerical Modeling and Performance Evaluation of Carbon Fiber-Reinforced Polymer-Strengthened Concrete Culverts against Water-Induced Corrosion. Infrastructures 2024, 9, 82. https://doi.org/10.3390/infrastructures9050082
Waqas HA, Bahrami A, Amin F, Sahil M, Saud Khan M. Numerical Modeling and Performance Evaluation of Carbon Fiber-Reinforced Polymer-Strengthened Concrete Culverts against Water-Induced Corrosion. Infrastructures. 2024; 9(5):82. https://doi.org/10.3390/infrastructures9050082
Chicago/Turabian StyleWaqas, Hafiz Ahmed, Alireza Bahrami, Fayiz Amin, Mehran Sahil, and Muhammad Saud Khan. 2024. "Numerical Modeling and Performance Evaluation of Carbon Fiber-Reinforced Polymer-Strengthened Concrete Culverts against Water-Induced Corrosion" Infrastructures 9, no. 5: 82. https://doi.org/10.3390/infrastructures9050082
APA StyleWaqas, H. A., Bahrami, A., Amin, F., Sahil, M., & Saud Khan, M. (2024). Numerical Modeling and Performance Evaluation of Carbon Fiber-Reinforced Polymer-Strengthened Concrete Culverts against Water-Induced Corrosion. Infrastructures, 9(5), 82. https://doi.org/10.3390/infrastructures9050082








