Towards Sustainable Road Pavements: Sound Absorption in Rubber-Modified Asphalt Mixtures
Abstract
1. Introduction
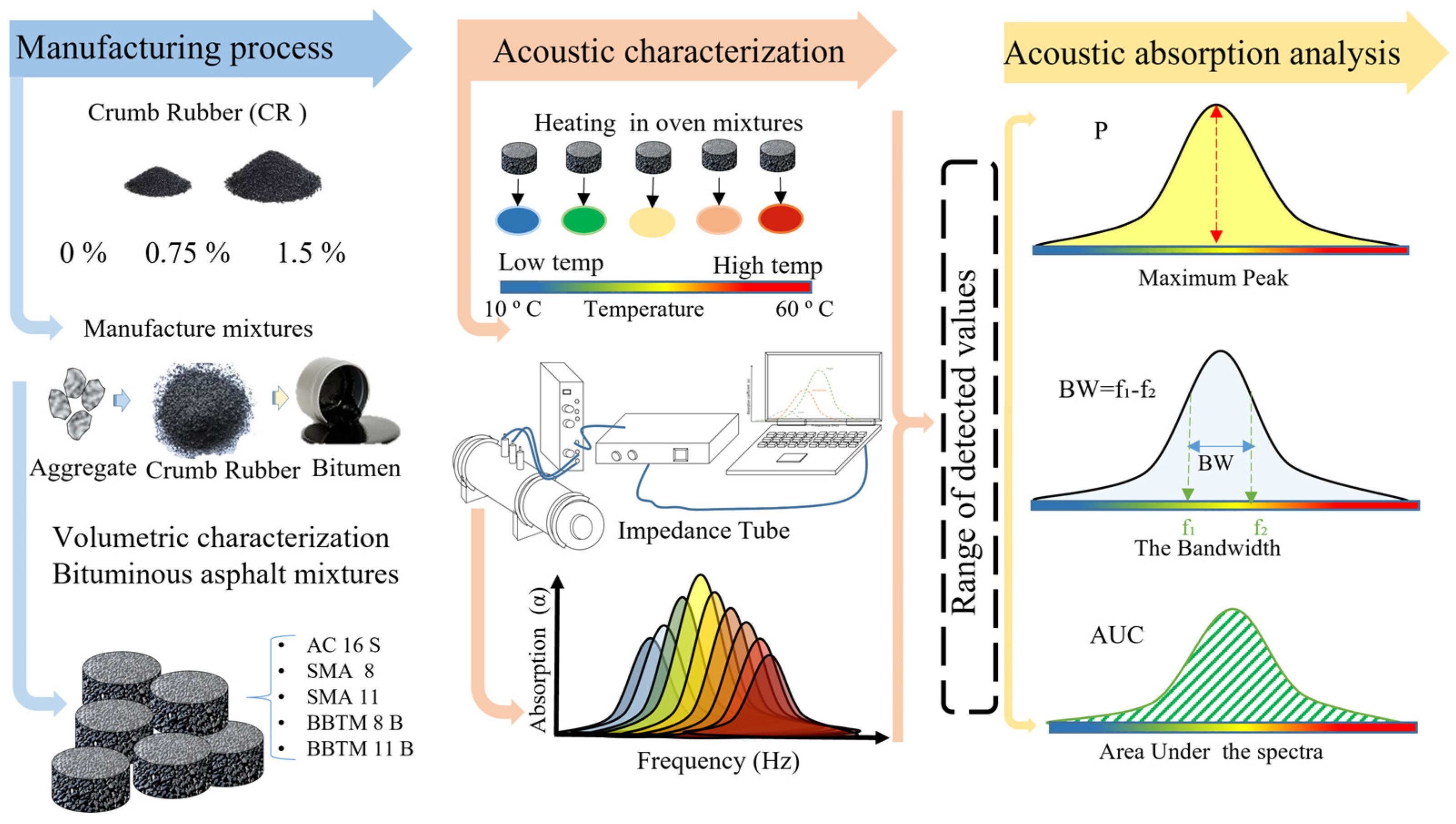
2. Methodology and Materials
2.1. Sound Absorption
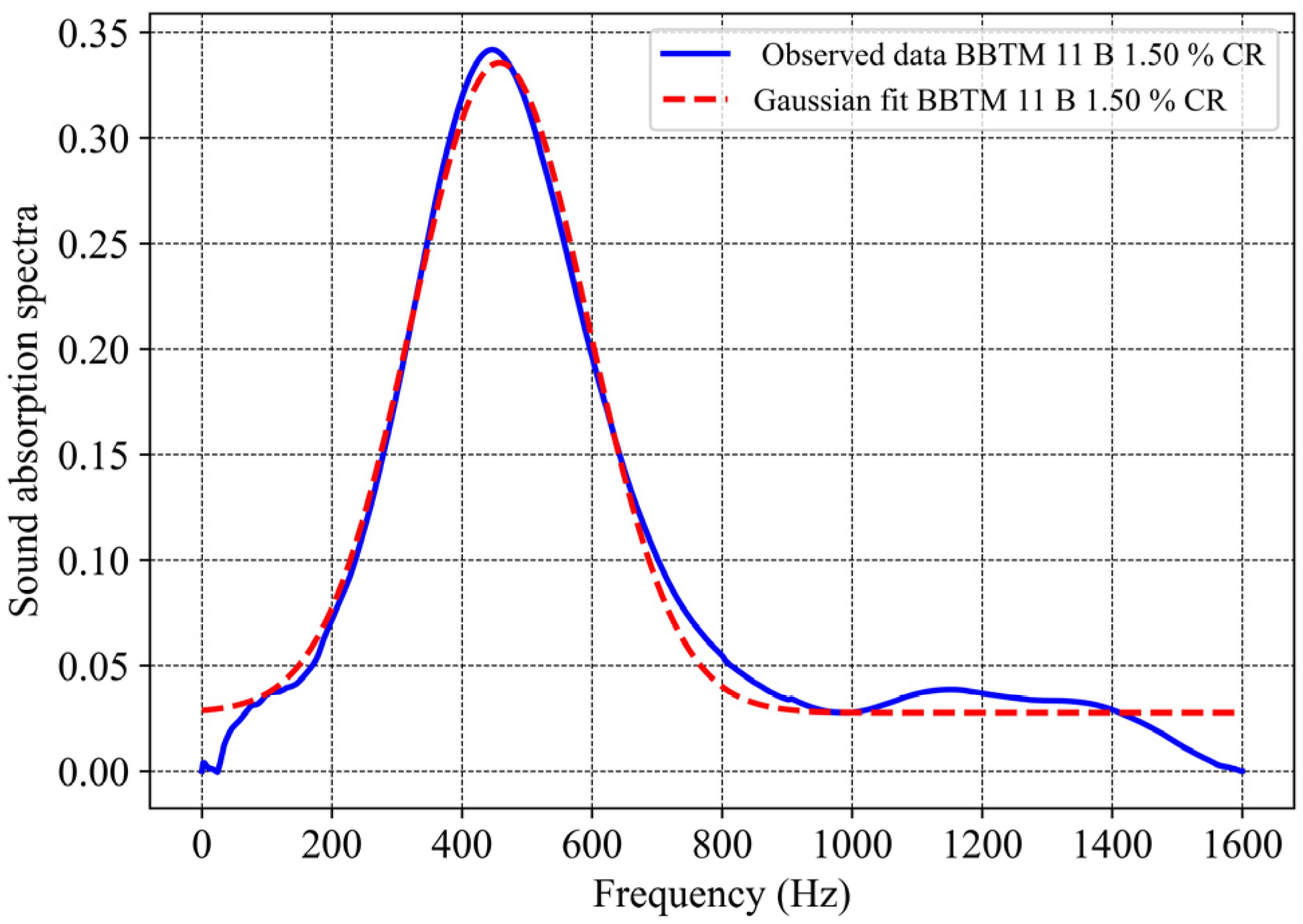
2.2. Sound Absorption Analysis by Gaussian Adjustment
2.3. Determination of Volumetric and Permeability Characteristics
2.4. Statistical Analysis
2.5. Aggregates
2.6. Crumb Rubber (CR)
2.7. Asphalt Mixture Investigation: Laboratory Experimental Activity
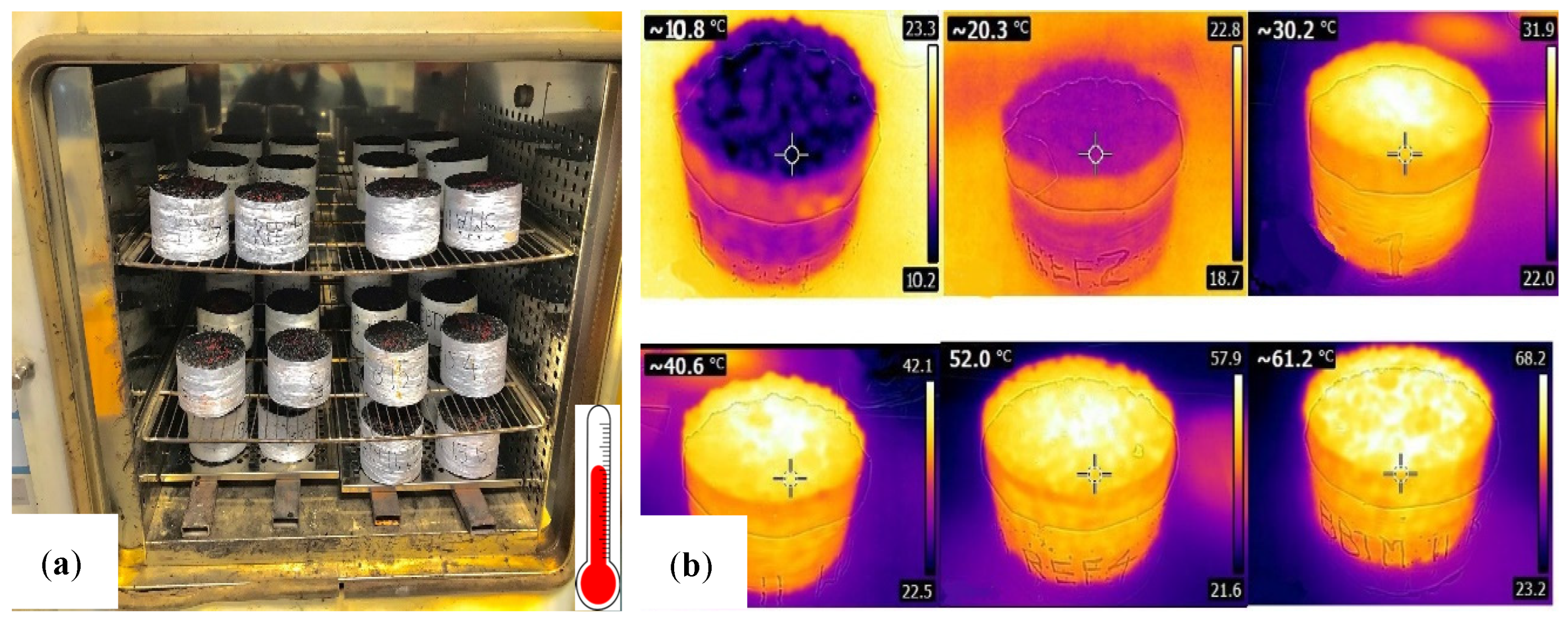
2.8. Thermal Conditioning for Absorption Measurement
3. Results and Discussion
3.1. Volumetric Characterization, Permeability, and Macrotexture
3.2. Sound Absorption Coefficient: Influence of Mixture Type, Temperature, and CR Content
3.3. Gaussian Goodness of Fit
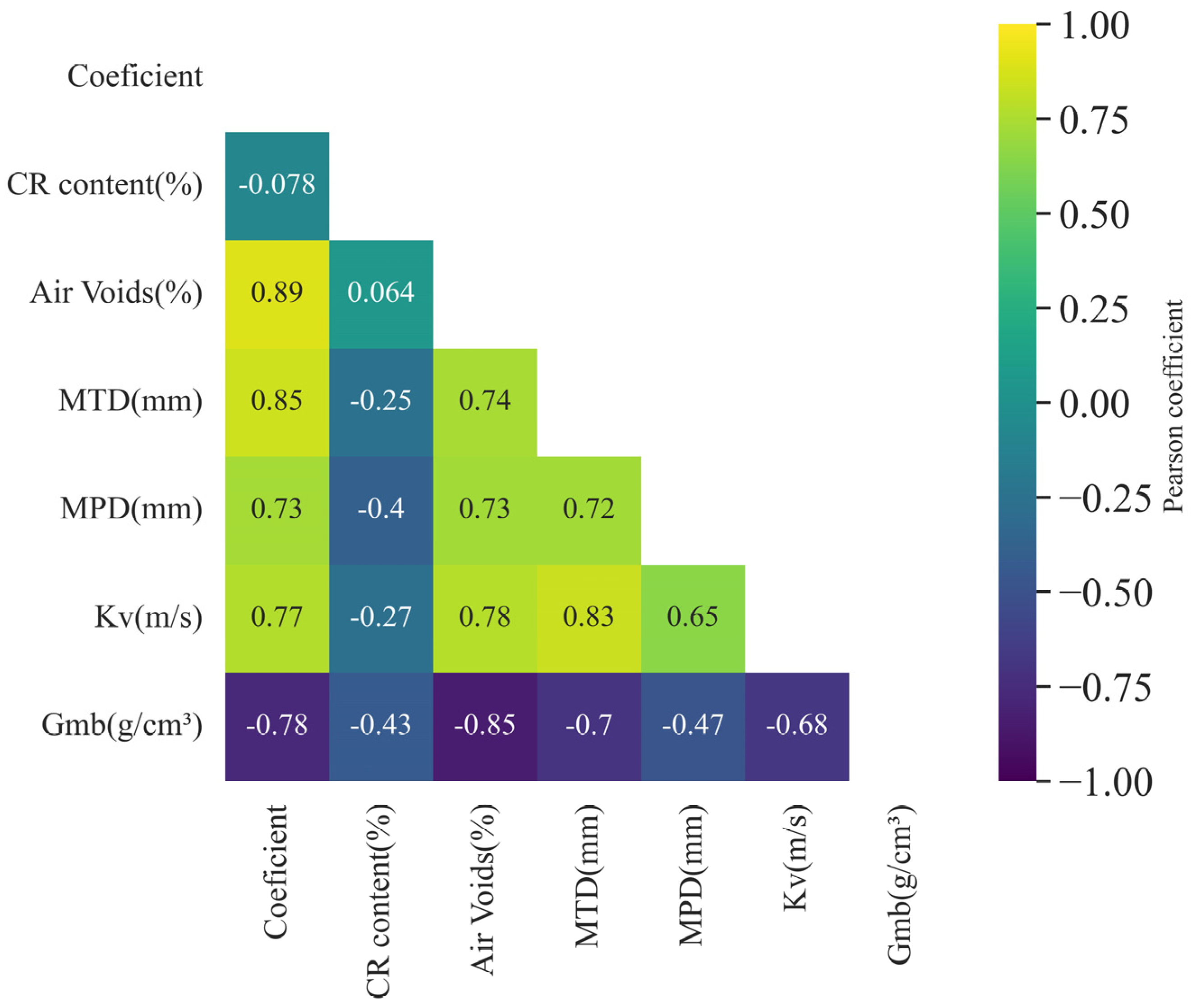
3.4. Regression Models of Asphalt Mixture Characteristics as a Function of Gaussian Parameters
4. Conclusions
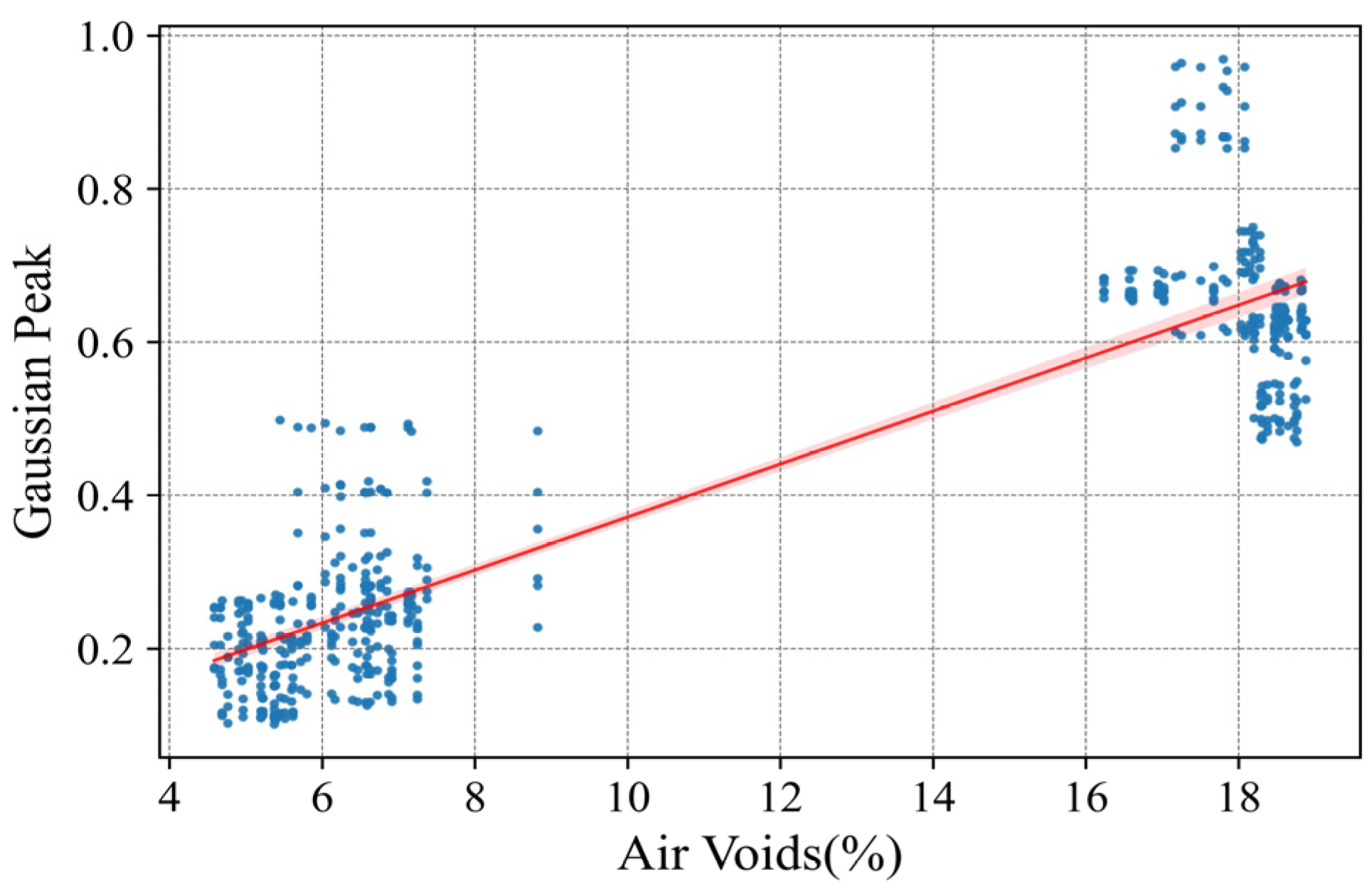
- The Peak (P) absorption improves with the air void content (Va) in asphalt mixtures. However, the rubber content (CR) and the temperature at which the measurement is made do not seem to influence the Peak parameter. The model fit is R2 = 0.788.
- The air void content (Va) tends to reduce the BandWidth (BW), while the crumb rubber content increases it. However, the model has limitations in terms of low goodness of fit, with R2 = 0.325.
- Void content positively affects the Area Under the Curve (AUC). On the other hand, rubber content slightly reduces the AUC. This model has a good fit with a coefficient of R2 = 0.738.
- The main factor affecting the sound absorption is clearly the void content of the asphalt mixture. The maximum sound absorption coefficient was obtained for asphalt mixtures with high air void content, in this research the discontinuous BBTM open mixtures.
- Crumb rubber has limited influence on the sound absorption of AC and SMA mixtures. In open-mixture-type BBTM it seems to slightly improve the sound absorption.
- The temperature (10 °C to 60 °C) has a limited influence on the results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- European Environment Agency. Environmental Noise in Europe—2020; European Environment Agency: Copenhagen, Denmark, 2020; p. 104. [Google Scholar]
- Klompmaker, J.O.; Hoek, G.; Bloemsma, L.D.; Wijga, A.H.; van den Brink, C.; Brunekreef, B.; Lebret, E.; Gehring, U.; Janssen, N.A.H. Associations of Combined Exposures to Surrounding Green, Air Pollution and Traffic Noise on Mental Health. Environ. Int. 2019, 129, 525–537. [Google Scholar] [CrossRef]
- EEA. EEA Report No 10/2014—Noise in Europe 2014; EEA: Copenhagen, Denmark, 2014; ISBN 978-92-9213-505-8. [Google Scholar]
- Sandberg, U. Tyre/Road Noise—Myths and Realities. In Proceedings of the 2001 International Congress and Exhibition on Noise Control Engineering, The Hague, The Netherlands, 27–30 August 2001; p. 22. [Google Scholar]
- Greer, G. Stone Mastic Asphalt—A Review of Its Noise Reducing and Early Life Skid Resistance Properties. In Proceedings of the 1st Australasian Acoustical Societies’ Conference 2006, ACOUSTICS 2006: Noise of Progress, Christchurch, New Zealand, 20–22 November 2006; pp. 319–323. [Google Scholar]
- Li, T. A Review on Physical Mechanisms of Tire-Pavement Interaction Noise. SAE Int. J. Veh. Dyn. Stab. NVH 2019, 3, 87–112. [Google Scholar] [CrossRef]
- Bennert, T.; Hanson, D.; Maher, A.; Vitillo, N. Influence of Pavement Surface Type on Tire/Pavement Generated Noise. J. Test. Eval. 2005, 33, 94–100. [Google Scholar] [CrossRef]
- Ling, S.; Yu, F.; Sun, D.; Sun, G.; Xu, L. A Comprehensive Review of Tire-Pavement Noise: Generation Mechanism, Measurement Methods, and Quiet Asphalt Pavement. J. Clean. Prod. 2021, 287, 125056. [Google Scholar] [CrossRef]
- Meiarashi, S.; Ishida, M.; Nakashiba, F.; Niimi, H.; Hasebe, M.; Nakatsuji, T. Improvement in the Effect of Drainage Asphalt Road Surface on Noise Reduction. Appl. Acoust. 1996, 47, 189–204. [Google Scholar] [CrossRef]
- Liao, G.; Heitzman, M.; West, R.; Wang, S.; Ai, C. Temperature Effects on the Correlations between Tire-Pavement Noises and Pavement Surface Characteristics. In Proceedings of the New Frontiers in Road and Airport Engineering—Selected Papers from the 2015 International Symposium on Frontiers of Road and Airport Engineering, IFRAE, Shanghai, China, 26–28 October 2015; pp. 219–232. [Google Scholar] [CrossRef]
- Vázquez, V.F.; Terán, F.; Paje, S.E. Dynamic Stiffness of Road Pavements: Construction Characteristics-Based Model and Influence on Tire/Road Noise. Sci. Total Environ. 2020, 736, 139597. [Google Scholar] [CrossRef]
- Cong, L.; Swiertz, D.; Bahia, H. Mix Design Factors to Reduce Noise in Hot-Mix Asphalt. Transp. Res. Rec. 2013, 2372, 17–24. [Google Scholar] [CrossRef]
- Bueno, M.; Luong, J.; Viñuela, U.; Terán, F.; Paje, S.E. Pavement Temperature Influence on Close Proximity Tire/Road Noise. Appl. Acoust. 2011, 72, 829–835. [Google Scholar] [CrossRef]
- Bühlmann, E.; Van Blokland, G. Temperature Effects on Tyre/Road-Noise-A Review of Empirical Research. In Proceedings of the Forum Acousticum, Krakow, Poland, 7–12 September 2014. [Google Scholar]
- Bendtsen, H.; Lu, Q.; Kohler, E. Temperature Influence on Road Traffic Noise: California OBSI Measurement Study; University of California Pavement Research Center: Davis, CA, USA, 2010; ISBN 9788792094476. [Google Scholar]
- Haider, M.; Conter, M.; Wehr, R.; Sandberg, U.; Anfosso, F. Project ROSANNE: Rolling Resistance, Skid Resistance, and Noise Emission Measurement Standards for Road Surfaces. In Proceedings of the INTERNOISE 2014—43rd International Congress on Noise Control Engineering: Improving the World through Noise Control, Melbourne, Australia, 16–19 November 2014. [Google Scholar]
- Ejsmont, J.; Sandberg, U.; Wieczko-Zurek, B.; Mioduszewski, P. Tyre/Road Noise Reduction by a Poroelastic Road Surface. In Proceedings of the INTERNOISE 2014—43rd International Congress on Noise Control Engineering: Improving the World through Noise Control, Melbourne, Austrilia, 16–19 November 2014; pp. 1–12. [Google Scholar]
- Bühlmann, E.; Schlatter, F.; Sandberg, U. Temperature Influence on Tire/Road Noise Measurements: Recently Collected Data and Discussion of Various Issues Related to Standard Testing Procedures. In Proceedings of the INTER-NOISE 2021—2021 International Congress and Exposition of Noise Control Engineering, Washington, DC, USA, 1 August 2021. [Google Scholar] [CrossRef]
- Del Pizzo, A.; Teti, L.; Moro, A.; Bianco, F.; Fredianelli, L.; Licitra, G. Influence of Texture on Tyre Road Noise Spectra in Rubberized Pavements. Appl. Acoust. 2020, 159, 107080. [Google Scholar] [CrossRef]
- Mioduszewski, P.; Taryma, S.; Woźniak, R. Temperature Influence on Tyre / Road Noise on Poroelastic Road Surface Based on Laboratory Measurements. Euronoise 2018, 2012, 2711–2718. [Google Scholar]
- Taryma, S.; Woźniak, R.; Ejsmont, J.; Mioduszewski, P.; Ronowski, G. Tire/Road Noise and Tire Rolling Resistance on the Prototype PERS Surface. IOP Conf. Ser. Mater. Sci. Eng. 2018, 421, 022035. [Google Scholar] [CrossRef]
- Sandberg, B.U. The Global Experience in Using Low-Noise Road Surfaces: A Benchmark Report. Hong Kong Environmental Protection Department Project No. AN 06-004 “Reviewing the Trial of Low Noise Road Surface (LNRS) in Hong Kong and Benchmarking the Experience on the Use of LNRS in Overseas Countries”; Sweden. 2009. Available online: https://www.yumpu.com/en/document/view/11548752/the-global-experience-in-using-low-noise-road (accessed on 15 February 2024).
- Vieira, T.; Sandberg, U.; Erlingsson, S. Negative Texture, Positive for the Environment: Effects of Horizontal Grinding of Asphalt Pavements. Road Mater. Pavement Des. 2019, 22, 1–22. [Google Scholar] [CrossRef]
- Sandberg, U. Road Traffic Noise the Influence of the Road Surface and Its Characterization; Elsevier: Amsterdam, The Netherlands, 1987; Volume 21. [Google Scholar]
- Anfosso-Lédée, F.; Pichaud, Y. Temperature Effect on Tyre-Road Noise. Appl. Acoust. 2007, 68, 1–16. [Google Scholar] [CrossRef]
- Luong, J.; Bueno, M.; Vázquez, V.F.; Paje, S.E. Ultrathin Porous Pavement Made with High Viscosity Asphalt Rubber Binder: A Better Acoustic Absorption? Appl. Acoust. 2014, 79, 117–123. [Google Scholar] [CrossRef]
- EN ISO 10534-1; Determination of Sound Absorption Coefficient and Acoustic Impedance in Impedance Tubes Part 1: Standing Wave Range Method. ISO: Geneva, Switzerland, 2002; pp. 32–34.
- EN 10534-2; Determination of Sound Absorption Coefficient and Acoustic Impedance in Impedance Tubes Part 2: Transfer Function Method. ISO: Geneva, Switzerland, 2002.
- Paje, S.E.; Bueno, M.; Terán, F.; Viñuela, U.; Luong, J. Assessment of Asphalt Concrete Acoustic Performance in Urban Streets. J. Acoust. Soc. Am. 2008, 123, 1439–1445. [Google Scholar] [CrossRef]
- Lalanne, C. Mechanical Vibration and Shock Measurements, 2nd ed.; Bruel & Kjaer: Nærum, Denmark, 1984; Volume 4, pp. 1–436. [Google Scholar]
- Iannace, G.; Ciaburro, G. Modelling Sound Absorption Properties for Recycled Polyethylene Terephthalate-Based Material Using Gaussian Regression. Build. Acoust. 2021, 28, 185–196. [Google Scholar] [CrossRef]
- Puyana-Romero, V.; Iannace, G.; Cajas-Camacho, L.G.; Garzón-Pico, C.; Ciaburro, G. Acoustic Characterization and Modeling of Silicone-Bonded Cocoa Crop Waste Using a Model Based on the Gaussian Support Vector Machine. Fibers 2022, 10, 25. [Google Scholar] [CrossRef]
- EN 12697-6; Test Methods for Hot Bituminous Mixtures Part 6: Determination of the Bulk Density of Bituminous Test Specimens by the Hydrostatic Method. Slovenian Institute for Standardization: Ljubljana, Slovenia, 2003.
- UNE-EN 12697-5:2003; Métodos de Ensayo Para Mezclas Bituminosas En Caliente Parte 5: Determinación de La Densidad Máxima. Asociación Española de Normalización y Certificación: Madrid, Spain, 2007.
- EN 13036-1; Road Surface Characteristics of Roads and Surfaces Test Methods Part 1: Measurement of the Depth of Pavement Surface Macrotexture by the Sand-Circle Method. Slovenian Institute for Standardization: Ljubljana, Slovenia, 2002.
- UNE-EN 12697-19; Mezclas Bituminosas Metodo de Ensayo Para Mezclas Bituminosas En Caliente Parte19: Permeabilidad de Las Probetas. Swiss Standards: Winterthur, Switzerland, 2013.
- Akoglu, H. User’s Guide to Correlation Coefficients. Turk. J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef]
- PG-3. General Technical Specifications for Road and Bridge Construction (PG-3). 2019. Available online: https://www.transportes.gob.es/carreteras/normativa-tecnica/17-pliegos-de-prescripciones-tecnicas-generales (accessed on 15 February 2024).
- EN 12697-34; Bituminous Mixtures December 2007 Test Methods for Hot Mix Asphalt Mixtures Part 34: Marshall Test. ISO: Geneva, Switzerland, 2007.
- EN 1426; Bitumen and Bituminous Binders Needle Penetration Determination. ISO: Geneva, Switzerland, 2007.
- Meiarashi, S.; Ishida, M.; Fujiwara, T.; Hasebe, M.; Nakatsuji, T. Noise Reduction Characteristics of Porous Elastic Road Surfaces. Appl. Acoust. 1996, 47, 239–250. [Google Scholar] [CrossRef]
- Mavridou, S.; Kehagia, F. Environmental Noise Performance of Rubberized Asphalt Mixtures: Lamia’s Case Study. Procedia Environ. Sci. 2017, 38, 804–811. [Google Scholar] [CrossRef]
- Kim, H.H.; Lee, S.J. Effect of Crumb Rubber on Viscosity of Rubberized Asphalt Binders Containing Wax Additives. Constr. Build. Mater. 2015, 95, 65–73. [Google Scholar] [CrossRef]
- Gallego Medina, J.; Tomas Raz, R.; Del Val Melus, J. Caracterizacion Mediante Ensayos Convencionales y Dinamicos de Mezclas Asfalticas Fabricadas Con Betun Modificado Con Caucho de Neumaticos. Available online: https://trid.trb.org/view/950625 (accessed on 28 October 2020).
- Vaitkus, A.; Vorobjovas, V.; Jagniatinskis, A.; Andriejauskas, T.; Fiks, B. Peculiarity of Low Noise Pavement Design under Lithuanian Conditions. Balt. J. Road Bridge Eng. 2014, 9, 155–163. [Google Scholar] [CrossRef]
- Irali, F.; Kivi, A.; Tighe, S.L.; Sangiorgi, C. Tire–Pavement Noise and Wearing Course Surface Characteristics of Experimental Canadian Road Pavement Sections. Can. J. Civ. Eng. 2015, 42, 818–825. [Google Scholar] [CrossRef]
- Shatanawi, K. The Effects of Crumb Rubber Particles on Highway Noise Reduction—A Laboratory Study; Clemson University: Clemson, SC, USA, 2008. [Google Scholar]
- Apaza, F.R.; Vázquez, V.F.; Paje, S.E.; Saiz, L.; Gulisano, F.; Gallego, J. The Potential Effect of Crumb Rubber on the Maximum Sound Absorption Performance of Asphalt Mixtures. Constr. Build. Mater. 2023, 389, 131789. [Google Scholar] [CrossRef]
- Apaza, F.R.; FVázquez, V.; Gallego, J.; EPaje, S.; Perez, R. Characterisation of the Sound Absorption of Bituminous Mixtures Modified with Rubber from End-of-Life Tires; Jorge, S., Geroge, W., Juan, G., Eds.; RAR2022: Malaga, Spain, 29 June 2022. [Google Scholar]
- Zhang, Y.; Li, H.; Abdelhady, A.; Yang, J. Effect of Different Factors on Sound Absorption Property of Porous Concrete. Transp. Res. D Transp. Environ. 2020, 87, 102532. [Google Scholar] [CrossRef]
- Sachakamol, P.; Dai, L. Parametric Influence on Prediction of Sound Absorption Coefficients for Asphalt Pavements. J. Environ. Inform. 2011, 18, 1–11. [Google Scholar] [CrossRef]
- John, T.; Kayhanian, M.; Harvey, J.T. Optimizing Rubberising Open Graded Friction Coruse (RHMA-O)Mix Desings for Water Quality Benefits: Phase I: Literature Review; University of California Pavement Research Center: Davis, CA, USA, 2020; p. 179. [Google Scholar]








| Classification Rules | Degree of Correlation |
|---|---|
| r = 0 | No correlation |
| 0 < |r| ≤ 0.19 | Very weak |
| 0.20 < |r| ≤ 0.39 | Weak |
| 0.40 < |r| ≤ 0.59 | Moderate |
| 0.60 < |r| ≤ 0.79 | Strong |
| 0.80 < |r| ≤ 1.00 | Very strong |
| |r| = 1 | Monotonic correlation |
| Sieve (mm) EN 933-1-13 | 2 | 1.5 | 1 | 0.5 | 0.25 | 0.125 | 0.063 |
|---|---|---|---|---|---|---|---|
| Pass (%) | 100 | 100 | 100 | 94.1 | 23.7 | 3.7 | 0.4 |
| Mixture | Max. Size (mm) | Type of Mixture | CR (%) | Binder Content (%) | MT (°C) | Digestion Temperature (°C) |
|---|---|---|---|---|---|---|
| AC 16 S—REF | 0.00 | 5.1 | ||||
| AC 16 S | 16 | AC 16 S—0.75% | 0.75 | 5.3 | 170 | 160 |
| AC 16 S—1.50% | 1.50 | 5.5 | ||||
| SMA 8—REF | 0.00 | 6.0 | ||||
| SMA 8 | 8 | SMA 8—0.75% | 0.75 | 6.1 | 170 | 160 |
| SMA 8—1.50% | 1.50 | 6.2 | ||||
| SMA 11—REF | 0.00 | 6.0 | ||||
| SMA 11 | 11.2 | SMA 11—0.75% | 0.75 | 6.1 | 170 | 160 |
| SMA 11—1.50% | 1.50 | 6.2 | ||||
| BBTM 8 B—REF | 0.00 | 5.0 | ||||
| BBTM 8 B | 8 | BBTM 8 B—0.75% | 0.75 | 5.1 | 170 | 160 |
| BBTM 8 B—1.50% | 1.50 | 5.2 | ||||
| BBTM 11 B—REF | 0.00 | 5.0 | ||||
| BBTM 11 B | 11.2 | BBTM 11 B—0.75% | 0.75 | 5.1 | 170 | 160 |
| BBTM 11 B—1.50% | 1.50 | 5.2 |
| Mixtures | CR (%) | MT (°C) | DT (°C) | Gmb (g/cm3) | Gmm (g/cm3) | Va (%) | Kv (m/s) | MTD (mm) |
|---|---|---|---|---|---|---|---|---|
| AC 16 S | 0.00 | 160 | 170 | 2.406 | 2.540 | 5.27 | *- | 0.985 |
| 0.75 | 160 | 170 | 2.358 | 2.487 | 5.24 | *- | 0.955 | |
| 1.50 | 160 | 170 | 2.295 | 2.424 | 5.35 | *- | 0.846 | |
| SMA 8 | 0.00 | 160 | 170 | 2.385 | 2.507 | 4.86 | 4.41 × 10−4 | 0.990 |
| 0.75 | 160 | 170 | 2.342 | 2.483 | 5.67 | 7.53 × 10−5 | 0.984 | |
| 1.50 | 160 | 170 | 2.296 | 2.461 | 6.73 | 7.18 × 10−4 | 0.932 | |
| SMA 11 | 0.00 | 160 | 170 | 2.349 | 2.517 | 6.66 | 1.97 × 10−4 | 1.607 |
| 0.75 | 160 | 170 | 2.316 | 2.483 | 6.73 | 9.26 × 10−4 | 1.320 | |
| 1.50 | 160 | 170 | 2.252 | 2.442 | 7.78 | 6.34 × 10−4 | 1.221 | |
| BBTM 8 B | 0.00 | 160 | 170 | 2.210 | 2.650 | 16.61 | 2.98 × 10−4 | 2.975 |
| 0.75 | 160 | 170 | 2.136 | 2.591 | 17.56 | 1.98 × 10−4 | 2.573 | |
| 1.50 | 160 | 170 | 2.117 | 2.592 | 18.34 | 1.93 × 10−4 | 1.934 | |
| BBTM 11 B | 0.00 | 160 | 170 | 2.148 | 2.643 | 18.72 | 2.79 × 10−4 | 3.054 |
| 0.75 | 160 | 170 | 2.140 | 2.634 | 18.76 | 3.05 × 10−4 | 2.873 | |
| 1.50 | 160 | 170 | 2.135 | 2.632 | 18.87 | 3.03 × 10−4 | 2.711 |
| Mixtures | CR (%) | No. Observations | R2 | Adjusted R2 | Result |
|---|---|---|---|---|---|
| AC 16 S | 0.00 | 801 | 0.923 | 0.923 | Accepted |
| 0.75 | 801 | 0.966 | 0.966 | Accepted | |
| 1.50 | 801 | 0.943 | 0.943 | Accepted | |
| SMA 8 | 0.00 | 801 | 0.986 | 0.984 | Accepted |
| 0.75 | 801 | 0.922 | 0.922 | Accepted | |
| 1.50 | 801 | 0.984 | 0.985 | Accepted | |
| SMA 11 | 0.00 | 801 | 0.924 | 0.924 | Accepted |
| 0.75 | 801 | 0.941 | 0.940 | Accepted | |
| 1.50 | 801 | 0.963 | 0.962 | Accepted | |
| BBTM 8 B | 0.00 | 801 | 0.969 | 0.968 | Accepted |
| 0.75 | 801 | 0.958 | 0.958 | Accepted | |
| 1.50 | 801 | 0.967 | 0.966 | Accepted | |
| BBTM 11 B | 0.00 | 801 | 0.993 | 0.931 | Accepted |
| 0.75 | 801 | 0.989 | 0.989 | Accepted | |
| 1.50 | 801 | 0.981 | 0.980 | Accepted |
| Coefficients | Statistics | 95% Confidence Interval for β | ||||
|---|---|---|---|---|---|---|
| β | Standard Error | t | p-Value | Lower Bound | Upper Bound | |
| Intercept | −0.0301 | 0.028 | 1.055 | 0.292 | −0.026 | 0.086 |
| Air voids (%) | 0.0708 | 0.002 | 44.611 | <0.001 | 0.068 | 0.074 |
| CR content (%) | −0.0061 | 0.015 | −0.396 | 0.693 | −0.036 | 0.024 |
| Temperature (°C) | 0.0005 | 0.001 | 0.919 | 0.358 | −0.001 | 0.002 |
| No. observations | 540 | |||||
| R2 | 0.788 | |||||
| Adjusted R2 | 0.787 | |||||
| Coefficients | Statistics | 95% Confidence Interval for β | ||||
|---|---|---|---|---|---|---|
| β | Standard Error | t | p-Value | Lower Bound | Upper Bound | |
| Intercept | 416.770 | 11.341 | 36.748 | <0.001 | 394.495 | 439.053 |
| Air voids (%) | −10.650 | 0.811 | −13.126 | <0.001 | −12.242 | −9.055 |
| CR content (%) | 79.450 | 7.864 | 10.103 | <0.001 | 64.004 | 94.900 |
| Temperature (°C) | −0.352 | −1.180 | 0.239 | −0.941 | 0.235 | |
| No. observations | 540 | |||||
| R2 | 0.327 | |||||
| Adjusted R2 | 0.323 | |||||
| Coefficients | Statistics | 95% Confidence Interval for β | ||||
|---|---|---|---|---|---|---|
| β | Standard Error | t | p-Value | Lower Bound | Upper Bound | |
| Intercept | 18.504 | 2.931 | 6.314 | <0.001 | 12.747 | 24.261 |
| Air voids (%) | 8.157 | 0.210 | 38.907 | <0.001 | 7.745 | 8.569 |
| CR content (%) | −5.921 | 2.032 | −2.914 | 0.004 | −9.913 | −1.929 |
| Temperature (°C) | 0.1338 | 0.077 | 1.734 | 0.084 | −0.018 | 0.285 |
| No. observations | 540 | |||||
| R2 | 0.740 | |||||
| Adjusted R2 | 0.738 | |||||
| Coefficients | Statistics | 95% Confidence Interval for β | ||||
|---|---|---|---|---|---|---|
| β | Standard Error | t | p-Value | Lower Bound | Upper Bound | |
| Intercept | 0.0424 | 0.020 | 2.164 | 0.031 | −0.004 | 0.081 |
| Air voids (%) | 0.0708 | 0.002 | 44.720 | <0.001 | 0.068 | 0.074 |
| No. observations | 540 | |||||
| R2 | 0.788 | |||||
| Adjusted R2 | 0.788 | |||||
| Coefficients | Statistics | 95% Confidence Interval for β | ||||
|---|---|---|---|---|---|---|
| β | Standard Error | t | p-Value | Lower Bound | Upper Bound | |
| Intercept | 416.77 | 11.341 | 36.748 | <0.001 | 394.495 | 439.053 |
| Air voids (%) | −10.65 | 0.811 | −13.126 | <0.001 | −12.242 | −9.055 |
| CR content (%) | 79.45 | 7.864 | 10.103 | <0.001 | 64.004 | 94.900 |
| No. observations | 540 | |||||
| R2 | 0.325 | |||||
| Adjusted R2 | 0.322 | |||||
| Coefficients | Statistics | 95% Confidence Interval for β | ||||
|---|---|---|---|---|---|---|
| β | Standard Error | t | p-Value | Lower Bound | Upper Bound | |
| Intercept | 18.504 | 2.931 | 6.314 | <0.001 | 12.747 | 24.261 |
| Air voids (%) | 8.157 | 0.210 | 38.907 | <0.001 | 7.745 | 8.569 |
| CR content (%) | −5.921 | 2.032 | −2.914 | 0.004 | −9.913 | −1.929 |
| No. observations | 540 | |||||
| R2 | 0.738 | |||||
| Adjusted R2 | 0.737 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Apaza, F.R.; Fernández Vázquez, V.; Paje, S.E.; Gulisano, F.; Gagliardi, V.; Saiz Rodríguez, L.; Gallego Medina, J. Towards Sustainable Road Pavements: Sound Absorption in Rubber-Modified Asphalt Mixtures. Infrastructures 2024, 9, 65. https://doi.org/10.3390/infrastructures9040065
Apaza FR, Fernández Vázquez V, Paje SE, Gulisano F, Gagliardi V, Saiz Rodríguez L, Gallego Medina J. Towards Sustainable Road Pavements: Sound Absorption in Rubber-Modified Asphalt Mixtures. Infrastructures. 2024; 9(4):65. https://doi.org/10.3390/infrastructures9040065
Chicago/Turabian StyleApaza, Freddy Richard, Víctoriano Fernández Vázquez, Santiago Expósito Paje, Federico Gulisano, Valerio Gagliardi, Leticia Saiz Rodríguez, and Juan Gallego Medina. 2024. "Towards Sustainable Road Pavements: Sound Absorption in Rubber-Modified Asphalt Mixtures" Infrastructures 9, no. 4: 65. https://doi.org/10.3390/infrastructures9040065
APA StyleApaza, F. R., Fernández Vázquez, V., Paje, S. E., Gulisano, F., Gagliardi, V., Saiz Rodríguez, L., & Gallego Medina, J. (2024). Towards Sustainable Road Pavements: Sound Absorption in Rubber-Modified Asphalt Mixtures. Infrastructures, 9(4), 65. https://doi.org/10.3390/infrastructures9040065









