Abstract
Once trusted, automated vehicles (AVs) will gradually appear in urban areas. Such a transition is an opportunity in transport planning to control undesired impacts and possibly mitigate congestion at a time when both conventional vehicles (CVs) and AVs coexist. This paper deals with the complex transport decision problem of designing part of the network that is exclusive for AVs through a nonlinear programming model. The objective function minimises the costs of travel times where vehicles circulate under user equilibrium. The model evaluates the benefits of having an AVs-dedicated infrastructure and the associated costs from the detouring of CVs. Three planning strategies are explored: incremental, long-term and hybrid planning. The first creates a subnetwork evolving incrementally over time. The second reversely designs a subnetwork from the optimal solution obtained at a ratio of 90% AVs. The third limits the incremental planning towards that optimal long-term solution. The model is applied to the city of Delft, in the Netherlands. Two scenarios are analysed, with and without AV-dedicated roads, at several AV penetration rates. We find that implementing dedicated roads for AVs reduces the overall costs and congestion up to 16%. However, CV detouring is inevitable at later network stages, increasing the total distance travelled (up to 8%) and congestion in the surroundings of AV subnetworks. Concerning the planning strategies, incremental planning is appropriate for starting in the initial stages and is the strategy that most tackles CV detouring. The hybrid or the long-term strategies are more suitable to be applied after a ratio of 50% AVs, and the hybrid planning is the strategy that most reduces delay.
1. Introduction
Transportation systems are fundamental for modern societies because their performance has a significant impact on social and economic development. Technology has been evolving significantly since the industrial revolution. In the nineteenth century, a clear shift happened from vehicles pulled by animals to public rail transport pulled by electricity. At the turn of the century, gas-powered vehicles rapidly emerged as fossil fuels became the primary source of energy. Nowadays, new forms of energy sources have been implemented like electric and hydrogen vehicles. During this technological advancement, people have always been responsible for the driving task and deciding the path. Driverless vehicles, departing from this human-centric perspective, will be the next shift in vehicular transportation.
There are projections that “fully automated vehicles (AVs) that operate on public roads among other traffic are unlikely to be on the market before the 2030s” [1] and some forecast the 2040s [2]. AVs level 4 will have an “urban and sub-urban pilot”, as well a “highway autopilot including a highway convoy”, while only AVs level 5 will be considered “fully automated passenger cars”.
Nieuwenhuijsen et al. [3] studied the diffusion of AVs using systems dynamics under a functional approach, by looking into the six levels of automation with different fleet sizes, technology maturity and average purchase price and utility. The model was applied to the Netherlands both for a base and an optimistic scenario (strong political support and technology development). They found that a market penetration of 10% of AVs level 4 will likely happen by 2027. AVs level 5 will achieve 90% market penetration somewhere between 2060 and 2080. Full deployment (100% of AVs level 5) will only occur after 2100.
As automated vehicles (AVs) enter the scene, understanding their role in the future of mobility is a critical challenge to be faced all over the world [4]. A functional deployment of AVs is first envisioned, gradually emerging over time with incompatibilities solved throughout this process. Shladover [5] presented a functional deployment roadmap, with some regions having Vehicle-to-Infrastructure (V2I) communication and other regions having separate dedicated lanes [5].
However, dedicated lanes encompass numerous practical challenges, and their implementation might not be easy. Nowadays, for example, bus and taxi dedicated lanes experience the unauthorised circulation and illicit parking of human-driven vehicles—the so-called conventional vehicles (CVs). In this paper, we are testing a scenario where, at some point, the deployment of AVs will happen in a dedicated road infrastructure, with AV subnetworks to deploy the first driverless vehicles, i.e., AVs level 4—a specific level of automation in which a vehicle drives automatically under certain conditions [6,7]. Restricted driving areas are not a novel practice; for instance, currently many urban centres ban the circulation of old vehicles to reduce air pollution. Legal aspects are involved, and traffic control in city centres might still be needed for pedestrians and bikes. In fact, from city authorities’ and other stakeholders’ perspectives, AV subnetworks will allow better traffic control, managing safety aspects and improving the efficiency of network elements such as traffic intersections. From an AV private owner’s perspective, AV subnetworks could be appreciated for their convenience and comfort, which could potentially motivate buying such vehicles. However, from the CV owner’s perspective, AV subnetworks could be unwelcome if they represent fewer route options, destinations hindrance and extra travel times.
The challenges tackled in this paper can be translated through the following research questions: Is the creation of AV subnetworks a viable strategy to deploy in urbanised regions? What is the best planning strategy throughout this transition process? How should the design of AV-only networks be created without excessively affecting CVs? In this paper, in order to address such questions, we define the road network design problem for AVs deployment (RNDP-AVs) through a nonlinear programming (NLP) mathematical model. The model assigns roads to fully automated vehicles as a function of the number of AVs in the city and their origins and destinations. The objective function comprises the minimisation of total travel time cost. A user equilibrium traffic assignment is considered which naturally becomes asymmetric as more road infrastructure is dedicated to AVs, thus reducing their travel times.
Furthermore, as more AVs enter the vehicle fleet, AV subnetworks will be required to be progressively expanded. The RNDP-AVs model is implemented and tested in three planning strategies: incremental, long-term and hybrid planning. In incremental planning, dedicated roads are added as the penetration rate grows. The long-term planning strategy backward-designs the AV subnetworks. Hybrid planning combines the previous strategies by reproducing the incremental planning limited to the optimal long-term solution.
For demonstration purposes, and to extract some first tentative conclusions about the possible results of the model, we apply it to a quasi-real case study of the city of Delft, in the Netherlands [8]. Three scenarios are created: a base scenario without AV subnetworks, a daily scenario that designs AV subnetworks considering the daily shifting demand and a peak-hour scenario that designs optimal AV subnetworks for the rush hour (9–10 a.m.). The experiment envisions the long-term for 100% of AVs, which, according to the current literature, may happen in 2100 [3].
The article is organised as follows. Section 2 presents the literature review. Section 3 introduces the RNDP-AVs and its analytical model formulated as an NLP problem. In Section 4, the application to the Delft case study is presented. Finally, Section 5 reports the main conclusions and presents some suggestions for future work.
2. Background
The literature regarding AVs is dispersed, and it has been increasing substantially in the last five years. Most of the research covers the upcoming impact of AVs, which can be divided into at least three levels of effect that somehow can be associated with time horizons: short-term, which involves traffic, travel choices and travel cost implications; medium-term, concerning infrastructure, vehicles, location choices and land-use implications; and long-term, focusing on societal implications [9].
Research is essentially focused on the first level, mostly on interurban traffic environments [10,11,12,13]. Hitherto, the literature has shown that AVs will generate comfort, traffic efficiency and safety on interurban roadways. We assume it will extend to urban environments, and the planning of the traffic operation of AVs stands as an opportunity to tackle urban problems. Yet, increasing comfort is usually depicted as a reduction in the value of travel time, which might influence AV travellers to take longer trips and therefore accept increased travel times. The traffic efficiency claimed by AVs’ cooperative adaptive cruise control system positively impacts road capacity, with reduced travel times [11]. How these two paradoxical factors work together in traffic equilibrium is still unknown, especially considering CVs’ adaptation to this future reality.
Our research focuses on the second-level implications, and the nature of this study fits into a road network design problem (RNDP) as it relates to a strategic decision support system for policy making and network improvement [14]. An RNDP is typically formulated as a bi-level problem to embrace both the stakeholders’ investment decisions and travellers’ behaviour, whilst at the same time decreasing the complex combinatorial nature of the problem. The problem is NP-hard and convexity is not guaranteed, making it difficult to solve by exact solution methods. Heuristics and metaheuristics are the alternative, yet a local optimum may be found instead of a global optimum solution [15].
Currently, most of the literature on network design is focused on dedicated lanes to first deploy AVs in urban environments [16,17]. On the topic of dedicated roads and AV subnetworks, ref. [18] proposed a bi-level framework for the optimal design of AV subnetworks, solved through a simulated annealing algorithm. However, their equilibrium analysis ignores CV trips that start and end inside AV subnetworks for simplification purposes, in a deterministic mixed routing problem that considers a system-optimal traffic assignment inside AV subnetworks and user equilibrium outside. The authors presented a numerical example where AVs compose 55% of all traffic and found that the social cost can be reduced by up to 21.4%, assuming that the road capacity triples in AV links. Similarly, ref. [19] proposed a bi-level network design model comprising the optimal design of the network involving AV links and congestion pricing to improve congestion. The authors use a relaxation-based method for solving the bi-level model. Ref. [20] introduced a bi-level problem for optimizing road networks for automated vehicles with dedicated links, dedicated lanes and mixed-traffic subnetworks that has been solved through heuristics.
A previous approach to solving this problem [21] involved a multiclass traffic assignment in mixed-integer programming through a system-optimal perspective, with simplifications like the minimisation of the average travel time in each road link rather than all passengers’ travel times—which is mandatory to achieve traffic equilibrium. Also, the authors used a constant traffic efficiency coefficient (25%), regardless of the penetration rate, in both regular and dedicated roads in a grid network experiment.
This RNDP, considering AVs and CVs in the same model, originates a multiclass traffic assignment—found in the literature [22,23,24]. Nevertheless, a multiclass traffic assignment can easily turn into an asymmetric assignment that naturally arises from each class’s differences [25,26,27]. Problems concerning the multiclass traffic assignment are resumed in two types of incoherence: behavioural and mathematical [28]. The behavioural incoherence happens if each class holds an individual travel time function or if links amongst the network have travel time functions differently depending on each class. To reduce the complexity while assuring convexity, a new variable is defined in this paper that aggregates the classes, so that AVs and CVs share a common link-travel-time function. This variable (total flow) embeds an added automated traffic efficiency. However, in some situations, a mathematical incoherence might appear because of the dependencies in the singular Jacobian matrix that imply a linear relationship between each class cost function and the weights used in the single flow variable grouping the classes [28]. In other words, mathematical incoherence happens when each class is distinguished by different costs (e.g., toll pricing or value of travsel time). In this study, we calculated the effects of such linearity, and we have concluded that such a rselationship resembles recent findings on AVs’ reduced value of travel time [29,30,31]—therefore, we accept the incoherence. This will be explained in the model section.
Nevertheless, there is an implicit asymmetric user equilibrium amongst classes that happens because part of the network is restricted to one class (network segregation), i.e., when dedicated roads are added. This means that, in origin–destination (O-D) pairs whose AVs encountered dedicated roads, their efficiency will allow them a reduction of travel time costs which will naturally be dissimilar to the travel time costs experienced by the CVs. In such cases, each class is under a user equilibrium traffic assignment. Contrariwise, in O-D pairs in which AVs only circulate in regular roads, both AVs and CVs share the same travel time function, and therefore, the user equilibrium prevails.
Our study considers a multiclass user equilibrium traffic assignment without explicit path enumeration (all possible paths are considered in the network between each O-D pair), which simultaneously analyses the increasing comfort and efficiency yield of the AVs. All travellers reach their destination using a CV or an AV, while the decision model evaluates travel costs based on the link performance (travel time) functions. Upgrading costs to transform a regular road (mixed traffic) into a dedicated road for AVs, e.g., for V2I connectivity, are also introduced in the paper. Another novelty of this paper is to propose and discuss the multi-stage planning of AV subnetworks over time.
3. The Road Network Design Problem for AVs Deployment (RNDP-AVs)
The problem that we address is how to design, on top of an existing road network, AV subnetworks to start the deployment of the first driverless vehicles (level 4 of automation). During this transition process, the network will be composed of regular roads (mixed traffic) and dedicated roads (automated traffic). Dedicated roads will have V2I connectivity installed, while regular roads will not. This single-level optimisation problem tackles both the dedicated roads decision problem and the traffic flow assignment problem in a nonlinear programming model.
All travellers reach their destination according to a user-optimum equilibrium, meaning that every passenger of each class (CV or AV) minimises their own travel time. We believe that, during this transition process, user equilibrium will still be the most realistic because system-optimum routing would be difficult to implement. The objective function minimises the total travel time cost, where each class of vehicles circulates under user equilibrium. The decision making occurs at every AV design stage, based on the AVs’ market penetration rate. Such a planning process is solved by mathematical optimisation. The global evaluation is not trivial, because dedicated roads implying a travel time reduction for AV passengers might also imply an increase in CVs’ travel times (detour). The model can evaluate the CVs’ detour, as the formulation includes a penalty variable to restrict CVs driving inside dedicated roads. The model respects all road links characteristics, ensuring link performance (travel time) functions.
3.1. Formulation of the RNDP-AVs Model
The assumptions of the problem are:
- AVs are assumed to be level 4 [6], meaning they can be driven manually outside dedicated roads but will assume autopilot mode inside AV subnetworks;
- AVs circulate everywhere, whereas CVs’ circulation is prohibited on AV subnetworks;
- Constant travel demand, i.e., an O-D matrix for AV drivers and another one for CV drivers;
- Each trip is assigned to an AV or a CV;
- Public authorities invest in each dedicated road to make it fit for AVs;
- A dedicated road comprises both directions dedicated to automated traffic.
To formulate the problem, we introduce the following notation:
Sets:
| : | set of nodes in the network, where is the number of nodes. |
| : | set of links of the road network where vehicles move. |
| : | set of O-D pairs that represent the trips demand in the network. |
| : | set of type of vehicles (mode) in the network: AV and CV |
| : | set of hours of the day |
Parameters:
| : | penetration rate of AVs in the vehicle fleet, between 0 and 1. |
| : | coefficient that reflects the efficiency of automated traffic on the road capacity in mixed traffic (MT) conditions, i.e., in regular roads. This coefficient can be compared to a passenger car unit, as it reflects the number of CVs to which an AV corresponds. Defined between 0 (an AV has no effect on traffic) and 1 (an AV is as efficient as a CV). |
| : | coefficient that reflects the maximum efficiency of automated traffic (AT), i.e., in dedicated roads, also between 0 and 1. |
| : | value of travel time inside cars, in monetary units per hour. |
| : | travel demand of mode from an origin, node , towards a destination, node , from period to period , . |
| : | minimum driving travel time in free-flow speed at each link , expressed in hours. |
| : | length of each link , expressed in kilometres. |
| : | capacity of each link , in vehicles for the period of analysis. |
| : | big number. |
Decision variables:
| : | binary variable equal to 1 if link is assigned for AV-only driving. |
| : | continuous variable that corresponds to the flow of vehicles in each link and each pair , from period to period , . |
| : | continuous variable that acts as penalty factor to avoid CV flow in dedicated roads, defined per link and pair , from period to period , . |
| : | continuous variable that represents the flow of AVs when a link is dedicated for AVs only (), regarding each O-D pair , from period to period , . This variable distinguishes AV benefits in mixed or automated traffic. |
The main decision variables are and . The remaining variables depend on the first ones through constraints.
Objective Function:
The objective function (1) minimises the total cost of all driving travel time costs under a user equilibrium traffic assignment formula [27] that works for each class of vehicles and according to the BPR function (2) that computes each link-travel-time function. The objective function is subject to the following Constraints (4)–(17).
Therefore, the objective function implemented in this paper is the following Expression (3).
Constraints:
Constraints (4)–(6) assure that, for each O-D pair, both AV and CV flows () are generated in the origin node (4) and absorbed in the destination node (5), with a flow equilibrium in the intermediate nodes (6).
Constraints (7) compute the total flow in each link . The AVs’ flow holds an efficiency benefit that is computed through the auxiliary variable . This benefit varies in mixed or automated-only traffic. The flow of CVs is kept, and a penalty flow happens if CVs circulate in AV-dedicated roads, which is annulled in the minimisation of the problem, forcing the detouring of CVs around AV subnetworks.
Constraints (8)–(10) define the penalty flow variables if CVs circulate in AV-dedicated roads. Constraints (8) and (9) assure that, for a dedicated road (), the penalty flow is identical to the CV flow. In regular roads, i.e., , the range is bounded to be in the interval for all . Yet the lower limit of that interval is naturally chosen since this is a minimisation problem. Constraints (10) assure that the penalty flow of link is null in regular roads; otherwise, it is limited to the road capacity .
Constraints (11)–(13) compute the variables that differentiate efficiency on dedicated and regular roads, i.e., automated and mixed traffic, respectively. In AV-dedicated roads, the variable assumes AV flow through Constraints (11) and (12), whereas in regular roads, this variable is null through Constraints (13).
Constraints (14) assure that a dedicated road for AVs comprises both directions of the road. Constraints (15) give a valid inequality so that the variable is only plausible to be considered when there is flow passing by.
Constraints (16) and (17) set the domain of the decision variables.
3.2. Progressive RNDP-AVs Model: AV Subnetworks Design throughout the Transition Process
The RNDP-AVs can be designed as the AVs penetration rate evolves by adding more dedicated roads, creating progressive AV subnetworks. Three urban transport planning strategies are tested:
- Incremental planning, i.e., dedicated roads are added incrementally as the penetration rate evolves. It starts with the computation of the first design stage, and henceforth, the solution from the precedent stage is maintained with new constraints;
- Long-term planning, i.e., the optimal solution at a long-term horizon. It starts by solving the RNDP-AVs for the last design stage (maximum penetration rate) and reversely reduces that subnetwork by limiting the creation of the decision variables at each stage;
- Hybrid planning, i.e., a mixed planning strategy combining both the incremental and long-term planning strategies. The model first computes the optimal long-term solution, e.g., 90% AVs. Henceforth, AV subnetworks network evolve incrementally towards the optimal final network design.
The pseudo-code used to run the incremental, the long-term and the hybrid planning strategies are detailed in the following Algorithms 1, 2, and 3, respectively. The following parameters are required for performing the dynamic programming:
| design stages, where is the latest with the maximum AV penetration considered. | |
| AVs penetration rate of stage . Note that . | |
| optimal solution ( vector) of each design stage . |
| Algorithm 1 Incremental planning | |
| 1: 2: while do 3: get 4: create all decision variables 5: if then 6: 7: end-if 8: function Objective Function 9: 10: end-function 11: 12: 13: Clear all decision variables 14: end | Starts calculating from the first design stage with the minimum penetration rate New constraints from prior design stage: dedicated roads from stage remain in stage . Save solution from design stage . |
| Algorithm 2 Long-term planning | |
| 1: 2: while do 3: get 4: if then 5: create all decision variables 6: function Objective Function 7: 8: end-function 9: else 10: create 11: create remaining decision variables, 12: function Objective Function 13: 14: end-function 15: end-if 16: 17: Clear all decision variables 18: 19: end | Starts calculating the last design stage starts with the maximum penetration rate (e.g., 90% of AVs). Calculation of the solutions in reverse Limits the solution space by evaluating only the dedicated roads that belong to the following design stage. |
| Algorithm 3 Hybrid planning | |
| 1: 2: create all decision variables 3: function Objective Function 4: 5: end-function 6: 7: Clear all decision variables 8: 9: while do 10: get 11: create all decision variables 12: if then 13: 14: end-if 15: function Objective Function 16: 17: end-function 18: 19: 20: Clear all decision variables 21: end | Starts calculating the last design stage starts with the maximum penetration rate (e.g., 90% of AVs). Starts calculating from the first design stage with the minimum penetration rate . Limits the solution space by evaluating only the dedicated roads that belong to the last design stage. New constraints from prior design stage: dedicated roads from stage remain in the stage . Save solution from design stage . |
4. Application to a Quasi-Real Case Study: The City of Delft
4.1. Setting up the Case Study
The application of the RNDP-AVs model is exemplified in a quasi-real case study: the city of Delft, in the Netherlands, located in the province of South Holland. Figure 1 shows all nodes (46) and road links (122) in the simplified network of Delft in a map of the region. The city centre is represented by node 3 and has the highest demand. The TU Delft campus is node 31, and major residential areas are in nodes 6 and 45. Two types of roads exist, one or two lanes per road direction, with a lane capacity of 1441 vehicles per hour, and the free flow speed is 50 and 70 km/h, respectively. These data come from a simplified traffic model of the city [8]. The application is for demonstration purposes, and the intention is to exemplify what type of results could be obtained from planning such networks.
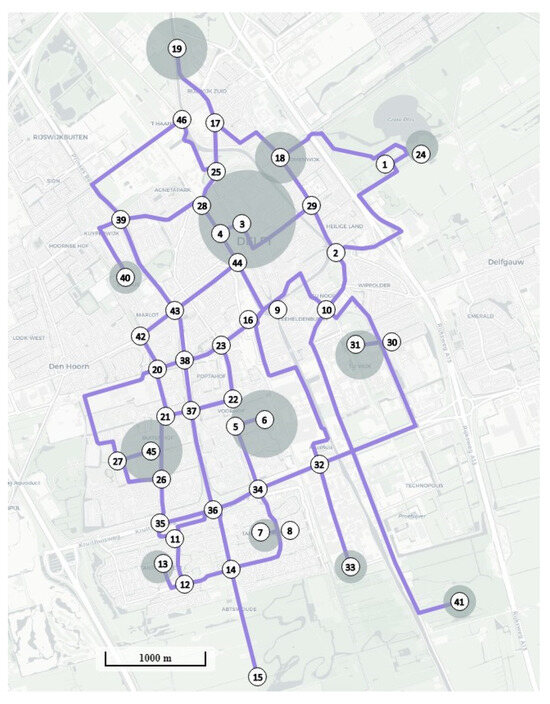
Figure 1.
Map of the case study with network (46 nodes and 122 road links) and centroids representation (grey circles), adapted from OpenLayers maps.
The original travel database (MON 2007/2008) was provided by the Dutch government and is available for transport research. The application is called a quasi-real case-study because the data is not completely real. Only the trips of families who travel inside the city during a whole working day in the year 2008 were obtained, ignoring external trips. The filtered dataset contains a collection of 152 trips from 29 households sampled. Sampling expansion factors for each family were given for a typical working day, usually varying from 200 to 1300. With this correction factor, the original dataset with 152 trips corresponds to 68,640 trips by 14,640 households, yielding an average sample rate of 0.2%. Therefore, 60,300 trips were considered through 58 OD pairs distributed between 12 centroids (see the grey circles in Figure 1, proportional to their demand) [8]. According to the dataset, the most congested hour (peak hour) is between 9 and 10 a.m., holding 15% of the daily trips.
The link performance function is the aforementioned BPR function (2) with the reference coefficients (). For increased realism, the coefficients would have to be estimated according to the reality of Delft. However, it is not our intention to reproduce current traffic in the city. The minimum travel time () is computed from the free-flow speed and rounded up to the nearest whole number in each link .
In this experiment, the design stages considered several AV penetration rates (): 0%, 10%, 25%, 50%, 75%, 90% and 100%. The study is envisioned up to an AV penetration rate of 100% of AVs—a rate that, according to Nieuwenhuijsen et al. (2018), will happen somewhere in 2100.
Traffic simulations that tested AVs with cooperative adaptive cruise control systems found a road capacity benefit in mixed traffic conditions [11]. A second-degree parabolic curve () was adapted from their results: for a 10% penetration rate of AVs, there is a benefit of 3%; when 50% of the vehicle fleet is automated, road capacity increases 22%; for 75% of AVs, a 39% increase is considered; and with 100%, a maximum benefit of 68% is reached. The AVs’ flow is discounted through a coefficient that has an inverse relationship with the adjusted capacity: in mixed traffic (regular roads), ; whereas in dedicated roads, each AV corresponds to 0.60 CV, .
The reference value of travel time spent inside CVs () in commuter trips in the Netherlands is considered to be EUR 10 per hour [29]. Since the total flow is a single variable and the cost function depends on the weights given to the variables, the AVs’ value of travel time is proportionally reduced in mixed and dedicated roads. Bearing in mind the inevitable mathematical incoherence mentioned in Section 2, we make use of this incoherence as the AV value of travel time decreases in an inversely proportional way to the road capacity gain that is given by the AVs. The AVs’ estimated values of travel time in the existing literature could drop as far as EUR 5.50 in the Netherlands for commuter trips [29]. In our experiment, CV passengers always have a higher value of travel time (10 EUR/h), whereas AV passengers have a reduced travel time cost. In dedicated roads, all traffic is automated, so the value of AVs’ travel time is EUR 5.95 per hour (). In regular roads with mixed traffic, the value of AVs’ travel time () varies accordingly to Figure 2.
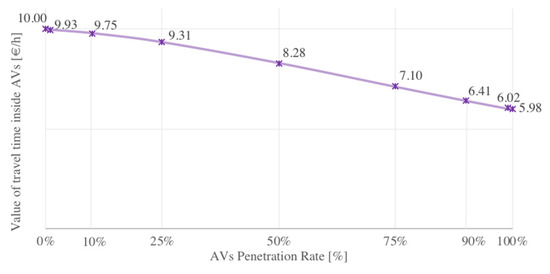
Figure 2.
Value of travel time as the AVs’ penetration rate evolves.
The RNDP-AVs model is applied for the Delft case study in three scenarios:
- Base Scenario without AV-dedicated road links, meaning that all vehicles circulate in mixed traffic conditions—see the results in Table 1. The base scenario is created to further compare its results with the Daily Scenario. Vehicles circulate everywhere in mixed traffic conditions, reflecting the impact of AVs’ deployment without any road traffic segregation. Constraints (18) are added to the prior RNDP-AVs formulation to replicate the Base Scenario.
 Table 1. Results of the Base Scenario without AV subnetworks applied to the whole day.
Table 1. Results of the Base Scenario without AV subnetworks applied to the whole day.
- Peak-Hour Scenario designs AV subnetworks only for the peak-hour demand, that in the Delft case study is between 9 and 10 a.m. (15% of the daily trips)—see the results in Table 2. This scenario is created to further compare and discuss the importance of considering the daily demand in this kind of road network design problem. Therefore, the experiments on this scenario will consider only the optimality analysis that represents the optimal solution and the minimisation of travel costs and network congestion.
 Table 2. Results of the Peak-Hour Scenario design with AV subnetworks.
Table 2. Results of the Peak-Hour Scenario design with AV subnetworks. - Daily Scenario designs AV subnetworks for the whole daily demand. It comprises only the travellers’ perspective by minimizing the overall total travel cost, balancing AVs’ travel savings and CVs’ extra travel time costs—see the results in Table 3. The Delft experiments are calculated throughout this transition process of AV deployment in four analyses; the optimality analysis shows the optimal solutions at each design stage (penetration rate), alongside the previously proposed planning strategies: the incremental, the long-term and the hybrid.
 Table 3. Results of Daily Scenario with AV subnetworks.
Table 3. Results of Daily Scenario with AV subnetworks.
The RNDP-AVs model was implemented in the Mosel language and solved using Xpress 8.1 [32] in a computer with a processor of 4.2 GHz Intel Core i7-7700K and 16 GB RAM. Our NLP problem was solved with the FICO Xpress-NLP SLP solver designed for large-scale nonconvex problems that uses a mixed-integer successive linear programming approach, combining branch and bound (BB) and successive linear programming (SLP). The reader may consult more information about the Xpress Solver [33] and other existing solvers [34]. Since the RNDP-AVs problem is convex, global optimality is guaranteed.
In optimality, the solutions were obtained within a tolerable computation time, less than 24 h for the whole process, involving seven design stages (penetration rates). In incremental planning (IP), the calculation took about 8 h. In long-term planning (LTP), it took less than 4 h, since the problem becomes less and less combinatorial as the algorithm reversely computes the RNDP-AVs. In hybrid planning (HP), the computation took over 12 h. For a penetration rate of 50% of AVs, the problem is more combinatorial than in the IP analysis, balancing the CV detour and the AV travel time savings.
4.2. User Equilibrium Validation
In traffic assignment problems, it is crucial to guarantee traffic behaviour. The user equilibrium assignment was first introduced by Wardrop [35], following which, it was analytically addressed by Beckmann et al. [36] with an optimisation model, founded on the Kuhn–Tucker conditions that guarantee the existence and the uniqueness of the solution. The user equilibrium assignment was later formulated by [37] through the inverse of the cost function. Ref. [38] combined the arc flow vector function, describing the assignment to an uncongested network, together with the arc cost vector function, with sufficient conditions for solution existence and uniqueness, mainly the continuity and monotonicity of the involved functions. Later, ref. [22] proposed a traffic assignment model that includes two type of vehicles in congested transportation networks, where arc flows depend on arc costs; thus, the equilibrium assignment searches for mutually consistent arc flows and costs.
The proposed RNDP-AVs objective function (1) uses the Beckmann function, whose arc costs (3) only depend on the link flow described in (7). Similarly, all auxiliary variables of the model depend on the arc flows, which depend on the arc cost itself—meaning that there is an interdependency of the auxiliary variables that depend primarily on the assignment of the arc flow that affects the cost function. Existence is guaranteed if both the arc flow and cost function are continuous (and the network is connected). Since the BRP function (arc cost function) is monotone strictly increasing and the sum of two continuous and increasing functions, uniqueness is guaranteed. Our proposed RNDP-AVs model uses integer variables () that are responsible for road traffic segregation that artificially design AV subnetworks. These integer variables are relaxed with the FICO Xpress-NLP SLP problem solver, and therefore convergence of the problem is guaranteed.
4.3. Mixed Traffic Conditions without AV Subnetworks
In the Base Scenario (Table 1), throughout this transition process (from 0% to 100% of AVs), costs reduce proportionally as the value of travel time spent inside AVs decreases (Figure 2). Total travel time sees a reduction of 4.7%, from 8915 to 8494 h. Network congestion decreases from 11% to 7%. The average degree of saturation reduces from 43% to 26%, leading to a total delay reduction from 484 to 66 h. Roadways above practical capacity (degree of saturation above 75%) drop from 86.67 to 5.47 kilometres, yet congested roadways (saturation above 100%) only start to be mitigated when AVs are 50%.
4.4. AV Subnetworks Designed for the Daily Traffic Demand
This section depicts the daily design of progressive AV subnetworks (Table 3 results). In the incremental planning (Figure 3), the design follows optimality at each stage if CVs are the majority of the vehicle fleet. For 10% of AVs, AV dedicated roads occupy 17.1% of the total network (30.54 km). For 90% of AVs, AV subnetworks are 34.3%. For a penetration rate of 100%, all the roads with traffic flow cover 89.9% of the network (160.40 km out of 178.51 km)—note that external demand to the city was not part of the dataset.
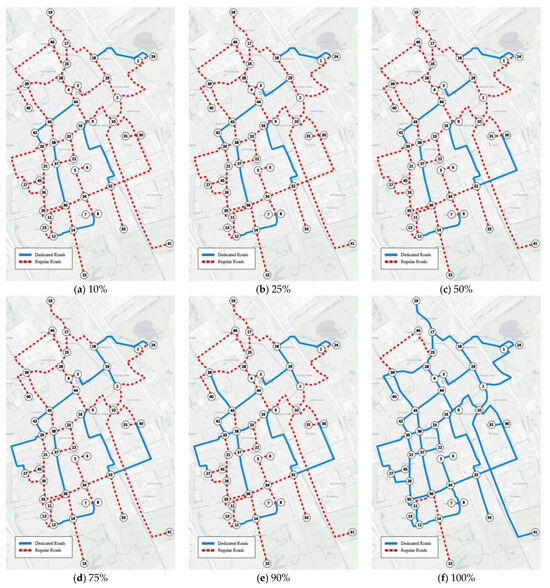
Figure 3.
Daily Scenario: AV subnetworks’ expansion under IP (Incremental Planning) strategy (a–f). AV dedicated roads (continuous thick lines) expand as the AV penetration rate (%) increases. Nodes are represented in Figure 1. All images are oriented north.
In a long-term planning design, AV subnetworks become relevant once AVs are the majority of the vehicle fleet. Figure 4 illustrates the expansion of AV subnetworks under LTP. AV subnetworks start at the penetration rate of 50% of AVs in three urban areas representing 17.8% of the network (31.71 km out of 178.51 km). At 100% of AVs, the road network needed is 74.6% of the original (133.11 km out of 178.51 km). Again, note that this experiment did not consider external demand to the city.
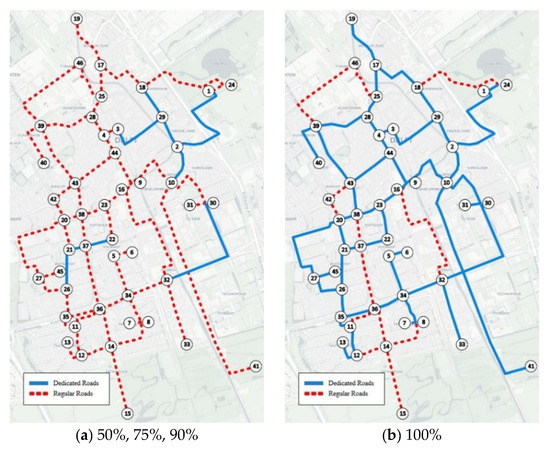
Figure 4.
Daily Scenario: AV subnetworks’ expansion under LTP (Long-Term Planning) strategy (a,b). AV dedicated roads (continuous thick lines) expand as the AV penetration rate (%) increases. Nodes are represented in Figure 1. All images are oriented north.
In hybrid planning, AV subnetworks are added incrementally by the combinatorial problem, yet limited to the optimal solution at the end of the process (100%)—74.6% (133.11 km out of 178.51 km) of the road network is enough to guarantee all road traffic. Figure 5 shows the AV subnetworks’ expansion. In the first half of the transition period, when AVs are still a minority of the vehicle fleet, only two roads are dedicated to AVs—2.9% of the network (5.25 km out of 178.51 km). AV subnetworks become relevant when AVs reach 50%, increasing from 14.5% (25.93 km out of 178.51 km) to 74.6%.
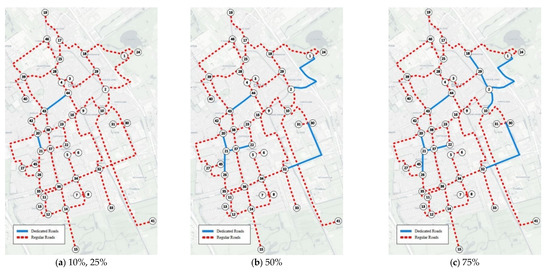
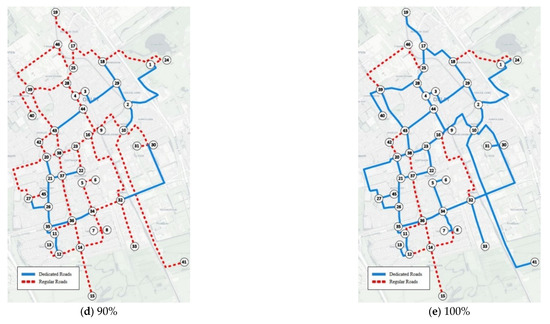
Figure 5.
Daily Scenario: AV subnetworks’ expansion under HP (Hybrid Planning) strategy (a–e). AV dedicated roads (continuous thick lines) expand as the AV penetration rate (%) increases. Nodes are represented in Figure 1. All images are oriented north.
4.5. Implications of AV Subnetworks
The following Figure 6 shows, for the Daily Scenario, the differential of the travel costs in every planning strategy—revealing that AV subnetworks might save 1.2% of the travel costs in comparison with the Base Scenario. The IP follows optimality until AVs are 50% of the fleet. Contrariwise, the LTP planning analysis is sided with optimality in the latest stages when AVs are 90% onwards. Both the IP and HP bring savings up to 0.8%.
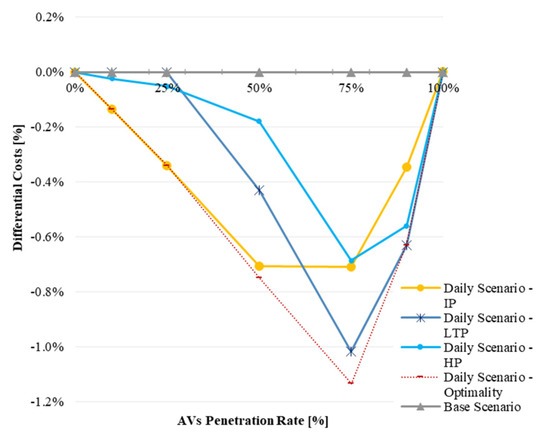
Figure 6.
Daily Scenario: travel costs variation.
Figure 7 depicts the total travel time, revealing that AV subnetworks imply higher total travel times up to 6.5% for CVs (Figure 8) and 3% for AVs (Figure 9). While the model minimises travel costs, it implicitly considers a reduction in AVs’ value of travel time in comparison to CVs’ value of travel time. The experiments showed that such a situation might happen to either a CV or an AV.
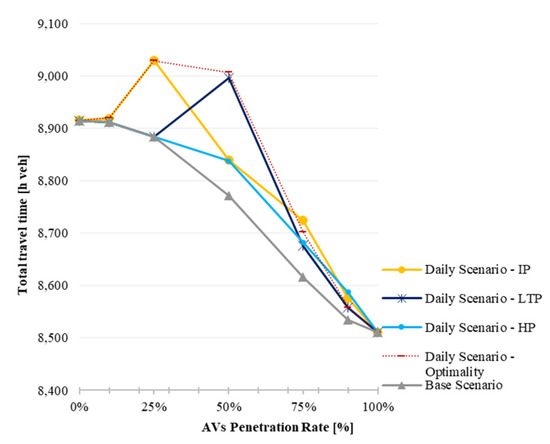
Figure 7.
Daily Scenario: total travel time.
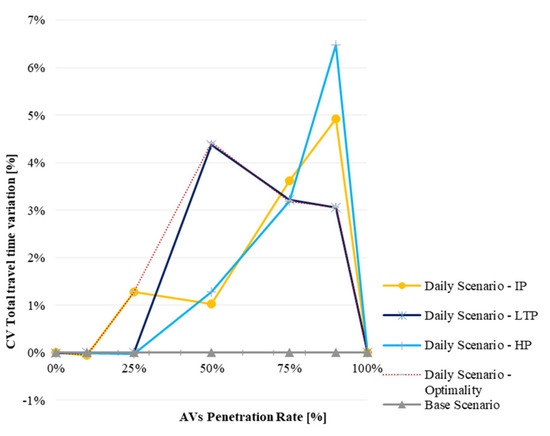
Figure 8.
Daily Scenario: CV total travel time variation.

Figure 9.
Daily Scenario: AV total travel time variation.
CV detouring naturally intensifies when AVs are 50%, or even sooner in the IP. According to Figure 10, Figure 11, Figure 12 and Figure 13, the total travel time of CV passengers (Figure 8) might increase in the following situations:
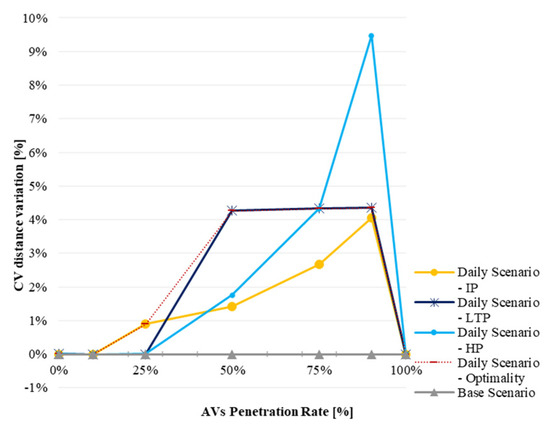
Figure 10.
Daily Scenario: CV total distance variation.
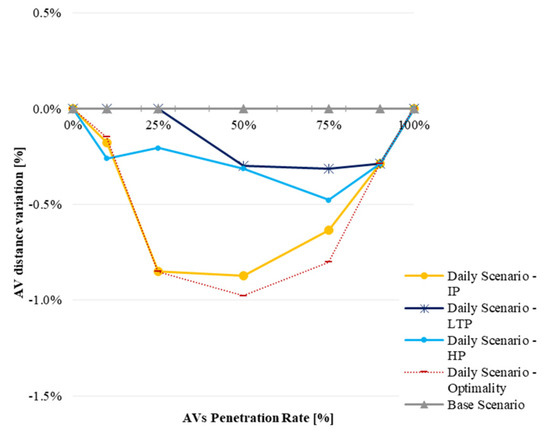
Figure 11.
Daily Scenario: AV total distance variation.
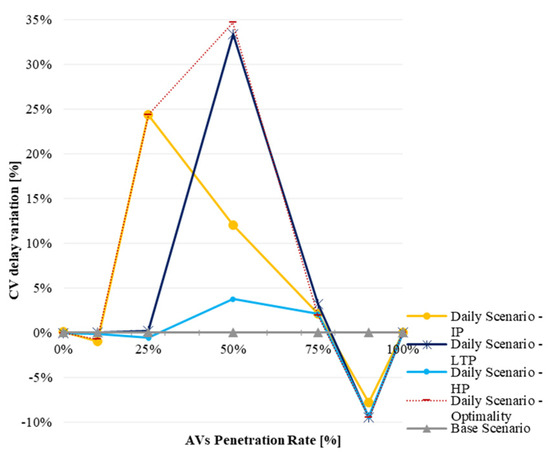
Figure 12.
Daily Scenario: CV total delay variation.
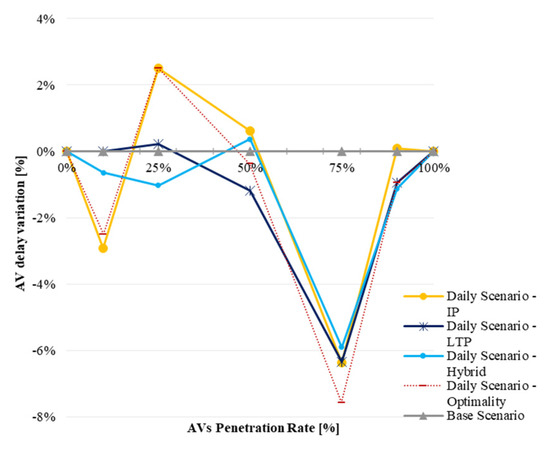
Figure 13.
Daily Scenario: AV total delay variation.
- CVs experience congestion in AV subnetworks’ surroundings that can be depicted by an increase in total CVs’ delay (see Figure 12). This occurs, for instance, at a penetration rate of 90%.
- CVs experience detouring away from AV subnetworks to reach their destination, which is depicted by an increase in CVs’ distance (see Figure 10). This occurs, for instance, at a penetration rate of 75%.
Conversely, total travel time might increase for AVs (Figure 9) in the following situations:
- As AVs’ value of travel time decreases, AV passengers might travel longer, which can be depicted by an increase in AVs’ delay while in congestion (see Figure 13). This occurs, for instance, at a penetration rate of 25%.
- AV trips might occur on shorter routes (lower distances) and experience higher travel times (Figure 11) This happens if AV subnetworks include roads with lower capacity/speed, when both AV delays and distance decrease. For example, this happens at a penetration rate of 10% in the IP and HP and of 50% in the LTP.
Figure 10 shows that CV detouring is unavoidable in the latest stages, increasing up to 10%. The “best” strategy to avoid CV detouring is the IP, if the design starts at a penetration rate of 25%. If the design starts at 50%, the outcome would be the optimality, which is not so beneficial. In addition, the IP strategy searches for shorter AV routes (Figure 11), which, while causing higher travel times, means that the IP design starts selecting lower-capacity roads. The IP design can increase the total delay of CV passengers (Figure 12) by about 25%. The LTP increases CV total delay to 35% for an AV penetration rate of 50%. The HP mitigates CV total delay and, for this indicator, is considered the “best” strategy. Similar conclusions can be drawn for AVs (Figure 13): the hybrid and the LTP strategies reduce delay up to 8%. AV subnetworks are important for reducing AV delays.
Figure 14, Figure 15, Figure 16 and Figure 17 evaluate congestion behaviour during this process. Figure 14 illustrates the average degree of saturation, which indicates that speed might increase on some roads. The IP design presents on average a lower degree of saturation; in Figure 15, for an AV penetration rate of 50%, the length of congested roads (DS ≥ 100%) is higher (8.14 km) than the Base Scenario—meaning that AV subnetworks from IP are not suitable at this design stage. The LTP (Figure 16) is suitable for an AV penetration rate of 50%, decreasing congestion on roads above practical capacity (DS ≥ 75%) on 4.60 km, yet worsening congested roads (DS ≥ 100%) on 1.77 km. HP (Figure 17) has a similar performance as the LTP, showing low performance in most of the transition process. Overall, AV subnetworks do not improve/mitigate congestion significantly, since the efficiency of AVs has an equally significant role in congestion in the Base Scenario.

Figure 14.
Daily Scenario: average degree of saturation.

Figure 15.
Daily Scenario: congestion with incremental planning.
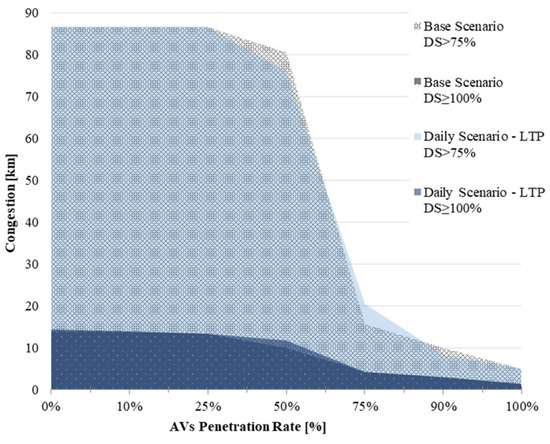
Figure 16.
Daily Scenario: congestion with long-term planning.
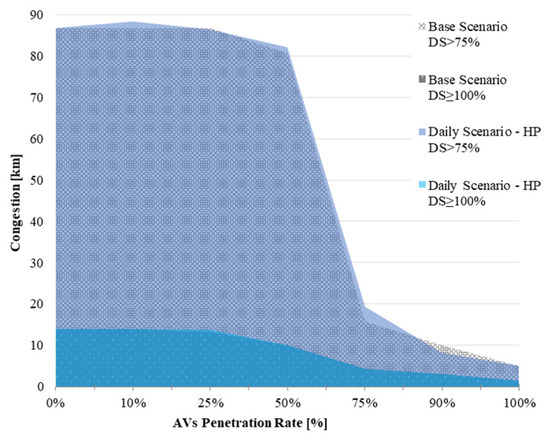
Figure 17.
Daily Scenario: congestion with hybrid planning.
4.6. Daily and Peak-Hour Design Comparison
The peak hour is usually considered in traffic design studies as it agglomerates most congestion problems. Therefore, this study was carried out to compare the feasibility on how deep and complex the RNDP-AVs takes place. The optimality of the Daily Scenario is now paralleled with the optimality of the Peak-Hour Scenario (9–10 a.m.) through Figure 18, and given a constant traffic demand throughout the process. The optimal zone (pink shadow) is between both optimality analyses, the Daily and Peak-Hour Designs. From 25% to 75%, the AV subnetworks in the Daily Scenario should be larger than in the Peak-Hour Scenario, whilst in the latest stages (from 90% of AVs onwards), the Peak-Hour Scenario would require larger AV subnetworks.
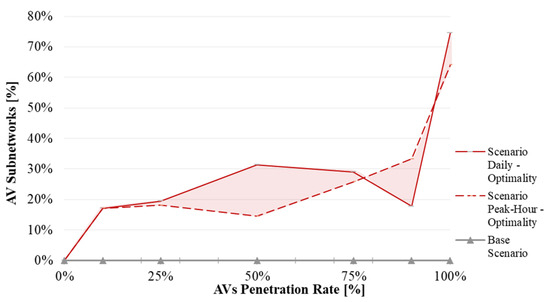
Figure 18.
Optimality design: daily and peak hour scenarios.
Nevertheless, the Daily Scenario presents, on average, only 1% heightened network congestion in the peak hour—yet it considers the daily traffic demand. For instance, for a penetration rate of 75%, the Daily Scenario produces 19% of network congestion in the peak hour (Table 3), against the 18% that would be obtained in the optimal Peak-Hour Scenario (Table 2), but still inferior to the Base Scenario, which would be 20% (Table 1). Similarly, for the average degree of saturation, the Daily Scenario produces, on average, an increase of 11% of the average degree of saturation against the peak-hour design, yet 3% less than the Base Scenario. This means that AV subnetworks found in the Delft experiments for the Daily Scenario are suitable and improve congestion in the peak hour.
4.7. Planning Design Strategies Overview
The strategy considered for the selection of dedicated roads is debatable and dependent on the desired results. Two patterns are noticeable: When most of the vehicles are conventional, the model aims to reduce CV detouring costs by selecting dedicated roads with a lower capacity and therefore lower speed, moving AV traffic away from regular roads. As more AVs are present in the system, the model aims to increase their cost savings by increasing the subnetwork’s dimensions. The expansion of the AVs subnetwork is condensed in Figure 19. The pink area considers the optimality of the peak-hour design.
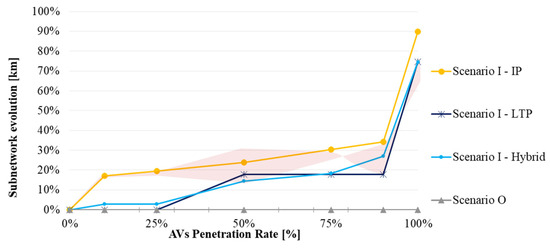
Figure 19.
AV subnetworks’ expansion in every planning strategy.
Amongst the planning strategies, the model balances the CV detouring extra costs and AV cost savings, given a penetration rate. This is why the incremental planning strategy starts avoiding CV detouring and forces an increase in the distances travelled by AVs in the early stages. On the other hand, the long-term planning starts from the optimal long-term network design, where 90% of the vehicles are automated and 10% are conventional. In this case, the model creates the network reversely by maximizing the travel time cost savings, which is naturally far from optimality at the early stages, because detouring is unavoidable—the reverse design gives preference to AVs savings and worsens CV detouring. Finally, the hybrid planning revealed surprising results because it proved that limiting the incremental planning to the optimal solution obtained in the long term strongly diminishes the negative effects of both the incremental and long-term planning strategies throughout the transition process. Moreover, in the first half of the transition period, the hybrid planning diminishes the extra travel costs that arise from implementing the long-term planning strategy; whilst, in the second half of the transition process, the hybrid planning diminishes the CV detouring that arises from implementing the incremental planning.
5. Conclusions and Future Work
In this paper, we proposed a road network design problem for the deployment of automated vehicles (RNDP-AVs) to design AV subnetworks in urban areas. The mathematical model is formulated as a nonlinear programming (NLP) problem. Our contribution is focused on the decision of which roads to dedicate to automated traffic and the progressive design of these AV subnetworks. It is focused on the transition process when the traffic equilibrium varies according to AVs’ operational efficiency and the decrease in the occupants’ value of travel time. Three planning strategies are proposed and compared: (1) incremental planning, where dedicated roads are added gradually as the AV penetration rate evolves; (2) long-term planning, where the subnetwork is reversely created from the long-term optimal solution; and (3) hybrid planning, where the subnetwork is limited from the early stages to reach the optimal final network design.
The RNDP-AVs model was applied to the network of the city of Delft. Three scenarios were performed: one without AV subnetworks, and a Peak-Hour Scenario that helps to evaluate the real impact of the Daily Scenario. All scenarios were implemented with seven AV penetration rates. The RNDP-AVs model proved to be an easy tool to guide the creation of AV subnetworks as a function of the penetration rate. The optimal solution can be obtained within an acceptable computation time for the combinatorial nonlinear decision problem. The incremental planning calculation time took 8 h. The long-term planning calculation time was about 4 h. The hybrid planning took 13 h.
AV subnetworks first appear in areas that are highly in demand (residential areas) and in which there is a compromise between the AV benefits, in terms of travel time cost savings, and CV detours. Through the Delft experiments conducted at each penetration rate, we found that AV subnetworks are a useful strategy to reduce the overall total travel cost, while degrading delay, degree of saturation and congestion. However, depending on which strategy is chosen for evolving this AV subnetwork and how early the design of AV subnetworks takes place, results differ. From a road safety perspective in urban areas, AV subnetworks might play an important role in segregating automated from mixed traffic as the design first induces AVs to shorter routes (lower distances) and lower speeds (higher travel times), which might be beneficial.
From the planning strategies applied to the Delft case study scenarios, we can draw the following conclusions:
- The incremental planning should start in the initial stages around AV penetration rates of 25%. The IP starts selecting lower-capacity roads (lower speeds), which leads to expanded AV subnetworks towards the end of the transition period, producing less CV detouring.
- Long-term planning is a fair strategy in the second half of the transition period, i.e., when the initial design stages occur once AVs are already a majority. For an equal share between AVs and CVs (50%), CVs will experience high detouring and delays, but that effect will be highly mitigated in the second half of the period.
- Hybrid planning revealed satisfactory results, reducing CV delays throughout the entire transition period, and it can be used to help design AV subnetworks from the beginning. The main disadvantage of this strategy is the CV detouring (longer trips, longer distances) in the latest stages, once AVs reach 90% of the vehicle fleet.
If CV detouring is considered the tie-breaking criteria regarding the decision as to the best planning strategy, incremental planning is the strategy that mitigates this problem the most. However, this decision also depends on the diffusion of AVs over time, because it will influence the penetration rate evolution during the deployment process. If the time lag from 1% to 50% of AVs is much longer than the time lag from 50% to 90% of AVs, the CV detouring would be very present, which reinforces that the incremental is the best strategy to be considered. Time plays an important role here, yet forecasts of the diffusion of AVs are still very uncertain and dependent on policy and technology evolution.
The application of the RNDP-AVs model points towards a need for designing a subnetwork for AVs. This model was formulated with the introduction of some simplifications and assumptions, as stated in Section 3. These simplifications and assumptions result in both limitations and future work opportunities. As limitations of the model, proper to any academic exercise, we have, for example, a constant mixed traffic efficiency coefficient and a constant road investment per kilometre. Furthermore, the application of the model has only been tested in the city of Delft, and does not consider external demand, because of data availability and the assumed focus on inner city traffic.
As for future work, the authors suggest an extended model joining the decision on AV subnetworks with the time lag decision. Similarly, an improved model joining together the decision about AV subnetworks and the strategic location problem for V2I communication sites (5 km of radius), as well traffic efficiency parameters that are more accurate, perhaps could be solved through heuristic methods [39,40], though more computationally costly to solve and the optimal solution might not be guaranteed. The same is true for other applications in bigger cities or larger networks. Another relevant improvement could be taking public transport as another alternative mode of transport, but it would involve both routes and schedules, transforming this road network design problem into a tricky combinatorial transit assignment problem [41]. Moreover, it is also possible to evolve to bi-level optimisation and add improvements such as other cost components involving pollution, noise reduction or other benefits, for example, freeing space in the city centre (e.g., parking and gas stations).
Author Contributions
Conceptualisation, formal analysis, writing—review and editing, L.C., G.H.d.A.C., B.v.A. and J.P.T.; methodology, validation, visualisation, data curation, investigation, writing—original draft preparation, L.C.; resources, supervision, project administration, G.H.d.A.C., B.v.A. and J.P.T.; software, funding acquisition, L.C., G.H.d.A.C. and B.v.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Portuguese Foundation for Science and Technology (FCT): the first author was supported by grant number PD/BD/113760/2015 under the MIT Portugal Programme in Transportation Systems.
Data Availability Statement
The data supporting this study’s findings are available from the corresponding author upon request.
Acknowledgments
The authors would like to thank FICO (Xpress software provider) for establishing a research agreement with the Department of Transport and Planning at TU Delft. Additionally, the first author gratefully acknowledges the opportunity to develop this study as a visiting PhD student at the Department of Transport and Planning at TU Delft. The authors would like to thank Kees van Goeverden for supplying a filtered database of Netherlands mobility in 2008/2009.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- European Transport Safety Council. Prioritising the Safety Potential of Automated Driving in Europe; European Transport Safety Council: Brussels, Belgium, 2016; Volume 22, Available online: http://etsc.eu/automated-driving-report/ (accessed on 2 January 2024).
- Toroyan, T.; Peden, M.M.; Iaych, K. WHO launches second global status report on road safety. Inj. Prev. 2013, 19, 150. [Google Scholar] [CrossRef] [PubMed]
- Nieuwenhuijsen, J.; de Almeida Correia, G.H.; Milakis, D.; van Arem, B.; van Daalen, E. Towards a quantitative method to analyze the long-term innovation diffusion of automated vehicles technology using system dynamics. Transp. Res. Part C Emerg. Technol. 2018, 86, 300–327. [Google Scholar] [CrossRef]
- Calvert, S.C.; Van Arem, B.; Heikoop, D.D.; Hagenzieker, M.; Mecacci, G.; De Sio, F.S. Gaps in the Control of Automated Vehicles on Roads. IEEE Intell. Transp. Syst. Mag. 2021, 13, 146–153. [Google Scholar] [CrossRef]
- Shladover, S.E. Progressive Deployment Steps Toward an Automated Highway System. Transp. Res. Rec. 2000, 1727, 154–161. [Google Scholar] [CrossRef]
- SAE. Taxonomy and Definitions for Terms Related to On-Road Motor Vehicle Automated Driving Systems; SAE IntInternational: Warrendale, PA, USA, 2018; Volume J3016_2018, pp. 1–12. [Google Scholar]
- Haitao, H.; Menendez, M.; Ilgin Guler, S. Analytical evaluation of flexible-sharing strategies on multimodal arterials. Transp. Res. Part A Policy Pract. 2018, 114, 364–379. [Google Scholar] [CrossRef]
- de Almeida Correia, G.H.; van Arem, B. Solving the User Optimum Privately Owned Automated Vehicles Assignment Problem (UO-POAVAP): A model to explore the impacts of self-driving vehicles on urban mobility. Transp. Res. Part B Methodol. 2016, 87, 64–88. [Google Scholar] [CrossRef]
- Milakis, D.; van Arem, B.; van Wee, B. Policy and society related implications of automated driving: A review of literature and directions for future research. J. Intell. Transp. Syst. 2017, 21, 324–348. [Google Scholar] [CrossRef]
- Kesting, A.; Treiber, M.; Helbing, D. Enhanced intelligent driver model to access the impact of driving strategies on traffic capacity. Philos. Trans. A. Math. Phys. Eng. Sci. 2010, 368, 4585–4605. [Google Scholar] [CrossRef]
- Calvert, S.C.; Van Den Broek, T.H.A.A.; Van Noort, M. Modelling cooperative driving in congestion shockwaves on a freeway network. In Proceedings of the 2011 14th International IEEE Conference on Intelligent Transportation Systems (ITSC), Washington, DC, USA, 5–7 October 2011; pp. 614–619. [Google Scholar] [CrossRef]
- Talebpour, A.; Mahmassani, H.S. Influence of connected and autonomous vehicles on traffic flow stability and throughput. Transp. Res. Part C Emerg. Technol. 2016, 71, 143–163. [Google Scholar] [CrossRef]
- Zhang, K.; Nie, Y.M. Mitigating the impact of selfish routing: An optimal-ratio control scheme (ORCS) inspired by autonomous driving. Transp. Res. Part C Emerg. Technol. 2018, 87, 75–90. [Google Scholar] [CrossRef]
- Magnanti, T.L.; Wong, R.T. Network Design and Transportation Planning: Models and Algorithms. Transp. Sci. 1984, 18, 1–55. [Google Scholar] [CrossRef]
- Bertsekas, D. Network Optimization: Continuous and Discrete Models; Athena Scientific: Nashua, NH, USA, 1998. [Google Scholar]
- Chen, Z.; He, F.; Zhang, L.; Yin, Y. Optimal deployment of autonomous vehicle lanes with endogenous market penetration. Transp. Res. Part C Emerg. Technol. 2016, 72, 143–156. [Google Scholar] [CrossRef]
- National Academies of Sciences. TRB Dedicating Lanes for Priority or Exclusive Use by Connected and Automated Vehicles; National Academies of Sciences: Washington, DC, USA, 2018. [Google Scholar] [CrossRef]
- Chen, Z.; He, F.; Yin, Y.; Du, Y. Optimal design of autonomous vehicle zones in transportation networks. Transp. Res. Part B 2017, 99, 44–61. [Google Scholar] [CrossRef]
- Ye, Y.; Wang, H. Optimal Design of Transportation Networks with Automated Vehicle Links and Congestion Pricing. J. Adv. Transp. 2018, 2018, 3435720. [Google Scholar] [CrossRef]
- Madadi, B.; Van Nes, R.; Snelder, M.; Van Arem, B. Optimizing road networks for automated vehicles with dedicated links, dedicated lanes, and mixed-traffic subnetworks. J. Adv. Transp. 2021, 2021, 8853583. [Google Scholar] [CrossRef]
- Conceição, L.; Correia, G.; Tavares, J.P.J.P. The deployment of automated vehicles in urban transport systems: A methodology to design dedicated zones. In Proceedings of the Transportation Research Procedia; 20th EURO Working Group on Transportation Meeting, EWGT 2017, Budapest, Hungary, 4–6 September 2017; pp. 4–6. [Google Scholar] [CrossRef]
- Cantarella, G.E.; Di Febbraro, A.; Gangi, M.D.; Giannattasio, O. Solving stochastic assignment to transportation networks with TVs and AVs. Transp. Res. Procedia 2019, 42, 7–18. [Google Scholar] [CrossRef]
- Luathep, P.; Sumalee, A.; Lam, W.H.K.; Li, Z.C.; Lo, H.K. Global optimization method for mixed transportation network design problem: A mixed-integer linear programming approach. Transp. Res. Part B Methodol. 2011, 45, 808–827. [Google Scholar] [CrossRef]
- Levin, M.W.; Boyles, S.D. A multiclass cell transmission model for shared human and autonomous vehicle roads. Transp. Res. Part C Emerg. Technol. 2016, 62, 103–116. [Google Scholar] [CrossRef]
- Dafermos, S. Traffic Equilibrium and Variational Inequalities. Transp. Sci. 1980, 14, 42–54. [Google Scholar] [CrossRef]
- Florian, M.; Hearn, D. Network Equilibrium Models and Algorithms Michael. Handbooks Oper. Res. Manag. Sci. 1995, 8, 485–550. [Google Scholar] [CrossRef]
- Sheffi, Y. Urban Transportation Network; Pretince Hall: Kent, OH, USA, 1985; Volume 4. [Google Scholar]
- Toint, P.; Wynter, L. Asymmetric multiclass traffic assignment: A coherent formulation. In Proceedings of the 15th ISTTT Meet, Adelaide, Australia, 16–18 July 2002. [Google Scholar]
- Yap, M.D.; Correia, G.; van Arem, B. Preferences of travellers for using automated vehicles as last mile public transport of multimodal train trips. Transp. Res. Part A Policy Pract. 2016, 94, 1–16. [Google Scholar] [CrossRef]
- de Almeida Correia, G.H.; Looff, E.; van Cranenburgh, S.; Snelder, M.; van Arem, B. On the impact of vehicle automation on the value of travel time while performing work and leisure activities in a car: Theoretical insights and results from a stated preference survey. Transp. Res. Part A Policy Pract. 2019, 119, 359–382. [Google Scholar] [CrossRef]
- Levin, M.W.; Boyles, S.D. Effects of autonomous vehicle ownership on trip, mode, and route choice. Transp. Res. Rec. 2015, 2493, 29–38. [Google Scholar] [CrossRef]
- FICO. Getting Started with Xpress Release 8.1; FICO: Bozeman, MT, USA, 2017. [Google Scholar]
- Fair Isaac Corporation. XPress Solver—Nonlinear Reference Manual. 2019. Available online: https://www.fico.com/fico-xpress-optimization/docs/latest/solver/nonlinear/HTML/GUID-4B40E940-6A38-342F-9531-A13E84FB1467.html (accessed on 7 July 2019).
- Kronqvist, J.; Bernal, D.E.; Lundell, A.; Grossmann, I.E. A review and comparison of solvers for convex MINLP. Optim. Eng. 2019, 20, 397–455. [Google Scholar] [CrossRef]
- Wardrop, J.G. Road paper. Some theoretical aspects of road traffic research. ICE Proc. Eng. Div. 1952, 1, 325–362. [Google Scholar] [CrossRef]
- Beckman, D.J.R.M.; McGuire, C.B.; Winsten, C.B.; Koopmans, T.C. Studies in the Economics of Transportation. OR 1956. [Google Scholar]
- Daganzo, C.F. Stochastic network equilibrium with multiple vehicle types and asymmetric, indefinite link cost jacobians. Transp. Sci. 1983, 17, 282–300. [Google Scholar] [CrossRef]
- Cantarella, G.E. A general fixed-point approach to multimode multi-user equilibrium assignment with elastic demand. Transp. Sci. 1997, 31, 107–128. [Google Scholar] [CrossRef]
- Efthymiou, D.; Chrysostomou, K.; Morfoulaki, M.; Aifantopoulou, G. Electric vehicles charging infrastructure location: A genetic algorithm approach. Eur. Transp. Res. Rev. 2017, 9, 27. [Google Scholar] [CrossRef]
- Brenna, M.; Lazaroiu, G.C.; Roscia, M.; Saadatmandi, S. Dynamic Model for the EV’s Charging Infrastructure Planning through Finite Element Method. IEEE Access 2020, 8, 102399–102408. [Google Scholar] [CrossRef]
- Wang, X.; Sun, C.; Wang, R.; Wei, T. Two-Stage Optimal Scheduling Strategy for Large-Scale Electric Vehicles. IEEE Access 2020, 8, 13821–13832. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).