Seepage Actions and Their Consequences on the Support Scheme of Deep-Buried Tunnels Constructed in Soft Rock Strata
Abstract
1. Introduction
2. Project Overview, Engineering Context and Rock Parameters
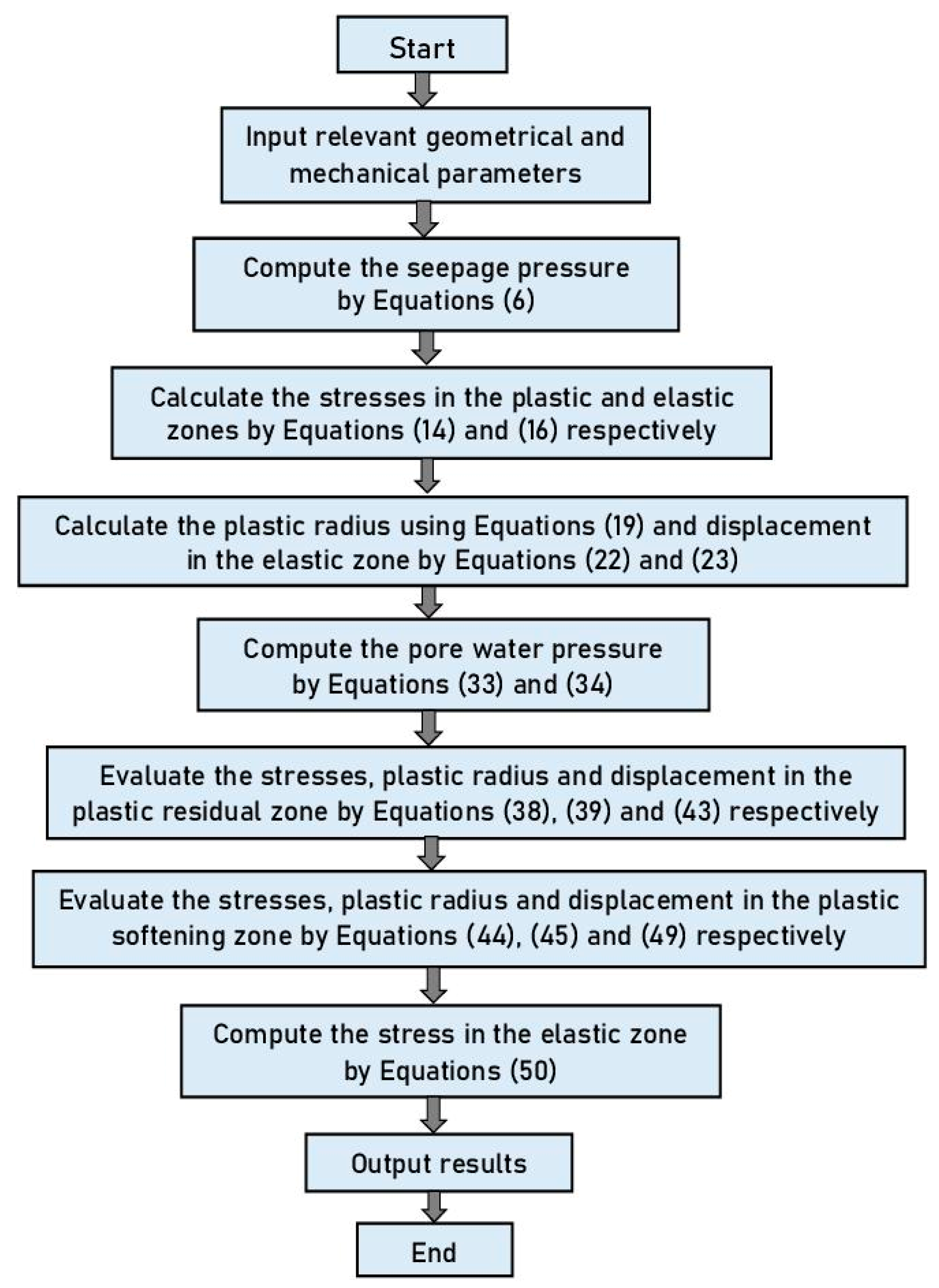
3. Adopted Mechanical Model of the Tunnel and Seepage Pressure Determination
4. Stress and Displacement Examination
4.1. Examination of Stress in the Plastic Zone
4.2. Examination of Stress in the Elastic Zone
5. Examining the Plastic Radius and the Displacement of the Host Rocks
6. Consideration of the Coupled Effect of Softening and Seepage
6.1. Stress, Plastic Radius and Displacements in the Plastic Residual Zone
6.1.1. Stress and Plastic Radius in the Plastic Residual Zone
6.1.2. Displacements in the Plastic Residual Zone
6.2. Stress, Plastic Radius and Displacements in the Plastic Softening Zone
6.2.1. Stress and Plastic Radius in the Plastic Softening Zone
6.2.2. Displacements in the Plastic Softening Zone
6.3. Stress in the Elastic Zone
7. Parametric Study and Discussion
7.1. Variation of Plastic Radius with Support Pressure
7.2. Variation of the Plastic Radius with the Principal Stress Coefficient
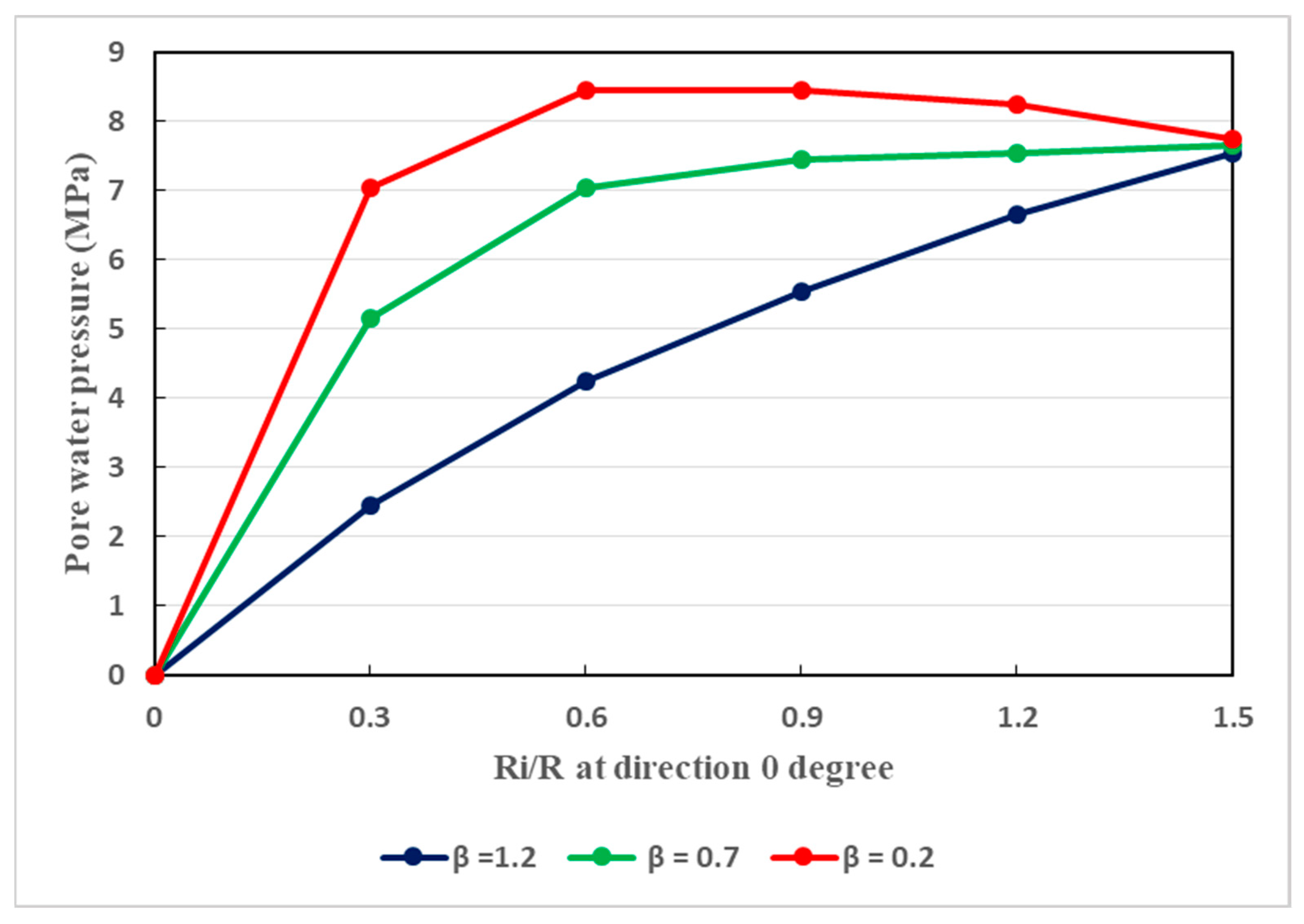
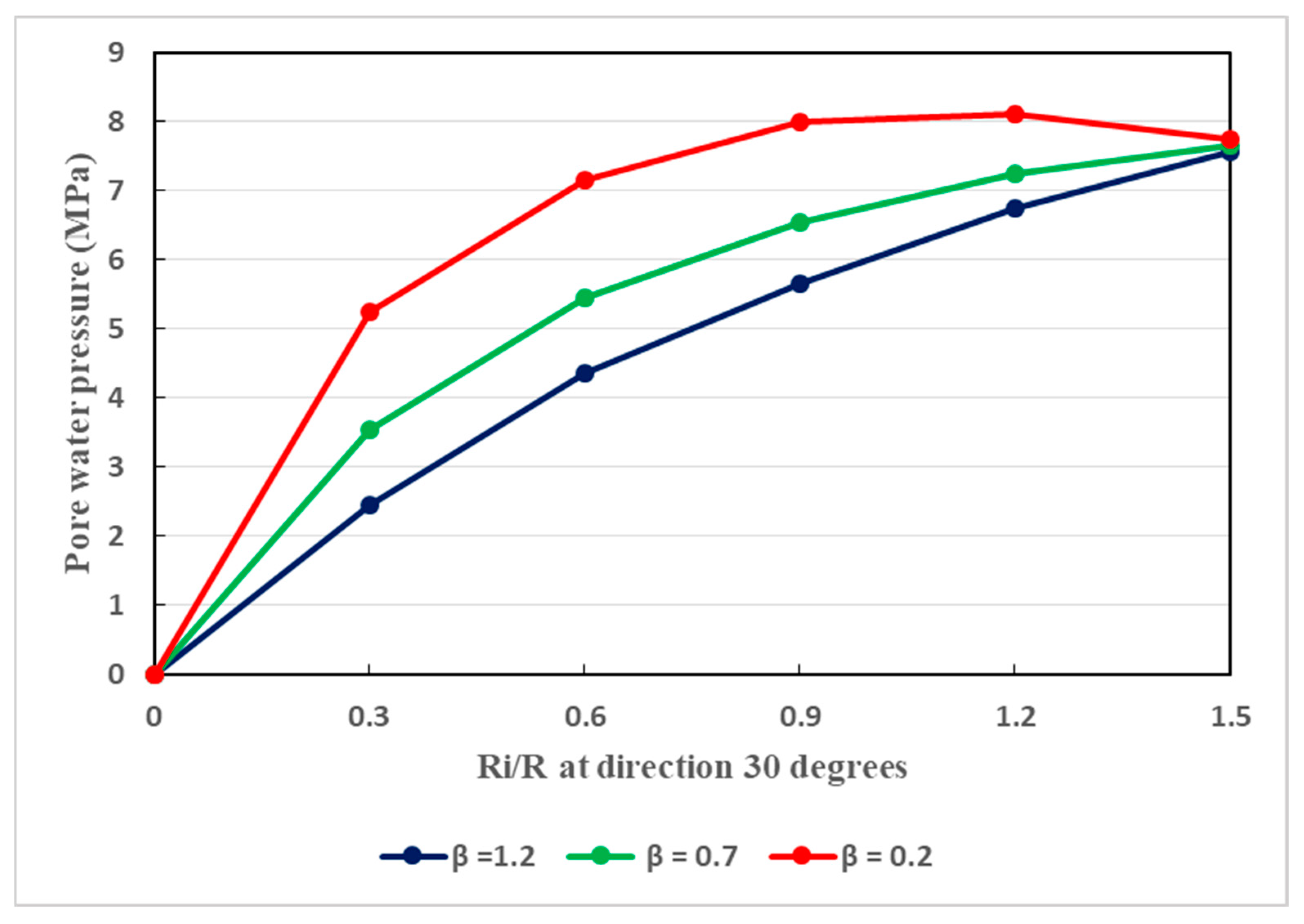
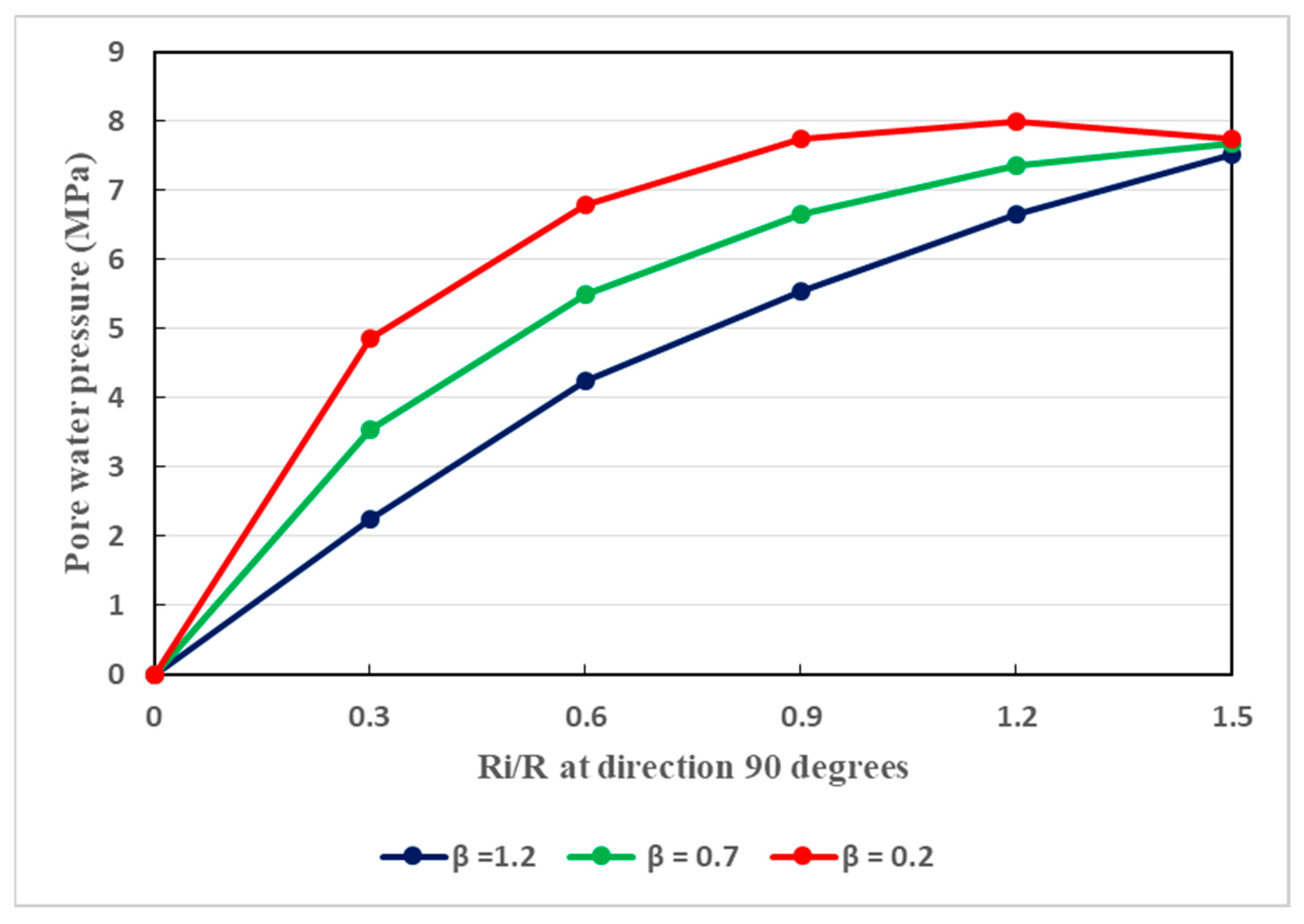
7.3. Variation of Pore Water Pressure in the Surrounding Rocks
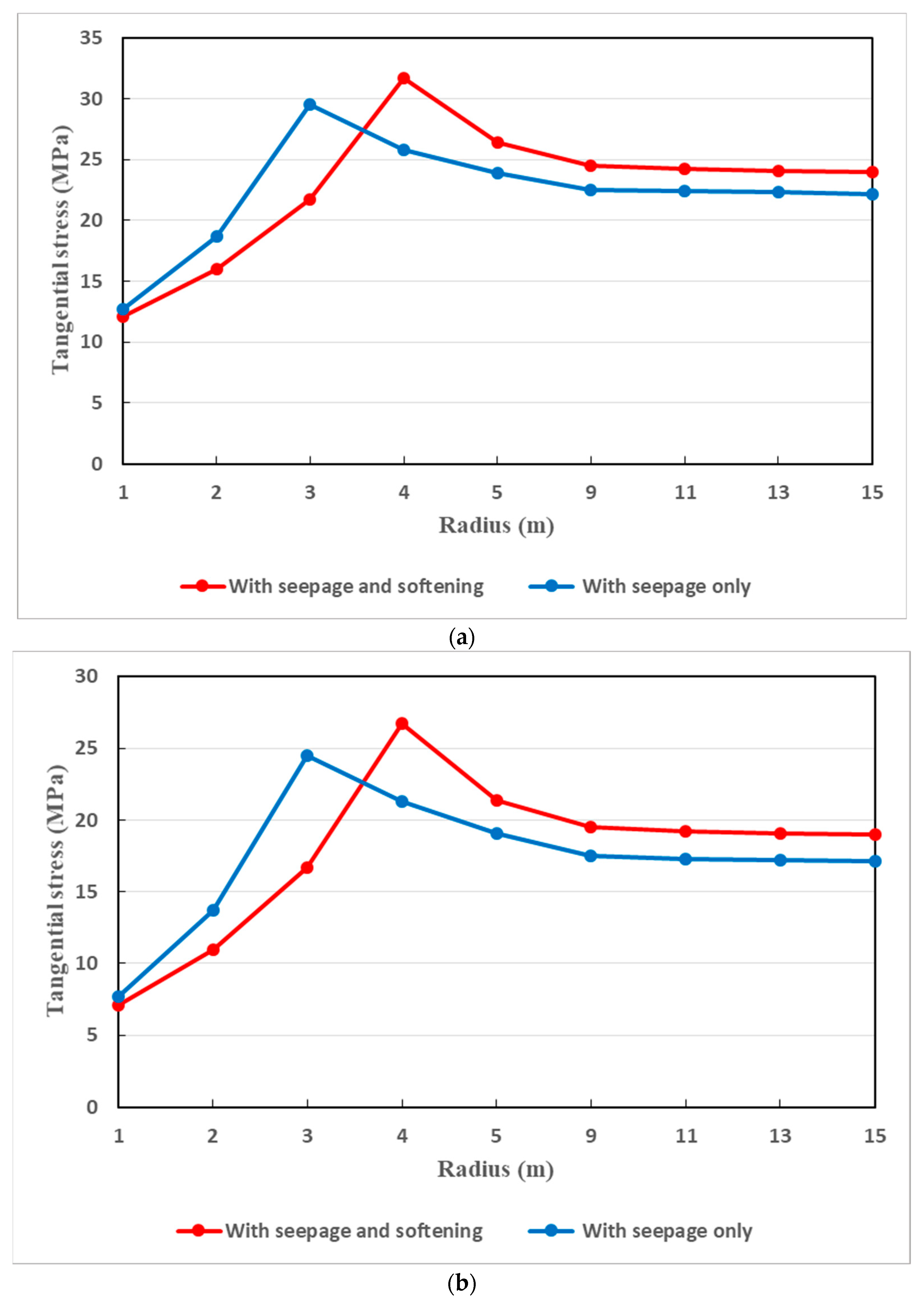
7.4. Variation of Tangential Stress in Surrounding Rocks
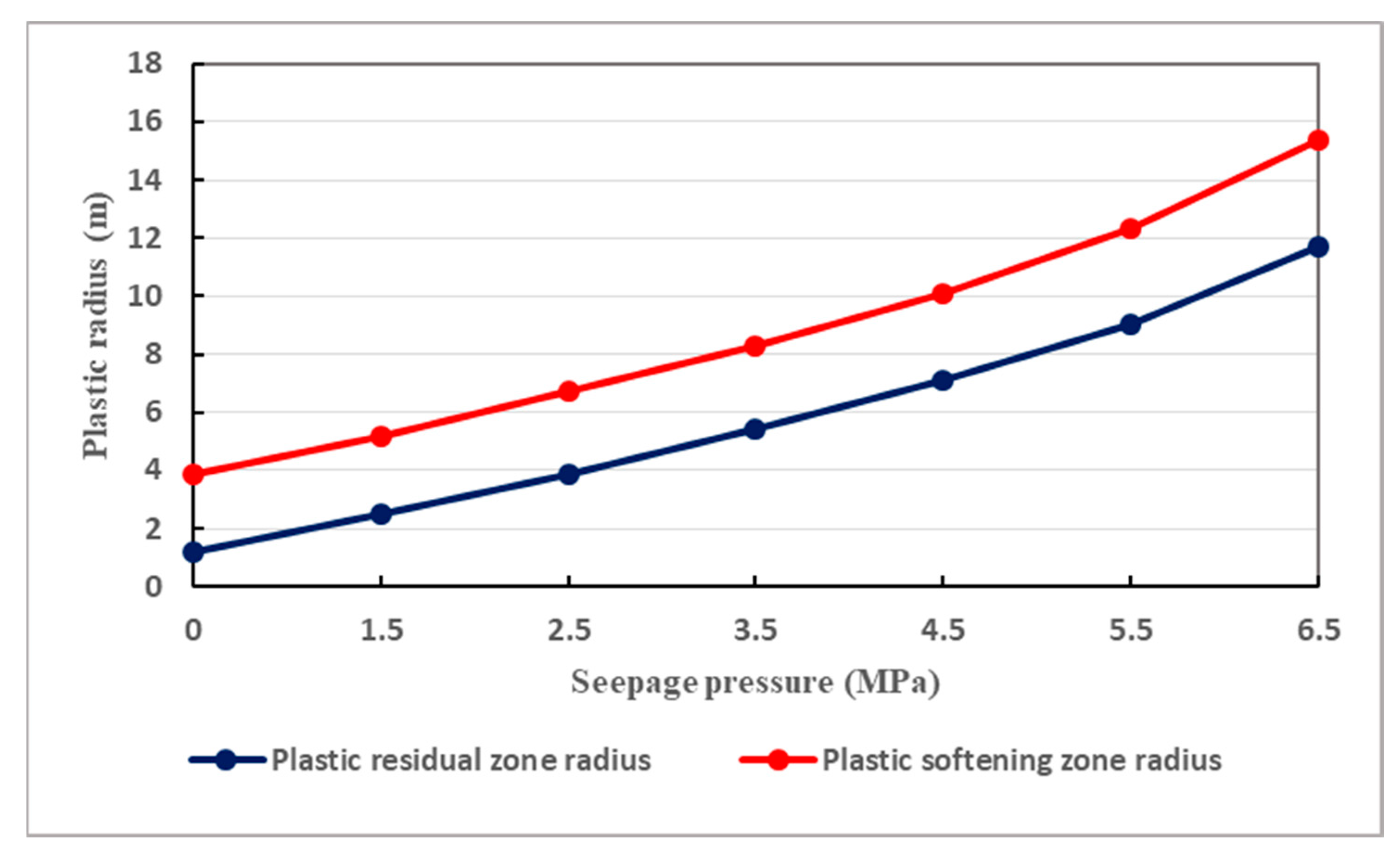
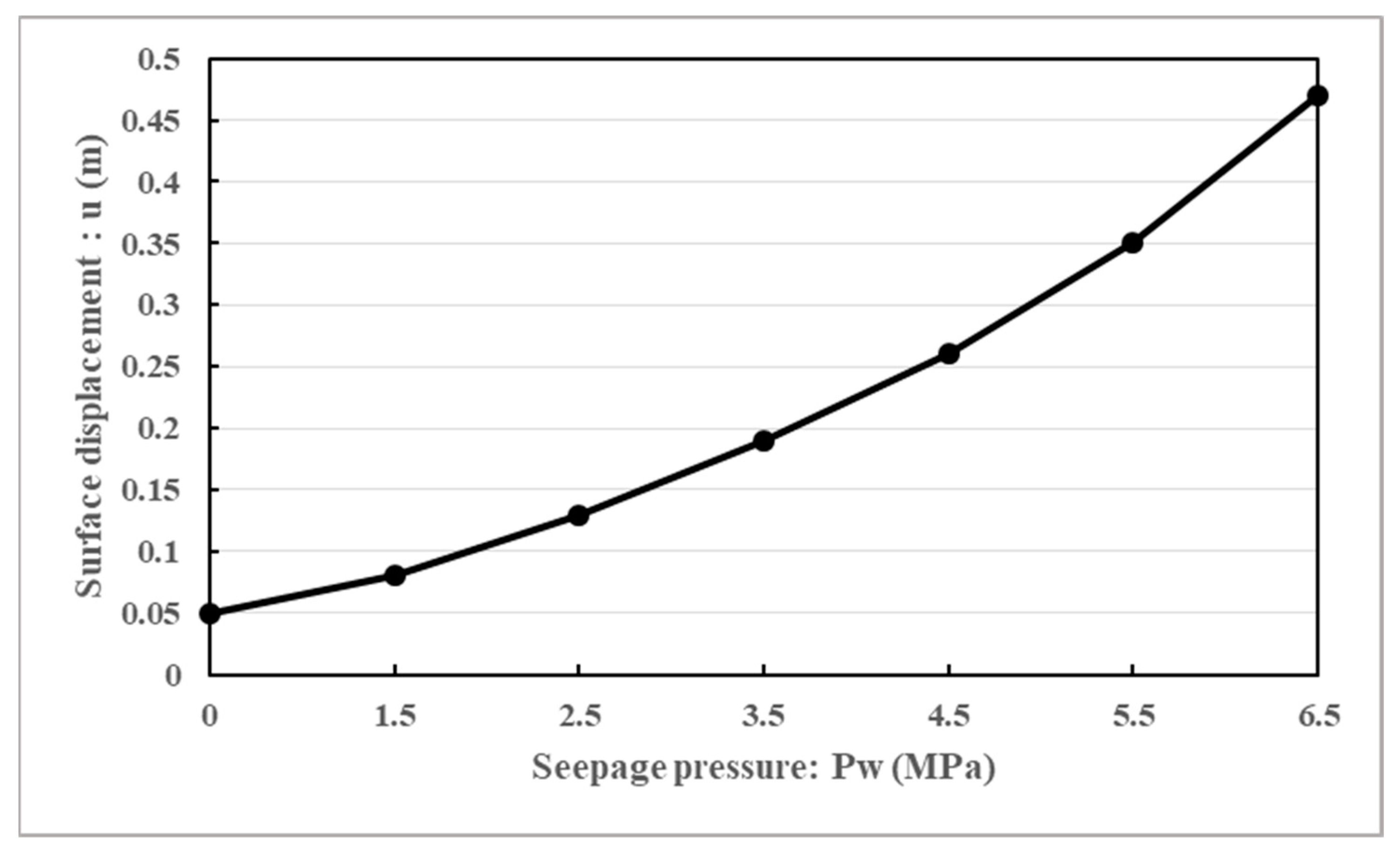
7.5. Influence of Seepage Pressure on the Tunnel Plastic Radii and Surface Displacements
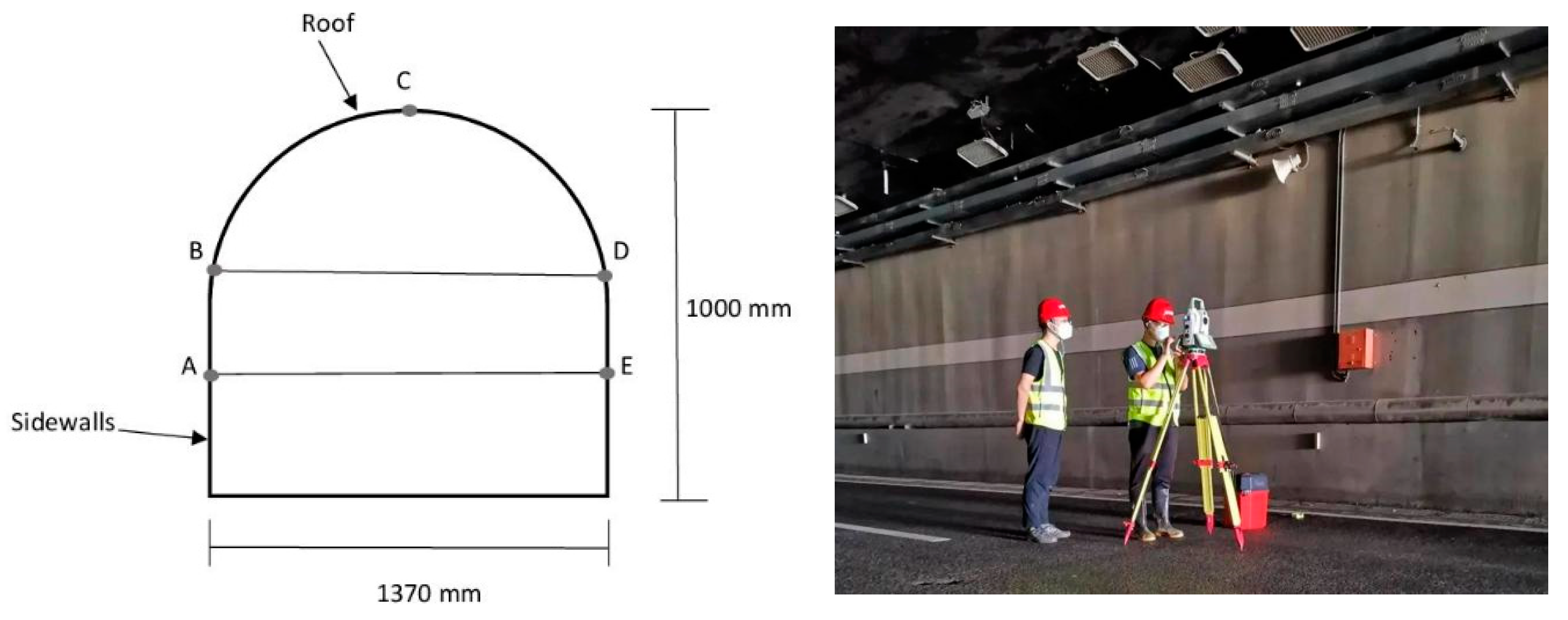
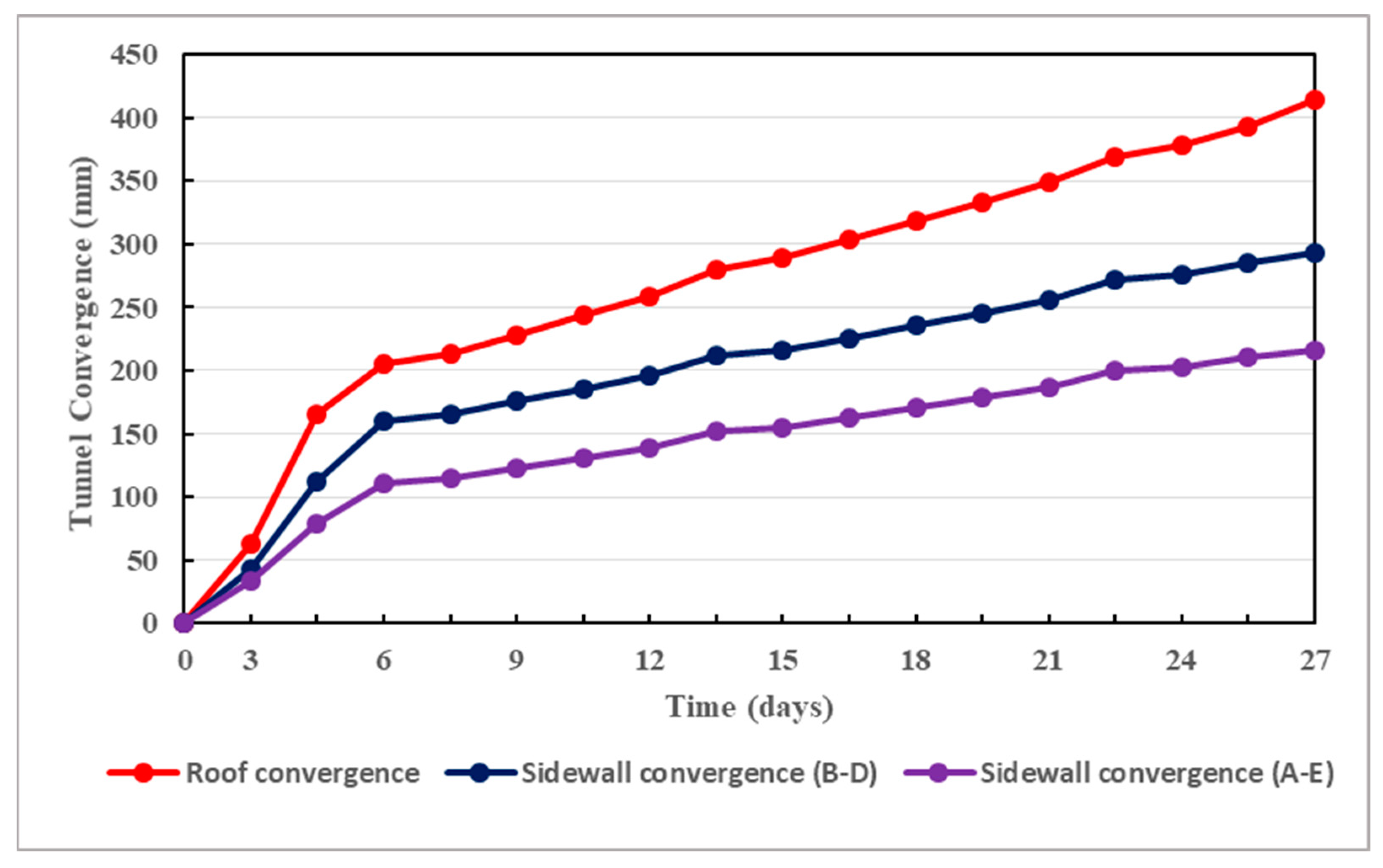
7.6. In Situ Measurements of Tunnel Convergence Deformation
7.7. Implications
- -
- Sufficiently large burial depth of the planned tunnel;
- -
- Complex soft rock conditions: broken argillaceous sandstone with low uniaxial compressive strength (<10 MPa);
- -
- Complex rock excavations: drill-and-blast with strictly controlled sequences;
- -
- Complex hydrological conditions: relatively water-rich zones, groundwater inflows into excavated areas are frequent.
8. Conclusions
- To effectively withstand the inevitable severe consequences caused by seepage actions, the support scheme of deep-buried tunnels, particularly tunnels constructed in soft rock environments, must be of highest resistance possible. It is thus necessary to design such supports in accordance with the complexity of the concerned rocky environments in order to confront the seepage actions.
- The plastic softening zone and the plastic residual zone are two constituents of the plastic zone of deeply buried tunnels. Their radius decreases by increasing the resistance of the support structure, under seepage conditions and under the combined effects of seepage and softening.
- The combined effects of water seepage and material softening are very dangerous for tunnel safety and stability. Such effects have the consequences of significantly increasing the plastic radii of deep soft rock tunnels. It is revealed that the more strongly the tunnel is supported, the more its plastic radii and therefore its deformations are reduced.
- In terms of scope, the plastic zone radii of deep soft rock tunnels are considerably affected by the principal stress coefficient. In fact, the highest values of the principal stress coefficient are favorable to small plastic radii. Accordingly, appropriate values of such coefficients must be adopted to ensure reasonable dissemination of tangential stress along the tunnel, which must be durably safe and stable.
- Throughout the surrounding rocks of deeply buried tunnels, the dissemination of pore water pressure is strongly affected by the uneven permeability coefficient under anisotropic seepage states. This conforms well to the actual situation where the host rocks are broken and therefore the seepage field is mainly anisotropic. Therefore, seepage actions cannot be ignored since they can affect the stability of deep soft rock tunnels in any direction.
- Owing to the inevitable severe consequences of seepage actions, deep-buried tunnels constructed in complex soft rocky media must be adequately monitored at all times, even if their support schemes are sufficiently resistant. In fact, proper long-term monitoring can effectively guarantee the safety and stability of such structures at all times. In this sense, reliable remote sensors show promise.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fernandez, G.; Alvarez, T.A., Jr. Seepage-Induced Effective Stresses and Water Pressures around Pressure Tunnels. J. Geotech. Eng. 1994, 120, 108–128. [Google Scholar] [CrossRef]
- Ohtsu, H.; Ohnishi, Y.; Taki, H.; Kamemura, K. A study on problems associated with finite element excavation analysis by the stress-flow coupled method. Int. J. Num. Anal. Meth. Geomech. 1999, 23, 1473–1492. [Google Scholar] [CrossRef]
- Rutqvist, J.; Stephansson, O. The role of hydromechanical coupling in fractured rock engineering. Hydrogeol. J. 2003, 11, 7–40. [Google Scholar] [CrossRef]
- Nam, S.W.; Bobet, A. Radial Deformations Induced by Groundwater Flow on Deep Circular Tunnels. Rock Mech. Rock Eng. 2007, 40, 23–39. [Google Scholar] [CrossRef]
- Shin, Y.J.; Song, K.-I.; Lee, I.M.; Cho, G.-C. Interaction between tunnel supports and ground convergence—Consideration of seepage forces. Int. J. Rock Mech. Min. Sci. 2011, 48, 394–405. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.-H.; Chen, J.-R. Elastoplastic Analysis of Surrounding Rocks of Submarine Tunnel with Consideration of Seepage. J. Highw. Transp. Res. Develop. 2013, 7, 73. [Google Scholar] [CrossRef]
- Fahimifar, A.; Ghadami, H.; Ahmadvand, M. An elasto-plastic model for underwater tunnels considering seepage body forces and strain-softening behavior. Eur. J. Environ. Civ. Eng. 2015, 19, 129–151. [Google Scholar] [CrossRef]
- Perazzelli, P.; Leone, T.; Anagnostou, G. Tunnel face stability under seepage flow conditions. Tunn. Undergr. Space Technol. 2014, 43, 459–469. [Google Scholar] [CrossRef]
- Jin-feng, Z.; Shuai-shuai, L.; Yuan, X.; Han-cheng, D.; Lian-heng, Z. Theoretical Solutions for a Circular Opening in an Elastic–brittle–plastic Rock Mass Incorporating the Out-of-plane Stress and Seepage Force. KSCE J. Civ. Eng. 2016, 20, 687–701. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, C.; Zhou, H.; Liu, N.; Zhang, Y.; Azhar, M.U.; Dai, F. The long-term safety of a deeply buried soft rock tunnel lining under inside-to-outside seepage conditions. Tunn. Undergr. Space Technol. 2017, 67, 132–146. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, C.; Wu, W.; Zhang, Y.; Ma, T. Analytical Solution for the External Stress Acting on the Lining in a Deep-Buried Circular TBM Tunnel Considering the Seepage Field. J. Appl. Mech. Technol. Phys. 2019, 60, 176–185. [Google Scholar] [CrossRef]
- Chen, Q.; Liang, L.; Zou, B.; Xu, C.; Kong, B.; Ma, J. Analytical Solutions of Steady a Seepage Field for Deep-Buried Tunnel with Grouting Ring Considering Anisotropic Flow. J. Mar. Sci. Eng. 2022, 10, 1861. [Google Scholar] [CrossRef]
- Di, Q.; Li, P.; Zhang, M.; Zhang, Q.; Wang, X. Analysis of face stability for tunnels under seepage flow in the saturated ground. Ocean Eng. 2022, 266, 112674. [Google Scholar] [CrossRef]
- Guo, Y.F.; Wang, H.N.; Jiang, M.J. An exact analytical approach for determining the seepage field around underwater twin tunnels with linings. Transp. Geotech. 2023, 42, 101050. [Google Scholar] [CrossRef]
- Niu, Y.; Ren, T.; Zhou, Q.; Jiao, X.; Shi, J.; Xiang, K.; Tao, J.; Zhai, Q.; Satyanaga, A. Analysis of Excavation Parameters on Face Stability in Small Curvature Shield Tunnels. Sustainability 2023, 15, 6797. [Google Scholar] [CrossRef]
- Li, S.; Liu, R.; Zhang, Q.; Zhang, X. Protection against water or mud inrush in tunnels by grouting: A review. J. Rock Mech. Geotech. Eng. 2016, 8, 753–766. [Google Scholar] [CrossRef]
- Liu, W.; Liang, J.; Xu, T. Tunnelling-induced ground deformation subjected to the behavior of tail grouting materials. Tunn. Undergr. Space Technol. 2023, 140, 105253. [Google Scholar] [CrossRef]
- Ou, Y.; Tian, G.; Chen, J.; Chen, G.; Chen, X.; Li, H.; Liu, B.; Huang, T.; Qiang, M.; Alfrendo, S.; et al. Feasibility Studies on the Utilization of Recycled Slag in Grouting Material for Tunneling Engineering. Sustainability 2022, 14, 11013. [Google Scholar] [CrossRef]
- Ren, D.J.; Shen, S.L.; Cheng, W.C.; Zhang, N.; Wang, Z.F. Geological formation and geo-hazards during subway construction in Guangzhou. Environ. Earth Sci. 2016, 75, 934. [Google Scholar] [CrossRef]
- Sousa, R.L.; Einstein, H.H. Lessons from accidents during tunnel construction. Tunn. Undergr. Space Technol. 2021, 113, 103916. [Google Scholar] [CrossRef]
- Wu, H.N.; Huang, R.Q.; Sun, W.J.; Long, S.; Xu, Y.S.; Liu, Y.B.; Du, S.J. Leaking behavior of shield tunnels under the Huangpu River of Shanghai with induced hazards. Nat. Hazards 2014, 70, 1115–1132. [Google Scholar] [CrossRef]
- Wongsaroj, J.; Soga, K.; Mair, R.J. Modelling of long-term ground response to tunnelling under St James’s Park, London. Géotechnique 2007, 57, 75–90. [Google Scholar] [CrossRef]
- Huang, Y.; Yu, Z.; Zhou, Z. Simulating Groundwater Inflow in the Underground Tunnel with a Coupled Fracture-Matrix Model. J. Hydrol. Eng. 2013, 18, 1557–1561. [Google Scholar] [CrossRef]
- Hu, Y.; Li, Y.A.; Lin, J.L.; Ruan, C.K.; Chen, S.J.; Tang, H.M.; Duan, W.H. Towards microstructure-based analysis and design for seepage water in underground engineering: Effect of image characteristics. Tunn. Undergr. Space Technol. 2019, 93, 103086. [Google Scholar] [CrossRef]
- Zhou, K.; Dou, L.; Gong, S.; Song, S.; Chai, Y.; Li, J.; Ma, X. Mechanical behavior of sandstones under water rock interactions. Geomech. Eng. 2022, 29, 627–643. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, Z.; Yang, J.; Pang, S.; Geng, J.; Li, W.; Zhang, X. Creep properties of siltstone-like materials with different unloading confining pressures under seepage. Front. Earth Sci. 2022, 10, 949916. [Google Scholar] [CrossRef]
- Peng, H.; Frenelus, W.; Zhang, J. Key factors influencing analytical solutions for predicting groundwater inflows in rock tunnels. Water Supply 2022, 22, 7982–8013. [Google Scholar] [CrossRef]
- El Tani, M.; Kamali, A.; Gholami, M.A. Analytic Assessment of the Water Table Drawdown, Seepage, and Back Pressure at Rudbar PSPP. Rock Mech. Rock Eng. 2019, 52, 2227–2243. [Google Scholar] [CrossRef]
- Gong, B.; Jiang, Y.; Okatsu, K.; Wu, X.; Teduka, J.; Aoki, K. The Seepage Control of the Tunnel Excavated in High-Pressure Water Condition Using Multiple Times Grouting Method. Processes 2018, 6, 159. [Google Scholar] [CrossRef]
- Zhang, Z.; Yin, T. A Coupled CFD–DEM Simulation of Slurry Infiltration and Filter Cake Formation during Slurry Shield Tunneling. Infrastructures 2018, 3, 15. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Z.; Jing, H.; Li, Y.; Wang, M. Study on the seepage characteristics of deep buried tunnels under variable high-pressure water heads. Bull. Eng. Geol. Environ. 2021, 80, 1477–1487. [Google Scholar] [CrossRef]
- Ding, W.; Tan, A.S.; Zhu, R.; Jiang, H.; Zhang, Q. Study on the Damage Process and Numerical Simulation of Tunnel Excavation in Water-Rich Soft Rock. Appl. Sci. 2021, 11, 8906. [Google Scholar] [CrossRef]
- Kacimov, A.R.; Obnosov, Y.V.; Šimůnek, J. Seepage to staggered tunnels and subterranean cavities: Analytical and HYDRUS modeling. Adv. Water Resour. 2022, 164, 104182. [Google Scholar] [CrossRef]
- Niu, X. Key Technologies of the Hydraulic Structures of the Three Gorges Project. Engineering 2016, 2, 340–349. [Google Scholar] [CrossRef]
- Yang, G.; Wang, X.; Wang, X.; Cao, Y. Analyses of Seepage Problems in a Subsea Tunnel Considering Effects of Grouting and Lining Structure. Mar. Georesources Geotechnol. 2016, 34, 65–70. [Google Scholar] [CrossRef]
- Wei, F.; Wang, H.; Zeng, G.; Jiang, M. Seepage flow around twin circular tunnels in anisotropic ground revealed by an analytical solution. Undergr. Space 2023, 10, 1–14. [Google Scholar] [CrossRef]
- Chen, S.-H. Hydraulic Structures; Springer: Berlin/Heidelberg, Germany, 2015; pp. 755–812. [Google Scholar] [CrossRef]
- Frenelus, W.; Peng, H. Evaluating the Time-Dependent Behavior of Deeply Buried Tunnels in Soft Rock Environments and Relevant Measures Guaranteeing Their Long-Term Stability. Appl. Sci. 2023, 13, 10542. [Google Scholar] [CrossRef]
- Peng, K.; Yi, G.; Luo, S.; Si, X. Stress Analysis and Spalling Failure Simulation on Surrounding Rock of Deep Arch Tunnel. Appl. Sci. 2023, 13, 6474. [Google Scholar] [CrossRef]
- Li, J. Key Technologies and Applications of the Design and Manufacturing of Non-Circular TBMs. Engineering 2017, 3, 905–914. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Fang, X. Iterative Formulas and Estimation Formulas for Computing Normal Depth of Horseshoe Cross-Section Tunnel. J. Irrig. Drain. Eng. 2010, 136, 786–790. [Google Scholar] [CrossRef]
- Bahmanikashkooli, A.; Zare, M.; Safarpour, B.; Safarpour, M. Application of Particle Swarm Optimization Algorithm for Computing Critical Depth of Horseshoe Cross Section Tunnel. APCBEE Procedia 2014, 9, 207–211. [Google Scholar] [CrossRef][Green Version]
- Bonini, M.; Debernardi, D.; Barla, M.; Barla, G. The mechanical behaviour of clay shales and implications on the design of tunnels. Rock Mech. Rock Eng. 2009, 42, 361–388. [Google Scholar] [CrossRef]
- Wu, K.; Shao, Z.; Qin, S.; Zhao, N.; Chu, Z. An Improved Nonlinear Creep Model for Rock Applied to Tunnel Displacement Prediction. Int. J. Appl. Mech. 2021, 13, 2150094. [Google Scholar] [CrossRef]
- Tunç, C.; Tunç, O. A note on the stability and boundedness of solutions to non-linear differential systems of second order. J. Assoc. Arab Univ. Basic Appl. Sci. 2017, 24, 169–175. [Google Scholar] [CrossRef]
- Zou, J.; Li, S. Theoretical solution for displacement and stress in strain-softening surrounding rock under hydraulic-mechanical coupling. Sci. China Technol. Sci. 2015, 58, 1401–1413. [Google Scholar] [CrossRef]
- Li, X.F.; Du, S.J.; Chen, B. Unified analytical solution for deep circular tunnel with consideration of seepage pressure, grouting and lining. J. Cent. South Univ. 2017, 24, 1483–1493. [Google Scholar] [CrossRef]
- Al-Ajmi, A.M.; Zimmerman, R.W. Stability analysis of vertical boreholes using the Mogi–Coulomb failure criterion. Int. J. Rock Mech. Min. Sci. 2006, 43, 1200–1211. [Google Scholar] [CrossRef]
- Komurlu, E.; Kesimal, A.; Hasanpour, R. In situ horizontal stress effect on plastic zone around circular underground openings excavated in elastic zones. Geomech. Eng. 2015, 8, 783–799. [Google Scholar] [CrossRef]
- Zou, Z.; Yang, J.; Wang, Z.; Liu, H. The Plastic Zone of Tunnel Surrounding Rock under Unequal Stress in Two Directions Based on the Unified Strength. Math. Probl. Eng. 2021, 2021, 8842153. [Google Scholar] [CrossRef]
- Frenelus, W.; Peng, H.; Zhang, J. Creep Behavior of Rocks and Its Application to the Long-Term Stability of Deep Rock Tunnels. Appl. Sci. 2022, 12, 8451. [Google Scholar] [CrossRef]
- Sterpi, D. An analysis of geotechnical problems involving strain softening effects. In. J. Numer. Anal. Meth. Geomech. 1999, 23, 1427–1454. [Google Scholar] [CrossRef]
- Wang, S.; Yin, S.; Wu, Z. Strain-softening analysis of a spherical cavity. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 182–202. [Google Scholar] [CrossRef]
- Wang, F.; Qian, D. Difference solution for a circular tunnel excavated in strain-softening rock mass considering decayed confinement. Tunn. Undergr. Space Technol. 2018, 82, 66–81. [Google Scholar] [CrossRef]
- Zareifard, M.R.; Shekari, M.R. Comprehensive solutions for underwater tunnels in rock masses with different GSI values considering blast-induced damage zone and seepage forces. Appl. Math. Model. 2021, 96, 236–268. [Google Scholar] [CrossRef]
- Song, F. Modelling Time-Dependent Plastic Behaviour of Geomaterials. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2021. [Google Scholar] [CrossRef]
- Manh, H.T.; Sulem, J.; Subrin, D.; Billaux, D. Anisotropic time-dependent modelling of tunnel excavation in squeezing ground. Rock Mech. Rock Eng. 2015, 48, 2301–2317. [Google Scholar] [CrossRef]
- Frenelus, W.; Peng, H.; Zhang, J. An Insight from Rock Bolts and Potential Factors Influencing Their Durability and the Long-Term Stability of Deep Rock Tunnels. Sustainability 2022, 14, 10943. [Google Scholar] [CrossRef]
- Sun, S.Q.; Li, S.C.; Li, L.P.; Shi, S.S.; Zhou, Z.Q.; Gao, C.L. Design of a Displacement Monitoring System Based on Optical Grating and Numerical Verification in Geomechanical Model Test of Water Leakage of Tunnel. Geotech. Geol. Eng. 2018, 36, 2097–2108. [Google Scholar] [CrossRef]
- Baji, H.; Li, C.Q.; Scicluna, S.; Dauth, J. Risk-cost optimised maintenance strategy for tunnel structures. Tunn. Undergr. Space Technol. 2017, 69, 72–84. [Google Scholar] [CrossRef]
- Elgamal, A.; Elfaris, N. Stability of Shield-Bored Tunnel for the Challenge of Nile Crossing. Infrastructures 2021, 6, 147. [Google Scholar] [CrossRef]
- Wu, G.; Chen, W.; Tian, H.; Jia, S.; Yang, J.; Tan, X. Numerical evaluation of a yielding tunnel lining support system used in limiting large deformation in squeezing rock. Environ. Earth Sci. 2018, 77, 439. [Google Scholar] [CrossRef]
- Gong, J.; Lambert, M.F.; Simpson, A.R.; Zecchin, A.C. Detection of Localized Deterioration Distributed along Single Pipelines by Reconstructive MOC Analysis. J. Hydraul. Eng. 2014, 140, 190–198. [Google Scholar] [CrossRef]
- Hognestad, H.O.; Kieffer, S. Pre-excavation grouting in rock tunneling—Dealing with high groundwater pressures. Geomech. Tunn. 2019, 12, 141–146. [Google Scholar] [CrossRef]
- Xu, S.; Ma, E.; Lai, J.; Yang, Y.; Liu, H.; Yang, C.; Hu, Q. Diseases failures characteristics and countermeasures of expressway tunnel of water-rich strata: A case study. Eng. Fail. Anal. 2022, 134, 106056. [Google Scholar] [CrossRef]
- Frenelus, W.; Peng, H. Towards Long-Term Monitoring of the Structural Health of Deep Rock Tunnels with Remote Sensing Techniques. Fratt. Ed. Integrità Strutt. 2023, 66, 56–87. [Google Scholar] [CrossRef]
- Tan, K.; Cheng, X.; Ju, Q.; Wu, S. Correction of Mobile TLS Intensity Data for Water Leakage Spots Detection in Metro Tunnels. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1711–1715. [Google Scholar] [CrossRef]
- Xu, X.; Shi, P.; Zhou, X.; Liu, W.; Yang, H.; Wang, T.; Yan, M.; Fan, W. A novel vision measurement system for health monitoring of tunnel structures. Mech. Adv. Mater. Struct. 2022, 29, 2208–2218. [Google Scholar] [CrossRef]
- Moser, F.; Lienhart, W.; Woschitz, H.; Schuller, H. Long-term monitoring of reinforced earth structures using distributed fiber optic sensing. J. Civ. Struct. Health Monit. 2016, 6, 321–327. [Google Scholar] [CrossRef]
- Monsberger, C.M.; Bauer, P.; Buchmayer, F.; Lienhart, W. Large-scale distributed fiber optic sensing network for short and long-term integrity monitoring of tunnel linings. J. Civ. Struct. Health Monit. 2022, 12, 1317–1327. [Google Scholar] [CrossRef]
- Kane, W.F.; Peters, D.C.; Speirer, R.A. Remote Sensing in Investigation of Engineered Underground Structures. J. Geotech. Eng. 1996, 122, 674–681. [Google Scholar] [CrossRef]
- Loganathan, K.; Najafi, M.; Kaushal, V.; Covilakam, M. Development of a Decision Support Tool for Inspection and Monitoring of Large-Diameter Steel and Prestressed Concrete Cylinder Water Pipes. J. Pipeline Syst. Eng. Pract. 2022, 13, 04021067. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhou, J.; Zhang, B.; Wang, H.; Huang, M. Statistical analysis of major tunnel construction accidents in China from 2010 to 2020. Tunn. Undergr. Space Technol. 2022, 124, 104460. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhao, J.; Li, S.; Jiang, Z.; Huang, F. A Unified Solution for Surrounding Rock of Roadway Considering Seepage, Dilatancy, Strain-Softening and Intermediate Principal Stress. Sustainability 2022, 14, 8099. [Google Scholar] [CrossRef]
- Luo, X.; Yu, C.; Wang, Y. Water control of water-rich deeply buried tunnel: An analytical model of a combined scheme. Geotech. Geol. Eng. 2023, 41, 3909–3922. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, Z.; Ren, L.; Zhang, R.; Zheng, L.; Zhang, L.; Zhang, Z.; Xie, J.; Liu, X. Analysis of Rock Mass Parameters and Plastic Zone of a Tunnel in Southwest Mountainous Area. KSCE J. Civ. Eng. 2023, 27, 5448–5459. [Google Scholar] [CrossRef]

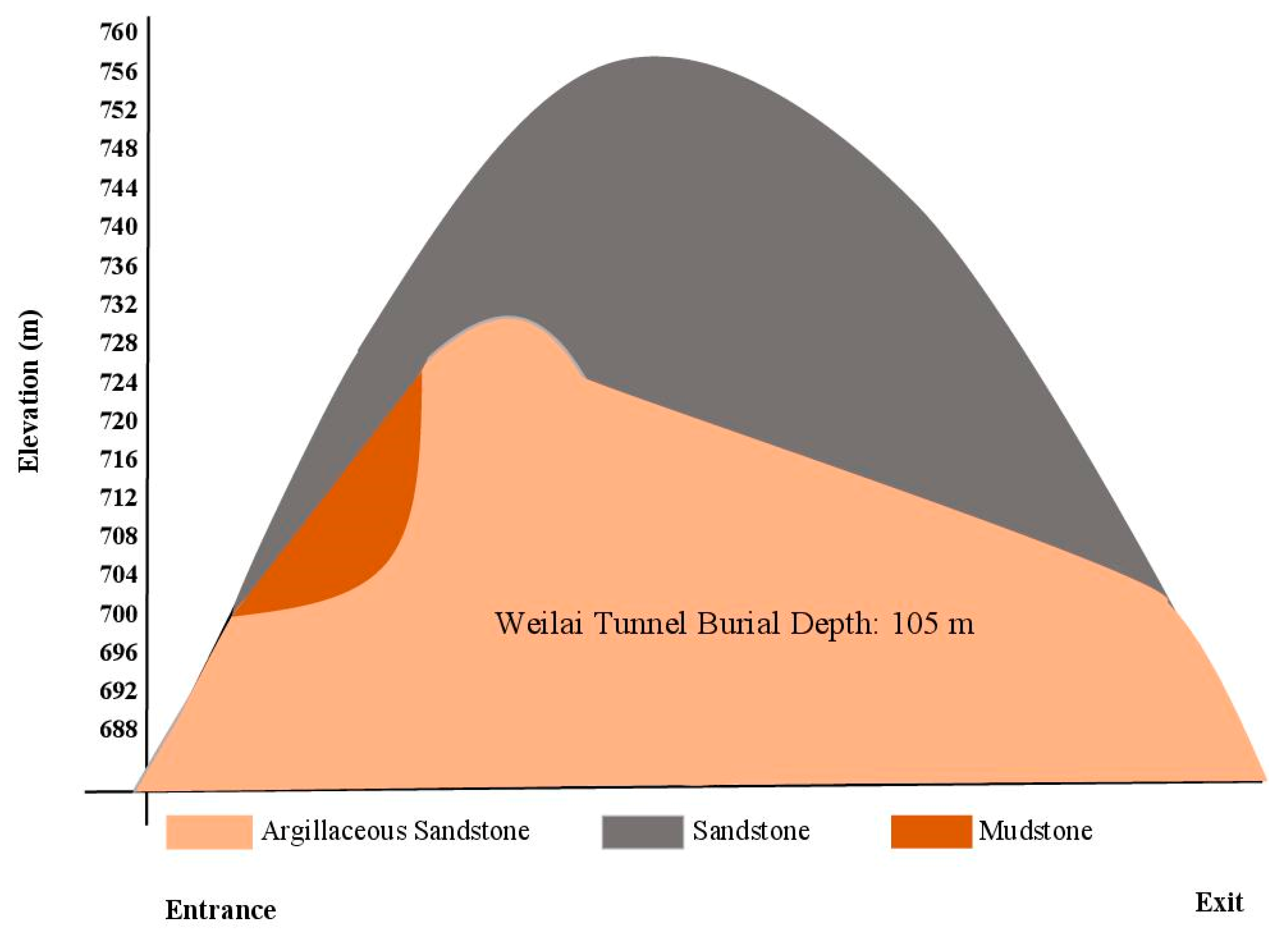
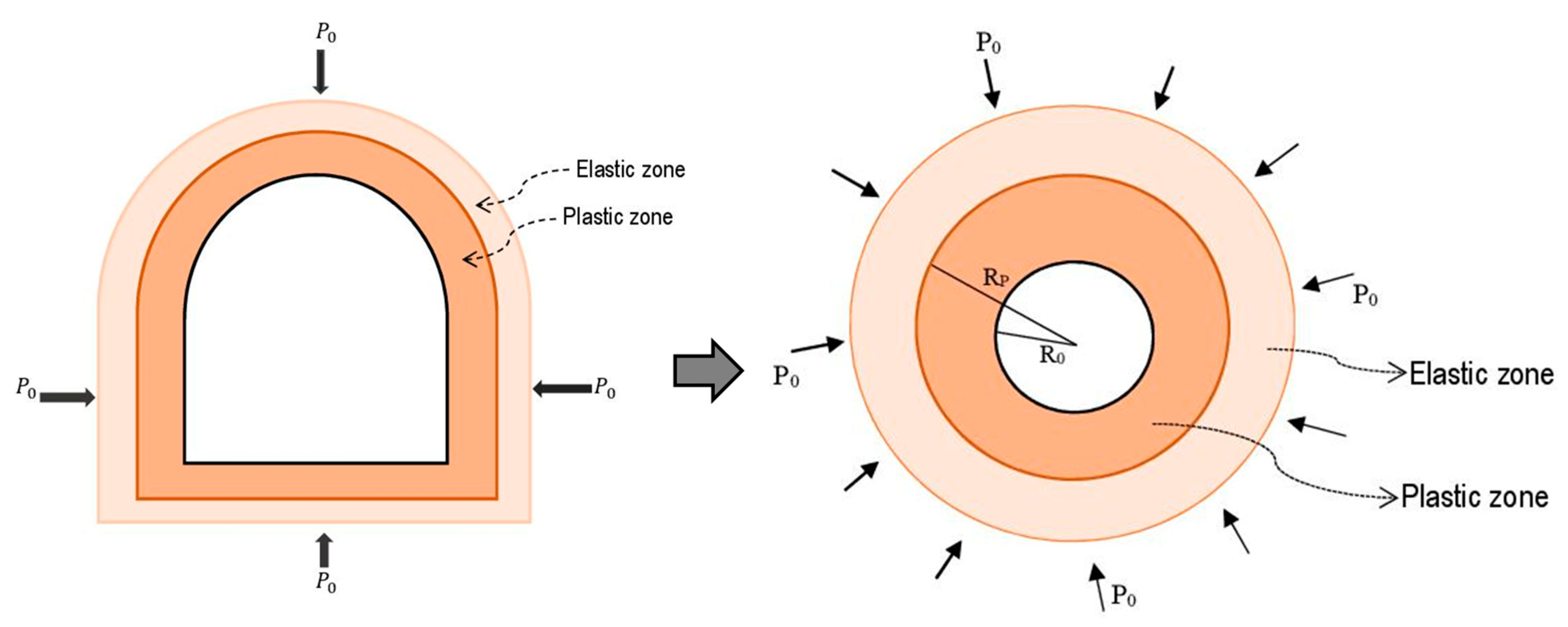
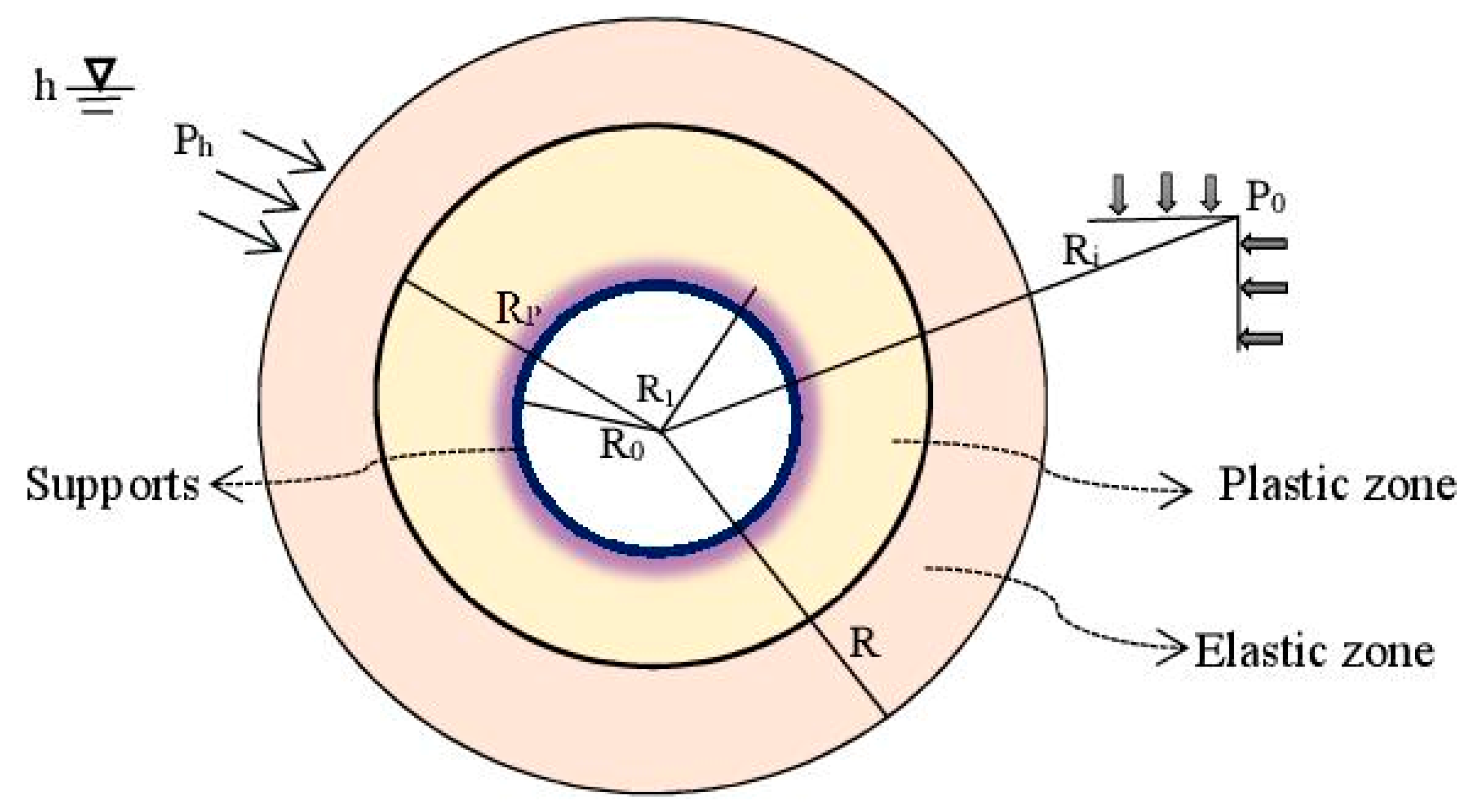
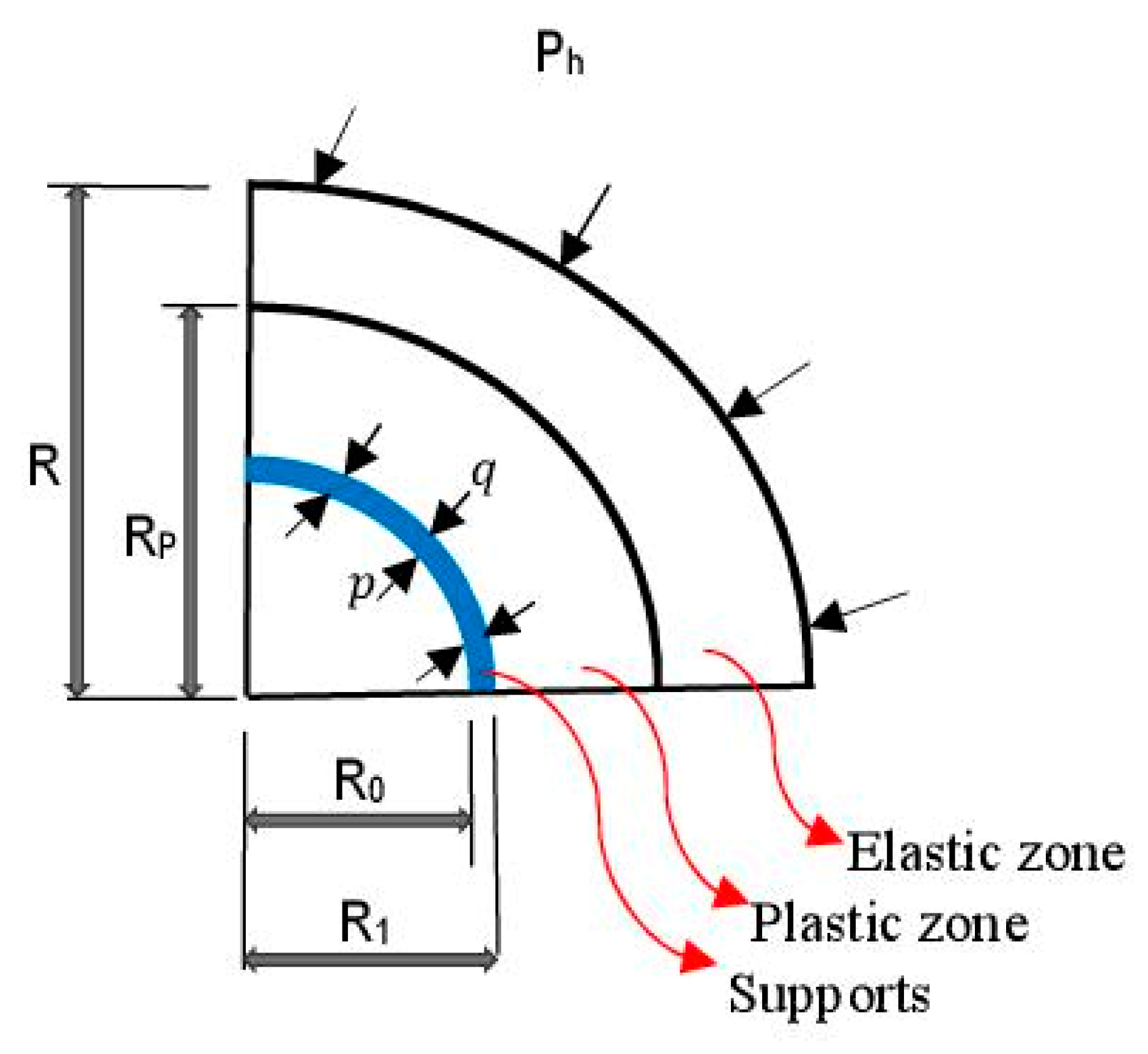






| Rock Type | Uniaxial Compressive Strength (MPa) | Elastic Modulus (GPa) | Poisson’s Ratio | Cohesion (MPa) | Internal Friction Angle (°) | Density (g/cm3) |
|---|---|---|---|---|---|---|
| Argillaceous sandstone | 10 | 2.2 | 0.23 | 5.06 | 30 | 0.24 |
| Rock Type | Uniaxial Compressive Strength (MPa) | Elastic Modulus (GPa) | Poisson’s Ratio | Cohesion (MPa) | Internal Friction Angle (°) | Density (g/cm3) |
|---|---|---|---|---|---|---|
| Argillaceous sandstone | 6.6 | 0.62 | 0.39 | 0.93 | 7.5 | 0.38 |
| Relevant Parameter Characteristics | Unit | Value |
|---|---|---|
| Initial hydrostatic stress | MPa | 10 |
| Hydraulic pressure | MPa | 5 |
| Residual internal friction angle | degree | 5.3 |
| Residual cohesion | kPa | 0.61 |
| Plastic softening parameter | - | 0.005 |
| Tunnel excavation radius | m | 6 |
| Tunnel net radius | m | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frenelus, W.; Peng, H.; Zhang, J. Seepage Actions and Their Consequences on the Support Scheme of Deep-Buried Tunnels Constructed in Soft Rock Strata. Infrastructures 2024, 9, 13. https://doi.org/10.3390/infrastructures9010013
Frenelus W, Peng H, Zhang J. Seepage Actions and Their Consequences on the Support Scheme of Deep-Buried Tunnels Constructed in Soft Rock Strata. Infrastructures. 2024; 9(1):13. https://doi.org/10.3390/infrastructures9010013
Chicago/Turabian StyleFrenelus, Wadslin, Hui Peng, and Jingyu Zhang. 2024. "Seepage Actions and Their Consequences on the Support Scheme of Deep-Buried Tunnels Constructed in Soft Rock Strata" Infrastructures 9, no. 1: 13. https://doi.org/10.3390/infrastructures9010013
APA StyleFrenelus, W., Peng, H., & Zhang, J. (2024). Seepage Actions and Their Consequences on the Support Scheme of Deep-Buried Tunnels Constructed in Soft Rock Strata. Infrastructures, 9(1), 13. https://doi.org/10.3390/infrastructures9010013






