Analyzing Wind Effects on Long-Span Bridges: A Viable Numerical Modelling Methodology Using OpenFOAM for Industrial Applications
Abstract
:1. Introduction
2. Modelling Assumptions
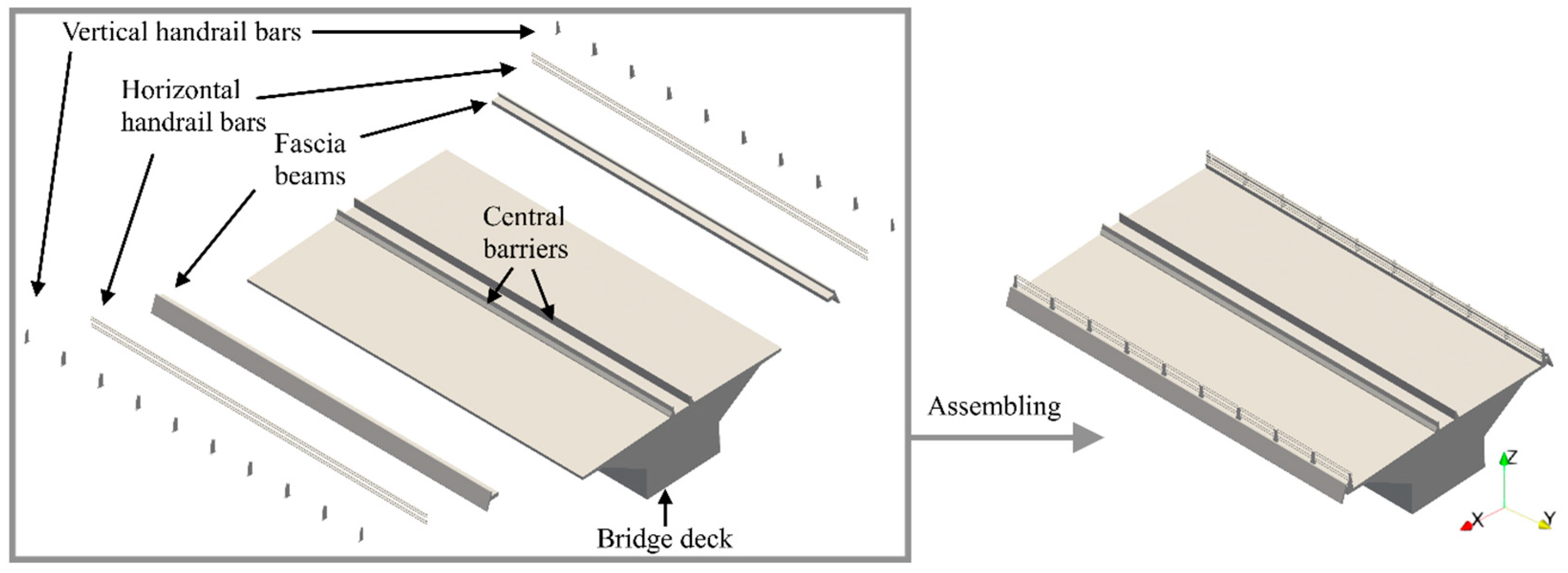
3. Geometry Development
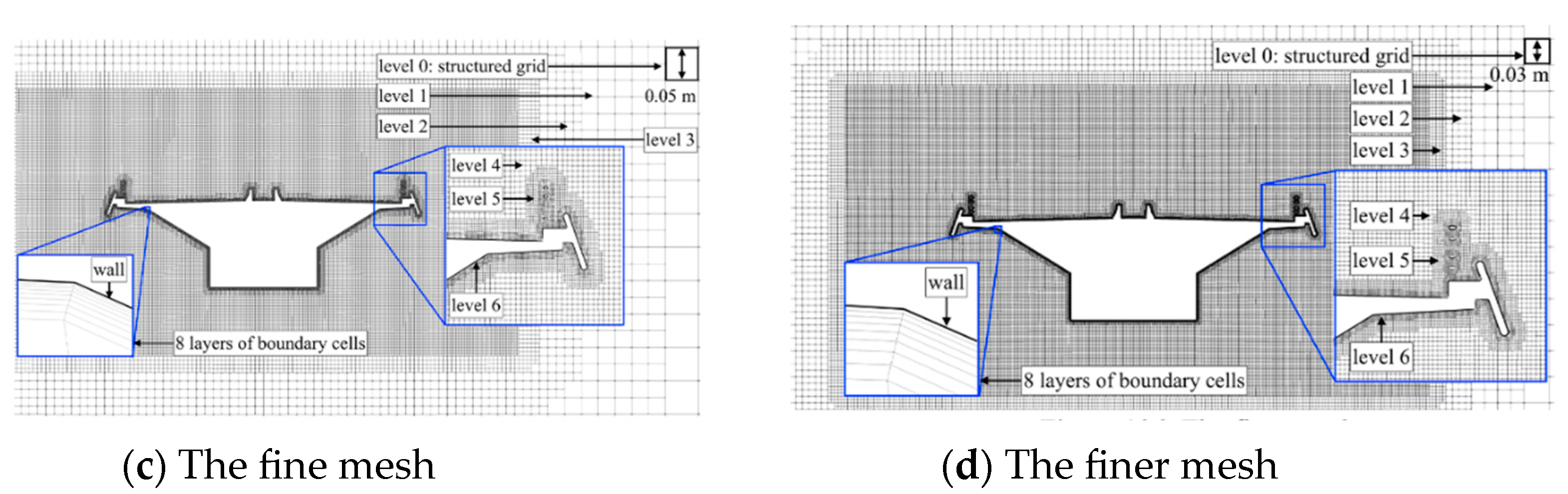
4. Creating the Mesh
5. Boundary Conditions
6. Discretization of the Equations—fvSchemes
7. Solving Algorithms—fvSolution
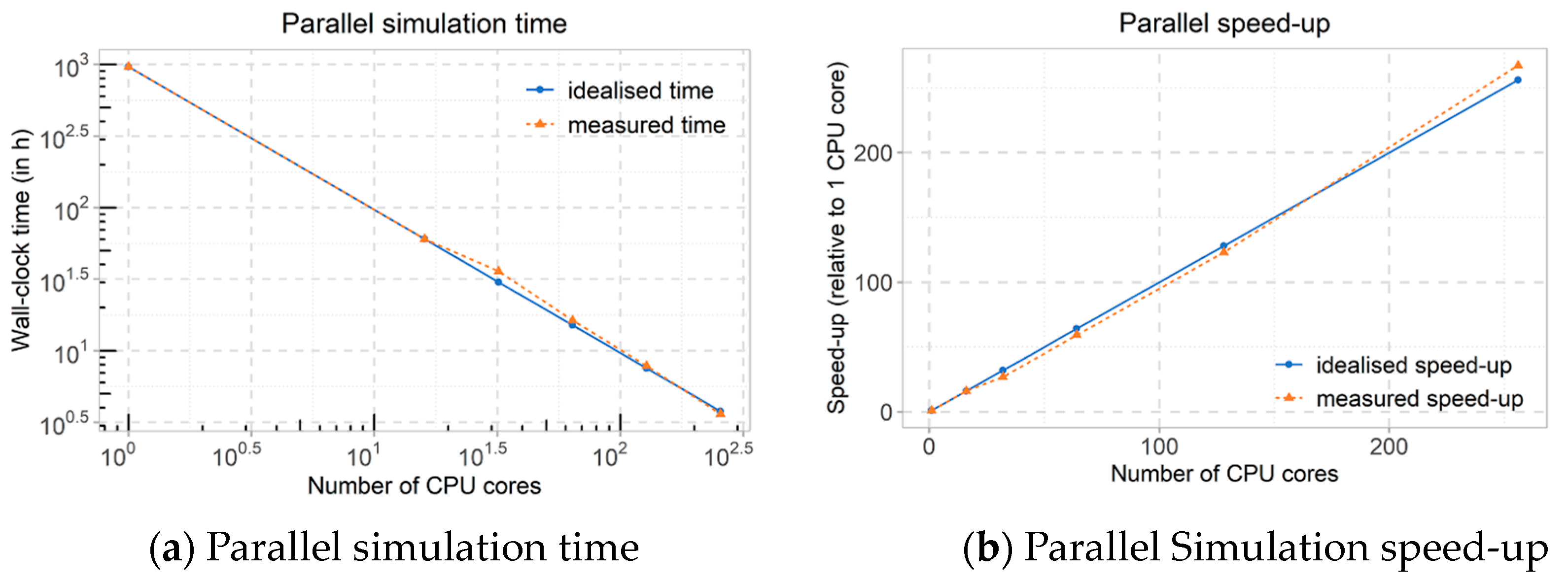
8. Parallel Configurations—decomposeParDict
9. Mesh Sensitivity Study
10. Post Processing
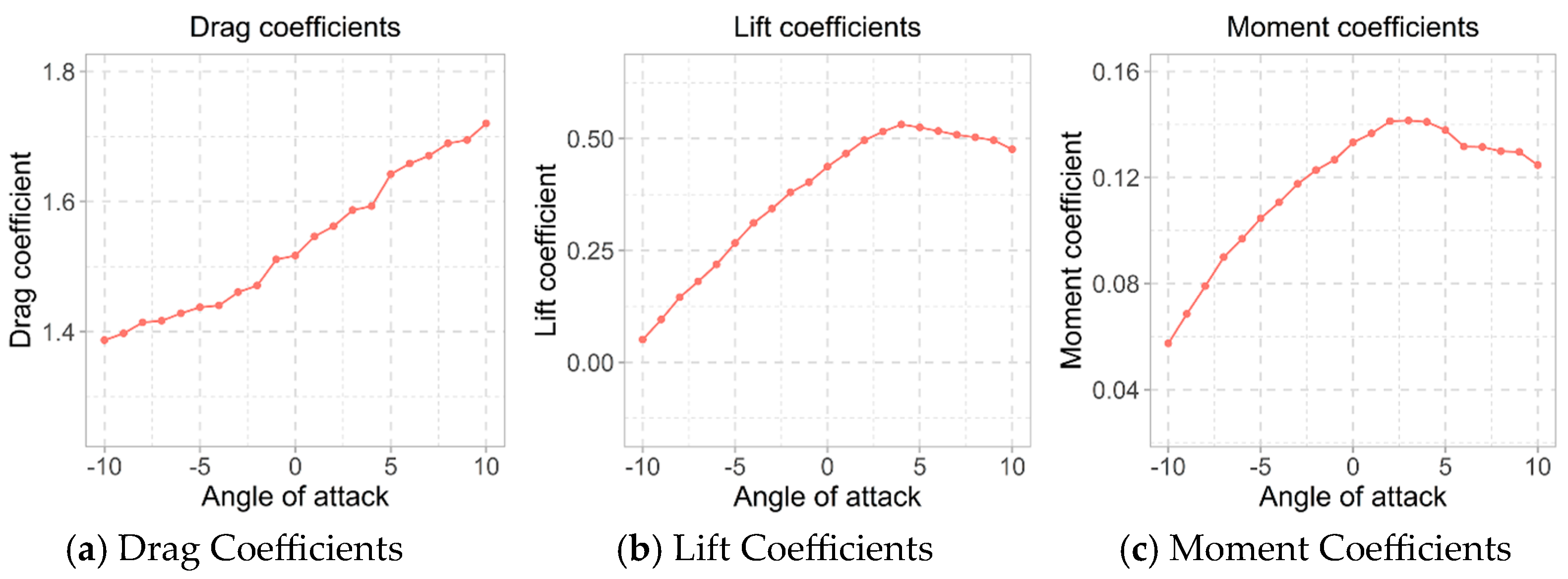
10.1. Aerodynamic Force Coefficients
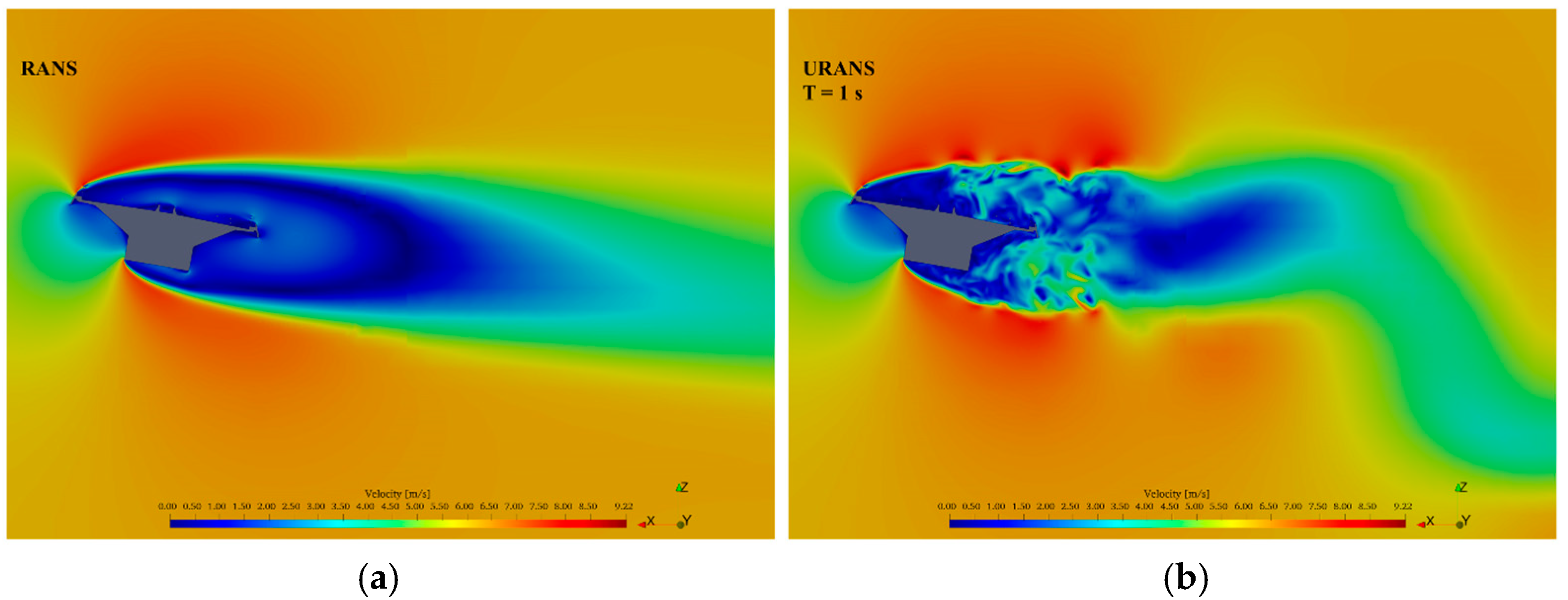
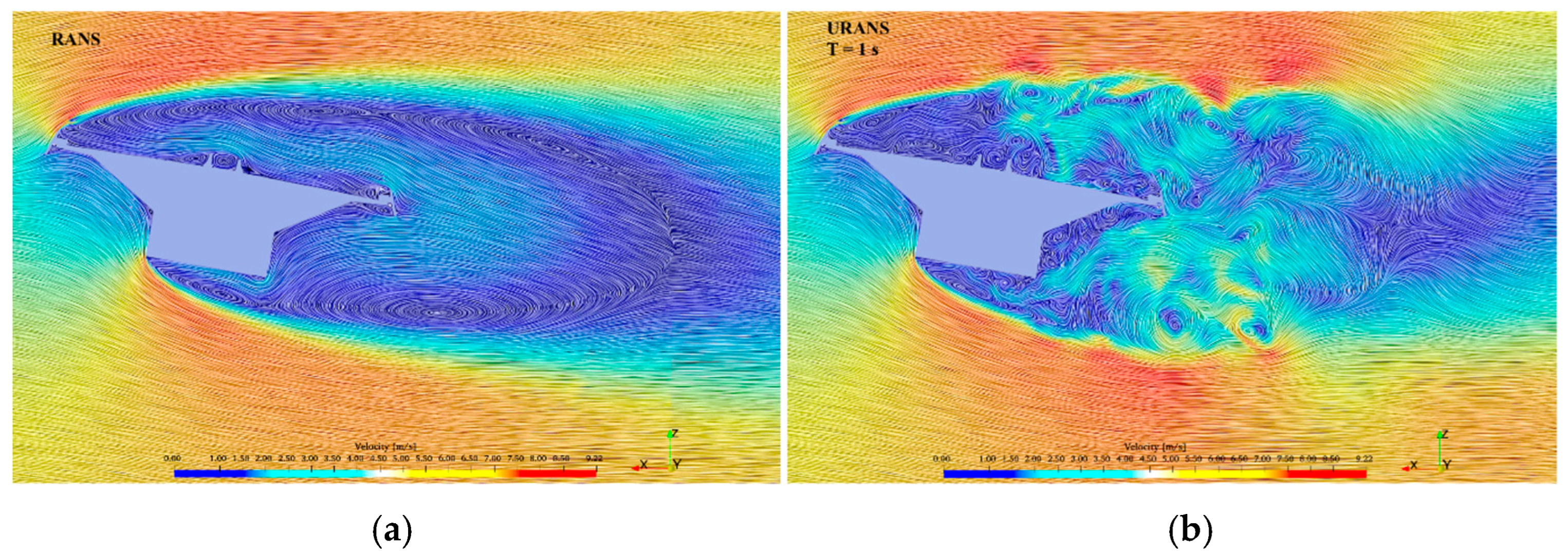
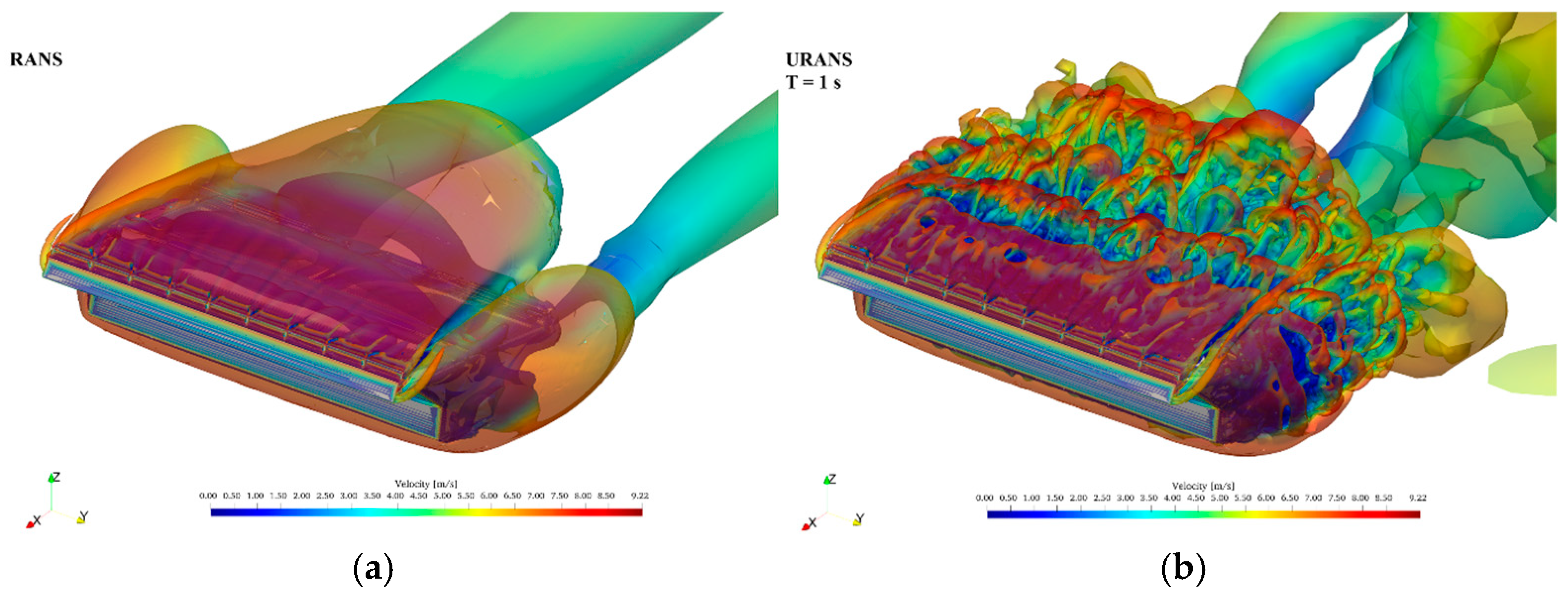
10.2. Visualization
11. Validation of the Methodology
12. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Simiu, E.; Yeo, D. Wind Effects on Structures: Modern Structural Design for Wind; Wiley Online Library: Hoboken, NJ, USA, 2019. [Google Scholar]
- Xu, Y.; Sun, D.; Ko, J.; Lin, J. Fully coupled buffeting analysis of Tsing Ma suspension bridge. J. Wind. Eng. Ind. Aerodyn. 2000, 85, 97–117. [Google Scholar] [CrossRef]
- Scanlan, R.H.; Tomko, J.J. Airfoil and bridge deck flutter derivatives. J. Eng. Mech. Div. 1971, 97, 1717–1737. [Google Scholar] [CrossRef]
- Wu, T.; Kareem, A. An overview of vortex-induced vibration (VIV) of bridge decks. Front. Archit. Civ. Eng. 2012, 6, 335–347. [Google Scholar] [CrossRef]
- Ge, Y.; Lin, Z.; Cao, F.; Pang, J.; Xiang, H. Investigation and prevention of deck galloping oscillation with computational and experimental techniques. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 2087–2098. [Google Scholar] [CrossRef]
- Ni, Y.; Wang, X.; Chen, Z.; Ko, J. Field observations of rain-wind-induced cable vibration in cable-stayed Dongting Lake Bridge. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 303–328. [Google Scholar] [CrossRef]
- Gao, D.; Chen, W.; Eloy, C.; Li, H. Multi-mode responses, rivulet dynamics, flow structures and mechanism of rain-wind induced vibrations of a flexible cable. J. Fluids Struct. 2018, 82, 154–172. [Google Scholar] [CrossRef]
- Sukamta; Guntorojati, I. Fariduzzaman Flutter analysis of cable stayed bridge. Procedia Eng. 2017, 171, 1173–1177. [Google Scholar] [CrossRef]
- Mei, H.; Wang, Q.; Liao, H.; Fu, H. Improvement of flutter performance of a streamlined box girder by using an upper central stabilizer. J. Bridg. Eng. 2020, 25, 04020053. [Google Scholar] [CrossRef]
- Niu, H.; Zhu, J.; Chen, Z.; Zhang, W. Dynamic performance of a slender truss bridge subjected to extreme wind and traffic loads considering 18 flutter derivatives. J. Aerosp. Eng. 2019, 32, 04019082. [Google Scholar] [CrossRef]
- Li, S.; Li, M.; Larose, G.L. Aerodynamic admittance of streamlined bridge decks. J. Fluids Struct. 2018, 78, 1–23. [Google Scholar] [CrossRef]
- Anas, S.; Alam, M.; Umair, M. Experimental and Numerical Investigations on Performance of Reinforced Concrete Slabs under Explosive-Induced Air-Blast Loading: A State-of-the-Art Review. In Structures; Elsevier: Amsterdam, The Netherlands, 2021; Volume 31, pp. 428–461. [Google Scholar] [CrossRef]
- Helgedagsrud, T.A.; Bazilevs, Y.; Mathisen, K.M.; Øiseth, O.A. Computational and experimental investigation of free vibration and flutter of bridge decks. Comput. Mech. 2019, 63, 121–136. [Google Scholar] [CrossRef]
- Jing, H.; He, X.; Wang, Z. Numerical modeling of the wind load of a two-dimensional cable model in rain–wind-induced vibration. J. Fluids Struct. 2018, 82, 121–133. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, Z. Free vibration numerical simulation technique for extracting flutter derivatives of bridge decks. J. Wind. Eng. Ind. Aerodyn. 2017, 170, 226–237. [Google Scholar] [CrossRef]
- Zhang, T.; Sun, Y.; Li, M.; Yang, X. Experimental and numerical studies on the vortex-induced vibration of two-box edge girder for cable-stayed bridges. J. Wind. Eng. Ind. Aerodyn. 2020, 206, 104336. [Google Scholar] [CrossRef]
- Selvam, R.P. Computational Fluid Dynamics for Wind Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Kuroda, S. Numerical simulation of flow around a box girder of a long span suspension bridge. J. Wind. Eng. Ind. Aerodyn. 1997, 67–68, 239–252. [Google Scholar] [CrossRef]
- Murakami, S.; Mochida, A. 3-D numerical simulation of airflow around a cubic model by means of the k-ϵ model. J. Wind Eng. Ind. Aerodyn. 1988, 31, 283–303. [Google Scholar] [CrossRef]
- Selvam, R.P.; Tarini, M.J.; Larsen, A. Computer modelling of flow around bridges using LES and FEM. J. Wind. Eng. Ind. Aerodyn. 1998, 77–78, 643–651. [Google Scholar] [CrossRef]
- Zhang, Y.; Cardiff, P.; Cahill, F.; Keenahan, J. Assessing the Capability of Computational Fluid Dynamics Models in Rep-licating Wind Tunnel Test Results for the Rose Fitzgerald Kennedy Bridge. CivilEng 2021, 2, 1065–1090. [Google Scholar] [CrossRef]
- Zhu, L.; McCrum, D.; Keenahan, J. Capability analysis of computational fluid dynamics models in wind shield study on Queensferry Crossing, Scotland. In Proceedings of the Institution of Civil Engineers-Bridge Engineering; Thomas Telford Ltd.: London, UK, 2022; pp. 1–13. [Google Scholar] [CrossRef]
- Zhu, L.; McCrum, D.; Sweeney, C.; Keenahan, J. Full-scale computational fluid dynamics study on wind condition of the long-span Queensferry Crossing Bridge. J. Civ. Struct. Health Monit. 2023, 13, 615–632. [Google Scholar] [CrossRef]
- Tang, H.; Li, Y.; Shum, K.; Xu, X.; Tao, Q. Non-uniform wind characteristics in mountainous areas and effects on flutter performance of a long-span suspension bridge. J. Wind. Eng. Ind. Aerodyn. 2020, 201, 104177. [Google Scholar] [CrossRef]
- Bruno, L.; Coste, N.; Fransos, D. Simulated flow around a rectangular 5:1 cylinder: Spanwise iscretization effects and emerging flow features. J. Wind. Eng. Ind. Aerodyn. 2012, 104–106, 203–215. [Google Scholar] [CrossRef]
- Bruno, L.; Fransos, D.; Coste, N.; Bosco, A. 3D flow around a rectangular cylinder: A computational study. J. Wind. Eng. Ind. Aerodyn. 2010, 98, 263–276. [Google Scholar] [CrossRef]
- Bruno, L.; Salvetti, M.V.; Ricciardelli, F. Benchmark on the Aerodynamics of a Rectangular 5:1 Cylinder: An overview after the first four years of activity. J. Wind. Eng. Ind. Aerodyn. 2014, 126, 87–106. [Google Scholar] [CrossRef]
- Mannini, C.; Marra, A.M.; Pigolotti, L.; Bartoli, G. The effects of free-stream turbulence and angle of attack on the aerodynamics of a cylinder with rectangular 5:1 cross section. J. Wind. Eng. Ind. Aerodyn. 2017, 161, 42–58. [Google Scholar] [CrossRef]
- Patruno, L.; Ricci, M.; de Miranda, S.; Ubertini, F. Numerical simulation of a 5:1 rectangular cylinder at non-null angles of attack. J. Wind. Eng. Ind. Aerodyn. 2016, 151, 146–157. [Google Scholar] [CrossRef]
- Mannini, C.; Šoda, A.; Schewe, G. Unsteady RANS modelling of flow past a rectangular cylinder: Investigation of Reynolds number effects. Comput. Fluids 2010, 39, 1609–1624. [Google Scholar] [CrossRef]
- Fransos, D.; Bruno, L. Edge degree-of-sharpness and free-stream turbulence scale effects on the aerodynamics of a bridge deck. J. Wind. Eng. Ind. Aerodyn. 2010, 98, 661–671. [Google Scholar] [CrossRef]
- Nieto, F.; Montoya, M.C.; Hernández, S.; Kusano, I.; Casteleiro, A.; Álvarez, A.J.; Jurado, J.; Fontán, A. Aerodynamic and aeroelastic responses of short gap twin-box decks: Box geometry and gap distance dependent surrogate based design. J. Wind. Eng. Ind. Aerodyn. 2020, 201, 104147. [Google Scholar] [CrossRef]
- Cid Montoya, M.; Hernández, S.; Nieto, F. Shape optimization of streamlined decks of cable-stayed bridges considering aeroelastic and structural constraints. J. Wind Eng. Ind. Aerodyn. 2018, 177, 429–455. [Google Scholar] [CrossRef]
- Montoya, M.C.; Nieto, F.; Hernández, S.; Kusano, I.; Álvarez, A.; Jurado, J. CFD-based aeroelastic characterization of streamlined bridge deck cross-sections subject to shape modifications using surrogate models. J. Wind. Eng. Ind. Aerodyn. 2018, 177, 405–428. [Google Scholar] [CrossRef]
- Álvarez, A.; Nieto, F.; Nguyen, D.; Owen, J.; Hernández, S. 3D LES simulations of a static and vertically free-to-oscillate 4:1 rectangular cylinder: Effects of the grid resolution. J. Wind. Eng. Ind. Aerodyn. 2019, 192, 31–44. [Google Scholar] [CrossRef]
- Mannini, C.; Sbragi, G.; Schewe, G. Analysis of self-excited forces for a box-girder bridge deck through unsteady RANS simulations. J. Fluids Struct. 2016, 63, 57–76. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Hargreaves, D.M.; Owen, J.S. Vortex-induced vibration of a 5:1 rectangular cylinder: A comparison of wind tunnel sectional model tests and computational simulations. J. Wind. Eng. Ind. Aerodyn. 2018, 175, 1–16. [Google Scholar] [CrossRef]
- Nieto, F.; Owen, J.; Hargreaves, D.; Hernández, S. Bridge deck flutter derivatives: Efficient numerical evaluation exploiting their interdependence. J. Wind. Eng. Ind. Aerodyn. 2015, 136, 138–150. [Google Scholar] [CrossRef]
- EN Eurocode 1—Actions on Structures—Part 1–4: General Actions—Wind Actions—Irish National Annex; CEN: Paris, France, 2010.
- CEN/TC 250. In Eurocode 1—Actions on Structures—Part 1–4: General Actions—Wind Actions. Third Draft: October 2019 Version; CEN: Paris, France, 2019.
- Keenahan, J. (Ed.) Reamonn MacReamoinn. CFD Development in Bridge Engineering, 2022. [Google Scholar]
- Zhang, Y.; Cardiff, P.; Keenahan, J. Wind-Induced Phenomena in Long-Span Cable-Supported Bridges: A Comparative Review of Wind Tunnel Tests and Computational Fluid Dynamics Modelling. Appl. Sci. 2021, 11, 1642. [Google Scholar] [CrossRef]
- Hu, C.; Zhao, L.; Ge, Y. Mechanism of suppression of vortex-induced vibrations of a streamlined closed-box girder using additional small-scale components. J. Wind. Eng. Ind. Aerodyn. 2019, 189, 314–331. [Google Scholar] [CrossRef]
- Li, H.; Chen, W.-L.; Xu, F.; Li, F.-C.; Ou, J.-P. A numerical and experimental hybrid approach for the investigation of aer-odynamic forces on stay cables suffering from rain-wind induced vibration. J. Fluids Struct. 2010, 26, 1195–1215. [Google Scholar] [CrossRef]
- Szabo, G.; Gyorgyi, J.; Kristof, G. Advanced flutter simulation of flexible bridge decks. Coupled Syst. Mech. 2012, 1, 133–154. [Google Scholar] [CrossRef]
- Zhang, Y.; Sweeney, C.; Cardiff, P.; Cahill, F.; Keenahan, J. Quantifying the Impact of Bridge Geometry and Surrounding Terrain: Wind Effects on Bridges. In Proceedings of the Institution of Civil Engineer: Bridge Engineering; Thomas Telford Ltd.: London, UK, 2023; pp. 1–18. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Lee, H.; Moon, J.; Chun, N.; Lee, H.E. Effect of beam slope on the static aerodynamic response of edge-girder bridge-deck. Wind Struct. 2017, 25, 157–176. [Google Scholar]
- Liu, L.; Zhang, L.; Wu, B.; Chen, B.; Aecom, P. Effect of Accessory Attachment on Static Coefficients in a Steel Box Girder for Long—Span Suspension Bridges. J. Eng. Sci. Technol. Rev. 2017, 10, 68–83. [Google Scholar] [CrossRef]
- Kusano, I.; Jakobsen, J.B.; Snæbjörnsson, J.T. CFD simulations of a suspension bridge deck for different deck shapes with railings and vortex mitigating devices. IOP Conf. Ser. Mater. Sci. Eng. 2019, 700, 012003. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Anina, H.; Rüdiger, H.; Stanko, B. Numerical simulations and experimental validations of force coefficients and flutter derivatives of a bridge deck. J. Wind Eng. Ind. Aerodyn. 2015, 144, 172–182. [Google Scholar]
- Zhang, H.; Xin, D.; Ou, J. Wake control using spanwise-varying vortex generators on bridge decks: A computational study. J. Wind. Eng. Ind. Aerodyn. 2019, 184, 185–197. [Google Scholar] [CrossRef]
- Chen, X.; Qiu, F.; Tang, H.; Li, Y.; Xu, X. Effects of secondary elements on vortex-induced vibration of a streamlined box girder. KSCE J. Civ. Eng. 2021, 25, 173–184. [Google Scholar] [CrossRef]
- Könözsy, L. The k-ω Shear-Stress Transport (SST) Turbulence Model. In A New Hypothesis on the Anisotropic Reynolds Stress Tensor for Turbulent Flows: Volume I: Theoretical Background and Development of an Anisotropic Hybrid k-omega Shear-Stress Transport/Stochastic Turbulence Model; Springer: Berlin/Heidelberg, Germany, 2019; pp. 57–66. [Google Scholar]
- Lien, F.-S.; Kalitzin, G. Computations of transonic flow with the v2–f turbulence model. Int. J. Heat Fluid Flow 2001, 22, 53–61. [Google Scholar] [CrossRef]
- Langtry, R.B.; Menter, F.R. Correlation-based transition modeling for unstructured parallelized computational fluid dy-namics codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar]
- Cécora, R.-D.; Eisfeld, B.; Probst, A.; Crippa, S.; Radespiel, R. Differential Reynolds stress modeling for aeronautics. AIAA J. 2015, 53, 739–755. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Spalart, P.R. Comments on the Feasibility of LES for Wings and on the Hybrid RANS/LES Approach. In Proceedings of the First AFOSR International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997; pp. 137–147. [Google Scholar]
- Solidworks; Dessault Systemes: Vélizy-Villacoublay, France, 2019.
- FreeCAD. 2016.
- An Introduction to ANSYS Fluent 2021; SDC Publications: Mission, KS, USA, 2021.
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Franke, J.; Hellsten, A.; Schlünzen, H.; Carissimo, B. Best Practice Guideline for the CFD Simulation of Flows in the Urban Environment. COST Action 732: Quality Assurance and Improvement of Microscale Meteorological Models (2007). In Proceedings of the 11th Conference on Harmonisation within Atmospheric Dispersion Modelling for Regulatory Purposes, Hamburg, Germany, May 2007. [Google Scholar]
- Greenshields, C.J. OpenFOAM User Guide; OpenFOAM Foundation Ltd.: London, UK, 2015; Volume 3, p. 47. [Google Scholar]
- Bradshaw, P.; Huang, G.P. The law of the wall in turbulent flow. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1995, 451, 165–188. [Google Scholar]
- Liu, F. A thorough Description of How Wall Functions are Implemented in OpenFOAM. Proceedings of CFD with OpenSource Software, 2016; Volume 34. [Google Scholar]
- Pinier, B.; Mémin, E.; Laizet, S.; Lewandowski, R. A model under location uncertainty to predict the mean velocity in wall bounded flows. arXiv 2018, arXiv:1812.02947. [Google Scholar]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. Ph.D. Thesis, Philosophy of the University, London, UK, June 1996. [Google Scholar]
- Barrett, R.; Berry, M.; Chan, T.F.; Demmel, J.; Donato, J.; Dongarra, J.; Eijkhout, V.; Pozo, R.; Romine, C.; Van der Vorst, H. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods. In Society for Industrial and Applied Mathematics; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar] [CrossRef]
- Van der Vorst, H.A. Bi-CGSTAB: A fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 1992, 13, 631–644. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. A Calculation Procedure for Heat, Mass and Momentum Transfer in Three-Dimensional Parabolic Flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Elsevier: Amsterdam, The Netherlands, 1983; pp. 54–73. [Google Scholar]
- Van Doormaal, J.P.; Raithby, G.D. Enhancements of the SIMPLE method for predicting incompressible fluid flows. Numer. Heat Transf. 1984, 7, 147–163. [Google Scholar]
- Issa, R. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Chevalier, C.; Pellegrini, F. PT-Scotch: A tool for efficient parallel graph ordering. Parallel Comput. 2008, 34, 318–331. [Google Scholar] [CrossRef]
- Venkatesh, T.; Sarasamma, V.; Rajalakshmy, S.; Sahu, K.C.; Govindarajan, R. Super-linear speed-up of a parallel multigrid Navier–Stokes solver on Flosolver. Curr. Sci. 2005, 88, 589–593. [Google Scholar]
- Cardiff, P.; Karač, A.; Ivanković, A. A large strain finite volume method for orthotropic bodies with general material ori-entations. Comput. Methods Appl. Mech. Eng. 2014, 268, 318–335. [Google Scholar]
- Ayachit, U. The ParaView Guide: A Parallel Visualization Application; Kitware, Inc.: Clifton Park, NY, USA, 2015. [Google Scholar]

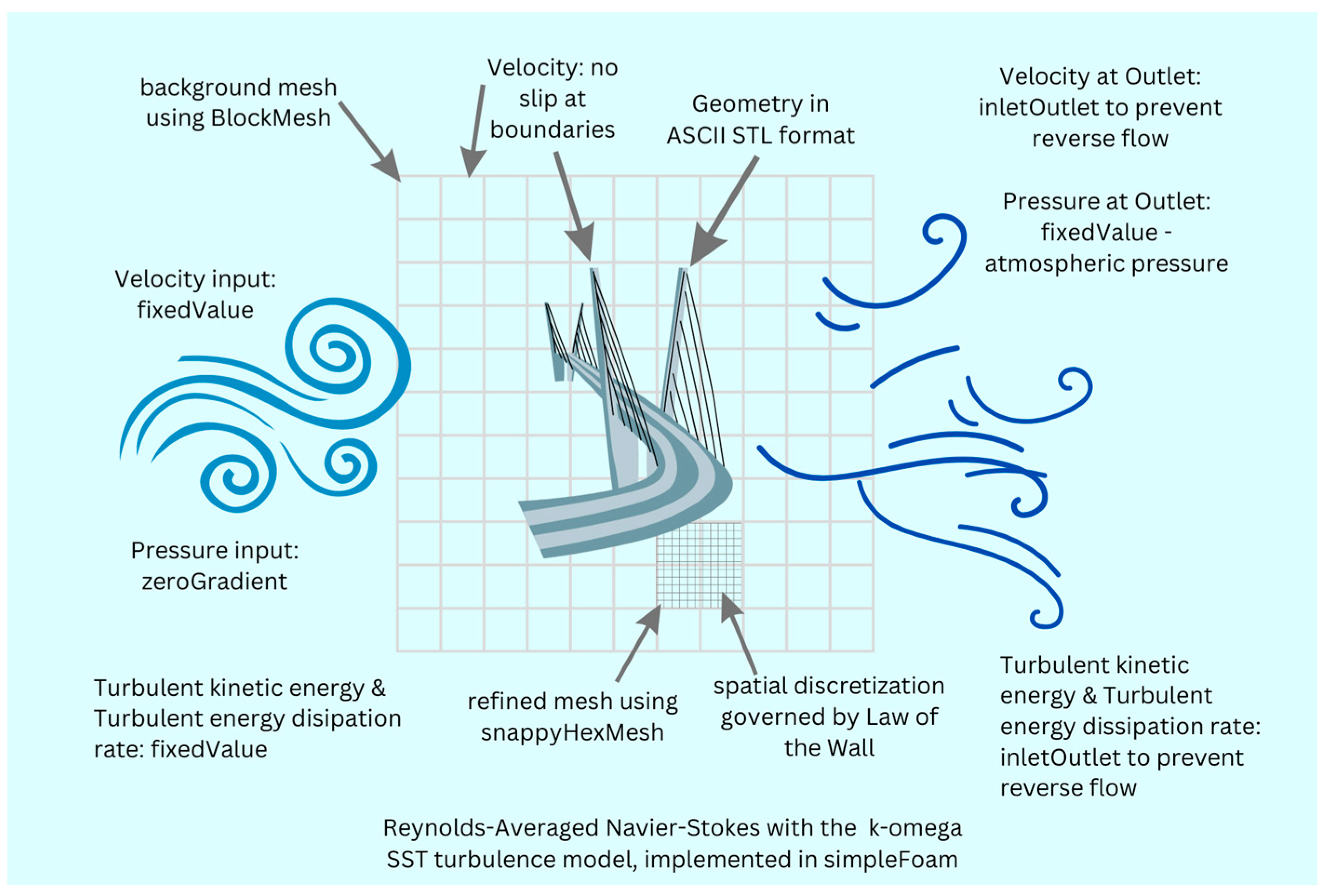











| Patch Name | Parameter | Type of Condition in OpenFOAM | Value | Unit |
|---|---|---|---|---|
| Inlet | U | fixedValue | P1 | m/s |
| p | zeroGradient | - | m2/s | |
| k | fixedValue | P2 | m2/s | |
| ω | fixedValue | P3 | s−1 | |
| νt | calculated | - | m2/s | |
| Outlet | U | inletOutlet | - | m/s |
| p | fixedValue | 0 | m2/s2 | |
| k | inletOutlet | - | m2/s2 | |
| ω | inletOutlet | - | s−1 | |
| νt | calculated | - | m2/s | |
| Side walls | U | noSlip | 0 | m/s |
| p | zeroGradient | - | m2/s2 | |
| k | kqRWallFunction | - | m2/s2 | |
| ω | omegaWallFunction | - | s−1 | |
| νt | nutkWallFunction | - | m2/s | |
| Bridge | U | noSlip | 0 | m/s |
| p | zeroGradient | - | m2/s2 | |
| k | fixedValue | 1 × 10− | m2/s2 | |
| ω | omegaWallFunction | - | s−1 | |
| νt | nutLowReWallFunction | - | m2/s |
| Number of CPU Cores | Wall-Clock Time (in h) | Speed-Up | Cells Per CPU Core |
|---|---|---|---|
| 1 | 965.28 (estimated) | - | 33,189,094 |
| 16 | 60.33 | 16 | 1,937,500 |
| 32 | 35.88 | 26.903 | 968,750 |
| 64 | 16.31 | 59.172 | 484,375 |
| 128 | 7.84 | 123.023 | 242,188 |
| 256 | 3.61 | 267.175 | 121,094 |
| Configurations | Coarse Mesh | Medium Mesh | Fine Mesh | Finer Mesh |
|---|---|---|---|---|
| −10° | 1,962,324 | 14,607,636 | 33,242,170 | 85,922,392 |
| 0° | 1,973,227 | 14,575,020 | 33,189,094 | 86,008,513 |
| 10° | 1,972,355 | 14,608,860 | 33,227,289 | 86,441,092 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; MacReamoinn, R.; Cardiff, P.; Keenahan, J. Analyzing Wind Effects on Long-Span Bridges: A Viable Numerical Modelling Methodology Using OpenFOAM for Industrial Applications. Infrastructures 2023, 8, 130. https://doi.org/10.3390/infrastructures8090130
Zhang Y, MacReamoinn R, Cardiff P, Keenahan J. Analyzing Wind Effects on Long-Span Bridges: A Viable Numerical Modelling Methodology Using OpenFOAM for Industrial Applications. Infrastructures. 2023; 8(9):130. https://doi.org/10.3390/infrastructures8090130
Chicago/Turabian StyleZhang, Yuxiang, Reamonn MacReamoinn, Philip Cardiff, and Jennifer Keenahan. 2023. "Analyzing Wind Effects on Long-Span Bridges: A Viable Numerical Modelling Methodology Using OpenFOAM for Industrial Applications" Infrastructures 8, no. 9: 130. https://doi.org/10.3390/infrastructures8090130
APA StyleZhang, Y., MacReamoinn, R., Cardiff, P., & Keenahan, J. (2023). Analyzing Wind Effects on Long-Span Bridges: A Viable Numerical Modelling Methodology Using OpenFOAM for Industrial Applications. Infrastructures, 8(9), 130. https://doi.org/10.3390/infrastructures8090130







