Evaluation of the Szapáry Long-Span Box Girder Bridge Using Static and Dynamic Load Tests
Abstract
1. Introduction
2. Testing the Szapáry Bridge on the Tisza River in Hungary
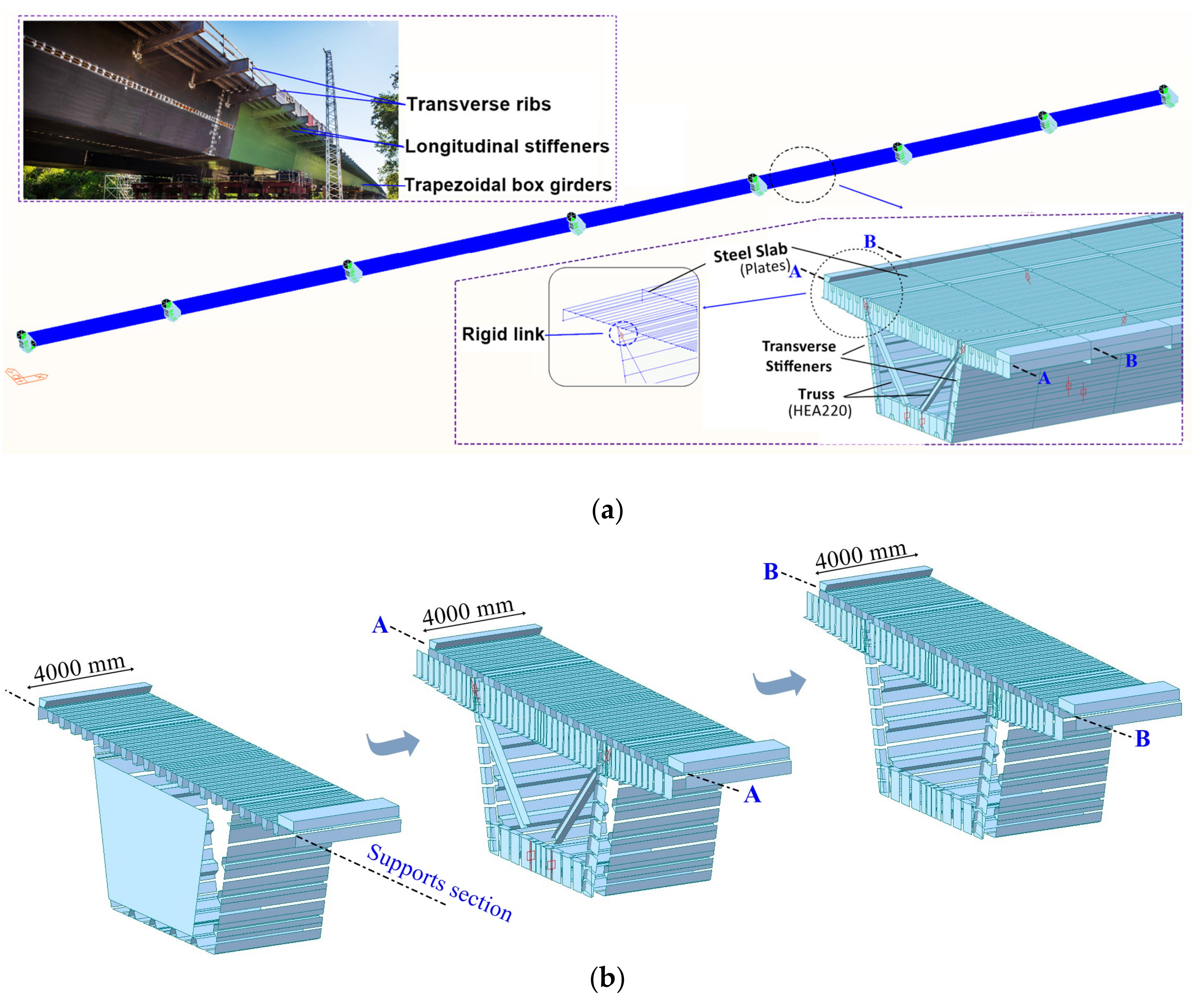
2.1. Description of the Szapáry Bridge
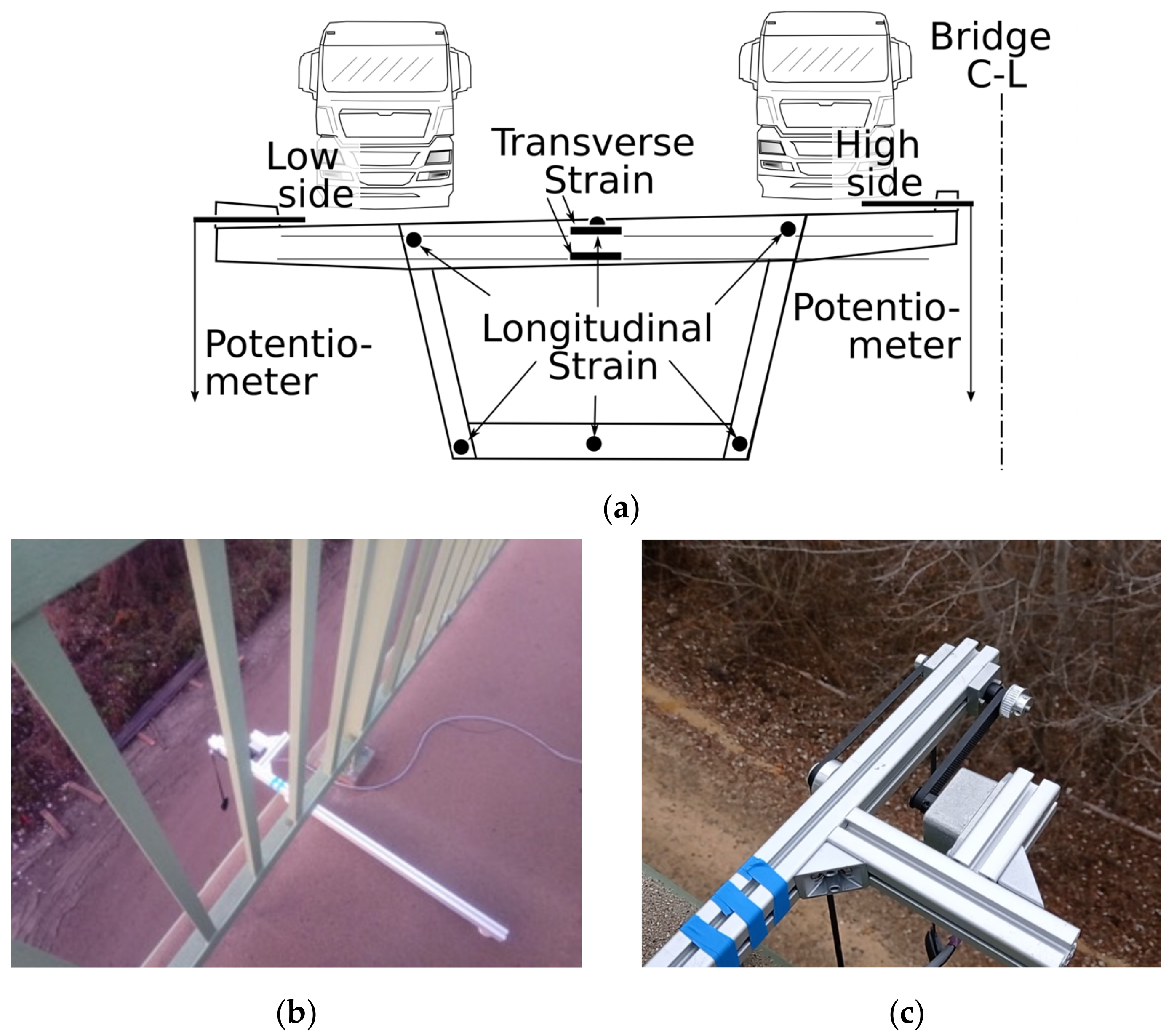
2.2. Experimental Program
Measurement of Deflections and Stresses
2.3. Tests Interpretation through Numerical Modeling
3. Field Tests and FEM Model: Results and Discussions
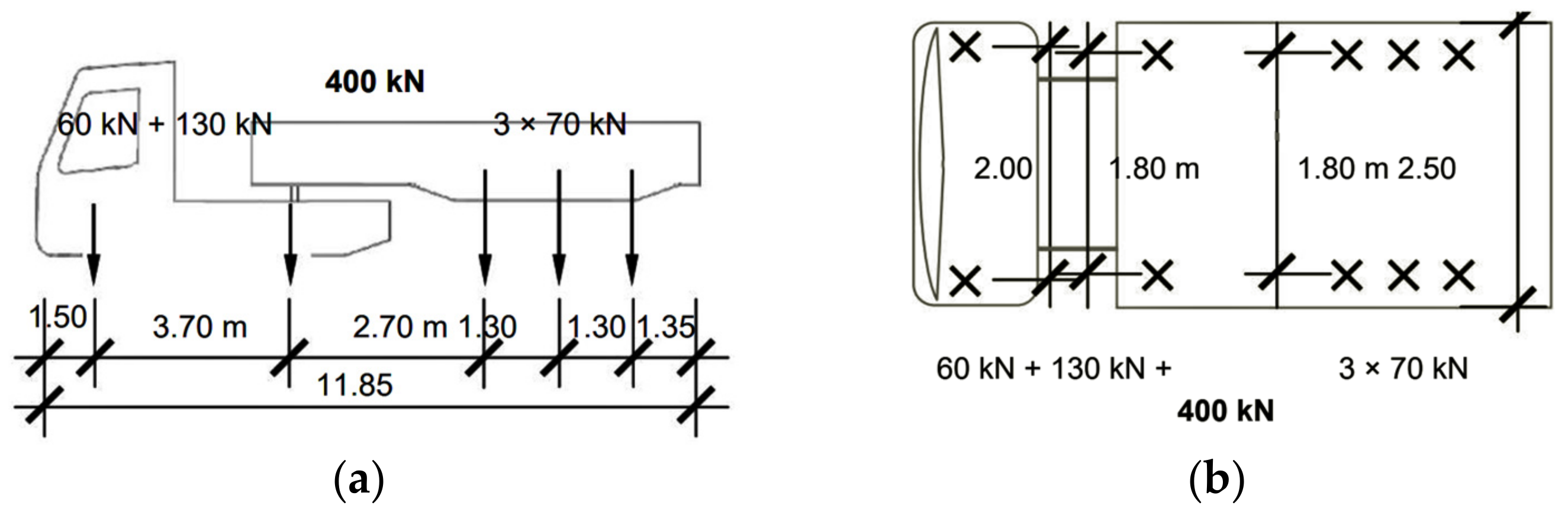
3.1. Bridge Deflection under Static Loadings
- (a)
- Load Configuration 01 (LC1)
- (b)
- Load Configuration 02 (LC2)
- (c)
- Load Configuration 03 (LC3)
- (d)
- Load Configuration 04 (LC4)
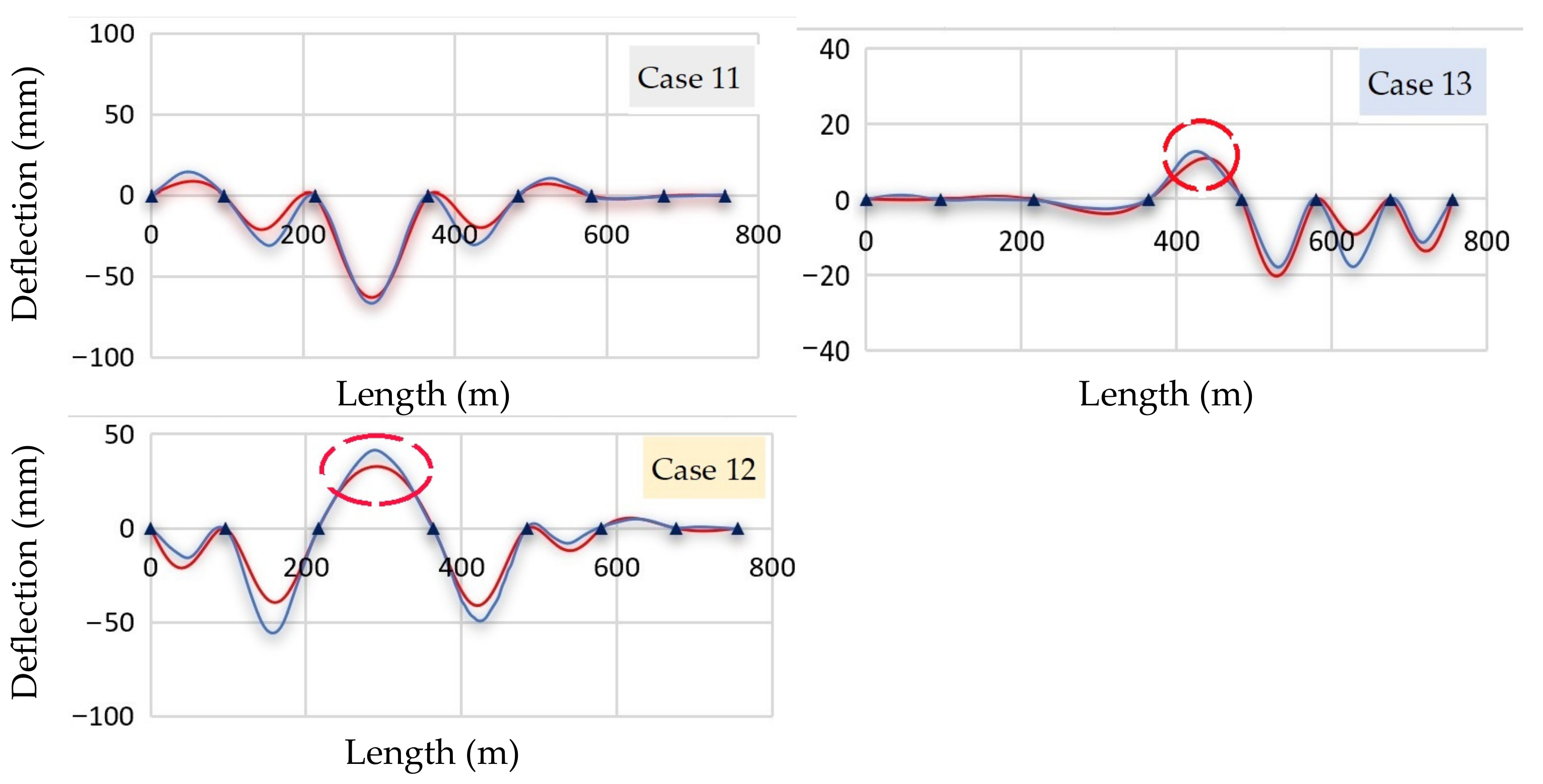
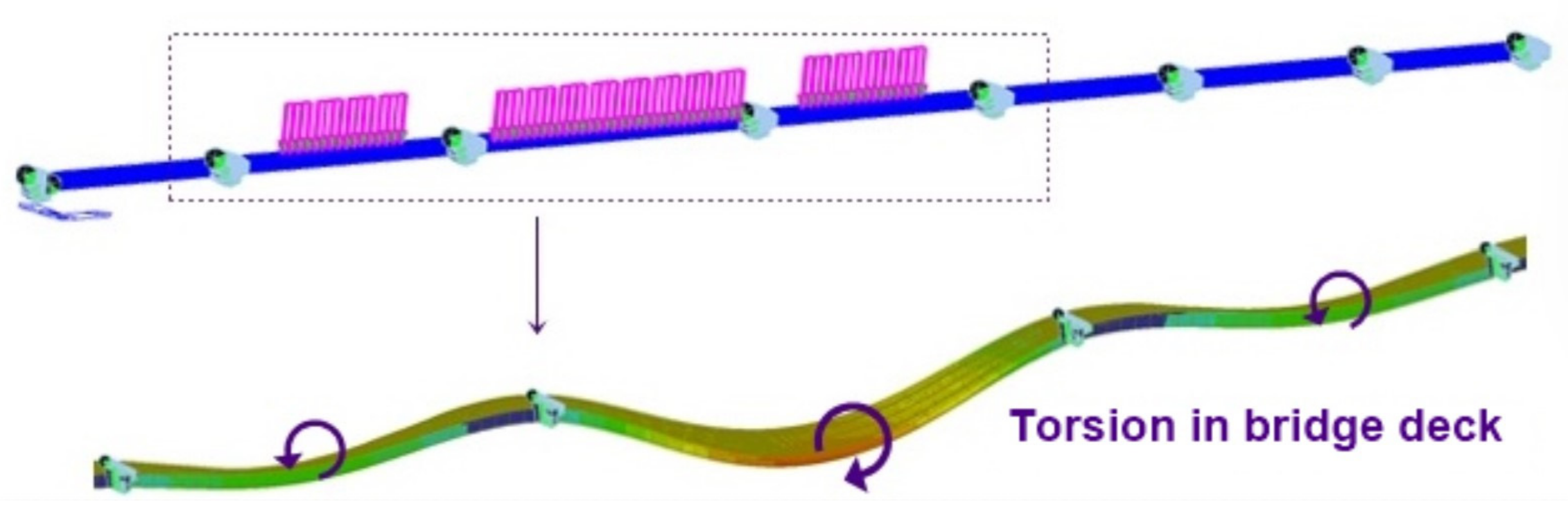
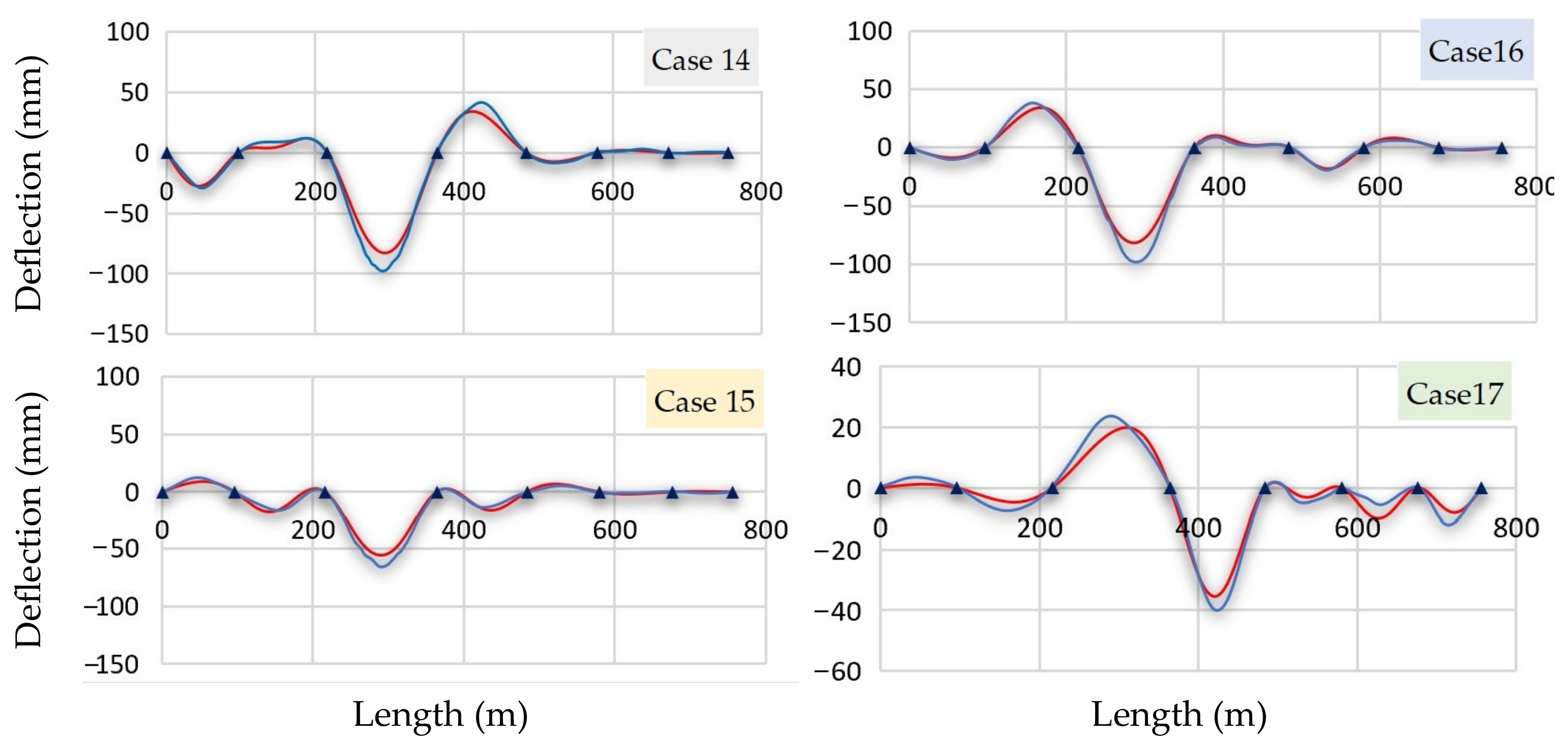
3.1.1. Discussion of Static Deflection Results
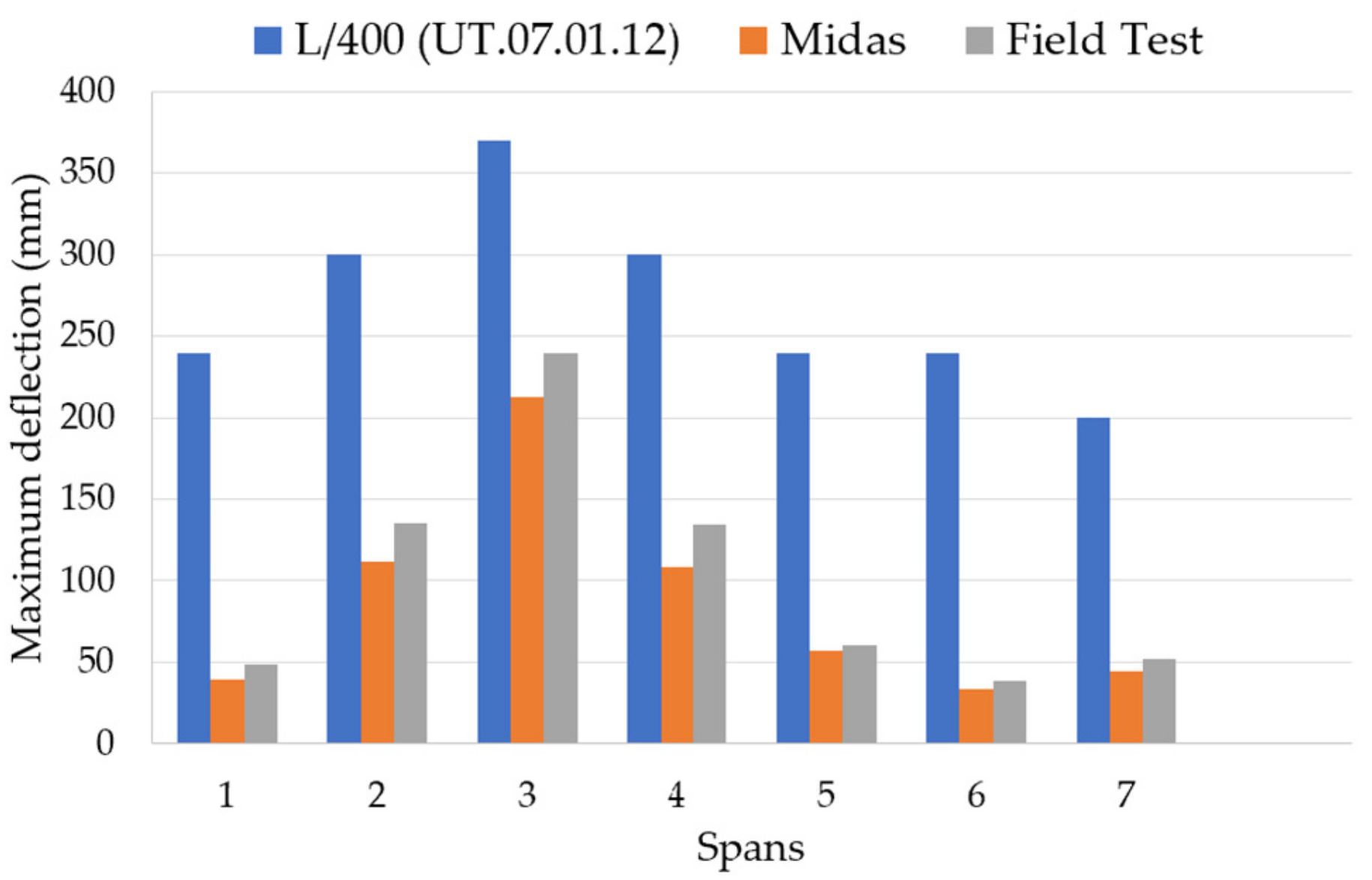
3.1.2. Deflection Limit Check
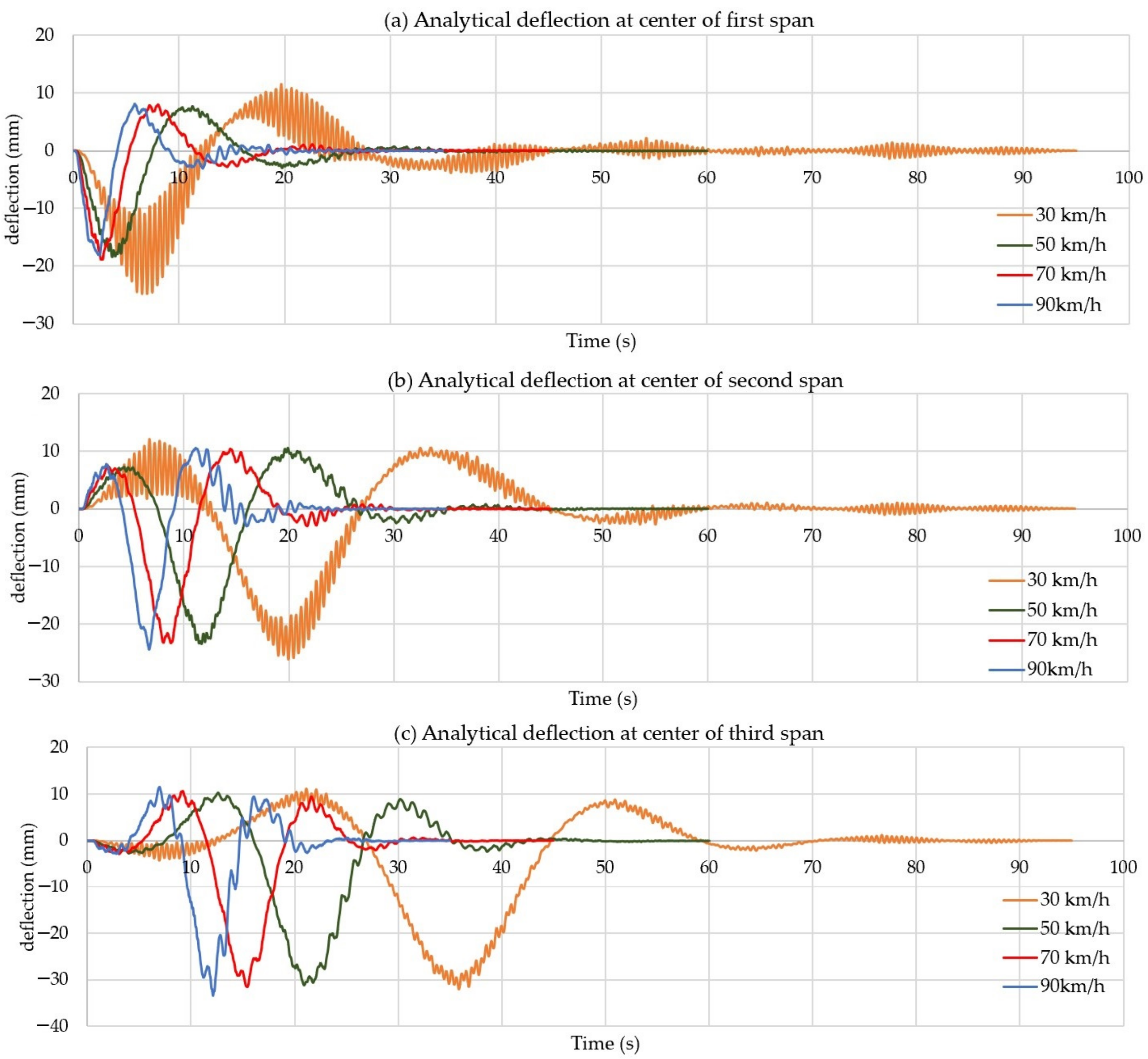
3.2. Bridge Deflection under Dynamic Loadings
4. Stresses in the Steel-Box Deck
5. Conclusions
- The finite-element model sufficiently represented the bridge field behavior and accurately estimated the deck deflection. This model can serve as a baseline for the as-built conditions of the structure and a starting point for the long-term monitoring of the Szapáry bridge.
- On the basis of the deflection comparison, the method proposed in this paper can be used for reliability and safety assessment of the bridge’s state under different loads. The information is more direct when compared to working exclusively with components and structural database. When combined with inspection and maintenance, it will provide valuable information on the bridge’s condition over time.
- The structural load-carrying capacity fulfilled the requirements of the original design. It confirmed an appropriate response for serviceability since the experimental deflections align well with the computed values according to the design provisions.
- However, critical load arrangements could damage the long-term bridge serviceability. Thus, designers should consider the many possible load combinations when evaluating deflections.
- For the box girder bridge design, multiple truck loading arrangements must account for any possible torsional action and damage that may occur.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hidayat, I.; Suangga, M.; Maulana, M.R. The effect of load position to the accuracy of deflection measured with LVDT sensor in I-girder bridge. IOP Conf. Ser. Earth Environ. Sci. 2018, 109, 012024. [Google Scholar] [CrossRef]
- Minsili, L.S.; Tchemou, G.; Louis, M.A.O.; Josette, M.L.A. Parametric Analysis of Vertical Deflections of Bridges under Moving. Sch. Bull. 2017, 3, 685–694. [Google Scholar]
- Birhane, F.N.; Kim, S.I.; Jang, S.Y. Long-term deflection of prestressed concrete bridge considering nonuniform shrinkage and crack propagation by equivalent load approach. Appl. Sci. 2020, 10, 7754. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, H.; Han, Q. Sensitivity Analysis of Factors Affecting down Deflection of Long-span Continuous Rigid Frame Bridge. IOP Conf. Ser. 2021, 781, 022048. [Google Scholar] [CrossRef]
- Robertson, I.N. Prediction of vertical deflections for a long-span prestressed concrete bridge structure. Eng. Struct. 2005, 27, 1820–1827. [Google Scholar] [CrossRef]
- Brownjohn, J.M.W.; Magalhaes, F.; Caetano, E.; Cunha, A. Ambient vibration re-testing and operational modal analysis of the Humber Bridge. Eng. Struct. 2010, 32, 2003–2018. [Google Scholar] [CrossRef]
- Bardakis, V.G.; Fardis, M.N. A displacement-based seismic design procedure for concrete bridges having deck integral with the piers. Bull. Earthq. Eng. 2011, 9, 537–560. [Google Scholar] [CrossRef]
- Ájpli, B.; Borzsák, P. e-UT 07.01.12—Structural Calculation. Design Code of Highway Bridges 2; Hungarian roads association: Budapest, Hungary, 2011. (In Hungarian) [Google Scholar]
- Dong, C.; Bas, S.; Debees, M.; Alver, N.; Catbas, F.N. Bridge Load Testing for Identifying Live Load Distribution, Load Rating, Serviceability and Dynamic Response. Front. Built Environ. 2020, 6, 1–14. [Google Scholar] [CrossRef]
- Lantsoght, E.O. Load Testing of Bridges; Proof Load Testing and the Future of Load Testing; CRC Press: London, UK, 2019; Volume 13. [Google Scholar] [CrossRef]
- Schacht, G.; Krontal, M.; Marx, S.; Bolle, G.; Wismar, H. Loading Tests of Existing Concrete Structures-Historical Development and Present Practise. In Proceedings of the Fib Symposium, Prague, Czech Republic, 8–10 June 2011. [Google Scholar]
- Jenkins, C.H.; Kjerengtroen, L.; Oestensen, H. Sensitivity of Parameter Changes in Structural Damage Detection. Shock. Vib. 1997, 4, 807239. [Google Scholar] [CrossRef]
- Dolati, S.S.K.; Caluk, N.; Armin, B.M.; Dolati, S.S.K. Non-Destructive Testing Applications for Steel Bridges. Appl. Sci. 2021, 11, 9757. [Google Scholar] [CrossRef]
- Zhu, Y.F.; Ren, W.X.; Wang, Y.F. Structural health monitoring on Yangluo Yangtze River Bridge: Implementation and demonstration. Adv. Struct. Eng. 2022, 25, 1431–1448. [Google Scholar] [CrossRef]
- Fang, I.-K.; Chen, C.-R.; Chang, I.-S. Field Static Load Test on Kao-Ping-Hsi Cable-Stayed Bridge. J. Bridg. Eng. 2004, 9, 531–540. [Google Scholar] [CrossRef]
- Ren, W.-X.; Lin, Y.-Q.; Peng, X.-L. Field Load Tests and Numerical Analysis of Qingzhou Cable-Stayed Bridge. J. Bridg. Eng. 2007, 12, 261–270. [Google Scholar] [CrossRef]
- Hassan, M.; Burdet, O.; Favre, R. Analysis and Evaluation of Bridge Behavior Under Static Load Testing Leading to Better Design and Judgment Criteria. In Proceedings of the Fourth Bridge Engineering Conference, Transportation Research Board (TRB), San Francisco, CA, USA, 28–30 August 1995. [Google Scholar]
- Galati, N.; Casadei, P.; Nanni, A. In-Situ Load Testing of Bridge a6101 Lexington, MO; Center for infrastructure engineering studies: Washington, DC, USA, 2005. [Google Scholar]
- Wang, X.; Wang, L.; Wang, H.; Ning, Y.; Huang, K.; Wang, W. Performance evaluation of a long-span cable-stayed bridge using non-destructive field loading tests. Appl. Sci. 2022, 12, 2367. [Google Scholar] [CrossRef]
- Zheng, X.; Du, H.; Zhang, R.; Ma, Q.; Gao, H. Static load test of RC T-beam bridge flexural strengthening with externally bonded steel plates. IOP Conf. Ser. Earth Environ. Sci. 2021, 791, 012018. [Google Scholar] [CrossRef]
- Cao, W.J.; Koh, C.G.; Smith, I.F.C. Enhancing static-load-test identification of bridges using dynamic data. Eng. Struct. 2019, 186, 410–420. [Google Scholar] [CrossRef]
- Bayraktar, A.; Türker, T.; Tadla, J.; Kurşun, A.; Erdiş, A. Static and dynamic field load testing of the long span Nissibi cable-stayed bridge. Soil Dyn. Earthq. Eng. 2017, 94, 136–157. [Google Scholar] [CrossRef]
- Sun, Z.; Siringoringo, D.M.; Fujino, Y. Load-carrying capacity evaluation of girder bridge using moving vehicle. Eng. Struct. 2021, 229, 111645. [Google Scholar] [CrossRef]
- Cantero, D.; Gonzáez, A.; Obrien, E.J. Comparison of bridge dynamic amplifications due to articulated 5-axle trucks and large cranes. Balt. J. Road Bridg. Eng. 2011, 6, 39–47. [Google Scholar] [CrossRef]
- Lak, M.A.; Degrande, G.; Lombaert, G. The effect of road unevenness on the dynamic vehicle response and ground-borne vibrations due to road traffic. Soil Dyn. Earthq. Eng. 2011, 31, 1357–1377. [Google Scholar] [CrossRef]
- Cantero, D.; Hester, D.; Brownjohn, J. Evolution of bridge frequencies and modes of vibration during truck passage. Eng. Struct. 2017, 152, 452–464. [Google Scholar] [CrossRef]
- Moussa, A.I.; Shahawy, M.A. Dynamic and static tests of prestressed concrete girder bridges in Florida. Struct. Res. Cent. 1993, 80. [Google Scholar]
- Hernandez, W.; Viviescas, A.; Riveros-Jerez, C.A. Vehicle Bump Testing Parameters Influencing Modal Identification of Long-Span Segmental Prestressed Concrete Bridges. Sensors 2022, 22, 1219. [Google Scholar] [CrossRef] [PubMed]
- Gatti, M. Structural health monitoring of an operational bridge: A case study. Eng. Struct. 2019, 195, 200–209. [Google Scholar] [CrossRef]
- Meixedo, A.; Ribeiro, D.; Santos, J.; Calçada, R.; Todd, M. Progressive numerical model validation of a bowstring-arch railway bridge based on a structural health monitoring system. J. Civ. Struct. Health Monit. 2021, 11, 421–449. [Google Scholar] [CrossRef]
- De Angelis, A.; Pecce, M.R. Model assessment of a bridge by load and dynamic tests. Eng. Struct. 2023, 275, 115282. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.; Zhou, Y.L.; Kang, J. Dynamic model updating for bridge structures using the kriging model and PSO algorithm ensemble with higher vibration modes. Sensors 2018, 18, 1879. [Google Scholar] [CrossRef] [PubMed]
- Sousa, H.; Cavadas, F.; Henriques, A.; Bento, J.; Figueiras, J. Bridge deflection evaluation using strain and rotation measurements. Smart Struct. Syst. 2013, 11, 365–386. [Google Scholar] [CrossRef]
- Gouda, L.P. Study on Parametric Behaviour of Single Cell Box Girder under Different Radius of Curvature. Master’s Thesis, National Institute of Technology Rourkela, Rourkela, India, 2013. [Google Scholar]
- MIDAS Civil. Midas User Manual; MIDAS Information Technology Co.: Seongnam, Republic of Korea, 2018. [Google Scholar]
- EN 1993-2; Eurocode 3: Design of steel structures—Part 2: Steel bridges. CEN-European Committee for Standardization: Brussels, Belgium, 2006.
- Gupta, P.K.; Singh, K.K.; Mishra, A. Parametric Study on Behaviour of Box-Girder Bridges Using Finite Element Method. Asian J. Civ. Eng. 2010, 11, 135–148. [Google Scholar]
- EN 1991-3; Eurocode 1: Basis of design and actions on structures—Part 2: Traffic loads on bridges. CEN-European Committee for Standardization: Brussels, Belgium, 2003.







 |
 |
 |
 |
| Cases | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| MaxError (mm) | 10.30 | 25.26 | 23.57 | 2.78 | 0.48 | 6.56 | 7.10 | 15.42 | 0.58 | 3.82 | 2.73 | 7.73 | 2.53 | 14.99 | 10.12 | 16.42 | 4.33 |
| MaxError (%) | 8.78 | 11.88 | 21.04 | 4.85 | 1.14 | 16.36 | 13.27 | 20.50 | 2.06 | 14.68 | 4.34 | 18.78 | 12.40 | 18.08 | 18.19 | 20.09 | 12.21 |
| Load Cases | Stress Variations (N/mm2) | |||||||
|---|---|---|---|---|---|---|---|---|
| Middle Top Plate Midspan | Middle Bottom Plate Midspan | Middle Top Plate Near Support | Middle Bottom Plate Near Support | |||||
| Measured | Analytical | Measured | Analytical | Measured | Analytical | Measured | Analytical | |
| 1 | −25.6 | −25.1 | 35.4 | 37.3 | 12.2 | 14 | −14.8 | −16.2 |
| 2 | −46.4 | −46.9 | 69.2 | 71.7 | 32.4 | 32.3 | −33.5 | −37.6 |
| 3 | 13.9 | 13.7 | −20.9 | −20.9 | 11.3 | 11.9 | −9.5 | −15.7 |
| 4 | 0.2 | −1.4 | 2.5 | 2 | 2.7 | 1 | −0.3 | −1.2 |
| 5 | 2 | 3 | −3.5 | −4.6 | 4.3 | 6.1 | −4.1 | −7.9 |
| 6 | −6.3 | −10.4 | 9.6 | 13.3 | 26.6 | 29.1 | −25.7 | −29.4 |
| 7 | −10.7 | −11.8 | 15.9 | 17.4 | 6 | 6.5 | −6.1 | −7.5 |
| 8 | 5.1 | 4.6 | −7.7 | −6.7 | −3.5 | −3.3 | 3.9 | 3.9 |
| 9 | −0.9 | −0.6 | 0.8 | 0.9 | 0.2 | 0.4 | −0.3 | −0.5 |
| 10 | 0.2 | 0.2 | −0.3 | −0.2 | −0.2 | −0.1 | 0.3 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brinissat, M.; Ray, R.P.; Kuti, R. Evaluation of the Szapáry Long-Span Box Girder Bridge Using Static and Dynamic Load Tests. Infrastructures 2023, 8, 91. https://doi.org/10.3390/infrastructures8050091
Brinissat M, Ray RP, Kuti R. Evaluation of the Szapáry Long-Span Box Girder Bridge Using Static and Dynamic Load Tests. Infrastructures. 2023; 8(5):91. https://doi.org/10.3390/infrastructures8050091
Chicago/Turabian StyleBrinissat, Marame, Richard Paul Ray, and Rajmund Kuti. 2023. "Evaluation of the Szapáry Long-Span Box Girder Bridge Using Static and Dynamic Load Tests" Infrastructures 8, no. 5: 91. https://doi.org/10.3390/infrastructures8050091
APA StyleBrinissat, M., Ray, R. P., & Kuti, R. (2023). Evaluation of the Szapáry Long-Span Box Girder Bridge Using Static and Dynamic Load Tests. Infrastructures, 8(5), 91. https://doi.org/10.3390/infrastructures8050091







