Study on Deflection-Span Ratio of Cable-Stayed Suspension Cooperative System with Single-Tower Space Cable
Abstract
:1. Introduction
2. Evaluation Method of Bridge Driving Comfort and Safety
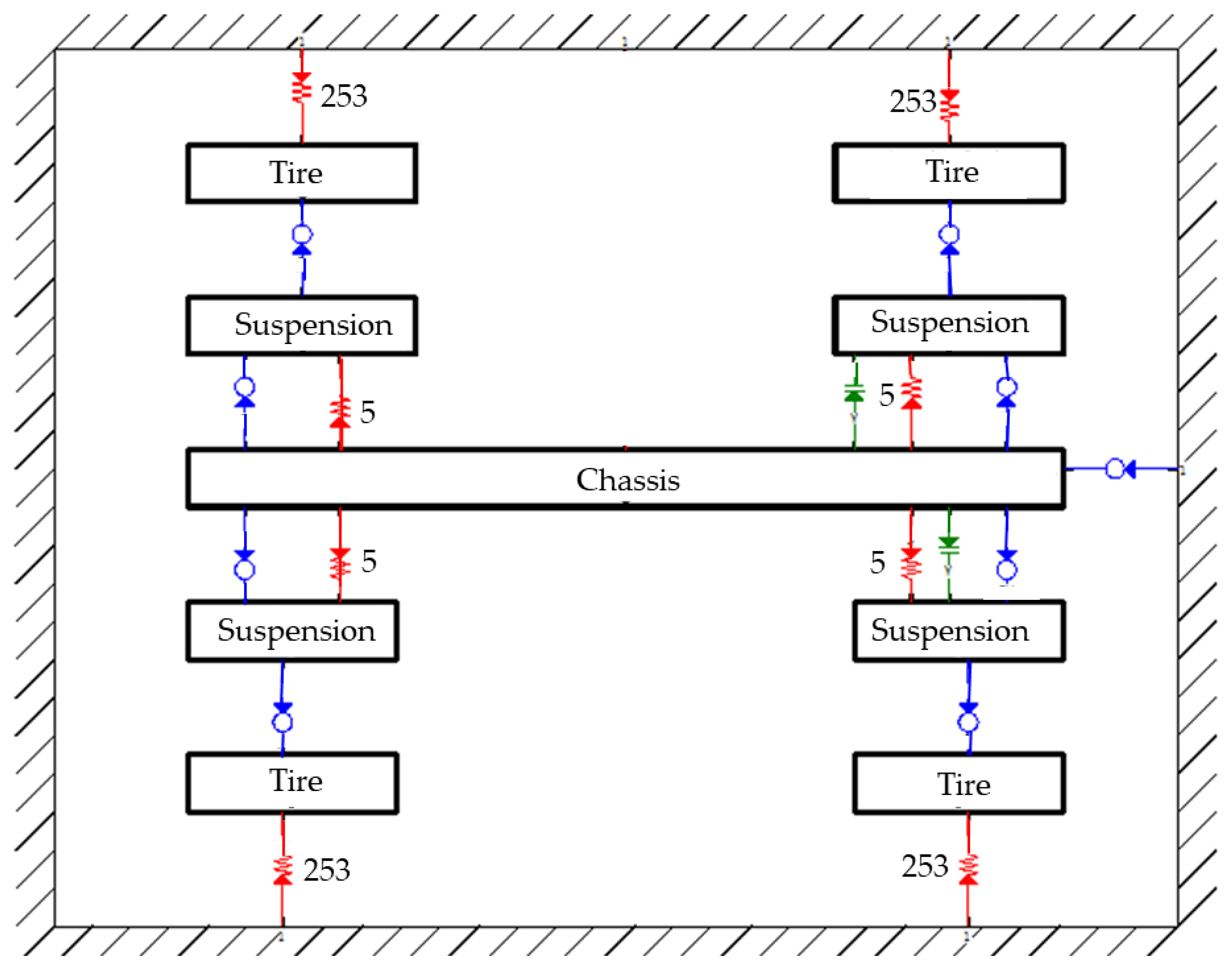
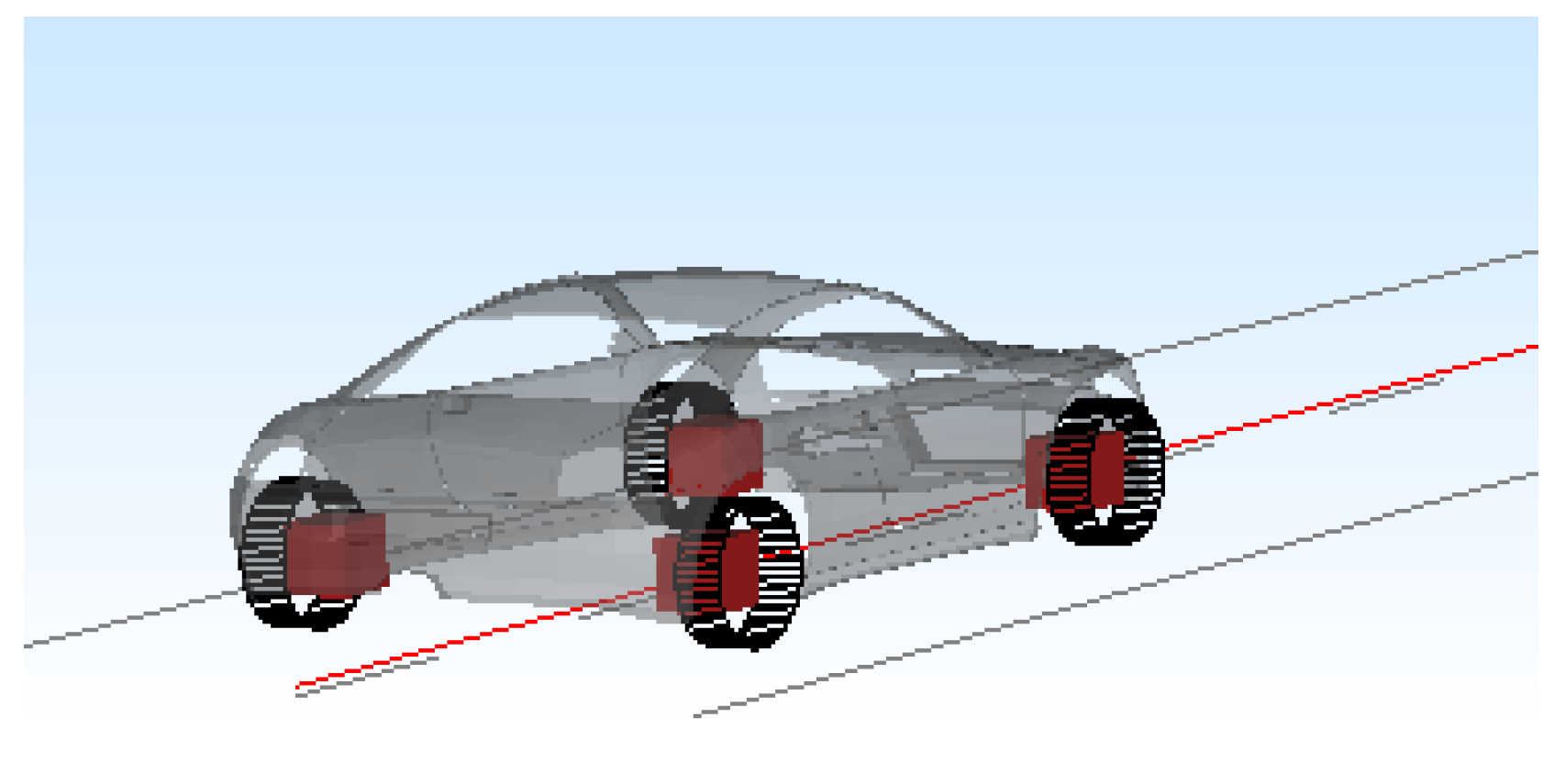
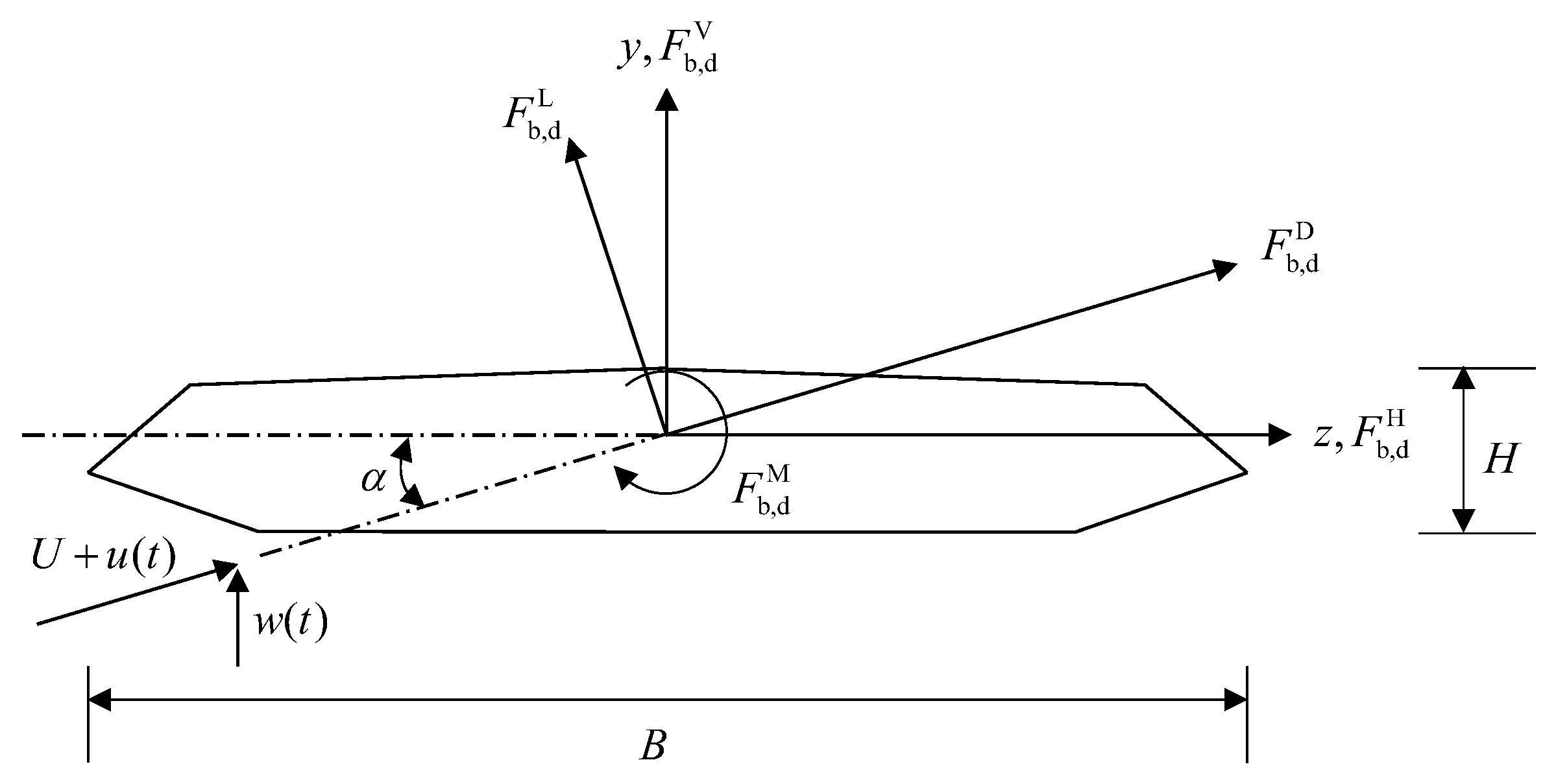
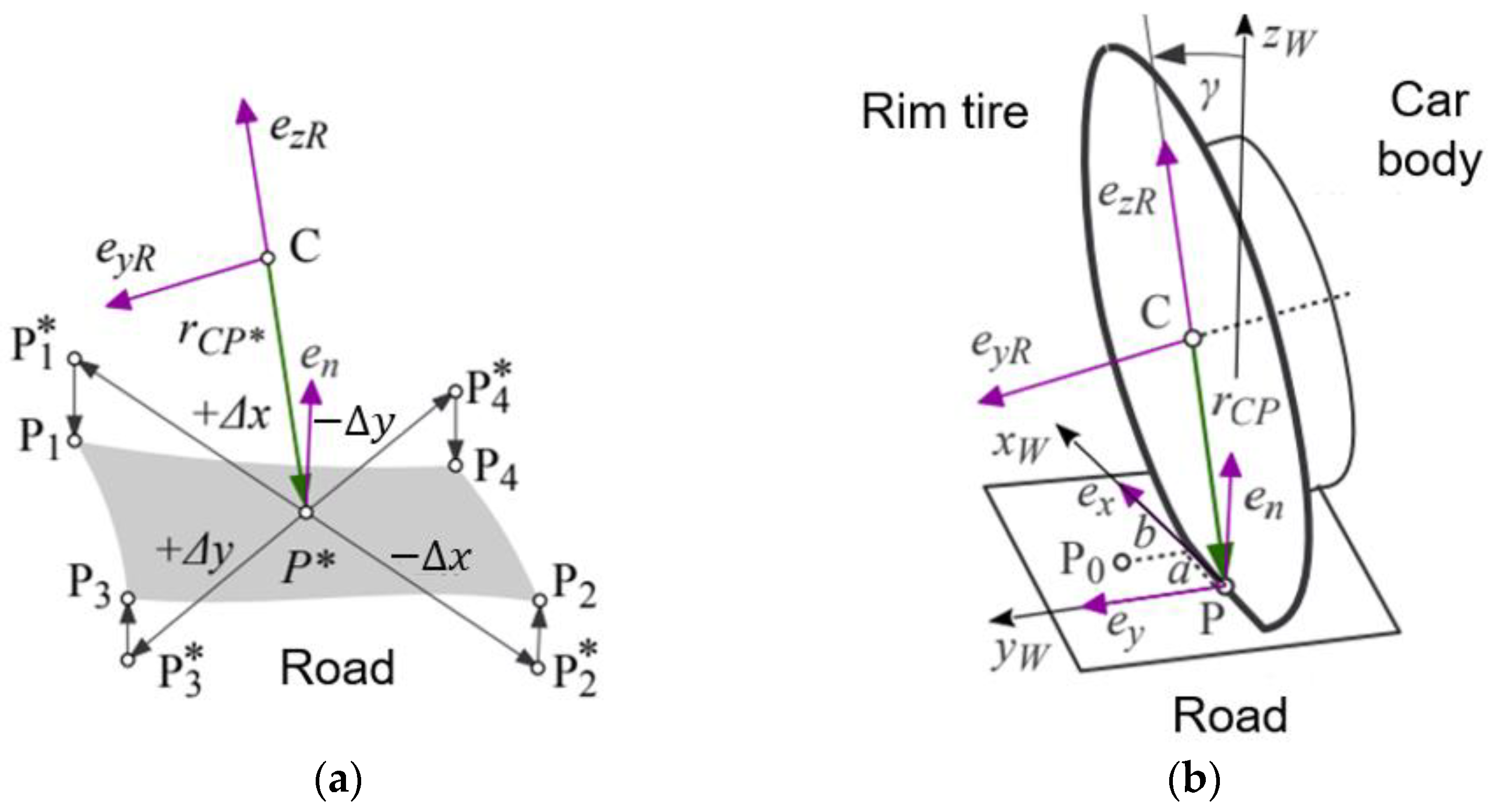
2.1. Dynamic Model of Bridges and Vehicles
2.2. Effect of Fluctuating Wind Field on Vehicle–Bridge System
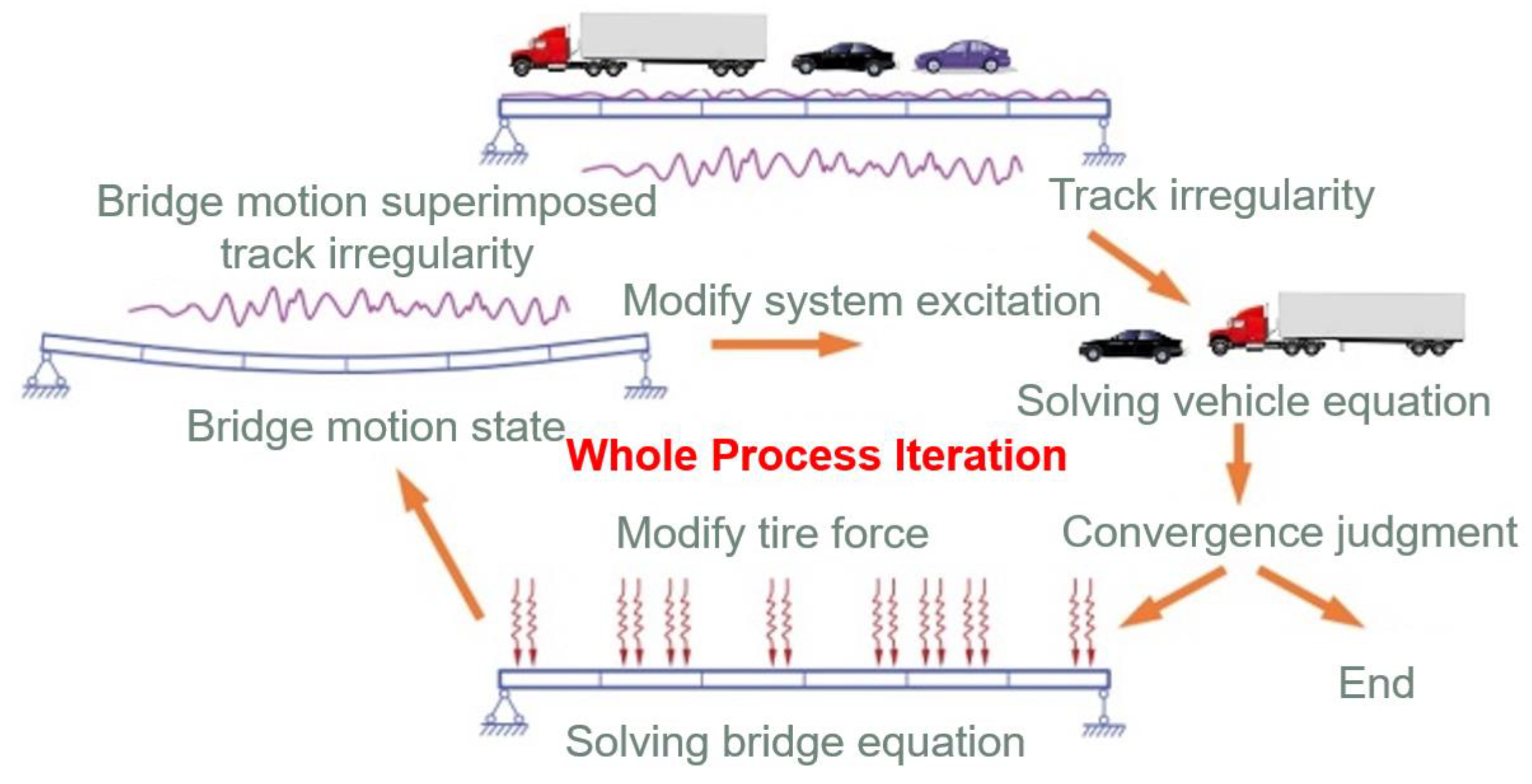
2.3. Vehicle–Bridge Interaction and Solution
2.4. Driving Comfort and Safety
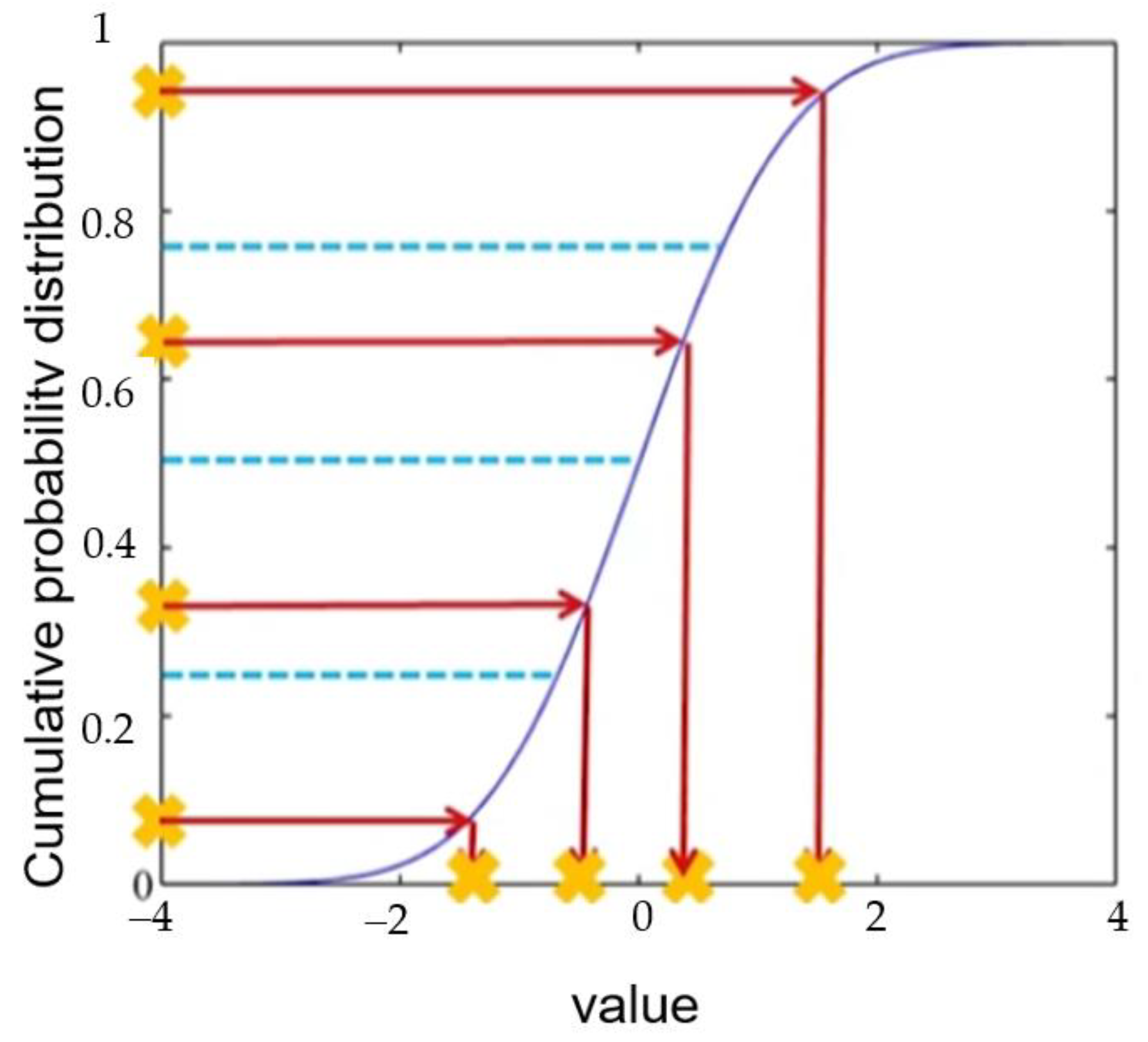
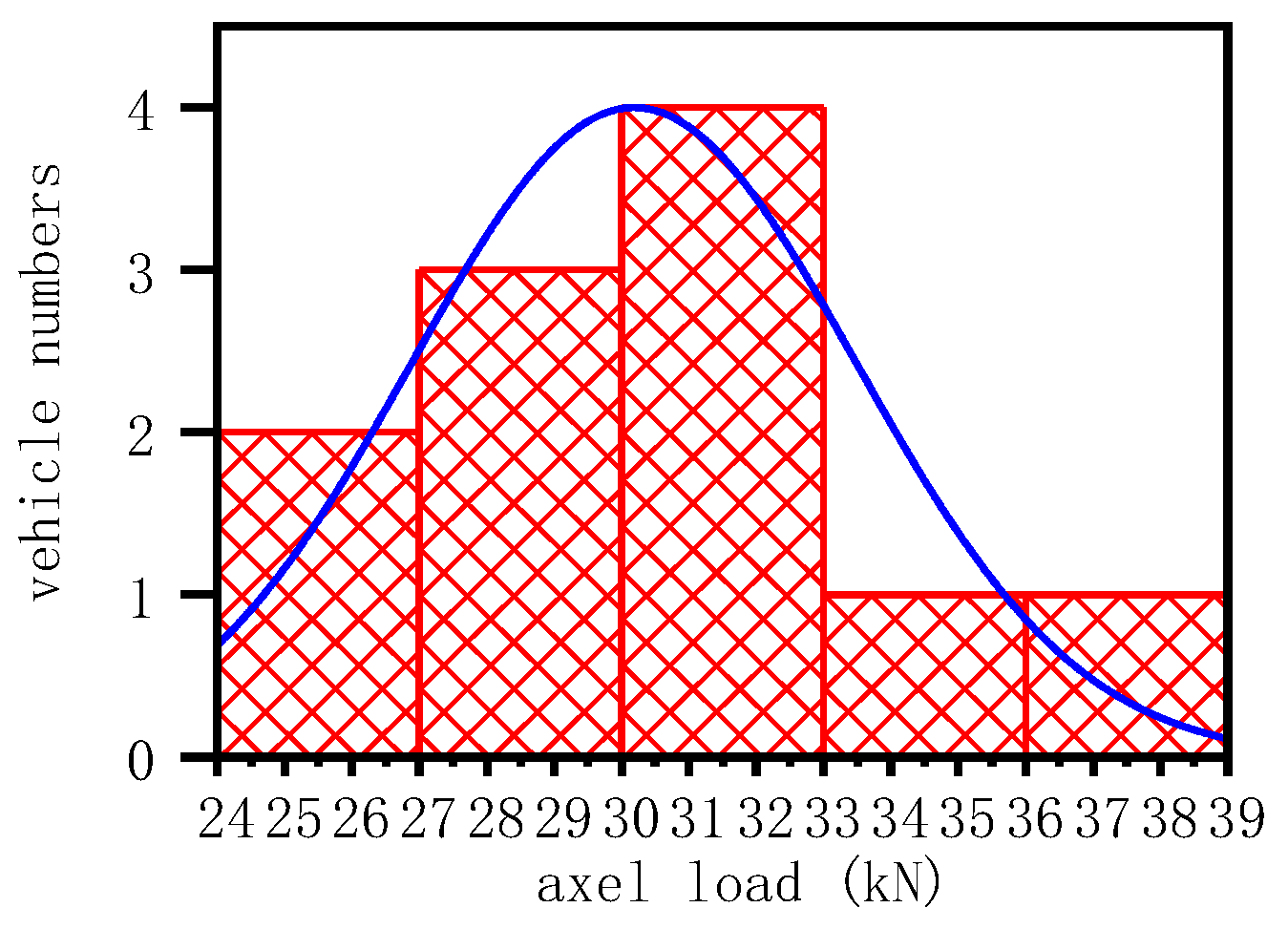
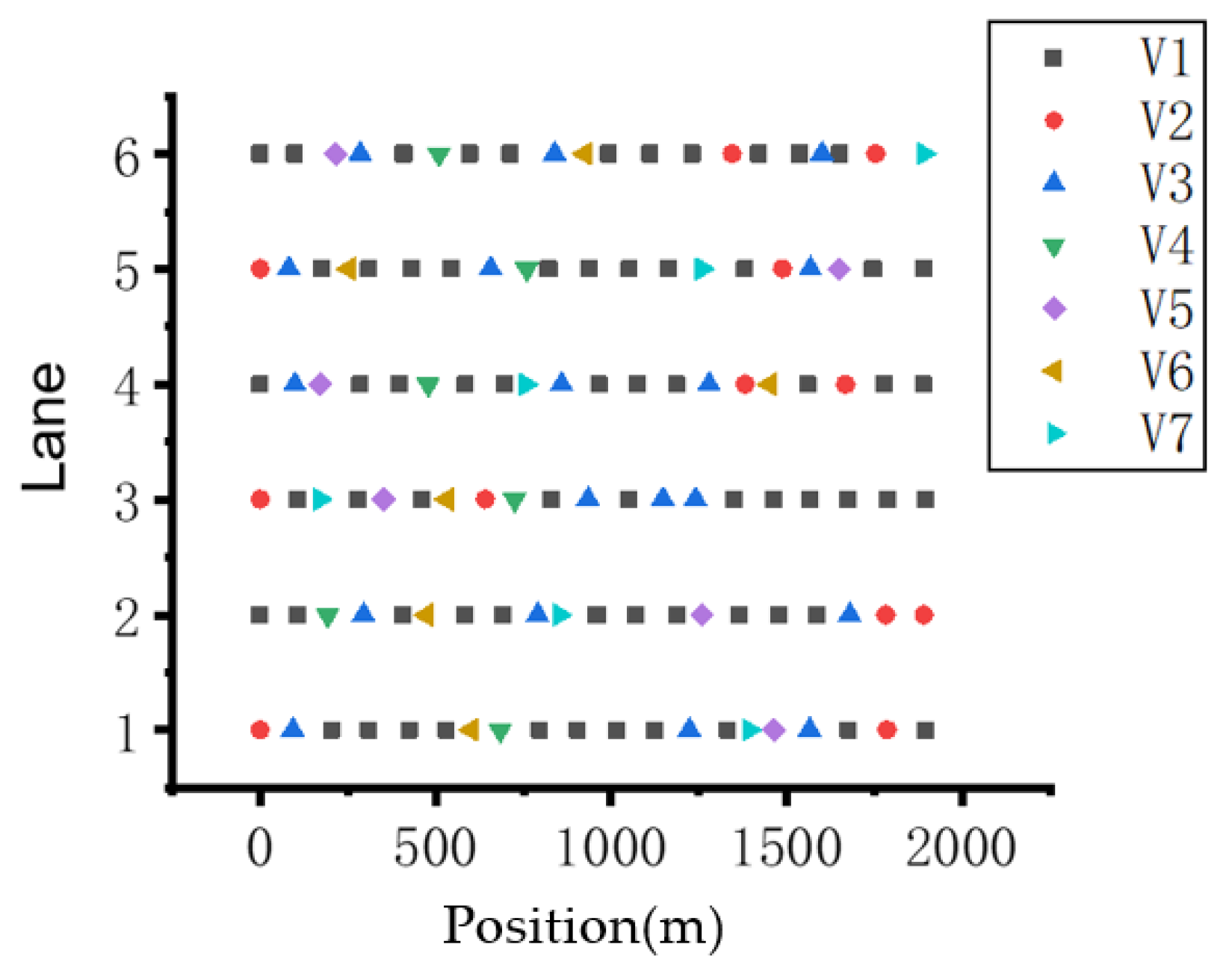
3. Simulation of Random Traffic Flow Based on Latin Hypercube Sampling
4. Bridge Driving Safety and Comfort Analysis for Cable-Stayed-Suspension Cooperative System
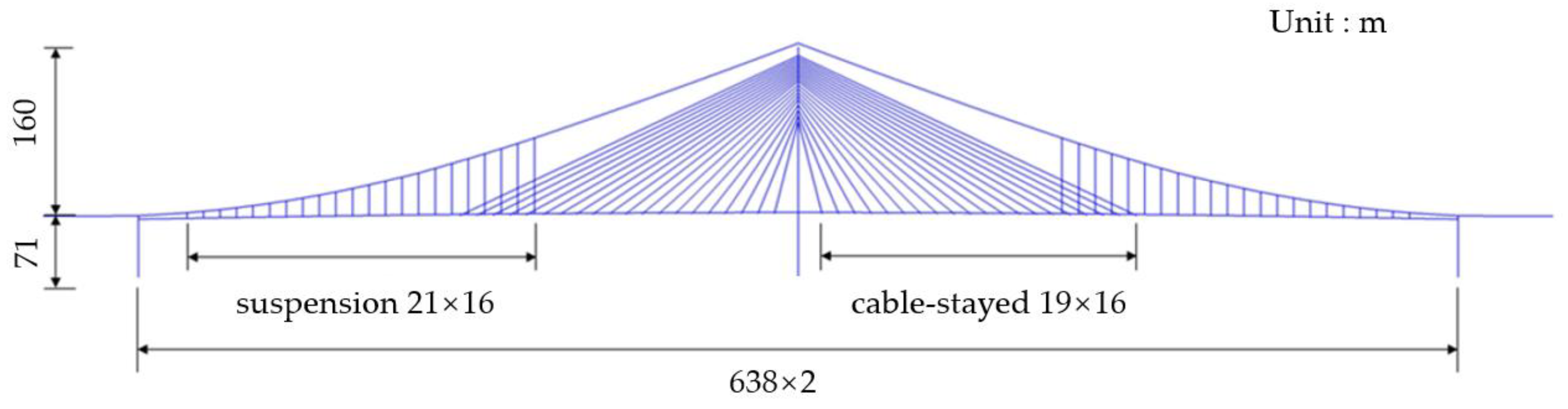
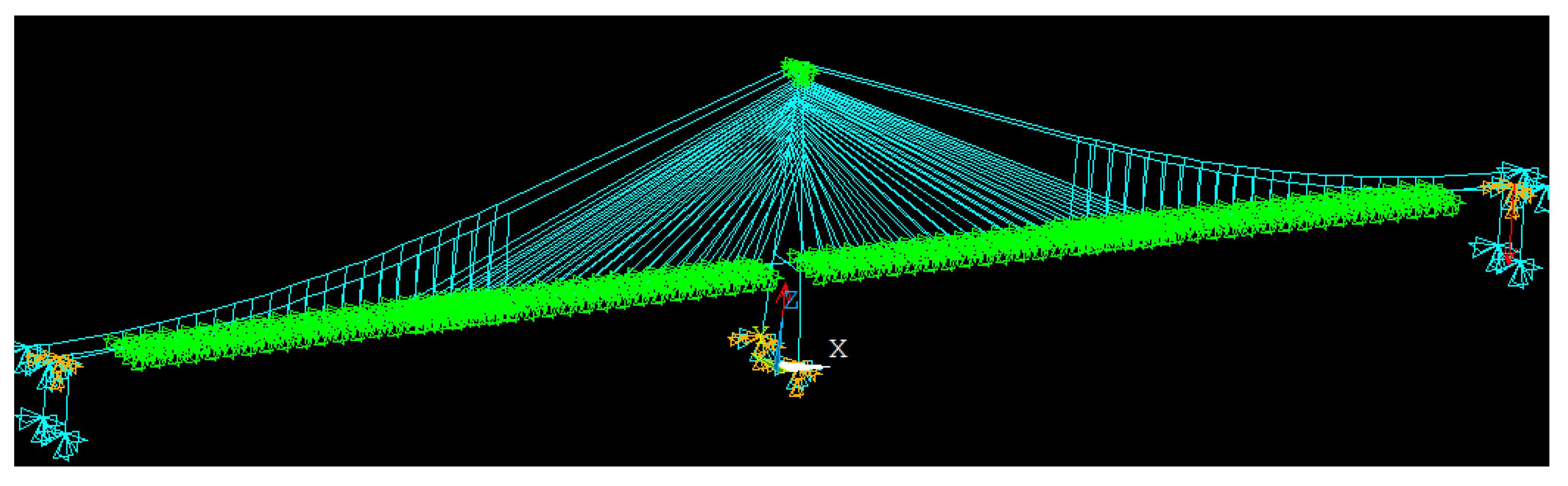
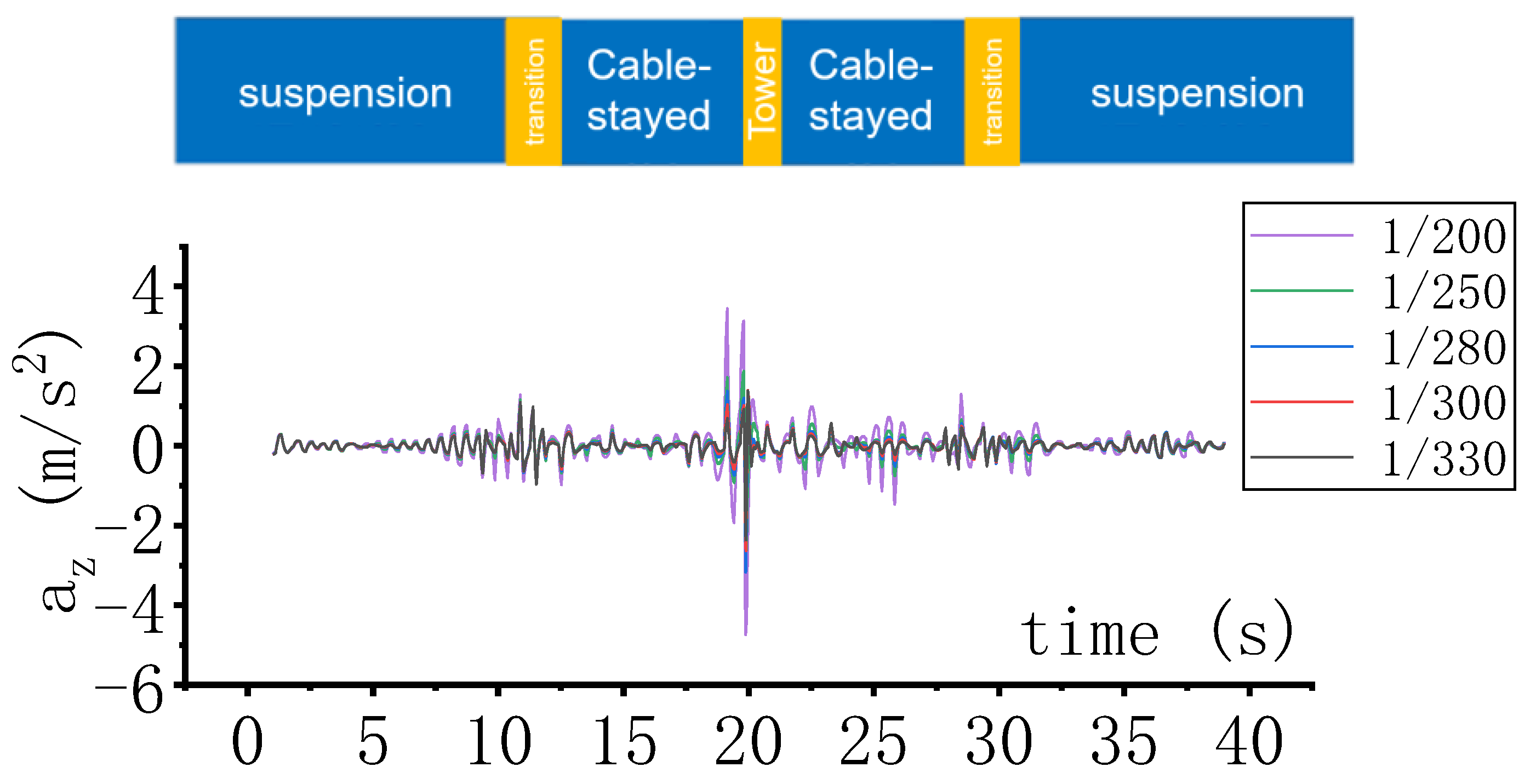
4.1. Conditions
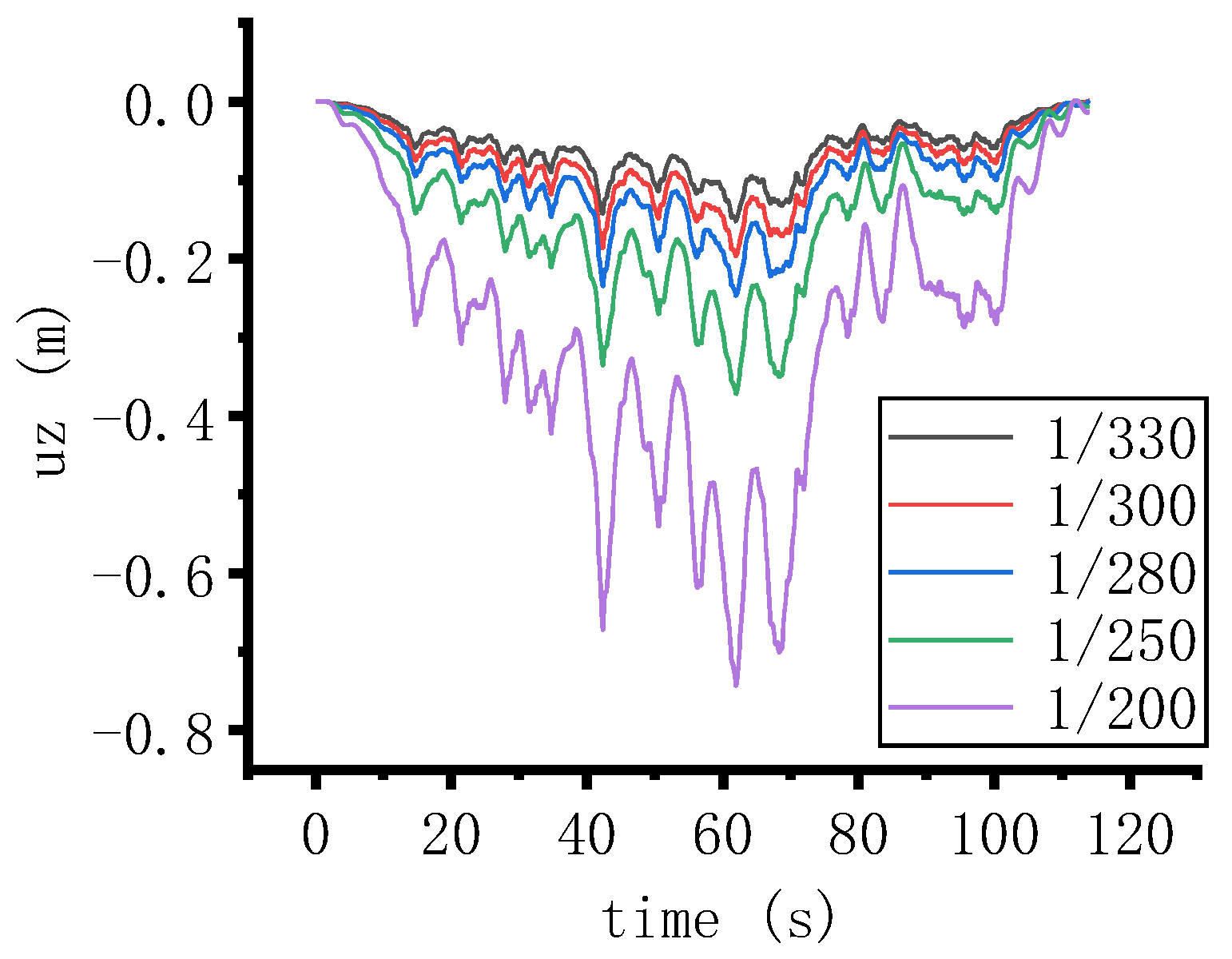
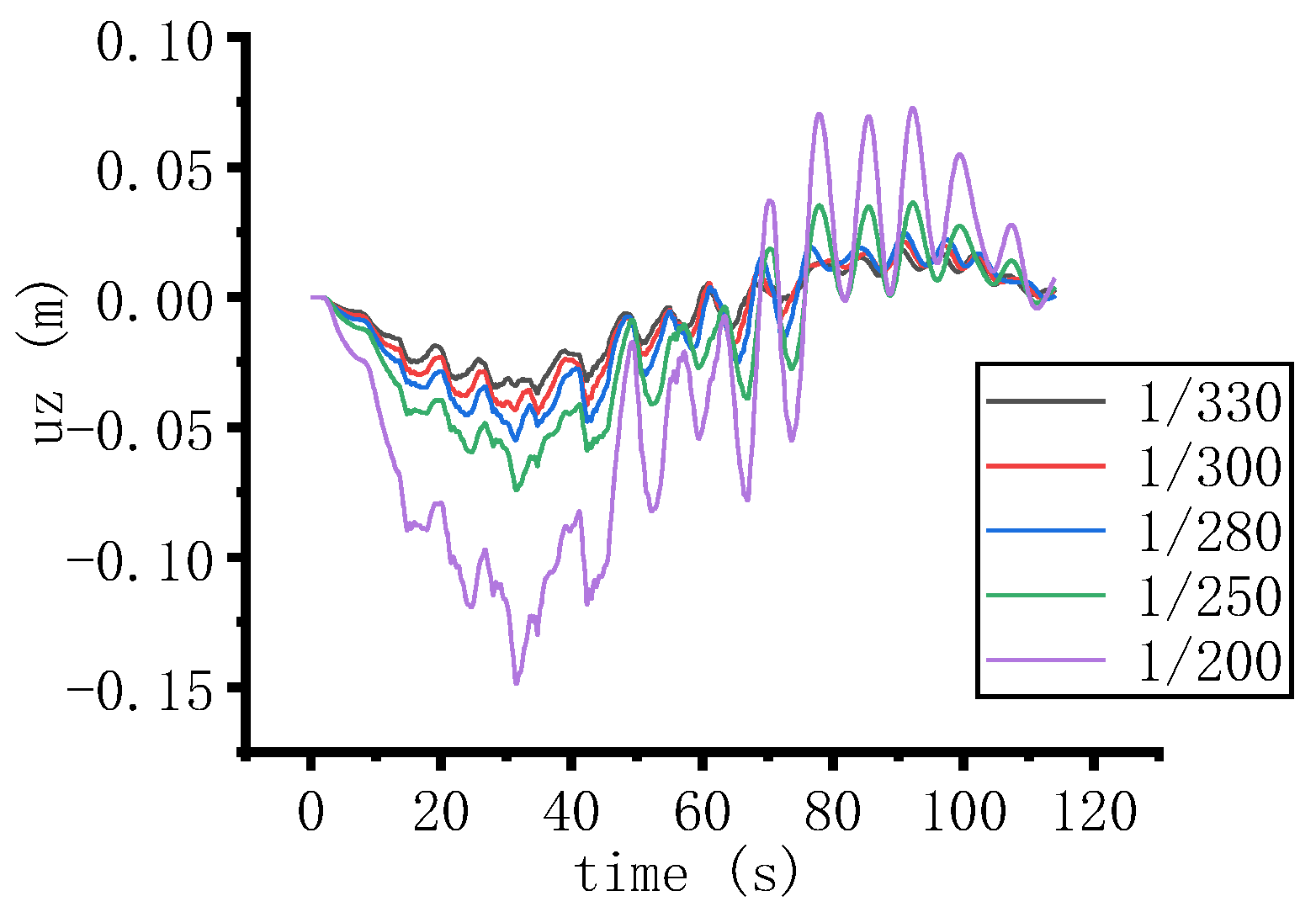
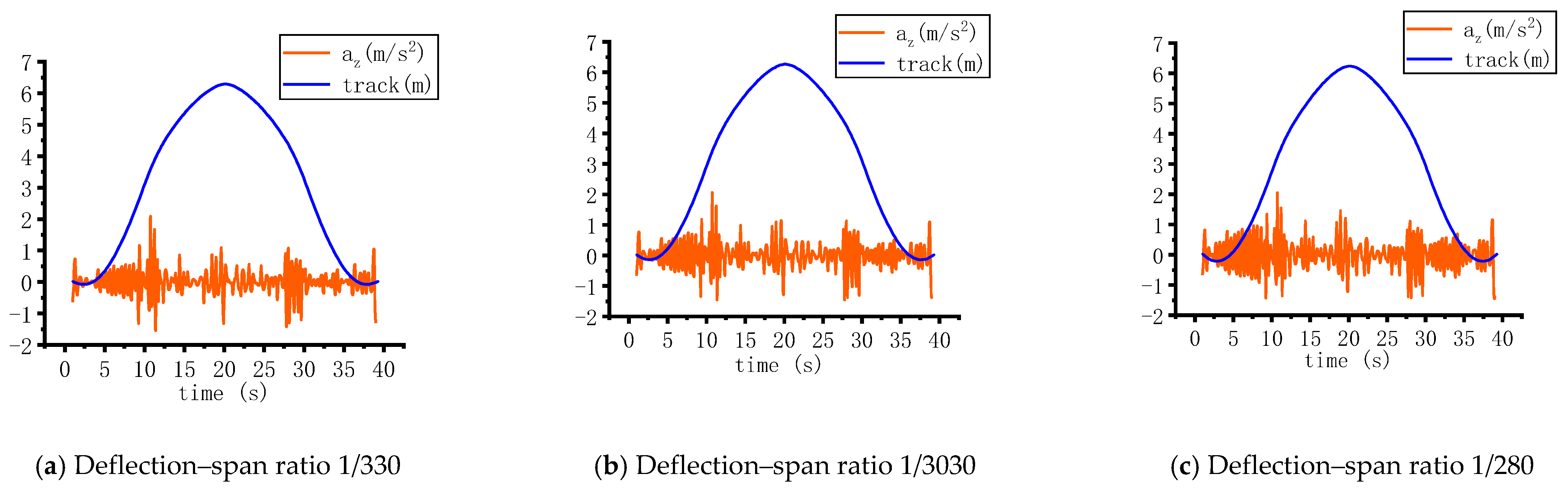
4.2. Vehicle Dynamic Response Analysis
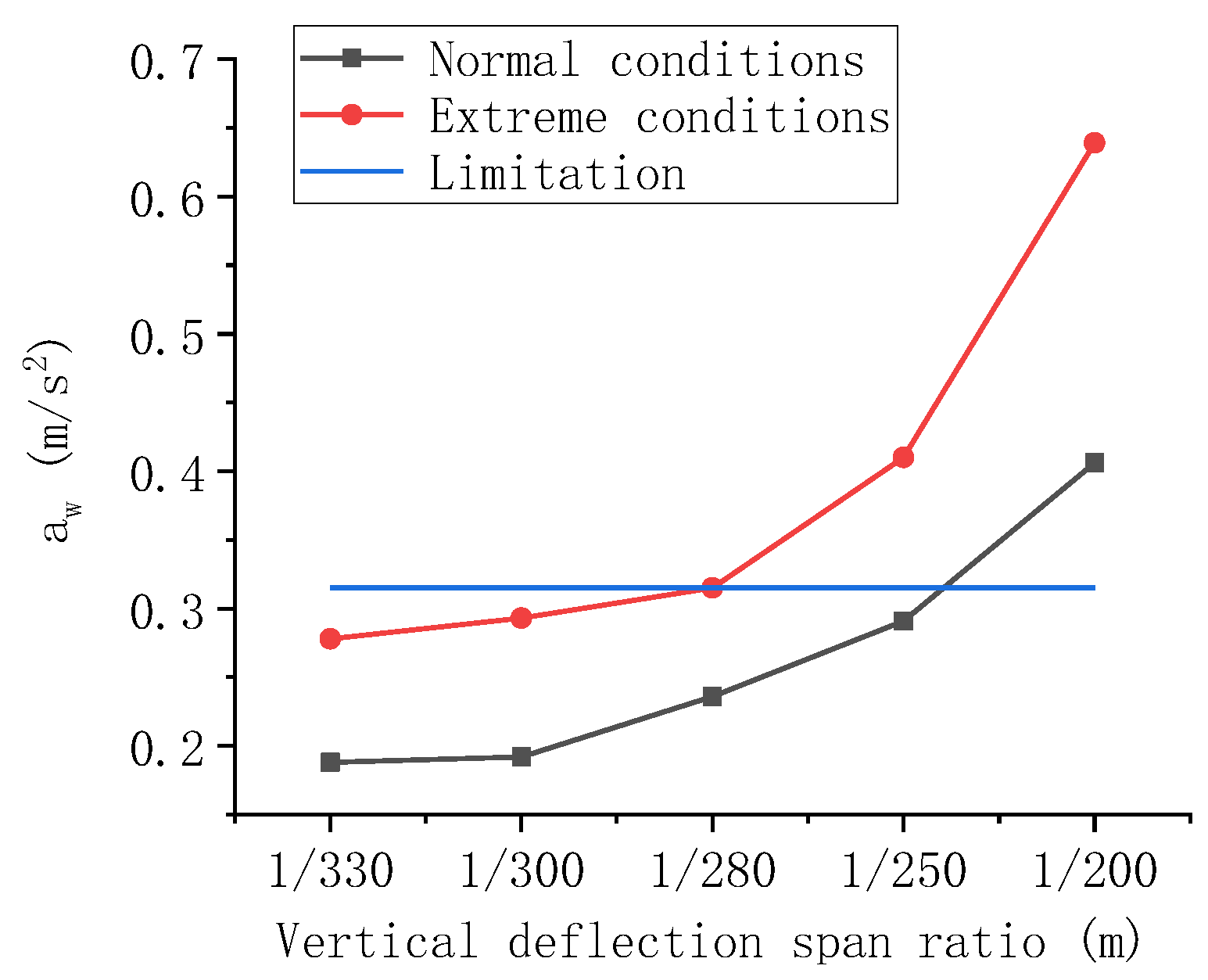
4.3. Evaluation of Driving Safety and Comfort and Limit Value of Bridge Deflection Ratio
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, F.; Huang, Z.; Guo, S.; Lei, J. Research on rail-road cable-stayed suspension bridge. Steel Constr. Chin. Engl. 2019, 34, 49–55. (In Chinese) [Google Scholar]
- Bryja, D.; Knawa, M. Computational model of an inclined aerial ropeway and numerical method for analyzing nonlinear cable-car interaction. Comput. Struct. 2011, 89, 1895–1905. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.G.; Rxnnquist, A.; Navik, P.; Liu, Z.D. Contact Wire Irregularity Stochastics and Effect on High-speed Railway Pantograph-Catenary Interactions. IEEE Trans. Instrum. Meas. 2020, 69, 8196–8206. [Google Scholar] [CrossRef]
- Duan, F.; Song, Y.; Gao, S.; Liu, Y.; Chu, W.; Lu, X.; Liu, Z. Study on Aerodynamic Instability and Galloping Response of Rail Overhead Contact Line Based on Wind Tunnel Tests. IEEE Trans. Veh. Technol. 2023, 1–11. [Google Scholar] [CrossRef]
- Larsen, A.; Larose, G.L. Dynamic wind effects on suspension and cable-stayed bridges. J. Sound Vib. 2015, 334, 2–28. [Google Scholar] [CrossRef]
- Huajun, B.; Wangqing, W.; Xu, S. Research on high-speed railway bridge design based on stiffness deformation requirements. World Bridges 2020, 48, 27–33. (In Chinese) [Google Scholar]
- Chen, J.; Lei, J.; Golden, O.; Hu, C. Study on structural characteristics and stiffness indexes of thousand-meter-scale road-rail suspension bridge. Railw. Stand. Des. 2022, 66, 54–61. (In Chinese) [Google Scholar]
- Lu, D.; Wei, H.; Yang, Y.; Wei, W. Research Progress on Theory and Application of Coupled Vibration of Highway Bridges and Vehicles. China J. Highw. Transp. 2018, 31, 38–54. [Google Scholar]
- Li, Y.; Long, J.; Xiang, H.; Ma, H.; He, M.; Xie, J. Transverse deflection-span ratio suggested value of an urban rail transit bridge based on a wind-vehicle-bridge system. J. Vib. Shock 2020, 39, 211–217. (In Chinese) [Google Scholar]
- Li, Y.; Xiang, H.; Liao, H. Study on wind shielding effect of wind screens based on coupling vibration theory of wind-vehicle-bridge(lines) systems. China Civ. Eng. J. 2014, 47, 97–102. (In Chinese) [Google Scholar]
- Li, X.; Gong, Z. Analysis of vehicle-included structure-borne noise characteristics of large-span steel bridge with different structure forms. J. Vib. Shock 2021, 40, 91–99. (In Chinese) [Google Scholar]
- Chen, H.; Zhang, W.; Li, J. Coupled dynamic response analysis of high-speed railway vehicle and track system under random track irregularities. J. Vib. Control 2020, 26, 1855–1869. [Google Scholar]
- Deng, L.; Duan, L.L.; He, W.; Ji, W. Study on Vehicle Model for vehicle-bridge coupling vibration of highway bridges in China. China J. Highw. Transp. 2018, 31, 92–100. (In Chinese) [Google Scholar]
- Kwasniewski, L.; Li, H.; Wekezer, J.; Malachowski, J. Finite element analysis of vehicle–bridge interaction. Finite Elem. Anal. Des. 2006, 42, 950–959. [Google Scholar] [CrossRef]
- Yuan, S. Development and Programing of Typical Vehicles Equation of Motion for Coupling Vibration between Highway Bridge and Vehicles. Master’s Thesis, Changan University, Xi’an, China, 2012. (In Chinese). [Google Scholar]
- Yu, M.; Yao, T.; Kong, L.; Shilin, L. A Review of Tire-asphalt Pavement Friction Measurement and Skid Resistance Model Study. J. Highw. Transp. Res. Dev. 2020, 37, 12–24. (In Chinese) [Google Scholar]
- Xiaohui, S.; Zeng, J.; Xin, J.; Zhao, J.; Zhao, P. Dynamic Dharacteristics and Parameter Analysis of Tire Model. J. Chongqing Univ. Technol. Nat. Sci. 2020, 34, 1–8. (In Chinese) [Google Scholar]
- Li, Y.; Xiang, H.; Qiang, S. Review on Coupling Vibration of Wind-vehicle-bridge System. China J. Highw. Transp. 2018, 31, 24–37. (In Chinese) [Google Scholar]
- Zhang, W.; Zhang, Z.; Zhang, X. Numerical investigation on the wind-field-dependence property of bridge section aero dynamic admittance. Acta Aerodyn. Sin. 2018, 36, 677–686. (In Chinese) [Google Scholar]
- Han, W.; Chen, A. Ride comfort assesment of vehicle running on long-span cable-stayed bridge under cross wind. China J. Highw. Transp. 2008, 21, 54–60. [Google Scholar]
- Lee, S.; Lee, S.; Lee, J.; Choi, S. A study on the evaluation of vehicle ride comfort using RMSV method. Int. J. Automot. Technol. 2018, 19, 69–76. [Google Scholar]
- Chen, N. The Safety of Road Vehicles Driven on Bridge Deck under Crosswind and Its Windproof Precautions. Ph.D. Thesis, Southwest Jiaotong University, Cheng’du, China, 2015. (In Chinese). [Google Scholar]
- Wang, J.; Huang, P.; Han, W.; Yuan, Y.; Zhou, G.; Xu, X. Fatigue Life Prediction of Concrete Bridges Based on Improved Damage Algorithm and MCMC Traffic Flow Simulation. J. Hunan Univ. Nat. Sci. 2021, 48, 31–43. (In Chinese) [Google Scholar]
- Qu, Z.; Liu, M.; Liu, J.; Cao, H.; Yang, G.; Liu, T. Latin hypercube sampling monte carlo simulation for the information flow time-delay of railway power supply system. China Railw. Sci. 2012, 33, 82–90. (In Chinese) [Google Scholar]
- Wang, D. Analysis of Vehicle-Bridge Coupled Vibration for Long-Span Suspension Bridge with Finite Element Model Updating under Random Traffic Flowing. Master’s Thesis, Chang’an University, Xi’an, China, 2008. [Google Scholar]
- Liu, F.; Luo, X. Influence of central buckle of main cable on mechanical properties of three-tower cable-stayed suspension cooperative system bridge. J. China Foreign Highw. 2016, 36, 143–146. (In Chinese) [Google Scholar]
- He, D.; Xiao, H. Influence of central buckle on mechanical property of combined cable-stayed and suspension bridge. Bridge Constr. 2020, 50, 23–28. (In Chinese) [Google Scholar]



| Level | aw (m/s2) | Comments |
|---|---|---|
| 1 | <0.315 | Comfortable |
| 2 | 0.315–0.630 | A little uncomfortable |
| 3 | 0.500–1.000 | Less comfortable |
| 4 | 0.800–1.600 | Uncomfortable |
| 5 | 1.250–2.500 | Very uncomfortable |
| 6 | >2.000 | Extremely uncomfortable |
| Symbol | Category | Ratio | Conversion Coefficient |
|---|---|---|---|
| V1 | Car | 40.6% | 1 |
| V2 | Bus | 5.8% | 2.0 |
| V3 | Buggy | 13.8% | 2.0 |
| V4 | Medium truck | 10.9% | 3.0 |
| V5 | Big truck | 10.1% | 4.0 |
| V6 | Trailers | 10.2% | 4.0 |
| V7 | Container truck | 8.6% | 4.0 |
| Conditions Number | Deflection–Span Ratio under Lane Load |
|---|---|
| 1 | 1/330 |
| 2 | 1/300 |
| 3 | 1/280 |
| 4 | 1/250 |
| 5 | 1/200 |
| Conditions Number | Maximum Displacement in Left Span (cm) | |
|---|---|---|
| Vehicle-Induced Static Displacement | Coupled Vibration Displacement | |
| 1 | 13.79 | 15.18 |
| 2 | 17.94 | 19.63 |
| 3 | 22.87 | 24.67 |
| 4 | 34.54 | 37.14 |
| 5 | 67.28 | 74.27 |
| Condition Number | Maximum Displacement in Left Span (cm) | |
|---|---|---|
| Vehicle-Induced Static Displacement | Coupled Vibration Displacement | |
| 1 | 2.7 | 3.71 |
| 2 | 4.37 | 4.46 |
| 3 | 5.32 | 5.50 |
| 4 | 6.35 | 7.44 |
| 5 | 12.35 | 14.88 |
| Deflection–Span Ratio | Single Car | Random Traffic Flow |
|---|---|---|
| 1/330 | 0.108 | 0.242 |
| 1/300 | 0.110 | 0.239 |
| 1/280 | 0.125 | 0.263 |
| 1/250 | 0.180 | 0.320 |
| 1/200 | 0.516 | 0.514 |
| Torsion Span Ratio | aw (m/s2) | RSF | SSF |
|---|---|---|---|
| 1/330 | 0.188 | 2.688 | 2.666 |
| 1/300 | 0.192 | 2.681 | 2.663 |
| 1/280 | 0.236 | 2.677 | 2.652 |
| 1/250 | 0.291 | 2.584 | 2.637 |
| 1/200 | 0.406 | 2.336 | 2.544 |
| Torsion Span Ratio | aw (m/s2) | RSF | SSF |
|---|---|---|---|
| 1/330 | 0.278 | 2.295 | 2.477 |
| 1/300 | 0.293 | 2.245 | 2.455 |
| 1/280 | 0.315 | 2.231 | 2.446 |
| 1/250 | 0.41 | 2.184 | 2.434 |
| 1/200 | 0.639 | 2.158 | 2.247 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, L.; Huang, Y.; Wei, X. Study on Deflection-Span Ratio of Cable-Stayed Suspension Cooperative System with Single-Tower Space Cable. Infrastructures 2023, 8, 62. https://doi.org/10.3390/infrastructures8030062
Xiao L, Huang Y, Wei X. Study on Deflection-Span Ratio of Cable-Stayed Suspension Cooperative System with Single-Tower Space Cable. Infrastructures. 2023; 8(3):62. https://doi.org/10.3390/infrastructures8030062
Chicago/Turabian StyleXiao, Lin, Yaxi Huang, and Xing Wei. 2023. "Study on Deflection-Span Ratio of Cable-Stayed Suspension Cooperative System with Single-Tower Space Cable" Infrastructures 8, no. 3: 62. https://doi.org/10.3390/infrastructures8030062
APA StyleXiao, L., Huang, Y., & Wei, X. (2023). Study on Deflection-Span Ratio of Cable-Stayed Suspension Cooperative System with Single-Tower Space Cable. Infrastructures, 8(3), 62. https://doi.org/10.3390/infrastructures8030062







