Development of Mathematical Models for Trucks and Cargo

Abstract

International trade allows countries to expand their markets and access goods and services that otherwise may not have been domestically available. As a result of international trade, the market is more competitive. This ultimately results in more competitive pricing and brings a cheaper product home to the consumer. The development of mathematical models to optimize the delivery of goods using a limited number of trucks is an urgent task for researchers around the world. The research goal was to use a developed mathematical model that allows one to optimize the performance of transportation tasks based on the selected parameters, both in terms of a particular truck and a fleet of trucks in the Russian region. The parameters (function, condition, cost, time, and quality) were set and an algorithm for the process of matching a specific truck and cargo was developed as part of the unit transportation task. A mathematical model has been developed for performing multiple freight tasks and operating a fleet of trucks, which considering such factors as cost, time, quality, and reputation, allows one to find an acceptable solution for a specific transportation task. A mathematical model was developed that considers such factors as cost, time, quality, and reputation, allowing one to find an acceptable solution for a particular transportation task. The simulation was performed in MATLAB 2018. The parameters of the simulations were a population size of 300, a maximum number of iterations of 2000, and a probability of selection of 0.85. From the 30 runs, the optional value was chosen as the best solution. The developed mathematical models have been tested for solving single and multiple transport problems under truck fleet simulation conditions. The results of the work can be used to optimize the operation of truck fleets in the Russian Federation and other countries.

1. Introduction

International trade allows countries to expand their markets and access goods and services that otherwise may not have been domestically available. As a result of international trade, the market is more competitive. This ultimately results in more competitive pricing and brings a cheaper product home to the consumer.

This statement was discussed in [1] from the point of multi-objective collaboration amongst shipping lines and marine terminal operations, in the article [2] from the point of vessel schedule recovery in liner shipping, in paper [3] from the point of uncertainties in liner shipping, and work [4] from the point of interrelations between sea hub ports and inland hinterlands. Cassiano et al. [5] proposed a conceptual model for Sustainability Urban Freight Transport.

The provision of transport services involves operating costs. The optimization of operating costs includes administrative, technical, and economic management levers associated with finding technical objects by people and the relationships occurring between the subjects of economic activity. During operation, vehicles at the enterprise are subject to physical aging, which leads to frequent economic or complete loss of their functional properties (economic productivity, efficiency, durability, and reliability). In addition, the vehicle’s operation is associated with some expenses, including operating costs. Therefore, a mathematical evaluation of the operating efficiency using information technology will solve the problems of vehicles’ reasonable use and improve the technical and economic indicators of the operational process under ongoing transportation conditions, also solving the related problems. This article provides the results of the development and use of mathematical models to optimize transport tasks.

1.1. Literature Review

There are many scientific works concerning the problem of optimization the transportation tasks. Transportation costs are the primary economic category that determines the relationship between transportation and other sectors of economic activity [6]. Cost is the primary criterion for choosing a carrier, rather than the carrier’s choice of using their means of transportation or transportation companies [7]. Transportation costs consist of such elements as the cost of delivery, the minimum weight of the cargo, loading and unloading devices, packaging and creation of cargo units, damage during transportation, and special services offered by the carrier, such as breaks during transportation [8]. It also impacts the cost of delivering transportation services, which is determined by vehicle economy and operating costs and depends on its technical condition. Key work processes that take place in a transport company are as follows [9]. Commissioning is the first operating step that includes, for example, transporting vehicles to the place of their use or storage and preparing them for operation [10,11]. Proper implementation of processes before commissioning has a significant effect on transforming vehicles in the subsequent phases of their operation. As for components, their functions, and ease of assembly, it is also essential to understand how long the vehicles and components remain unchanged in a particular phase [12]. The operation is the most important in all business processes. The operating process is related to the maintenance of vehicles in complete working conditions.

In contrast, the renewal or upgrade processes are related to maintenance and repair, collection, and transfer of information to the vehicle manufacturers about damages, causes, and consequences [13]. Labor-intensive implementation of maintenance processes depends on the condition of the operated vehicles, their quality, proper operation, the intensity of destructive factors, the cost of repair work, and others [14]. Reliable information on the maintenance and renewal status of vehicles and their units is required for adequate planning and implementation of service processes. Unfortunately, diagnostic studies conducted in transportation companies are usually not entirely valid, making it difficult to perform maintenance and repair [15]. The liquidation process is the ending phase of using vehicle assets. Usually, this phase implies the sale of the vehicle or complete/partial disassembly into spare parts for further reuse or for using material and components they are made of as waste.

The use of vehicles is related to numerous predictable events, usually called “issues” that standard methods cannot resolve. An issue often occurs due to changes in the vehicle’s technical condition, and the cause of such change is unknown. From a technical perspective, the vehicle’s operating system can be divided into [16,17]: (1) Deviance—a system failure occurs, and the cause is unknown; (2) Optimization—assessment of how to marginally improve system functions; (3) Innovativeness—redesign of the system.

The main problem in the exploitation of transport resources arises when deciding on the mode and purpose of transportation. For an appropriate decision, it is necessary to determine the object status or the type of action sequence required to apply in a particular situation. The effectiveness of the decision is directly related to the promptness of its implementation. Recent decisions to optimize transport operating costs concern not only economic but also environmental issues [18]. Also, it should be taken into account that the operating costs depend on many factors, such as the specific number of vehicles on the site, the availability of spare parts, and the task schedule [19]. Quality decisionmaking requires computerized decision support systems to enhance expert assessment of the solution’s effectiveness through an information support modeling process. Due to the specifics of transport companies, where vehicles have difficult access to diagnostic stations or service stations, strategic management models alone cannot be used as the vehicles used must comply with international standards in the transportation sector [20].

Vehicle operation optimization tasks may be defined as follows: 1. Adapting the supply of transportation services to changes in demand in terms of quantity and quality; 2. Accomplishing transportation tasks with a minimum total cost, i.e., operating costs of the system for a more extended period. Accordingly, the main goals of exploiting the transport system can be formulated. The goal, in this case, will be to support the maintenance process, specifying the best maintenance strategy with known input and output parameters of the primary decision variable. It is necessary to define rules for making decisions that will form the basis of the automated decision-making procedure, e.g., computer simulation of signal changes in analyzed machine states for different decision options. Evaluation of the vehicle’s operation forms the basis for optimal solution development in the planning and implementation of transport use and maintenance processes, allowing the system to achieve the required level of reliability and operational safety. Applied methods to evaluate operation processes can be classified into two main groups: analysis of the system condition at a specific time or during a specific period, including predicting future reserves, and the so-called direct measurement methods. The deterministic approach is used to generate retrospective assessments of methods for measuring direct effects [21]. By generating forward-looking estimates of system performance, the model may be stochastic. When assessing prospective virtual techniques, including functions of computer simulation for operating processes and changes in the condition of vehicles and their aggregates, each decision to control the operational process is implemented in a complex operating system. Transport companies must introduce such systems by analyzing data concerning such parameters as the status of the operation, efficiency in the operating process, presence of threats, operational system efficiency, and efficacy of assigned subsystems.

The values of the decision-making indicators (process indicators within the operating system) can be determined for each mode of transport, the entire transport undertaking, and their subsets. The vehicle operating system requires the commencement of operational and monitoring tasks. Furthermore, such a system comprises a subsystem for planning and reporting decisions [22]. The information collection and processing management system requires rational and targeted actions crucial to adopting optimal decisions. The complexity of processes to make optimal decisions about reducing operating costs requires developing an algorithm to make decisions and gather the necessary information. Problems resulting from individual processes may be grouped according to the time they arose during the operation. The literature identifies such vehicle operating problems in the transport structure [23] as optimizing routes, optimizing the choice of freight transport, and optimizing the selection of vehicle drivers.

The problems of the maintenance process include [7]: optimizing the reliability of vehicles in service in the transport sector; optimizing the condition and structure of the type, quantity, and cost of spare parts and minimizing their maintenance and restoration costs; optimizing the transport reliability structure (reducing the damage rate); and improving spare parts supply processes.

Problems of process management include [12]: reducing vehicle mileage, idling time, and stopping time; optimizing vehicle booking; optimizing calendar performance; optimizing the use of human resources in service processes (outages and inspections); optimizing the control system; adapting the type and quantity of transport activities to skills and tasks; optimizing vehicle purchases from a consumer perspective (technical state–cost); and optimizing the method for updating a company’s vehicle fleet. Solving these problems necessitates creating a model for the vehicle operating system in terms of regular transport with a particular focus on its hierarchical structure and work algorithms.

At present, there is a desire to continuously improve the efficiency of transport companies, with an ever-increasing demand for quality requirements and more stringent formal and legal regulations. Therefore, one of the critical elements that drive business development is using IT technologies and telecommunications more efficiently. Computer support for the maintenance subsystem (repair services) in transportation businesses may be implemented through independent computer programs such as CMMS (computerized maintenance management system), often in combination with existing or future Enterprise Resource Planning System (ERP) class systems, and through modules (or functions) of more complex ERP systems [24]. Manufacturers and distributors of computer software often fail to identify potential issues and costs associated with the implementation and use of systems, listing only the benefits of systems that, in most cases, include more efficient use of commercial resources that are expected to provide: reduced production costs, reduced inventory requirements, reduced damage to vehicles, etc. [24]. The absence of a precise, consistent, and unified method for describing the properties of the goods offered makes their valuation and comparison difficult [25,26]. Methods for evaluating information technologies of the maintenance support system and optimizing the selection of these systems for an enterprise can be divided into two main groups: (1) Objective methods based on mathematically optimized problems; (2) Subjective approaches based on the analysis of the selected criteria and their respective contributions.

It is proposed to evaluate the services of supporting IT systems and optimize the selection of those systems within a specific enterprise [16,27]. The constant desire to reduce operating costs at transport enterprises to minimize downtime and emergencies, preventive services, and the constant increase in the safety requirements for the use of vehicles specify the need to use IT-support systems. The main objectives that can be achieved by implementing and using electronic systems efficiently will improve the efficiency and quality of the processes implemented.

1.2. Aims and Objectives of the Study

The research goal is to use a mathematical model that allows one to optimize the transport task in the Russian region, based on the chosen parameters, both in the conditions of a particular truck and a fleet of trucks. To fulfill this goal, it is necessary to perform the following tasks:

-

establish parameters for matching truck and cargo to perform single and multiple transportation tasks,

-

apply the developed mathematical models under the conditions of simulating the operation of a particular truck/truck fleet to determine the effectiveness of the developed models,

-

give recommendations on the use of the developed mathematical models.

The next part of the article includes the following main sections: 2. Materials and Methods; 3. Results; 4. Discussion; 5. Conclusions; 6. Abbreviations; 7. Notations; 8. Author Contributions and References.

2. Materials and Methods

The methodology of this investigation was partially taken from work [28]. In that work, studies were carried out and a mathematical model was developed to optimize the task of finding a match between the characteristics of the truck and the load. The experimental data were obtained from one of the transport enterprises of Saint-Petersburg, Russian Federation. Performing DP (delivery performance) transportation tasks require sensible truck scheduling. There is consistency between trucks, DP tasks, and loads. The TC (truck and cargo) matching parameters were converted into matching parameters between DP tasks and trucks.

There are some important indicators of matching transport tasks and trucks: function (cargo type, truck type), state (done, completed, and in progress for transport task; works, idle, and in repair for the truck), expenses (required value corresponding to weight and volume of cargo for transport task; fare for the truck), time (transport period for transport task and period of shipment for the truck), quality (friendliness of cargo supplier for transport task and reputation, driver experience, driver level, and information security of the truck supplier for the truck), and distance (source for transport task and truck location). 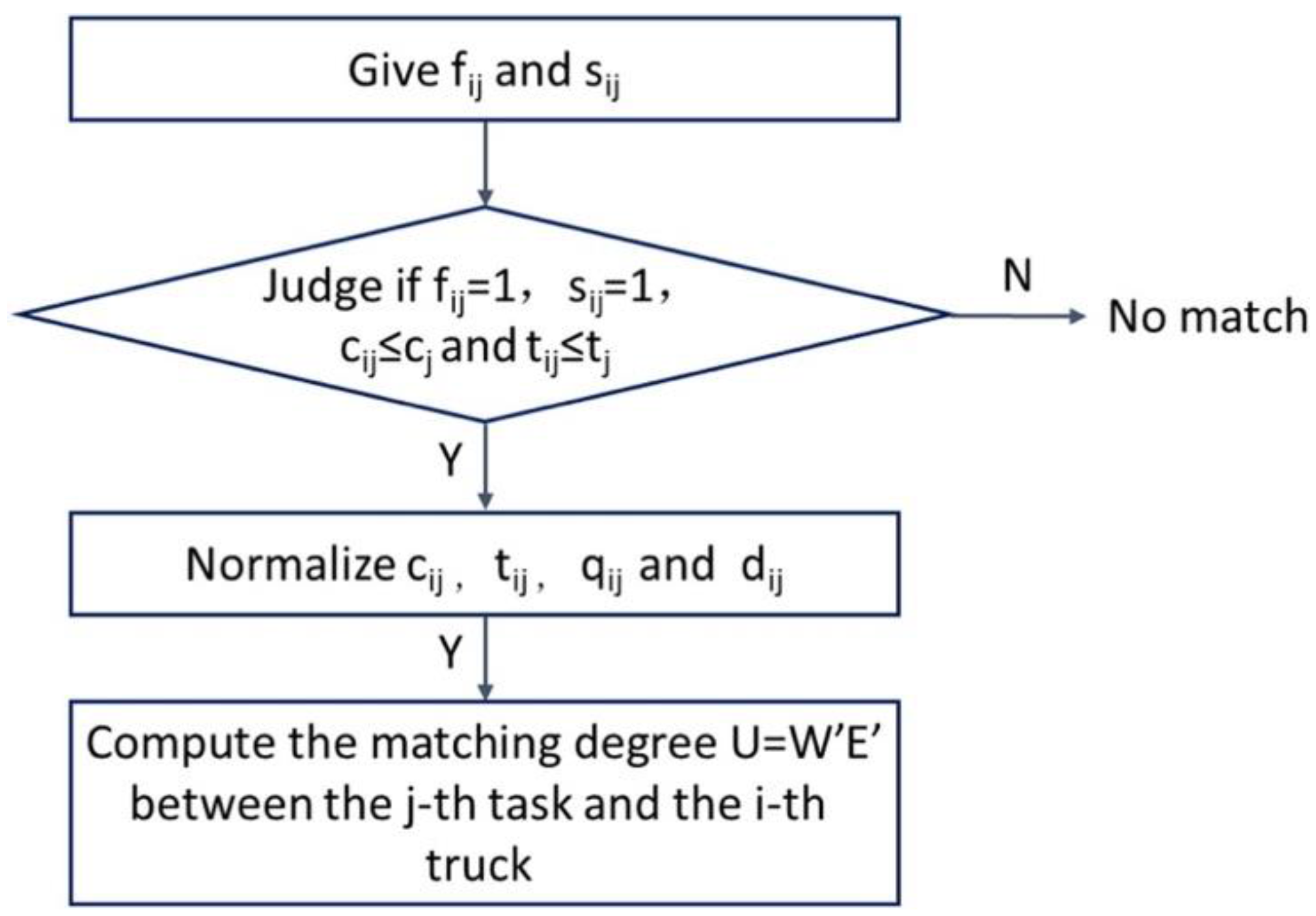Figure 1 shows the algorithm of the truck and task connection.

Where $f_j, s_j, c_j, t_j, q_j,w_j d_j$—function, state, cost, time, quality, weight, and distance for DP transport task $L_j$, respectively. Characteristics of the truck $E_i$, suitable for the task $L_j$, can be described as:

$$E_{ij}=\left\{f_{ij}, s_{ij}, c_{ij}, t_{ij}, q_{ij}, d_{ij}\right\}$$

(1)

$f_{ij}$ reflects whether the truck meets the functional requirements of the transport task $L_j$; $s_{ij}$—the condition of the truck (e.g., idle and under repair); $c_{ij}$—whether the truck meets the cost requirements of the task $L_j$; $t_{ij}$—whether the truck meets the time requirements of the task $L_j$; $q_{ij}$—whether the truck meets the quality requirements of the task $L_j$; and $d_{ij}$ displays the current coordinates of the truck. Feature matching between tasks and trucks was performed in three steps:

Step 1: Feature-state matching.

If $i-\mathrm{th}$ truck has the function of performing $j-\mathrm{th}$ task, $f_{ij}=1$; otherwise, $f_{ij}=0$. In the latter case, $i-\mathrm{th}$ truck is not suitable for $j-\mathrm{th}$ task, and the feature comparison stops.

If $i-\mathrm{th}$ truck is idle and $j-\mathrm{th}$ task is performed, $c_{ij}=1$; otherwise, $c_{ij}=0$. In the latter case, $i-\mathrm{th}$ truck is not suitable for $j-\mathrm{th}$ task, and the feature comparison stops.

Step 2: Matching cost, time, weight, and distance.

According to the definitions of truck characteristics and task characteristics, the cost, time, quality, and distance of $j-\mathrm{th}$ task can be described by the vector:

$$L_j^{\prime }=\left\{c_j, t_j, q_j, d_j\right\}$$

(2)

If $j-\mathrm{th}$ task is performed by $i-\mathrm{th}$ truck, then the cost, time, quality, and distance of $j-\mathrm{th}$ task can be described by another vector $\left\{c_{ij}, t_{ij}, q_{ij}, d_{ij}\right\}$.

If $c_{ij}\le c_i$, and $t_{ij}\le t_i$, it is necessary to go to step 3. Otherwise $i-\mathrm{th}$ truck does not match $j-\mathrm{th}$ task, and the feature comparison stops.

Step 3. One needs to set the values of the parameters $c_{ij}, t_{ij}, q_{ij}, d_{ij}$ as:

$$W^{\prime }=\{w_1^{\prime }, w_2^{\prime }, w_3^{\prime }, w_4^{\prime }\}$$

(3)

Next, it is necessary to adjust $t_{ij}$, for:

$$t_{ij}^{\prime }=\left|t_{ij}-t_i\right|,$$

(4)

adjust $d_{ij}$, for:

$$d_{ij}^{\prime }=\sqrt{{\left(d_{ij}-d_i\right)}^2+{\left(d_{ij}-d_i\right)}^2},$$

(5)

and then normalize $\left\{c_{ij}, t_{ij}^{\prime }, q_{ij}, d_{ij}^{\prime }\right\}$, to get the vector $E^{\prime }$. After that, one needs to determine the degree of compliance ($U$) between $i-\mathrm{th}$ truck and $j-\mathrm{th}$ task using a weighted factor analysis and add the trucks with the highest 2–5 degrees of matching to the set of candidate trucks for the j-th task:

$$U=W^{\prime }{E}^{\prime }$$

(6)

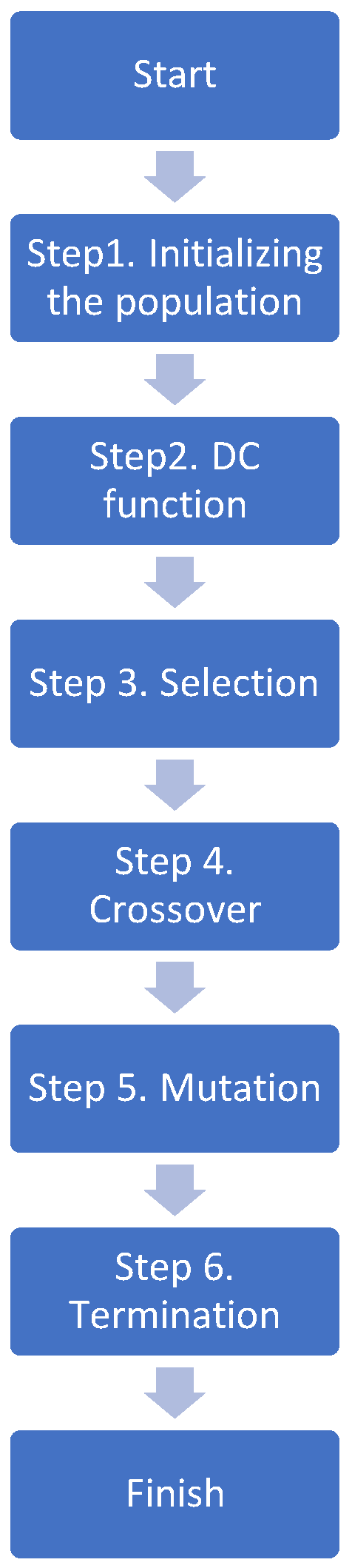
The GA (genetic algorithm) is an intelligent approach to global search that mimics natural evolution. With excellent adaptability, search efficiency, reliability, and parallelization, GA provides a suitable tool to solve the TC matching problem. Thus, the model was solved by GA in the following steps:

Step 1: Initializing the population.

Each solution has been written as a matrix. For example, solution X can be described as:

$$X=\left(\begin{array}{cccc}0& 0& 0& 0\\ 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$$

(7)

The solution means that truck 2 performs task 1, truck 3 performs task 2, truck 4 performs task 3, and truck 5 performs task 5.

The initial population was randomly generated.

Step 2: DC function.

In the TC matching model, the target function pursues the maximum DC and has been directly adopted as the GA (genetic algorithm) fitness function. Given the power limitations of the model, the penalty factor k was introduced as a DC function. If a person is an admissible solution, then k is 1; otherwise, k < 1. Then the individual DC function can be set as:

$$\begin{gathered} D{C}_i=k·\left(1-\sqrt{w_c^2+w_t^2+w_s^2}-\sqrt{{(w_c{\overline{C}}_z)}^2+{(w_t{\overline{T}}_z)}^2+{(w_s{\overline{S}}_z)}^2}/\sqrt{w_c^2+w_t^2+w_s^2}\right)· \\ (1-arccos\frac{w_c^2{\overline{C}}_z+w_t^2{\overline{T}}_z+w_s^2{\overline{S}}_z}{\sqrt{w_c^2+w_t^2+w_s^2}}/\pi /2) \end{gathered}$$

(8)

Step 3: Selection.

Let N be the population size. Then the probability of choosing the i-th individual can be obtained by the roulette method:

$$p_i=f_i/{{\displaystyle \sum }}_{i=1}^M{f}_i$$

(9)

Step 4: Crossover.

During crossover, the single-point crossover operator was used to create a new generation of individuals. The probability of crossover is usually $p_c\in \left[0.4, 0.99\right]$. For each person, a random number $r_i$ was generated in the interval [0, 1]. If $p_c>r_i$, then the individual was taken after the crossover ancestor.

Step 5: Mutation.

A basic bitwise mutation operator has been adopted for mutation. The probability of mutation is usually $p_m\in \left[0.0001, 0.1\right]$. For each person, a random number $r_i^{\prime }$ was generated in the interval [0, 1]. If $p_c>r_i$, then the individual was considered to be the parent of the mutation.

Step 6: Termination.

GA was stopped as soon as the number of iterations reached a specified maximum number. The maximum number of iterations is the maximum allowed cycles of genetic operations. To assess the accuracy of the GA model, methods to estimate the mean absolute error (MAPE), root mean square error (RMSE), and standard deviation error (SDE) were used. Statistical data processing was performed in the Statistics program.

The Figure 2 is shown below:

3. Results

The characteristics of each DP task were compared with the characteristics of the DP trucks. A set of candidate trucks for each task was constructed in advance. The features of the j-th DP problem were expressed as $L_j=\left\{1,1,84651,265,93.5\%,\left(25.38,36.46\right)\right\}$. The characteristics of 10 DP trucks, optional for this task, were described as $E_{1j}, E_{2j}\dots E_{10j}$ and given in

Table 1. Parameters of 10 trucks.

Truck	Function, ${\mathit{f}}_{\mathit{i}\mathit{j}}$	Condition, ${\mathit{s}}_{\mathit{i}\mathit{j}}$	Price, Rubles, ${\mathit{c}}_{\mathit{i}\mathit{j}}$	Time, Min., ${\mathit{t}}_{\mathit{i}\mathit{j}}$	Quality, %	Coordinates, km
$M_1$	1	1	42,274	243	94.9	20.36, 29.88
$M_2$	1	1	44,723	222	93.6	42.49, 30.68
$M_3$	1	1	45,397	219	95.8	32.36, 30.77
$M_4$	1	0	51,547	195	97.4	22.06, 29.54
$M_5$	1	1	43,119	168	96.2	39.23, 37.29
$M_6$	1	1	45,542	319	93.2	27.42, 40.26
$M_7$	1	1	39,519	219	92.6	28.78, 33.44
$M_8$	1	1	41,277	154	94.3	38.92, 37.90
$M_9$	0	1	50,600	202	95.8	21.92, 29.81
$M_{10}$	1	1	46,633	211	96.2	38.92, 47.90

.

Initially, $E_{ij}, E_{2j}, E_{3j}, E_{5j}, E_{7j}, E_{8,j}, E_{10j}$ were scanned based on $f_{ij}=1$, $s_{ij}=1$, $c_{ij}\le c_i$, $t_{ij}\le t_j$. Then, $t_{ij}^{\prime }$ and $d_{ij}^{\prime }$ were calculated and all parameters were normalized (

Table 2. Normalized parameters of DP complex of trucks.

Truck	Price, Rubles, ${\mathit{c}}_{\mathit{i}\mathit{j}}$	Time, Min., ${\mathit{t}}_{\mathit{i}\mathit{j}}$	Quality, %	Distance
$M_1$	0.1461	0.3907	0.1430	0.1438
$M_2$	0.1436	0.1421	0.1410	0.0707
$M_3$	0.1288	0.1302	0.1444	0.1424
$M_5$	0.1432	0.0539	0.1450	0.1885
$M_7$	0.1563	0.1302	0.1395	0.2872
$M_8$	0.1496	0.0464	0.1421	0.0951
$M_{10}$	0.1324	0.1065	0.1450	0.0724

).

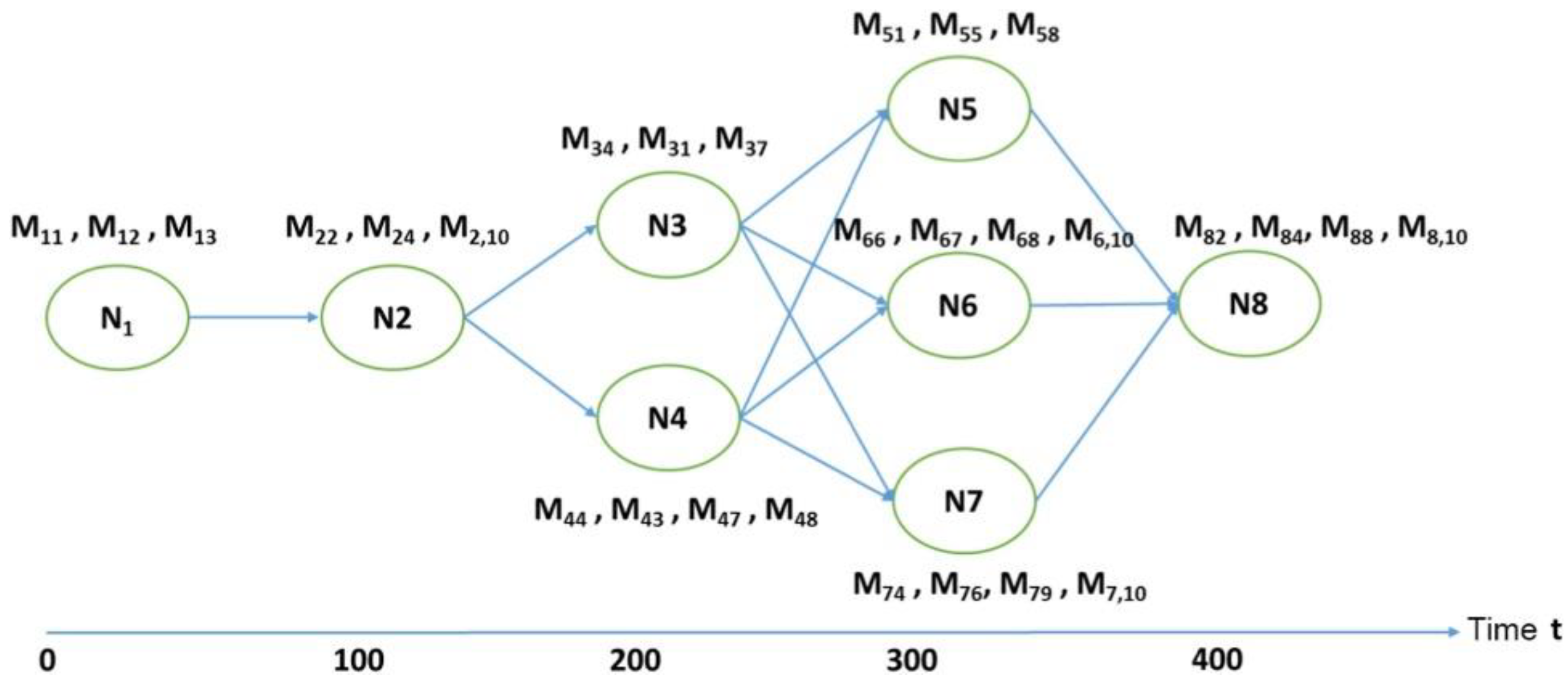
Let the weight vector $W^{\prime }$ be $\left\{0.3, 0.2, 0.3, 0.2\right\}$. Then, the degree of correspondence between the set of trucks ($M_1$, $M_2$, $M_3$, $M_5$, $M_7$, $M_8$, $M_{10}$) and the j-th task can be calculated as (0.1936, 0.1279, 0.1365, 0.1349, 0.1722, 0.1158, and 0.1190, respectively). One can see that truck number 1 and 7 must work for this task. Figure 3 shows the tasks, candidates, and sequences of tasks.

The operating time of each truck is 8 h per day from 9:00 a.m. to 5:00 p.m. Thus, the time t at 9:00 a.m. was set as 0 min, and at 5:00 p.m. as 480 min.

Table 3. DP transport task set demand parameters.

Task	Price, Rubles	Time, Min.	Time Window $({\mathit{T}}_{\mathit{j}1}, {\mathit{T}}_{\mathit{j}2})$	Reputation, %
$N_1$	67.9	62	15,75	95.9
$N_2$	72.3	64	62,122	94.8
$N_3$	54.9	96	203,263	93.3
$N_4$	94.6	120	194,254	96.4
$N_5$	43.5	63	277,337	93.2
$N_6$	84.0	105	281,341	95.2
$N_7$	69.3	99	293,353	96.6
$N_8$	42.6	80	365,425	97.3

shows the values of price, time, time window, and reputation requirements for a set of DP transportation tasks.

Table 4. Parameters of truck delivery.

Task	Candidate Trucker	Price, Rubles	Time, Min.	Reputation, %
$N_1$	$M_{11}$	66.2	62	99.9
	$M_{12}$	57.9	79	98.8
	$M_{13}$	73.1	68	99.5
$N_2$	$M_{22}$	72.5	64	99.8
	$M_{24}$	85.2	75	99.7
	$M_{2,10}$	74.6	83	98.4
$N_3$	$M_{34}$	54.4	96	99.3
	$M_{31}$	71.2	88	96.8
	$M_{37}$	71.4	101	96.5
$N_4$	$M_{44}$	93.9	120	97.4
	$M_{43}$	85.2	137	99.5
	$M_{47}$	90.8	113	99.8
	$M_{48}$	85.4	128	98.4
$N_5$	$M_{51}$	43.9	63	98.2
	$M_{55}$	51.1	59	99.0
	$M_{58}$	47.5	47	97.6
$N_6$	$M_{66}$	84.8	105	99.2
	$M_{67}$	71.6	92	98.3
	$M_{68}$	76.3	120	99.9
	$M_{6,10}$	74.5	112	96.9
$N_7$	$M_{74}$	74.6	99	98.6
	$M_{76}$	67.3	124	97.9
	$M_{77}$	67.3	100	99.5
	$M_{79}$	63.6	103	98.3
$N_8$	$M_{82}$	40.9	80	98.3
	$M_{84}$	43.6	56	97.3
	$M_{88}$	44.9	76	97.8
	$M_{8,10}$	48.6	69	99.4

shows the price, time, and reputation provided by the candidate truck.

Table 5. Cost and time of inter-task connection.

Connection	Cost		Time
	Symbol	Rubles	Symbol	Min.
$M_{12}\to M_{22}$	$c_{2221}$	3241.4	$t_{2221}$	22
$M_{24}\to M_{34}$	$c_{4342}$	4529.4	$t_{4342}$	34
$M_{24}\to M_{44}$	$c_{4442}$	3787.3	$t_{4442}$	39
$M_{13}\to M_{51}$	$c_{1513}$	699.5	$t_{1513}$	15
$M_{37}\to M_{67}$	$c_{7673}$	554.5	$t_{7673}$	12
$M_{47}\to M_{67}$	$c_{7674}$	5348.3	$t_{7674}$	41
$M_{48}\to M_{68}$	$c_{8684}$	3505.8	$t_{8684}$	30
$M_{58}\to M_{88}$	$c_{8885}$	3343.8	$t_{8885}$	29
$M_{68}\to M_{88}$	$c_{8886}$	486.2	$t_{8886}$	18
$M_{6,10}\to M_{8,10}$	$c_{10,8,10,6}$	418.0	$t_{10,8,10,6}$	17
$M_{7,10}\to M_{8,10}$	$c_{10,8,10,7}$	563.0	$t_{10,8,10,7}$	16

shows the inter-task price and inter-task time for one task.

The authors performed a simulation in MATLAB 2018. The parameters of simulations were a population size of 300; a maximum number of 2000 iterations; a probability of selection of 0.85; $P_m$, 0.85; and $P_c$, 0.15. The program was run 30 times. From the 30 runs the optional value was chosen as the best solution. The best solution X if W = (0.5, 0.25, 0.25) can be expressed as (see

Table 6. Matrix of the best solution.

0	1	0	0	0	0	0	0
0	0	1	0	0	0	0	0
1	0	0	0	0	0	0	0
0	0	0	0	0	1	0	0
0	0	0	0	1	0	0	0
0	0	0	0	0	0	0	0
0	0	0	1	0	0	0	0
0	0	0	0	0	0	0	1
0	0	0	0	0	0	0	0
0	0	0	0	0	0	1	0

).

Analyzing the given data, one can conclude that task 2 is best suited for truck 1; truck 2—tasks 3 and 6; truck 3—task 1; truck 4—task 6; truck 5—task 5; truck 7—task 4; truck 8—task 8; and truck 10—task 7.

It can be concluded that using the task sequence shown in Figure 3 and also the parameters of truck delivery (Table 4) and cost and time of inter-task connection (Table 5) using the simulation in MATHLAB 2018 we found the best solution for these tasks. Thus, the developed algorithm can be used for the optimization of truck-cargo tasks.

4. Discussion

Direct transportation refers to the mode of transportation when the driver drives a trailer to a certain place, after which they leave this trailer and take a new trailer for delivery to another place. Vehicle matching cannot be realized without efficient LIS (logistics information sharing) platforms. In the late 20th century, several countries developed and implemented LIS platforms. In particular, the Felixstowe Cargo Processing System (FCPS) was introduced in the UK, DAKOSY in Germany, Tradegate in Australia, and PORTNET in Singapore [29]. The use of these platforms can significantly improve the logistical capabilities of these countries. Swedish retailers [30] investigated a LIS platform in different channel systems. Authors of [31] proposed the use of a blockchain and the Internet of Things (IoT) for developing a new LIS platform. The work [32] developed a model of a local LIS platform that encompasses core components, the scope of implementation, stakeholder interests, and operational interests.

Nourinejad et al. [33] developed a dynamic unbalanced truck outsourcing model that tracks ridership, free and busy vehicle outsourcing, and modeled and priced ridership in nonequilibrium bilateral markets. Lehmann [34] investigated the problem of using numerous contract matching. Considering the efficiency of truck use, authors of [35] investigated the planning of the small truckload market. Based on feedback from both truck and freight suppliers, researchers of [36] established a TC model for truck logistics platforms in China. Yu et al. Authors of [37] improved the balance algorithm for the TC matching model. Improvements concerned a more detailed study of the characteristics of the truck and cargo. Each trip was evaluated in terms of truck efficiency, cargo handling, and current location and time.

The work [38] described the aims and limitations of the TC model and developed an evolutionary algorithm to solve this problem. A penalty-based fading adaptation method was created to select the optimal quantum individual when there is no strong admissible solution in the early phase of the quantum swarm; the QIE algorithm completion mechanism was optimized for quantum swarm maturity [39,40]. Authors of [41] implemented the least squares support vector method (LS-SVM) for TC matching. In general, TC matching research has mainly focused on distributional network matching and matching efficiency. There are few reports on intelligent TC matching based on complex LIS platforms [42,43].

The work by Rojas Viloria et al. [44] reviewed optimization models within 79 reviewed publications, of which 31 studied logistics applications of parcel deliveries, 28 of them as a single approach where the only focus is delivery and three had multiple applications (e.g., humanitarian and delivery). Concerning the optimization objectives, 22 papers dealt with parcel delivery operations aimed at optimizing a single objective related to time (59%), distance (18%), cost (18%), and covered area/demand (5%). It can be noted that the current study’s approach to optimization (function, condition, cost, time, and quality) is fully consistent with the latest research in this area, and, therefore, is modern.

To summarize, there are many studies on macro-level matching problems (e.g., LIS platforms). Meanwhile, few scholars have dealt with such detailed issues as TC matching. In addition, previous TC comparison studies have usually involved a single truck supplier and have not considered the new concept of truck fleets. Thus, this paper is the original study on TC comparison in terms of truck fleet utilization.

5. Conclusions

This paper considered the task of optimizing a fleet of trucks in terms of freight delivery efficiency. The parameters (function, state, cost, time, and quality) were established and an algorithm for the process of comparing a particular truck and cargo within a single transportation task was developed. The above-mentioned parameters included some sub-parameters: function (cargo type, truck type), state (done, completed, and in progress for transport task; works, idle, and in repair for the truck), expenses (required value corresponding to weight and volume of cargo for transport task; fare for the truck), time (transport period for transport task and period of shipment for the truck), quality (friendliness of cargo supplier for transport task and reputation, driver experience, driver level, and information security of the truck supplier for the truck), and distance (source for transport task and truck location for the truck).

When there is a need to perform multiple freight tasks in a truck fleet environment, a mathematical model was developed that considers such factors as cost, time, quality, and reputation, allowing one to find an acceptable solution for a particular transportation task. The authors performed a simulation in MATLAB 2018. The parameters of simulations are a population size of 300; the maximum number of 2000 iterations; a probability of selection of 0.85; $P_m,$0.85; and $P_c$, 0.15. The program was run 30 times. From the 30 runs the optional value was chosen as the best solution. The above theoretical developments have been successfully applied to solve single and multiple transport problems under truck fleet simulation conditions. It is necessary to highlight that the results of this investigation have some limitations concerning the conditions of the experiment (population size of 300; the maximum number of 2000 iterations; and probability of selection of 0.85). The work results can be used to optimize the operation of truck fleets in the conditions of Russia and other countries.