State-of-the-Art Review on Probabilistic Seismic Demand Models of Bridges: Machine-Learning Application
Abstract
:1. Introduction
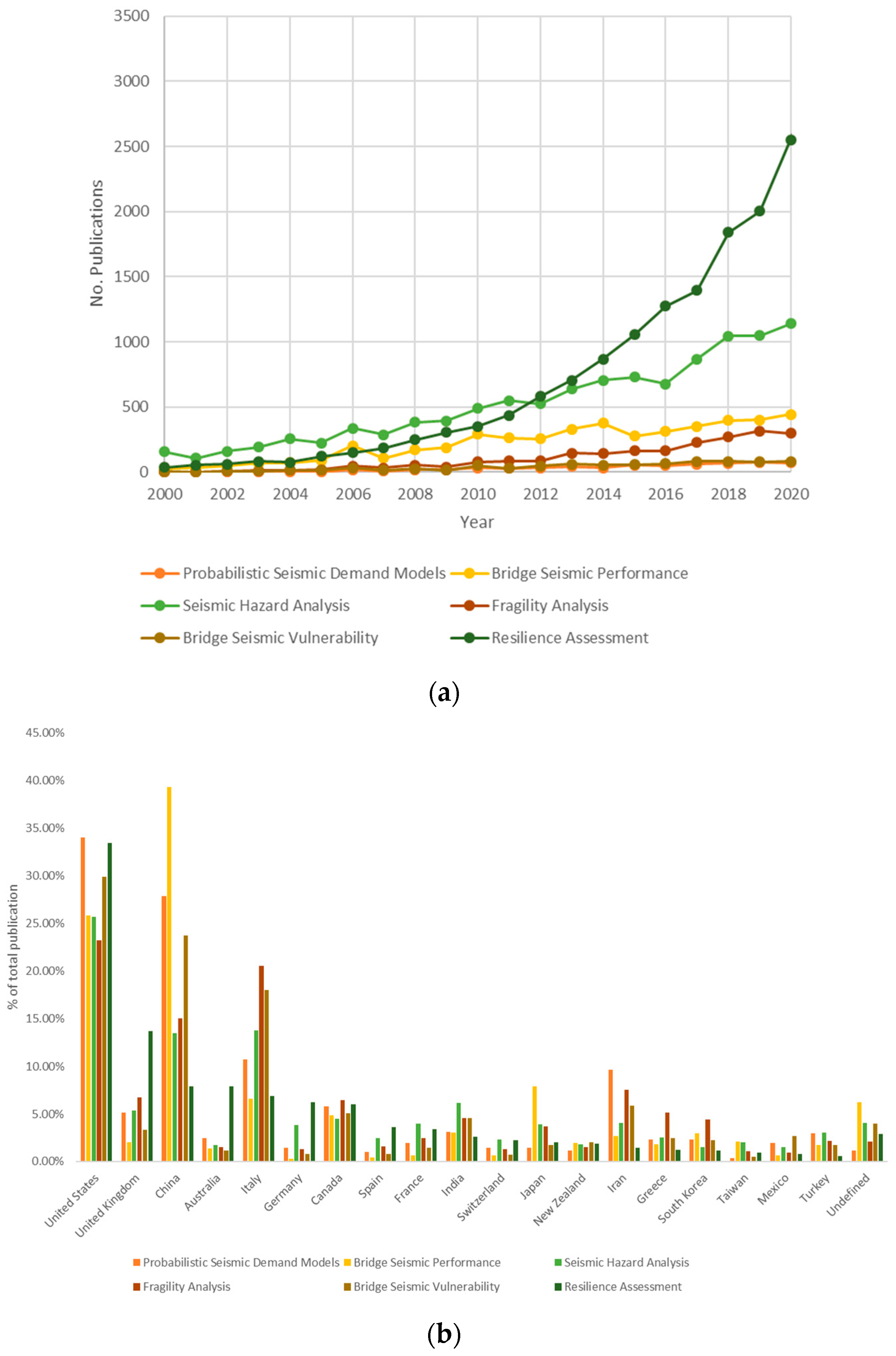
Literature Search Strategy
2. Seismic Vulnerability Assessment Using PSDMs
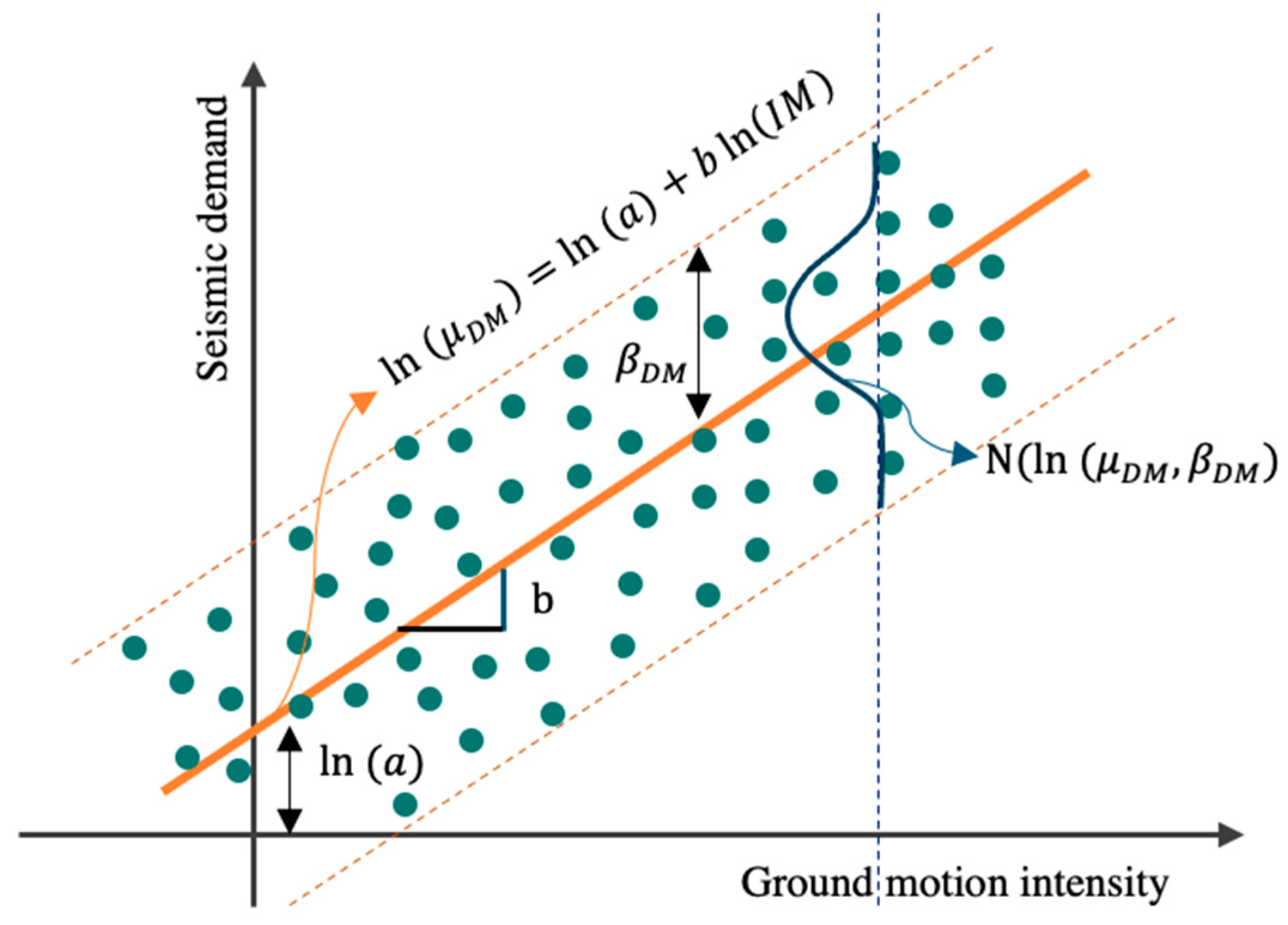
2.1. Description of PSDM and Univariate Linear Model
2.2. Alternative Statistical Models for Seismic Demand Regression
2.3. Multivariate Linear Regression and Feature Selection Techniques
2.3.1. Stepwise Regression
2.3.2. LASSO
2.4. Seismic Vulnerability Methodology Using Polynomial RSM
2.5. Random Forest
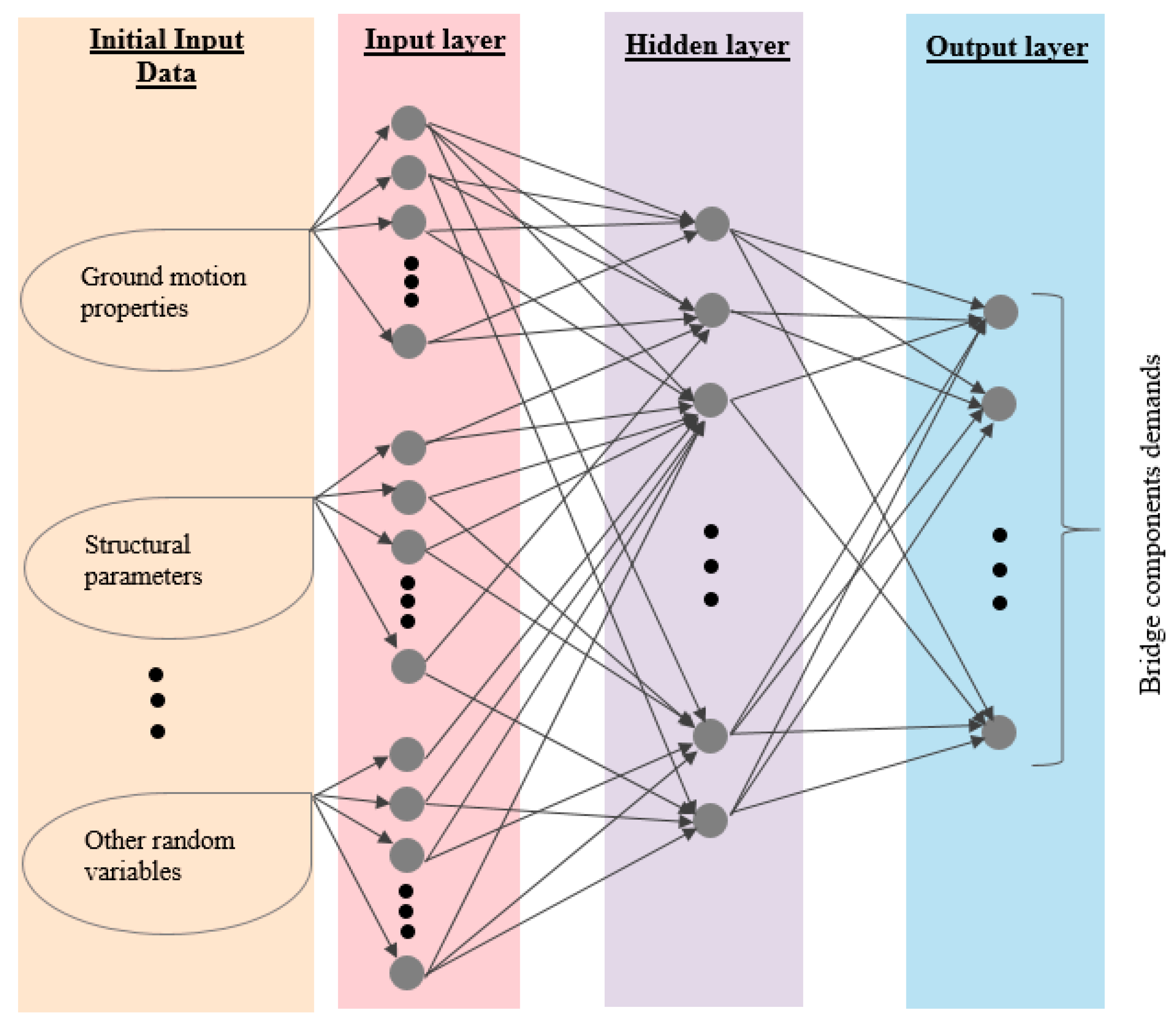
2.6. Artificial Neural Network
2.7. Surrogate Models
2.8. Multivariate Multiple Linear Regression
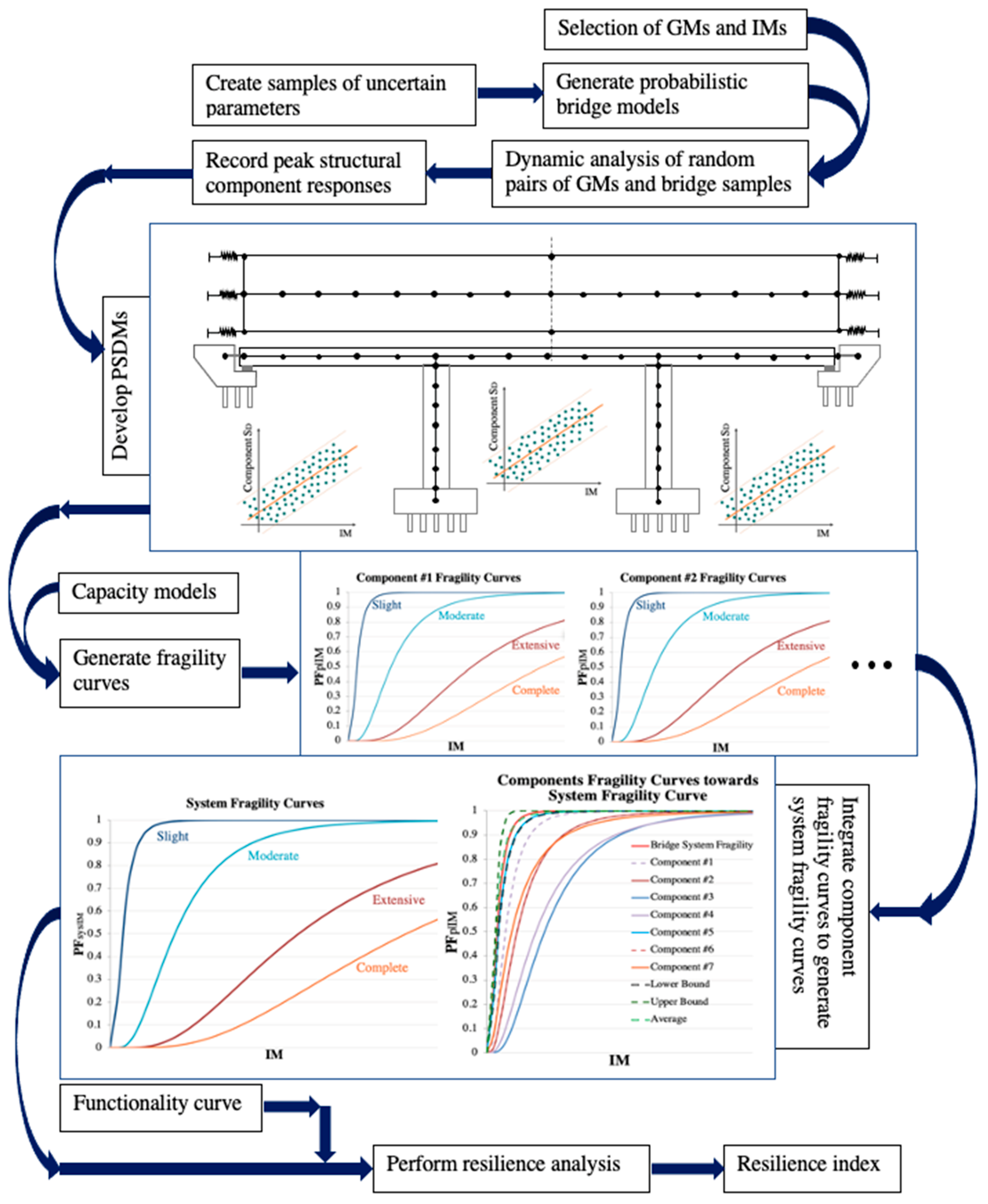
3. Application of the Demand Models to the Seismic Hazard Analysis
3.1. Fragility Curves
3.2. Resilience
4. Discussion
4.1. Comparative Analysis of Highlighted Methodologies
4.2. Challenges to Be Addressed in Future Research
- The primary reason for the popularity of the univariate conventional model is its simplicity. However, the growing advanced statistical and ML methodologies make it feasible to develop efficient yet simple PSDMs with the most influential set of predictors that would be practical to infer. Despite the existing variety of ML algorithms, there is a gap between all the theoretical aspects and the engineering applications related to the PSDMs. Although there has been a growing body of research to implement the recently developed ML methodologies, such methods have not yet been widely applied in PSDMs, and more studies are needed to apply novel ML approaches on various bridge types. Their application in seismic resilience assessment is also yet to be explored.
- The log-normality assumption of the demand and capacity needs to be reassessed. As mentioned in the previous sections, a couple of more recent studies proved that this assumption is not compatible with all demands and bridge types. The distribution type can lead researchers to choose the appropriate ML algorithm since every algorithm has its own underlying assumptions for the input and output distribution.
- Generally, a PSDM model correlates selective input parameters to a specific demand parameter. Although some of the proposed response surface models provide higher accuracy, using too many predictors, on one hand, increases the chance of overfitting and on the other hand, makes the final model impractical to implement in practice. To this end, the design of the experiment or a prior sensitivity analysis was commonly performed to consider specific input parameters in each round of analyses. In fact, this issue can be currently addressed effortlessly as a part of developing the model, using the capabilities of ML approaches such as the feature selecting techniques (such as elastic net, stepwise regression, LASSO, and random forest) that are embedded in the model-training algorithms. These techniques have been used by a few researchers for basic models, but they should be considered as an essential step to integrate with more complex models such as PRSM.
- As mentioned earlier (see section titled Description of PSDM and Univariate Linear Model), the selection of appropriate IMs is critical for developing a practical PSDM. However, in the conventional form of PSDM (i.e., Equations (2) and (3)), a single IM is chosen to estimate demands. A variety of IMs exists that their level of importance as an input variable in the PSDM needs to be assessed. This can lead to PSDMs with multiparameter IM to include parameters such as the PGA, PGV, etc. As stated earlier, some studies proposed an optimal intensity measure for specific bridge types by iteratively varying IMs in the models while monitoring the resulting variations in the estimated demand. However, these findings may not be generalized to bridges with different characteristics since each study is limited to a particular bridge type and specific structural parameters. For example, spectral acceleration could be a suitable candidate for bridge components whose response is significantly correlated with Sa. This typically happens when the corresponding response has not yet reached a highly inelastic range, and its seismic demand is governed by a single fundamental mode of vibration. On the contrary, alternative IMs need to be investigated to take the effect of inelasticity and the higher modes of vibration. There yet remains a principal milestone to identify the IMs that are highly correlated with the demands of various components of a bridge and to propose a more generalized recommendation for the selection of efficient IMs in developing PSDMs.
- Previous studies investigated PSDMs for a variety of EDPs (commonly selected arbitrarily or based on engineering judgment) among which the demands associated with the bridge column failure are found to be the most common primary demand in estimating the vulnerability of the bridge system. In order to incorporate the results of PSDMs into the fragility and resilience evaluation of bridges, the PSDMs of the various bridge components need to be derived individually; then, individual fragilities are generated for each component, and these fragilities are combined in a later step to determining the fragility of the bridge system. In this process, the correlation between the EDPs is often assumed, as noted in previous literature. However, this correlation could alter the overall conclusions. Thereby, further research is required to investigate the influence of this correlation on the fragility and resilience analysis. Moreover, the correlation between the responses of the different bridge components can be analyzed using advanced ML approaches to improve the overall assessment. Moreover, there is a potential to incorporate all EDPs of interest into a single multivariate PSDM. In fact, such a model could not only replace the costly derivation of the system’s fragility from individual fragilities but would also be able to capture the correlation between different EDPs.
- Overall, for the prediction of bridge demands, the application of tree-based ML algorithms and the polynomial orders higher than two and nonlinear methods is limited. Previous studies found decision tree and ANN algorithms effective in terms of capturing the complexity in data. Among the available tree-based methods, only random forest has been tested by a few researchers; hence, future research can investigate the performance of other bagging and boosting algorithms such as least squares boosting. Furthermore, it was noted that the application of ANN in this field is very limited. In this ML approach, the number of hidden layers and the number of nodes influence the efficiency of the ANN algorithm [94]. As stated, previous studies that applied ANN only used one hidden layer and assumed a particular number of nodes for their analysis. However, on the application of ANN for estimating the bridge , further studies are needed to determine the optimal number of hidden layers as well as the number of nodes to optimize the model efficiency.
- As described, PSDMs are extensively used to generate analytical fragility curves that are used to estimate the resilience of bridges. To this end, relatively few studies have focused on applying different ML algorithms to improve fragility functions. In particular, most studies parameterized fragility functions that are primarily developed through logistic regression. Thus, research needs to explore the performance of other methods in terms of fragility analysis of bridges.
- Similar to the fragility analysis, the relevant studies on the resilience assessment of bridges need to be expanded. As it is shown in the Resilience section, there is no clear consensus in resilience and lifecycle assessment using PSDMs. The literature is in agreement that the failure absorption patterns upon seismic event occurrence can be simplified as a sudden drop in functionality/performance with an associated probability of exceedance. However, the main difference in approaches seems to be focused on formulating the recovery trajectories. While many have proposed a variety of analytical trajectories to account for different scenarios, some have simplified the recovery/restoration patterns as a sudden rise in functionality with mean recovery time, driven by expert judgment.
4.3. Potential Future Developments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ang, A.-S.; De Leon, D. Modeling and analysis of uncertainties for risk-informed decisions in infrastructures engineering. Struct. Infrastruct. Eng. 2005, 1, 19–31. [Google Scholar] [CrossRef]
- Mackie, K.; Stojadinovic, B. Probabilistic Seismic Demand Model for California Highway Bridges. J. Bridge Eng. 2001, 6, 468–481. [Google Scholar] [CrossRef] [Green Version]
- Shome, N.; Cornell, C.A.; Bazzurro, P.; Carballo, J.E. Earthquakes, Records, and Nonlinear Responses. Earthq. Spectra 1998, 14, 469–500. [Google Scholar] [CrossRef]
- Cornell, C.A.; Krawinkler, H. Progress and challenges in seismic performance assessment. PEER CTR News 2000, 3, 1–3. [Google Scholar]
- Hwang, H.; Jernigan, B.J.; Lin, W.Y. Evaluation of seismic damage to Memphis bridges and highway systems. J. Bridge Eng. 2000, 5, 322–330. [Google Scholar] [CrossRef]
- Gardoni, P.; Mosalam, K.M.; DER Kiureghian, A. Probabilistic seismic demand models and fragility estimates for RC bridges. J. Earthq. Eng. 2003, 7, 79–106. [Google Scholar] [CrossRef]
- Nielson, B.G. Analytical Fragility Curves for Highway Bridges in Moderate Seismic Zones. Doctoral Dissertation, Georgia Institute of Technology, Atlanta, GA, USA, 2005. [Google Scholar]
- Padgett, J.E.; DesRoches, R. Methodology for the development of analytical fragility curves for retrofitted bridges. Earthq. Eng. Struct. Dyn. 2008, 37, 1157–1174. [Google Scholar] [CrossRef]
- Zhong, J.; Gardoni, P.; Rosowsky, D.; Haukaas, T. Probabilistic Seismic Demand Models and Fragility Estimates for Reinforced Concrete Bridges with Two-Column Bents. J. Eng. Mech. 2008, 134, 495–504. [Google Scholar] [CrossRef]
- Ramanathan, K.N. Next Generation Seismic Fragility Curves for California Bridges Incorporating the Evolution in Seismic Design Philosophy. Doctoral Dissertation, Georgia Institute of Technology, Atlanta, GA, USA, 2012. [Google Scholar]
- Soleimani, F. Fragility of California Bridges-Development of Modification Factors. Doctoral Dissertation, Georgia Institute of Technology, Atlanta, GA, USA, 2017. [Google Scholar]
- Freddi, F.; Padgett, J.E.; Dall’Asta, A. Probabilistic seismic demand modeling of local level response parameters of an RC frame. Bull. Earthq. Eng. 2017, 15, 1–23. [Google Scholar] [CrossRef]
- Ma, H.-B.; Zhuo, W.-D.; Lavorato, D.; Nuti, C.; Fiorentino, G.; Marano, G.C.; Greco, R.; Briseghella, B. Probabilistic seismic response and uncertainty analysis of continuous bridges under near-fault ground motions. Front. Struct. Civ. Eng. 2019, 13, 1510–1519. [Google Scholar] [CrossRef]
- Maleki, S. Deck modeling for seismic analysis of skewed slab-girder bridges. Eng. Struct. 2002, 24, 1315–1326. [Google Scholar] [CrossRef]
- Shamsabadi, A.; Rollins, K.M.; Kapuskar, M. Nonlinear soil–abutment–bridge structure interaction for seismic performance-based design. J. Geotech. Geoenviron. Eng. 2007, 133, 707–720. [Google Scholar] [CrossRef]
- Monteiro, R.; Delgado, R.; Pinho, R. Probabilistic Seismic Assessment of RC Bridges: Part I—Uncertainty Models. In Structures; Elsevier: Amsterdam, The Netherlands, 2016; Volume 5, pp. 258–273. [Google Scholar]
- Xie, Y.; Zhang, J.; Desroches, R.; Padgett, J.E. Seismic fragilities of single-column highway bridges with rocking column-footing. Earthq. Eng. Struct. Dyn. 2019, 48, 843–864. [Google Scholar] [CrossRef]
- Xie, Y.; DesRoches, R. Sensitivity of seismic demands and fragility estimates of a typical California highway bridge to uncertainties in its soil-structure interaction modeling. Eng. Struct. 2019, 189, 605–617. [Google Scholar] [CrossRef]
- Padgett, J.E.; Desroches, R. Sensitivity of Seismic Response and Fragility to Parameter Uncertainty. J. Struct. Eng. 2007, 133, 1710–1718. [Google Scholar] [CrossRef] [Green Version]
- Soleimani, F.; Vidakovic, B.; DesRoches, R.; Padgett, J. Identification of the significant uncertain parameters in the seismic response of irregular bridges. Eng. Struct. 2017, 141, 356–372. [Google Scholar] [CrossRef]
- Soleimani, F.; Mangalathu, S.; DesRoches, R. A comparative analytical study on the fragility assessment of box-girder bridges with various column shapes. Eng. Struct. 2017, 153, 460–478. [Google Scholar] [CrossRef]
- Mangalathu Sivasubramanian Pillai, S. Performance Based Grouping and Fragility Analysis of Box-Girder Bridges in California. Doctoral Dissertation, Georgia Institute of Technology, Atlanta, GA, USA, 2017. [Google Scholar]
- Huang, Q.; Gardoni, P.; Hurlebaus, S. Probabilistic Seismic Demand Models and Fragility Estimates for Reinforced Concrete Highway Bridges with One Single-Column Bent. J. Eng. Mech. 2010, 136, 1340–1353. [Google Scholar] [CrossRef]
- Bin Ma, H.; Zhuo, W.D.; Yin, G.; Sun, Y.; Chen, L.B. A Probabilistic Seismic Demand Model for Regular Highway Bridges. Appl. Mech. Mater. 2016, 847, 307–318. [Google Scholar] [CrossRef]
- Seo, J.; Linzell, D.G. Use of response surface metamodels to generate system level fragilities for existing curved steel bridges. Eng. Struct. 2013, 52, 642–653. [Google Scholar] [CrossRef]
- Ghosh, J.; Padgett, J.E.; Dueñas-Osorio, L. Surrogate modeling and failure surface visualization for efficient seismic vulnerability assessment of highway bridges. Probab. Eng. Mech. 2013, 34, 189–199. [Google Scholar] [CrossRef]
- Pan, Y.; Agrawal, A.K.; Ghosn, M. Seismic Fragility of Continuous Steel Highway Bridges in New York State. J. Bridg. Eng. 2007, 12, 689–699. [Google Scholar] [CrossRef]
- Seo, J.; Linzell, D.G. Probabilistic Vulnerability Scenarios for Horizontally Curved Steel I-Girder Bridges under Earthquake Loads. Transp. Res. Rec. J. Transp. Res. Board 2010, 2202, 206–211. [Google Scholar] [CrossRef]
- Seo, J.; Linzell, D.G. Horizontally curved steel bridge seismic vulnerability assessment. Eng. Struct. 2012, 34, 21–32. [Google Scholar] [CrossRef]
- Park, J.; Towashiraporn, P. Rapid seismic damage assessment of railway bridges using the response-surface statistical model. Struct. Saf. 2014, 47, 1–12. [Google Scholar] [CrossRef]
- Seo, J.; Park, H. Probabilistic seismic restoration cost estimation for transportation infrastructure portfolios with an emphasis on curved steel I-girder bridges. Struct. Saf. 2017, 65, 27–34. [Google Scholar] [CrossRef]
- Du, A.; Padgett, J.E.; Shafieezadeh, A. Adaptive IMs for improved seismic demand modeling of highway bridge portfolios. In Proceedings of the 11th National Conference in Earthquake Engineering, Los Angeles, CA, USA, 25–29 June 2018. [Google Scholar]
- Mangalathu, S.; Jeon, J. Stripe-based fragility analysis of multispan concrete bridge classes using machine learning techniques. Earthq. Eng. Struct. Dyn. 2019, 48, 1238–1255. [Google Scholar] [CrossRef]
- Soleimani, F. Analytical seismic performance and sensitivity evaluation of bridges based on random decision forest framework. Structures 2021, 32, 329–341. [Google Scholar] [CrossRef]
- Pang, Y.; Dang, X.; Yuan, W. An Artificial Neural Network Based Method for Seismic Fragility Analysis of Highway Bridges. Adv. Struct. Eng. 2014, 17, 413–428. [Google Scholar] [CrossRef]
- Mangalathu, S.; Heo, G.; Jeon, J.-S. Artificial neural network based multi-dimensional fragility development of skewed concrete bridge classes. Eng. Struct. 2018, 162, 166–176. [Google Scholar] [CrossRef]
- Kameshwar, S.; Padgett, J.E. Response and fragility assessment of bridge columns subjected to barge-bridge collision and scour. Eng. Struct. 2018, 168, 308–319. [Google Scholar] [CrossRef]
- Kameshwar, S.; Padgett, J.E. Multi-hazard risk assessment of highway bridges subjected to earthquake and hurricane hazards. Eng. Struct. 2014, 78, 154–166. [Google Scholar] [CrossRef]
- Du, A.; Padgett, J.E. Multivariate surrogate demand modeling of highway bridge structures. In Proceedings of the 12th Canadian Conference on Earthquake Engineering, Quebec City, QC, Canada, 17–20 June 2019; pp. 17–20. [Google Scholar]
- Choe, D.-E.; Gardoni, P.; Rosowsky, D.; Haukaas, T. Seismic fragility estimates for reinforced concrete bridges subject to corrosion. Struct. Saf. 2009, 31, 275–283. [Google Scholar] [CrossRef]
- Zhong, J.; Gardoni, P.; Rosowsky, D. Bayesian Updating of Seismic Demand Models and Fragility Estimates for Reinforced Concrete Bridges with Two-Column Bents. J. Earthq. Eng. 2009, 13, 716–735. [Google Scholar] [CrossRef]
- Zakeri, B.; Padgett, J.E.; Amiri, G.G. Fragility Analysis of Skewed Single-Frame Concrete Box-Girder Bridges. J. Perform. Constr. Facil. 2014, 28, 571–582. [Google Scholar] [CrossRef]
- Tondini, N.; Stojadinovic, B. Probabilistic seismic demand model for curved reinforced concrete bridges. Bull. Earthq. Eng. 2012, 10, 1455–1479. [Google Scholar] [CrossRef]
- Soleimani, F.; Yang, C.S.W.; DesRoches, R. The Effect of Superstructure Curvature on the Seismic Performance of Box-Girder Bridges with In-Span Hinges. In Structures Congress; American Society of Civil Engineers: Reston, VA, USA, 2017; pp. 469–480. [Google Scholar]
- Abbasi, M.; Zakeri, B.; Amiri, G.G. Probabilistic Seismic Assessment of Multiframe Concrete Box-Girder Bridges with Unequal-Height Piers. J. Perform. Constr. Facil. 2016, 30, 04015016. [Google Scholar] [CrossRef]
- Noori, H.Z.; Amiri, G.G.; Nekooei, M.; Zakeri, B. Seismic Fragility Assessment of Skewed MSSS-I Girder Concrete Bridges with Unequal Height Columns. J. Earthq. Tsunami 2016, 10, 1550013. [Google Scholar] [CrossRef] [Green Version]
- Soleimani, F. Propagation and quantification of uncertainty in the vulnerability estimation of tall concrete bridges. Eng. Struct. 2020, 202, 109812. [Google Scholar] [CrossRef]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis, 5th ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013. [Google Scholar]
- Miller, A. Subset Selection in Regression; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso: A retrospective. J. R. Stat. Soc. 2011, 73, 267–288. [Google Scholar] [CrossRef]
- Shafieezadeh, A.; Ramanathan, K.; Padgett, J.E.; DesRoches, R. Fractional order intensity measures for probabilistic seismic demand modeling applied to highway bridges. Earthq. Eng. Struct. Dyn. 2012, 41, 391–409. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef] [Green Version]
- Heidari, A.A.; Faris, H.; Aljarah, I.; Mirjalili, S. An efficient hybrid multilayer perceptron neural network with grasshopper optimization. Soft Comput. 2019, 23, 7941–7958. [Google Scholar] [CrossRef]
- Huang, D.-S. Radial basis probabilistic neural networks: Model and application. Int. J. Pattern Recognit. Artif. Intell. 1999, 13, 1083–1101. [Google Scholar] [CrossRef]
- Bugmann, G. Normalized Gaussian Radial Basis Function networks. Neurocomputing 1998, 20, 97–110. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Simpson, T. Comparative studies of metamodelling techniques under multiple modelling criteria. Struct. Multidiscip. Optim. 2001, 23, 1–13. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Jekabsons, G.; Zhang, Y. Adaptive basis function construction: An approach for adaptive building of sparse polynomial regression models. Mach. Learn. 2010, 1, 127–155. [Google Scholar]
- Rosipal, R.; Krämer, N. Overview and Recent Advances in Partial Least Squares. In International Statistical and Optimization Perspectives Workshop “Subspace, Latent Structure and Feature Selection”; SLSFS 2005; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3940, pp. 34–51. [Google Scholar]
- Jeong, S.-H.; Elnashai, A.S. Probabilistic fragility analysis parameterized by fundamental response quantities. Eng. Struct. 2007, 29, 1238–1251. [Google Scholar] [CrossRef]
- Mangalathu, S.; Soleimani, F.; Jeon, J.-S. Bridge classes for regional seismic risk assessment: Improving HAZUS models. Eng. Struct. 2017, 148, 755–766. [Google Scholar] [CrossRef]
- Yu, O.; Allen, D.L.; Drnevich, V.P. Seismic vulnerability assessment of bridges on earthquake priority routes in Western Kentucky. In Lifeline Earthquake Engineering; ASCE: Reston, VA, USA, 1991; pp. 817–826. [Google Scholar]
- Sichani, M.E.; Padgett, J.E.; Bisadi, V. Probabilistic seismic analysis of concrete dry cask structures. Struct. Saf. 2018, 73, 87–98. [Google Scholar] [CrossRef]
- Jeon, J.-S.; Mangalathu, S.; Song, J.; Desroches, R. Parameterized Seismic Fragility Curves for Curved Multi-frame Concrete Box-Girder Bridges Using Bayesian Parameter Estimation. J. Earthq. Eng. 2017, 23, 954–979. [Google Scholar] [CrossRef]
- Balomenos, G.P.; Kameshwar, S.; Padgett, J.E. Parameterized fragility models for multi-bridge classes subjected to hurricane loads. Eng. Struct. 2020, 208, 110213. [Google Scholar] [CrossRef]
- Muntasir Billah, A.H.M.; Shahria Alam, M. Seismic fragility assessment of highway bridges: A state-of-the-art review. Struct. Infrastruct. Eng. 2015, 11, 804–832. [Google Scholar] [CrossRef]
- Hosseini, S.; Barker, K.; Ramirez-Marquez, J.E. A review of definitions and measures of system resilience. Reliab. Eng. Syst. Saf. 2016, 145, 47–61. [Google Scholar] [CrossRef]
- Woods, D.D. Four concepts for resilience and the implications for the future of resilience engineering. Reliab. Eng. Syst. Saf. 2015, 141, 5–9. [Google Scholar] [CrossRef]
- Henry, D.; Ramirez-Marquez, J.E. Generic metrics and quantitative approaches for system resilience as a function of time. Reliab. Eng. Syst. Saf. 2012, 99, 114–122. [Google Scholar] [CrossRef]
- Hajializadeh, D.; Imani, M. RV-DSS: Towards a resilience and vulnerability-informed decision support system framework for interdependent infrastructure systems. Comput. Ind. Eng. 2021, 156, 107276. [Google Scholar] [CrossRef]
- Sharma, N.; Tabandeh, A.; Gardoni, P. Resilience analysis: A mathematical formulation to model resilience of engineering systems. Sustain. Resilient Infrastruct. 2018, 3, 49–67. [Google Scholar] [CrossRef] [Green Version]
- Decò, A.; Bocchini, P.; Frangopol, D.M. A probabilistic approach for the prediction of seismic resilience of bridges. Earthq. Eng. Struct. Dyn. 2013, 42, 1469–1487. [Google Scholar] [CrossRef]
- Jia, G.; Tabandeh, A.; Gardoni, P. Life-Cycle Analysis of Engineering Systems: Modeling Deterioration, Instantaneous Reliability, and Resilience. In Risk and Reliability Analysis: Theory and Applications; Springer International Publishing: Cham, Switzerland, 2017; pp. 465–494. [Google Scholar]
- Sharma, N.; Tabandeh, A.; Gardoni, P. Regional resilience analysis: A multiscale approach to optimize the resilience of interdependent infrastructure. Comput. Civ. Infrastruct. Eng. 2020, 35, 1315–1330. [Google Scholar] [CrossRef]
- Applied Technology Council (ATC). Database on the Performance of Structures Near Strong-Motion Recordings: 1994 Northridge, California, Earthquake; Rep. No. ATC-38; Applied Technology Council: Redwood City, CA, USA, 2000. [Google Scholar]
- Briaud, J.-L.; Gardoni, P.; Yao, C. Statistical, Risk, and Reliability Analyses of Bridge Scour. J. Geotechnol. Geoenviron. Eng. 2014, 140, 04013011. [Google Scholar] [CrossRef]
- FEMA. HAZUS-MH MR4–Earthquake Model User Manual; FEMA: Washington, DC, USA, 2009. [Google Scholar]
- Applied Technology Council (ATC). Earthquake Damage Evaluation Data for California; Applied Technology Council: Redwood City, CA, USA, 1985. [Google Scholar]
- Karamlou, A.; Bocchini, P. Computation of bridge seismic fragility by large-scale simulation for probabilistic resilience analysis. Earthq. Eng. Struct. Dyn. 2015, 44, 1959–1978. [Google Scholar] [CrossRef]
- Gidaris, I.; Padgett, J.E.; Barbosa, A.; Chen, S.; Cox, D.; Webb, B.; Cerato, A. Multiple-Hazard Fragility and Restoration Models of Highway Bridges for Regional Risk and Resilience Assessment in the United States: State-of-the-Art Review. J. Struct. Eng. 2017, 143, 04016188. [Google Scholar] [CrossRef]
- Bocchini, P.; Decò, A.; Frangopol, D. Probabilistic functionality recovery model for resilience analysis. In Proceedings of the Bridge Maintenance, Safety, Management, Resilience and Sustainability, Stresa, Italy, 8–12 July 2012; pp. 1920–1927. [Google Scholar]
- Bocchini, P.; Frangopol, D.M. Optimal Resilience- and Cost-Based Postdisaster Intervention Prioritization for Bridges along a Highway Segment. J. Bridge Eng. 2012, 17, 117–129. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Banerjee, S. Retrofit Optimization for Resilience Enhancement of Bridges under Multihazard Scenario. J. Struct. Eng. 2016, 142, 4015012. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Reinhorn, A.M.; Bruneau, M. Seismic resilience of a hospital system. Struct. Infrastruct. Eng. 2010, 6, 127–144. [Google Scholar] [CrossRef]
- Kafali, C.; Grigoriu, M. Rehabilitation decision analysis. In ICOSSAR’05: Proceedings of the Ninth International Conference on Structural Safety and Reliability; IOS Press: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Hazus, M.H. Multi-Hazard Loss Estimation Methodology: Earthquake Model Hazus-MH MR5 Technical Manual; FEMA: Washington, DC, USA, 2011. [Google Scholar]
- Zhou, Y.; Banerjee, S.; Shinozuka, M. Socio-economic effect of seismic retrofit of bridges for highway transportation networks: A pilot study. Struct. Infrastruct. Eng. 2010, 6, 145–157. [Google Scholar] [CrossRef]
- Venkittaraman, A.; Banerjee, S. Enhancing resilience of highway bridges through seismic retrofit. Earthq. Eng. Struct. Dyn. 2014, 43, 1173–1191. [Google Scholar] [CrossRef]
- Chang, L.; Peng, F.; Ouyang, Y.; Elnashai, A.S.; Spencer, B.F., Jr. Bridge seismic retrofit program planning to maximize postearthquake transportation network capacity. J. Infrastruct. Syst. 2012, 18, 75–88. [Google Scholar] [CrossRef]
- Pang, Y.; Wei, K.; Yuan, W. Life-cycle seismic resilience assessment of highway bridges with fiber-reinforced concrete piers in the corrosive environment. Eng. Struct. 2020, 222, 111120. [Google Scholar] [CrossRef]
- Fu, Z.; Gao, R.; Li, Y. Probabilistic Seismic Resilience-Based Cost–Benefit Analysis for Bridge Retrofit Assessment. Arab. J. Sci. Eng. 2020, 45, 8457–8474. [Google Scholar] [CrossRef]
- Vishwanath, B.S.; Banerjee, S. Life-Cycle Resilience of Aging Bridges under Earthquakes. J. Bridge Eng. 2019, 24, 04019106. [Google Scholar] [CrossRef]
- Rafiq, M.; Bugmann, G.; Easterbrook, D. Neural network design for engineering applications. Comput. Struct. 2001, 79, 1541–1552. [Google Scholar] [CrossRef]
- Soleimani, F. Probabilistic seismic analysis of bridges through machine learning approaches. Structures 2022, 38, 157–167. [Google Scholar] [CrossRef]
- Soleimani, F.; Liu, X. Artificial neural network application in predicting probabilistic seismic demands of bridge components. Earthq. Eng. Struct. Dyn. 2021, 51, 612–629. [Google Scholar] [CrossRef]
- Soleimani, F.; Hajializadeh, D. Bridge seismic hazard resilience assessment with ensemble machine learning. Structures 2022, 38, 719–732. [Google Scholar] [CrossRef]

| Study | Bridge Demand Parameters | Intensity Measure | Investigated Input Uncertain Variables in the Formulation | Bridge Type | Methodology |
|---|---|---|---|---|---|
| Huang, Q., Gardoni, P., and Hurlebaus, S., 2010 [23] | Seismic univariate deformation and shear, bivariate deformation–shear demands | Pseudo-spectral acceleration and peak ground velocity | 12 parameters including span length, column height, column diameter-to-superstructure depth ratio, reinforcement nominal yield strength, concrete nominal strength, longitudinal reinforcement ratio, transverse reinforcement ratio, degree of skew, bridge dead load, pile soil stiffness, abutment models, two-span ratio | Reinforced concrete highway bridge with single-column bent and two spans | Correction term as a set of explanatory functions; using Bayesian updating approach |
| Ma, H.B., Zhuo, W.D., Yin, G., Sun, Y., and Chen, L.B., 2016 [24] | Maximum drift ratio at top of piers | The spectral acceleration at the fundamental period with 5% damping | One parameter: fundamental period (T) | Single column, regular continuous concrete highway bridges with three spans in China—8 representative regular highway bridges | Multiplicative factor as a function of fundamental period |
| Soleimani, 2017 [11] | Column curvature ductility, abutment displacement | Spectral acceleration at 1.0 s | One parameter corresponding to a geometric irregularity such as skew angle, tall column height, and unbalanced frame stiffness ratio | Box-girder concrete bridges in California | Mathematical optimization techniques; Levenberg–Marquardt method; Bayesian updating |
| Xie, Y., Zhang, J., DesRoches, R., and Padgett, J. E., 2019 [17] | Uplift demand (column drift ratio and normalized uplift angle) | Peak ground velocity, frequency duration, cumulative absolute velocity of exceedance, frequency at the largest spectral velocity | Rocking frequency parameter, effective height | Single-column concrete box-girder bridge with rocking isolation in California | General linear model with stepwise regression |
| Soleimani, F., Vidakovic, B., DesRoches, R., and Padgett, J. E., 2017 [20] | Column curvature ductility, foundation rotation and displacement, displacement of deck, abutment, bearing, and shear key | Spectral acceleration at 1.0 s | 42 categorical and numerical parameters including modeling, structural, material, and geometric characteristics of bridges | Concrete box-girder bridges in California with: (i) skew angle, (ii) a frame with unbalanced stiffness, and (iii) tall column heights | General linear model with LASSO |
| Xie, Y. and DesRoches, R., 2019 [18] | Column displacement ductility, displacements of abutment, foundation, bearing, and shear key | Spectral acceleration at 1.0 s | 18 random variables corresponding to soil-structure interaction that cover different soil zones | A two-span prestressed concrete box-girder bridge in California and supported on diaphragm abutments and a two-column central bent | General linear model with stepwise regression and LASSO |
| Seo and Linzell, 2013 [25] | Peak radial bearing deformations, peak tangential bearing deformations, peak radial abutment deformations directly adjacent to the bearing seats, peak tangential abutment deformations directly adjacent to the bearing seats, column curvature ductility | Peak ground acceleration | 13 macrolevel and microlevel parameters; number of spans, maximum span length, deck width, maximum column height, radius of curvature, girder spacing, cross-frame spacing, damping ratio, compressive and tensile strength and Young’s modulus of concrete, steel reinforced modulus and yield strength | Horizontally curved steel I-girder bridges in Pennsylvania, New York, and Maryland | 2nd order polynomial response surface model |
| Ghosh, J., Padgett, J.E., and Dueñas-Osorio, L., 2013 [26] | Column curvature ductility, longitudinal and transverse deformations of bearings and abutment | Spectral acceleration at the geometric mean of periods in the longitudinal and transverse directions | 10 parameters including steel strength, elastomeric bearing pad friction and gap and bar area, column reinforcing bar area, shear modulus of elastomeric bearing pads, concrete cover depth, column height, midspan length, number of columns per bent | Multispan (three-span three columns per bent) simply supported concrete girder bridge | 2nd order polynomial response surface model, multivariate adaptive regression splines, radial basis function networks, and support vector machines |
| Pan, Y., Agrawal, A.K., and Ghosn, M., 2007 [27] | Pier curvature, high and low type rocker bearing displacement | Peak ground acceleration, moment magnitude, and epicentral distance | Not available | Continuous multispan I-girder steel highway bridge in New York | General linear model and 2nd order polynomial response surface model |
| Seo and Linzell, 2010, 2012 [28,29] | Peak radial bearing deformations, peak tangential bearing deformations, peak radial abutment deformations directly adjacent to the bearing seats, peak tangential abutment deformations directly adjacent to the bearing seats, column curvature ductility | Peak ground acceleration | Number of spans, maximum span length, radius of curvature, girder spacing, cross-frame spacing | Horizontally curved steel I-girder bridges in Pennsylvania, New York, and Maryland | 2nd order polynomial response surface model |
| Park and Towashirapor, 2014 [30] | Seismic damage of bearings, piers, and abutments in terms of the maximum value of a response, such as displacement or curvature | Peak ground acceleration | Physical configuration of the bridge including the number of spans, span length, and pier height | Five span steel-plate girder bridges in Korea | 2nd order polynomial response surface model |
| Seo and Park, 2017 [31] | Peak responses corresponding to radial and tangential abutment components, radial and tangential bearing components, and pier columns | Peak ground acceleration | Number of spans, maximum span length, deck width, maximum column height, radius of curvature, girder spacing, cross-frame spacing | Curved steel I-girder bridges in Eastern United States | 2nd order polynomial response surface model |
| Du, A., Padgett, J. E., and Shafieezadeh, A., 2018 [32] | Column drift, displacement of expansion bearings and displacement of fixed bearings | One parameter from spectral acceleration and geometric mean of spectral accelerations at several periods, a total of four one-parameter adaptive IMs and two fractional-order adaptive IMs | 16 structure-related parameters for concrete bridge class and 14 structure-related parameters for slab bridge class | Two case-study highway bridge classes (multispan simply supported concrete girder bridges and multispan continuous slab) in Central and Southeastern United States | 2nd order polynomial response surface model with stepwise regression |
| Mangalathu and Jeon, 2019 [33] | Column curvature ductility, displacement of abutment and bearing, and superstructure unseating | Spectral acceleration at 1.0 s | 23 parameters including geometric, material, and structural modeling characteristics | Three four-span concrete box-girder bridges in California | Random forest |
| Soleimani, 2021 [34] | Column curvature ductility, displacement of deck, abutment, and bearing | Spectral acceleration at 1.0 s | 24 parameters including geometric, material, and structural modeling characteristics | Multispan concrete box-girder bridges with tall piers within low, medium, and high column height ratios | Random forest |
| Pang, Y., Dang, X., and Yuan, W., 2014 [35] | Curvatures of cross sections of columns, displacements of bearings and abutments | Peak ground acceleration | 16 selected material properties (four parameters for the confined concrete and three parameters for the unconfined concrete) and geometric parameters (span length, column height, deck width, column diameter, gap between girder and abutment and concrete cover) | Three-span continuous bridge with two columns per bent in China | Multilayer radial basis function neural networks |
| Mangalathu, S., Heo, G., and Jeon, J.S., 2018 [36] | Curvature ductility of column, maximum displacement of abutments, maximum deformation of bearing, maximum unseating deformation of superstructure | Spectral acceleration at 1.0 s | 23 parameters including categorical variables (e.g., the number of columns per bent, backfill type), numerical variables (e.g., the number of spans, the number of columns), and continuous variables (e.g., span length, concrete compressive strength) | Two-, three-, and four-span skewed concrete box-girder bridge with single and two columns per bent and seat abutment | Artificial neural networks with sigmoid activation function (one hidden layer with 10 neurons) |
| Kameshwar and Padgett, 2018 [37] | Shear and moment demands on bridge columns | Peak ground acceleration | 32 parameters design and geometric parameters related to superstructure, column, and sub-structure elements together with soil parameters and the barge collision conditions | Simply supported bridges (with six simply supported spans) on navigable waterways with large circular, elliptical, or wall type columns supported on pile foundations | 4th order polynomial response surface model with stepwise regression |
| Kameshwar and Padgett, 2014 [38] | Peak column curvature ductility, abutment and bearing displacements | Peak ground acceleration | Concrete nominal strength, reinforcement yield strength, span length, column height and diameter, width of deck, number of spans, longitudinal and transverse reinforcement ratios | Multispan simply supported concrete girder bridges located in South Carolina | Polynomial response surface models with three orders, adaptive basis function construction, multivariate adaptive regressive splines, and radial basis function interpolation |
| Du and Padgett, 2019 [39] | Column drift ratio, longitudinal and transverse deformation of expansion bearings and fixed bearings, abutment deformations | Spectral acceleration at the geometric mean of periods in the longitudinal and transverse directions | 14 parameters for concrete bridges 16 parameters for steel bridges | Two case studies: simply supported concrete girder and continuous steel girder bridge type | Multivariate linear regression, linear and partial kernel 2nd and 3rd order (L-PLSR and K-PLSR), artificial neural networks with a single hidden layer |
| Study | Key Aspects | Applicability Case Studies |
|---|---|---|
| Gardoni, P., Mosalam, K.M., and Der Kiureghian, A., 2003 [6]; Choe, D. E., Gardoni, P., Rosowsky, D., and Haukaas, T., 2009 [40]; Zhong, J., Gardoni, P., and Rosowsky, D., 2009 [41]; Huang, Q., Gardoni, P., and Hurlebaus, S., 2010 [23] | Produced probabilistic model from deterministic; moderate bias; improve accuracy | General type of bridges |
| Ma, H.B., Zhuo, W.D., Yin, G., Sun, Y., and Chen, L.B., 2016 [24] | Proposed simplified empirical expression for drift ratio of the bridge columns | General type of bridges |
| Soleimani, 2017 [11] | Proposed modified PSDMs to derive EDPs of irregular bridges; stiffness frames of bridges | Irregular bridges including skew angle, tall piers, and unbalanced stiffness frames of bridges. |
| Xie, Y., Zhang, J., DesRoches, R., and Padgett, J.E., 2019 [17] | Accounted for rocking isolation parameters; estimated full contact damage, rocking, and overturning probability of the bridge column | General type of bridges |
| Soleimani, F., Vidakovic, B., DesRoches, R., and Padgett, J.E., 2017 [20] | Identified influential uncertain parameters for bridges with geometric irregularities | Bridges with geometric irregularities |
| Xie and Desroches, 2019 [18] | Investigated the sensitivity of seismic demands to variation in its soil-structure interaction (SSI) modeling parameters | Typical highway bridge |
| Seo and Linzell, 2013 [25]; Seo and Linzell, 2010 [28]; Seo and Linzell, 2012 [29] | Examined the influence of important parameters on their seismic response | Horizontally curved steel I-girder |
| Gosh, J., Padgett, J.E., and Dueñas-Osorio, L., 2013 [26] | Explored four different metamodeling strategies to predict bridge responses | General type of bridges |
| Pan Y., Agrawal, A.K., and Ghosn, M., 2007 [27] | Performed an analytical seismic fragility analysis along with sensitivity assessment if seismic response to variations in superstructure mass, gap size, concrete compressive strength, reinforcing bar yield stress, friction coefficient of expansion bearing, and abutment wall–soil stiffness | Typical steel highway bridge |
| Park and Towashiraporn, 2014 [30] | Used response surface model to median and variation in seismic damage | Steel-plate-girder bridges |
| Du, A., Padgett, J.E., and Shafieezadeh, A., 2018 [32] | Established systematic optimization process to adaptively identify the optimal IM parameters to characterize the correlation between IMs and structural responses | General type of bridges |
| Seo and Park, 2017 [31] | Generated restoration curves | Portfolio of regional curved I-girder bridges |
| Mangalathu and Jeon, 2019 [33] | Generated bridge-specific fragility curves using random forest | General type of bridges |
| Soleimani, 2021 [34] | Conducted sensitivity analysis of seismic demands | Bridges with tall piers |
| Pang, Y., Dang, X., and Yuan, W., 2014 [35] | Proposed an artificial neural network-based prediction scheme to replace the extremely time-consuming process in traditional analytical fragility methodologies | General type of bridges |
| Mangalathu, S., Heo, G., and Jeon, J.S., 2018 [36] | Investigated the applicability of artificial neural network in the generation of seismic fragility curves for regional risk assessment of bridges to reduce computationally intensive procedure | General type of bridges |
| Kameshwar and Padgett, 2018 [37] | Developed parameterized polynomial response surface models to predict the shear and flexural response for a wide range of bridge characteristics and collision conditions without model-based simulation | General type of bridges |
| Kameshwar and Padgett, 2014 [38] | Generated parametric bridge fragility functions for bridges with different geometric and structural properties given exposure to different hazard types | General type of bridges |
| Du and Padgett, 2019 [39] | Provided a comparative study of four different multivariate surrogate demand modeling approaches | General type of bridges |
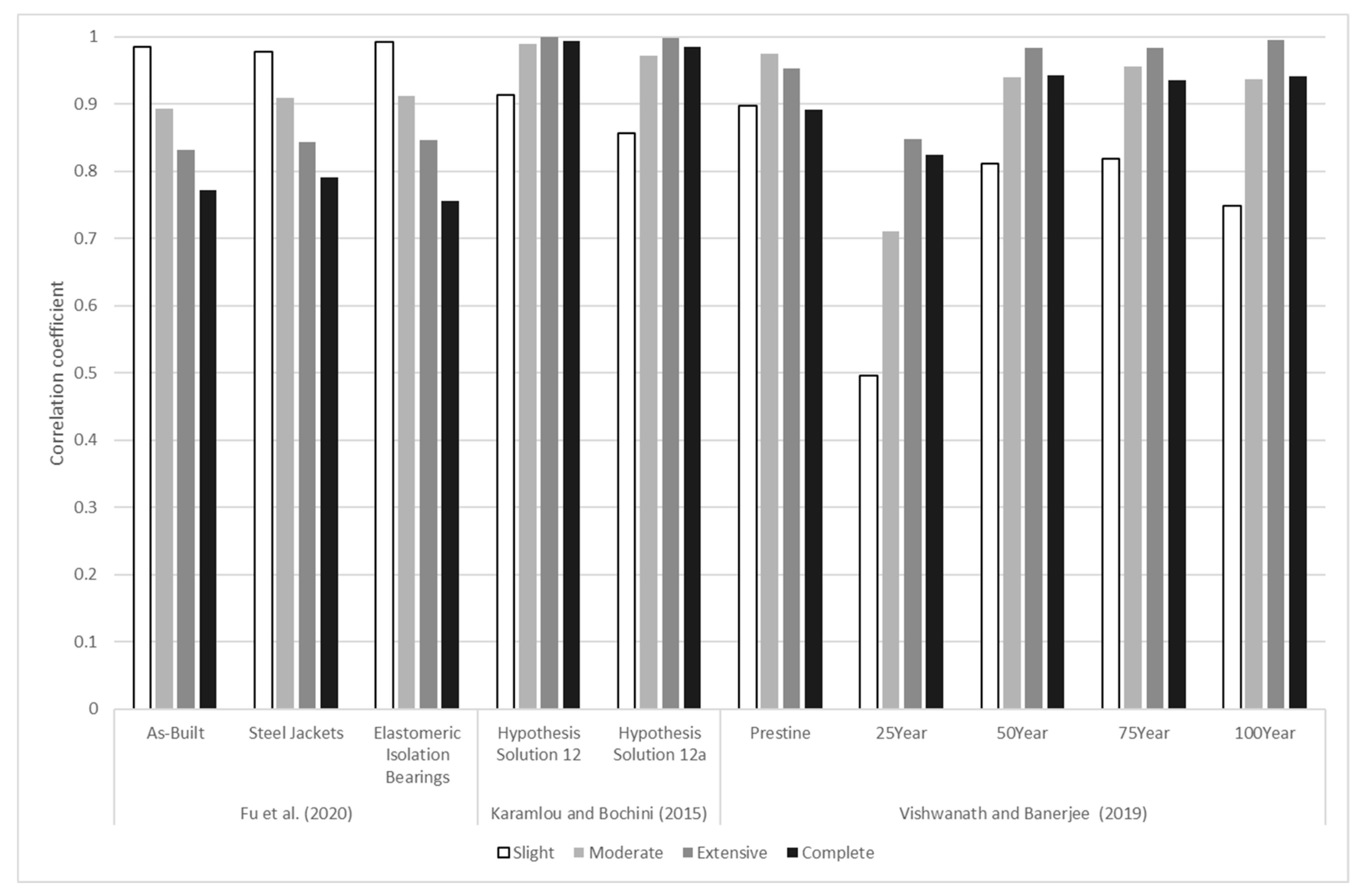
| Study | Fragility Models | Resilience Quantification Technique | Recovery Trajectory Profile | Correlation Coefficient Range between Resilience and Fragility Curves | Resilience as Lifecycle Analysis | Resilience Metric Reporting System |
|---|---|---|---|---|---|---|
| Pang, Wei, and Yuan (2020) [91] | Analytical fragility using PSDMs in Equations (3) and (4) | Equation (24) | Equation (26) with positive negative exponential, and trigonometric recovery profile | [0.7–0.9] | ✔ | Resilience as a function of time of occurrence and peak ground acceleration |
| Fu, Gao, and Li (2020) [92] | Analytical fragility using PSDMs in Equations (3) and (4) | Equation (24) | And Equation (26) to define and and using experimental data for constant parameters | [0.77–0.98] | ✘ | Resilience as a function of peak ground acceleration |
| Karamlou and Bocchini (2015) [80] | Analytical fragility using PSDMs in Equations (3) and (4) | Equation (24) | ATC-13 | [0.85–0.99] | ✔ | Resilience as a function of peak ground acceleration |
| Venkittaraman and Banerjee (2014) [89] | Simulation-based analytical fragility without using PSDMs | Equation (24) | Linear, negative exponential, and trigonometric | N/A resilience is not reported as a function of PGA | ✔ | Resilience as a function of recovery or control time |
| Vishwanath and Banerjee (2019) [93] | Simulation-based analytical fragility without using PSDMs | Equation (24) | Equation (26) and sigmoidal recovery profile | [0.49–0.99] | ✔ | Resilience as a function of age and peak ground acceleration |
| Method | Fundamental Advantages | Featured Disadvantages/Drawbacks |
|---|---|---|
| Unidimensional linear regression |
|
|
| Modification factors |
|
|
| Multiparameter general linear regression models, stepwise regression, LASSO |
|
|
| Polynomial regression |
|
|
| Random forest |
|
|
| Artificial neural networks |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soleimani, F.; Hajializadeh, D. State-of-the-Art Review on Probabilistic Seismic Demand Models of Bridges: Machine-Learning Application. Infrastructures 2022, 7, 64. https://doi.org/10.3390/infrastructures7050064
Soleimani F, Hajializadeh D. State-of-the-Art Review on Probabilistic Seismic Demand Models of Bridges: Machine-Learning Application. Infrastructures. 2022; 7(5):64. https://doi.org/10.3390/infrastructures7050064
Chicago/Turabian StyleSoleimani, Farahnaz, and Donya Hajializadeh. 2022. "State-of-the-Art Review on Probabilistic Seismic Demand Models of Bridges: Machine-Learning Application" Infrastructures 7, no. 5: 64. https://doi.org/10.3390/infrastructures7050064
APA StyleSoleimani, F., & Hajializadeh, D. (2022). State-of-the-Art Review on Probabilistic Seismic Demand Models of Bridges: Machine-Learning Application. Infrastructures, 7(5), 64. https://doi.org/10.3390/infrastructures7050064






