Structural Performance of Acute Corners on Skewed Bridge Decks Using Non-Linear Modeling of the Deck Parapet
Abstract
:1. Introduction
2. Materials and Methods
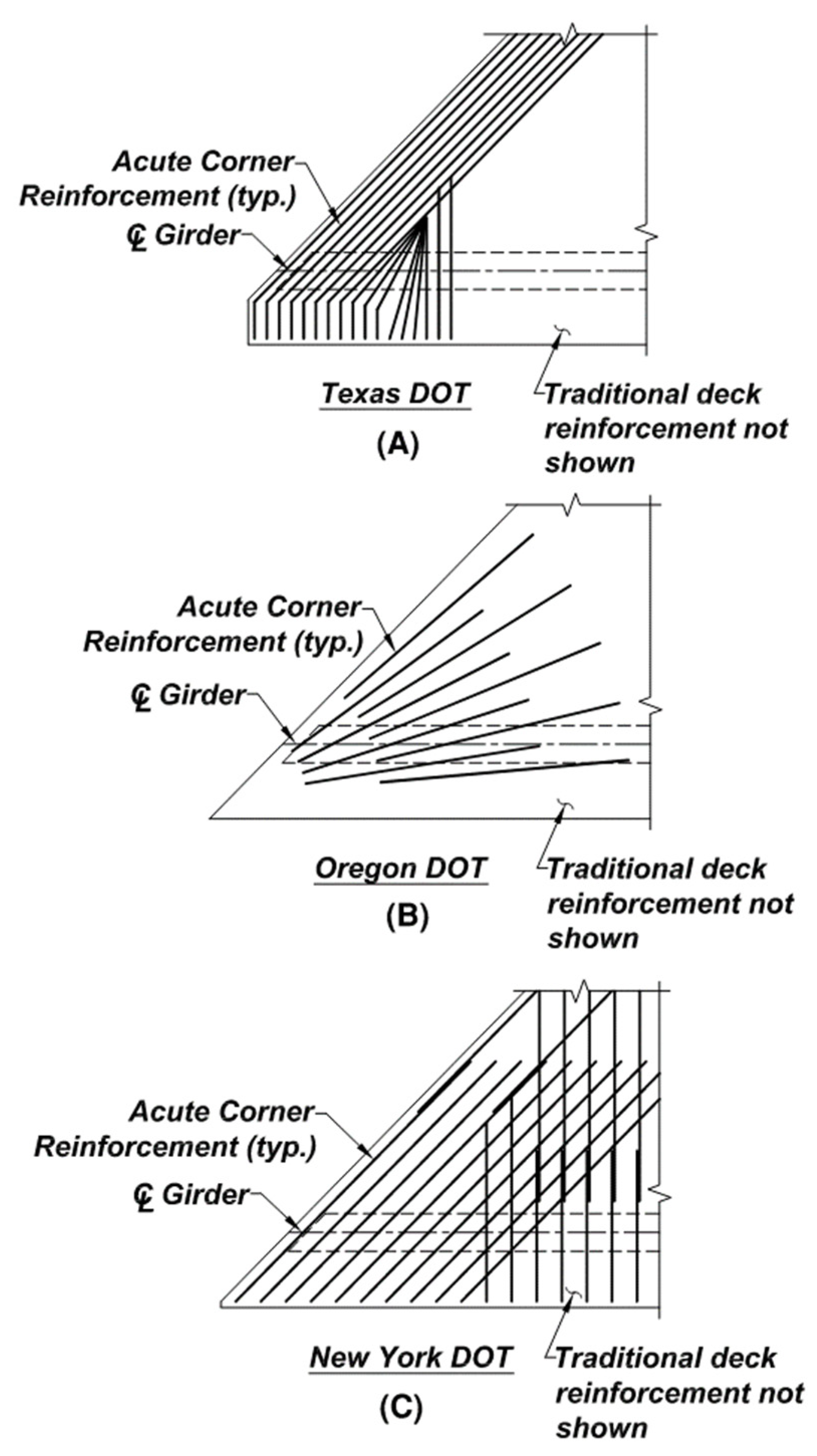
2.1. Current Practice in the Design of Acute Corner Reinforcement Details
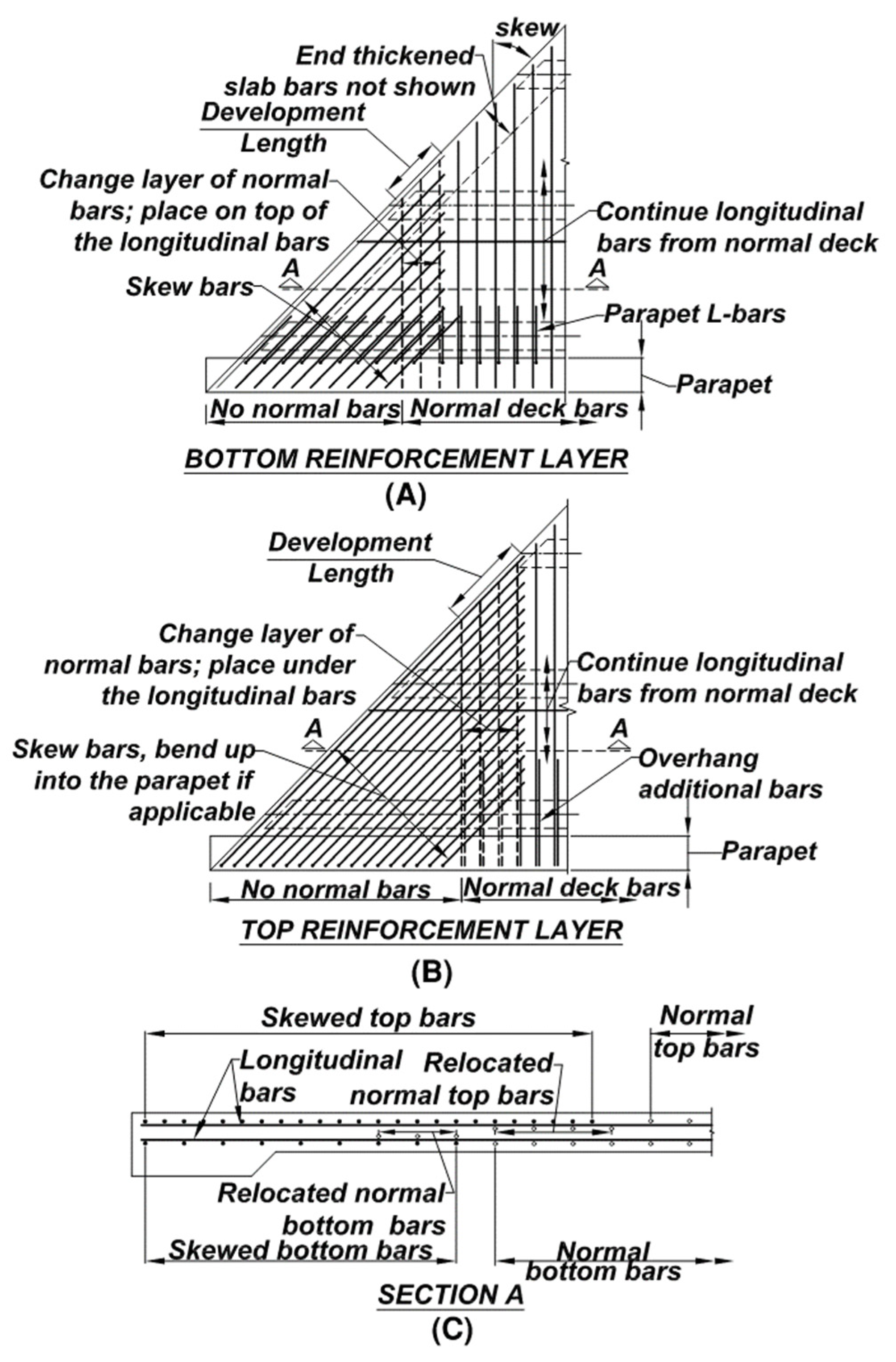
2.2. Proposed Detail for Acute Corner Reinforcing
2.3. AASHTO Design Requirements
2.3.1. Overhang Design
2.3.2. Parapet Design
2.4. Analytical Evaluation
2.4.1. Selection of Models
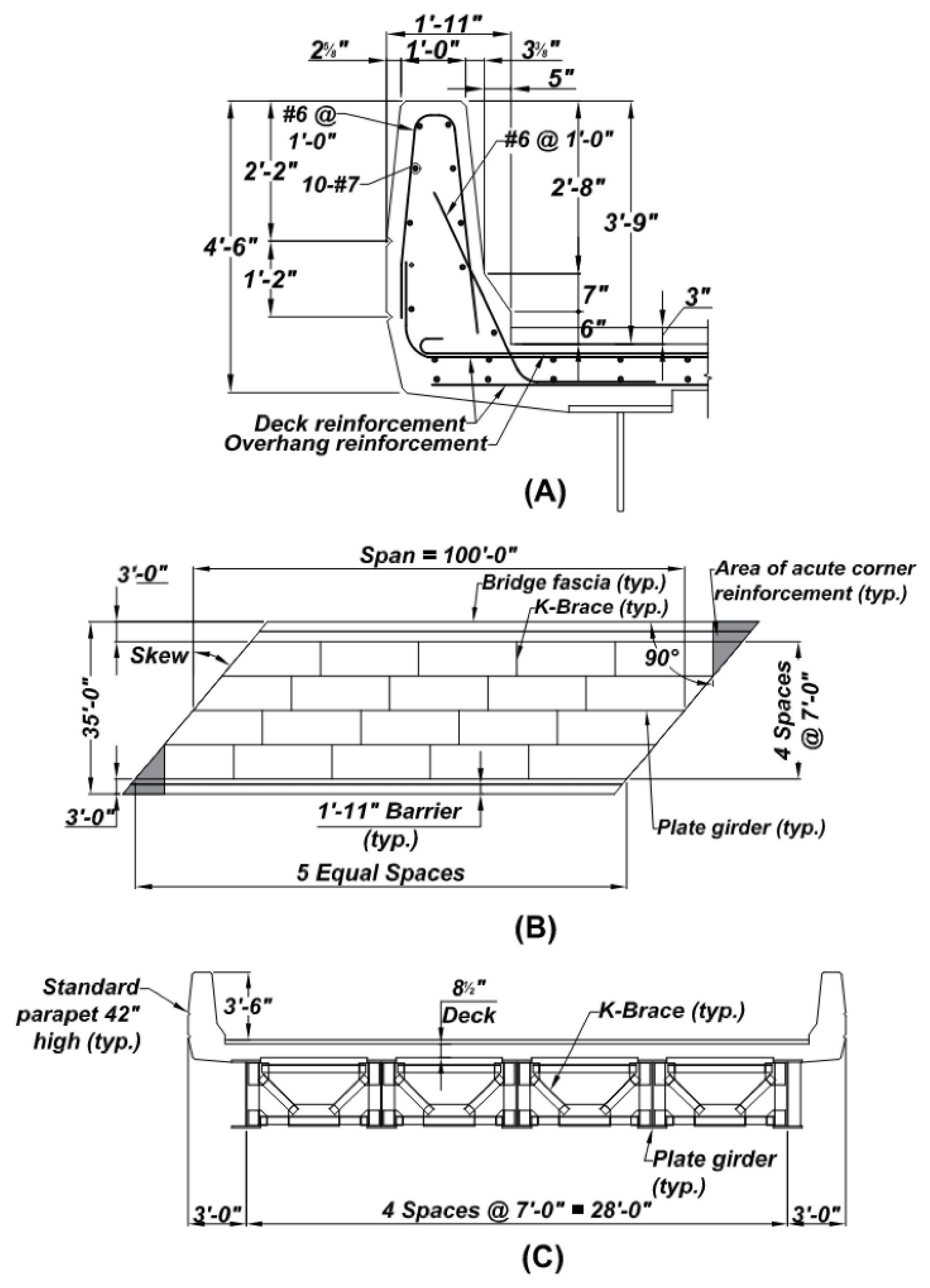
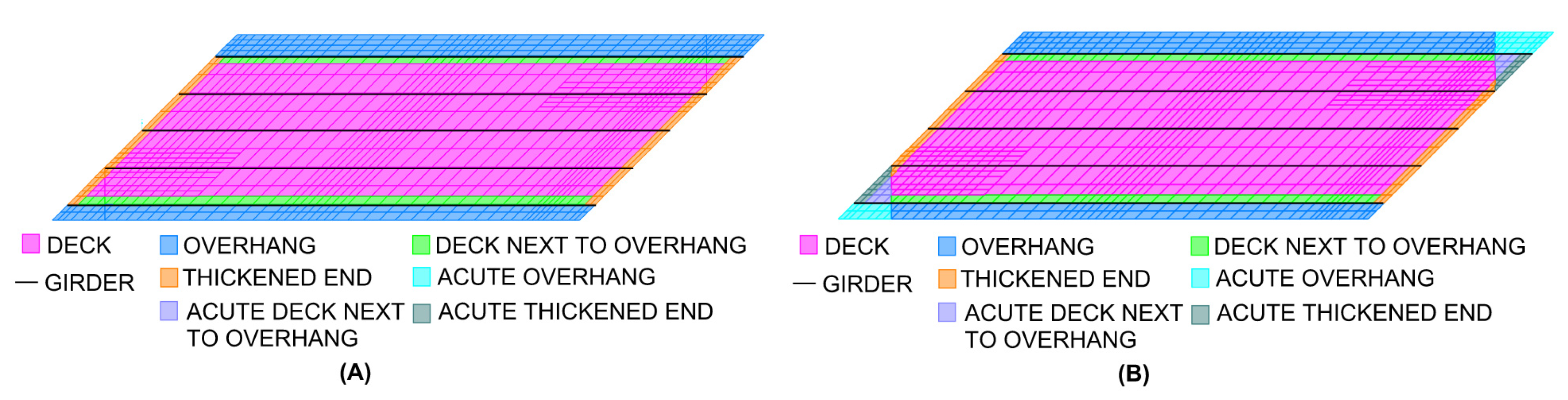
2.4.2. Model Geometry
2.4.3. Material Properties and Element Selection
2.4.4. Reinforcement Design
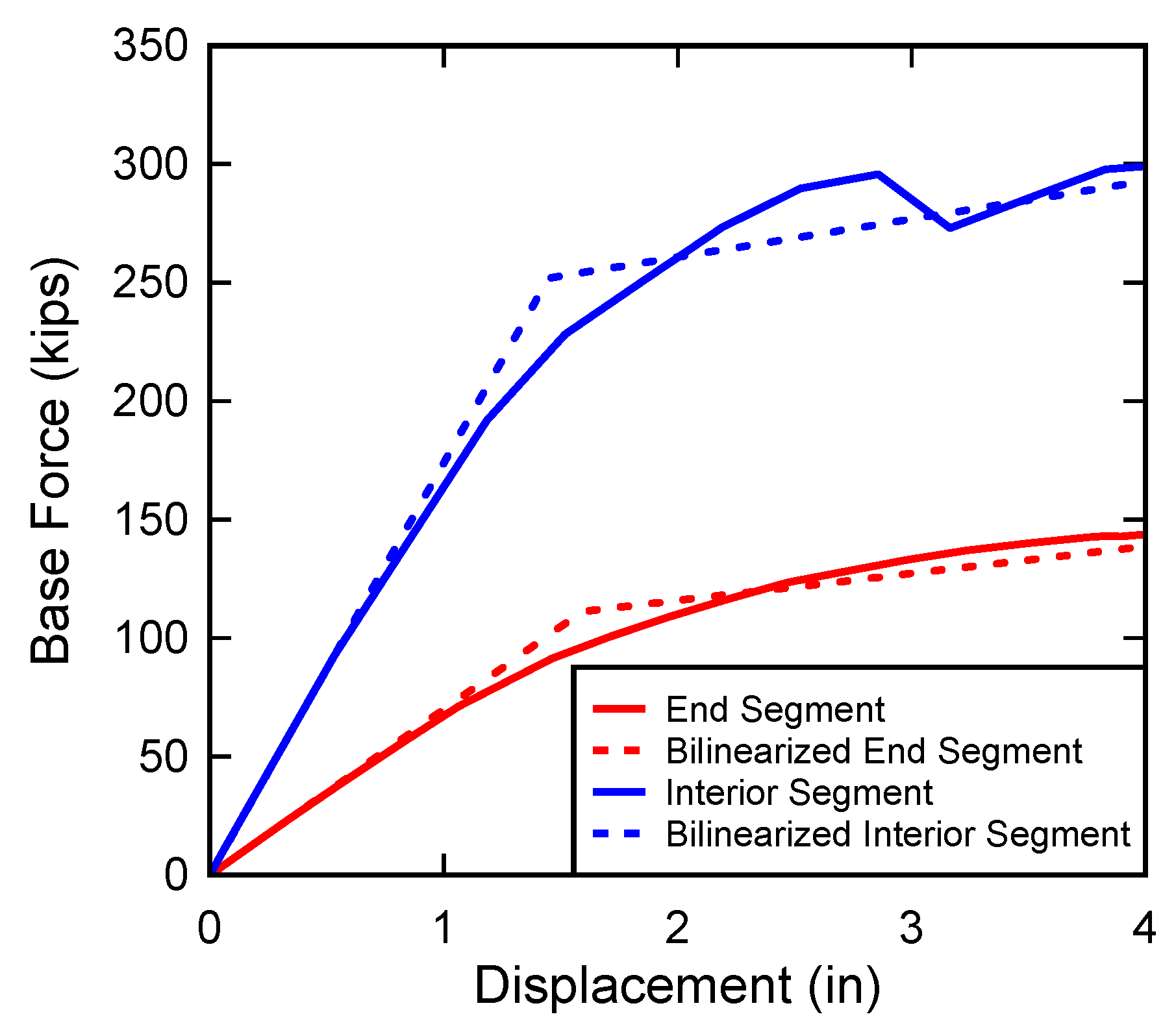
2.4.5. Verification of Parapet Behavior
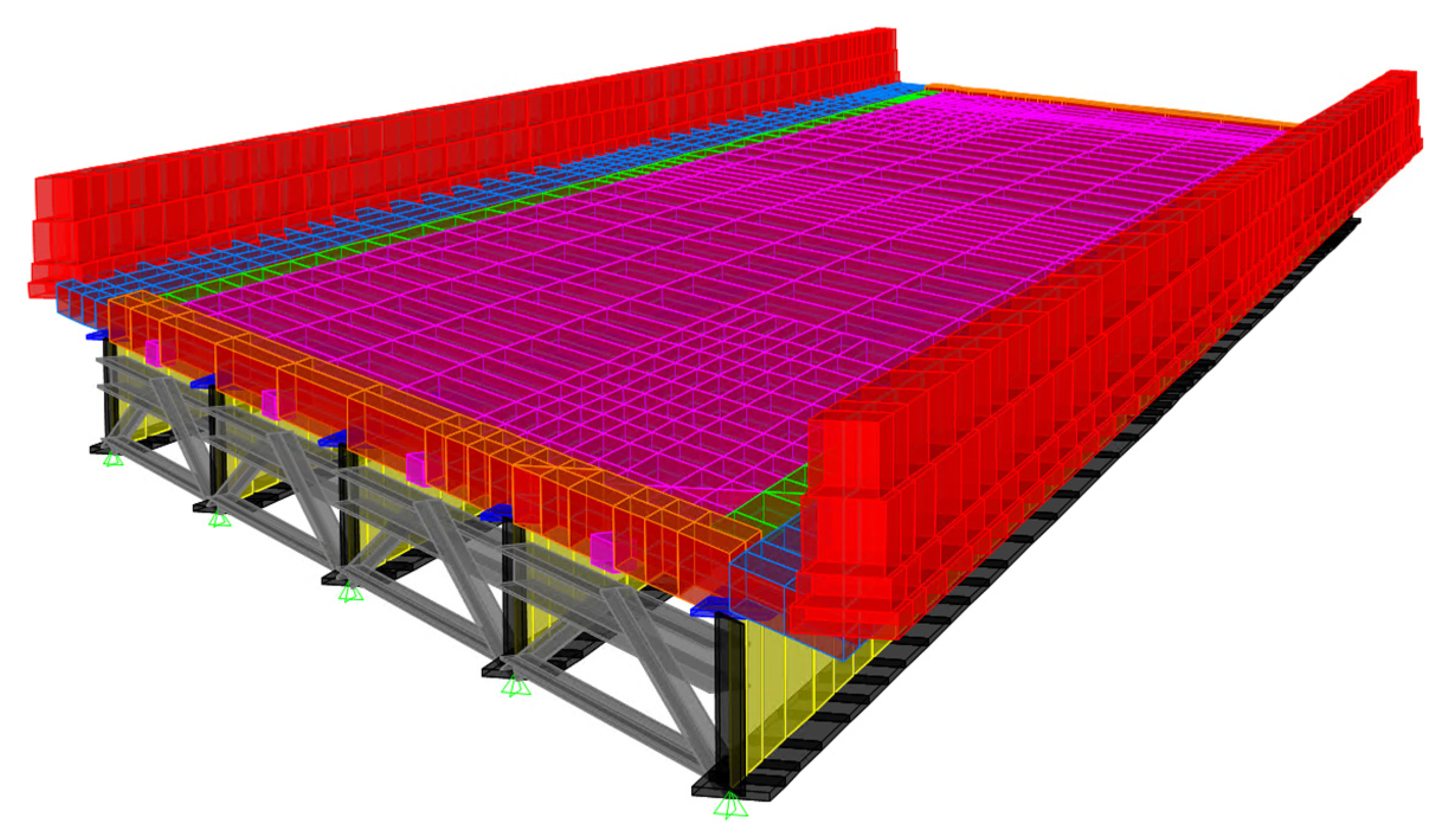
2.4.6. Model Assembly
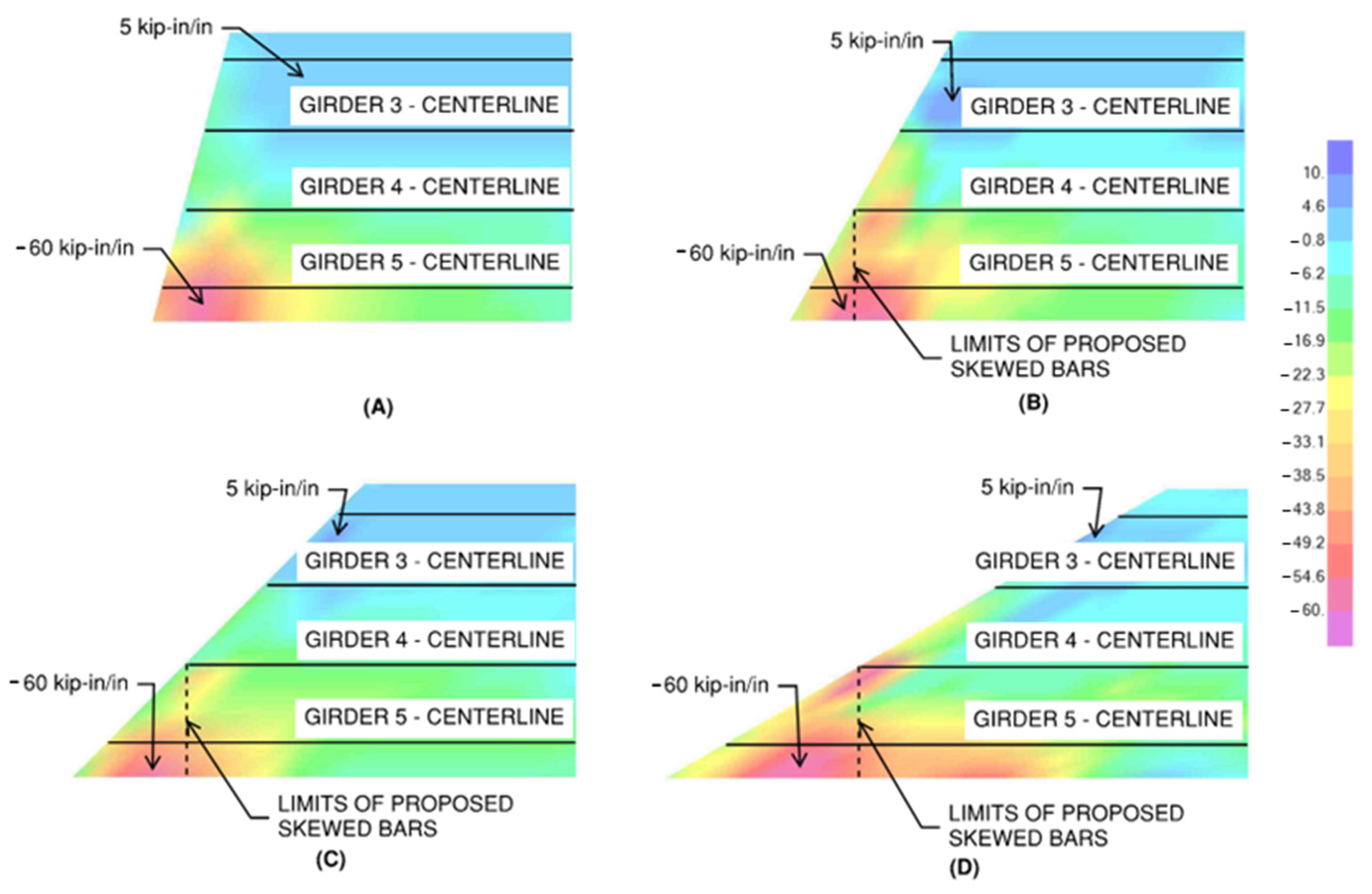
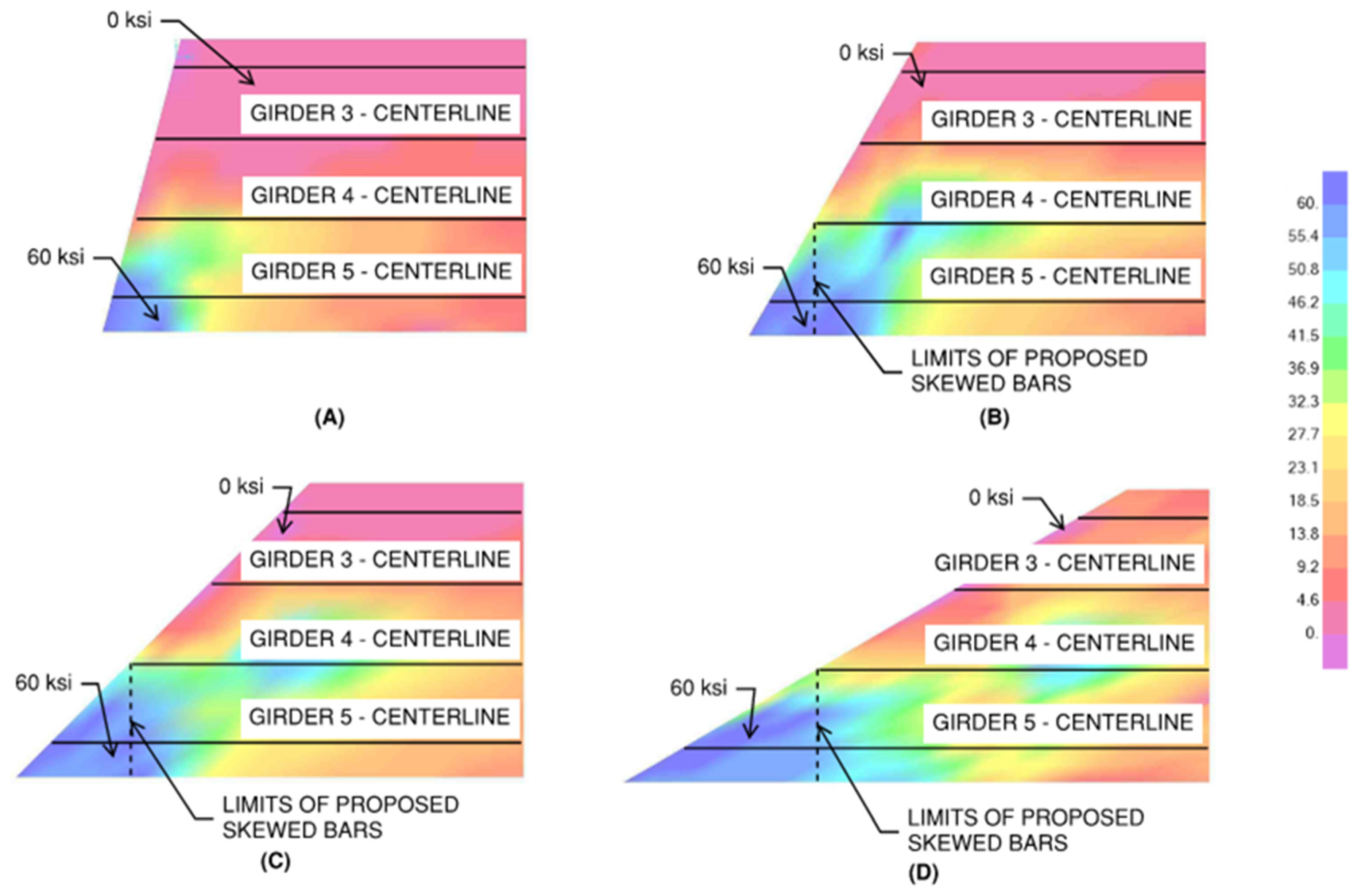
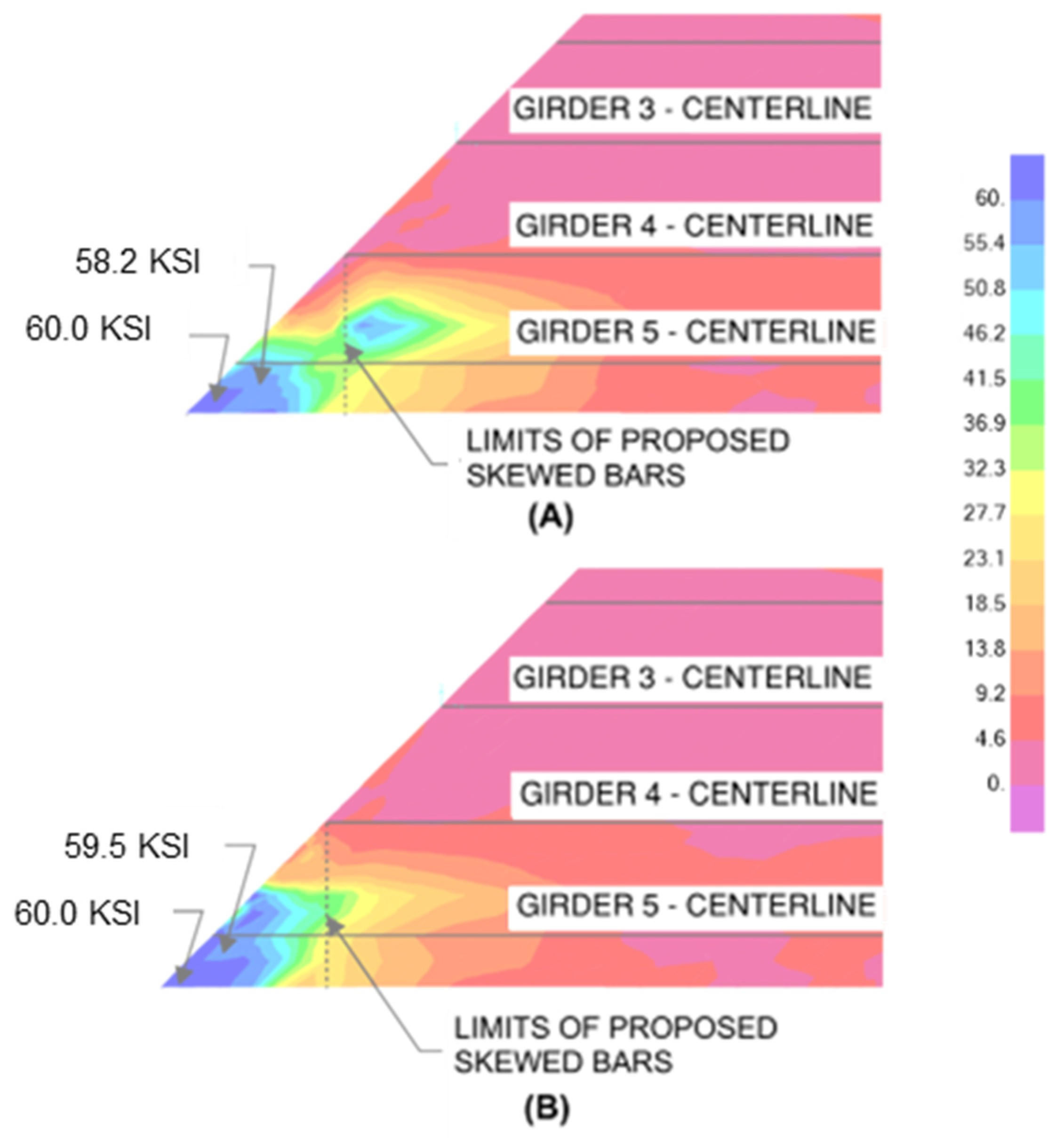
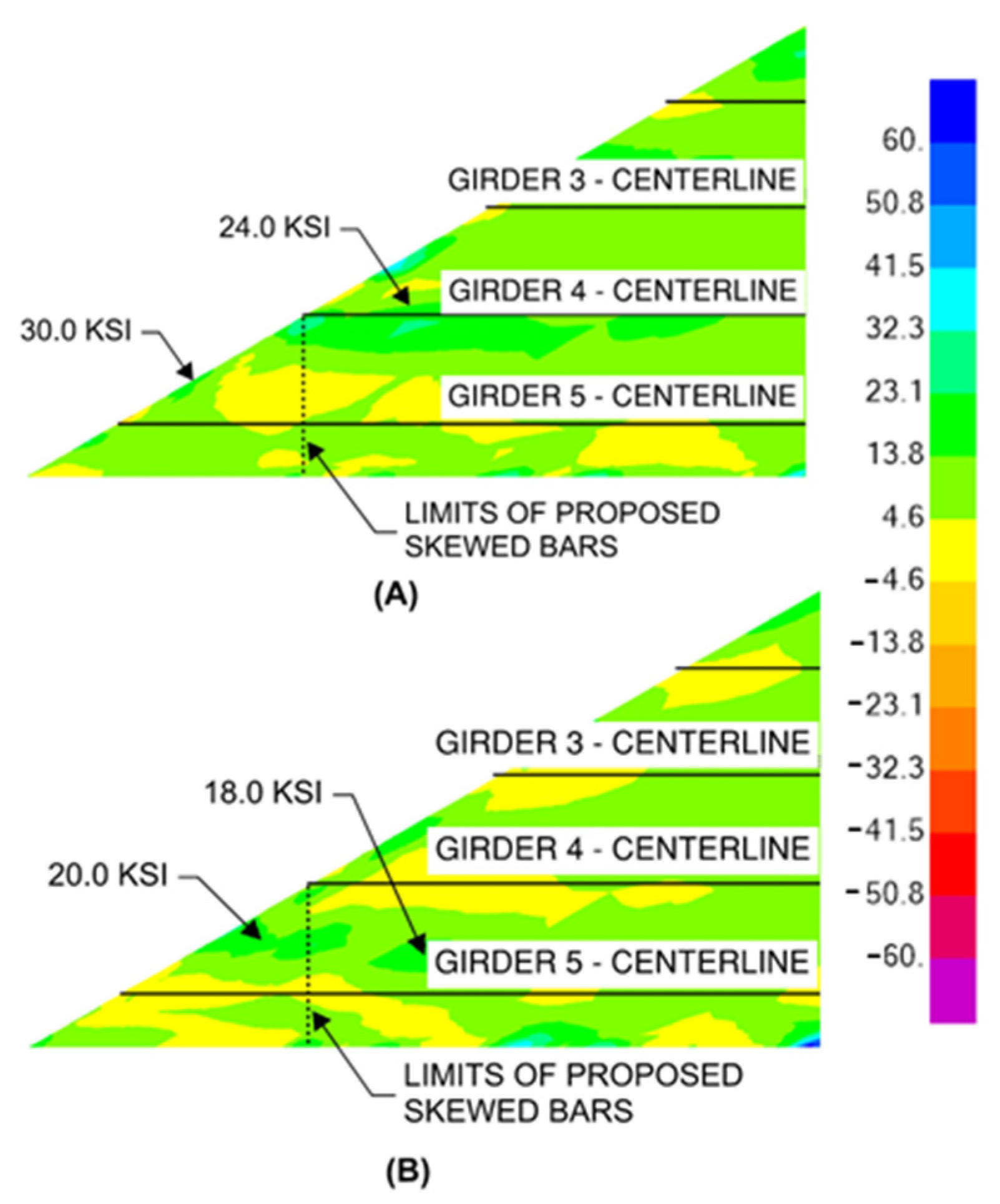
3. Results
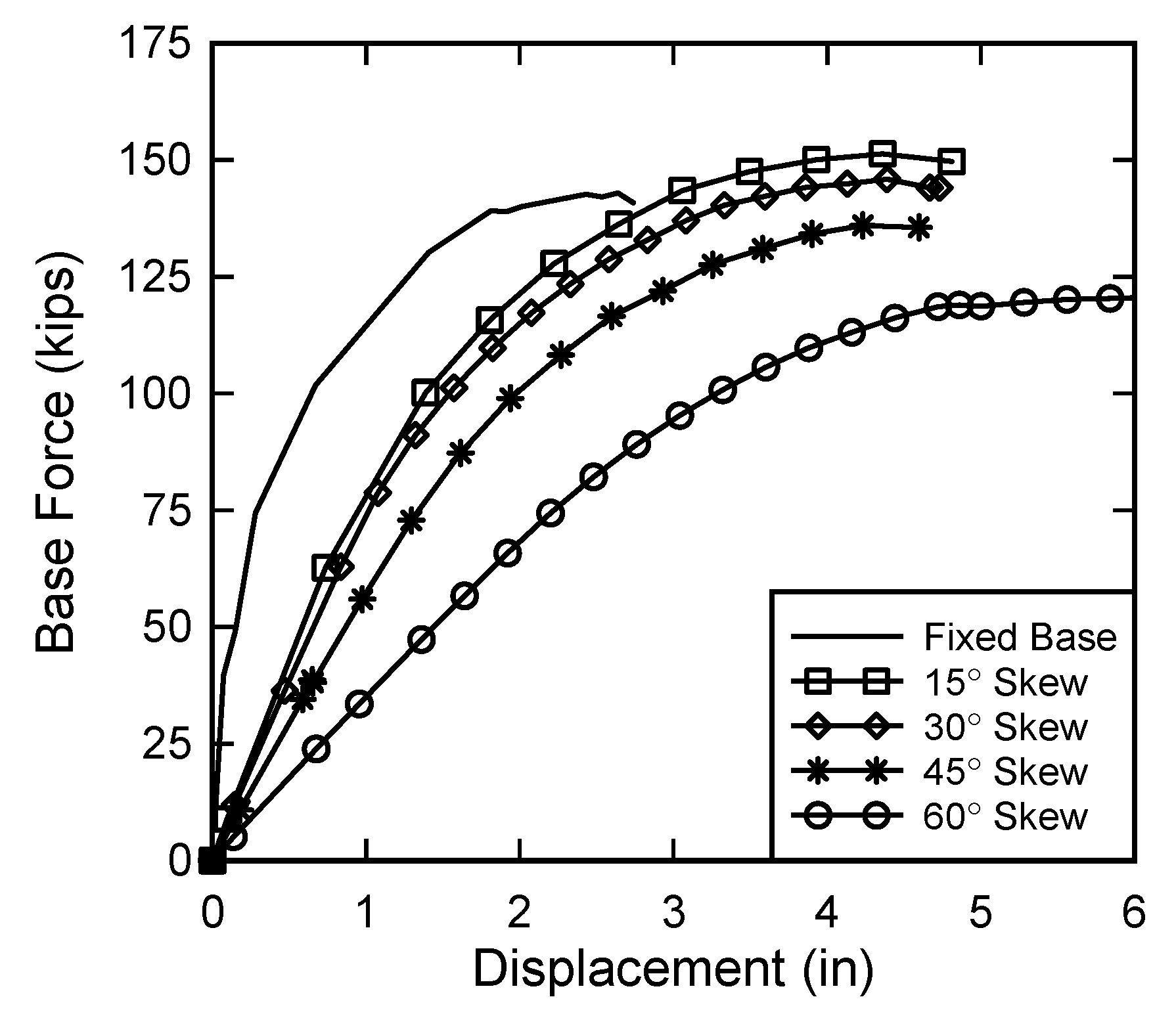
3.1. Plastic Behavior of the Parapet on the Bridge Deck
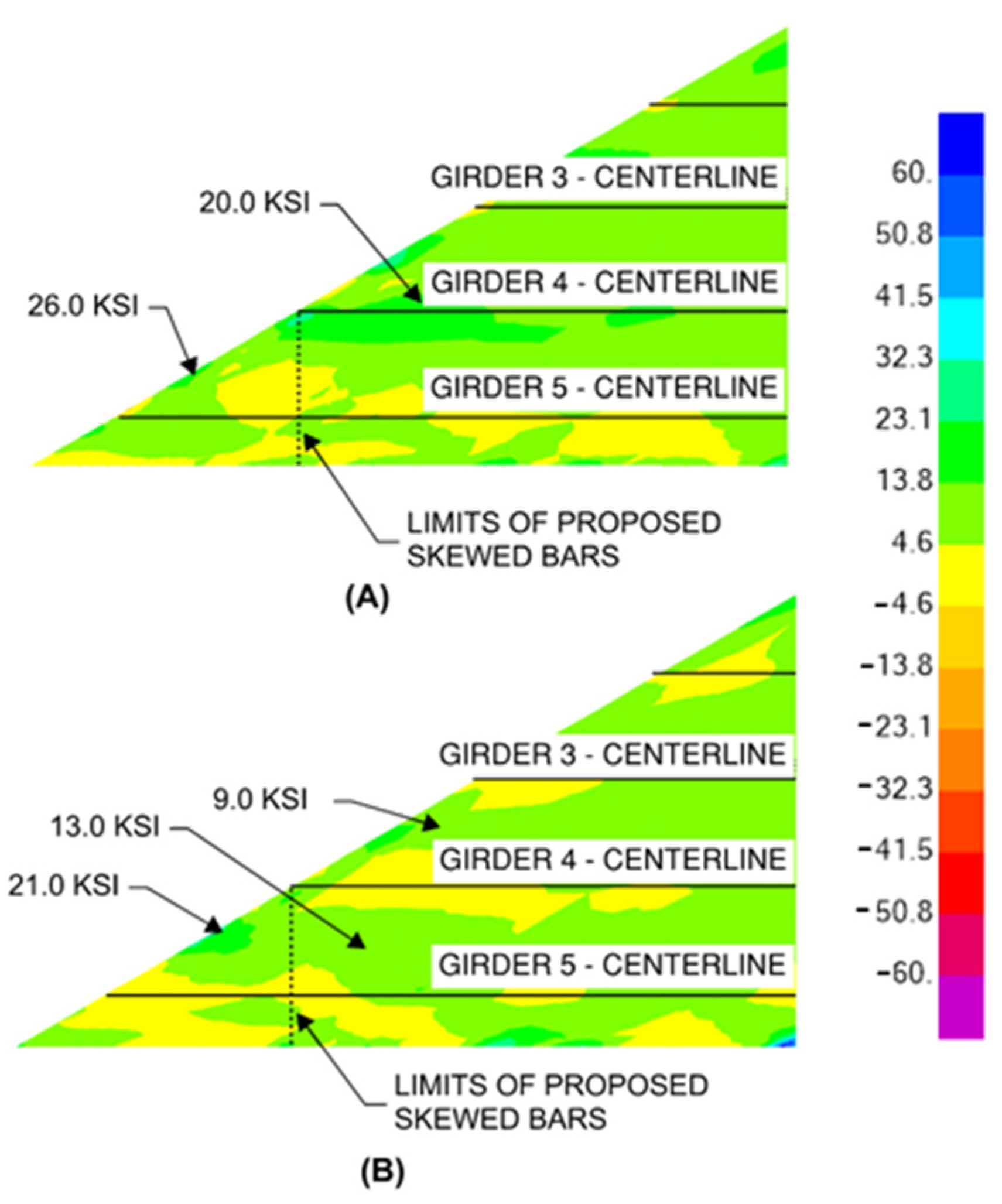
3.2. Deck Design Case 1
3.3. Deck Design Cases 2 and 3
3.4. Strength I and Service I Analysis
4. Discussion
5. Conclusions
- A simplified detail based on modifying the CTDOT standard detail was proposed. The key detailing changes include reducing the area of special reinforcement detailing, placing bars along the skew to provide adequate development length, and removing the thickened slab at the acute corner.
- The analysis showed the proposed detail satisfies AASHTO’s strength design requirements for all skew angles studied including 15°, 30°, 45°, and 60°. The modeling methodology described can be used to study any additional skew angles of interest.
- Due to the recent modifications for crash test loading, the proposed detail should be reevaluated under MASH test levels prior to implementation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Coletti, D.; Chavel, B.; Gatti, W.J. Challenges of skew in bridges with steel girders. Transp. Res. Rec. 2011, 2251, 47–56. [Google Scholar] [CrossRef]
- Chavel, B.W. Steel Bridge Design Handbook: Bridge Deck Design; Federal Highway Administration. Office of Bridge Technology: Chicago, IL, USA, 2012.
- Kun, C.; Yang, Z.; Chouw, N. Seismic performance of skewed bridges with simultaneous effects of pounding and supporting soil. Eng. Struct. 2018, 174, 26–38. [Google Scholar] [CrossRef]
- Serdar, N.; Folić, R. Vulnerability and optimal probabilistic seismic demand model for curved and skewed RC bridges. Eng. Struct. 2018, 176, 411–425. [Google Scholar] [CrossRef]
- Wang, Y.; Ibarra, L.; Pantelides, C. Effect of incidence angle on the seismic performance of skewed bridges retrofitted with buckling-restrained braces. Eng. Struct. 2020, 211, 110411. [Google Scholar] [CrossRef]
- Ghanem, A.; Moon, D. Seismic Fragility Assessment of Skewed Reinforced Concrete Bridges. In Proceedings of the 17th World Conference on Earthquake Engineering (17WCEE), Sendai, Japan, 27 September–2 October 2021. [Google Scholar]
- Gupta, T.; Sandhu, D. Seismic response of horizontally curved bridges in combination with skewed abutments. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 36, pp. 864–878. [Google Scholar]
- Phan, V.-T.; Nguyen, D.-D. Correlation Between Seismic Intensity Measures and Response of Skewed Bridges. In Recent Advances in Earthquake Engineering; Springer: Singapore, 2022; pp. 25–36. [Google Scholar]
- Fu, G.; Dimaria, J.; Zhuang, Y.; Feng, J. Bridge Deck Corner Cracking on Skewed Structures; Department of Transportation, Construction and Technology Division: Lansing, MI, USA, 2007. [Google Scholar]
- Okumus, P.; Diaz Arancibia, M. Sources, mitigation and implications of skew-related concrete deck cracks in girder bridges. Struct. Infrastruct. Eng. 2021, 17, 1612–1625. [Google Scholar] [CrossRef]
- Diaz Arancibia, M.; Rugar, L.; Okumus, P. Role of skew on bridge performance. Transp. Res. Rec. 2020, 2674, 282–292. [Google Scholar] [CrossRef]
- Solae, C.; Chorzepa, M.G.; Durham, S.A.; Kim, S.S. Investigation of cracks observed on a skewed bridge constructed using self-propelled modular transporters. J. Perform. Constr. Facil. 2020, 34, 04020098. [Google Scholar] [CrossRef]
- Chorzepa, M.G.; Solae, C.; Durham, S.; Kim, S.S. Development of Possible Solutions to Eliminate or Reduce Deck Cracking on Skewed Bridges Built by Using the Accelerated Bridge Construction Method; Department of Transportation, Office of Performance-Based: Atlanta, GA, USA, 2019. [Google Scholar]
- Arancibia, M.D.; Okumus, P. Load Distribution and In-Plane Superstructure Movements on Highly Skewed Steel Girder Bridges. In Developments in International Bridge Engineering; Springer: Singapore, 2021; pp. 107–114. [Google Scholar]
- American Association of State Highway and Transportation Officials. AASHTO LRFD Bridge Design Specifications; American Association of State Highway and Transportation Officials, Highway Subcommittee on Bridges and Structures: Washington, DC, USA, 2020. [Google Scholar]
- Connecticut Department of Transportation. Bridge Design Manual; Connecticut Department of Transportation: Newington, CT, USA, 2019.
- Texas Department of Transportation. TxDOT Bridge Design Manual; Texas Department of Transportation: Austin, TX, USA, 2021.
- Oregon, D. Bridge Design Manual; Oregon Department of Transportation: Salem, OR, USA, 2021. Available online: http://www.oregon.gov/ODOT (accessed on 18 April 2022).
- New York State Department of Transportation. Standard Bridge Detail Sheets; New York State Department of Transportation: Albany, NY, USA, 2021.
- CSi. CSiBridge 2017; Computers and Structures: Berkeley, CA, USA, 2016. [Google Scholar]
- Mackie, K.R.; Scott, M.H. Implementation of nonlinear elements for seismic response analysis of bridges. Pract. Period. Struct. Des. Constr. 2019, 24, 04019011. [Google Scholar] [CrossRef]
- Khan, E.; Lobo, J.A.; Linzell, D.G. Live load distribution and dynamic amplification on a curved prestressed concrete transit rail bridge. J. Bridge Eng. 2018, 23, 04018029. [Google Scholar] [CrossRef]
- Gupta, T.; Kumar, M. Flexural response of skew-curved concrete box-girder bridges. Eng. Struct. 2018, 163, 358–372. [Google Scholar] [CrossRef]
- Abdel-Mohti, A.; Pekcan, G. Seismic response of skewed RC box-girder bridges. Earthq. Eng. Eng. Vib. 2008, 7, 415–426. [Google Scholar] [CrossRef]
- Sofi, F.A.; Steelman, J.S. Nonlinear flexural distribution behavior and ultimate system capacity of skewed steel girder bridges. Eng. Struct. 2019, 197, 109392. [Google Scholar] [CrossRef]
- Huang, H.; Shenton, H.W.; Chajes, M.J. Load distribution for a highly skewed bridge: Testing and analysis. J. Bridge Eng. 2004, 9, 558–562. [Google Scholar] [CrossRef]
- Huo, X.S.; Zhang, Q. Effect of skewness on the distribution of live load reaction at piers of skewed continuous bridges. J. Bridge Eng. 2008, 13, 110–114. [Google Scholar] [CrossRef]
- Théoret, P.; Massicotte, B.; Conciatori, D. Analysis and design of straight and skewed slab bridges. J. Bridge Eng. 2012, 17, 289–301. [Google Scholar] [CrossRef]
- Connecticut Department of Transportation. New Bridge Design Standard Practice; Connecticut Department of Transportation: Newington, CT, USA, 2005.
- Gurkalo, F.; Du, Y.; Poutos, K.; Jimenez-Bescos, C. The nonlinear analysis of an innovative slit reinforced concrete water tower in seismic regions. Eng. Struct. 2017, 134, 138–149. [Google Scholar] [CrossRef]
- Chung, W.; Sotelino, E.D. Nonlinear finite-element analysis of composite steel girder bridges. J. Struct. Eng. 2005, 131, 304–313. [Google Scholar] [CrossRef]
- Recalde, B.R.B.; Gastal, F.P.S.L.; Bessa, V.D.A.; Schwetz, P.F. Numerical analysis of waffle slabs in flexure considering the effects of concrete cracking. Rev. IBRACON Estrut. Mater. 2015, 8, 225–247. [Google Scholar] [CrossRef] [Green Version]

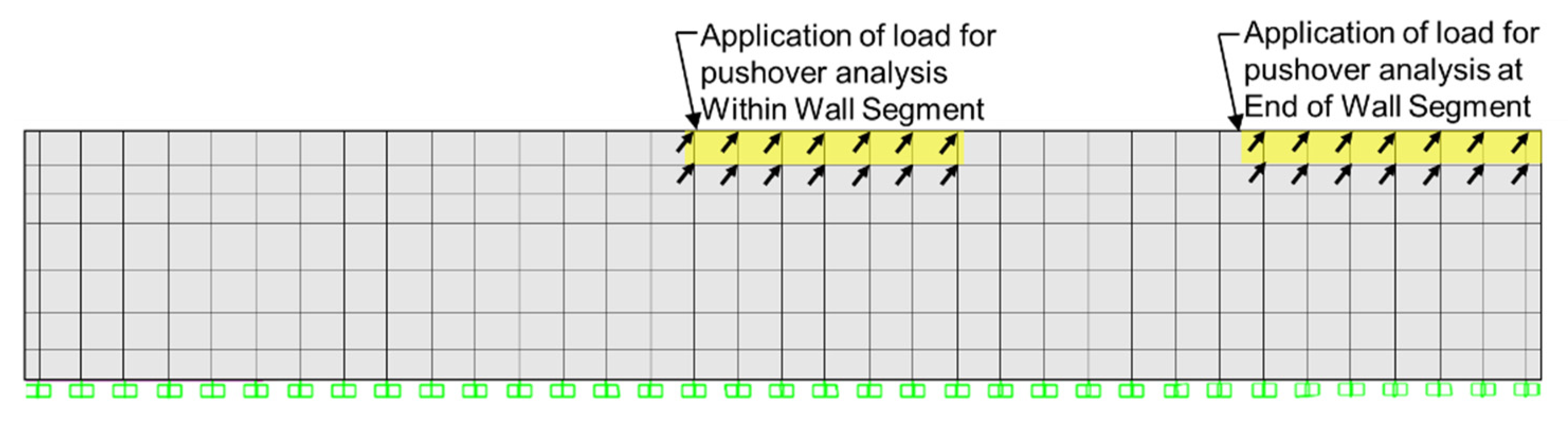





| Failure Plane | Location | Rw (kips) | Lc (ft) |
|---|---|---|---|
| Failure Plane 1 | Within Wall Segment | 262.59 | 15.29 |
| Failure Plane 1 | End of Wall Segment | 116.94 | 6.81 |
| Failure Plane 2 | Within Wall Segment | 217.57 | 10.72 |
| Failure Plane 2 | End of Wall Segment | 107.95 | 5.32 |
| Location | Method | Yield Strength (kips) | Resistance, Rw (kips) | Displacement at Rw (in) | Yield Line Extent, Lc (ft) |
|---|---|---|---|---|---|
| End of Parapet | Yield Line | N/A | 108 | N/A | 5.30 |
| End of Parapet | Pushover | 110 | 110 | 2.95 | 4.80 |
| Middle of Parapet | Yield Line | N/A | 218 | N/A | 10.7 |
| Middle of Parapet | Pushover | 228 | 228 | 1.92 | 13.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mawson, J.; Mehr, M.; Constant, J.; Zaghi, A.E.; Hain, A. Structural Performance of Acute Corners on Skewed Bridge Decks Using Non-Linear Modeling of the Deck Parapet. Infrastructures 2022, 7, 77. https://doi.org/10.3390/infrastructures7060077
Mawson J, Mehr M, Constant J, Zaghi AE, Hain A. Structural Performance of Acute Corners on Skewed Bridge Decks Using Non-Linear Modeling of the Deck Parapet. Infrastructures. 2022; 7(6):77. https://doi.org/10.3390/infrastructures7060077
Chicago/Turabian StyleMawson, Jessica, Masoud Mehr, Jodi Constant, Arash E. Zaghi, and Alexandra Hain. 2022. "Structural Performance of Acute Corners on Skewed Bridge Decks Using Non-Linear Modeling of the Deck Parapet" Infrastructures 7, no. 6: 77. https://doi.org/10.3390/infrastructures7060077
APA StyleMawson, J., Mehr, M., Constant, J., Zaghi, A. E., & Hain, A. (2022). Structural Performance of Acute Corners on Skewed Bridge Decks Using Non-Linear Modeling of the Deck Parapet. Infrastructures, 7(6), 77. https://doi.org/10.3390/infrastructures7060077






