Risk-Based Criticality Assessment for Smart Critical Infrastructures
Abstract
:1. Introduction
2. Background and Related Work
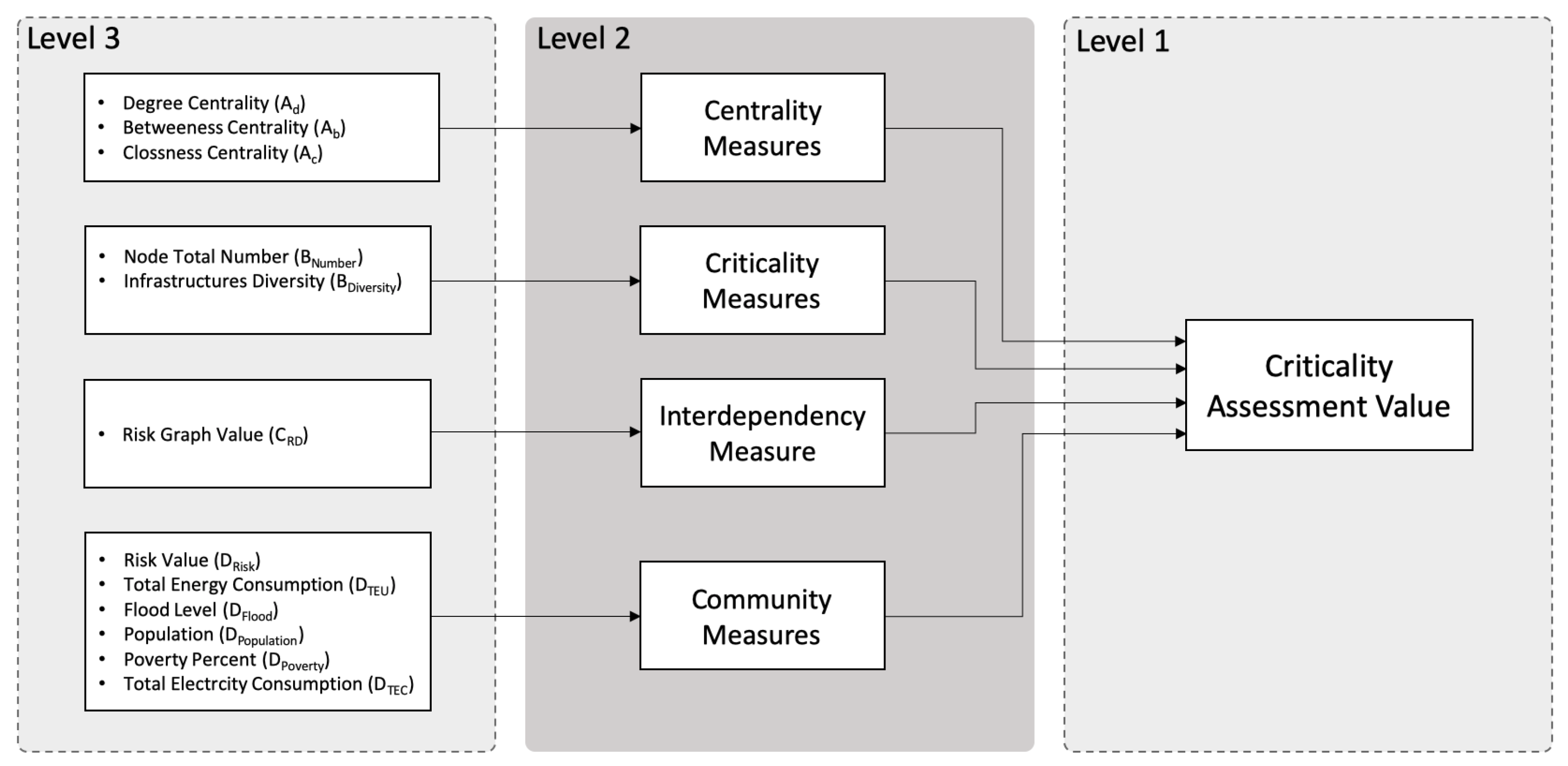
3. Criticality Assessment Process Development
3.1. Identify Measures and Data Acquisition
3.1.1. Centrality Measures
3.1.2. Criticality Measures
3.1.3. Interdependence Measures
3.1.4. Community Measures
3.2. Weighting and Ranking Critically Factors
3.3. Feature Selection
4. Case Study
- Method LMG: Based on sequential but takes care of the dependence on orderings by averaging over orderings;
- Method Last: Measures the increase in for each regressor when including this regressor as the last of the p regressors;
- Method First: To compare the values from p regression models with one regressor only;
- Method Pratt: Multiply the standardized coefficient with the marginal correlation.
5. Result
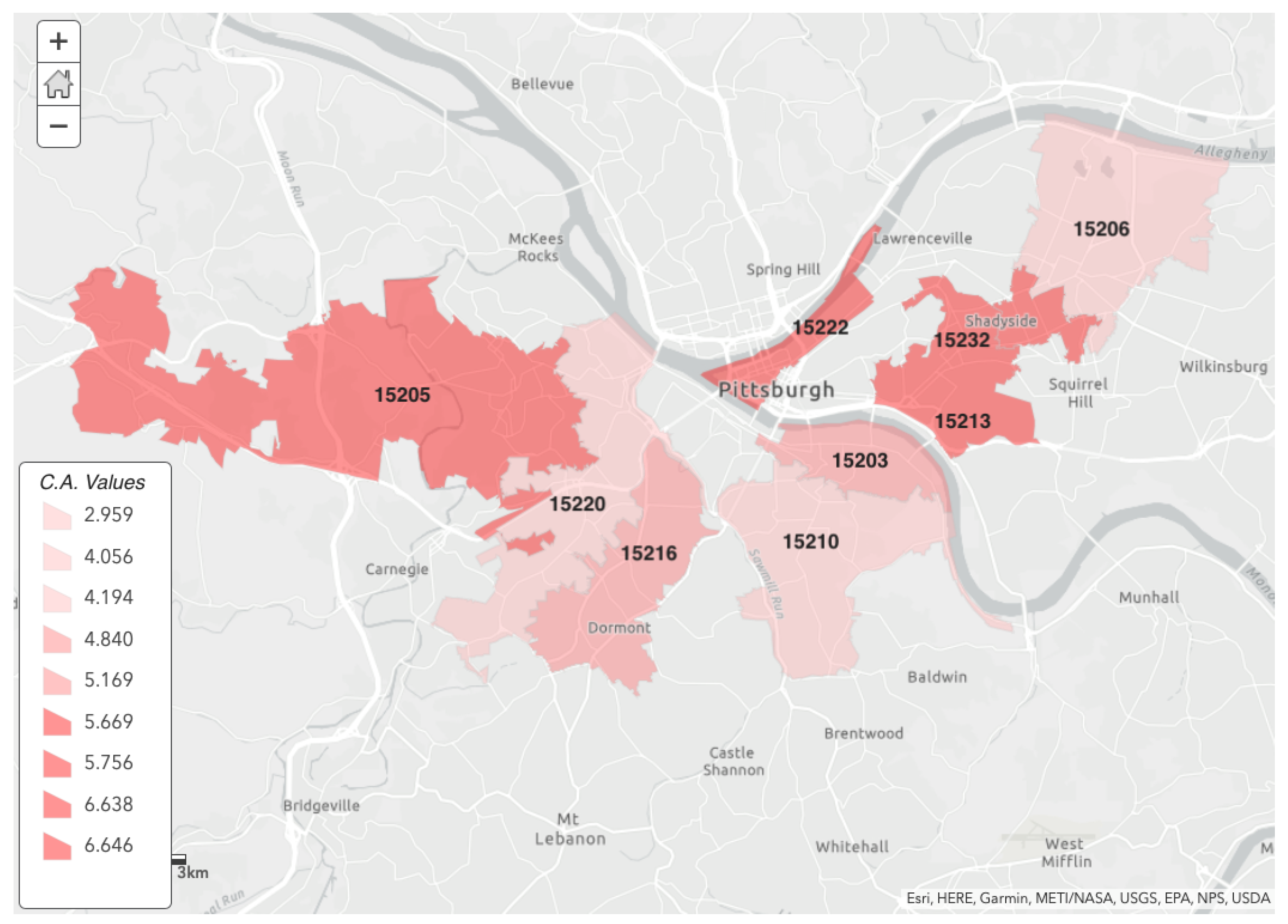
5.1. Zip Code Based
5.2. Neighborhood Based
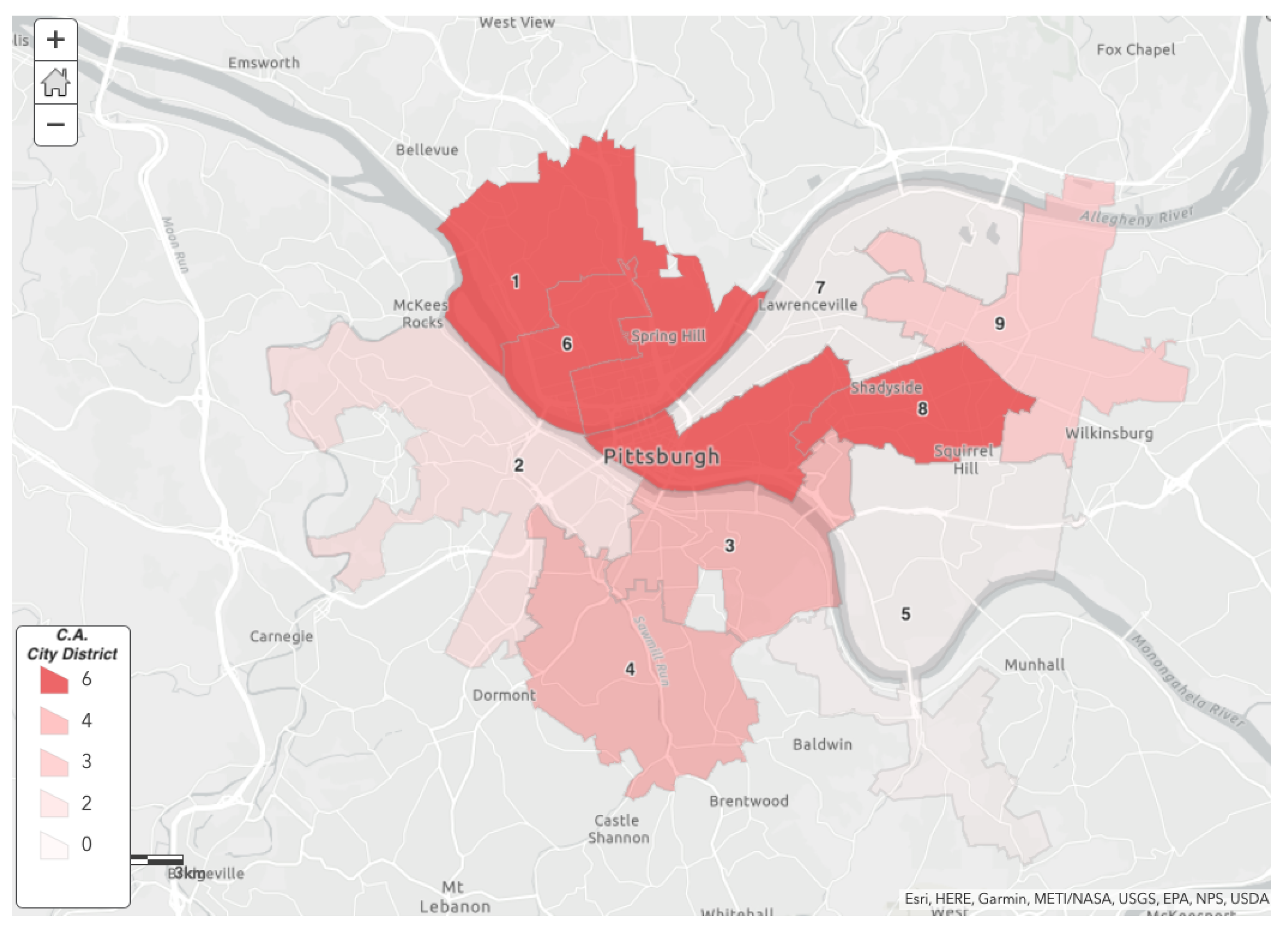
5.3. City Council District
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fisher, R.; Bassett, G.; Buehring, W.; Collins, M.; Dickinson, D.; Eaton, L.; Haffenden, R.; Hussar, N.; Klett, M.; Lawlor, M.; et al. Constructing a Resilience Index for the Enhanced Critical Infrastructure Protection Program; Technical Report; Argonne National Lab (ANL): Argonne, IL, USA, 2010. [Google Scholar]
- Nanab, C.; Sansavini, G.; Krögerc, W.; Heinimann, H. A quantitative method for assessing the resilience of infrastructure systems. In Proceedings of the PSAM 2014–Probabilistic Safety Assessment and Management, Berlin, Germany, 14–18 June 2014. [Google Scholar]
- Longstaff, P.H.; Armstrong, N.J.; Perrin, K.; Parker, W.M.; Hidek, M.A. Building resilient communities: A preliminary framework for assessment. Homel. Secur. Aff. 2010, 6, 1–23. [Google Scholar]
- Department of Homeland Security. Critical Infrastructure Sectors|Homeland Security. 2018. Available online: https://www.cisa.gov/critical-infrastructure-sectors (accessed on 20 July 2021).
- Eisenberg, D.A.; Park, J.; Seager, T.P. Sociotechnical network analysis for power grid resilience in South Korea. Complexity 2017, 2017, 3597010. [Google Scholar] [CrossRef] [Green Version]
- Stergiopoulos, G.; Kotzanikolaou, P.; Theocharidou, M.; Gritzalis, D. Risk mitigation strategies for critical infrastructures based on graph centrality analysis. Int. J. Crit. Infrastruct. Prot. 2015, 10, 34–44. [Google Scholar] [CrossRef]
- Wang, Z.; Ran, Z.; Chen, X.; Liang, Y.; Ren, Z.; He, Y. Critical Node Identification for Electric Power Communication Network Based on Topology and Services Characteristics. MATEC Web Conf. 2018, 246, 03023. [Google Scholar] [CrossRef]
- Gómez, J.F.; Martínez-Galán, P.; Guillén, A.J.; Crespo, A. Risk-Based Criticality for Network Utilities Asset Management. IEEE Trans. Netw. Serv. Manag. 2019, 16, 755–768. [Google Scholar] [CrossRef]
- Dick, K.; Russell, L.; Souley Dosso, Y.; Kwamena, F.; Green, J.R. Deep learning for critical infrastructure resilience. J. Infrastruct. Syst. 2019, 25, 05019003. [Google Scholar] [CrossRef]
- Van Bodegom, A.; Koopmanschap, E. The COVID-19 Pandemic and Climate Change Adaptation; Wageningen Centre for Development Innovation: Wageningen, The Netherlands, 2020; pp. 1–24. [Google Scholar]
- Alqahtani, A.; Tipper, D.; Kelly-Pitou, K. Locating Microgrids to Improve Smart City Resilience. In Proceedings of the Resilience Week 2018, RWS 2018, Denver, CO, USA, 20–23 August 2018. [Google Scholar] [CrossRef]
- Danielsson, P.E. Euclidean distance mapping. Comput. Graph. Image Process. 1980, 14, 227–248. [Google Scholar] [CrossRef] [Green Version]
- Patel, B. Producing reliable power in the hospital setting. Power Eng. 2011, 115, 20–24. [Google Scholar]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef] [Green Version]
- Rinaldi, S.M. Modeling and simulating critical infrastructures and their interdependencies. In Proceedings of the Hawaii International Conference on System Sciences, Big Island, HI, USA, 5–8 January 2004. [Google Scholar] [CrossRef]
- Zio, E.; Sansavini, G. Modeling interdependent network systems for identifying cascade-safe operating margins. IEEE Trans. Reliab. 2011, 60, 94–101. [Google Scholar] [CrossRef] [Green Version]
- Ouyang, M.; Hong, L.; Mao, Z.J.; Yu, M.H.; Qi, F. A methodological approach to analyze vulnerability of interdependent infrastructures. Simul. Model. Pract. Theory 2009, 17, 817–828. [Google Scholar] [CrossRef]
- Kotzanikolaou, P.; Theoharidou, M.; Gritzalis, D. Assessing n-order dependencies between critical infrastructures. Int. J. Crit. Infrastruct. 6 2013, 9, 93–110. [Google Scholar] [CrossRef]
- Alqahtani, A.; Tipper, D.; Kelly-Pitou, K.; Amy, B. Identifying Vulnerable Critical Infrastructure Zones in Smart Cities. In Proceedings of the 2020 16th International Conference on the Design of Reliable Communication Networks DRCN 2020, Milan, Italy, 24–27 March 2020. [Google Scholar]
- Dodge, Y. The Oxford Dictionary of Statistical Terms; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Bruce, P.; Bruce, A. Practical Statistics for Data Scientists: 50 Essential Concepts; O’Reilly Media, Inc.: Newton, MA, USA, 2017. [Google Scholar]
- Bottenberg, R.A.; Ward, J.H. Applied Multiple Linear Regression; 6570th Personnel Research Laboratory, Aerospace Medical Division, Air Force: Lackland Air Force Base, TX, USA, 1963; Volume 63. [Google Scholar]
- City-Data Bank. 2020. Available online: https://www.city-data.com (accessed on 19 July 2021).
- ESRI. ArcGIS Desktop: Release 10.2. 2013. Available online: https://www.esri.com (accessed on 20 July 2021).
- U.S. Census Bureau. Data Sources Include the United States Postal Service. 2020. Available online: https://www.unitedstateszipcodes.org (accessed on 20 July 2021).
- Jones, D.N. Defining City Neighborhoods an Imprecise Process. Pittsburgh-Post-Gaz 2020. Available online: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&cad=rja&uact=8&ved=2ahUKEwjRnPq97Pz0AhWPohQKHVkJC3UQFnoECAwQAQ&url=https%3A%2F%2Fwww.post-gazette.com%2Flocal%2Fcity%2F2006%2F06%2F05%2FDefining-city-neighborhoods-an-imprecise-process%2Fstories%2F200606050129&usg=AOvVaw3ynvSPoTr2lFo9zV77AE6b (accessed on 20 July 2021).
- City Council, District Information, Neighborhoods. 2020. Available online: www.pittsburghpa.gov/council (accessed on 20 July 2021).



| Risk Dependence (i,j) | |||||
|---|---|---|---|---|---|
| VL | L | M | H | VH | |
| VL | 0–0.05 | 0–0.05 | 0–0.05 | 0–0.05 | 0–0.05 |
| L | 0–0.05 | 0.05–0.25 | 0.05–0.25 | 0.05–0.25 | 0.05–0.25 |
| M | 0–0.05 | 0.05–0.25 | 0.25–0.5 | 0.25–0.5 | 0.25–0.5 |
| H | 0–0.05 | 0.05–0.25 | 0.25–0.5 | 0.5–0.75 | 0.5–0.75 |
| VH | 0.05–0.25 | 0.05–0.25 | 0.25–0.5 | 0.5–0.75 | 0.75–1 |
| Risk Dependence (i,j) | |||||
|---|---|---|---|---|---|
| VL | L | M | H | VH | |
| VL | 1 | 2 | 3 | 4 | 5 |
| L | 2 | 3 | 4 | 5 | 6 |
| M | 3 | 4 | 5 | 6 | 7 |
| H | 4 | 5 | 6 | 7 | 8 |
| VH | 5 | 6 | 7 | 8 | 9 |
| Zip Code | ||||
|---|---|---|---|---|
| 15211 | 13 | 6 | 0 | 0.90 |
| 15235 | 28 | 14 | 0 | 0.4 |
| 15106 | 8 | 24 | 0 | 0.28 |
| 15214 | 6 | 20 | 0 | 0.53 |
| 15216 | 13 | 38 | 11 | 0.20 |
| 15206 | 27 | 88 | 35 | 0.08 |
| 15217 | 23 | 82 | 18 | 0.11 |
| 15205 | 29 | 88 | 87 | 0.07 |
| 15203 | 13 | 40 | 26 | 0.18 |
| 15219 | 24 | 68 | 157 | 0.08 |
| Sector | Zip Code | Coennected Nodes | Impact | Likehood | RD | C |
|---|---|---|---|---|---|---|
| communication | 15106 | 6 | 9 | 0.25 | 2.25 | 9.5 |
| Energy | 15106 | 5 | 6 | 0.5 | 3 | |
| Energy | 15106 | 5 | 6 | 0.5 | 3 | |
| Healthcare | 15106 | 2 | 1 | 0.25 | 0.25 | |
| Healthcare | 15106 | 2 | 1 | 0.25 | 0.25 | |
| Healthcare | 15106 | 2 | 1 | 0.25 | 0.25 | |
| Healthcare | 15106 | 2 | 1 | 0.25 | 0.25 | |
| Healthcare | 15106 | 2 | 1 | 0.25 | 0.25 |
| Zip Code | ||||||
|---|---|---|---|---|---|---|
| 15206 | 9 | 215.5 | 2 | 31,216 | 24.65% | 2,861,972 |
| 15203 | 12 | 361.8 | 1 | 32,482 | 23.17% | 1,401,579 |
| 15210 | 3 | 172.5 | 3 | 28,320 | 29.10% | 1,890,664 |
| 15205 | 4 | 250.3 | 3 | 13,352 | 34.05% | 2,870,500 |
| 15208 | 4 | 183.5 | 4 | 31,850 | 23.82% | 1,052,736 |
| 15201 | 12 | 365.9 | 1 | 22,586 | 13.04% | 1,919,123 |
| 15216 | 4 | 114.8 | 4 | 19,204 | 34.50% | 1,656,714 |
| 15213 | 4 | 155.2 | 4 | 24,691 | 9.52% | 4,615,921 |
| 15219 | 16 | 86.0 | 1 | 1999 | 28.46% | 3,576,810 |
| 15120 | 6 | 593.8 | 2 | 9613 | 19.99% | 1,393,654 |
| 15222 | 16 | 74.1 | 1 | 29,621 | 8.61% | 2,897,465 |
| Feature | Importance | Measure | Importance |
|---|---|---|---|
| Number of Nodes | 1.178 | Criticality | 1.216 |
| Diversity of Nodes | 1.177 | ||
| Degree | 2.563 | Centrality | 1.614 |
| Betweeness | 2.861 | ||
| Closeness | 3.008 | ||
| Interdependence | - | Interdependence | 2.828 |
| Risk Value | 3.299 | Community | 1.156 |
| Electricity Use | 6.739 | ||
| Flooding Level | 3.355 | ||
| Population | 7.271 | ||
| Poverty Percent | 7.524 | ||
| Energy | 8.393 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almaleh, A.; Tipper, D. Risk-Based Criticality Assessment for Smart Critical Infrastructures. Infrastructures 2022, 7, 3. https://doi.org/10.3390/infrastructures7010003
Almaleh A, Tipper D. Risk-Based Criticality Assessment for Smart Critical Infrastructures. Infrastructures. 2022; 7(1):3. https://doi.org/10.3390/infrastructures7010003
Chicago/Turabian StyleAlmaleh, Abdulaziz, and David Tipper. 2022. "Risk-Based Criticality Assessment for Smart Critical Infrastructures" Infrastructures 7, no. 1: 3. https://doi.org/10.3390/infrastructures7010003
APA StyleAlmaleh, A., & Tipper, D. (2022). Risk-Based Criticality Assessment for Smart Critical Infrastructures. Infrastructures, 7(1), 3. https://doi.org/10.3390/infrastructures7010003






