Performance Evaluation of a Hybrid PSO Enhanced ANFIS Model in Prediction of Traffic Flow of Vehicles on Freeways: Traffic Data Evidence from South Africa
Abstract
1. Introduction
1.1. Research Motivations
1.2. Resarch Contributions
- This research provides an exciting opportunity to advance our knowledge of applying metaheuristics models in the traffic flow of vehicles on freeways.
- This study offers some important insights on how to collect, divide, and use traffic data to model vehicles’ traffic flow.
- This is the first study to undertake a comprehensive investigative analysis of the South Africa Road transportation system focusing on the country’s freeways.
- Finally, this study makes a major contribution to research on traffic flow prediction by demonstrating how off-peak and on-peak are significant factors in predicting traffic flow.
1.3. Research Organization
2. Related Studies
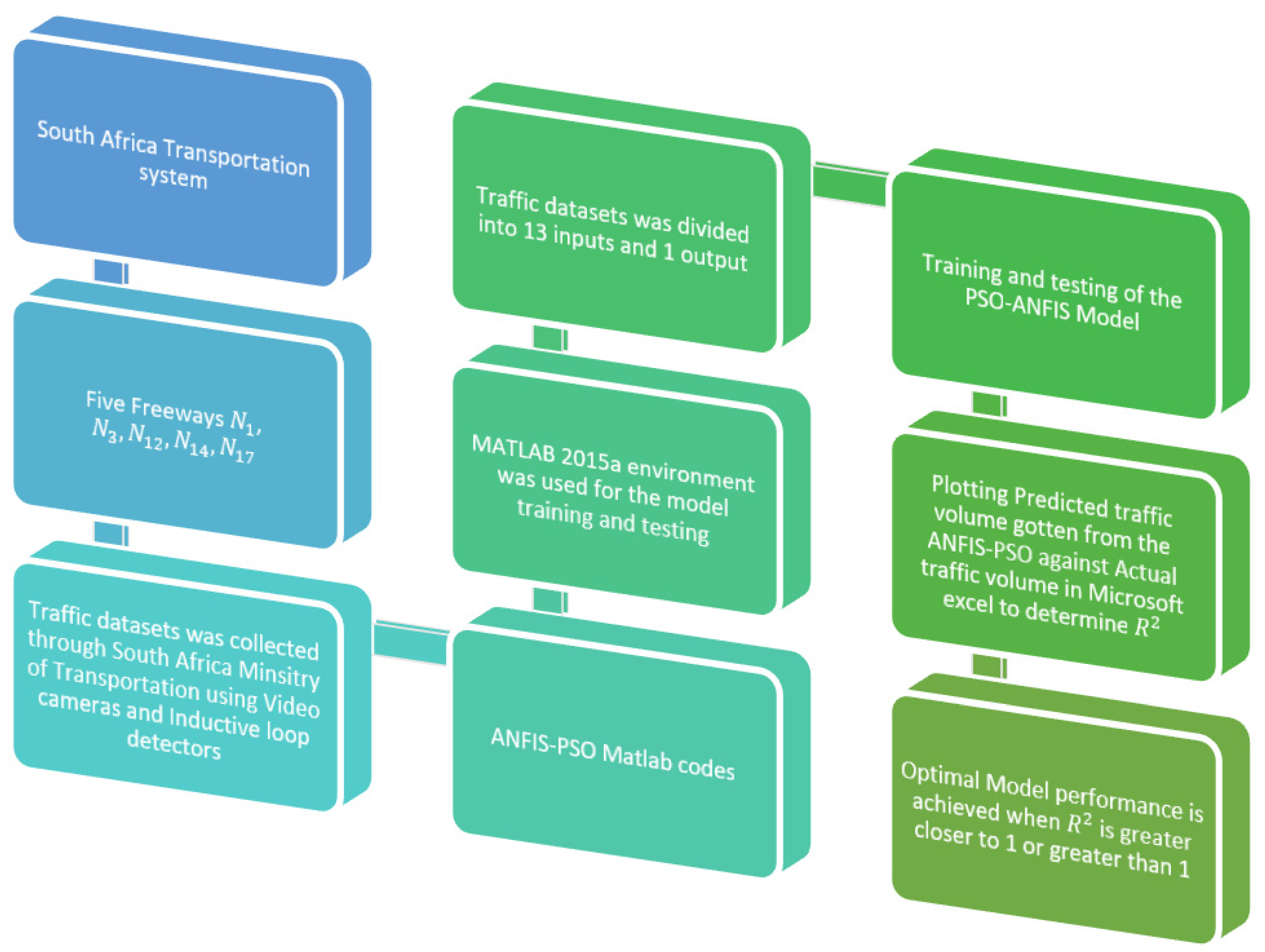
3. Methodology
3.1. Research Design
3.2. Location of the Research
3.3. Traffic Data
3.4. Equipment Used in the Collection of Traffic Data
3.4.1. Inductive Loop Detector
3.4.2. Video Cameras
- (a)
- An image processing system can be defined as a video camera situated overhead at a position above the freeway that is used to capture real-time traffic flow images and video images of the traffic flow of vehicles.
- (b)
- Telecommunication system can be defined as advanced innovative and a telephone line that transfers images and video streams to the image processing system.
- (c)
- Image processing system such as a computer that processes frames of a video clip used for traffic data extraction on freeways.
3.5. The Five Freeways Vehicular Traffic Flow
3.6. Model Development
- whereis represented by the time step,
- are known as the input parameters
- indicates the system output parameter
- represents the fuzzy sets
- is known as the crisp variables
- ❖ 1000 maximum iteration must be achieved.
- ❖ The model training run in the MATLAB environment will be stopped only when the objective functions don’t achieve the required parameter.
Performance Evaluation of ANFIS-PSO Model
- Root Mean Square Error (RMSE)
- 2.
- Determination of Coefficientwhere;
4. Results and Discussions
5. Conclusions and Recommendations
- The findings of this research suggest that, in general, the accuracy and effectiveness of the ANFIS-PSO model are suitable for predicting optimal performance parameters of traffic flow of vehicles at freeways.
- The evidence from this study suggests that it is significant to understand and identify common features of vehicular traffic flow and how it affects the traffic volume of vehicles at major freeways.
- This study has achieved the successful development of an adaptive neuro-fuzzy inference system optimized by particle swarm optimization for modelling vehicular traffic flow at freeways.
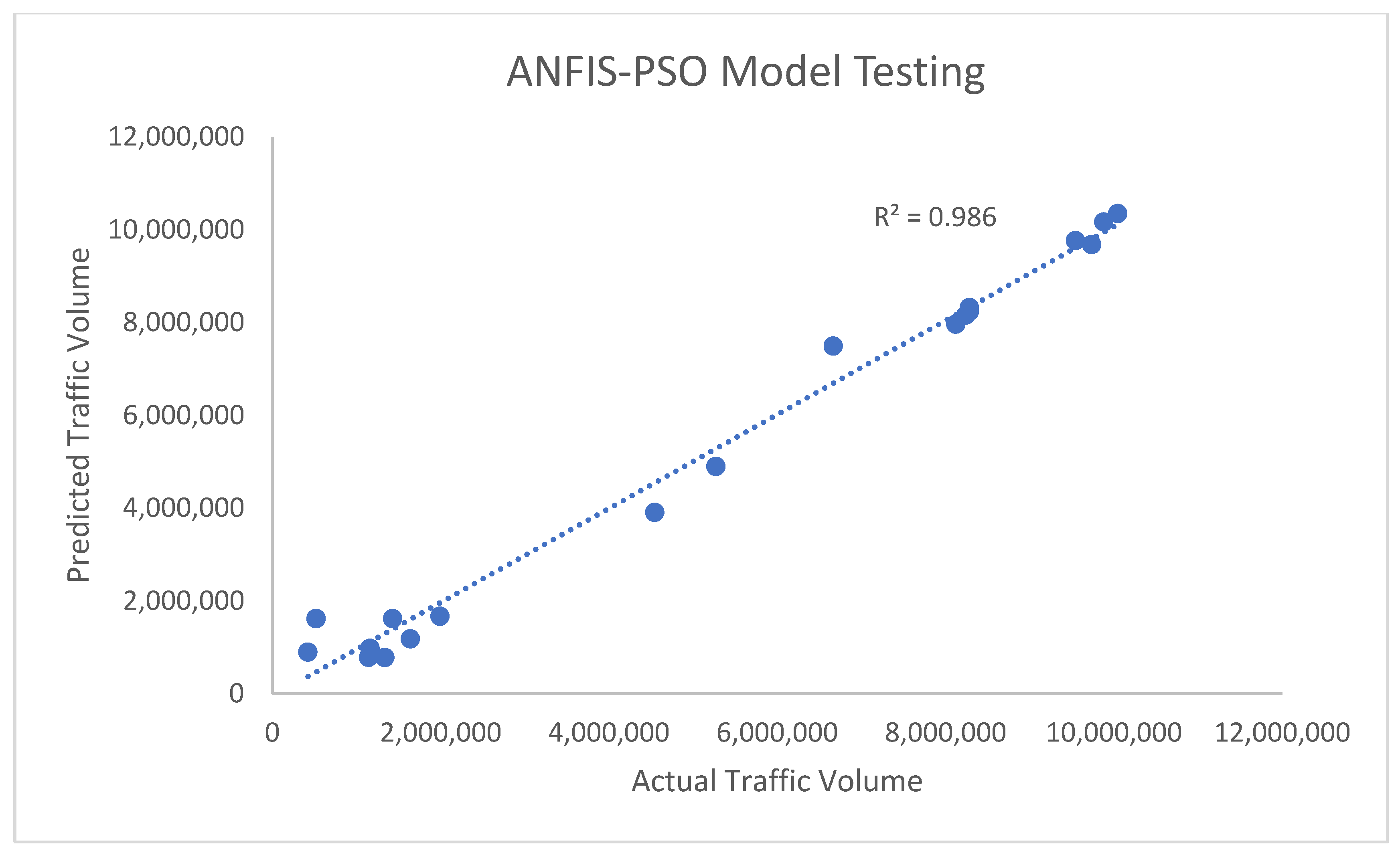
- The second major finding was that the, from the results obtained during the ANFIS-PSO model training and testing of traffic datasets from each freeway, it could be deduced that there is an optimum performance of the ANFIS-PSO model. The effectiveness and efficiency of the ANFIS-PSO model are better than the conventional models well actuated and feed controller in different traffic flow conditions.
- The Multiple regression analysis for both the ANFIS-PSO model training and testing (0.9978 and 0.9860) provides an excellent predictive approach compared to other predictive models. In congruence with past literature, in which various predictive models were used, the ANFIS-PSO model possesses a high predictability level. This result has proven that the ANFIS-PSO model can model the traffic flow of vehicles at freeways with high accuracy by creating an agglomeration of appropriate fuzzy rules and neuron weights. The most significant advantage of ANFIS-PSO over other models discovered in this research is the ability of the model to calculate suitable regression values for the input and output traffic variables, considering the membership functions associated with those variables.
- In general, the results of this research have shown the ANFIS-PSO model’s capability to address the primary shortcoming of artificial neural networks without evaluating the structure of the network and the trapping of the local optimum performance.
- This research extends our knowledge of metaheuristic models in predicting the traffic flow of vehicles at freeways. It also significantly adds to the growing body of literature regarding the combination of particle swarm optimization to existing heuristics models.
5.1. Recommendations
- It would be interesting to assess the impacts of COVID-19 on the traffic flow of vehicles using other metaheuristics models such as ANN-PSO and ANFIS-GA.
- Further work needs to be done to establish whether other existing traffic flow variables can be used to model traffic flow using conventional and artificial intelligence models.
- Further research needs to examine the links between traffic flow variables such as traffic volume, traffic density, speed, and time.
- A natural progression of this work will be in exploring areas of determining and evaluating the feasibilities of traffic volume prediction using different types of swarm and evolutionary optimization algorithms
- Finally, further research needs to explore the significance difference between application of spatiotemporal and metaheuristics models in the modelling of vehicular traffic flow using traffic data from road intersections or freeways.
5.2. Limitations
- The number of traffic data used; it is always important when predicting to make use of a large volume of data to achieve optimal performance as much as possible.
- During the traffic data collection, the traffic flow of vehicles might have been affected by extreme weather, vehicular accidents on the freeways, and other unforeseeable factors.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Freeways | Dates | Number of Lanes | Lane Descriptions | Traffic Flow Directions | Number of Vehicles | Longitude | Type of Pavement | Latitude | Length (km) |
|---|---|---|---|---|---|---|---|---|---|
| 01—Lane to Johannesburg | Southbound | ||||||||
| 02—Middle Lane to Johannesburg | Southbound | ||||||||
| 03—Lane to Johannesburg | Southbound | ||||||||
| N 1 | 15 July 2019–24 July 2019 | 4 | 04—On-Ramp joining N3 | Southbound | 21,097,152 | 26.1669 | Asphalt | 29.0961 | 1940 |
| 05—lane from N1 | Southbound | ||||||||
| 06—Middle Lane from N1 | Southbound | ||||||||
| 07—Lane from N1 (Polokwane) | Southbound | ||||||||
| 01—Lane to Johannesburg | Northbound | ||||||||
| 02—Middle Lane to Johannesburg | Northbound | ||||||||
| N 3 | 15 July 2019–24 July 2019 | 3 | 03—Middle Lane to Johannesburg | Northbound | 12,240,260 | 28.341483 | Asphalt | −26.468419 | 579 |
| 04—Lane to Johannesburg | Northbound | ||||||||
| 05—The Off-Ramp to R10 1N | Southbound | ||||||||
| N 12 | 15 July 2019–24 July 2019 | 01—lane to Johannesburg | Southbound | 20,448,023 | 29.227533 | Asphalt | −25.922341 | 1353 | |
| 02—Middle Lane to Johannesburg | Southbound | ||||||||
| 03—Middle Lane to Johannesburg | Southbound | ||||||||
| 04—Lane to Johannesburg | Southbound | ||||||||
| 05—Off-Ramp to Ultra city | Southbound | ||||||||
| 06—Fastlane, Off-Ramp | Southbound | ||||||||
| 07—Off-Ramp to Samrand Avenue | Southbound | ||||||||
| 01—lane to Johannesburg | Southbound | ||||||||
| 02—Middle Lane to Johannesburg | Southbound | ||||||||
| N 14 | 15 July 2019–24 July 2019 | 4 | 03—Middle Lane to Johannesburg | Southbound | 16,051,124 | 27.847201 | Asphalt | −26.033668 | 1195 |
| 04—Lane to Johannesburg | Southbound | ||||||||
| 05—Off-Ramp to R56 2 | Southbound | ||||||||
| 01—lane to Johannesburg | Southbound | ||||||||
| 02—Middle Lane to Johannesburg | Southbound | ||||||||
| N 17 | 15 July 2019–24 July 2019 | 4 | 03—Middle Lane to Johannesburg | Southbound | 18,262,048 | 30.9885 | Asphalt | −26.2126 | 330 |
| 04—Lane to Johannesburg | Southbound | ||||||||
| 05—Off-Ramp to New Road | Southbound |
| Light Vehicle | Long Truck | Medium Truck | Short Truck | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dates and Period of the Day | Speed (km/h) | Number of Light Veicles | Time (s) | Speed (km/h) | Number of Long Trucks | Time (s) | Speed (km/h) | Number of Medium Trucks | Time (s) | Speed (km/h) | Number of Short Trucks | Time (s) | Traffic Density (Vehicles/km) | Traffic Volume (Number of Vehicles/Time) |
| 15 July 2019 | ||||||||||||||
| 1 | 115 | 1438 | 230 | 87 | 44 | 298 | 92 | 29 | 282 | 97 | 51 | 276 | 223 | 574 868 |
| 2 | 65 | 29,934 | 489 | 49 | 197 | 960 | 59 | 188 | 591 | 70 | 625 | 542 | 4421 | 5,416,190 |
| 3 | 106 | 18,213 | 245 | 81 | 308 | 321 | 85 | 277 | 315 | 95 | 1056 | 278 | 2836 | 6,882,973 |
| 4 | 103 | 22,344 | 255 | 82 | 321 | 316 | 85 | 263 | 308 | 97 | 865 | 271 | 3399 | 7,996,735 |
| 5 | 109 | 3071 | 244 | 81 | 140 | 319 | 83 | 70 | 349 | 93 | 96 | 285 | 482 | 1,163,614 |
| 16 July 2019 | ||||||||||||||
| 1 | 111 | 1234 | 237 | 82 | 115 | 313 | 84 | 35 | 306 | 95 | 54 | 277 | 205 | 504,994 |
| 2 | 60 | 28,844 | 565 | 52 | 258 | 833 | 52 | 206 | 750 | 65 | 635 | 586 | 4278 | 4,544,699 |
| 3 | 107 | 24,793 | 241 | 83 | 338 | 310 | 88 | 332 | 298 | 99 | 1437 | 264 | 3843 | 9,543,915 |
| 4 | 103 | 22,577 | 254 | 81 | 269 | 318 | 86 | 258 | 302 | 98 | 919 | 270 | 3432 | 8,120,977 |
| 5 | 110 | 3432 | 241 | 81 | 162 | 320 | 84 | 91 | 315 | 95 | 94 | 278 | 540 | 1,323,411 |
| 17 July 2019 | ||||||||||||||
| 1 | 113 | 1005 | 233 | 85 | 84 | 305 | 91 | 43 | 286 | 103 | 56 | 256 | 170 | 425,123 |
| 2 | 76 | 31,392 | 422 | 67 | 225 | 540 | 70 | 234 | 520 | 84 | 758 | 378 | 4658 | 6,666,994 |
| 3 | 106 | 25,480 | 243 | 82 | 376 | 313 | 87 | 331 | 297 | 99 | 1503 | 266 | 3956 | 9,737,896 |
| 4 | 103 | 22,999 | 254 | 82 | 299 | 313 | 87 | 271 | 298 | 97 | 932 | 272 | 3500 | 8,284,089 |
| 5 | 110 | 3736 | 240 | 82 | 141 | 313 | 86 | 74 | 303 | 94 | 108 | 282 | 580 | 1,431,353 |
| 18 July 2019 | ||||||||||||||
| 1 | 113 | 1114 | 232 | 86 | 95 | 301 | 88 | 31 | 299 | 94 | 65 | 283 | 186 | 468,260 |
| 2 | 74 | 31,060 | 430 | 65 | 287 | 582 | 65 | 240 | 580 | 83 | 751 | 398 | 4620 | 6,469,966 |
| 3 | 106 | 25,977 | 244 | 83 | 351 | 311 | 88 | 345 | 297 | 98 | 1521 | 270 | 4028 | 9,880,675 |
| 4 | 103 | 23,051 | 254 | 81 | 308 | 319 | 84 | 258 | 311 | 95 | 870 | 278 | 3498 | 8,244,838 |
| 5 | 110 | 3876 | 240 | 79 | 152 | 334 | 83 | 70 | 317 | 97 | 115 | 270 | 602 | 1,481,270 |
| 19 July 2019 | ||||||||||||||
| 1 | 113 | 1296 | 233 | 84 | 85 | 309 | 87 | 56 | 298 | 96 | 51 | 281 | 213 | 531,622 |
| 2 | 58 | 28,408 | 691 | 48 | 283 | 991 | 49 | 233 | 981 | 64 | 686 | 630 | 4230 | 3,682,757 |
| 3 | 104 | 27,970 | 248 | 81 | 383 | 317 | 85 | 356 | 305 | 97 | 1522 | 273 | 4319 | 10,412,641 |
| 4 | 102 | 24,080 | 256 | 81 | 351 | 316 | 85 | 257 | 307 | 98 | 916 | 270 | 3658 | 8,571,413 |
| 5 | 110 | 5306 | 240 | 82 | 126 | 317 | 85 | 72 | 314 | 101 | 111 | 260 | 802 | 1,993,989 |
| 20 July 2019 | ||||||||||||||
| 1 | 110 | 1853 | 241 | 84 | 84 | 311 | 82 | 32 | 321 | 97 | 52 | 269 | 289 | 710,172 |
| 2 | 111 | 13,178 | 232 | 83 | 213 | 312 | 85 | 141 | 307 | 103 | 421 | 257 | 1993 | 5,135,566 |
| 3 | 109 | 22,552 | 237 | 82 | 205 | 315 | 89 | 202 | 296 | 104 | 656 | 254 | 3374 | 8,544,563 |
| 4 | 108 | 17,034 | 241 | 81 | 172 | 321 | 86 | 120 | 310 | 106 | 426 | 248 | 2536 | 6,335,493 |
| 5 | 110 | 5717 | 240 | 79 | 48 | 324 | 88 | 42 | 298 | 102 | 71 | 258 | 840 | 2,103,922 |
| 21 July 2019 | ||||||||||||||
| 1 | 110 | 1700 | 244 | 82 | 36 | 319 | 86 | 22 | 306 | 97 | 21 | 266 | 254 | 623,026 |
| 2 | 113 | 7266 | 231 | 84 | 112 | 311 | 85 | 67 | 307 | 106 | 156 | 248 | 1086 | 2,821,822 |
| 3 | 114 | 17,208 | 227 | 85 | 111 | 302 | 95 | 132 | 279 | 112 | 340 | 234 | 2542 | 6,737,959 |
| 4 | 110 | 19,043 | 236 | 84 | 128 | 309 | 93 | 122 | 281 | 112 | 350 | 234 | 2806 | 7,167,665 |
| 5 | 112 | 3940 | 236 | 85 | 59 | 306 | 81 | 39 | 327 | 103 | 65 | 258 | 586 | 1,490,162 |
| 22 July 2019 | ||||||||||||||
| 1 | 113 | 1290 | 231 | 85 | 51 | 304 | 90 | 29 | 290 | 100 | 53 | 261 | 203 | 520,392 |
| 2 | 64 | 31,003 | 525 | 54 | 225 | 806 | 56 | 188 | 809 | 71 | 608 | 496 | 4575 | 5,240,023 |
| 3 | 107 | 23,657 | 243 | 82 | 435 | 315 | 87 | 346 | 300 | 97 | 1468 | 270 | 3701 | 9,095,988 |
| 4 | 103 | 22,292 | 256 | 81 | 293 | 317 | 85 | 256 | 307 | 98 | 834 | 268 | 3382 | 7,948,635 |
| 5 | 110 | 2989 | 242 | 80 | 138 | 324 | 81 | 83 | 322 | 93 | 84 | 283 | 471 | 1,145,786 |
| 23 July 2019 | ||||||||||||||
| 1 | 113 | 1258 | 232 | 84 | 122 | 308 | 88 | 34 | 294 | 92 | 45 | 288 | 208 | 522,734 |
| 2 | 66 | 30,007 | 507 | 57 | 219 | 771 | 58 | 214 | 662 | 73 | 673 | 456 | 4445 | 5,280,114 |
| 3 | 106 | 24,620 | 245 | 81 | 351 | 317 | 86 | 323 | 305 | 97 | 1516 | 272 | 3830 | 9,350,828 |
| 4 | 103 | 22,522 | 255 | 81 | 282 | 320 | 86 | 257 | 306 | 97 | 886 | 272 | 3421 | 8,063,400 |
| 5 | 110 | 3297 | 240 | 81 | 124 | 317 | 82 | 65 | 318 | 95 | 83 | 276 | 510 | 1,259,688 |
| 24 July 2019 | ||||||||||||||
| 1 | 113 | 1040 | 233 | 85 | 92 | 302 | 84 | 41 | 314 | 93 | 49 | 283 | 175 | 434,026 |
| 2 | 66 | 29,983 | 509 | 59 | 265 | 630 | 58 | 199 | 698 | 75 | 697 | 481 | 4449 | 5,273,322 |
| 3 | 106 | 25,084 | 244 | 81 | 357 | 319 | 85 | 340 | 305 | 97 | 1479 | 274 | 3894 | 9,518,832 |
| 4 | 103 | 23,049 | 254 | 81 | 325 | 318 | 87 | 261 | 302 | 97 | 937 | 274 | 3510 | 8,284,807 |
| 5 | 110 | 3488 | 240 | 81 | 157 | 321 | 79 | 74 | 336 | 95 | 101 | 277 | 546 | 1,339,216 |
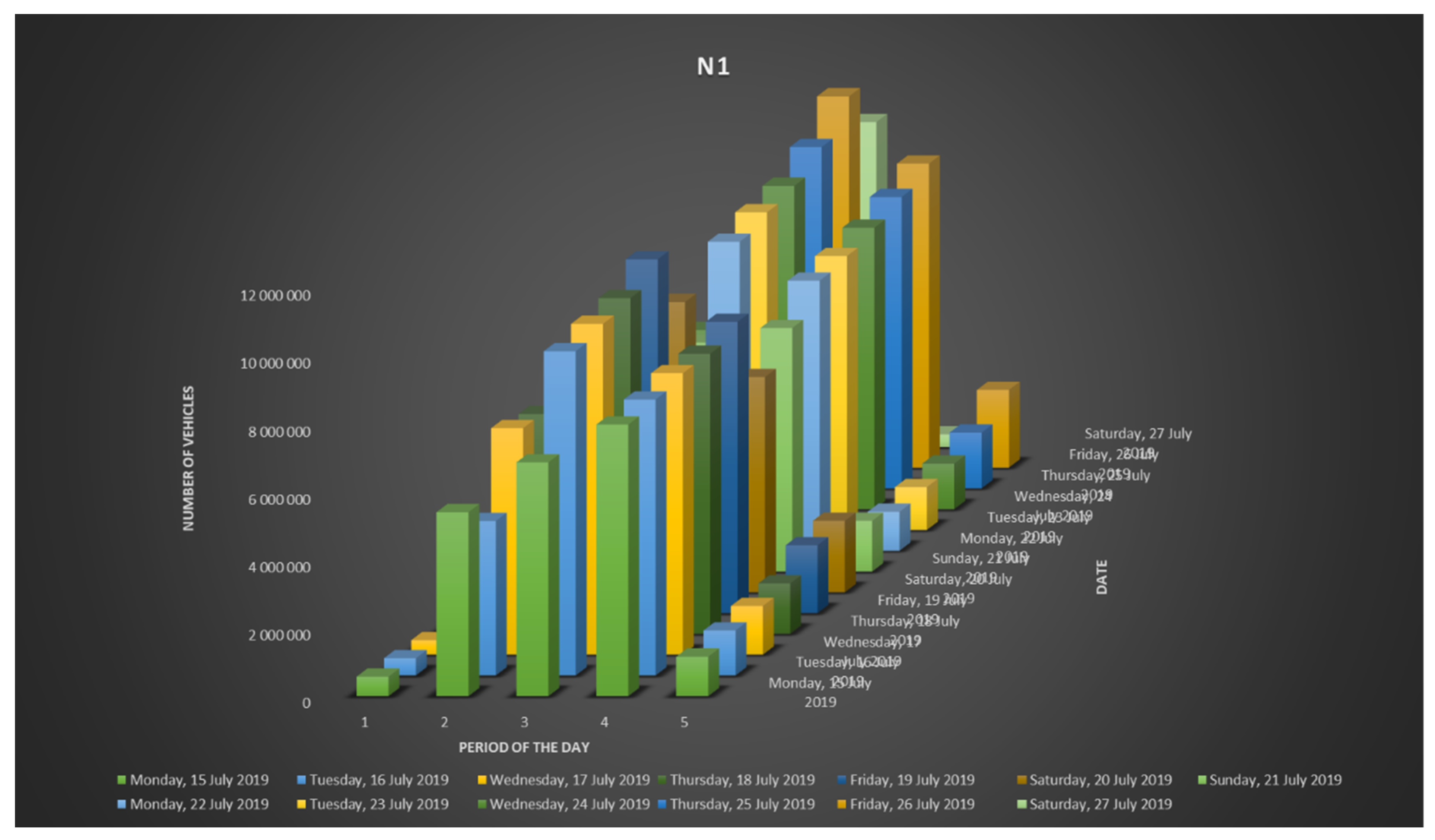
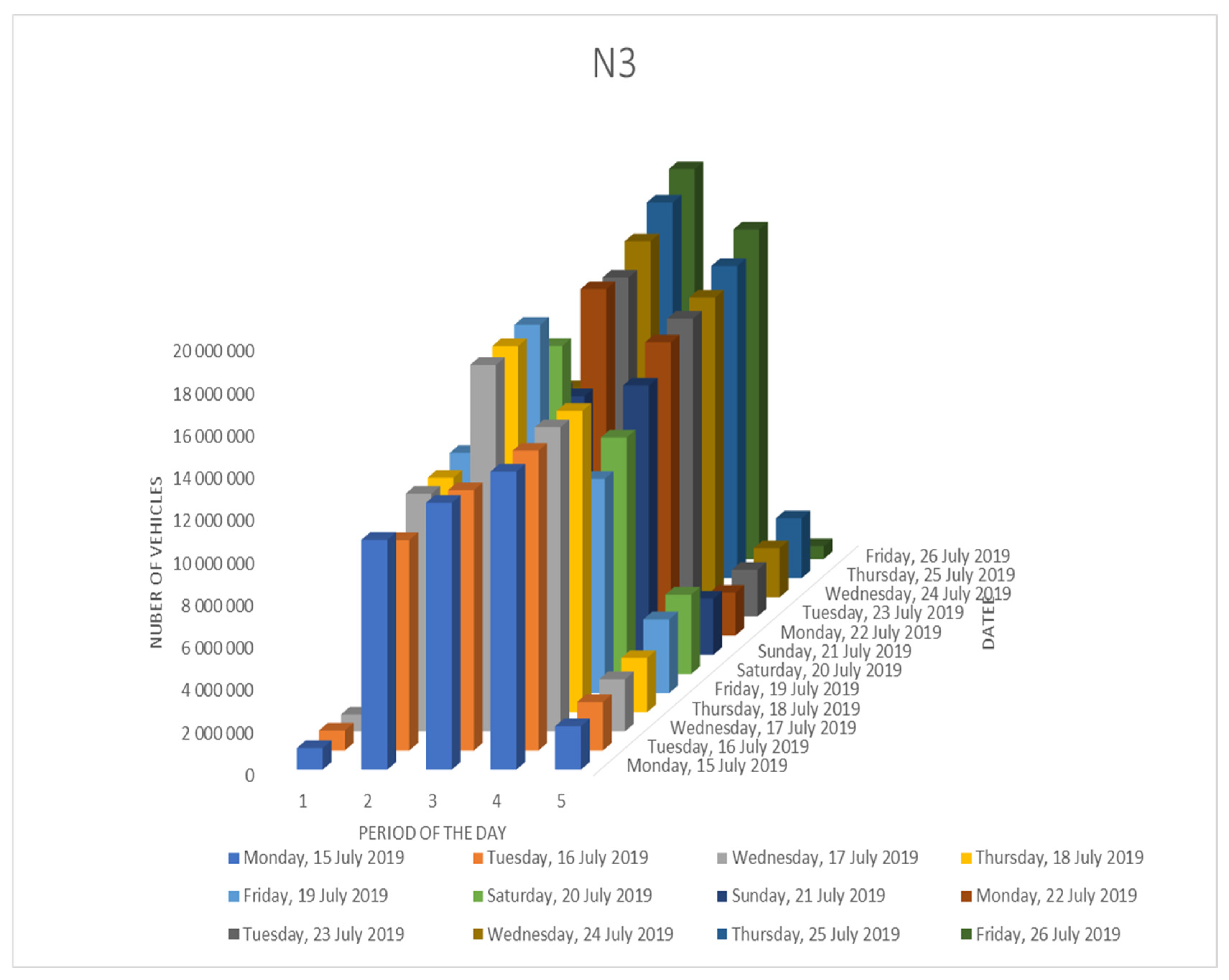

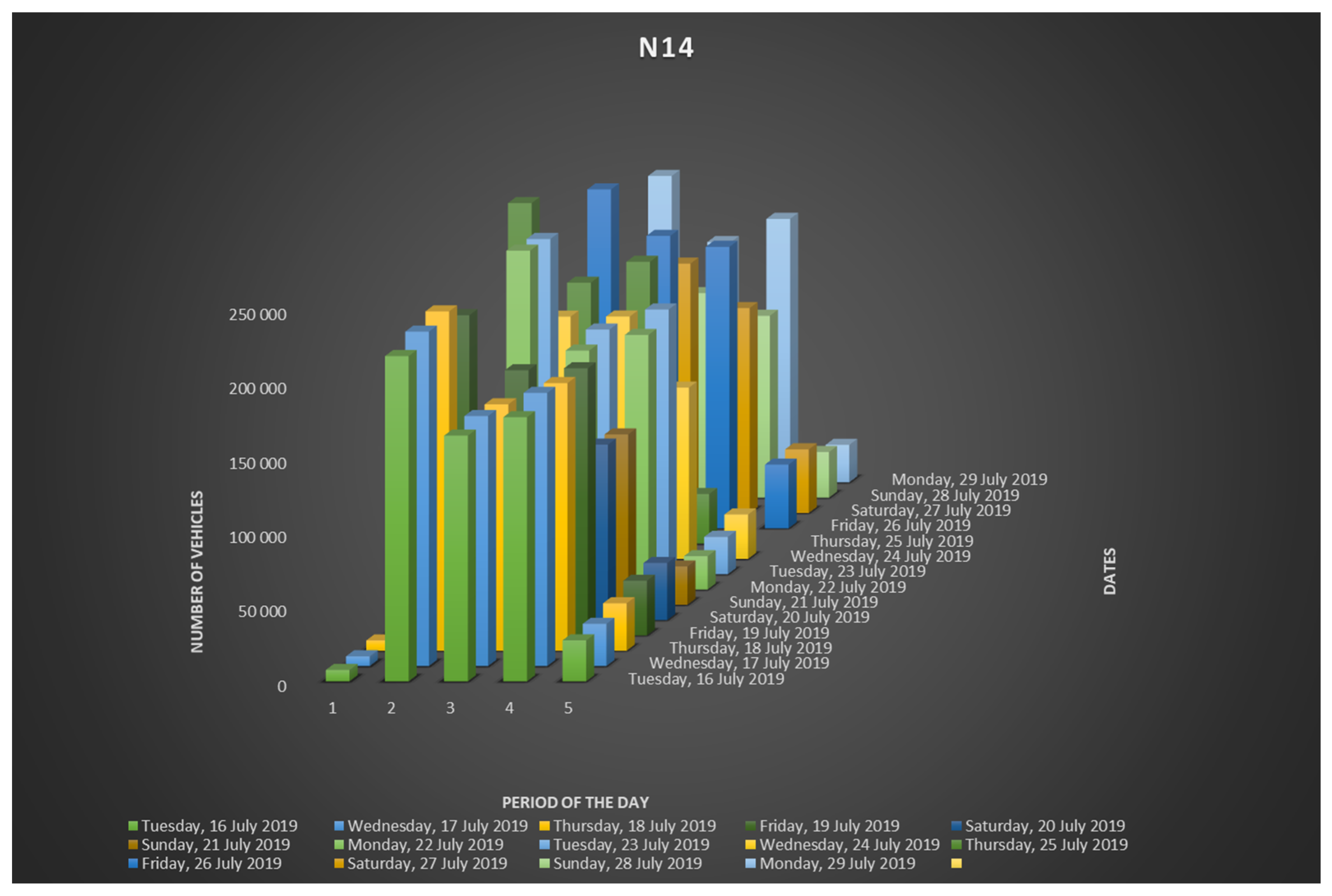

- 1: 00:00:00–04:59:59 (Off-peak),
- 2: 05:00:00–09:59:59 (On-peak)
- 3: 10:00:00–14:59:59 (On-peak)
- 4: 15:00:00–19:59:59 (On-peak)
- 5: 20:00:00–23:59:59 (Off-peak).
References
- Wang, W.; Zhang, H.; Li, T.; Guo, J.; Huang, W.; Wei, Y.; Cao, J. An interpretable model for short term traffic flow prediction. Math. Comput. Simul. 2020, 171, 264–278. [Google Scholar] [CrossRef]
- Deng, S.; Jia, S.; Chen, J. Exploring spatial-temporal relations via deep convolutional neural networks for traffic flow prediction with incomplete data. Appl. Soft Comput. 2019, 78, 712–721. [Google Scholar] [CrossRef]
- Emami, A.; Sarvi, M.; Bagloee, S.A. Short-term traffic flow prediction based on faded memory Kalman Filter fusing data from connected vehicles and Bluetooth sensors. Simul. Model. Pract. Theory 2020, 102, 102025. [Google Scholar] [CrossRef]
- Li, F.; Liao, S.S.; Cai, M. A new probability statistical model for traffic noise prediction on free flow roads and control flow roads. Transp. Res. Part D Transp. Environ. 2016, 49, 313–322. [Google Scholar] [CrossRef]
- Aramini, B.; Fan, J. Technique for myasthenia gravis: Subxiphoid approach. Thorac. Surg. Clin. 2019, 29, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Candini, O.; Grisendi, G.; Foppiani, E.M.; Brogli, M.; Aramini, B.; Masciale, V.; Spano, C.; Petrachi, T.; Veronesi, E.; Conte, P.; et al. A novel 3D in vitro platform for pre-clinical investigations in drug testing, gene therapy, and immuno-oncology. Sci. Rep. 2019, 9, 7154. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Su, X.; Wang, Y.; Lin, Y.; Li, Z.; Li, Y. Robust causal dependence mining in big data network and its application to traffic flow predictions. Transp. Res. Part C Emerg. Technol. 2015, 58, 292–307. [Google Scholar] [CrossRef]
- Taghipour, A.; Frayret, J.-M. Negotiation-based coordination in supply chain: Model and discussion. In Proceedings of the 2010 IEEE International Conference on Systems, Man and Cybernetics, Istanbul, Turkey, 10–13 October 2010; pp. 1643–1649. [Google Scholar]
- Vosooghidizaji, M.; Taghipour, A.; Canel-Depitre, B. Supply chain coordination under information asymmetry: A review. Int. J. Prod. Res. 2020, 58, 1805–1834. [Google Scholar] [CrossRef]
- Shang, Q.; Lin, C.; Yang, Z.; Bing, Q.; Zhou, X. A hybrid short-term traffic flow prediction model based on singular spectrum analysis and kernel extreme learning machine. PLoS ONE 2016, 11, e0161259. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wang, J.; Fan, R.; Zhang, Y.; Guo, Q.; Siddique, C.; Ban, X.J. Short-term traffic state prediction from latent structures: Accuracy vs. efficiency. Transp. Res. Part C Emerg. Technol. 2020, 111, 72–90. [Google Scholar] [CrossRef]
- Brockmann, D.; Hufnagel, L.; Geisel, T. The scaling laws of human travel. Nature 2006, 439, 462–465. [Google Scholar] [CrossRef]
- Qin, H.; Li, H.; Zhao, X. Development status of domestic and foreign smart city. Glob. Presence 2010, 9, 50–52. [Google Scholar]
- Ukaegbu, U.; Tartibu, L.; Laseinde, T.; Okwu, M.; Olayode, I. A deep learning algorithm for detection of potassium deficiency in a red grapevine and spraying actuation using a raspberry pi3. In Proceedings of the 2020 International Conference on Artificial Intelligence, Big Data, Computing and Data Communication Systems (icABCD), Durban, South Africa, 6–7 August 2020; pp. 1–6. [Google Scholar]
- Ukaegbu, U.F.; Tartibu, L.K.; Okwu, M.O.; Olayode, I.O. Development of a Light-Weight Unmanned Aerial Vehicle for Precision Agriculture. Sensors 2021, 21, 4417. [Google Scholar] [CrossRef] [PubMed]
- An, S.-H.; Lee, B.-H.; Shin, D.-R. A survey of intelligent transportation systems. In Proceedings of the 2011 Third International Conference on Computational Intelligence, Communication Systems and Networks, Bali, Indonesia, 26–28 July 2011; pp. 332–337. [Google Scholar]
- Castro-Neto, M.; Jeong, Y.-S.; Jeong, M.-K.; Han, L.D. Online-SVR for short-term traffic flow prediction under typical and atypical traffic conditions. Expert Syst. Appl. 2009, 36, 6164–6173. [Google Scholar] [CrossRef]
- Chen, H.; Rakha, H.A. Real-time travel time prediction using particle filtering with a non-explicit state-transition model. Transp. Res. Part C Emerg. Technol. 2014, 43, 112–126. [Google Scholar] [CrossRef]
- Severino, A.; Pappalardo, G.; Curto, S.; Trubia, S.; Olayode, I.O. Safety Evaluation of Flower Roundabout Considering Autonomous Vehicles Operation. Sustainability 2021, 13, 10120. [Google Scholar] [CrossRef]
- Al-Kadi, O.; Al-Kadi, O.; Al-Sayyed, R.; Alqatawna, J.F. Road scene analysis for determination of road traffic density. Front. Comput. Sci. 2014, 8, 619–628. [Google Scholar] [CrossRef]
- Chin, A.T. Containing air pollution and traffic congestion: Transport policy and the environment in Singapore. Atmos. Environ. 1996, 30, 787–801. [Google Scholar] [CrossRef]
- Rosenlund, M.; Forastiere, F.; Stafoggia, M.; Porta, D.; Perucci, M.; Ranzi, A.; Nussio, F.; Perucci, C.A. Comparison of regression models with land-use and emissions data to predict the spatial distribution of traffic-related air pollution in Rome. J. Expo. Sci. Environ. Epidemiol. 2008, 18, 192–199. [Google Scholar] [CrossRef]
- Krzyżanowski, M.; Kuna-Dibbert, B.; Schneider, J. Health Effects of Transport-Related Air Pollution; WHO Regional Office Europe: Copenhagen, Denmark, 2005. [Google Scholar]
- Qian, Z.S.; Rajagopal, R. Optimal dynamic parking pricing for morning commute considering expected cruising time. Transp. Res. Part C Emerg. Technol. 2014, 48, 468–490. [Google Scholar] [CrossRef]
- De Gier, J.; Garoni, T.M.; Rojas, O. Traffic flow on realistic road networks with adaptive traffic lights. J. Stat. Mech. Theory Exp. 2011, 2011, P04008. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, F.-Y.; Wang, K.; Lin, W.-H.; Xu, X.; Chen, C. Data-driven intelligent transportation systems: A survey. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1624–1639. [Google Scholar] [CrossRef]
- INRIX. Inrix Parking Solutions. 2017. Available online: http://www2.inrix.com/parking-solutions (accessed on 20 October 2021).
- Olayode, O.; Tartibu, L.; Okwu, M. Application of Artificial Intelligence in Traffic Control System of Non-Autonomous Vehicles at Signalized Road Intersection. Proc. CIRP 2020, 91, 194–200. [Google Scholar] [CrossRef]
- Isaac, O.O.; Tartibu, L.K.; Okwu, M.O. Prediction and Modelling of Traffic Flow of Human-Driven Vehicles at a Signalized Road Intersection Using Artificial Neural Network Model: A South Africa Road Transportation System Scenario. Transp. Eng. 2021, 6, 100095. [Google Scholar]
- Olayode, I.O.; Tartibu, L.K.; Okwu, M.O. Traffic Flow Prediction at Signalized Road Intersections: A Case of Markov Chain and Artificial Neural Network Model. In Proceedings of the 2021 IEEE 12th International Conference on Mechanical and Intelligent Manufacturing Technologies (ICMIMT), Cape Town, South Africa, 13–15 May 2021; pp. 287–292. [Google Scholar]
- Yang, X.; Yu, Q.; He, L.; Guo, T. The one-against-all partition based binary tree support vector machine algorithms for multi-class classification. Neurocomputing 2013, 113, 1–7. [Google Scholar] [CrossRef]
- Petković, D.; Ćojbašić, Ž.; Nikolić, V.; Shamshirband, S.; Kiah, M.L.M.; Anuar, N.B.; Wahab, A.W.A. Adaptive neuro-fuzzy maximal power extraction of wind turbine with continuously variable transmission. Energy 2014, 64, 868–874. [Google Scholar] [CrossRef]
- Deng, Y.; Ren, Z.; Kong, Y.; Bao, F.; Dai, Q. A hierarchical fused fuzzy deep neural network for data classification. IEEE Trans. Fuzzy Syst. 2016, 25, 1006–1012. [Google Scholar] [CrossRef]
- Chen, C.P.; Zhang, C.-Y.; Chen, L.; Gan, M. Fuzzy restricted Boltzmann machine for the enhancement of deep learning. IEEE Trans. Fuzzy Syst. 2015, 23, 2163–2173. [Google Scholar] [CrossRef]
- Olayode, I.O.; Tartibu, L.K.; Okwu, M.O.; Severino, A. Comparative Traffic Flow Prediction of a Heuristic ANN Model and a Hybrid ANN-PSO Model in the Traffic Flow Modelling of Vehicles at a Four-Way Signalized Road Intersection. Sustainability 2021, 13, 10704. [Google Scholar] [CrossRef]
- Liebig, T.; Piatkowski, N.; Bockermann, C.; Morik, K. Dynamic route planning with real-time traffic predictions. Inf. Syst. 2017, 64, 258–265. [Google Scholar] [CrossRef]
- Smith, B.L.; Williams, B.M.; Oswald, R.K. Comparison of parametric and nonparametric models for traffic flow forecasting. Transp. Res. Part C Emerg. Technol. 2002, 10, 303–321. [Google Scholar] [CrossRef]
- Chen, C.; Hu, J.; Meng, Q.; Zhang, Y. Short-time traffic flow prediction with ARIMA-GARCH model. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden, Germany, 5–9 June 2011; pp. 607–612. [Google Scholar]
- Li, J.-Q. Discretization modeling, integer programming formulations and dynamic programming algorithms for robust traffic signal timing. Transp. Res. Part C Emerg. Technol. 2011, 19, 708–719. [Google Scholar] [CrossRef]
- Aifadopoulou, G.; Bratsas, C.; Koupidis, K.; Chatzopoulou, A.; Salanova, J.-M.; Tzenos, P. Short-Term Prediction of the Traffic Status in Urban Places Using Neural Network Models. In The 4th Conference on Sustainable Urban Mobility; Springer: Cham, Switzerland; Skiathos Island, Greece, 2018; pp. 181–188. [Google Scholar]
- Olayode, I.O.; Tartibu, L.K.; Okwu, M.O.; Ukaegbu, U.F. Development of a Hybrid Artificial Neural Network-Particle Swarm Optimization Model for the Modelling of Traffic Flow of Vehicles at Signalized Road Intersections. Appl. Sci. 2021, 11, 8387. [Google Scholar] [CrossRef]
- Vlahogianni, E.I.; Karlaftis, M.G.; Golias, J.C. Optimized and meta-optimized neural networks for short-term traffic flow prediction: A genetic approach. Transp. Res. Part C Emerg. Technol. 2005, 13, 211–234. [Google Scholar] [CrossRef]
- Nellore, K.; Hancke, G.P. A survey on urban traffic management system using wireless sensor networks. Sensors 2016, 16, 157. [Google Scholar] [CrossRef]
- Bratsas, C.; Koupidis, K.; Salanova, J.-M.; Giannakopoulos, K.; Kaloudis, A.; Aifadopoulou, G. A comparison of machine learning methods for the prediction of traffic speed in urban places. Sustainability 2020, 12, 142. [Google Scholar] [CrossRef]
- Barchi, A.C.; Ito, S.; Escaramboni, B.; de Oliva Neto, P.; Herculano, R.D.; Miranda, M.C.R.; Passalia, F.J.; Rocha, J.C.; Núñez, E.G.F. Artificial intelligence approach based on near-infrared spectral data for monitoring of solid-state fermentation. Process Biochem. 2016, 51, 1338–1347. [Google Scholar] [CrossRef]
- Adnan, M.M.; Sarkheyli, A.; Zain, A.M.; Haron, H. Fuzzy logic for modeling machining process: A review. Artif. Intell. Rev. 2015, 43, 345–379. [Google Scholar] [CrossRef]
- Almási, A.-D.; Woźniak, S.; Cristea, V.; Leblebici, Y.; Engbersen, T. Review of advances in neural networks: Neural design technology stack. Neurocomputing 2016, 174, 31–41. [Google Scholar] [CrossRef]
- Olayode, I.O.; Tartibu, L.K.; Okwu, M.O. Application of Fuzzy Mamdani Model for Effective Prediction of Traffic Flow of Vehicles at Signalized Road Intersections. In Proceedings of the 2021 IEEE 12th International Conference on Mechanical and Intelligent Manufacturing Technologies (ICMIMT), Cape Town, South Africa, 13–15 May 2021; pp. 219–224. [Google Scholar]
- Ali, M.; Ghatol, A. A neuro-fuzzy inference system for student modeling in web-based intelligent tutoring systems. In Proceedings of International Conference on Cognitive Systems; Citeseer: New Delphi, India, 2004; pp. 14–19. [Google Scholar]
- Khameneh, N.B.; Arabalibeik, H.; Salehian, P.; Setayeshi, S. Abnormal red blood cells detection using adaptive neuro-fuzzy system. In Medicine Meets Virtual Reality; IOS Press BV: Amsterdam, The Netherlands, 2012; pp. 30–34. [Google Scholar]
- Fang, H. Adaptive neurofuzzy inference system in the application of the financial crisis forecast. Int. J. Innov. Manag. Technol. 2012, 3, 250. [Google Scholar]
- Chakrapani, Y.; Soundararajan, K. Adaptive neuro-fuzzy inference system based fractal image compression. Int. J. Recent Trends Eng. 2009, 2, 47. [Google Scholar]
- Patil, S.; Mandal, S.; Hegde, A.; Alavandar, S. Neuro-fuzzy based approach for wave transmission prediction of horizontally interlaced multilayer moored floating pipe breakwater. Ocean Eng. 2011, 38, 186–196. [Google Scholar] [CrossRef]
- Topalov, A.V.; Kayacan, E.; Oniz, Y.; Kaynak, O. Adaptive neuro-fuzzy control with sliding mode learning algorithm: Application to antilock braking system. In Proceedings of the 2009 7th Asian Control Conference, Hong Kong, China, 27–29 August 2009; pp. 784–789. [Google Scholar]
- Dastranj, M.R.; Ebroahimi, E.; Changizi, M.; Sameni, E. Control DC motorspeed with adaptive neuro-fuzzy control (ANFIS). Aust. J. Basic Appl. Sci. 2011, 5, 1499–1504. [Google Scholar]
- Cheng, C.-B.; Lee, E. Applying fuzzy adaptive network to fuzzy regression analysis. Comput. Math. Appl. 1999, 38, 123–140. [Google Scholar] [CrossRef][Green Version]
- Loukas, Y.L. Adaptive neuro-fuzzy inference system: An instant and architecture-free predictor for improved QSAR studies. J. Med. Chem. 2001, 44, 2772–2783. [Google Scholar] [CrossRef]
- Cai, C.; Du, D.; Liu, Z. Battery state-of-charge (SOC) estimation using adaptive neuro-fuzzy inference system (ANFIS). In The 12th IEEE International Conference on Fuzzy Systems, 2003, FUZZ’03, St. Louis, MO, USA, 25–28 May 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 2, pp. 1068–1073. [Google Scholar]
- Do, L.N.; Vu, H.L.; Vo, B.Q.; Liu, Z.; Phung, D. An effective spatial-temporal attention based neural network for traffic flow prediction. Transp. Res. Part C Emerg. Technol. 2019, 108, 12–28. [Google Scholar] [CrossRef]
- Yang, B.; Sun, S.; Li, J.; Lin, X.; Tian, Y. Traffic flow prediction using LSTM with feature enhancement. Neurocomputing 2019, 332, 320–327. [Google Scholar] [CrossRef]
- Tang, J.; Chen, X.; Hu, Z.; Zong, F.; Han, C.; Li, L. Traffic flow prediction based on combination of support vector machine and data denoising schemes. Phys. A Stat. Mech. Appl. 2019, 534, 120642. [Google Scholar] [CrossRef]
- Zhao, L.; Zhou, Z.; Lu, H.; Fujita, H. Parallel computing method of deep belief networks and its application to traffic flow prediction. Knowl.-Based Syst. 2019, 163, 972–987. [Google Scholar] [CrossRef]
- Zaki, J.; Ali-Eldin, A.; Hussein, S.E.; Saraya, S.F.; Areed, F.F. Framework for Traffic Congestion Prediction. Int. J. Sci. Eng. Res. 2016, 7, 1205–1210. [Google Scholar]
- Chaulya, S.; Prasad, G. Mine transport surveillance and production management system. In Sensing and Monitoring Technologies for Mines and Hazardous Areas; Elsevier: Amsterdam, The Netherlands, 2016; pp. 87–160. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN ‘95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar] [CrossRef]
- Bashir, Z.; El-Hawary, M. Applying wavelets to short-term load forecasting using PSO-based neural networks. IEEE Trans. Power Syst. 2009, 24, 20–27. [Google Scholar] [CrossRef]
- Yu, W.; Li, X. Fuzzy identification using fuzzy neural networks with stable learning algorithms. IEEE Trans. Fuzzy Syst. 2004, 12, 411–420. [Google Scholar] [CrossRef]
- Yuan, X.; Wang, L.; Yuan, Y. Application of enhanced PSO approach to optimal scheduling of hydro system. Energy Convers. Manag. Res. News 2008, 49, 2966–2972. [Google Scholar] [CrossRef]
- Kennedy, J. The behavior of particles. In International Conference on Evolutionary Programming; Springer: San Diego, CA, USA, 25–27 March 1998; pp. 579–589. [Google Scholar]
- Shoorehdeli, M.A.; Teshnehlab, M.; Sedigh, A.K.; Khanesar, M.A. Identification using ANFIS with intelligent hybrid stable learning algorithm approaches and stability analysis of training methods. Appj. Soft Comput. 2009, 9, 833–850. [Google Scholar] [CrossRef]
- Basser, H.; Karami, H.; Shamshirband, S.; Akib, S.; Amirmojahedi, M.; Ahmad, R.; Jahangirzadeh, A.; Javidnia, H. Hybrid ANFIS–PSO approach for predicting optimum parameters of a protective spur dike. Appl. Soft Comput. 2015, 30, 642–649. [Google Scholar] [CrossRef]








| Input Variables | Output Variables |
|---|---|
| Traffic density | Traffic Volume |
| Number of light vehicles | |
| The average speed of light vehicles | |
| Time of day of light vehicles | |
| The average speed of a long truck | |
| Time of day of long truck | |
| Number of long trucks | |
| The average speed of a medium truck | |
| Time of day of medium truck | |
| Number of medium trucks | |
| Number of short trucks | |
| The average speed of a short truck | |
| Time of day of short truck |
| Freeways | Training | Testing | Total |
|---|---|---|---|
| 71 | 25 | 96 | |
| 100 | 30 | 130 | |
| 95 | 20 | 115 | |
| 100 | 30 | 130 | |
| 151 | 28 | 179 | |
| 517 | 133 | 650 |
| Size of the Population | Maximum Number of Iterations | Inertia Weight | Inertia Weight Damping Ratio | Coefficient of Personal Learning | Coefficient of Global Learning |
|---|---|---|---|---|---|
| 50 | 1000 | 1 | 0.99 | 1 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olayode, I.O.; Severino, A.; Tartibu, L.K.; Arena, F.; Cakici, Z. Performance Evaluation of a Hybrid PSO Enhanced ANFIS Model in Prediction of Traffic Flow of Vehicles on Freeways: Traffic Data Evidence from South Africa. Infrastructures 2022, 7, 2. https://doi.org/10.3390/infrastructures7010002
Olayode IO, Severino A, Tartibu LK, Arena F, Cakici Z. Performance Evaluation of a Hybrid PSO Enhanced ANFIS Model in Prediction of Traffic Flow of Vehicles on Freeways: Traffic Data Evidence from South Africa. Infrastructures. 2022; 7(1):2. https://doi.org/10.3390/infrastructures7010002
Chicago/Turabian StyleOlayode, Isaac Oyeyemi, Alessandro Severino, Lagouge Kwanda Tartibu, Fabio Arena, and Ziya Cakici. 2022. "Performance Evaluation of a Hybrid PSO Enhanced ANFIS Model in Prediction of Traffic Flow of Vehicles on Freeways: Traffic Data Evidence from South Africa" Infrastructures 7, no. 1: 2. https://doi.org/10.3390/infrastructures7010002
APA StyleOlayode, I. O., Severino, A., Tartibu, L. K., Arena, F., & Cakici, Z. (2022). Performance Evaluation of a Hybrid PSO Enhanced ANFIS Model in Prediction of Traffic Flow of Vehicles on Freeways: Traffic Data Evidence from South Africa. Infrastructures, 7(1), 2. https://doi.org/10.3390/infrastructures7010002









