Model Bridge Span Traversed by a Heavy Mass: Analysis and Experimental Verification
Abstract
:1. Introduction
1.1. Structural Health Monitoring Issues
1.2. External Load Categories
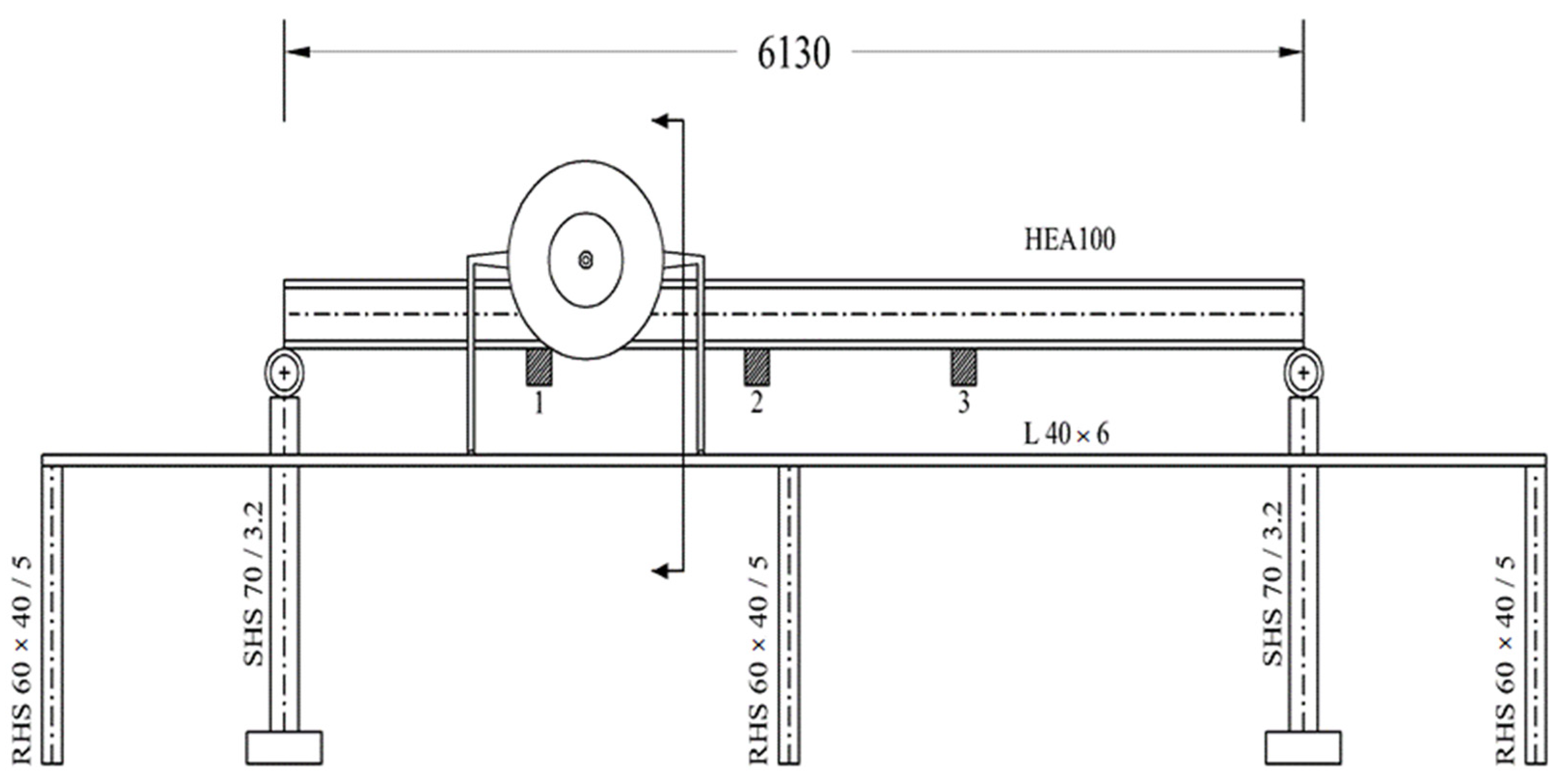
2. Experimental Setup
3. Beam Models for the Bridge Deck on Flexible Supports
4. Mathematical Models for Moving Loads
4.1. Stationary Mass Reference Case
4.2. Moving Load Case
4.3. Moving Heavy Mass Case
5. Numerical Implementation for the Heavy Mass Case
5.1. Numerical Details
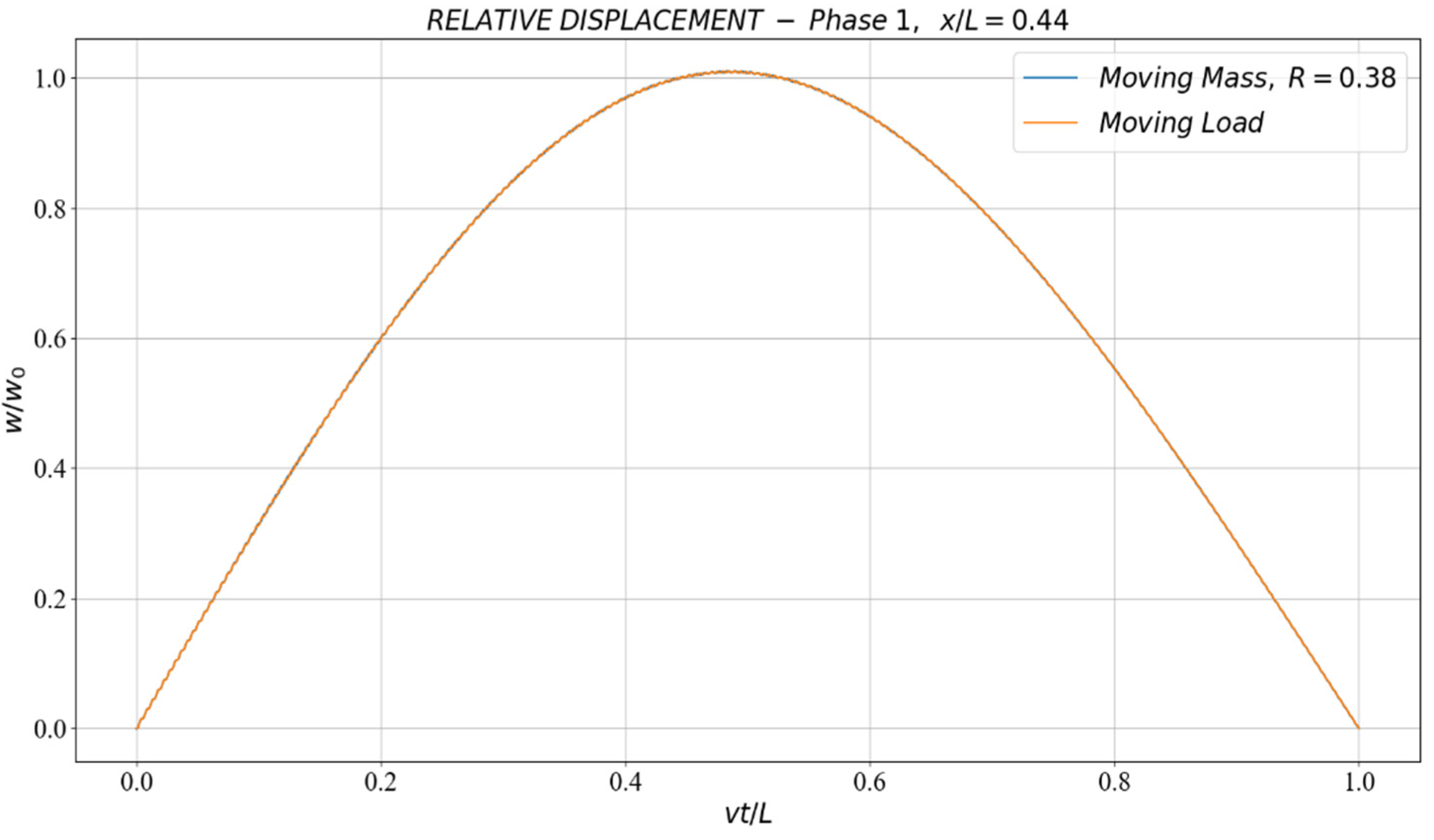
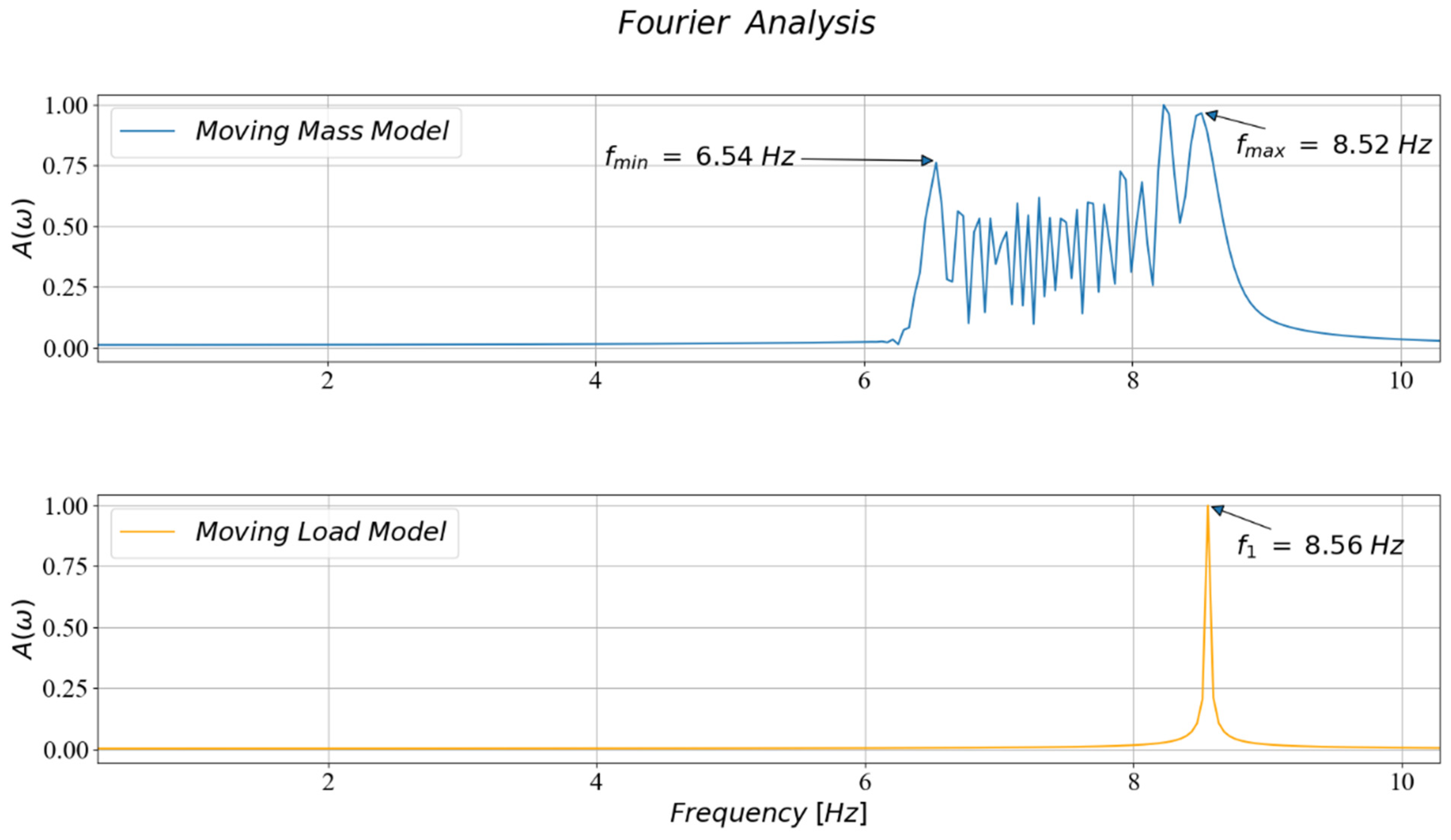
5.2. Numerical Results
6. The Effect of a Moving Mass Inertia
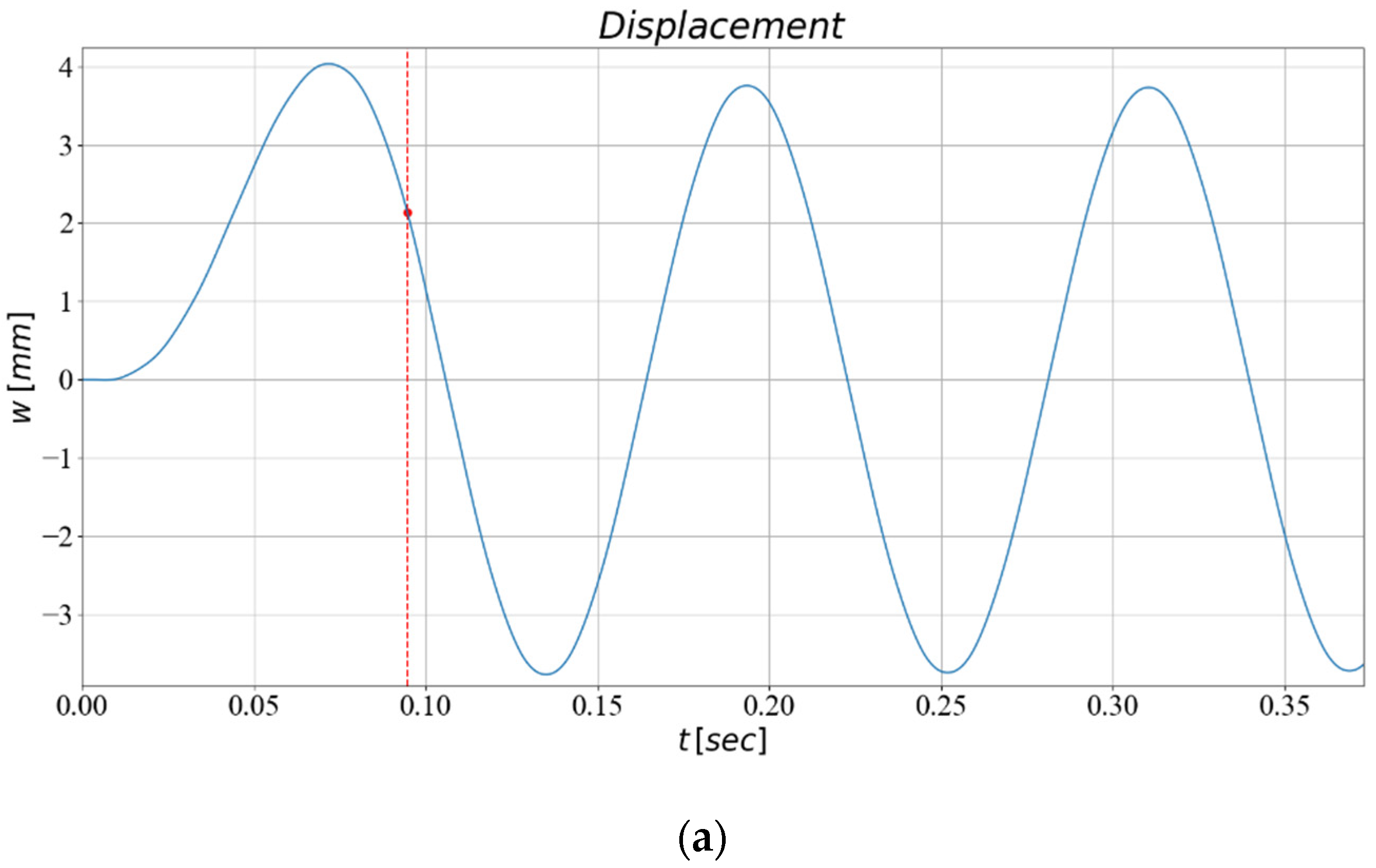
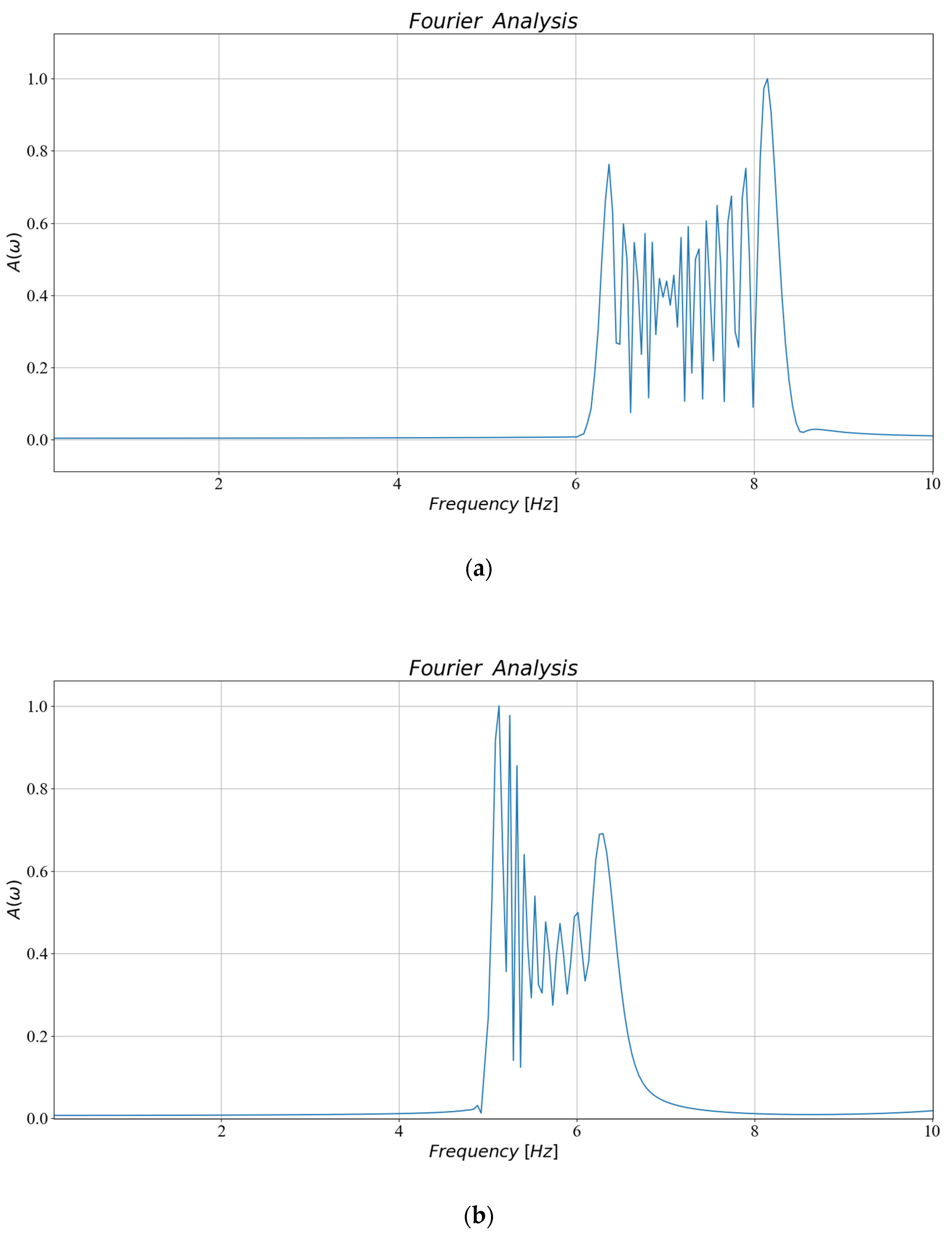
7. Experimental Validation
Discussion of the Results
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. The Eigenproblem for Flexible end Supports
References
- Renaudot, A. Etude de l’influence des charges en mouvement sur la résistance des ponts métalliques à poutres droites. Ann. des Ponts et Chaussées 1861, 1, 145–204. [Google Scholar]
- Fryba, L. Vibrations of Solids and Structures under Moving Loads; Noordhoff International Publishers: Groningen, NL, USA, 1972. [Google Scholar]
- Liu, K.; Roeck, G.D.; Lombaert, G. The effect of dynamic train-bridge interaction on the bridge response during a train passage. J. Sound Vib. 2009, 325, 240–251. [Google Scholar] [CrossRef]
- Green, M.F.; Cebon, D. Dynamic interaction between heavy vehicles and highway bridges. Comput. Struct. 1997, 62, 253–264. [Google Scholar] [CrossRef] [Green Version]
- Green, M.F.; Cebon, D. Dynamic response of highway bridges to heavy vehicle loads: Theory and experimental validation. J. Sound Vib. 1994, 170, 51–78. [Google Scholar] [CrossRef]
- Johansson, C. Simplified Dynamic Analysis of Railway Bridges under High-Speed Trains. Licentiate Thesis, Kungl Tekniska Hogskolan, Stockholm, Sweden, 2013. [Google Scholar]
- Bajer, C.I.; Dyniewicz, B. Numerical Analysis of Vibrations in Structures under Moving Loads; Springer: Heidelberg, Germany, 2012. [Google Scholar]
- Rao, S.S. Vibrations of Continuous Systems; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Kausel, E. Advanced Structural Dynamics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- O’Rourke, T.D. Critical infrastructure, interdependencies, and resilience. BRIDGE-Wash.-Natl. Acad. Eng. 2007, 37, 22. [Google Scholar]
- Do, T.V.; Pham, T.M.; Hao, H. Dynamic response and failure modes of bridge columns under vehicle collision. Eng. Struct. 2018, 156, 243–259. [Google Scholar] [CrossRef]
- Tang, Q.; Du, C.; Hu, J.; Wang, X.; Yu, T. Surface rust detection using ultrasonic waves in a cylindrical geometry by finite element simulation. Infrastruct. 2018, 3, 29. [Google Scholar] [CrossRef] [Green Version]
- Azim, R.; Gul, M. Data-driven damage identification technique for railroad bridges utilizing principal component strain response. Struct. Infrastruct. Eng. 2020, 17, 1019–1035. [Google Scholar] [CrossRef]
- Ellingwood, B.R.; Naus, D.J. Condition assessment and maintenance of aging structures in critical facilities, a probabilistic approach. In Case Studies in Optimal Design and Maintenance Planning Civil Infrastructure Systems; Frangopol, D.M., Ed.; ASCE Structural Engineering Institute: Reston, VA, USA, 1999; pp. 45–56. [Google Scholar]
- Ying, Y.; Garrett, J.H., Jr.; Oppenheim, I.J.; Soibelman, L.; Harley, J.B.; Shi, J.; Jin, Y. Toward Data-Driven Structural Health Monitoring: Application of Machine Learning and Signal Processing to Damage Detection. J. Comput. Civ. Eng. 2013, 27, 667–680. [Google Scholar] [CrossRef]
- Smarsly, K.; Law, K.H. A migration-based approach towards resource-efficient wireless structural health monitoring. Adv. Eng. Inform. 2013, 27, 625–635. [Google Scholar] [CrossRef]
- Adams, D. Health Monitoring of Structural Materials and Components: Methods with Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Peeters, B.; De Roeck, G. One-year monitoring of the Z24-Bridge: Environmental effects versus damage events. Earthq. Eng. Struct. Dyn. 2001, 30, 149–171. [Google Scholar] [CrossRef]
- Sohn, H.; Dzwonczyk, M.; Strasser, E.G.; Kiremidjian, A.S.; Law, K.H.; Meng, T. An experimental study of temperature effect on modal parameters of the Alamosa Canyon bridge. Earthq. Eng. Struct. Dyn. 1999, 28, 879–897. [Google Scholar] [CrossRef]
- ArcelorMittal Europe. Orange Book. 2021. Available online: https://orangebook.arcelormittal.com/design-data/uk-na/beams/he/section-properties-dimensions-and-properties/ (accessed on 30 August 2021).
- Dormand, J.R.; Prince, P.J. A family of embedded Runge-Kutta formulae. J. Comput. Appl. Math. 1980, 6, 19–26. [Google Scholar] [CrossRef] [Green Version]





| Bernoulli–Euler Beam | ||||||
| 8.56 | 34.23 | 77.01 | 136.9 | 213.9 | 308.0 | 419.3 |
| Rayleigh Beam | ||||||
| 8.55 | 34.20 | 76.86 | 136.4 | 212.8 | 305.7 | 414.9 |
| Eigenfrequency Number | Reference Beam without a Stationary Mass | |||
|---|---|---|---|---|
| 1 | 8.56 | 7.39 | 6.97 | 6.61 |
| 2 | 34.22 | 26.43 | 27.87 | 34.22 |
| 3 | 77.01 | 66.55 | 77.01 | 59.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dadoulis, G.I.; Manolis, G.D. Model Bridge Span Traversed by a Heavy Mass: Analysis and Experimental Verification. Infrastructures 2021, 6, 130. https://doi.org/10.3390/infrastructures6090130
Dadoulis GI, Manolis GD. Model Bridge Span Traversed by a Heavy Mass: Analysis and Experimental Verification. Infrastructures. 2021; 6(9):130. https://doi.org/10.3390/infrastructures6090130
Chicago/Turabian StyleDadoulis, Georgios I., and George D. Manolis. 2021. "Model Bridge Span Traversed by a Heavy Mass: Analysis and Experimental Verification" Infrastructures 6, no. 9: 130. https://doi.org/10.3390/infrastructures6090130
APA StyleDadoulis, G. I., & Manolis, G. D. (2021). Model Bridge Span Traversed by a Heavy Mass: Analysis and Experimental Verification. Infrastructures, 6(9), 130. https://doi.org/10.3390/infrastructures6090130







