Abstract
With the increasing demand for the efficiency of wind energy projects due to challenging market conditions, the challenges related to maintenance planning are increasing. In this paper, a condition-based monitoring system for wind turbines (WTs) based on data-driven modeling is proposed. First, the normal condition of the WTs key components is estimated using a tailor-made artificial neural network. Then, the deviation of the real-time measurement data from the estimated values is calculated, indicating abnormal conditions. One of the main contributions of the paper is to propose an optimization problem for calculating the safe band, to maximize the accuracy of abnormal condition identification. During abnormal conditions or hazardous conditions of the WTs, an alarm is triggered and a proposed risk indicator is updated. The effectiveness of the model is demonstrated using real data from an offshore wind farm in Germany. By experimenting with the proposed model on the real-world data, it is shown that the proposed risk indicator is fully consistent with upcoming wind turbine failures.
1. Introduction
The number and size of wind turbines (WTs) are increasing, and operation and maintenance costs constitute up to 30% of the total energy cost of WTs [1]. Therefore, the cost of operation and maintenance is a serious problem for most WT operators [2]. Figure 1a shows the breakdown of operational expenditures of an offshore wind farm [3] Therefore, using an effective health monitoring system prevents huge repair and unsupplied wind energy costs [4]. WTs are usually faced with severe weather conditions, mostly off-shore ones, e.g., extreme high/low temperature, high humidity, severe wind speed, and direct sunlight. Moreover, WTs include many mechanical moving systems, which increase the probability of WT failure [5].
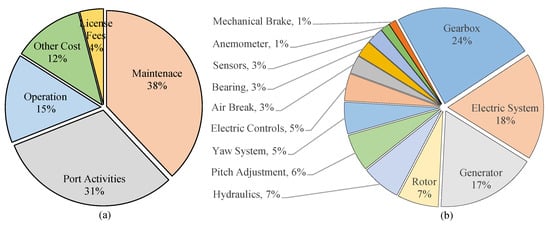
Figure 1.
(a) Breakdown of operational expenditures of an offshore wind farm [3]; (b) the contribution of WT components in the WT failure [7].
Prioritizing the WTs component failure provides a deeper understanding of the maintenance scheduling problem [6]. Figure 1b shows the primary causes of WT downtime [7]. In a report from the National Renewable Energy Lab, the failure rates of the key components of a WT have been investigated [7]. Based on this report, three elements that comprise the WT drivetrain—the gearbox, generator, and main shaft/bearing—cause about 44% of the total WT downtime. Moreover, the electric parts of the WT, i.e., generator, transformer, converter, and control system, cause about 40% of the total WT failures. Thus, the four leading causes of WTs failures can be listed as gearbox, generator, transformer, and converter. Regarding this matter, the condition of all of them are considered in this paper for proper health monitoring of the WTs.
Temperature monitoring of the WTs key component provides relevant information on the state of its health condition [8]. The temperature of the WT key components should be maintained in a safe range and must not overpass throughout the normal operating conditions [9]. An exceeded temperature over the safe band may address an anomaly in the corresponding component of the WT, e.g., rotor over-speed, aging, short circuits, and lubrication failure. Thus, the temperature monitoring method is an acceptable approach for health monitoring of the WTs and can be applied for the diagnosis stage of maintenance management system [10].
Since the bearing is one of the critical components of the WT, the bearing temperature is considered for the condition monitoring of WT in [11]. Temperature higher than the allowed limit indicates the probability of bearing malfunction, such as: issues on lubrication, electrical leakage through the shaft, aging, and variability of external loads. In case of not perfect bearing operation, the characteristics of the lubricating oil will change, which can result in more fatigue loads [12]. Thus, the bearing is not efficient enough, and leads to loss of energy during the bearing operation and an increase in the bearing oil temperature.
A rise in the temperature of WT components can be due to many factors. It is usually difficult to identify the main source of the abnormal temperature [13]. If the temperature of a component increases due to a failure, it affects the temperature of the nearby components. Thus, the nearby sensors may transfer incorrect data in the higher temperature, while there isn’t any problem in the the corresponding component, but it is affected due to the nearby components [14]. Actually, it is very difficult to indicate the main reason of abnormal temperatures in all of the sensors. Therefore, a coordinated monitoring system should record the temperature of all components and perform an integrated assessment. In addition, with WTs in different locations, the sensor data received via the SCADA system, the interpretation of the SCADA data and the trustworthy analysis of the alarms can be another problem in this domain [15].
A bearing’s degradation model has been addressed in [16] to estimate the real-time remaining useful life (RUL). In this method, the SCADA data provides the WT bearings temperatures and the relative temperature is calculated by means of moving average. The performance degradation model is determined using the Wiener process with linear fluctuations. The parameters of this model are tuned using the maximum likelihood estimation method. The results of this study indicated that the real-time RUL estimation method can be more effective compared to the traditional methods. The first measured data above the safe band of the bearing temperature considered by inverse Gaussian distribution that can lead to enhancement in WT operation and maintenance strategies [17].
The converter is one of the important components in WT and has a considerable failure rate. Thus, detection or prediction of upcoming failures are crucial in WT condition monitoring systems. Authors in [18] present a method for WT converter fault detection using convolutional neural network models that are developed using data from the WT SCADA. The proposed method begins with the selection of fault indicator variables, and then the fault indicator variable data are extracted from the WT SCADA system. Convolutional neural network models using the generated data to extract features from the radar charts and analyze feature characteristics for fault detection. Power transformers in WTs are exposed to mechanical, thermal, and electrical stresses during the operation period. The authors in [19] propose an improved aging model of transformers using the Frequency Response Analysis (FRA) method for the detection of faults and the location of mechanical deformations of their live parts and the correlation function is used to determine the level of fault detected. Another important component of a WT is its generators. Since the generator includes both mechanical and electrical parts, it has a considerable contribution to WT failures. The authors of [20] develop a test case for the detection of damage to the slip rings of the WT generator. A principal component regression is adopted, directed to the temperature collected in the slip ring. Moreover, using the data collected at the nearby WT on the farm, it is possible to identify the incoming fault approximately one day before the occurrence of a failure [20]. Transformation is another important component in a WT. The most common faults for WT transformers are combustion, and an abnormal increase in electrical resistance was frequently detected in a large number of windings and lead bars. To solve these problems, the authors at [21] propose a series of characterization methods to investigate assembly structure, matrix materials, and macro/microscopic morphologies of failed transformers. A temperature simulation experiment was also carried out on [21] to evaluate normal operating conditions. Analysis results in [21] showed that improper installation, unreasonable design, unqualified fabrication, and improper maintenance were the main causes of WT transformer failure.
The relationship between WT component temperature variation and WT health condition was investigated in [22]. It has been addressed that the probability of failure occurrence can be calculated by studying the overheating behavior of the WT’s bearing. The outcomes of [22] indicated that it is possible to predict the failure occurrence even one month earlier, which is a brilliant result. Bayesian inference can be appropriate for prediction of the WT failures, and it offers a compensation between model performance and computational efficiency. The contributions of this paper are listed as follows:
- Introducing an optimal risked-based methodology for WT condition monitoring;
- Proposing an artificial neural network-based model for estimating the normal condition of WT key components;
- Presenting a real-time risk indicator, which is used in the health monitoring and anomaly detection of WT.
In this paper, an optimal temperature-based condition monitoring is proposed for WTs. In the first stage, the normal condition of the WT’s key components, i.e., gearbox, converter, generator, and transformer, has been estimated through an artificial neural network model. In the second stage, the deviation of real-time measurement with reference to the estimated values has been calculated. The estimated values provide the healthy conditions of the WT components and any deviations from these reference values can be marked as an anomaly. In this paper, a risk indicator is also introduced, which is calculated on the basis of a safe band. The safe band represents the maximum acceptable deviation between the real-time temperature measurement and the estimated normal conditions for the WT key component’s temperature. Therefore, the calculation of the safe band plays an important role in the calculation of the risk indicator. One of the main contributions of this paper is to propose a flowchart and modeling for the optimal calculation of the safe band to increase the accuracy of the WT condition monitoring system. Finally, the effectiveness of the model has been proved using the real data of an offshore wind farm in Germany.
The rest of the paper is structured as follows: Section 2 presents background on different maintenance strategies of WT. The conceptual framework of the proposed model of condition monitoring has been explained in Section 3, and its corresponding mathematical modeling is addressed in Section 4. The results of numerical studies are discussed in Section 5 and finally Section 6 concludes the paper.
2. Condition-Based Maintenance of WT
Figure 2 shows different clusters of maintenance strategies [23]. The main maintenance strategies are corrective and preventive. Preventive maintenance considers scheduling some actions before failures occur, while corrective maintenance is carried out after failures. Preventive maintenance strategies can be categorized into two sub-clusters [24]; namely: predetermined or scheduled maintenance and condition-based maintenance (CBM). Predetermined maintenance is activated based on an established time schedule. CBM is an appropriate way of designing maintenance programs based on real-time conditions of the system [25,26]. The system conditions are usually evaluated through equipment used to quantify the physical condition of the system [27], e.g., temperature data, vibration data, current/voltage waveform analysis data, acoustic emission data, or oil analysis data. The CBM method plays an important role in optimal maintenance scheduling to prevent under- or over-maintenance costs [28]. For preventing such problems, optimal maintenance scheduling has to be applied using health monitoring on the key components [29]. A health monitoring system provides continuous evaluation of normal conditions of the WT key components and calculates an optimal maintenance scheduling [30]; as a result, it enhances the efficiency of the maintenance program and consequently increases the reliability of the system.
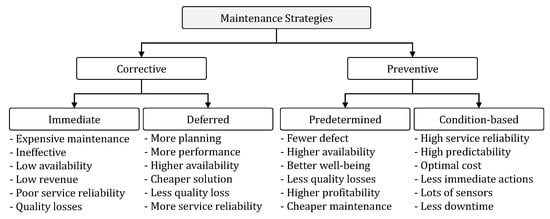
Figure 2.
Clusters of maintenance strategies [23].
3. Optimal Temperature-Based Condition Monitoring Framework
Today, several information sources exist within a wind farm that can assist in decision-making during a maintenance scheduling process, but sometimes they are not integrated enough into the comprehensive modeling of the system. This section describes an integrated predictive maintenance framework in which several tools are integrated to assist the process of asset management in a wind farm. In order to make a trade-off between enhancing the short-term reliability of each individual WT and reducing the maintenance costs, an optimal temperature-based condition monitoring framework proposed which is shown in Figure 3. As it is seen in Figure 3, the proposed framework includes four main parts, which are explained in-detail as follows:
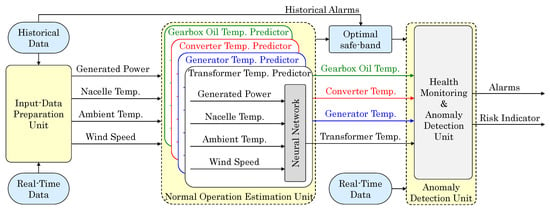
Figure 3.
Proposed optimal temperature-based condition monitoring framework for WTs.
Input-Data Preparation Unit: This unit provides the input-data for the proposed model. There are two sources of data i.e., the historical or logged data and the real-time measurement data. The out-put data of this unit not only includes the real-time measurements of the different sensors that are suitable for the real-time calculations, but also includes the historical data that has been used for the training of the ANN. These input data consist of ambient temperature (°C), wind speed (m/s), nacelle temperature (°C), and the amount of active generated power (kW) of the wind turbine.
Normal Operation Estimation Unit: In this stage, the input-data from the previous unit are entered into four independent neural network predictors, which are trained properly during the normal operation of the WT, i.e., when there are no reported components alarms. The goal of this unit is to estimate the normal (or healthy) condition of the system. Thus, in this stage, we are able to diagnose the healthy conditions of the WT main components based on the operating conditions. As it is indicated in the Introduction section, temperature monitoring is an appropriate way for analyzing the health condition of the WT main components. In this stage, there are four neural network predictors, and all of them receive the same input-data, which are prepared in the previous unit and predict different temperatures, i.e., the temperature of gearbox oil, converter, generator winding, and transformer oil.
Optimal Safe-Band Calculator: The safe band represents the maximum acceptable or tolerable deviation between the real-time temperature measurement and the estimated normal conditions for the temperature of the WT key components. Therefore, the calculation of the safe band plays an important role in the calculation of the risk indicator and enhancing the precision of the WT condition monitoring system. In this unit, the dependency of the historical alarms with the risky conditions of the WT has been evaluated in different safe-band values.
Health Monitoring and Anomaly Detection Unit: This stage is the heart of the proposed framework, which is shown in Figure 3. Normal operation estimation unit provides some temperature data as a benchmark to represent the healthy condition of the WT main components, and in parallel the real-time values of these parameters are entered into the Health Monitoring and Anomaly Detection Unit from the measurement units. The real-time values—from the sensors/measurement devices—and normal estimated values are compared with each other and the amount of the deviations between these two values are calculated. More deviation represents the more risky situation. These deviations between real and expected conditions may be more or less severe for the component’s life. Another important contribution of this paper is introducing the risk indicator, which is calculated based on the proposed deviations. It can be interpreted as symptoms leading to possible failure modes.
4. Mathematical Modeling
In this section, the mathematical formulation of the proposed framework in Figure 3 is presented. Thus, this section is divided into three sub-sections; i.e., (1) modeling of Normal Condition, which is based on training an appropriate artificial neural network; (2) modeling of risk Indicator, which includes the mathematical formulation for modeling the condition of the system and, finally; (3) modeling of safe band optimization, which address the an optimization problem.
4.1. Modeling of Normal Conditions
It is important to model the expected normal condition or baseline for a component or subsystem at different operating points. Consequently, any deviation from this condition can lead to a failure mode. The prediction of the normal condition of the main WT components is based on the following steps:
- Collecting the measured data from WT and analyzing their cross-dependency;
- Defining a set of failure modes based on the collected data;
- Formulating the normal condition model based on the normal operation condition of the system (excluding the failure periods);
- Validating the proposed model in a test (or study) period.
Figure 4 shows the proposed diagram of normal operation estimation unit, which indicates the interconnections between the input, output data, and the Artificial Neural Network (ANN) model. For more clarification, the procedure proposed in Equation (1) for the calculation of normal or healthy condition models, the creation of a model for the prediction of the transformer oil temperature of a WT will be explained. This model can used for prediction of the temperature of the transformer oil using input data; i.e., active generated power , nacelle temperature , ambient temperature , wind speed , and transformer oil temperature in the last time interval . t is the index of operating time and j is the number of the wind turbine. Not only does this model consider the real-time WT operating point, i.e., , , , and , but it also uses the former estimated value of the parameter to prevent a huge variation in the temperature of the WT key components. Indeed, it models a dependency during the operating time and represents the thermal inertia over the study period. Equation (1) represents the mathematical relation between the input and output data:
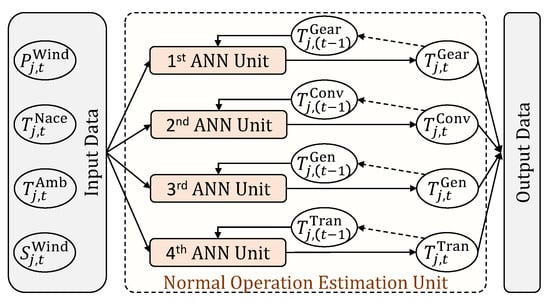
Figure 4.
Internal interconnections of the diagnosis stage.
A Multi-Layer Perceptron (MLP) ANN is used in this study, which is one of the feed-forward ANN models. Our tuned ANN consists of three layers; each layer includes 20 neurons and its activation function is identity. The mean absolute error (MAE) for the test data of gearbox, converter, generator, and transformer are 2.6, 3.2, 2.9, and 3.8 °C, respectively, which is completely satisfactory. The programming environment is Python 3.7 and Jupyter Notebook as an integrated development environment (IDE). Two extra libraries, namely Pandas framework and SciKit-learn, have been used for data manipulation and machine learning solutions, respectively. The hardware consisted of 10 GB of RAM and 4 CPU cores (Intel® Xeon® Gold 5120 Processor, 2.20 GHz).
4.2. Modeling of Risk Indicator
The real-time monitoring of deviations with respect to the mentioned normal condition is an appropriate indicator, which represents the amount of stress on a component. Thus, this indicator can provide suitable information regarding its health condition. In other words, such deviation-based indicator addresses the possible failure of the component in the very near future, which may cause unavailability for the WT. Therefore, it can be used as a risk indicator of a failure mode. In Equation (4), a condition equation has been presented for calculating the deviations of each component during the operating time of the system. For calculating the deviation , the maximum acceptable amount of each variable, which can be considered as the temperature cap , is defined in Equation (3). above the estimated value provides the maximum tolerable amount of the temperature in each main component of the WT. Let’s define the , the set of main components of WT, as follows:
where is a safe band in which the temperature of each main component of the WT can be increased up to this upper limit and is still tolerable. However, if the temperature of a component exceeds this limit, the condition of that component is hazardous and should be considered a potential anomaly. These anomalies would be detected as deviation between the temperature of the WT component and the maximum tolerable limit as addressed in (4).
Since the temperature of four key components of the WT are considered in the health monitoring model, the risk indicator should be extracted from all of them. In Equation (5), individual deviations of each WT’s main component are added together to represent the total deviation :
A failure of a component occurring can be interpreted as the evolution of these deviations as a symptom. These symptoms can be diagnosed by logging the deviations over the operating time of the WT. In the mathematical terms, the risk indicator can be formulated by Equation (6) as an accumulation of logged deviations regarding the normal condition or healthy condition during the operation time:
Due to some errors in the model precision, it is probable to be some momentary deviations, which are not caused by some physical faults, but are due to the lack of model precision. To reduce the impacts of this issue, as indicated in (6), a cumulative risk indicator is introduced to reduce the impacts of these small deviations. Therefore, the proposed cumulative risk indicator will increase considerably when there are some continuous deviations over a period of time and not just in a snapshot of a time.
4.3. Modeling of Safe Band Optimization
Figure 5 shows the proposed safe band optimization flowchart. First, the safe band is considered to be zero and the corresponding deviation is calculated. Then, the safe band increases in intervals of 0.1 degrees until all calculated deviations are greater than zero. Then, the optimization coefficient , which is one of the contributions of the paper, is computed based on the calculated deviations and historical alarms. Equation (7) represents the mathematical formulation for modeling the proposed optimization coefficient:
where is the binary alarm data of WT j in time t and is defined as follows:
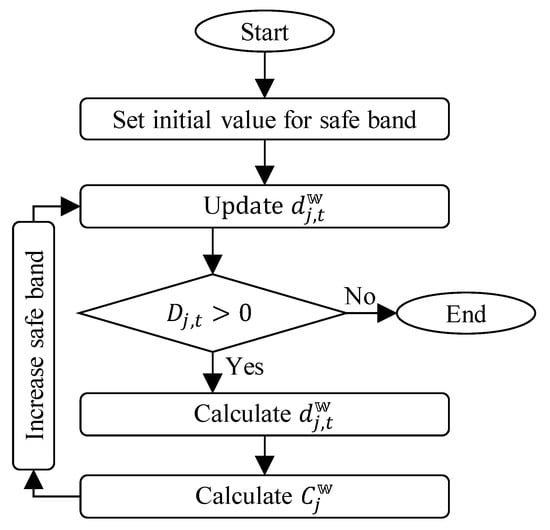
Figure 5.
The proposed safe band optimization flowchart.
By substituting (5) and (4) in (7), a function between the optimization coefficient and the safe band could be proposed as:
If the safe band value is too small, we probably have a lot of deviations, which will result in the denominator being larger than the numerator in Equation (7). In this case, the proposed is very small. However, if the secure band value is too large, the deviations will be very small and consequently the numerator will be close to zero and then the proposed will be small again. Thus, there should be a maximum value for the proposed , which represents the optimal value of the safe band with the best compatibility between calculated deviations and the historical alarms.
5. Results
The proposed model has been applied on the real data of an offshore wind farm in Germany, which includes 30 WTs. The data were logged for two years from October 2016 to October 2018 with the sample rate of 10 min. We used the first 18 months of the data set as the training part and consequently the last 6 months as the test data. The results that are shown in this section are extracted from the test data.
Figure 6 present the input data of the proposed framework. Figure 6a represents the wind speed (m/S) and the active generated power (kW) of a WT. The ambient and nacelle temperature (°C) are shown in Figure 6b. As it is shown in this figure, the inside temperature of the nacelle is about 15–20 °C higher than the ambient temperature, which is rooted in the operation of the WT and the cooling system.
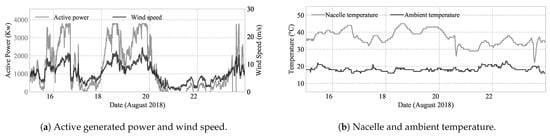
Figure 6.
Input data: (a) active generated power and wind speed; (b) nacelle and ambient temperature.
As it could be seen in Figure 7, the optimization coefficient is maximized in a certain amount of the safe band. Thus, the optimal value for the safe band is 10.8 °C. This amount for the safe band is taken into account in the remaining simulations.
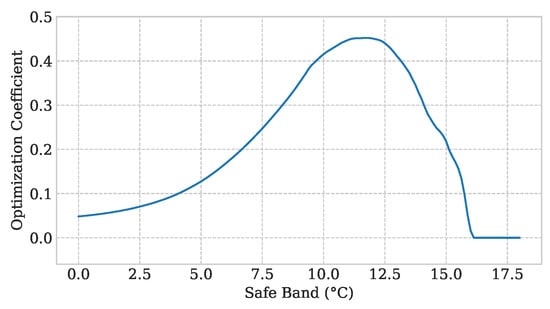
Figure 7.
Variation of the proposed optimization coefficient by changing the amount of safe-band.
Figure 8 addresses the results of the study which includes both normal conditions of the WT key components and its corresponding deviations. In Figure 8, the green line shows the estimated value, which represents the normal or healthy conditions of the system as well as the safe band, which is calculated 10.8 °C more than the estimated value. The red line addresses the measurement data. The deviation, which has been defined by Equation (4), is shown in the second axis in blue color. As it can be seen in Figure 8, if the measurement data (red line) increases more than the maximum value of the safe band, a deviation will be reported.
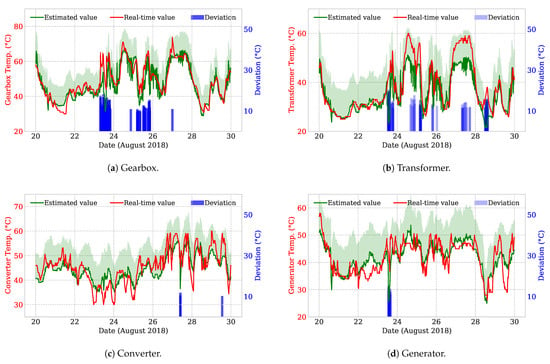
Figure 8.
First axis (in red): measurement data, safe band (indicated in fade-green color) and normal estimated value; Second axis (in blue): its corresponding deviation value.
The accuracy of “detecting failures” compared to the “historical failures” during the test period was different for different components of wind turbines. The accuracy for Gearbox was 94%, for Transformer was 91%, for Generator was 90%, and for converter was 87%.
By precisely observing Figure 8, different characteristics and behaviors could be observed between the variation of the real-time measurements and the estimated data. For example, the variation of the real-time measurement data in Figure 8c,d is much higher compared to the estimated data, while the estimated data vary more smoothly. In addition, the variation of the estimated data in Figure 8b, especially on 25 and 27 August, is greater than the real-time measurement data. Assuming that the sensor data do not meet the frequency requirements of the thermal signal, this may be due to the thermal inertia of the system, e.g., the oil temperature in Figure 8b. Thus, the question may come to mind regarding whether the high frequency variation of the oil temperature estimate is feasible. To answer this question, we try to consider the thermal inertia in our proposed model for the ANN model (Figure 4). However, from Figure 8a,b, it can be understood that it does not work in an ideal manner. In other words, considering the thermal inertia in the model by estimating the current values based on the previous values, it has been expected to have smoother variations. However, as it can be seen in Figure 8a,b, this was not perfect. In this sense, we began to study the thermal inertia of the oil temperature both in the gearbox and in the transformer in physical terms and not only in mathematical terms such as future work in order to analyze the estimated values and develop a physical model to demonstrate that oil temperatures in these mechanisms can change at such a high frequency as indicated in 27 August in Figure 8b. In fact, in this paper, we proposed an optimal value of the safe band to cover the mismatch between the variation frequency of the real-time measurements and the estimated normal values. However, the main concern regarding this mismatch would be some additional deviation data (blue bars) in Figure 8a,b (for example, those for days 23–24 and 28–29 in Figure 8b). To mitigate the impacts of this problem, we proposed a cumulative risk indicator in (6) to reduce the impacts of these small deviations. In other words, the proposed cumulative risk indicator will be affected when there are some continuous deviations over a period of time and not just in a snapshot of a time.
Figure 9 illustrates the variation of the risk indicator over a 4-month of the test period with respect to temperature deviations of the gearbox, generator, converter, and transformer to the normal condition model that estimates its healthy operation condition. Using the deviation information included in Figure 8 and using Equations (5) and (6), the values of the risk indicator have been calculated. The representation of these values in Figure 9 is for four months and is able to detect abnormalities of temperature deviation in the key components of WT. By focusing on the variation of the proposed risk indicator of the gearbox (blue line), it can be seen that there is huge growth in the second week of July. The gearbox did not show a considerable deviation from its normal expected condition for about first three weeks of July 2018. However, around the second week of July 2018, something happened in the gearbox, which caused high values of deviations and an important change in the value of the risk indicator. An amount of stress for this failure mode appeared. A process of rapid degradation was observed from this moment with a progressive increase in the risk indicator values and also the slope of the curve represented. An interesting point regarding the gearbox is that it was working without any failure during all of those 4-month periods. However, the change in the slope of the gearbox risk indicator represents the need for an appropriate maintenance program as soon as possible to prevent occurring sever damages to the gearbox and consequently huge maintenance costs.
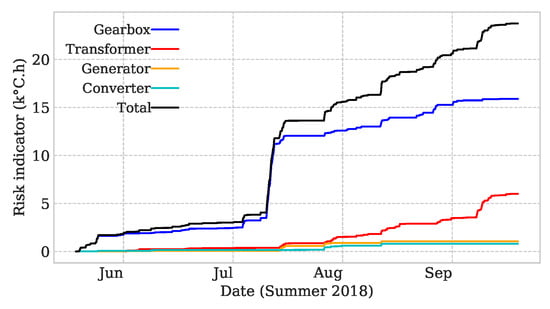
Figure 9.
Variation of the risk indicator during Summer 2018.
6. Conclusions
This paper proposes a model for optimal condition monitoring and anomaly detection for key components of wind turbines (WT) based on their continuous temperature monitoring. The normal condition is generated by a model using an artificial neural network that is trained during normal operation of the WT in order to estimate the expected temperature values of the key components of the WT under different operating conditions. The deviations are calculated with respect to the normal conditions, which are the main inputs for the assessment of the risk indicator. This paper not only presented the definition of this risk indicator, but also developed a method for calculating this indicator in an optimal manner. From the results of this study, which was extracted from real data of a wind farm in Germany, it was shown that it is possible to predict the upcoming failure of WT components before occurring, which gives us a reasonable understanding of the lifespan of the WTs and how their operation and maintenance could be enhanced.
Author Contributions
The following Contribution were made by the authors: Methodology and conceptualisation: all authors; Data collection, S.H. and I.K.; Algorithm and code development: A.R. and P.T.B.; Design the Proof of Concept: all authors; Validation of results: P.T.B. and D.B.; review and editing: all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This project has been partially funded by Federal Ministry for Economic Affairs and Energy under Grant No. 0350008 (Smart Grid Cyber-Resilience Lab) and also partially through the direct funding from EWE AG.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No publicly available datasets were used.
Acknowledgments
The authors would like to thank EWE Offshore Service & Solutions (OSS) for providing data, which enabled the research and they also acknowledge the scientific and technical help provided by staff in the EWE DataLab.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| ANN | artificial neural network |
| CBM | condition-based maintenance |
| Conv | converter |
| CPU | central processing unit |
| IDE | integrated development environment |
| Gear | gearbox |
| Gen | generator |
| MAE | mean absolute error |
| MLP | multi-layer Perceptron |
| RAM | random-access memory |
| RUL | remaining useful life |
| SCADA | supervisory control and data acquisition |
| Trans | transformer |
| WT | wind turbine |
References
- Bosch, J.; Staffell, I.; Hawkes, A.D. Global levelised cost of electricity from offshore wind. Energy 2019, 189, 116357. [Google Scholar] [CrossRef]
- Babazadeh, D.; Van Hertem, D.; Nordström, L. Study of centralized and distributed coordination of power injection in multi-TSO HVDC grid with large off-shore wind integration. Electr. Power Syst. Res. 2016, 136, 281–288. [Google Scholar] [CrossRef]
- Board, R.A. Value Breakdown for the Offshore Wind Sector; Technical Report for the Renewables Advisory Board (RAB) by BVG Associates; RAB, 2010; pp. 1–20. Available online: https://assets.publishing.service.gov.uk.glasswall-icap.com/government/uploads/system/uploads/attachment_data/file/48171/2806-value-breakdown-offshore-wind-sector.pdf (accessed on 16 March 2021).
- Chandrasekhar, K. Gaussian processes for structural health monitoring of wind turbine blades. Renew. Sustain. Energy Rev. 2019, 64, 91–105. [Google Scholar]
- Teimourzadeh Baboli, P. Flexible and overall reliability analysis of hybrid AC–DC microgrid among various distributed energy resource expansion scenarios. IET Gener. Transm. Distrib. 2016, 10, 3978–3984. [Google Scholar] [CrossRef]
- Parsa Moghaddam, M.; Teimourzadeh Baboli, P.; Alishahi, E.; Lotfifard, F. Flexible load following the wind power generation. In Proceedings of the 2010 IEEE International Energy Conference, Manama, Bahrain, 18–22 December 2010; pp. 802–807. [Google Scholar]
- Sheng, S.; Link, H.; LaCava, W.; van Dam, J.; McNiff, B.; Veers, P.; Keller, J.; Butterfield, S.; Oyague, F. Wind Turbine Drivetrain Condition Monitoring during GRC Phase 1 and Phase 2 Testing; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2011.
- Stetco, A.; Dinmohammadi, F.; Zhao, X.; Robu, V.; Flynn, D.; Barnes, M.; Keane, J.; Nenadic, G. Machine learning methods for wind turbine condition monitoring: A review. Renew. Energy 2019, 133, 620–635. [Google Scholar] [CrossRef]
- Han, Q.; Chu, F. Condition Monitoring of Wind Turbines Using Adaptive Control Charts. In Proceedings of the 13th International Conference on Damage Assessment of Structures; Springer: Berlin/Heidelberg, Germany, 2020; pp. 606–617. [Google Scholar]
- Zhang, P.; Lu, D. A Survey of Condition Monitoring and Fault Diagnosis toward Integrated O&M for Wind Turbines. Energies 2019, 12, 2801. [Google Scholar]
- Xu, Q.; Fan, Z.; Jia, W.; Jiang, C. Quantile regression neural network-based fault detection scheme for wind turbines with application to monitoring a bearing. Wind Energy 2019, 22, 1390–1401. [Google Scholar] [CrossRef]
- Fava, G.M.; Liberatore, S.; Moaveni, B. Estimating Fatigue in the Main Bearings of Wind Turbines Using Experimental Data. In Dynamics of Civil Structures; Springer: Berlin/Heidelberg, Germany, 2020; Volume 2, pp. 163–171. [Google Scholar]
- Solimine, J.; Niezrecki, C.; Inalpolat, M. An experimental investigation into passive acoustic damage detection for structural health monitoring of wind turbine blades. Struct. Health Monit. 2020, 19, 1711–1725. [Google Scholar] [CrossRef]
- Teimourzadeh Baboli, P.; Damavandi, M.Y.; Parsa Moghaddam, M.; Haghifam, M. A mixed integer modeling of micro energy-hub system. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Zhang, F.; Wen, Z.; Liu, D.; Jiao, J.; Wan, H.; Zeng, B. Calculation and Analysis of Wind Turbine Health Monitoring Indicators Based on the Relationships with SCADA Data. Appl. Sci. 2020, 10, 410. [Google Scholar] [CrossRef]
- Pan, Y.; Hong, R.; Chen, J.; Wu, W. A hybrid DBN-SOM-PF-based prognostic approach of remaining useful life for wind turbine gearbox. Renew. Energy 2020, 152, 138–154. [Google Scholar] [CrossRef]
- Teimourzadeh Baboli, P.; Parsa Moghaddam, M. Allocation of network-driven load-management measures using multiattribute decision-making. IEEE Trans. Power Deliv. 2010, 25, 1839–1845. [Google Scholar] [CrossRef]
- Xiao, C.; Liu, Z.; Zhang, T.; Zhang, X. Deep Learning Method for Fault Detection of Wind Turbine Converter. Appl. Sci. 2021, 11, 1280. [Google Scholar] [CrossRef]
- Milić, S.D.; Ilić, D.; Ponjavić, M. Fault detection using FRA in order to improve the aging model of power transformer. Facta Univ. Ser. Electron. Energetics 2020, 33, 413–427. [Google Scholar] [CrossRef]
- Astolfi, D.; Castellani, F.; Natili, F. Wind turbine generator slip ring damage detection through temperature data analysis. Diagnostyka 2019, 20, 3–9. [Google Scholar] [CrossRef]
- Zhu, Y.M.; Gong, Y.; Yang, Z.G. Failure analysis on over-temperature combustion of transformers in 4 MW offshore wind turbines. Eng. Fail. Anal. 2019, 96, 211–222. [Google Scholar] [CrossRef]
- Uzunoğlu, B. An Adaptive Bayesian Approach with Subjective Logic Reliability Networks for Preventive Maintenance. IEEE Trans. Reliab. 2019, 916–924. [Google Scholar] [CrossRef]
- Artigao, E.; Martín-Martínez, S.; Honrubia-Escribano, A.; Gómez-Lázaro, E. Wind turbine reliability: A comprehensive review towards effective condition monitoring development. Appl. Energy 2018, 228, 1569–1583. [Google Scholar] [CrossRef]
- Leite, G.d.N.P.; Araújo, A.M.; Rosas, P.A.C. Prognostic techniques applied to maintenance of wind turbines: A concise and specific review. Renew. Sustain. Energy Rev. 2018, 81, 1917–1925. [Google Scholar] [CrossRef]
- Zhou, P.; Yin, P. An opportunistic condition-based maintenance strategy for offshore wind farm based on predictive analytics. Renew. Sustain. Energy Rev. 2019, 109, 1–9. [Google Scholar] [CrossRef]
- Babazadeh, D.; Muthukrishnan, A.; Mitra, P.; Larsson, T.; Nordström, L. Real-time estimation of AC-grid short circuit capacity for HVDC control application. IET Gener. Transm. Distrib. 2017, 11, 838–846. [Google Scholar] [CrossRef]
- Ghamlouch, H.; Fouladirad, M.; Grall, A. The use of real option in condition-based maintenance scheduling for wind turbines with production and deterioration uncertainties. Reliab. Eng. Syst. Saf. 2019, 188, 614–623. [Google Scholar] [CrossRef]
- Song, S.; Li, Q.; Felder, F.A.; Wang, H.; Coit, D.W. Integrated optimization of offshore wind farm layout design and turbine opportunistic condition-based maintenance. Comput. Ind. Eng. 2018, 120, 288–297. [Google Scholar] [CrossRef]
- Tziavos, N.I.; Hemida, H.; Dirar, S.; Papaelias, M.; Metje, N.; Baniotopoulos, C. Structural health monitoring of grouted connections for offshore wind turbines by means of acoustic emission: An experimental study. Renew. Energy 2020, 147, 130–140. [Google Scholar] [CrossRef]
- Traylor, C.; DiPaola, M.; Willis, D.J.; Inalpolat, M. A computational investigation of airfoil aeroacoustics for structural health monitoring of wind turbine blades. Wind Energy 2020, 23, 795–809. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).