1. Introduction
The concept of autonomous vehicles (AVs) has been under development since the 1990s [
1,
2], when the first field experiment performed on a freeway was conducted in San Diego, California. Autonomous vehicles have already started to appear on roads across the globe. Clearly, as the AV market expands, transportation professionals and researchers must address an array of challenges before AV becomes a reality. Several government and industry entities have begun to deploy demonstrations and field tests of the technology [
3,
4,
5,
6]. Centers for testing and validation, education, products, and standards for AV have been established and a variety of conferences are being organized to discuss the planning and modeling for AVs [
6]. Currently, researchers, scientists, and engineers are investing significant resources to develop supporting technologies. This vibrant state of development has motivated the proposed program.
Autonomous vehicles have numerous advantages [
7]. Since more than 90% of fatal vehicle collisions are attributed to human error, AV technologies can substantially reduce deaths and injuries from vehicle collisions. Autonomous vehicles can also reduce traffic congestion, reduce carbon dioxide emissions, increase the highway capacity, reduce fuel consumption, improve public transportation services, and provide more efficient parking. On two-lane highways, the driver’s decision to overtake may be risky, since a driver has to judge the operational behavior of opposing and impeding vehicles and decide to pass in a very short amount of time. In addition, the speed plan of the passing vehicle is based on the driver’s perception of its dynamic properties.
In autonomous overtaking, prediction, decision making, and continuous monitoring of vehicle performance are performed by an onboard system. The operation of autonomous vehicles is based on planning the movement trajectory, as well as other reference trajectories. The system searches for an optimal way to bypass obstacles while maintaining traffic safety. For overtaking on two-lane highways, the vehicle’s on-board system must estimate the distance and time required for the passing maneuver and distribute the passing vehicle speed and steering angle based on conflicting criteria. Therefore, the optimization of passing vehicle control for safe and efficient passing maneuvers of autonomous vehicles can be achieved.
Numerous researchers have addressed the issues of planning motion reference lines and control parameters for autonomous vehicles and attempted to find the best trajectories, speed plans, and state-space sequences. Schwarting et al. [
8] considered the concept of parallel autonomy, where autonomous control works as an option to monitor and correct driver errors (called shared control). The work initially focused on curvilinear road profiles for which the optimal trajectory of motion was determined using nonlinear model predictive control (MPC), which allowed a consideration of turns and avoidance of moving and static obstacles. Both kinematic and dynamic models were used as vehicle models. The optimization model included a probabilistic collision estimate, and geometric and physical (tire-road adhesion) constraints. The intervention parameter was used to assess the degree to which the system is involved in driver actions. The optimization algorithm provided fast convergence. The only limitation of this work is that the acceleration input parameter is not related to the engine’s potential.
Talamino and Sanfeliu [
9] presented a technique for planning a movement trajectory and speed plan of an autonomous vehicle in urban areas based on G
2-splines. The polynomial fitting involved iterations equivalent to the optimization of curvature parameters. To simulate a sufficiently long path, a fifth-degree polynomial was used. However, such polynomials are often unstable between nodes. For the speed distribution, a third-degree polynomial was proposed, where the transition time was determined based on the values of parameters (speeds and accelerations) at the end points. Acceleration was limited to the maximum value and was not related to the parameters of the power plant. Not enough information about the overtaking maneuver parameters was provided. González et al. [
10] reviewed the methods used to plan autonomous vehicle movement. Graph algorithms were mainly used to determine the minimum maneuver path on the surrounding space grid. The State Lattice algorithm executed path searching using state-space mesh generation. Sampling-Based Planners generated random state-spaces and looked for their ties. A rapidly exploring random tree (RRT) made it possible to use structured spaces. Lines and circles, closed curves, polynomial curves, Bézier curves, and spline curves were used to represent the path forecast. A numerical method for optimizing a function subject to different constraints was used.
Gu et al. [
11] proposed a planning method that automatically discovers tactical maneuver patterns and fuses pattern reasoning trajectories based on the idea of using pseudo-homology along with characterizing workspace regions. Different patterns can be extracted, depending on the spatial area where the trajectory terminates (region-based distinction), how it gets there around the obstacles (homology-based distinction), and what overtaking (if any) order it follows (sequence-based distinction). A series of virtual tests were conducted and confirmed the effectiveness of the method. Wang et al. [
12] considered the process of building an optimal overtaking route based on minimizing the probability of the vehicles’ presence in the area with close coordinates. An integration process was used to solve the nonlinear optimization. Kala and Warwick [
13] considered the process of overtaking based on the conditions of maximum speed movement, but limited acceleration. A speed plan was not considered for overtaking. Testing of the model was carried out at low speeds, with a large distance between the approaching vehicles.
Babu et al. [
14] presented an MPC framework based on path speed decomposition for autonomous driving. The concept of a time scaled collision cone, which constrains and formulates forward-speed quadratic optimization, was presented. Collision modeling between rectangular objects was presented. The planned vehicle was reduced to a point and the dynamic obstacle was enlarged using the concept of the Minkowski sum. The autonomous driving scenarios were validated with computations of lane change, overtaking, and merging maneuvers among multiple dynamic obstacles. Tomas-Gabarron et al. [
15] considered how to trace the optimum trajectory of a high-speed vehicle that changed its lateral position within a time interval. Four different functions were proposed, along with their relative merits. The presence of Gaussian noise in the sensors’ measurements was studied regarding its influence on the final trajectories. Different performance criteria for the optimization of such maneuvers were presented, as well as an analysis on how path deviations can be minimized by using trajectory smoothing techniques, such as the Kalman filter. Liu et al. [
16] focused on speed profile planning for a given path represented by a set of waypoints. The speed profile was generated using temporal optimization that searched the time stamps for all waypoints. Non-convex temporal optimization was approximated by a set of quadratic programs that were solved iteratively using a slack convex feasible algorithm to speed up computations. Other interesting developments of motion planning and control can be found elsewhere [
17,
18,
19,
20,
21].
This paper presents a new technique of speed planning for the overtaking of autonomous vehicles on two-lane highways. The methodology consists of two main analytical tools. The first tool is a heuristic algorithm that determines the time and distance required for a safe passing maneuver. The algorithm relies on uncertainty-based thresholds of the opposing and impeding vehicles and the minimum and maximum performances of the passing vehicle. The second tool is a quadratic optimization model that determines the optimal speed distribution to ensure a smooth path for the passing vehicle. If needed, the speed plan is updated during the maneuver. The proposed method focuses on finding a rational scheme for vehicle limiting performances. The method aims to simultaneously satisfy several competing objectives, such as a sufficient overtaking time, trajectory smoothness, energy consumption, and collision avoidance. The reason for implementing this approach is that if overtaking is performed with the maximum vehicle performance, there will be a risk of losing lateral stability (due to random external forces) and energy consumption will be high. However, this scenario provides the minimum time and reduces the probability of a head-on collision. On the other hand, if overtaking is performed slowly, a good stability and controllability will be ensured, but there may not be enough of a safety margin at the end of the maneuver.
4. Quadratic Optimization Model
4.1. General
After the rational values of tp and Xp are determined using the heuristic algorithm previously described, the desired trajectory of motion is determined using a kinematic model. Such a model makes path planning simpler and faster and provides a smooth curve that can be adjusted, depending on the priorities of the kinematic parameters. This curve can serve as a reference for the control implementation of laws of the autonomous vehicle during maneuver realization.
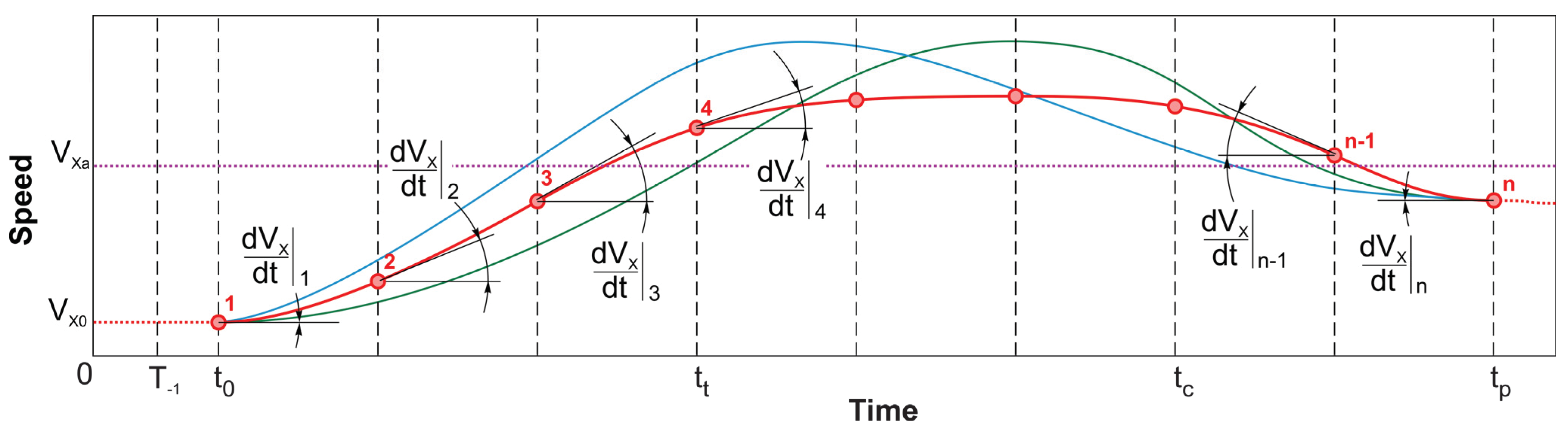
Suppose that the overtaking maneuver is being planned for a relatively straight road section. Then, the formation of the longitudinal and transversal components of the speed plan can be considered independent. Consider the process of forming the longitudinal component of vehicle speed according to the direction of road marking lines (
Figure 6). The values of the time and distance required for overtaking (
tp,
Xp) are determined before the maneuver starts at time
t0. Obviously, there are many realizations of the distribution of the speed’s longitudinal component, such that their integral over the time interval (
tp − t0) equals the distance
Xp. These curves will at least differ in the value of
VX and its derivative
dVX/dt (acceleration) at the nodal points.
The speed distribution must also satisfy various requirements, such as technical, operational, economic, and safety requirements, which may be conflicting. The technical requirements are associated with the propulsion system to ensure the required vehicle’s performance under external constraints, such as a slope, road resistance, tire adhesion, and head wind. That is, the curvature of the speed plan should be comparable to the curvature of the output characteristics of a power unit operating in the transient mode. The operational requirements ensure that the traction and steering controls are smooth by imposing restrictions related to the vehicle’s steerability and stability. Therefore, significant speed and acceleration are undesirable at the moments of lane change. The economic requirements aim to minimize the work of the vehicle power unit by minimizing vehicle acceleration, since more fuel consumption occurs at the moments of speed change. From this perspective, the cumulative derivative of the speed plan curve should also be minimal. The safety requirements limit the maximum speed, acceleration, angular speed of the steering wheel, and time spent near the impeding vehicle.
4.2. Objective Function
The objective function of the model minimizes the speed variation, acceleration variation, and sharpness (differences between tangent coefficients of adjacent nodes). Therefore, the optimal speed distribution is written as
where
J denotes the objective function;
WV,
WA, and
WS denote the weighting factors of speed, acceleration, and sharpness, respectively; and
JV, JA, and
JS denote corresponding integral functions.
The speed integral function is given by
where the last member that does not contain the variable
qi (see Equation (A4),
Appendix A) is omitted.
The speed integral must correspond to the distance
Sp, considering Equations (A1), (A3), (A8), and (A10) (
Appendix A). For the integral function
JV’’,
where
g = (
gb1,
gb2, …,
gbn)
T,
E = (
E4,
E4, …,
E4)
T,
E4 denotes the identity matrix of the dimension
4 × 4, and
Mq denotes the transition matrix from the vector
q of degrees of freedom to the vector
qf of repeating degrees of freedom of all finite elements (FE). Note that in adjacent FE, the values of the nodes on the right and left are repeated in the vector
qf (e.g.,
q3i and
q4i are equal to
q1(i+1) and
q2(i+1), respectively). Therefore, the excess degrees of freedom must be reduced by grouping node values instead of FE. That is,
qf = Mq·q.Now consider the integral of the square of speed
V2(
t), considering Equation (A11) (
Appendix A):
In vector-matrix form, Equation (22) can be written as
where
Z4 = zero matrix (
4 × 4).
The integral functions of the acceleration and sharpness are similar to Equation (22). Considering Equation (23) and Equations (A12) and (A13) (
Appendix A), they yield
where
G and
K denote the matrices formed in the same format as
D in Equation (23).
By leaving only the members containing the variables, the problem becomes equivalent to quadratic optimization. By substituting Equations (20)–(25), the objective function of Equation (19) becomes
where
H denotes the equivalent of Hessian for combined speed, acceleration, and sharpness factors, and
L denotes the vector reflecting the average level of speed.
4.3. Constraints
4.3.1. Lane Change-Related Constraint
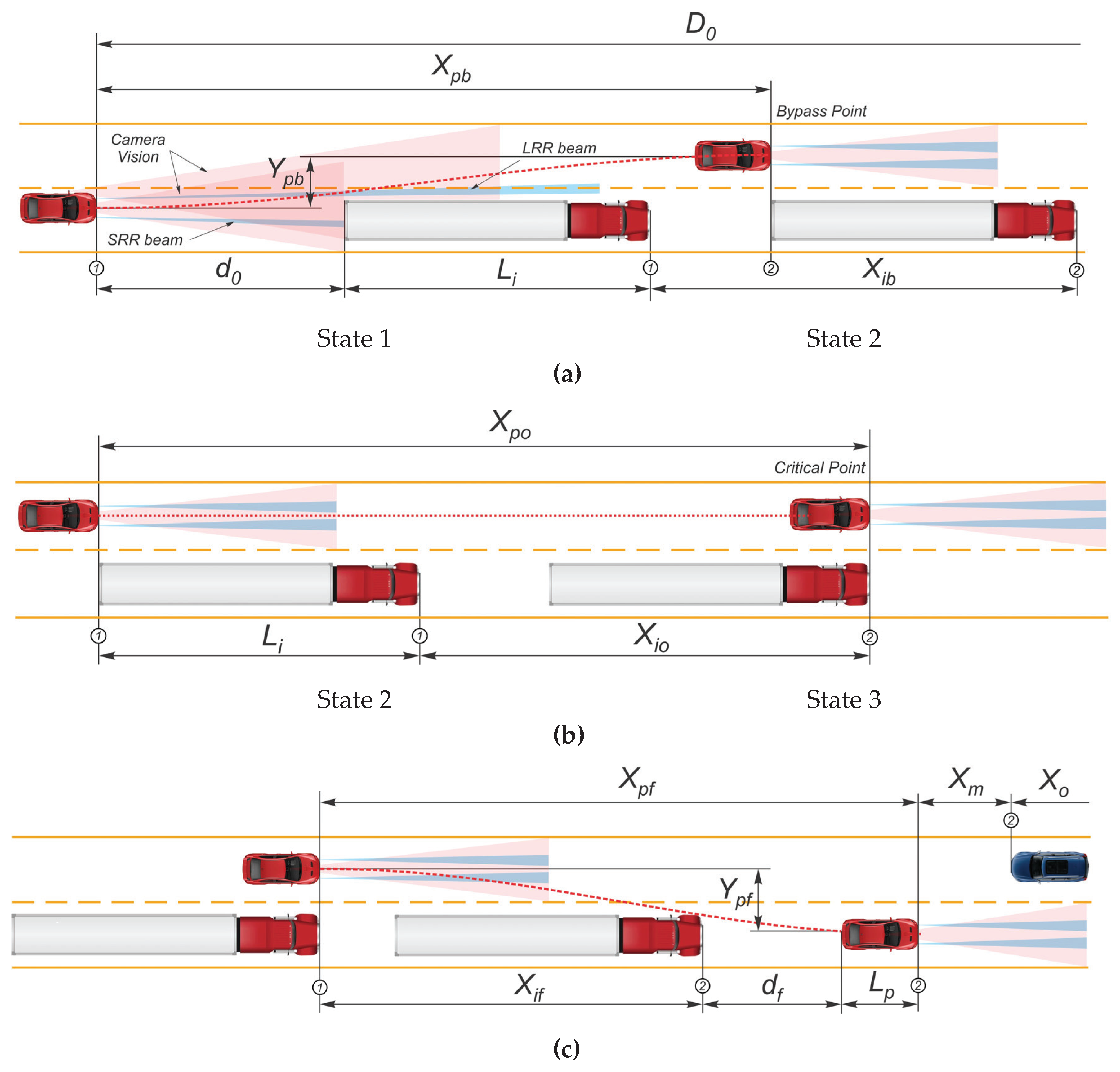
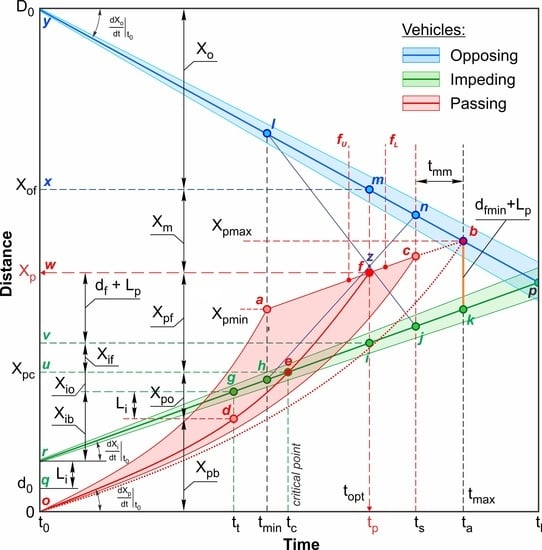
The lane change is the first phase depicted in
Figure 1a. The maneuver starts from a position that satisfies the condition of avoiding a blind spot and determines the length of the impeding vehicle (i.e., extremely close to the dashed marking line). The main requirement is that the full departure in the opposite lane should be completed before reaching the rear of the impeding vehicle. This approach ensures maximum security, especially before outrunning a long impeding vehicle, since its lateral behavior (possible swinging of a semitrailer) is unpredictable. Additionally, the tracking of the opposing vehicle’s position and speed is retained until the departure to the opposite lane. In an extreme case, a transverse movement may be allowed, where the minimum safe side distance between the passing and impeding vehicles is provided.
The time required for the passing vehicle to pass from State 1 to 2 (
Figure 1a) is
tt (
Figure 3). Then, the longitudinal component of the path is
The condition for achieving State 2 (
Figure 1a) is
The time
tt can be determined iteratively (
Figure 3) after the distribution of the longitudinal speed, based on Equations (27) and (28), considering
Xpb = Xp(
tt). According to a possible slight decrease in the impeding vehicle speed,
Xpb may correspond to a small longitudinal gap between the front of the passing vehicle and the rear of the impeding vehicle. Thus,
The path’s transverse component is
where
VY(
t) is represented similar to Equation (21).
4.3.2. Location in Opposite Lane Constraint
The upper limit of the passing vehicle transversal movement
Ypo may correspond to its position in the middle of the opposite lane. Possible deflections of this position are restricted by safe clearance to the road edge (
Figure 1b). A lower limit of this clearance is the minimum safe distance between passing and impeding vehicles. Therefore, for
Xpo and
Ypo,
where
tc can be found iteratively according to the condition when the passing and impeding vehicles are abreast at the critical point (State 3,
Figure 1b), considering
Xp(
tc)
= Xpb + Xpo (Point
e,
Figure 3).
According to a possible slight increase in the impeding vehicle speed, the passing vehicle’s front can be a little ahead of the front of the impeding vehicle. Thus,
4.3.3. Maneuver Completion
The lane change planning is similar to the first phase. Thus,
4.4. Preparing the Reference Trajectories
As a result of the optimization, the components of speeds (
VX,
VY)
T in global coordinates are determined. Therefore, it is necessary to transfer the speeds to the local coordinates of the passing vehicle (
Vx,
Vy)
T, in order to allow it to consider its maneuvering. Since the yaw angle
φ is small,
and
The ideal forecast for the yaw angle can be obtained as a tangent to the motion trajectory:
Therefore, to track a virtual trajectory, a state vector corresponding to the capabilities of the current measurements may be used: absolute displacements in global coordinates Xp, Yp; speeds in local coordinates Vx, Vy; and the yaw angle φ. As additional parameters, which can be directly measured on a vehicle, the accelerations that are components of the optimized speed plans reduced to the vehicle local coordinates may be used, as well as the yaw rate, which can be estimated indirectly as dφ/dt considering Equation (36).
5. Updating the Speed Plan
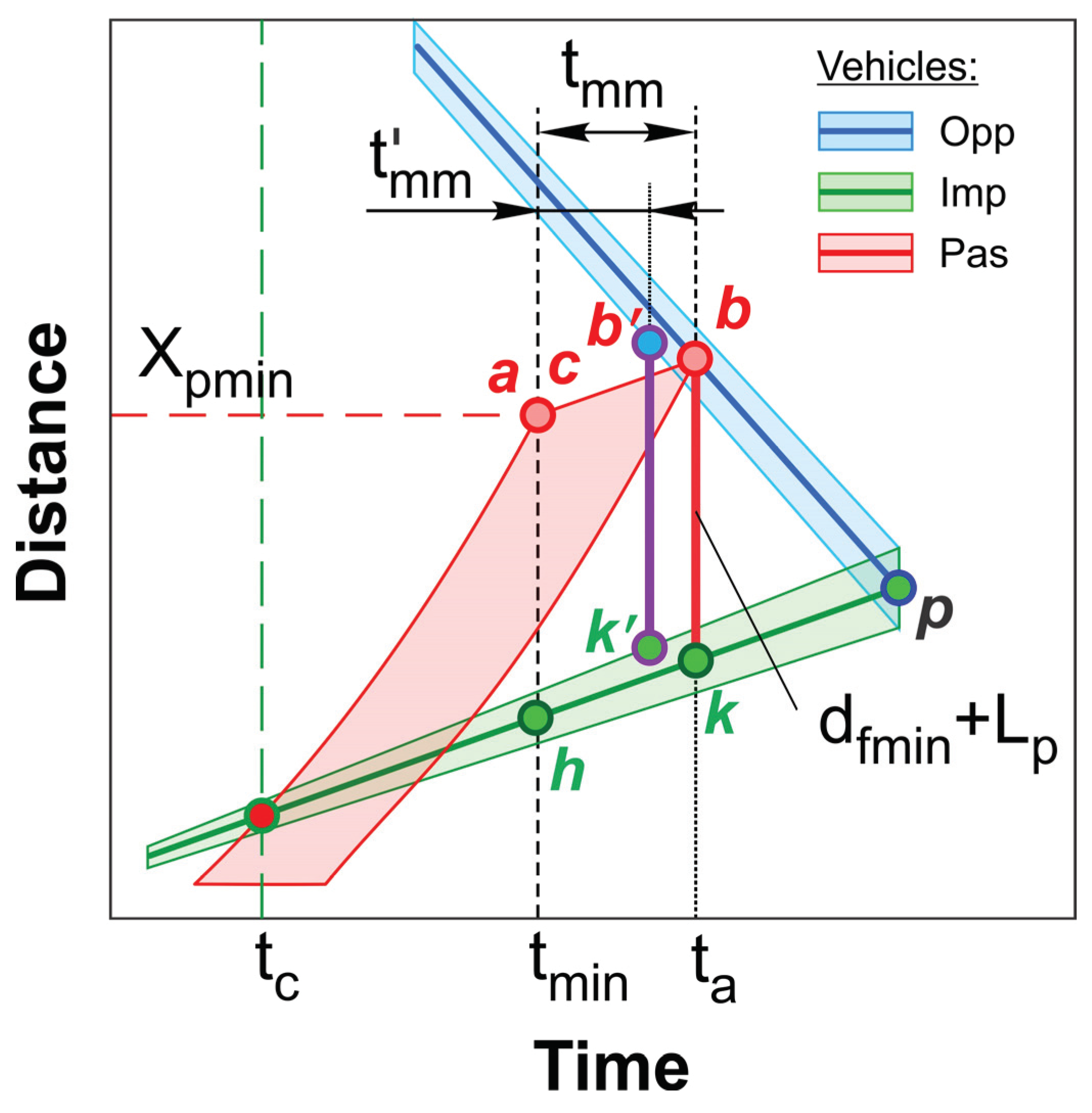
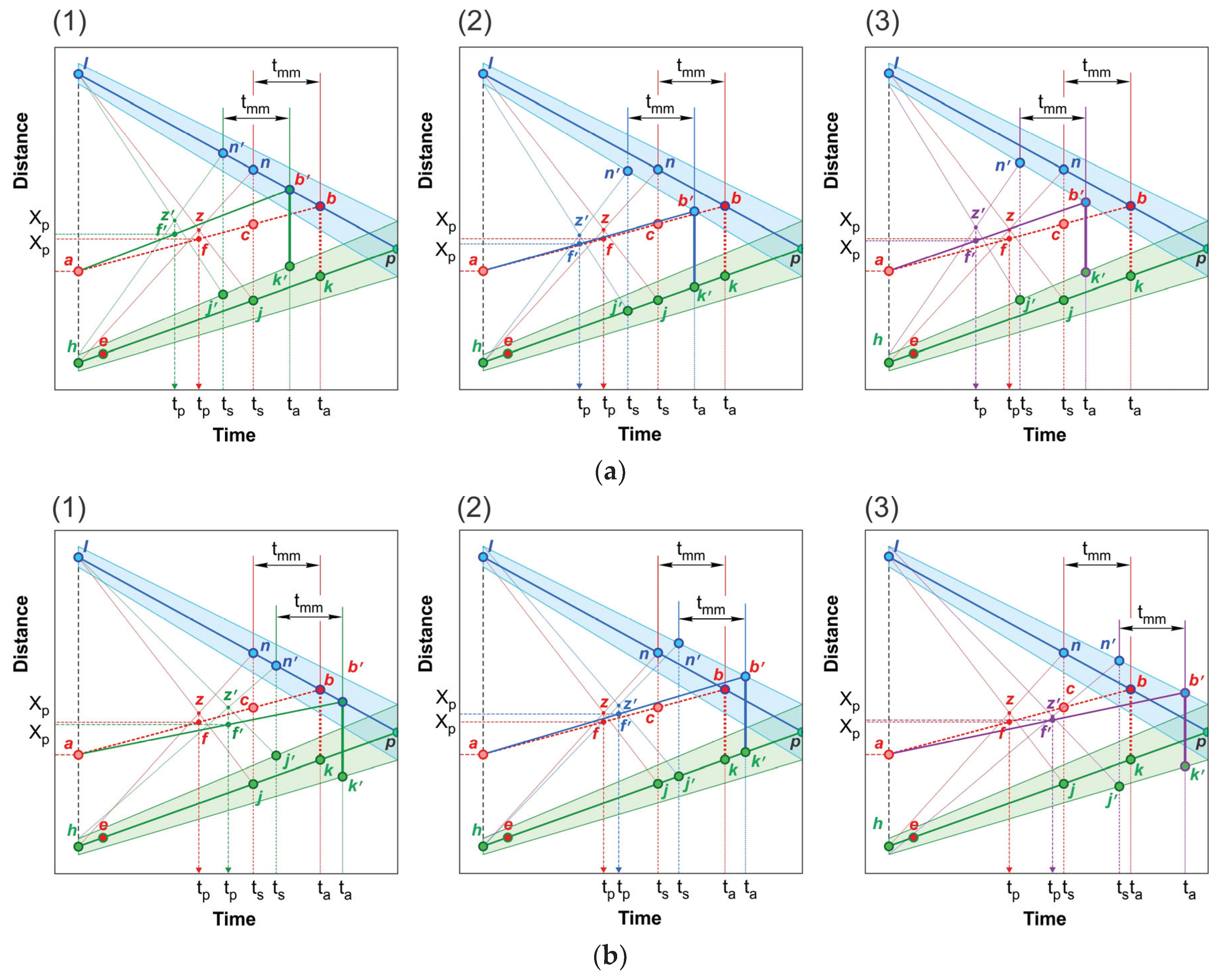
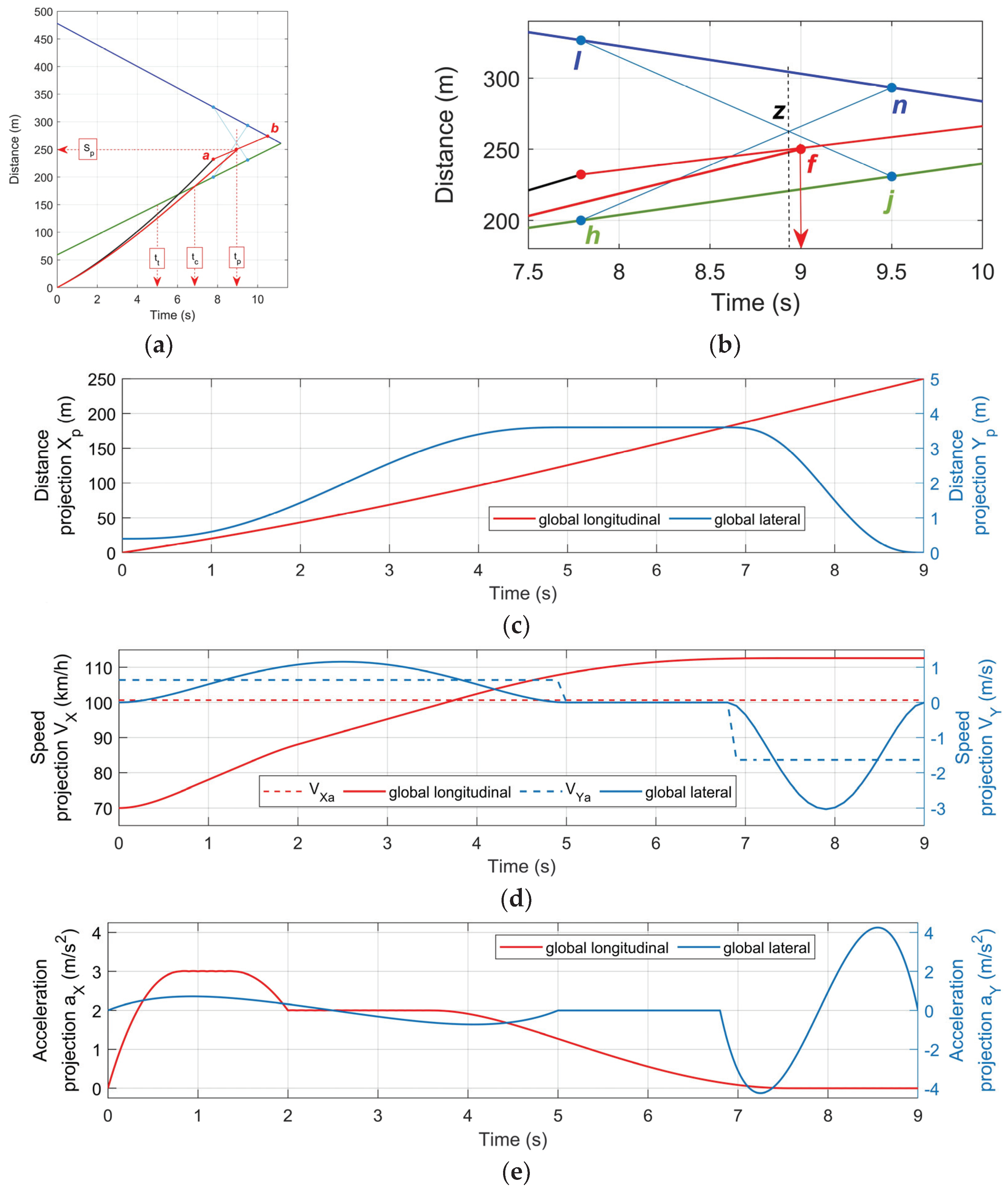
Each subsequent measurement determines the new position of the linear forecast. As previously mentioned, the influence of the fluctuations in the participants’ speed on the forecast reliability during the maneuver should be analyzed to avoid a redundant number of predictions. In
Figure 3, the deviations in the proximity of Point
f are shown, where the threshold values of changes in speeds of the opposing and impeding vehicles are reached. In
Figure 7a1, the speed of the impeding vehicle increases in such a way that the linear curve exceeds the upper boundary prior to the moment
ta, and the segment
b’k’ slightly goes up (green), along the path curve of the impeding vehicle. Basically, the value of the minimum required distance
dfmin depends on the difference between the speeds of the passing and impeding vehicles, and, thus, will vary with the fluctuations in movement modes of the overtaking participants. However, the changes will not have a significant affect, and therefore,
dfmin can be considered constant in the vicinity of Point
ta. The determination of
dfmin is described elsewhere [
24,
25]. The bias of the intersection point of the trapezoid diagonals in
z’ leads to shifting of the optimal Point
f’ up to the left. The required time
t’p becomes shorter and the needed space
X’p becomes larger. This may be explained by the significant sensitivity of the forecast to the impeding vehicle’s speed changes.
In the case of
Figure 7a2, the opposing vehicle speed increases and the upper boundary limit is violated. In this case, the inclination angles of the segments
ab and
ab’ are practically the same. However, even though the required time has decreased
t’p < tp, unlike the previous case, the required space
X’p decreases due to the larger space needed for the opposing vehicle. The most critical case is when the speed fluctuations of both the opposing and impeding vehicles reach the threshold boundaries simultaneously (
Figure 7a3). The displacement of the minimum space segment
dfmin + Lp for completing the maneuver can be so significant that the time
t’s approaches the preset time
tp, and the margin
tmm in relation to the minimum performance mode will not be provided. Point
t’p is located the furthest from Point
tp, even though the space required for the maneuver may remain almost unchanged
X’p ≈ Xp. Similarly, a decrease in the speed of opposing and impeding vehicles will give a lower limit of time fluctuations
fL (
Figure 3). However, such decreases are not dangerous, and it makes sense to only recalculate the forecast to save energy and increase the movement stability. Based on the described scheme, it is possible to determine the allowable level of deviations, at which the margin of minimum safety is kept without the necessary recalculation.
Therefore, for the case depicted in
Figure 7b1, the diminished impeding vehicle speed means that a shorter distance and longer period are needed:
X’p < Xp and
t’p > tp. For the case in
Figure 7b2, the diminished opposing vehicle speed demonstrates the need for a longer distance and time because of the reduced space
Xo for the opposing vehicle:
X’p > Xp and
t’p > tp. For the case in
Figure 7b3, the diminished speeds of both opposing and impeding vehicles move Point
z’ quite far from
z, providing a longer time in almost the same space:
X’p ≈Xp and
t’p > tp. This may cause the double margin time
tmm with unreasonable energy consumption. Therefore, the passing vehicle speed mode may be reduced.
Other possible combinations, where one of the vehicles increases its speed and the other decreases its speed approximately simultaneously, give solutions that are not superior in nature to the changes discussed in
Figure 7. Note that measurements of
dn are available prior to the moment of alignment with the rear of the impeding vehicle, after which the last
dn value may be fixed, and measurements of
Dn can be carried out until the critical point. Recalculation after the critical point is possible if the next impeding vehicle appears in the lane, which does not provide a proper pocket or harshly reduces its speed.
Obviously, even in the automatic mode of maneuver execution, deviations of the passing vehicle speed are possible due to the influence of various random factors. However, within the thresholds set by
fU,
fL (
Figure 3), forecast recalculation is not required. Therefore, the autonomous control system must adjust the speed mode of the passing vehicle not only according to measurement changes, but also considering the matching with its own reference curve (
of in
Figure 3).
The condition under which the specified safety level is retained and the forecast does not require recalculation is
where
t’a denotes the instantaneous value of the hypothetical accident time compatible with predefined
ta;
tpr = Δ
tpr +
p·Δ
tm = (
m+p)·Δ
tm, where
p denotes the number of spare measurement cycles, by default,
p = 2; and
tun denotes the unaccounted time expenses (e.g., engine transition mode and control delay).
Hence,
t’a can be recalculated using Equation (13) for every
n-th measurement at
tn as follows:
As can be seen, the expression does not contain any absolute value, except for vehicles’ lengths, and only uses relative measurements, making it independent of the passing vehicle state parameters, including variance regarding its reference curve.
7. Application
The purpose of this application is to achieve stable control and ensure that the Plant state parameters fit those generated by the proposed methodology. The application involved setting initial conditions data, defining the parameters of the AMPC controller, and determining the desired reference tracks for speed, acceleration, and displacement in the global coordinates.
7.1. Initial Conditions Data
The Matlab/Simulink example for simulating overtaking was used [
26]. According to the measurements, at time
T−1 =
−0.1 s, the initial data vector is formed as follows:
where the linear dimensions are given in
m and speeds in
km/h. Using the technique described in [
22], for the case of ideal motion conditions, the necessary values yield
tmin =
7.79 s and
Sfmin =
25 m. The minimum time margin was set as
tmm =
1 s. Substituting these values into Equations (12)–(18) and (27)–(33) gives the following rational values (
Figure 9a,b): overtaking global longitudinal projection
Xp = 250 m, overtaking time
tp =
8.9 ≈ 9 s, bypass time during lane change
tt =
5.1 s, and time to the critical Point
tc = 6.9 s.
7.2. Parameters of the AMPC Controller
The sampling time = 0.1 s, prediction horizon = 10 s, and control horizon = 2 s. The plant model has four states with two measured outputs. Weights: manipulated variable (steering angle) = 0 and manipulated variable rate (steering angle rate) = 0.1; output variables: lateral displacement = 0.8 and yaw angle = 0.1; constraints: −0.2 ≤ steering angle (rad) ≤ 0.2, −0.2 ≤ steering angle (rad/s) ≤ 0.2, 0 ≤ lateral displacement (m) ≤ 3.6, and −0.1 ≤ yaw angle (rad) ≤ 0.1.
7.3. Reference Speeds, Accelerations, and Displacements
Using the proposed optimization model, the desired reference tracks for speed, acceleration, and displacement in the global coordinates were determined, using the time grid with the increment of
0.1 s (
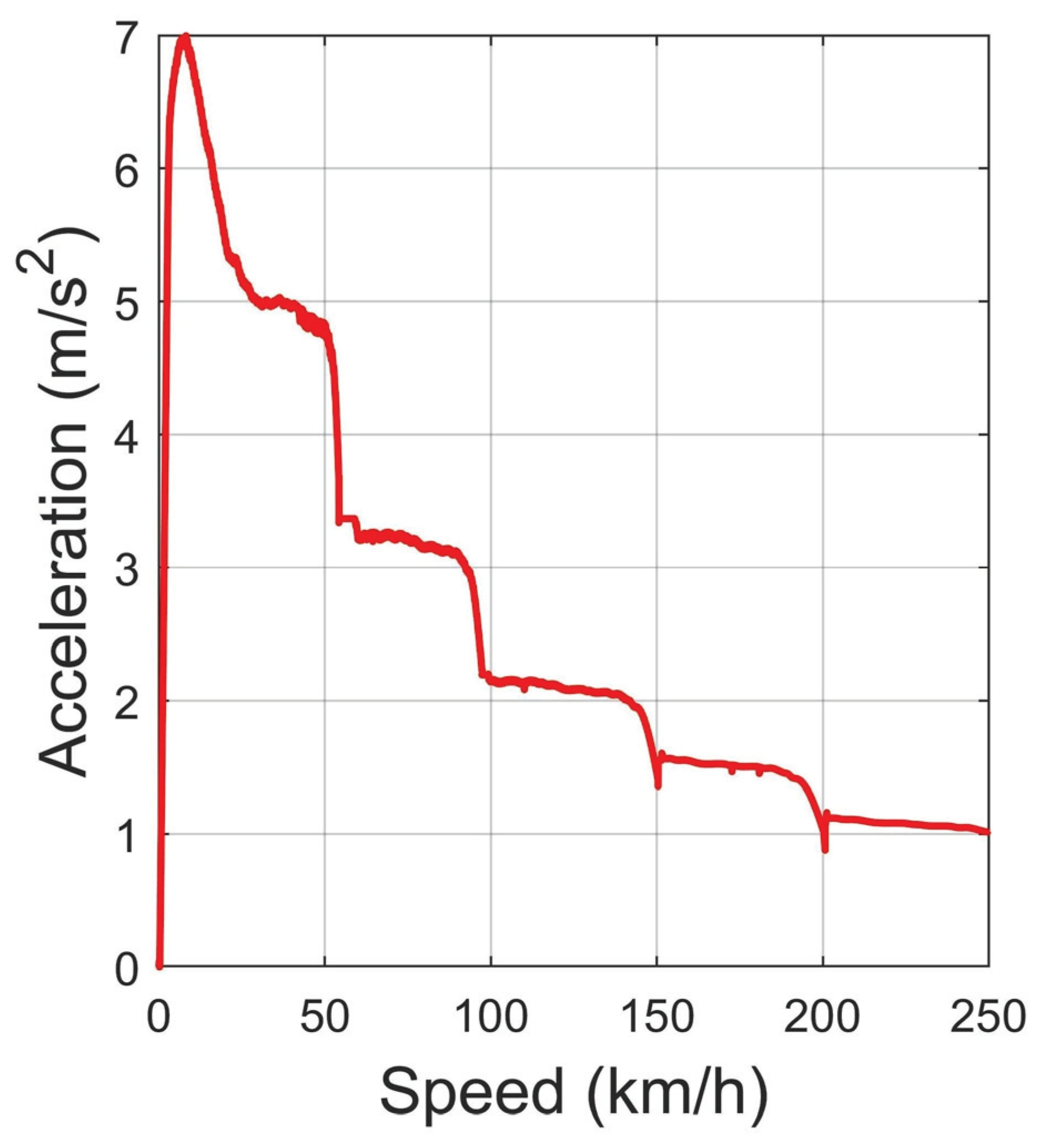
Figure 9c–e). Note that the setting of linear constraints in Equation (40) should be consistent with the thresholds of the vehicle performance set by the distribution of acceleration upon speed (
Figure 4) for the current conditions. This means that each speed value to be optimized in a time grid node is tied to the maximum possible acceleration at this speed, which creates non-linear constraints. In this regard, for each set of speed and acceleration thresholds in the optimization process, some rationale is needed, as previously described. Another difficult point before optimization is setting the final values of the speed and acceleration, since they significantly affect the trend of the entire speed plan. The speed value in the last node close to the average speed
VXa (
Figure 9d) may lead to the appearance of such a peak near the critical point, when the longitudinal accelerations in the phase of maneuver completion are negative and larger than the absolute value of
0.5 m/s2. That would mean the use of service braking and activation of the vehicle’s working brake system. From the point of view of ensuring the maximum vehicle stability during the lane change, it is undesirable to use the tire longitudinal force values close to those which may considerably reduce the tire’s lateral adhesion. In connection with the foregoing, it may be recommended to focus on the value of the speed
Vpf at which the distribution of the speed plan requires decelerations, provided only by limiting the engine power consumption. In this case, the selected value
Vpf ensures maneuver completion with acceleration close to zero.
As can be seen, the combination of the plan for longitudinal speeds and accelerations fits the performance limitations well in
Figure 4. At the same time, the projection curve of the overtaking path on the global
X axis clearly corresponds to
250 m (
Figure 9d). This, when copied to
Figure 9a’s curve, shows that in the initial phase, the vehicle uses a potential close to the upper limit (black line). The next important point is the conditionality of the weighting factors in the optimization of Equation (19). Note that the ratio of weight coefficients significantly changes the optimization picture in connection with the change of priorities. Increasing the
WV coefficient very much reduces the speed consumption, but significantly increases the need for acceleration at the beginning of the maneuver. The increase of the
WA coefficient reduces the cumulative consumption of acceleration, but does not provide smoothness in the boundary zones of the speed plan, and the peak speed value rises. Increasing the
WS coefficient distributes speeds evenly over time.
Therefore, in the current case of optimizing the longitudinal plan, the stable engine’s performance is the most important, minimizing abrupt transitions in its control; respectively, the values for the entire overtaking maneuver are chosen: WV = 0.2, WA = 0.2, and WS = 0.6. In the distribution of transverse speeds of the bypass phase, the priority is divided between the control smoothness and the cumulative acceleration intake: WV = 0.2, WA = 0.4, and WS = 0.4. In the final phase, due to the lane change at high speeds, the main priority is focused on reducing the lateral accelerations, respectively: WV = 0.1, WA = 0.6, and WS = 0.3. It is obvious, however, that priorities may vary, depending on the situation.
It should also be noted that the value of the vehicle’s initial lateral position does not correspond to the lane center, but is offset by 0.4 m from the dashed line to ensure the conditions previously described.
Figure 10 shows the overtaking results by predicting the lateral offset and yaw angle. As can be seen in
Figure 10a, at the 9th second of overtaking, the trajectory longitudinal component practically corresponds to the pre-set one, with a final value of
Xp = 250 ≈ 249.4 m, and the transverse component
Yp is strictly within
3.6 m, but has a residual of
0.23 m at the time
tp = 9 s. At this moment, the passing vehicle is almost in the middle of its lane and continues stable movement, i.e., the situation is uncritical. The AMPC controller calculates the discrete control signal based on the information on the previous value and reference tracks. However, it is almost impossible to avoid tracking delay completely. The same effect can be observed in relation to the lateral speed
VY (
Figure 10b), which coincides in terms of shape and values with the initial one in
Figure 9d, but lags a bit in time.
In general, by using the vehicle refined models of
Plant and
Model (
Figure 8) and including a larger number of state parameters for tracking and other measures, the model convergence can be improved.
8. Concluding Remarks
This article has presented a methodology for distributing the speed in the longitudinal and lateral directions when a vehicle is overtaking on two-lane highways in an automated mode. An advantage of the kinematic technique used in the model is its ability to predict both speed and acceleration references, providing subsequent tracking control based on sensor measurements. In addition, this technique can be successfully used as a component of the model predictive control for generating reference trajectories. Based on this study, the following comments are offered.
In this study, the ‘kinematic model’ was not exactly used in the sense of a vehicle model, but the output kinematic parameters of the vehicle motion were used to predict both the trajectory and the overtaking mode, considering the speed distribution directly and acceleration distribution indirectly, as part of the FE speed model. In this regard, we followed the well-established trend of planning motion paths with various curves and graphs, as presented in the literature [
17]. However, we obtained trajectories as integrals of the velocity plans. Unlike other studies, the proposed approach focused on using an FE grid that simultaneously ensured a high accuracy and compliance with the real capabilities of the vehicle engine-drive system. In particular, the interaction between possible speeds and the respective accelerations was considered.
In the quadratic optimization model for the speed-plan distribution, three measures were considered (speed, acceleration, and sharpness). The two parameters (tp and Xp) characterize the average speed Vxa and are obviously not enough, because many curves integrable in the interval (t0, tp) can give the same Xp. In addition, the vehicle’s ability to increase speed is a function of the speed and depends on the vehicle’s characteristics (i.e., acceleration is a 3D surface as a function of vehicle speed and throttle activation level). Therefore, in this study, it was assumed that the speed nodes are interconnected by curves over time, differentiable at least twice (i.e., providing smoothness). Then, the derivatives at the nodes which reflect the slope (acceleration) and the curvature (sharpness) were included as members of the objective function, along with their weights. Since this is an FE model of the curve, no other parameters except for the nodal Vx, dVx/dt, and d2Vx/dt2 can be included, because only the nodes need to be distributed, consistent with the vehicle technical features.
The general idea of using the overtaking heuristic algorithm is to guarantee maneuver completion, prior to the maneuver beginning, with at least the minimum safety margin. The algorithm emanates from individual vehicle operational properties. This allows the maximum and minimum performances to be predicted for given initial conditions. Therefore, considering possible changes due to random factors, for example, the algorithm will provide a decision to only pass when maneuver safety is ensured. In addition, the algorithm can foresee the situation when a vehicle must have a power margin, and whether maneuver completion requires additional acceleration to prevent a possible collision. Note that cancelling the overtaking maneuver is possible. However, within the framework of the presented algorithm, cancellation could happen in occasional situations (e.g., sudden swinging of the impeding vehicle). In this case, a switch to another algorithm is needed and this should be investigated in the future.
Determination of the required overtaking time is based on the safety margin and adequate engine power. These criteria allow possible adjustments of the power consumption and safety time, depending on the situation changes and priorities. A simple, but quite effective, technique was proposed in the heuristic algorithm for finding one rational curve from an infinite number of possible realizations. This is the reason why two additional derivatives (acceleration and sharpness) were used for finding the best speed distribution. All these measures aim at ensuring strict vehicle power stability and consequently, safety. In addition, by considering the lateral acceleration and yaw rate (indirectly) in the steering control prognosis, motion instability and possible sideslip can be prevented. Therefore, maneuver safety has been adequately incorporated in the proposed framework.
In this study, the roadway is assumed to be straight, with ideal surface friction and no external forces (e.g., gusts of wind). In addition, the road is assumed to have very gentle vertical curvature. These assumptions are necessary, since sensor measurements can be particularly affected by the slope and direction of the road, being unable to measure the position and speed of the opposing vehicles in various circumstances. Fortunately, this does not represent a limitation of the model, since overtaking maneuvers on two-lane highways are not permitted on sharp vertical curves because they require very long vertical curves that are expensive to construct [
27,
28].
Further research can be conducted to improve the algorithm for finding the optimal speed distribution for overtaking. Areas of focus may include: (1) influence of the final speed of the maneuver on the nature of the optimal speed plan; (2) influence of the weight coefficients on the speed plan; and (3) modeling of obstacle avoidance in autonomous overtaking. By grouping the longitudinal and lateral components of the reference trajectories, the kinematic technique can be used to simulate the obstacle-avoidance trace for autonomous vehicles. In addition, a sensitivity analysis of the proposed framework can be conducted to understand the impact of certain problem parameters on the overall results, including the effect of uncertainty.