Path and Control Planning for Autonomous Vehicles in Restricted Space and Low Speed
Abstract
1. Introduction
2. Kinematic Models of Autonomous Motion
2.1. Single Vehicle
2.1.1. Passenger Car
2.1.2. Long Truck with Steered Rear Axle
2.2. Articulated Vehicles
2.2.1. Conventional Tractor-Semitrailer Vehicle
2.2.2. Tractor-Semitrailer Vehicle with Semitrailer’s Steered Axles
3. Optimization Model
3.1. Basic Model
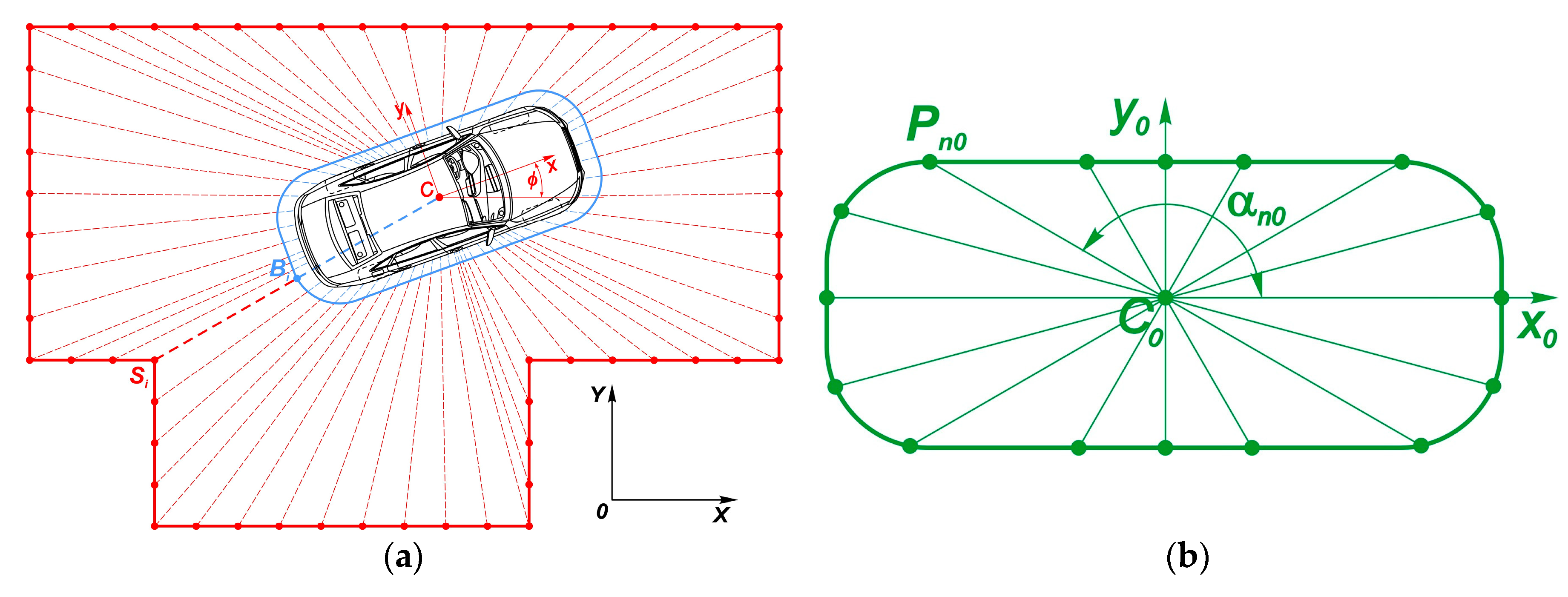
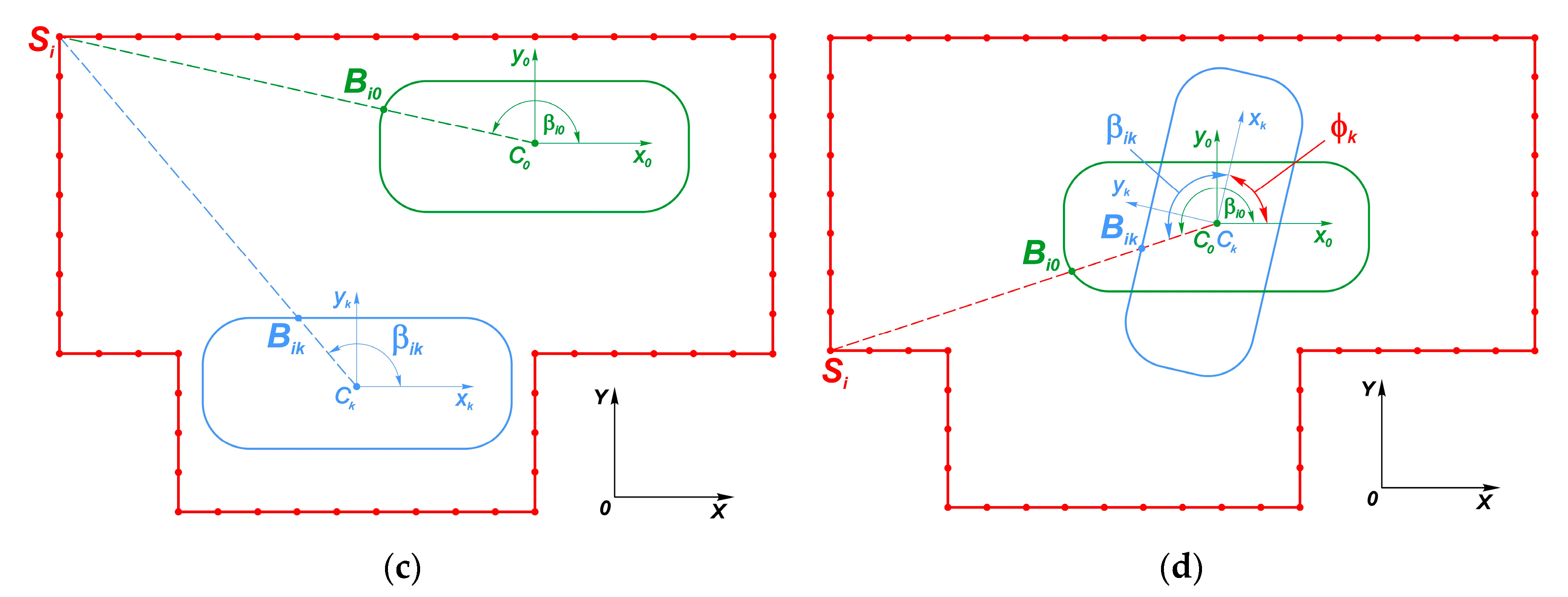
3.2. Operational and Physical Constraints
3.2.1. Case 1: Vehicle Yaw Rate
3.2.2. Case 2: Parking in Restricted Space
3.2.3. Case 3: Circular Motion
4. Simulation
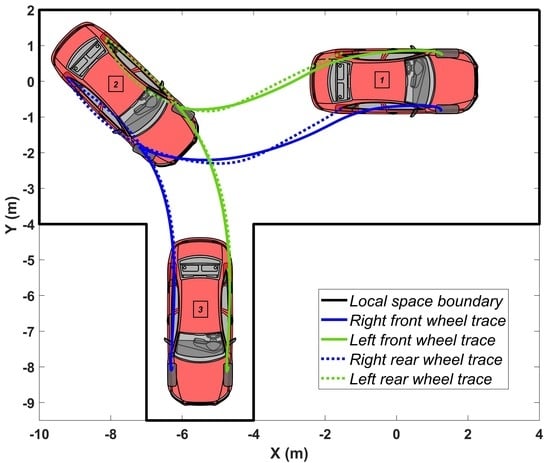
4.1. Simulation of Passenger Car
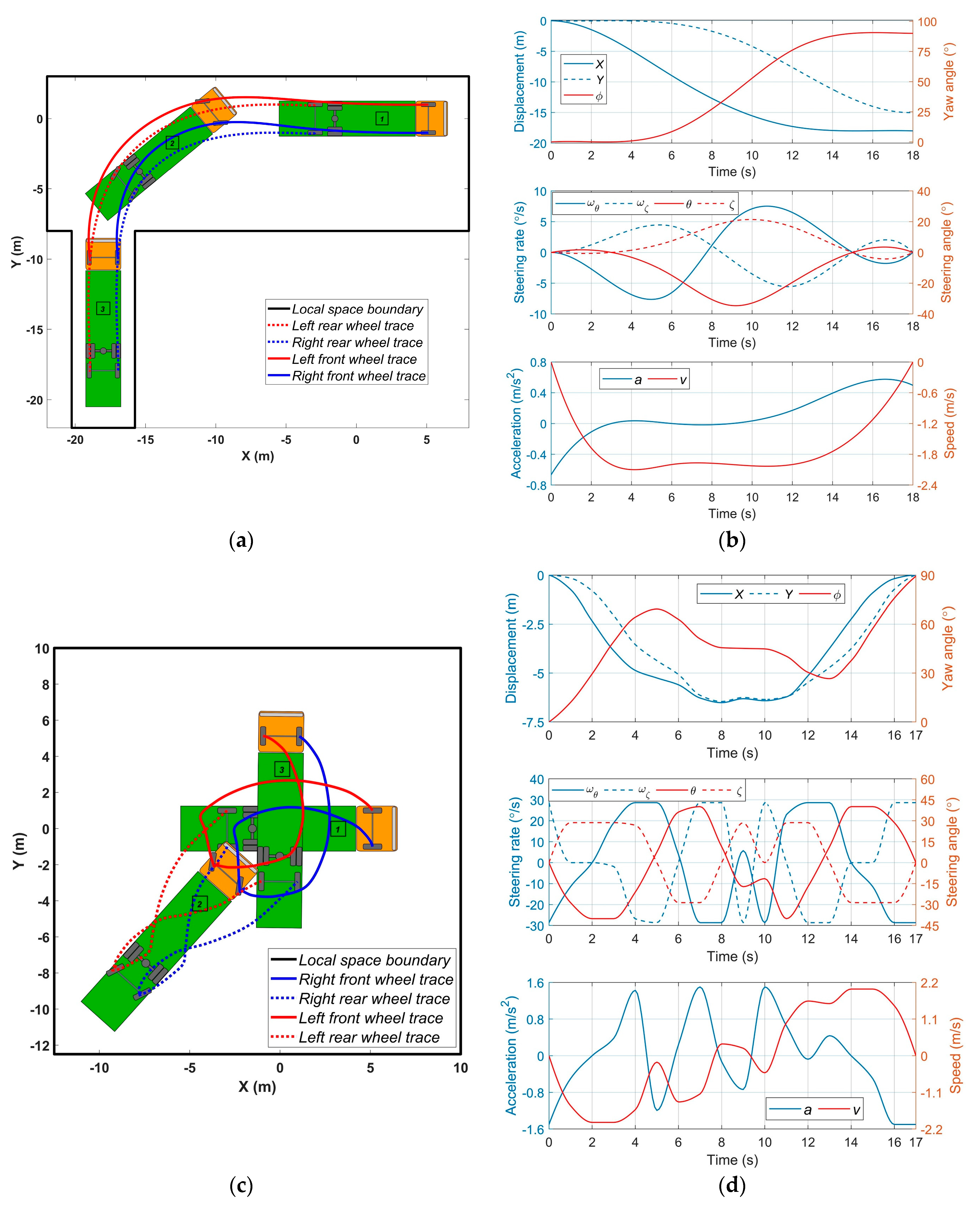
4.2. Simulation of Long Single Truck with Steered Rear Axle
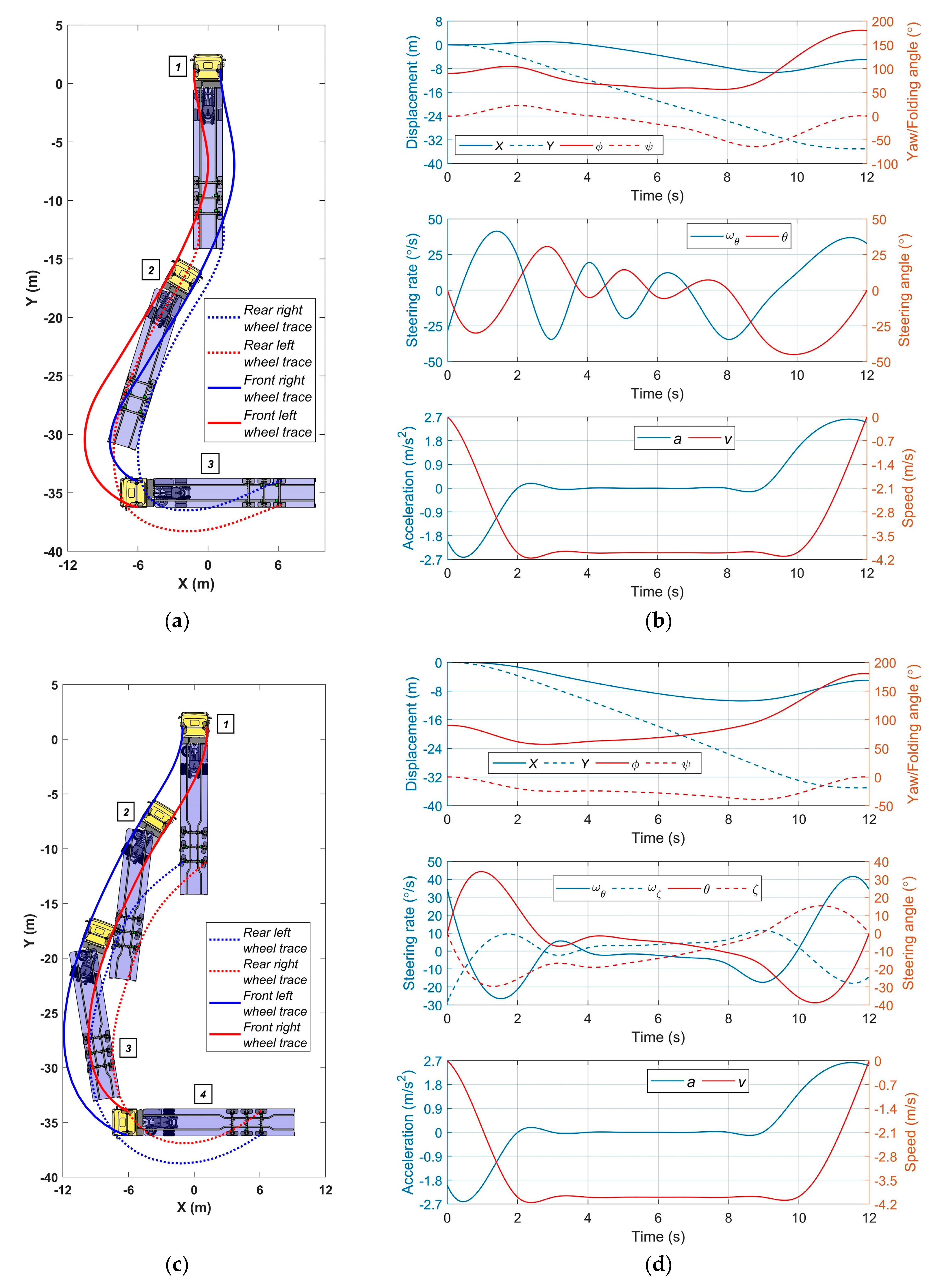
4.3. Simulation of Articulated Vehicles
4.4. Results and Discussion
5. Conclusions
- Based on the positive results in all the simulations, the use of kinematic models’ trajectories for the tracking is quite suitable for low speeds, when the trajectories are supposed to be represented by smooth curves. However, the shape of control signals reflects, to a greater measure, the disadvantages of kinematic models’ indirect control (by acceleration) and to a lesser measure reflects the direct control parameter (throttle position and power).
- The presented original algorithms consider the indirect parameter - the intrusion into a vehicle safety contour (or the excess of a pre-set level by control points) to model the inequality constraints. The proposed idea has shown the adequate accuracy in assessing the inadmissible distances to a vehicle body. The simplicity and versatility can be marked as an advantage of the proposed method, and the fact that it is a part of the optimization process and not just a geometric technique. The proposed technique can also be easily used for simulating the avoidance of moving and stationary obstacles.
- The cost function form significantly affects the forecast, depending on the accepted optimality criteria. The advantage of the specified NMPC is the ability to use any functions, both linear and non-linear, and their combinations. Unlike the lane change at high speeds, where the smoothness is required and quadratic forms are frequently used, the linear functions and quasi-optimal solutions are often quite adequate at low speeds. Thus, it was revealed that the cost function’s linear components work better where changes of vehicle model speed’s signs are expected, and a shorter maneuvering path is needed. Quadratic forms provide more smoothed control and allow better coordination of combined control (the case of several steered axles).
- This project may be considered as a test phase of a comprehensive study of parking/docking algorithms for autonomous vehicles. The results have argued the applicability of kinematic models and the quality of forecast in general. Within the expansion of elaborating the automated parking algorithms, it is planned to include the following issues: mapping the parking space using the SLAM methods, improving the constraint evaluation algorithm to an adaptive level, creating and testing the alternative algorithms for constraints, developing dynamic vehicle models with real-world control parameters, implementing nonlinear and adaptive MPC methods for the tracking task, and combining the parking computing techniques into one automated option for HIL-testing.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AV | Autonomous vehicle |
| CAV | Conventional articulated vehicle |
| EKF | Extended Kalman filter |
| HIL | Hardware-in-the-loop |
| NMPC | Nonlinear model predictive control |
| SLAM | Simultaneous localization and mapping |
| SQP | Sequential quadratic programming |
| TSV | Tractor-semitrailer vehicle |
| TSV-SSA | Tractor- semitrailer vehicle with semitrailer’s steered axles |
References
- Lee, B.; Wei, Y.; Guo, I.Y. Automatic parking of self-driving car based on Lidar. International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2017, 42, 241–246. [Google Scholar]
- Lee, H.; Chun, J.; Jeon, K. Autonomous back-in parking based on occupancy grid map and EKF SLAM with W-band radar. In Proceedings of the International Conference on Radar (RADAR), Brisbane, Australia, 27–30 August 2018; pp. 1–4. [Google Scholar]
- Lin, L.; Zhu, J.J. Path planning for autonomous car parking. In Proceedings of the ASME Dynamic Systems and Control Conference, Atlanta, GA, USA, 30 September–October 3 2018; Volume 3. [Google Scholar]
- Pérez-Morales, D.; Domínguez-Quijada, S.; Kermorgant, O.; Martinet, P. Autonomous parking using a sensor-based approach. In Proceedings of the IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016. [Google Scholar]
- Luca, R.; Troester, F.; Gall, R.; Simion, C. Environment mapping for autonomous driving into parking lots. In Proceedings of the IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 28–30 May 2010; pp. 1–6. [Google Scholar]
- Zhou, J.; Navarro-Serment, L.E.; Hebert, M. Detection of parking spots using 2D range data. In Proceedings of the IEEE International Conference on Intelligent Transportation Systems, Anchorage, AK, USA, 16–19 September 2012; pp. 1280–1287. [Google Scholar]
- Heinen, M.R.; Osorio, F.S.; Heinen, F.J.; Kelber, C. SEVA3D: Using artificial neural networks to autonomous vehicle parking control. In Proceedings of the IEEE International Joint Conference on Neural Network, Vancouver, BC, Canada, 16–21 July 2006; pp. 4704–4711. [Google Scholar]
- Kiss, D.; Tevesz, G. Autonomous path planning for road vehicles in narrow environments: An efficient continuous curvature approach. J. Adv. Transp. Intell. Auton. Transp. Syst. Des. Simul. 2017. [Google Scholar] [CrossRef]
- Wang, Y.; Jha, D.K.; Akemi, Y. A two-stage RRT path planner for automated parking. In Proceedings of the 13th IEEE Conference on Automation Science and Engineering, Xi’anChina, 20–23 August 2017; pp. 496–502. [Google Scholar]
- Ballinas, E.; Montiel, O.; Castillo, O.; Rubio, Y.; Aguilar, L.T. Automatic parallel parking algorithm for a car-like robot using fuzzy PD+1. Control. Eng. Lett. 2018, 26, 447–454. [Google Scholar]
- Petrov, P.; Fawzi, N. Automatic vehicle perpendicular parking design using saturated control. In Proceedings of the IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies, Amman, Jordan, 3–5 November 2015; pp. 1–6. [Google Scholar]
- Gupta, A.; Rohan, D.; Mohit, A. Autonomous parallel parking system for Ackerman steering four wheelers. In Proceedings of the IEEE International Conference on Computational Intelligence and Computing Research, Coimbatore, India, 28–29 December 2010; pp. 1–6. [Google Scholar]
- Tazaki, Y.; Okuda, H.; Suzuki, T. Parking Trajectory Planning Using Multiresolution State Roadmaps. IEEE Trans. Intell. Veh. 2017, 2, 298–307. [Google Scholar] [CrossRef]
- Suhr, J.K.; Jung, H.G. Automatic parking space detection and tracking for underground and indoor environments. IEEE Trans. Ind. Electron. 2016, 63, 5687–5698. [Google Scholar] [CrossRef]
- Diachuk, M.; Easa, S.M.; Hassein, U.; Shihundu, D. Modeling passing maneuver based on vehicle characteristics for in-vehicle collision warning systems on two-lane highways. Transp. Res. Record 2019, 2673, 165–178. [Google Scholar] [CrossRef]
- Diachuk, M.; Easa, S.M. Guidelines for roundabout circulatory and entry widths based on vehicle dynamics. J. Traffic Transp. Eng. 2018, 5, 361–371. [Google Scholar] [CrossRef]
- Garcia, C.E.; Prett, D.M.; Morari, M. Model predictive control: Theory and practice—A survey. Automatica 1989, 25, 335–348. [Google Scholar] [CrossRef]
- Lu, Y.; Arkun, Y. Quasi-Min-Max MPC algorithms for LPV systems. Automatica 2000, 36, 527–540. [Google Scholar] [CrossRef]
- MathWorks. Available online: www.mathworks.com (accessed on 1 August 2019).




| Type of Motion | Restrictions 1 | Initial Conditions |
|---|---|---|
| Parallel reverse parking | −40 ° ≤ θ ≤ 40 °; −2 m/s ≤ v ≤ 2 m/s; −34 °/s ≤ ωθ ≤ 34 °/s; −1 m/s2 ≤ a ≤ 1 m/s2 | Ts = 1 s; p = 14; q0 = (0, 0, 0, 0, 0)T; qf = (−7.65, −5, 0, 0, 0)T |
| Perpendicular reverse parking | −40 ° ≤ θ ≤ 40 °; −2 m/s ≤ v ≤ 2 m/s; −34 °/s ≤ ωθ ≤ 34 °/s; −1 m/s2 ≤ a ≤ 1 m/s2 | Ts = 0.5 s; p = 14; q0 = (0, 0, 0, 0, 0)T; qf = (−5.5, −6.8, π/2, 0, 0)T |
| Perpendicular forward parking | −40 ° ≤ θ ≤ 40 °; −2 m/s ≤ v ≤ 2 m/s; −34 °/s ≤ ωθ ≤ 34 °/s; −1 m/s2 ≤ a ≤ 1 m/s2 | Ts = 1 s; p = 16; q0 = (0, 0, 0, 0, 0)T; qf = (−5.5, −6.8, −π/2, 0, 0)T |
| Circular motion 2,3 | −40 ° ≤ θ ≤ 40 °; Rout = 10 m, H = 2.3 m; Rin = Rout – H; −28 °/s ≤ ωθ ≤ 28 °/s; 0.95·vdes m/s ≤ v ≤ 1.25·vdes m/s; −2 m/s2 ≤ a ≤ 2.5 m/s2 | Ts = 1 s; p = 16; βC0 = −π·7/9; βCf = π·5/6; q0 = (Rav·cos(βC0), Rav·sin(βC0), π/2 +βC0, arctan(2·L/Rav), vdes)T; qf = (Rav·cos(βCf), Rav·sin(βCf), π/2 +βCf, arctan(2·L/Rav), vdes)T |
| Type of Motion | Restrictions 1 | Initial Conditions |
|---|---|---|
| Perpendicular reverse parking | −40° ≤ θ ≤ 40°; −30° ≤ ζ ≤ 30; −2 m/s ≤ v ≤ 2 m/s; −6 °/s ≤ ωθ ≤ 6 °/s; −6 °/s ≤ ωζ ≤ 6 °/s; −0.7 m/s2 ≤ a ≤ 0.7 m/s2 | Ts = 3 s; p = 6; q0 = (0, 0, 0, 0, 0, 0)T; qf = (−18, −15, π/2, 0, 0, 0)T |
| Parking with changing position on the spot | −40° ≤ θ ≤ 40°; −30° ≤ ζ ≤ 30; −2 m/s ≤ v ≤ 2 m/s; −28 °/s ≤ ωθ ≤ 28 °/s; −28 °/s ≤ ωζ ≤ 28 °/s; −1.5 m/s2 ≤ a ≤ 1.5 m/s2 | Ts = 1 s; p = 18; q0 = (0, 0, 0, 0, 0, 0)T; qf = (0, 0, π/2, 0, 0, 0)T |
| Circular motion 2,3 | −40° ≤ θ ≤ 40°; −30°≤ ζ ≤ 30°; 0.95·vdes m/s ≤ v ≤ 1.25·vdes m/s; Rout = 15 m, H = 4.5 m; Rin = Rout – H; −28 °/s ≤ ωθ ≤ 28 °/s; −28 °/s ≤ ωζ ≤ 28 °/s; −2 m/s2 ≤ a ≤ 2.0 m/s2 | Ts = 1 s; p = 13; βC0 = −135°; βCf = 140°; q0 = (Rav·cos(βC0), Rav·sin(βC0), π/2 +βC0, arctan(2·L10/Rav), −arctan(2·l10/Rav), vdes)T; qf = (Rav·cos(βCf), Rav·sin(βCf), π/2 +βCf, arctan(2· L10/Rav), −arctan(2·l10/Rav), vdes)T |
| Type of Automated Vehicle (AV) | Type of Motion | Restrictions 1 | Initial Conditions |
|---|---|---|---|
| Conventional TSV | Docking (unconstrained space) | −90° ≤ ψ ≤ 90°; −45° ≤ θ ≤ 45°; −4 m/s ≤ v ≤ 4 m/s; −34 °/s ≤ ωθ ≤ 34 °/s; −2.0 m/s2 ≤ a ≤ 2.5 m/s2 | Ts = 1 s; p = 12; q0 = (0, 0, π/2, 0, 0, 0)T; qf = (−5, −35, π, 0, 0, 0)T |
| Circular Motion 2 | Inequality constraint of Equation (56); Rout = 15 m, H = 5 m; Rin = Rout – H; −40° ≤ ψ ≤ 40°; −45° ≤ θ ≤ 45°; 0.95·vdes m/s ≤ v ≤ 1.25·vdes m/s; −34 °/s ≤ ωθ ≤ 34 °/s; −0.5 m/s2 ≤ a ≤ 0.5 m/s2 | Ts = 1 s; p = 9; βC0 = −160°; βCf = 140°; q0 = (Rav·cos(βC0), Rav·sin(βC0), π/2 +βC0, π·11/60, arctan(2·L1/Rav), vdes)T; qf = (Rav·cos(βCf), Rav·sin(βCf), π/2+βCf, π·11/60, arctan(2·L1/Rav), vdes)T | |
| TSV-SSA | Docking (unconstrained space) | −90° ≤ ψ ≤ 90°; −40° ≤ θ ≤ 40°; −35° ≤ ζ ≤ 35°; −4 m/s ≤ v ≤ 4 m/s; −34 °/s ≤ ωθ ≤ 34 °/s; −34 °/s ≤ ωζ ≤ 34 °/s; −2.0 m/s2 ≤ a ≤ 2.5 m/s2 | Ts = 1 s; p = 12; q0 = (0, 0, π/2, 0, 0, 0, 0)T; qf = (−5, −35, π, 0, 0, 0, 0)T |
| Circular motion 3 | Inequality constraint of Equation (56); Rout = 15 m, H = 4 m; Rin = Rout – H; 30° ≤ ψ ≤ 35°; 15° ≤ θ ≤ 20°; −15° ≤ ζ ≤ −10°; 0.95·vdes m/s ≤ v ≤ 1.05·vdes m/s; −34 °/s ≤ ωθ ≤ 34 °/s; −28 °/s ≤ ωζ ≤ 28 °/s; −0.5 m/s2 ≤ a ≤ 0.5 m/s2 | Ts = 1 s; p = 9; βC0 = -100; βCf = 200°; q0 = (Rav·cos(βC0), Rav·sin(βC0), π/2 +βC0, π/6, arctan(2·L1/Rav), -arctan(2·L1/Rav), vdes)T; qf = (Rav·cos(βCf), Rav·sin(βCf), π/2 +βCf, π/6, arctan(2·L1/Rav), -arctan(2·L1/Rav), vdes)T |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diachuk, M.; Easa, S.M.; Bannis, J. Path and Control Planning for Autonomous Vehicles in Restricted Space and Low Speed. Infrastructures 2020, 5, 42. https://doi.org/10.3390/infrastructures5050042
Diachuk M, Easa SM, Bannis J. Path and Control Planning for Autonomous Vehicles in Restricted Space and Low Speed. Infrastructures. 2020; 5(5):42. https://doi.org/10.3390/infrastructures5050042
Chicago/Turabian StyleDiachuk, Maksym, Said M. Easa, and Joel Bannis. 2020. "Path and Control Planning for Autonomous Vehicles in Restricted Space and Low Speed" Infrastructures 5, no. 5: 42. https://doi.org/10.3390/infrastructures5050042
APA StyleDiachuk, M., Easa, S. M., & Bannis, J. (2020). Path and Control Planning for Autonomous Vehicles in Restricted Space and Low Speed. Infrastructures, 5(5), 42. https://doi.org/10.3390/infrastructures5050042