Numerical and Experimental Investigations of Asphalt Pavement Behaviour, Taking into Account Interface Bonding Conditions
Abstract
1. Introduction
2. Analytical Solution Background and Improvement
2.1. Analytical Solution Background
2.1.1. At the Surface, z = 0
2.1.2. Between the Layers i and i + 1, 0 < z < H
2.1.3. At the Lowest Layer, i = n, z ≥ H
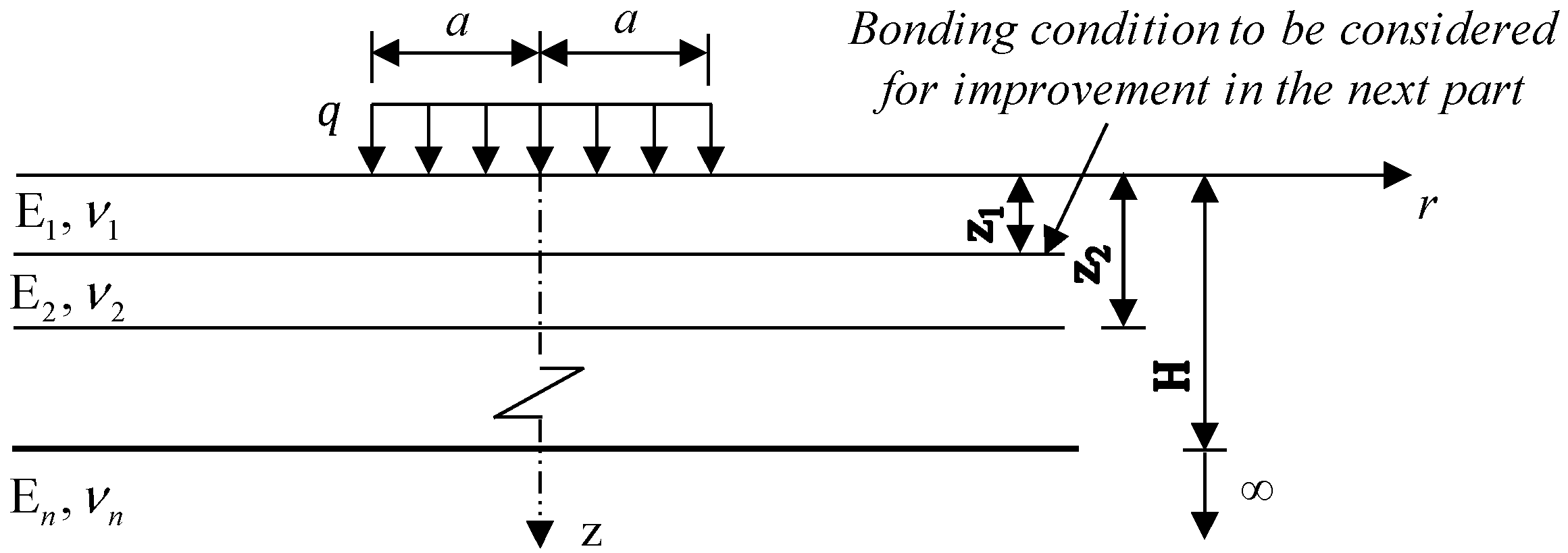
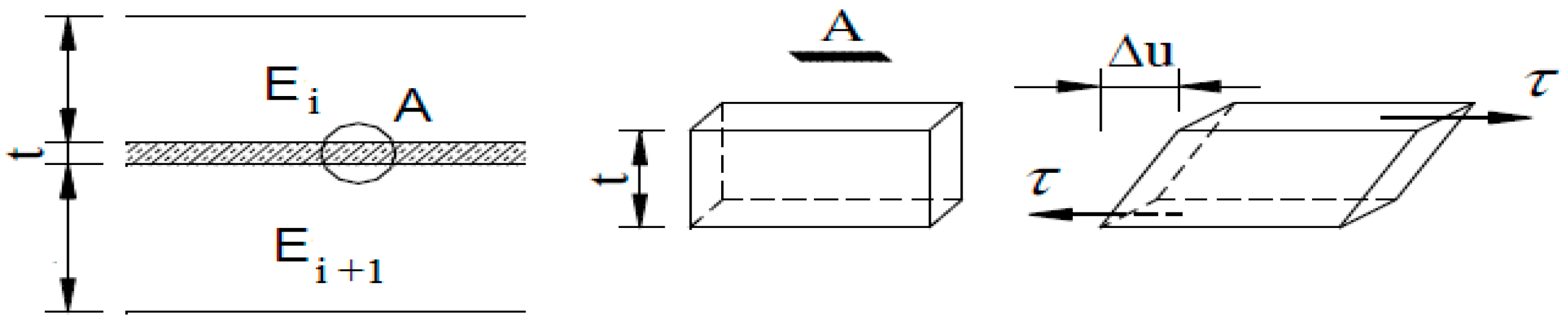
2.2. Improvement Taking into Account Actual Bonding Condition
2.3. Numerical Implementation and Backcalculation Principle
3. Sensitivity Analysis
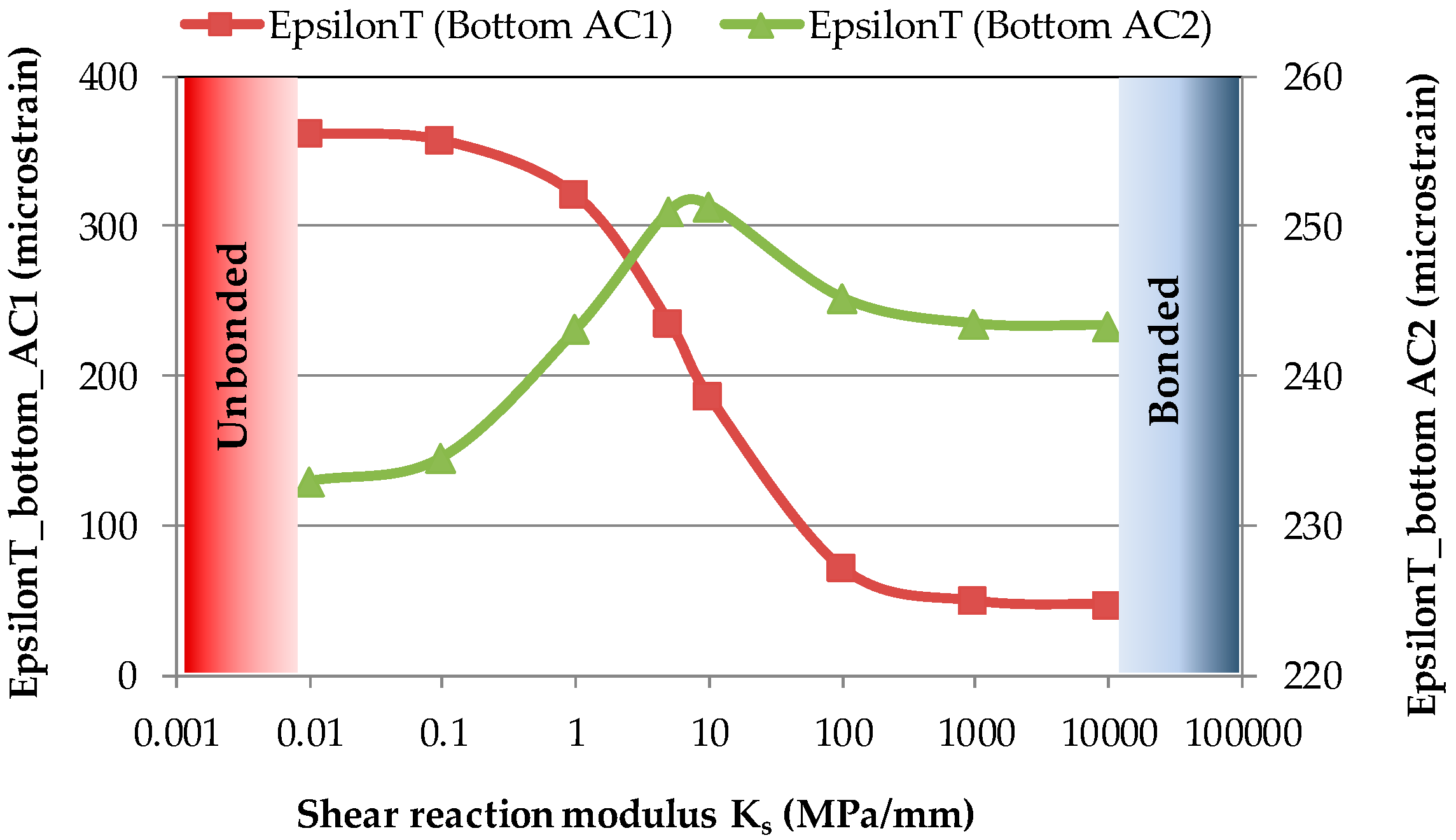
3.1. Strain Sensitivity to the Interface Bonding Conditions
- Ks ≤ 0.1 MPa/mm: Poor bond to unbonded.
- 0.1 MPa/mm < Ks < 100 MPa/mm: Partially bonded
- Ks ≥ 100 MPa/mm: Good bond to fully bonded.
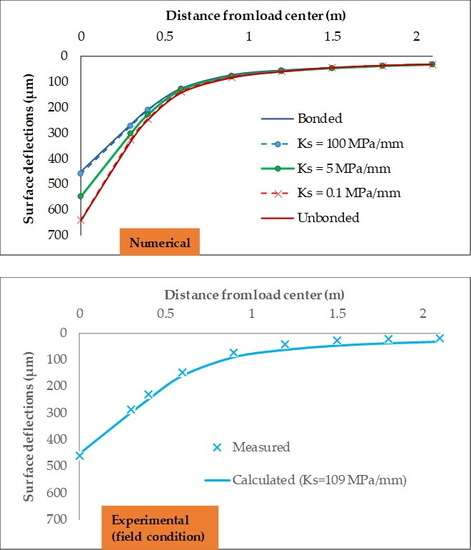
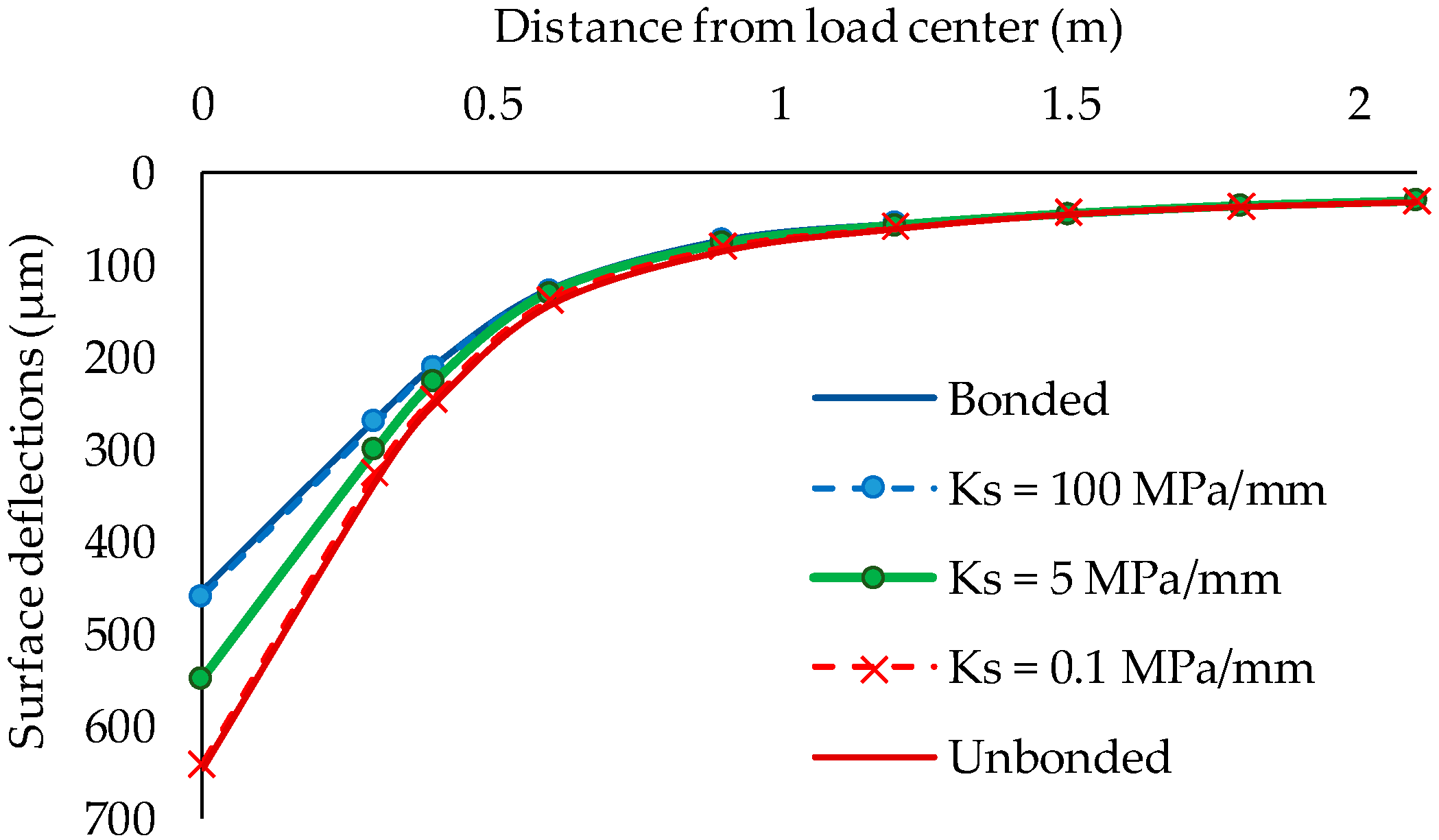
3.2. Deflection Sensitivity to the Interface Bonding Conditions
4. Evaluation of Pavement Interface Bonding Condition in an Experimental Case Study
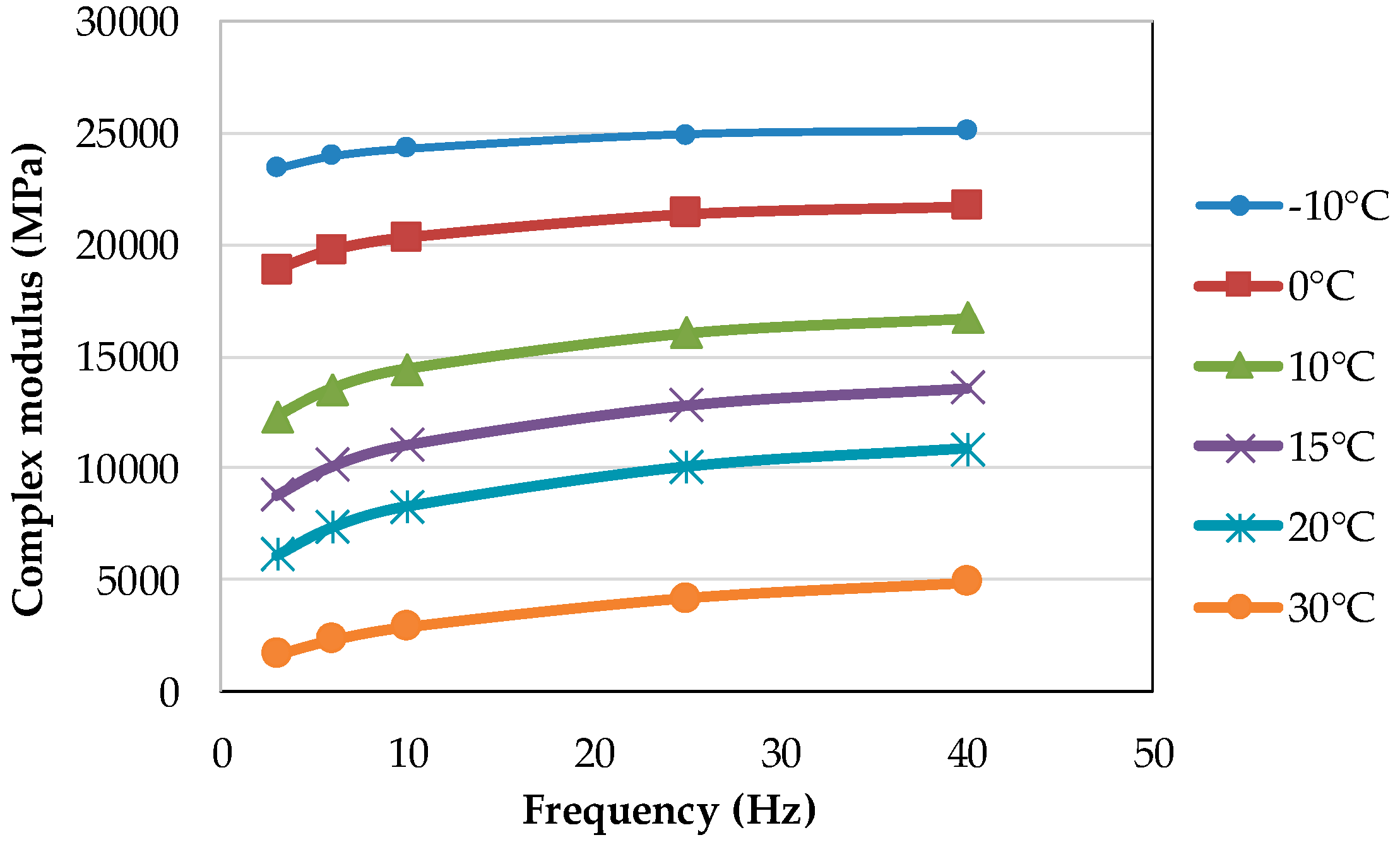
4.1. Pavement Structures and Materials Characteristics
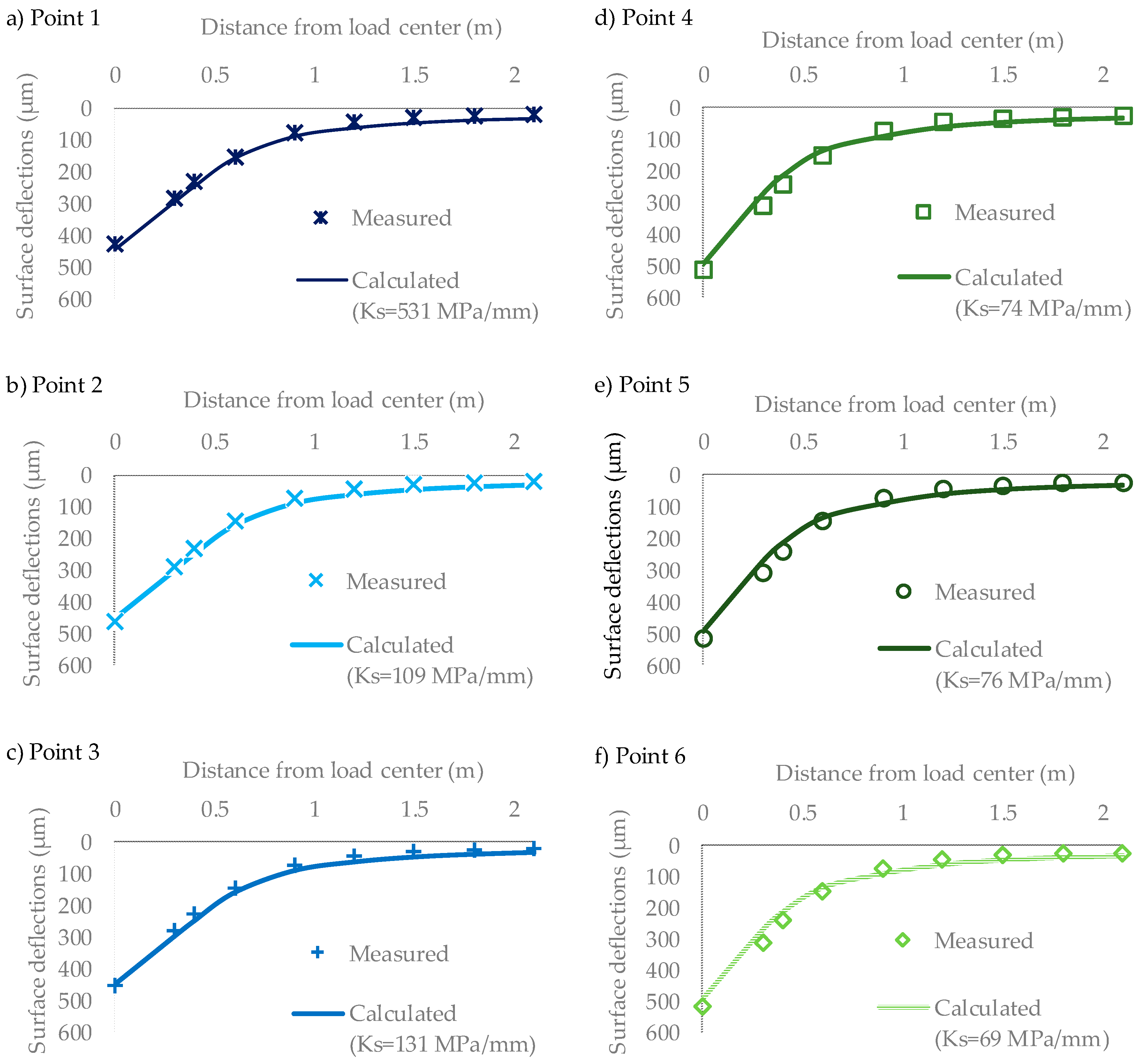
4.2. Evaluation of Bonding Condition at the Interface of the Asphalt Layers
5. Conclusions
- The numerical sensitivity analysis showed clearly the influence of interface bonding condition on pavement responses under the loading of an FWD. It allows classifying the interface bonding condition depending on the shear reaction modulus: poor bond to unbonded for Ks ≤ 0.1 MPa/mm; partially bonded for 0.1 MPa/mm < Ks < 100 MPa/mm; good bond to fully bonded for Ks ≥ 100 MPa/mm.
- In the experimental case study on two full-scale pavement structures, the presented original procedure made it possible to determine an actual value of Ks for each evaluated pavement position and to differentiate the interface bonding level of the two investigated pavement structures.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Burmister, D.M. The theory of stress and displacements in layered systems and applications to the design of airport runways. Highw. Res. Board Proc. 1943, 23, 126–144. [Google Scholar]
- Burmister, D.M. The general theory of stress and displacements in layered soil systems. I. J. Appl. Phys. 1945, 16, 89–94. [Google Scholar] [CrossRef]
- Burmister, D.M. The general theory of stress and displacements in layered soil systems. II. J. Appl. Phys. 1945, 16, 126–127. [Google Scholar] [CrossRef]
- Burmister, D.M. The general theory of stress and displacements in layered soil systems. III. J. Appl. Phys. 1945, 16, 296–302. [Google Scholar] [CrossRef]
- Huang, Y. Pavement Analysis and Design, 2nd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2003. [Google Scholar]
- Romanoschi, S.; Metcalf, J. Characterization of asphalt concrete layer interfaces. Transp. Res. Rec. J. Transp. Res. Board 2001, 1778, 132–139. [Google Scholar] [CrossRef]
- Zofka, A.; Maliszewski, M.; Bernier, A.; Josen, R.; Vaitkus, A.; Kleizienė, R. Advanced shear tester for evaluation of asphalt concrete under constant normal stiffness conditions. Road Mater. Pavement Des. 2015, 16 (Suppl. 1), 187–210. [Google Scholar] [CrossRef]
- Canestrari, F.; Ferrotti, G.; Parti, M.N.; Santagata, E. Advanced testing and characterization of interlayer shear resistance. Transp. Res. Rec. J. Transp. Res. Board 2005, 1929, 69–78. [Google Scholar] [CrossRef]
- Canestrari, F.; Ferrotti, G.; Lu, G.; Millien, A.; Partl, M.; Petit, C. Mechanical testing of interlayer bonding in asphalt pavements. In Advances in Interlaboratory Testing and Evaluation of Bituminous Materials; Partl, M., Bahia, H.U., Canestrari, F., de la Roche, C., Di Benedetto, H., Piber, H., Sybilski, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 303–360. [Google Scholar] [CrossRef]
- West, R.C.; Zhang, J.; Moore, J. Evaluation of Bond Strength between Pavement Layers; NCAT Report 05–08; National Center for Asphalt Technology: Auburn, AL, USA, 2005. [Google Scholar]
- Raab, C.; Partl, M.N.; Abd El Halim, A.O. Evaluation of interlayer shear bond devices for asphalt pavements. Balt. J. Road Bridge Eng. 2009, 4, 176–195. [Google Scholar] [CrossRef]
- Leutner, R. Untersuchung des Schichtenverbundes beim bituminösen Oberbau. Bitumen 1979, 41, 84–91. [Google Scholar]
- Destrée, A.; De Visscher, J. Impact of tack coat application conditions on the interlayer bond strength. Eur. J. Environ. Civ. Eng. 2017, 21, 3–13. [Google Scholar] [CrossRef]
- Petit, C.; Chabot, A.; Destree, A.; Raab, C. Recommendation of RILEM TC 241-MCD on Interface Debonding Testing in Pavements. Mater. Struct. 2018, 51, 96. [Google Scholar] [CrossRef]
- Diakhate, M.; Millien, A.; Petit, C.; Phelipot-Mardelé, A.; Pouteau, B. Experimental investigation of tack coat fatigue performance: Towards an improved lifetime assessment of pavement structure interfaces. Constr. Build. Mater. 2011, 25, 1123–1133. [Google Scholar] [CrossRef]
- Freire, R.; Di Benedetto, H.; Sauzéat, C.; Pouget, S.; Lesueur, D. Linear Viscoelastic Behaviour of Geogrids Interface within Bituminous Mixtures. KSCE J. Civ. Eng. 2018, 22, 2082–2088. [Google Scholar] [CrossRef]
- Kobisch, R.; Peyronne, C. L’ovalisation: Une nouvelle méthode de mesure des déformations élastiques des chaussées. Bull Liaison Lab Ponts Chauss 1979, 102, 59–71. [Google Scholar]
- Goacolou, H.; Keryell, P.; Kobisch, R.; Poilane, J.P. Utilisation de l’ovalisation en auscultation des chaussées. Bull Liaison Lab Ponts Chauss 1983, 128, 65–75. [Google Scholar]
- Alavi, S.; Lecates, J.F.; Tavares, M.P. Falling Weight Deflectometer Usage; The National Academies Press: Washington, DC, USA, 2007. [Google Scholar] [CrossRef][Green Version]
- Le, M.T.; Nguyen, Q.H.; Nguyen, M.L. Numerical analysis of double-layered asphalt pavement behaviour taking into account interface bonding conditions. In Proceedings of the CIGOS 2019-Innovation for Sustainable Infrastructure, Hanoi, Vietnam, 31 October–1 November 2019. [Google Scholar] [CrossRef]
- Goodman, R.E.; Taylor, R.L.; Brekke, T.L. A model for the Mechanics of Jointed Rocks. J. Soil Mech. Found. Div. 1968, 94, 637–659. [Google Scholar]
- The MathWorks. MATLAB and Statistics Toolbox Release 2012b; The MathWorks, Inc.: Natick, MA, USA, 2012. [Google Scholar]
- Le, V.P.; Lee, H.J.; Flores, J.M.; Kim, W.J.; Baek, J. New approach to construct master curve of damaged asphalt concrete based on falling weight deflectometer back-calculated moduli. J. Transp. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Nguyen, M.L.; Blanc, J.; Kerzreho, J.P.; Hornych, P. Review of glass fibre grid use for pavement reinforcement and APT experiments at IFSTTAR. Road Mater. Pavement Des. 2013, 14, 287–308. [Google Scholar] [CrossRef]
- Nguyen, N.L.; Dao, V.D.; Nguyen, M.L.; Pham, D.H. Investigation of Bond between Asphalt Layers in Flexible Pavement. In Proceedings of the 8th RILEM International Conference on Mechanisms of Cracking and Debonding in Pavements, Nantes, France, 7–9 June 2016. [Google Scholar] [CrossRef]
- RILEM TC 272-PIM. Available online: https://www.rilem.net/groupe/272-pim-phase-and-interphase-behaviour-of-bituminous-materials-359 (accessed on 15 January 2020).
| Layer | E (MPa) | Poisson’s Ratio | Nominal 1 Thickness (cm) | Actual 2 Thickness S-I (cm) | Actual 2 Thickness S-II (cm) | |
|---|---|---|---|---|---|---|
| 1 | Asphalt surface | 9000 | 0.35 | 6.5 | 6.6 | 6.3 |
| Interface | - | - | - | - | - | |
| 2 | Asphalt base | 9000 | 0.35 | 4.5 | 4.6 | 3.9 |
| 3 | Subgrade | 184 | 0.35 | 290 | 290 | 290 |
| 4 | Concrete raft | 55000 | 0.25 | - | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, M.-T.; Nguyen, Q.-H.; Nguyen, M.L. Numerical and Experimental Investigations of Asphalt Pavement Behaviour, Taking into Account Interface Bonding Conditions. Infrastructures 2020, 5, 21. https://doi.org/10.3390/infrastructures5020021
Le M-T, Nguyen Q-H, Nguyen ML. Numerical and Experimental Investigations of Asphalt Pavement Behaviour, Taking into Account Interface Bonding Conditions. Infrastructures. 2020; 5(2):21. https://doi.org/10.3390/infrastructures5020021
Chicago/Turabian StyleLe, Minh-Tu, Quang-Huy Nguyen, and Mai Lan Nguyen. 2020. "Numerical and Experimental Investigations of Asphalt Pavement Behaviour, Taking into Account Interface Bonding Conditions" Infrastructures 5, no. 2: 21. https://doi.org/10.3390/infrastructures5020021
APA StyleLe, M.-T., Nguyen, Q.-H., & Nguyen, M. L. (2020). Numerical and Experimental Investigations of Asphalt Pavement Behaviour, Taking into Account Interface Bonding Conditions. Infrastructures, 5(2), 21. https://doi.org/10.3390/infrastructures5020021