Abstract
Moisture susceptibility is still one of the primary causes of distress in flexible pavements, reducing the pavements’ durability. A very large number of tests are available to evaluate the susceptibility of a binder aggregate combination. Tests can be conducted on the asphalt mixture, either in a loose or compacted form, or on the individual components of an asphalt pavement. Apart from various mechanisms and models, fundamental concepts have been proposed to calculate the thermodynamic tendency of a binder aggregate combination to adhere and/or debond under wet conditions. The aim of this review is to summarize literature findings and conclusions, regarding these concepts as carried out in the CEDR project FunDBits. The applied test methods, the obtained results, and the validation or predictability of these fundamental approaches are discussed.
1. Introduction
Moisture in asphalt pavement structures can lead to phenomena such as stripping, raveling, and pothole formation, limiting the lifetime and durability of the pavement. Moisture sensitivity has been studied extensively in the literature, resulting in an enormous number of possible test procedures, which have been classified into various levels [1]. The first level consists of tests, conducted on the individual components, traditionally comprising of the binder, the aggregate, and possible additives. Nowadays this level will also include renewable, as well as secondary (waste) materials [2,3,4]. The next level includes tests conducted on loose asphalt mixture, while subsequent levels consider tests involving compacted asphalt mixtures, and finally compacted mixture in a pavement under field conditions. It is obvious that the number of parameters and the test complexity increase as tests move from the individual components to the pavement level.
Commonly, in the literature, the occurrence of moisture damage is divided into adhesive or cohesive failure. Adhesive failure being a loss of adhesion between the aggregate and the binder interface. This will result in clean aggregate surfaces after failure [5,6]. Cohesive failure occurs if moisture weakens the binder or mastic phase leading to a failure inside this binder or mastic film. In this case, the aggregates will still be covered with bitumen after failure. In addition to this, a third possibility has been identified where damage is caused by the fracture of aggregates, particularly when the mixture is subjected to freezing [5,7,8]. The actions by which damage occurs can be further divided into at least five different mechanisms, detachment, displacement, spontaneous emulsification, pore pressure, and hydraulic scour. An overview is given by Little et al. [9].
Moreover, also, various mechanisms have been proposed to explain adhesion between bitumen and aggregates [6,10]; including a chemical reaction [11], a thermodynamic approach based on surface energies [8], molecular orientation [12], molecular dynamics [13], and mechanical adhesion [14]. In asphalt pavements, moisture damage is most likely related to a combination of mechanisms, which depend on the pavement materials, the mix design, the traffic loading, and the climatic conditions. Due to this complexity, a large number of possible parameters have been identified, but it is not clear which of these are decisive and determine the behavior [15].
In the literature, two fundamental concepts have been proposed to calculate thermodynamic work of adhesion and debonding in the presence of moisture between a binder and an aggregate. The first one is the surface energy component concept which was first applied by Texas A&M researchers to bitumen and aggregates and who developed also the methodologies for the measurement of surface energies for bitumen, respectively aggregates [8]. Another concept is based on the Hamaker equation, which was developed for materials having only Lifshitz–Vander Waals interactions [16]. This concept has also been applied to bitumen aggregate adhesion.
The aim of this paper is to summarize literature findings and conclusions, regarding the test methods, results, and the validation or predictability of these fundamental approaches. The current paper is based on activities conducted for the Project FunDBitS (Functional Durability-related Bitumen Specification, CEDR Transnational Road Research programme Call 2013: Energy Efficiency—Materials and Technology) [17], updated with recent literature.
2. Concepts to Calculate the Bitumen–Aggregate Adhesion
2.1. Calculation of Adhesive Bond Strength and Debonding by Water from Surface Energy Components
Researchers at Texas A&M University have applied the methodology of measuring surface energy components as a base to calculate the adhesion of bitumen to an aggregate surface [8]. They also developed and evaluated the most suitable test methods to determine surface energy components for bitumen and for aggregates. In this concept, surface energy components of bitumen and aggregates are derived separately, and the data allow calculating the interfacial work of adhesion in dry, as well as in wet conditions. The concept is based on the Van Oss–Chaudhury–Good (VCG) theory of wettability and is very well explained in for example, [16,18,19,20,21,22,23].
The surface free energy (SFE) of a material is defined as the amount of work required to create a unit area of a new surface of that specific material in a vacuum [20,24,25,26]. This surface energy can be divided into different parts (Equation (1)); a first part, relating to Liftshitz–van der Waals interactions and referred to as γLW and a second part referring to asymmetrical polar interactions, described as acid–base interactions γAΒ or electron acceptor, respectively donor parts. The Lifshitz–van der Waals component of the surface energy comprises the following interactions: Keesom (dipole–dipole interactions), Debye (dipole-induced–dipole interactions), and London dispersion forces (induced dipole–induced dipole interactions). In literature, it was shown later that the LW part should only include the London dispersive interactions, while Keesom and Debye interactions should be included in the acid–base part [27]. In this paper, the notation LW part is kept, although it refers to the dispersive part only.
- γ—total surface energy;
- γLW—dispersive part of the surface energy;
- γAB—acid base part of the surface energy;
- γ+—Lewis acid component or electron acceptor of surface energy;
- γ−—Lewis base or electron donor component of surface energy.
The interaction of two materials in vacuum or the free energy change of adhesion (ΔG12) between two materials 1 and 2 can be formulated as a function of their respective surface energy components as shown in Equation (2). The free energy change is equal in magnitude but has the opposite sign as the work of adhesion, W12.
The subscripts 1 and 2 refer to the respective surface energy components of the two substances 1 and 2. Equation (2) shows that the interaction of two materials in vacuum is always negative, meaning there is always an attraction. Equation (2) cannot be zero since for all materials γLW is a finite and positive number. Based on Equation (2), it is possible to calculate the surface energy components for an unknown substance by measuring the surface energy of the unknown versus at least three probe compounds of known surface energy components. From these three liquids at least two need to have (known) polar parts. Different options are available to test this experimentally and they will be discussed briefly in the experimental part.
Once the surface components for bitumen and aggregates are determined, their interfacial work of adhesion, the dry bond strength, can be calculated using Equation (2), where the subscripts 1 and 2 refer to the two substances tested, in this case, aggregate and bitumen. If in this equation, material 1 and 2 would be the same substance it becomes equal to two times the surface energy of this material (2γ in Equation (1)). Therefore, twice the surface energy of bitumen is related to the cohesive strength or bond energy of bitumen. The cohesive bond energy of a material is defined as the amount of work required to fracture the material to create two new surfaces of a unit area each, in a vacuum. Numerically this is equal to twice the total surface free energy of the material (Equation (3)). A higher magnitude of cohesive bond energy implies that more energy is required for a crack to propagate due to fracture.
Finally, consider a three-phase system comprising of bitumen, aggregate, and water represented by material 1 and 2 in medium 3, respectively (Equation (4)). If the medium water displaces bitumen from the bitumen–aggregate interface several processes occur. The interface bitumen–aggregate is lost, and this is associated with external work, −γ12. At the same time, during this process, two new interfaces are created: between bitumen and water and between aggregate and water. The work needed for the formation of these two new interfaces is γ13 + γ23. Therefore, the total work needed for water to displace bitumen from the surface of the aggregate is γ13 + γ23 − γ12 (Equation (5)). In terms of free energy, the resulting free energy of adhesion of component 1 and 2 in medium 3 can be expressed using the same relations but with opposite signs.
In order to take both the LW and polar part into account, Equation 5 must be calculated as follows in Equation (6):
When ΔGa132 < 0 it indicates that there is an attraction between component 1 and 2 also when immersed in medium 3, and in this case, a displacement will not happen for a system in thermodynamic equilibrium. For ΔGa132 > 0 the interaction between 1 and 2 becomes repulsive. The magnitude of work of debonding can differ significantly depending on the surface energy components of bitumen and aggregates. Similarly, for describing the interaction between molecules or particles of material 1 suspended in liquid 3 one can write (Equation (7)). The latter is the driving force for phase separation of adhesives in aqueous media (Equation (8)). A large negative value would indicate a good resistance to debonding while a large positive value indicates easier stripping due to water, for systems in thermodynamic equilibrium. For practically all bitumen–aggregate systems the work of debonding W132 is negative or ΔGa132 is positive indicating that debonding in the presence of water is thermodynamically favorable.
If the polar surface free energy components of a hydrophobic material (or two similar hydrophobic materials) are negligibly small, then the most important parameter in Equation (7) is . This parameter represents the polar contribution to the cohesive energy of water. The value is −102 mJ/m2 and is present in all types of interactions when immersed in water. In fact, this term is the main contributor to the interfacial attractions between nonpolar materials immersed in an H-bonding material such as water.
Based on three parameters: the dry adhesion, the cohesive strength of bitumen, and the free energy of adhesion in the water, two related energy ratios have been proposed: ER1 and ER2 according to Equations (8) and (9), respectively. In literature, the ratio between the adhesive bond energy values in the dry condition and in the presence of water, ER1, can be used to predict the moisture sensitivity of asphalt mixtures [16]. Another ratio ER2 can be used; in this parameter the adhesive bond energy in the dry state is diminished with the bitumen cohesion, and this value is divided by the bitumen aggregate adhesion in the presence of water. In order to accommodate the effects of aggregate micro-texture on the bitumen–aggregate bond strength in the presence of moisture both bond parameters can also be multiplied by the specific surface area (SSA) of the aggregates. The procedure on how to calculate these parameters is very well described in the literature [9,19,20,28,29,30], but is it not fully clear which of these parameters is best suited to predict moisture damage. The term ΔGa12 in Equations (8) and (9) refers to the interfacial free energy of adhesion between bitumen and aggregate in a vacuum (or air), while ΔGa132 refers to the wet adhesion.
In the paper by Bhasin et al. [19], the free energy ratios calculated separately for the acid–base components, as shown in Equation (10), were used. The authors observed that the portion of the bond energy that results from the interaction of the acid component of asphalt and the base component of aggregate contributes the most to the total adhesive bond strength of the mixture [19]. Still, other combinations have been proposed by Hamedi and Moghadas Nejad [31].
In addition to the VCG method, other methods to calculate adhesion are also often used, such as for example, the Owens–Wendt (OW) method, also known as the Kaelble method. In the OW method, SFE is a sum of two components: a dispersive (D) and a polar (P) part, where the dispersive part reflects only dispersive interactions, and the polar part is a sum of polar, hydrogen, inductive, and acid–base interactions. In the OW method, a minimum of two known solvents or media are needed to calculate the SFE components.
2.2. Calculation of Adhesive Bond Strengths in Various Media Based on the Hamaker Equation
Researchers at KTH (Royal Institute of Technology in Stockholm, Sweden) have used the Hamaker equation to estimate the interaction of bitumen and aggregate/mineral components having air or water as an intervening medium [32]. The Hamaker equation is used to estimate the van der Waals interaction, including dispersive, Keesom, and Debye interactions. The Hamaker’s equation (Equation (11)) is composed of two parts: a first part describes the polar contribution and a second part—the dispersive contribution. In this Equation (11), subscripts 1 and 2 refer in this case to bitumen and aggregate while subscript 3 refers to the medium, either air or water. Calculations of Hamaker’s polar part require accurate dielectric data, in particular, dielectric constants and for the dispersive part the refractive index of the interacting materials and the intervening medium.
- εi—the static dielectric constant for material/medium I (in vacuum ε3 = 1);
- ni—the refractive index of the material/medium I, in the visible region (in vacuum n3 = 1);
- h—Planck’s constant (= 6.6261 × 10−34 Js);
- k—Boltzmann constant (= 1.3807 × 10−23 J/K);
- T—the absolute temperature;
- υ—the main electronic absorption frequency (typically ± 3 × 1015 s−1).
If Hamaker’s equation equals zero, there is no net force and the bodies are neither pulled together nor pushed apart. If the net force is positive then the bodies will adhere, if the net force is negative repulsion will occur. For most material combinations, the Hamaker equation is positive and the van der Waals force is attractive. The van der Waals force is always attractive between two surfaces of the same material and always attractive in a vacuum. The Hamaker’s equation can be negative and repulsive for two different material surfaces interacting through a liquid medium (A123). Relations between the Hamaker constant and the dispersive part of the surface energy have been proposed: For example, Israelachvili [33] has calculated the Hamaker constants of different liquids from their refractive indices and the surface tensions of these liquids using the following Equation (12):
- rii—the separation distance between interacting atoms or molecules;
- γLW—the dispersive part of the surface energy.
Israelachvili [33] found a very good agreement between the calculated surface tension of saturated hydrocarbons and the corresponding experimental values using Equation (12) and r = 0.2054 nm. However, this was not true for polar substances. Israelachvili [33] concluded that Equation (12) may not be used to calculate the surface free energies of highly polar liquids, where short-range forces other than dispersion forces (e.g., hydrogen bonds) are involved. Later, the value for r was corrected (by the same author) to a value of 0.165 nm.
3. Summary of Experimental Studies Based on SFE Approach
3.1. Overview of Test Procedures to Determine Surface Energies
An overview of experimental methods, as was observed in the literature survey, to determine SFE or SFE components of bitumen and aggregates is presented in Table 1. The calculation method, if applicable is indicated. In the Owens–Wendt (OW) concept, SFE is a sum of two components: a dispersion (D) and a polar (P) part, while in the Van Oss–Chaudhury–Good (VCG) theory, SFE is calculated based on three components; a disperse, an acid, and a base component. The most popular test methods include the Wilhemy plate test (WP) and the universal sorption device (USD) for respectively, bitumen and aggregates. Due to its simplicity and because it can be used for both bitumen and aggregates, the sessile drop test is also used a lot. These three tests are briefly explained in the next paragraphs.

Table 1.
Literature overview indicating the test methods used to determine surface energies of bitumen and aggregate.
The Wilhelmy plate method also referred to as plate method, was proposed by researchers from Texas A&M University to investigate bitumen [18,35]. Later, this test was applied by other researchers as referred to in Table 1. In this test, a thin bitumen coated glass plate is immersed or withdrawn from probe liquid at a slow and constant speed. The dynamic contact angles that develop between the bitumen film and the liquid are obtained, by comparing the weight of the sample slide in air to its weight in the liquid after correcting for buoyancy. The basic principle is schematically illustrated in Figure 1. The dynamic contact angle measured during the immersion process is called the advancing contact angle (a wetting process), while the dynamic contact angle measured during the withdrawal process is called the receding contact angle (a de-wetting process). Theoretically, for a surface that does not undergo any permanent change by meeting the probe liquid, the advancing and receding contact angles should be the same. However, in most cases, differences are observed [20] and they have been attributed to chemical and morphological heterogeneities of the surface, or also to roughness, swelling, rearrangement, inter-diffusion, and/or surface deformation. In the case of bitumen, it has been attributed to surface heterogeneities, and in bitumen, the advancing contact angles are used to determine surface energy components [20]. In the latter study, the effect of the choice of probe liquids on the precision of the SFE determination was investigated. In principle, for the OW method it would be enough to determine the contact angles with two known probe liquids and for VCG calculation with three probe liquids. However, if two or more of the probe liquids have similar surface free energy components, the calculated surface free energy components of bitumen will be very sensitive to small errors in the measurement of contact angles. It was advised by Texas A&M to use five probe liquids.
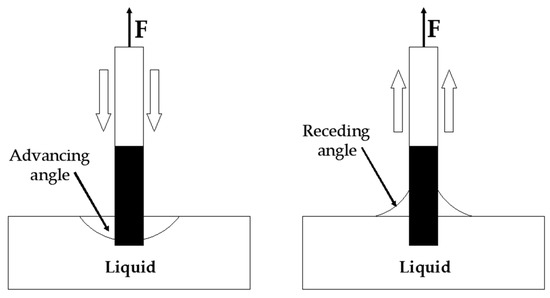
Figure 1.
Schematic illustration of Wilhelmy plate technique [35].
The sessile drop method is based on a direct measurement of the contact angle of a known liquid on the surface of the material being tested [18]. This approach is very well described in other references such as [52]. While the plate technique measures a dynamic contact angle in a quasi-equilibrium state, the sessile drop approach usually measures a static contact angle although it can also be used in a dynamic mode. As in the case of Wilhelmy plate method, the three unknown surface energy components of a solid under investigation can be calculated once the contact angles of at least three known liquids on this substrate are measured. In this test, a drop (about 2 to 3 mm in diameter) of a probe liquid is dispensed on a horizontal, flat surface of the material being tested (this can be a bitumen film or a flat stone surface), and the contact angle is measured. In Figure 2, different contact angles are shown as a function of the degree of wetting. For a complete wetting, the contact angle is zero, while for two materials that have no wetting the contact angle is 180 °C. In that case, the drop will roll on the surface. Instead of working with known probe liquids, it is also possible to use solid substrates with known surface energy characteristics and use sessile drop measurements to determine the SFE components of an unknown liquid.
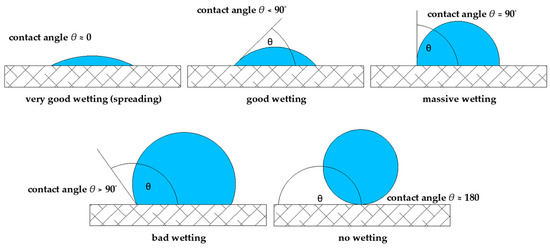
Figure 2.
Overview of contact angles as a function of the wetting behavior [52].
Bitumen and aggregate can be tested using this method. In both cases, the sample needs to be flat and smooth, and aggregates are very often polished. Therefore, the surface does not represent a natural crushed state. In addition, since each measurement is made using a single drop that covers only an area of about 2 to 3 mm in diameter, the application of this test on heterogeneous aggregate surfaces will require a lot of repeats on different locations, in order to get a reasonable average representative of the whole surface area. Additionally, it has also been reported that nonpolar liquids cannot be used on high-energy aggregates surfaces since complete wetting occurs, resulting in a zero-contact angle. The quality of the drop pictures is also very important as stated in [56]. A summary of possible errors related with this technique is provided by Rudawska et al. [62].
The universal sorption device (USD) is a gravimetric sorption technique, used to measure the sorption characteristics of selected vapors on aggregate surfaces. According to literature it can be used in a static or dynamic way. Again, the sorption tests need to be conducted with at least three vapors with known surface energy components in order to be able to calculate the three SFE components of an unknown aggregate. Sorption methods are particularly suitable since they can accommodate different sample sizes, irregular shapes, mineralogy’s, and surface textures associated with aggregates. In the method used by Texas A&M University, an aggregate fraction passing a 4.75 mm sieve and retained on a 2.36 mm sieve is tested. The chamber, including the suspended aggregate fraction, is vacuumed and the solute is injected into the system. A highly sensitive magnetic suspension balance is used to measure the amount of solute adsorbed on the surface of the aggregate at predetermined increasing levels of relative pressure. Little and Bhasin [20] noted that the specific surface area (SSA) of the aggregates is a required input to be able to compute SFE components. The methodology of using the universal sorption device is applicable only when the probe vapor molecules are adsorbed due to physical adsorption and not chemisorption [20]. Experiments by Texas A&M University have confirmed that the adsorption of the selected probe vapors on typical aggregate surfaces such as granite, limestone, and gravel is mostly due to physical adsorption. However, if aggregates are coated with chemically active materials and are used for testing, it must be ensured that the probe vapors do not react with the coating. Little and Bhasin [20] also show that clean aggregates are needed and physically adsorbed impurities such as water vapor, etc., need to be removed, as they will influence the SFE components. Water molecules and other impurities when adsorbed to the clean aggregate surface will lower its surface energy.
3.1.1. SFE Measurement Results on Bituminous Binders
In Table 2, values obtained for surface energy measurements on unmodified bitumen are shown. All these data are based on the Wilhelmy plate method combined with the VCG calculation procedure. Only data on unmodified binders are summarized, and the data are first grouped by the laboratory where they have been tested, and secondly by the reported publication date.

Table 2.
Overview of typical values of surface energies for unmodified bituminous binders, using the Wilhelmy plate test.
There seems to be a good agreement in the total surface energy levels found, although the levels found by Bahramian [39], and Zhang et al. [22] are slightly higher. Bahramian [39] also showed in his project slightly higher levels in the polar parts as compared to other references. In general, for bituminous binders, the polar parts are much smaller compared to the dispersive parts.
Standard deviations on the surface energy components have been reported for example in [18] and [39]. These standard deviations are small compared to the measured levels for the total and dispersive parts, but they are large for polar, acid, and base parts, indicating that these parts cannot be measured very accurately. Especially the small acid and base parts have sometimes very large standard deviations. In the paper by Luo et al. [42], the obtained levels are lower as compared to the other references because these authors added a correction to the Wilhelmy plate method. This correction takes into account the slight curvature of the liquid surface next to the plate. For some of the samples, this correction resulted in a change of more than 10% in the cohesive energy components.
Comparisons of different tests methods, using the same sample set, were reported in [18,20,32,35,39]. For example, for the comparison between the sessile drop method and the Wilhelmy plate tests, Little and Bhasin [20] reported that both test methods produce results for the LW component with adequate precision. There was a trend between LW parts of both methods (R2 = 0.59), but sessile drop measurements systematically resulted in larger dispersive parts, attributed to differences in the test methodologies. Differences were also reported in the acid components; a larger value was obtained using the Wilhelmy plate method. In the paper by Bahramian [39], a similar comparison was conducted, in this case, almost no differences were observed between both methods.
In the paper by Hirsch and Friemel-Göttlich [53], sessile drop measurements of probe liquids on a bitumen surface were used to determine SFE components of bitumen (OW calculation), in this study the author reported that especially for soft binders, very small polar components were obtained. This was related to separation effects at the bitumen surface. Normally bitumen is heated, covered on a glass plate, and afterward allowed to cool to room temperature. During this cooling, the surface will optimize its surface energy by selectively placing compounds with small surface energy at the surface. Especially, the accumulation of smaller more mobile paraffin at the surface can reduce the surface energy. The authors in [53] could avoid this phenomenon by using a freshly microtome-cut bitumen surface instead of an air-cooled surface. Unfortunately, in the paper the comparison of both surfaces is not included, only measured data on microtome-cut surfaces are reported. These indicate rather larger polar SFE components as compared to other references. The author also expected these effects in polymer modified binders.
Interesting results were also obtained by Khan et al. [54], he used the sessile drop method to determine the three SFE components. Additionally, for three binders, he compared several preparation methods of the bitumen surfaces. In method A, he first mixed the additives with the binders, this was either an adhesion improver or an emulsifier, and used the standard method to prepare a sample. This is heating a binder, preparing a hot surface, and leaving it in air to cool down. In addition to this, in method B, he prepared bitumen surfaces without additives in the standard way, and placed these surfaces underwater, in which the additives were mixed. After removing this surface from the water, the SFE components were determined. The data clearly showed that the effect of a surfactant or an emulsifier was only observed in method B. Only those surfaces that had been into contact with the water, had developed a clear polar part in their surface energy components.
The effects of testing time and temperature on SFE component determination is discussed in the papers [35,52,53,56]. A linear decrease in total surface energy with temperature has been reported, and all binders seem to vary in a very similar way, for 30 °C increase, the total surface energy decreases between 2 and 2.5 mN/m2.
In many studies, different bituminous binders show differences in the total and dispersive parts of the surface energy and also small differences in acid or base parts as reported in the papers [18,20,35]. However, at this moment, it is not clear how these differences relate to other bitumen parameters, and/or to the bitumen chemistry. Korn [52] has reported that paraffinic binders have larger total surface energies compared to naphthenic bitumen, but paraffinic binders have a lower polar part. In the papers [53,57] only very little variation was observed in the total surface energies of various commercial binders, while in the paper [53], it was noted that more differences could be observed when comparing polar and dispersive parts, but the author also indicated that the errors bars on these parts are rather large. The influences of bitumen modification, antistrip additives and ageing on the surface energy, and its components are summarized in Table 3. In conclusion, it seems that the effect of additives such as antistrip agents is very hard to detect in SFE measurements. Moreover, polymer or wax modification does not result in large changes, and for aging different trends are reported.

Table 3.
Overview of effect of bitumen type and bitumen modification including use of additives on surface energy and SFE components.
3.1.2. SFE Measurement Results on Aggregates
Aggregates consist of an assemblage of one or more minerals, while minerals have a definite chemical composition and an ordered atomic arrangement as described in [18]. Consequently, it is expected that the surface of aggregates is rather heterogeneous. In the papers [52,53,63], aggregate types are divided into acid and basic types; acid aggregates consist mainly of quartz (silica dioxide or SiO2) and are generally considered as water sensitive aggregates. The reason is that SiO2 can form strong hydrogen bonds with water resulting in strong interactions. The author also reports that on these surfaces even after heating it is very likely that a monomolecular layer of water will remain. On the other hand, basic aggregates consist mainly of calcite and are considered as good adhering aggregates. Therefore, in general terms, bad adhering aggregates may include quartz, quartzite, hornblende, biotite, orthoclase, while good adhering aggregates comprise, e.g., basalt, augite, and olivine. Hirsch and Friemel-Göttlich [53] note that the chemical components at the stone surface with a high affinity for bitumen are in general elements such as Al, Fe, Mg, and Ca, while elements with a low affinity are Na and K. The reason given is that Ca2+ and Mg2+ ions form water-insoluble salts, while K+ and Na+ form water-soluble salts, with a negative effect on the bitumen stone adhesion. A similar observation was in [64], where it was shown that alkali feldspars induced a weak interface with bitumen. Lyne et al. [65,66] has given a literature overview on the effect of specific elements on the moisture sensitivity of bitumen—aggregate adhesion. Minerals containing alkali metals are prone to stripping and iron compounds are considered beneficial. Magnesium and calcium are also considered advantageous. The total picture of the effect of aluminum and silica is less clear. Hefer [18] has noted that carbonates may result in weak boundaries if the pH of the water drops below 6, since then, the carbonates may dissolve leading to failure.
Surface energy measurements on aggregates indicate much more variation between the surface energy components compared to the values observed for various bituminous binders. Little and Bhasin [20] have reported that the total surface energy is typically in the range of 50 up to 400 mJ/m2 for aggregates. The magnitude of the LW component is smaller (30 to 60 mJ/m2) compared to the magnitude of the base component (200 to 1000 mJ/m2). Most aggregates have a small magnitude of the acid component ranging from 0 up to100 mJ/m2, so the total polar part of the surface energy is not necessarily high and can still be small depending on the acid component. Hirsch and Friemel-Göttlich [52] noted that differences in the total surface energy and the distribution between dispersive and polar parts can be larger between aggregates belonging to the same class of aggregates compared to aggregates belonging to different classes. In the particular case in [53], when two quartzite aggregate types showed larger differences than what is observed between quartzite and granite types.
In the collected papers, large variations between aggregates were observed, even for aggregates that differ only slightly in their mineralogical composition. For example, in the papers [26,41], two limestone type of aggregates, consisting both for 96% of the mineral calcite, still showed a very large difference between the surface energy components. Regarding standard deviations, these are reported, for example, by Bhasin [28] and they are low compared to the measured values, except if an SFE component is very small.
Different test methods are available and have been used to evaluate the SFE of aggregates. From a comparison of different methods, the following conclusions were obtained:
- Inverse gas chromatography is not very successful for aggregates as stated by Hefer [18] as the retention time measured may correspond to only the high-energy functional groups present on the surface of the material and not to an average value as reported in the papers [20,28];
- The use of contact angle methods such as the sessile drop method are limited as they require a flat stone surface; and a large number of repeats are needed [53];
- Static and dynamic vapor sorption measurements are very suited for aggregates with irregular shapes as concluded in the papers [34,35];
- Atomic force microscopy (AFM) also requires a very flat surface and moreover, only a very small area is scanned at a given time as reported in the papers [34,35];
- Micro calorimetry characterizes only the enthalpy change and could only be used if entropy would turn out to be negligible as stated in the papers [34,35].
In several references the effects of polishing have been discussed. Hirsch and Friemel-Göttlich [53] have investigated the surface roughness after polishing and concluded that even after polishing differences in surface flatness still exists between different aggregates. In this case, slight variations in the surface hardness could, after polishing result in very small imperfections on the surface. The researchers tried to avoid the influence of surface irregularities by using the same sample preparation for all the aggregates, and by performing a larger number of contact angle measurements on different locations on the stone surface. The author also investigated the difference between cutting, scrubbing and polishing, when measuring contact angles with water. The polished stones gave the lowest contact angles. The author concluded that irregularities, which may be larger after cutting and scrubbing, hinder the wetting of liquids on the surface. This study also compared static and dynamic contact angles between probe liquids on stone surfaces. For some surface types differences between both contact angles were seen, while for others these were very similar. If differences were observed these could be attributed to the surface roughness. In this study, the author decided to determine the SFE components of the aggregates (polar and dispersive only) using dynamic contact angles. There is still a lot of discussion on the validity of methods that measure liquid contact angles for solids which are not easily prepared into a flat plane as stated by Miller [58].
In some references, the effect of using “freshly-cut” or “aged” aggregates is discussed. Korn [52] noted that after crushing, there is a reorganization of polar substances at the surface, and by adsorption of substances from the air (water molecules and dust) the surface energy of the aggregate decreases until after a few months a stable situation has been installed. Schellenberger [67] noted that freshly cut aggregates have a worse moisture sensitivity behavior compared to aggregates that have been stored for some time. Hefer [18] noted that possible reactions at the stone surface when water is absorbed are presented. Little and Bhasin [20] noted that for two aggregate types no differences due to aggregate storage could be observed. This was explained by the fact that crushed aggregates may within a few seconds after crushing accumulate surface contamination from the environment.
Miller et al. [58,59] evaluated the possibility to catalogue mineral properties, with the aim to relate the mineralogy to the surface energy components and also to check if it is possible to assign surface energy values to aggregates coming from a specific quarry. This last objective can only be possible if the surface energies of aggregates are not dependent upon the moment and at which point in the quarry they are taken. This last condition was however not met. Additionally, a simple relation between mineralogical composition and surface energy could not be developed because it was not always possible to draw clear correlations between surface chemistry and surface energy. The reasons for this observation are not so clear. Hirsch and Friemel-Göttlich [53] reported that determining the chemical and functional groups as active sites is useful to understand interfacial reactions but does not explain the magnitude or strength of these sites. Additionally, measured values of organic and inorganic coatings seemed to play an important role and also the influence of varying surface roughness was unclear.
Regarding aggregate modifications, in the paper by Arabani et al. [21] the influence of a polyethylene (PE) precoating of three types of aggregates was evaluated. The data clearly show that PE treatment decreases the polar components of the aggregates and increases the dispersive part. However, the base component was for all aggregates higher after modification. There was no explanation for this last observation. In the literature, numerous papers have evaluated the effect of hydrated lime. In the papers [18,53], it was postulated that hydrated lime ties up carboxylic acids and 2-quinolones in the bitumen, with the formation of insoluble calcium organic salts, which prevent these functionalities from reacting with a siliceous surface to form water-sensitive bonds. This leaves important active sites on the siliceous surface to form strong water-resistant bonds with nitrogen groups in bitumen (amines) resulting in a reduction of the water sensitivity of asphalt mixtures. In the paper by Moghadas Nejad et al. [40] the SFE components of the aggregates with and without hydrate lime treatment were determined, and the authors showed that hydrated lime treatment reduces the acid SFE and increases the base SFE of the two types of aggregates. However, Little and Bhasin [20] reported that the methodology of using the universal sorption device is applicable only when the probe vapor molecules are adsorbed due to physical adsorption and not due to chemisorption. It is unclear if this condition is met in the case of hydrated lime.
3.1.3. Dry and Wet Adhesion
Once the SFE components of bitumen and aggregate are determined, the dry and wet bond strengths can be calculated. In literature, normally dry bond strengths are positive and wet bond strengths become negative as stated by Hefer [18] indicating an attraction between bitumen and aggregate when dry that becomes a repulsion when wet. Miller et al. [59] investigated a large range of minerals and for some of these, free energies of adhesion between bitumen and these minerals were still negative even in the presence of water. These were typically minerals with a low acid and a low base component. Therefore, the latter minerals do not have a thermodynamically drive for an adhesive debonding. The fact that this was not observed for any of the aggregates studied was explained by the fact that aggregates are combinations of different minerals, resulting in average values. Grenfell et al. [26] reported that a limestone aggregate, which had small acid and base components, also showed a negative free energy of adhesion with bitumen. A similar observation was made by Porot et al. [61]. In this case, all investigated aggregates showed negative free energies of adhesion in the presence of water, which may also be related to difficulties in the exact determination of acid and base components.
3.2. Sessile Drop Measurements in Dry and Wet Conditions
In some studies [49,52,53,56,57,67,68,69,70], the bitumen–aggregate affinity is derived from contact angle measurements, between bitumen drops in direct contact with a (flat) aggregate surface. In such tests, surface energy components are not determined, however, later tests allow a direct measurement of bitumen–aggregate interaction, which can be measured both in air, as well as in water. Therefore, a short summary of these types of tests is included.
Korn [52] has developed a procedure to measure contact angles of bitumen drops on substrates in air and in water. In this proposal, the temperatures for wetting and respectively, de-wetting by water are determined by the bitumen softening points. In the first step, a procedure to bring equally sized drops of bitumen on a substrate is described. For this purpose, the bitumen was heated, in this case, up to 150 °C, while the substrate was kept at room temperature. Several drops of bitumen were placed on the substrate using a needle. Afterwards, the covered substrates were heated to a temperature, 25 to 30 °C above the softening point. The contact angle data of bitumen to the substrate in air were recorded after 10 min at 70 °C. Subsequently, the substrate with the wetted bitumen drop was placed underwater at a temperature which is 5 °C below the R&B softening point, in this example at 40 °C. The drop contact angle was measured again after 2 h of storage underwater. The difference in contact angle before and after water storage is then calculated. Threshold values for the change after 2 h respectively 24 h water storage have been set and used as a measure of the resistance to stripping.
Several references have applied this type of tests as described in the papers [52,56,68], while Schellenberger [66] is using a similar approach, measuring contact angle underwater while adapting slightly the procedure. Korn [52] observed clear differences between stone types and between various bitumen types, especially in case of bitumen modified with antistrip additives, waxes, or polymers. However, it should be noted that for polymer and wax modified bitumen the wetting temperatures needed to be considerably higher, because of the increased viscosity. The authors also noted that differences in surface texture influenced the contact angles, and finally, that there is no relation between the total surface energy of a binder and the wetting of this binder on a particular stone.
Schellenberger [67] mentioned that the procedure was adapted, and, in this test, all unmodified binders gave rather low contact angles, so a good wetting was not achieved. The test could clearly show the effect of additives, which was also aggregate type dependent. Furthermore, the author noted that this test cannot be used to investigate PmB’s, as it does not allow preparing small drops when the bitumen is polymer modified. In the paper, the effect of additives was confirmed in rolling bottle tests and in boiling water tests. Nehrings [68] used the same procedure as Korn [52] to evaluate the effect of adhesion improvers, however, no effect was observed when measuring contact angles in the dry situation, only the water conditioning step allowed to distinguish the binders. Wistuba [56] conducted very similar tests as Korn [52], the authors report the need for minimum standards for image quality, in order to improve the repeatability and reproducibility of the test method.
In the papers [49,52,57,69,70], contact angles were only evaluated in the dry situation. Some studies described in the papers [49,53,69] indicate that effects of additives such as adhesion promotors can be observed even when testing dry contact angles, while other papers [57,70] indicate that these tests cannot differentiate binders with and without adhesion promotors.
In summary, it seems that contact angle measurements in the dry and wet state may be a successful way to estimate the water sensitivity. However, at this moment the validation is mainly limited to comparing binders with and without adhesion improvers, or other modifications. There are still a lot of open questions with regard to this test such as: should binders be compared at an equal viscosity state or at an equal temperature, what is the effect of using a polished or a flat aggregate surface and what about the accuracy, how large is the effect of a minor unevenness or a scratch on the spreading of bitumen drops.
3.3. Correlations between SFE Measurements and Water Sensitivity Observations
3.3.1. Correlations between Calculated Bond Strengths and Laboratory Tests Indicative of Moisture Damage
Table 4, is a selection of research papers, investigating the validation of surface energy predictions based on laboratory tests. The number of test samples from each study, as well as the water conditioning and test procedures are included in Table 4, while the findings are summarized in the next paragraphs.

Table 4.
Overview of papers investigating relations between laboratory tests and predicted performance based on surface energy calculations (the findings are summarized in the text).
Apeagyei et al. [71] evaluated six combinations and determined compressive strength ratios, between wet and dry conditioned tests. In this paper, possible correlations between predicted and tested ratios were not presented. Instead, from the surface energies of binder and aggregate, and from the measured compressive strength ratios, a new parameter, the percentage of the surface area of aggregate exposed to water was calculated. According to the authors, this percentage is a significant index to quantify the level of adhesive fracture. In this study, the water conditioning took place prior to testing the asphalt mixture samples, but the authors concluded that the introduction of moisture in either a liquid or vapor state during cyclic loading may well be more damaging than simply moisture conditioning an asphalt concrete sample prior to testing. The authors also noted a filler effect: This essentially occurs when a filler is intimately mixed or dispersed with the binder. In fact, hydrated lime intimately mixed with the bitumen may provide a filler effect that not only stiffens the mixture at high temperatures but also provides a toughening effect that leads to increased fatigue life and increased low-temperature fracture resistance.
In the papers [20,28,30], 12 binder–aggregate combinations were investigated, the authors came to the following conclusions: the SSA, the specific surface are of the aggregates, is a parameter that should be added to the surface energy parameters to predict the moisture sensitivity. When including SSA, correlations improved, and residual errors decreased. Moreover, in general, the correlation between the SFE parameters and the ratio of dry versus wet fatigue life was better than the correlation with the ratio of dynamic modulus in tension. The best correlations of 0.84, 0.83 were obtained between the fatigue ratio (wet/dry) versus log (ER1*SSA) and versus log (ER2*SSA), respectively.
Howson et al. [24] investigated six binder–aggregate combinations, based on uniaxial pull-off tests using a DSR. For each test, the total work of fracture was derived. The latter was higher for limestone as compared to andesite (for each binder and at each conditioning level). The change in the total work of fracture compared to the dry sample was calculated (in limestone this tended to increase with conditioning time, in andesite this tended to decrease). The average of this change related well to the values given by the energy parameter (ER2), R2 = 0.89. A lot more conclusions were obtained in this paper: for example, the authors noted an effect of the aggregate type, even if the failure was purely cohesive. They also noted changes in the patterns of (cohesively) fractured surfaces after water conditioning, and proposed a mechanism based on an increased ability of the binders to flow, as well as cavitation and fibril formation due to the action of water. The authors also noted that an increase in film thickness resulted in increases in total work of fracture, as it allowed more energy to be dissipated in the bulk of the viscoelastic asphalt binder.
Hirsch and Friemel-Göttlich [53] compared surface energies and rolling bottle tests on 25 binder–aggregate. Two criteria for the assessment were used; stone coverage should be larger if γ stone is large and γ binder is low. Additionally, the bond between aggregate and binder is stronger if the distribution of polar to dispersive parts is more equal. In this study, these assumptions could not be confirmed, and no correlations were obtained. The reasons for this are not clear but the fact that SSA was not included in the predictions was stated as a reason, a second reason could be related to the possibility that the binder forms a good adhering, but brittle film which could break during the rolling bottle test; or a strong cohesive binder film is formed, which is not well adhering, but not breaking during rolling action.
Arabani et al. [21] used three aggregate–binder combinations and each aggregate was tested in three states; without treatment, after coating it with low density poly(ethylene), and again after coating with high density poly(ethylene). Therefore, in fact, a total of nine combinations was tested. Unfortunately, in the paper no direct comparison of bond strength ratios to predicted levels based on the surface energies was shown. Clear effects of the coating with polyethylene were observed and discussed.
Wasiuddin [55] compared results of a modified pull-off test (PATTI) to SFE free energy calculations for several aggregate binder combinations and binders modified with sasobit and liquid anti strip. The results did not correlate well. In this study, a new moisture conditioning procedure was proposed, able to produce adhesive failure which can be quantified by the modified pull-off test. For this purpose, plain glass plates, coated with bitumen, were placed overnight in an oven at 64 °C in submerged condition. This conditioning resulted in most cases in an adhesive failure, but for some of the modified samples the failure was still either a mixed-mode (between cohesive and adhesive failure) or a fully cohesive failure. The authors also noted that in the submerged condition, water can develop randomly distributed, micro and macro scale cylindrical holes in the bitumen film. These holes penetrate up to the asphalt–substrate interface and start replacing asphalt film from the substrate surface, causing adhesive failure or stripping. Maybe this observation is related to the high temperature of 64 °C, at which sample conditioning took place.
Liu et al. [41] tested three limestone types and three granite types of aggregates with various binders. Differences in moisture sensitivity of the mixtures were observed based on the test method used: the boiling water test (BWT) and the rolling bottle test (RBT) were the most discriminative tests while the static immersion and the ultrasonic test were the least sensitive. The results for the total water immersion test had mixed success. The BWT and RBT ranked limestone combinations better compared to the granite combinations. The correspondence between SFE calculated and measured water-sensitivity was partially correct, the mixtures that performed worst or best in RBT and BWT were identified. Furthermore, the authors concluded that the magnitude of the work of debonding in the presence of water was found to be aggregate type dependent which suggests that the physicochemical properties of aggregates may play a more significant role in the generation of moisture damage, than bitumen properties.
Grenfell et al. [26] evaluated two aggregates, limestone and granite, using three binders. In this study the rolling bottle tests were well predicted by SFE calculations. All four aggregate–bitumen bond energy parameters (ER1, ER2, ER1*SSA, and ER2*SSA) could be used to predict moisture sensitivity of asphalt mixtures. Threshold values of (0.75 for ER1, 0.50 for ER2, 0.50 for ER1*SSA, and 0.35 for ER2*SSA) were defined to separate ‘good’ from ‘poor’ moisture damage performing aggregate–bitumen combinations. The authors concluded that surface energy properties of the materials combined with the parameters obtained by conventional moisture sensitivity assessment techniques can contribute towards the development of a material screening protocol for determining the best combinations of bitumen and aggregates for the local road material providing better bitumen–aggregate adhesion and less susceptibility to moisture damage/stripping.
Apeagyei et al. [71] followed the indirect stiffness versus conditioning time; generally, stiffness decreased with conditioning time (and consequently water content) except at low exposure times where low water content was associated with a slight but repeatable increase in stiffness. In this paper, the reversibility of moisture damage was investigated, this is the stiffness degradation in wet specimens being fully recovered upon specimen drying. The effect of moisture exposure on durability was found to be reversible as moisture conditioned asphalt mixtures that had lost up to 80% of the initial stiffness upon drying fully recovered. This was associated with a plasticization process, softening the bulk mastic, and moving the critical stress concentration location from the interfacial region of the aggregate-mastic bond into the bulk mastic. Micro-CT scans of the asphalt mixtures internal structure suggest moisture diffusion was mainly restricted to the bulk mastic and not the aggregate–mastic interface. The results suggest that cohesive rather than adhesive failure dominate the durability of asphalt mixtures under the long-term moisture exposure used in this study. In another paper by Apeagyei et al. [15] the worse moisture resistance of the granite mastics compared with the limestone mastic bonds could be explained, in part, by the dominant mineral phases in the granite. The three dominant minerals in granite, namely albite, feldspar, and quartz have been associated with poor adhesion and interfacial failure. A good correlation was found between the thermodynamic work of adhesion and debonding, and the practical work of adhesion of the aggregate–mastic bonds. This suggests that physical adsorption controls the moisture damage in aggregate–mastic bonds. In this paper the authors also noted an increase in cohesive strength with moisture exposure, which was related to a plasticization effect.
Zhang et al. [22] noted that differences in the water sensitivity tests could be explained by the water absorption and mineral compositions of the aggregates. They concluded that based on the peel test, the moisture absorption and mineralogical compositions of aggregate were considered as two important factors to moisture sensitivity. This phenomenon suggests that in a susceptible asphalt mixture, the effect of aggregate may be more influential than the effect of bitumen. The SATS test and the peel test showed similar moisture sensitivity results demonstrating the good correlation between these two mechanical tests. However, the surface energy tests, and the mechanical tests cannot correlate in terms of moisture sensitivity evaluation. For the aggregates considered in this research, the surface-energy-based method did not correlate well with the peel test for moisture sensitivity evaluation.
Hamedi and Moghadas Nejad [31] tested combinations of eight aggregates and four binders. Four SFE calculated parameters were used, of which two showed a good correlation with the laboratory tests: EP1 defined as the difference between the surface energy of adhesion of asphalt–aggregate and water–aggregate divided by the surface energy of adhesion of asphalt–aggregate. Additionally, EP2, which is the ratio between the surface energy of adhesion of asphalt–aggregate (in dry conditions) to the difference between surface energy of adhesion in dry and wet conditions. Both parameters showed a good correlation with the tensile strength ratio. The R squares for these parameters were 0.82 and 0.81, respectively. The authors observed that these relations worsened slightly when including SSA, which they related to difficulties in the measurement of SSA. The authors also noted that the biggest shortcoming of thermodynamics is that it does not dictate rate; it shows in which direction things will go, when in equilibrium conditions. In the papers [45,60], 24 combinations were investigated. In this study, apart from the SSA of the aggregates, the authors also tested the AFT (asphalt film thickness) and the permeability of the asphalt mixtures. A multiple regression model was applied to predict the moisture susceptibility of asphalt mixtures based on thermodynamic parameters and the three other parameters (permeability, SSA, and AFT). A good model was obtained, showing that the combination of these parameters can predict the occurrence of moisture damage in asphalt mixtures, measured by the modified Lottman indirect tension test. The results of the coefficients also showed that the highest positive impact on asphalt mixture strength against moisture is caused by SSA, indicating that this parameter is certainly an important one [45]. In the paper by Azarion et al. [60], the authors noted that a comparison between variables based on the coefficients is not possible since the variables all had different sizes. The model showed that all parameters were significant.
Porot el al. [46] found that according to SFE calculations all combinations should have been well resistant to moisture damage, which did not correspond to the experimental test results. In this project, four aggregates and three binders were tested using various test methods.
In conclusion, Table 4 demonstrates that a large number of laboratory test procedures have been used to validate SFE component calculations, including binder pull-off and peeling tests, mastic cohesion strength and adhesion tests, asphalt mixture tensile tests, stiffness, dynamic modulus and fatigue tests, rolling bottle and boiling water tests. In some cases, very good relations between predicted water sensitivity levels, based on the SFE concept and measured performances were obtained, [15,20,26,28,29,30,40,51], while in other cases relations were less good or even nonexistent as reported in [22,41,46,53,55]. It is clear that SFE parameters are important, but the overview of findings suggests that very often other properties need to be included when estimating the moisture susceptibility in laboratory tests or in practice. An important property of the aggregate, indicated by many papers [9,19,20,29,30,31,44,45,78], is the SSA, which is related to the aggregate roughness or texture. Of course, this property will be of less importance in tests where the aggregate surface is polished. Other parameters that have been considered include the binder film thickness and asphalt mixture porosity [24,45]. Again, in tests where the binder film thickness is constant, this parameter will not show up. Similar observations can be made for the water conditioning step, if the water needs to penetrate a large aggregate substrate before reaching the aggregate binder bond, probably the water permeability and water uptake of the aggregate will start to become important. In addition, the temperature at which the water conditioning is conducted will also have an influence on the results. Temperatures as high as 64 °C have been used, and due to the high temperature susceptibility of bitumen, one can expect a different behavior at high temperatures as compared to a conditioning conducted at 20 °C. For example, Wasiuddin [55] noted that where 64 °C was used during the water conditioning, binder flow, and cavitation were observed, which is probably related to this high temperature conditioning. Correlations between SFE and rolling bottle tests have been found to be weak [46,55]. The obvious reason for this, is the presence of a mechanical action in the rolling bottle test, which is not covered by SFE calculations. In addition, most likely in the rolling bottle test the mechanical action dominates over the SFE driven equilibrium conditions. Hirsch and Friemel-Göttlich [53] explained the lack of correlation by the formation of a good adhering but brittle film breaking under the rolling action and the formation of a strong cohesive, but less good adhering film. Furthermore, a number of papers also showed the importance of the filler type, which may need to be included. Finally, a reversibility of moisture damage has also been demonstrated.
The overview indicates that the set of properties, needed to obtain good relations between predicted and tested performances, depends very much on the experimental test setup, including the water conditioning regime.
As explained in several papers [15,46,51,55,79], water may cause a change in the damage location; in the dry state, the damage typically occurs in the binder or mastic phase, being the weakest bond, referred to as cohesive failure, while under wet conditions, the damage occurs in the aggregate–binder interface, referred to as adhesive failure. Depending on the time given, and the degree of water penetration, mixed behavior is also possible. Apeagyei et al. [15] observed a weakening of the mastic due to the presence of water. In their paper, it was postulated that the damage in the presence of water would still be cohesive and take place in the weakened mastic phase. If the failure location changes between wet and dry states, the use of a wet versus dry ratio becomes questionable. This ratio can be high because of a high moisture resistance, or because the water did not reach the aggregate–binder interface, or because already in the dry state the cohesive properties had a low value. In fact, the percentual area of the binder aggregate bond exposed to water may be a better indicator, as explained by Kim et al. [25].
To validate the SFE concept, in a first step it is legitimate to remove as much as possible other parameters, so that the significance of SFE parameters can be demonstrated. In further steps other parameters such as SSA, binder film thickness, and porosity could be included, to further evaluate their importance. Studies evaluating all or at least a large number of parameters are needed to further clarify the relationships between each of these properties, and to possibly rank them according to their importance. In the study of Hamedi and Moghadas Nejad [45], where indirect tensile tests on asphalt cores were conducted, it seems that the SSA of the aggregate is certainly one of the decisive parameters.
3.3.2. Correlations between Calculated Bond Strengths and Field Experience
When evaluating field behavior, external parameters come into play; which examine the conditions outside of the asphalt mixture system, such as traffic and weather fluctuations.
In the papers [19,20,28,36], bond strength calculations and the various energy ratios were compared for eight mixtures with known field performance. The comparison of field performance with the bond energy parameters, ER1 and ER2, and the energy ratios multiplied with the SSA shows that all ratios can distinguish good from poor performing field mixtures. For each ratio, threshold values of the bond energy parameter could be derived. The authors concluded that bond energy parameters can be used to segregate mixtures based on their moisture sensitivity, but that these data cannot be used for qualitative comparisons between various parameters. Since, unlike laboratory tests, it is difficult to control and quantify the moisture sensitivity of field mixtures on a uniform scale due to the differences in environmental and field conditions that influence these mixtures. Masad et al. [36] combined the use of surface energy components with DMA data on mastics are described to predict fatigue and healing in further detail. This approach is not discussed in this report. Bhasin et al. [19] used the same data but, in this case, they were ranked according to the ratio of the total free energy ratios and the free energy ratios calculated separately for the polar components. In this paper [19], for both energy ratios threshold values to identify moisture susceptible binder aggregate combinations were proposed. The authors concluded that the portion of the bond energy that results from the interaction of the acid component of binder and the base component of aggregate contributes the most to the total adhesive bond strength of the mixture.
4. Summary of Experimental Studies Based on the Hamaker Approach
The Hamaker equation is applicable to nonpolar materials and materials which have polar but no directional bonds, as for example hydrogen bonds. Three papers have been published that evaluate the adhesion between bitumen and aggregate both in the dry and wet state.
Lyne et al. [32] calculated Hamaker constants of a typical bitumen with several aggregates, based on dielectric and refractive index data, which were obtained from the literature. These Hamaker constants were calculated, for the intervening medium air and also for the medium water. When changing the intervening medium from air to water, the part of the Hamaker constant related to polar interactions increased, while the part related to dispersive interactions decreased a lot. It is expected that molecular forces related to dipoles increase with polar liquids such as water, while dispersive interactions decrease. For air as an intervening medium, the polar part contributed 1% of the total Hamaker value. For water as an intervening medium, the polar part contributed 9% to 25 % of the total interaction. The calculation showed that if water comes in between the aggregate and the bitumen, the interaction forces between bitumen and aggregate decrease by 80%–90%. This reduction is the main reason for stripping. The authors also showed that the dispersive part, derived from refractive index data is dominant in the bitumen stone interaction, in air, and also in water. As the dispersive terms are dominating, the data also imply that adhesion increases (dry as well as in water) as the refractive index of the aggregate and the bitumen are larger. In this paper [32], the ranking of the field performance of several aggregates, derived from literature data [80], corresponded to the ranking based on the calculation of the Hamaker constant.
Lyne et al. [65,66] focused on the variation in the dispersive component of minerals via their refractive indices, which were found in the literature. In this study, it was assumed that the bitumen–air–aggregate and the bitumen–water–aggregate adhesive interaction can be represented by the dispersive component of the Hamaker’s constant. The data indicated that aggregates and minerals that have a refractive index, higher than a cutoff value of around 1.6 are expected to be less susceptible to stripping. This is represented in Figure 3.

Figure 3.
High refractive index value for aggregates and minerals classified according to their degree of resistance to stripping (P—poor, F—fair, and G—good) [65,80].
In this paper [66], the authors also related stripping and refractive index values to the elemental composition of the minerals. Some relations were found: (1) alkali metals tend to lower the refractive index and (2) alkali earth metals and transition metals tend to maintain the refractive index above 1.6. The authors concluded that the elemental composition of minerals has a clear influence on the refractive index and therefore also on the dispersive interaction ability with bitumen. However, it was also indicated that other mechanisms that are not dependent on an interaction may still occur, such as alkali metals, which form water-soluble salts, and which will contribute to stripping when present in higher concentrations.
Lyne et al. [65,66] evaluated several bitumen aggregate combinations. In this study, the refractive indexes were measured using ellipsometry, which allowed calculating the dispersive component of the Hamaker constant. Three aggregates and seven binders were included in the study. Regarding the binders, the refractive indices varied only in the second decimal place, between n = 1.550 and n = 1.598, while the spread in refractive index among the three aggregate samples was much larger. This observation corresponds to the observation that the stone surface determines the adhesion behavior more compared to the bituminous binders. From the refractive index data on bitumen, the cohesive energy of the binders was estimated as the dispersive component of the Hamaker equation in the medium air and water. In the paper, adhesive and cohesive energies were compared, based on the refractive index of the aggregate. If the aggregate had a refractive index that is higher than the binder, the link bitumen–aggregate would be stronger compared to bitumen–bitumen, and cohesive failure of the bitumen will be more likely. If the aggregate has a refractive index of the same magnitude as the bituminous binder, then an adhesive failure will be as likely as a cohesive failure. The critical refractive index value, discriminating good from fair aggregates was reported previously to be 1.6. This value is very close to the refractive index measured on bitumen and is, therefore, a threshold for cohesive versus adhesive failure. This observation indicates that stripping is related to a bitumen–aggregate adhesion and happens when the bitumen–aggregate adhesion is weaker than the bitumen cohesion.
5. Conclusions
When summarizing the test results of the SFE components of bitumen, typically the SFE is composed of a large dispersive part, sometimes accompanied by a small acid and/or base component. There is some variation between different binders, but it is small, and it is not clear how this relates to other properties. Softer binders tend to have lower polar components and slight differences between naphthenic and paraffinic bitumen have been observed. The effect of bitumen modifications is very small. Regarding test precision, it seems to be very difficult to measure the small parts, acid and base accurately. When comparing the different methods to determine the surface energy components, rather large differences between different test methods have been noted. It was also reported that the sample state has an effect a microtome-cut surface of bitumen is different compared to an air-cooled bitumen surface [53], and [54] showed differences between water-treated and air-cooled samples. These observations indicate that for a multicomponent material such as bitumen, care is needed when properties are derived from measurements made on the samples’ surface. As bitumen consists of a very large numbers of different molecules, it could very well be that an air-cooled surface, and this is the one that is investigated in most studies, is different from the surface composition that adheres to the aggregate. Indications of chemical and microstructural differences between air-cooled and fractured bitumen surfaces have been noted [81,82] and recently microscopy studies have demonstrated differences in bitumen surfaces depending on the type of contact liquid [83]. In addition, also for polymers variations in surface energies depending upon the contact medium have been observed by Awaja et al. [84]. This seems to point out that SFE measurements on air-cooled surfaces are different from the state of the binder as it is when against a stone surface.
With respect to aggregates, it was observed that there is a much larger variation between the SFE components of aggregates compared to the variation seen for bitumen. Aggregates typically have large base components, although when looking at minerals there are specific minerals that have only small acid and base components. There are basically two test methods commonly used for aggregates, the universal sorption test and the sessile drop method. In both cases, the sample preparation of the aggregates is critical. For example, there is still a question if possible absorbed water layers or other impurities on the aggregate surface have been removed or need to be removed, which has not yet been fully answered. In turn, the time after cutting or heating the aggregates may also have an effect. For the sessile drop test, the flatness or the absence of sufficient flatness has been reported to influence the test result. In this test, only a very small area of the aggregate is tested. As aggregates are known to be nonuniform, and can also differ between the individual stone particles, a lot of repeats are needed to obtain a full view of the variation. In the universal sorption device, a larger amount of aggregates is tested, averaging internal variations. Regarding the test precision, it seems, as for bitumen, difficult to measure the smallest SFE parts accurately.
Regarding the calculation of bond strengths, small differences in acid and base components of the bitumen can have a large effect on the adhesive bond strengths in dry and in wet conditions, especially for aggregates with a large mostly base component. Consequently, small errors in the acid base determination of the bitumen can have a large effect.
Regarding the validation, a number of studies have shown good correlations between laboratory tests and the predicted behavior, while there are also papers where correlations were less good. It is clear that, in addition to SFE based calculations, other parameters need to be taken into account in order to make good predictions. Other parameters such as the SSA, the binder film thickness, the asphalt permeability have been proposed. In this respect, it is not clear how important and which role SFE based properties can play, within the mixture of all possible influences.
In another approach, the change in bitumen drops after they have obtained good adhesion were followed while being submerged in water. This approach seems promising, but also in this case questions about the effect of binder viscosity, temperature, and the influence of aggregate flatness need to be addressed. Finally, the Hamaker approach, which is mainly relating bitumen–aggregate adhesion to dispersive interactions [32,65,66], seems to be able to establish a ranking between different aggregate types. Nevertheless, for this approach, a laboratory validation including various bitumens is not yet available. Moreover, also in this case, possible sample and/or more suitable surface preparation effects have not been studied in detail. Additionally, again, also the Hamaker approach relates only to equilibrium conditions.
In general, fundamental questions with regard to moisture damage mechanisms as they take place in asphalt mixtures remain. It is still not fully clear which mechanism, or combination of mechanisms induce moisture damage, and how these depend on conditions such as temperature, the particular mix design, binder aging, the traffic, the water exposure time, and possibly the presence of other pavement failures. The use of SFE based properties can be regarded as a promising element, in this complex interplay of properties.
Author Contributions
Writing—original draft preparation and editing, H.S. and S.V.; writing—review and editing, P.K.D.M. All authors have read and agreed to the published version of the manuscript.
Funding
The research was partly funded by the CEDR Transnational Road Research Programme Call 2013: Energy Efficiency—Materials and Technology through the project FunDBitS (Functional Durability-related Bitumen Specification). Funding countries included Germany, Norway, UK, Austria, The Netherlands, and Slovenia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lu, Q.; Harvey, J.T.; Monismith, C.L. Investigation of Conditions for Moisture Damage in Asphalt Concrete and Appropriate Laboratory Test Methods: Summary Report, University of California, Pavement Research Center UC Davis and Berkeley. Available online: http://www.ucprc.ucdavis.edu/PDF/UCPRC-SR-2005-01.pdf (accessed on 26 January 2020).
- Skaf, M.; Pasquini, E.; Revilla-Cuesta, V.; Ortega-Lopez, V. Performance and durability of porous asphalt mixtures manufactured exclusively with electric steel slag. Materials 2019, 12, 3306. [Google Scholar] [CrossRef] [PubMed]
- Ingrassia, L.P.; Lu, X.; Ferrotti, G.; Canestrari, F. Renewable materials in bituminous binders and mixtures: Speculative pretext or reliable opportunity? Resour. Conserv. Rec. 2019, 144, 209–222. [Google Scholar] [CrossRef]
- Ma, J.; Sun, D.; Pang, Q.; Sun, G.; Hu, M.; Lu, T. Potential of recycled concrete aggregate pretreated with waste cooking oil residue for hot mix asphalt. J. Clean. Prod. 2019, 221, 469–479. [Google Scholar] [CrossRef]
- Terrel, R.; Al-Swailmi, S. Water Sensitivity of Asphalt–Aggregate Mixes: Test Selection. In SHRP Report A-403; National Research Council: Washington, DC, USA, 1994; p. 183. Available online: http://onlinepubs.trb.org/onlinepubs/shrp/SHRP-A-403.pdf (accessed on 10 October 2019).
- Caro, S.; Masad, E.; Bhasin, A.; Little, D.N. Moisture susceptibility of asphalt mixtures, Part 1: mechanisms. Int. J. Pavement Eng. 2008, 9, 81–98. [Google Scholar] [CrossRef]
- Abuawad, I.M.A. Mechanical and Surface Free Energy Characterization of Asphalt Concrete for Moisture Damage Detection. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign County, IL, USA, 2016; p. 179. Available online: https://pdfs.semanticscholar.org/7260/8d5a5564df3fbeec1c50857d5b759fa86c72.pdf (accessed on 13 February 2020).
- Cheng, D.; Little, D.N.; Lytton, R.; Holste, J.C. Surface energy measurement of asphalt and its application to predicting fatigue and healing in asphalt mixtures. Transp. Res. Rec. 2002, 1810, 44–53. [Google Scholar] [CrossRef]
- Little, D.L.; Allen, D.H.; Bhasin, A. Modeling and Design of Flexible Pavements and Materials; Springer International Publishing AG: Cham, Switzerland, 2018; p. 693. [Google Scholar] [CrossRef]
- Caro, S.; Masad, E.; Bhasin, A.; Little, D.N. Moisture susceptibility of asphalt mixtures, Part 2: Characterisation and modelling. Int. J. Pavement Eng. 2008, 9, 99–114. [Google Scholar] [CrossRef]
- Bagampadde, U.; Isacsson, U.; Kiggundu, B.M. Classical and Contemporary Aspects of Stripping in Bituminous Mixes. RMPD 2004, 5, 7–43. [Google Scholar] [CrossRef]
- Ensley, E.K. Multilayer adsorption with molecular orientation of asphalt on mineral aggregate and other substrates. J. Appl. Chem. Biotechnol. 1975, 25, 671–682. [Google Scholar] [CrossRef]
- Yao, H.; Dai, Q.; You, Z. Chemo-physical analysis and molecular dynamics (MD) simulation of moisture susceptibility of nano hydrated lime modified asphalt mixtures. Constr. Build. Mater. 2015, 101, 536–547. [Google Scholar] [CrossRef]
- Terrel, R.L.; Shute, J.W. Summary Report on Water Sensitivity. Report SHRP-A/IR-89-003; Strategic Highway Research Program, National Research Council: Washington, DC, USA, 1989; p. 102. Available online: http://onlinepubs.trb.org/Onlinepubs/shrp/shrp-A-IR-89-003/SHRP-AIR-003.pdf (accessed on 10 October 2019).
- Apeagyei, A.K.; Grenfell, J.R.A.; Airey, G.D. Moisture-induced strength degradation of aggregate–asphalt mastic bonds. RMPD 2014, 15, 239–262. [Google Scholar] [CrossRef]
- Van Oss, C.J.; Chaudhury, M.K.; Good, R.J. Interfacial Lifshitz-van der Waals and polar interactions in macroscopic systems. Chem. Rev. 1988, 88, 927–941. [Google Scholar] [CrossRef]
- Vansteenkiste, S.; Soenen, H. Correlation between Bitumen and Asphalt Properties. In Project report FunDBitS. CEDR Call 2013: Energy Efficient–Materials and Technology; 2016; p. 51. Available online: https://www.cedr.eu/download/other_public_files/research_programme/call_2013/energy_efficiency/fundbits/D.2e_bitumen-aggregate-interaction.pdf (accessed on 6 September 2019).
- Hefer, A.W. Adhesion in Bitumen-Aggregate Systems and Quantification of the Effects of Water on the Adhesive Bond. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2004; p. 222. Available online: http://hdl.handle.net/1969.1/1457 (accessed on 9 September 2019).
- Bhasin, A.; Masad, E.; Little, D.; Lytton, R. Limits on Adhesive Bond Energy for Improved Resistance of Hot-Mix Asphalt to Moisture Damage. Transp. Res. Rec. 2006, 1970, 3–13. [Google Scholar] [CrossRef]
- Little, D.N.; Bhasin, A. Using surface energy measurements to select materials for asphalt pavement. In Final Report for National Cooperative Highway Research Program RRD 316; National Cooperative Highway Research Program: Washington, DC, USA, 2007. [Google Scholar] [CrossRef]
- Arabani, M.; Hamedi, G.H. Using the surface free energy method to evaluate the effects of polymeric aggregate treatment on moisture damage in hot-mix asphalt. J. Mater. Civ. Eng. 2011, 23, 802–811. [Google Scholar] [CrossRef]
- Zhang, J.; Airey, G.D.; Grenfell, J.; Apeagyei, A.K. Moisture sensitivity examination of asphalt mixtures using thermodynamic, direct adhesion peel and compacted mixture mechanical tests. Road Mater. Pavement Des. 2016, 19, 120–138. [Google Scholar] [CrossRef]
- Alvarez, A.E.; Ovalles, E.; Caro, S. Assessment of the effect of mineral filler on asphalt–aggregate interfaces based on thermodynamic properties. Constr. Build. Mater. 2012, 28, 599–606. [Google Scholar] [CrossRef]
- Howson, J.; Masad, E.; Little, D.; Kassem, E. Relationship between bond energy and total work of fracture for asphalt binder-aggregate systems. Road Mater. Pavement Des. 2012, 13, 281–303. [Google Scholar] [CrossRef]
- Kim, S.-H.; Jeong, J.-H.; Kim, N. Use of Surface Free Energy Properties to Predict Moisture Damage Potential of Asphalt Concrete Mixture in Cyclic Loading Condition. KSCE J. Civ. Eng. 2003, 7, 381–387. [Google Scholar] [CrossRef]
- Grenfell, J.; Ahmad, N.; Liu, Y.; Apeagyei, A.; Large, D.; Airey, G. Assessing asphalt mixture moisture susceptibility through intrinsic adhesion bitumen stripping and mechanical damage. RMPD 2014, 15, 131–152. [Google Scholar] [CrossRef]
- Kloubek, J. Development of methods for surface free energy determination using contact angles of liquids on solids. Adv. Colloid. Interfac. 1992, 38, 99–142. [Google Scholar] [CrossRef]
- Bhasin, A. Development of Methods to Quantify Bitumen-Aggregate Adhesion and Loss of Adhesion Due to Water. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2006; p. 158. Available online: http://hdl.handle.net/1969.1/5934 (accessed on 9 September 2019).
- Bhasin, A.; Howson, J.; Masad, E.; Little, D.N.; Lytton, R.L. Effect on modification processes on bond energy of asphalt binders. Transp. Res. Rec. 2007, 1998, 29–37. [Google Scholar] [CrossRef]
- Bhasin, A.; Little, D.N.; Vasconcelos, K.L.; Masad, E. Surface free energy to identify moisture sensitivity of materials for asphalt mixes. Transp. Res. Rec. 2007, 2001, 37–45. [Google Scholar] [CrossRef]
- Hamedi, G.H.; Moghadas Nejad, F. Using energy parameters based on the surface free energy concept to evaluate the moisture susceptibility of hot mix asphalt. RMPD 2015, 16, 239–255. [Google Scholar] [CrossRef]
- Lyne, A.L.; Birgisson, B.; Redelius, P. Interaction forces between mineral aggregates and bitumen calculated using the hamaker constant. RMPD Spec. Issue Asph. Technol. 2010, 11, 305–323. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Van der Waals forces in biological systems. Q. Rev. Biophys. 1973, 6, 341–387. [Google Scholar] [CrossRef]
- Hefer, A.; Little, D. Towards Quantification of Adhesion and Water Stripping in Bituminous Materials Using Modern Surface Energy Theory. In Proceedings of the 24th South African Transport Conference (SATC2005), Pretoria, South Africa, 12 July 2005; pp. 115–124. Available online: https://repository.up.ac.za/bitstream/handle/2263/6314/015.pdf;sequence=1 (accessed on 9 September 2019).
- Hefer, A.; Little, D.N. Adhesion in Bitumen-Aggregate Systems and Quantification of the Effects of Water on the Adhesive Bond. In Technical Report ICAR-505-1; Texas A&M University: College Station, TX, USA, 2005; p. 218. Available online: http://hdl.handle.net/2152/35371 (accessed on 9 September 2019).
- Masad, E.; Zollinger, C.; Bulut, R.; Little, D.N.; Lytton, R.L. Characterization of HMA moisture damage using surface energy and fracture properties. Assoc. Asph. Paving Technol. Proc. Tech. Sess. 2006, 75, 713–754. [Google Scholar]
- Wasiuddin, N.M.; Zaman, M.M.; O’Rear, E.A. Effect of Sasobit and Aspha-min on wettability and adhesion between asphalt binders and aggregates. Transp. Res. Rec. 2008, 2051, 80–89. [Google Scholar] [CrossRef]
- Howson, J.E.; Bhasin, A.; Masad, E.; Lytton, R.; Little, D. Development of a Database for Surface Energy of Aggregates and Asphalt Binder. In Report FHWA/TX-09/5-4524-01-1; Federal Highway Administration/Texas Deptartment of Transportation: Austin, TX, USA, 2009; p. 76. Available online: http://tti.tamu.edu/documents/5-4524-01-1.pdf (accessed on 9 September 2019).
- Bahramian, A. Evaluating surface energy components of asphalt binders using wilhelmy plate and sessile drop techniques. In Degree Project in Highway and Railway Engineering; KTH: Stockholm, Sweden, 2012; p. 40. Available online: https://www.diva-portal.org/smash/get/diva2:601925/FULLTEXT01.pdf (accessed on 9 September 2019).
- Moghadas Nejad, F.; Hamedi, G.H.; Azarhoosh, A.R. Use of surface free energy method to evaluate effect of hydrate lime on moisture damage in hot-mix asphalt. J. Mater. Civ. Eng. 2013, 25, 1119–1126. [Google Scholar] [CrossRef]
- Liu, Y.; Apeagyei, A.; Ahmad, N.; Grenfell, J.; Airey, G. Examination of moisture sensitivity of aggregate–bitumen bonding strength using loose asphalt mixture and physico-chemical surface energy property tests. Int. J. Pavement. Eng. 2014, 15, 657–670. [Google Scholar] [CrossRef]
- Luo, R.; Zhang, D.; Zeng, Z.; Lytton, R. Effect of surface tension on the measurement of surface energy components of asphalt binders using the Wilhelmy Plate Method. Constr. Build. Mater. 2015, 98, 900–909. [Google Scholar] [CrossRef]
- Shafabakhsh, G.H.; Faramarzi, M.; Sadeghnejad, M. Use of surface free energy method to evaluate the moisture susceptibility of sulfur extended asphalts modified with antistripping agents. Constr. Build. Mater. 2015, 98, 456–464. [Google Scholar] [CrossRef]
- Hamedi, G.H. Evaluating the effect of asphalt binder modification using nanomaterials on the moisture damage of hot mix asphalt. RMPD 2016, 18, 1375–1394. [Google Scholar] [CrossRef]
- Hamedi, G.H.; Moghadas Nejad, F. Evaluating the effect of mix design and thermodynamic parameters on moisture sensitivity of hot mix asphalt. J. Mater. Civ. Eng. 2017, 29, 04016207. [Google Scholar] [CrossRef]
- Porot, L.; Soenen, H.; Besamusca, J.; Apeagyei, A.; Grenfell, J.; Vansteenkiste, S.; Chailleux, E.; Gaudefroy, V.; Chaturabong, P.; Tozzo, C.; et al. Bituminous Binder. In Testing and Characterization of Sustainable Innovative Bituminous Materials and Systems; RILEM State-of-the-Art Reports 24, Partl; Porot, L., Di Benedetto, H., Canestrari, F., Marsac, P., Tebaldi, G., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 15–74. [Google Scholar] [CrossRef]
- Kakar, M.R.; Hamzah, M.O.; Akhtar, M.N.; Saleh, J.M. Evaluating the Surface Free Energy and Moisture Sensitivity of Warm Mix Asphalt Binders Using Dynamic Contact Angle. Adv. Civ. Eng. 2019, 19, 15. [Google Scholar] [CrossRef]
- Koc, M.; Bulut, R. Characterization of warm mix asphalt additives using direct contact angle measurements and surface free energies. In Proceedings of the Transportation Research Board 93rd Annual Meeting, Washington, DC, USA, 12–16 January 2014. [Google Scholar]
- Aguiar-Moya, J.P.; Salazar-Delgado, J.; Baldi-Sevilla, A.; Leiva-Villacorta, F.; Loria-Salazar, L. Effect of aging on adhesion properties of asphalt mixtures with the use of bitumen bond strength and surface energy measurement tests. Transp. Res. Rec. 2015, 2505, 57–65. [Google Scholar] [CrossRef]
- Ji, J.; Liu, L.; Suo, Z.; Zhai, P.; Yang, X.; You, Z. Adhesion Evaluation of Asphalt-Aggregate Interface Using Surface Free Energy Method. Appl. Sci. Basel 2017, 7, 156. [Google Scholar] [CrossRef]
- Moraes, R.; Velasquez, R.; Bahia, H. Using bond strength and surface energy to estimate moisture resistance of asphalt-aggregate systems. Constr. Build. Mater. 2017, 130, 156–170. [Google Scholar] [CrossRef]
- Korn, S. Beurteilung der Benetzbarkeit und des Adhäsionsvermögens von Bitumen mittels Kontaktwinkelmessungen. Ph.D. Thesis, Hamburg University of Applied Sciences, Hamburg, Germany, 2004. [Google Scholar]
- Hirsch, V.; Friemel-Göttlich, B. Bestimmung des adhäsiven Potentials von Bitumen und Gesteinsoberflächen mit Hilfe der Kontaktwinkel-messmethode. In Berichte der Bundesanstalt für Straßenwesen Straßenbau (BAsT); Heft S 59; Bergisch Gladbach, Germany, 2009; Available online: https://bast.opus.hbz-nrw.de/opus45-bast/frontdoor/deliver/index/docId/71/file/S59.pdf (accessed on 9 September 2019).
- Khan, A.; Redelius, P.; Kringos, N. Evaluation of adhesive properties of mineral-bitumen interfaces in cold asphalt mixtures. Constr. Build. Mater. 2016, 125, 1005–1021. [Google Scholar] [CrossRef]
- Wasiuddin, N.M.; Saltibus, N.E.; Mohammad, L.N. Novel moisture-conditioning method for adhesive failure of hot- and warm-mix asphalt binders. Transp. Res. Rec. 2011, 2208, 108–117. [Google Scholar] [CrossRef]
- Wistuba, M.P.; Grothe, H.; Grönniger, J.; Handle, F. Adhesion of bitumen: Screening and evaluating laboratory testing techniques. Proceedings of 5th Eurasphalt & Eurobitume Congress, Istanbul, Turkey, 13–15 June 2012; p. 12. [Google Scholar]
- Radenberg, M. Einfluss der chemischen, rheologischen und physikalischen Grundeigenschaften von Straßenbaubitumen auf das Adhäsionsverhalten unterschiedlicher Gesteinskörnungen. In Schlussbericht; 16639 N/1, Bochum, Germany, 2014; p. 104. Available online: http://www.lvw.ruhr-uni-bochum.de/mam/content/forschung/projekte/bericht_aif_igf_16639_n-1.pdf (accessed on 9 September 2019).
- Miller, C.M. Adhesion and the Surface Energy Components of Natural Minerals and Aggregates. Master’s Thesis, Texas A&M University, College Station, TX, USA, 2010; p. 218. Available online: http://hdl.handle.net/1969.1/ETD-TAMU-2010-08-8237 (accessed on 9 September 2019).
- Miller, C.; Little, D.N.; Bhasin, A. Surface energy characteristics of natural minerals and their impact of aggregate-bitumen bond strengths and asphalt mixture durability. Transp. Res. Rec. 2012, 2267, 45–55. [Google Scholar] [CrossRef]
- Azarion, Y.; Shirmohammadi, H.; Hamedi, G.H.; Saedi, D. Model for Predicting Moisture Susceptibility of Asphalt Mixtures Based on Material Properties. J. Mater. Civ. Eng. 2019, 31. [Google Scholar] [CrossRef]
- Porot, L.; Besamusca, J.; Soenen, H.; Apeagyei, A.; Grenfell, J.; Sybilski, D. Bitumen/aggregate affinity – RILEM Round Robin test. In 8th RILEM International Symposium on Testing and Characterization of Sustainable and Innovative Bituminous Materials; Canestrari, F., Partl, M.N., Eds.; Springer: Dordrecht, The Netherlands, 2016; RILEM 11; pp. 153–164. [Google Scholar] [CrossRef]
- Rudawska, A.; Jacniacka, E. Analysis for determining surface free energy uncertainty by the Owen-Wendt method. Int. J. Adhes. Adhes. 2009, 29, 451–457. [Google Scholar] [CrossRef]
- Cui, S.; Blackman, B.R.K.; Kinlock, A.J.; Taylor, A.C. Durability of asphalt mixtures: Effect of aggregate type and adhesion promoters. Int. J. Adhes. Adhes. 2014, 54, 100–111. [Google Scholar] [CrossRef]
- Horgnies, M.; Darque-Ceretti, E.; Fezai, H.; Felder, E. Influence of the interfacial composition on the adhesion between aggregates and bitumen: Investigations by EDX, XPS and peel tests. Int. J. Adhes. Adhes. 2011, 31, 238–247. [Google Scholar] [CrossRef]
- Lyne, A.L.; Redelius, P.; Collin, M.; Birgisson, B. Characterization of stripping properties of stone material in asphalt. Mater. Struct. 2013, 46, 47–61. [Google Scholar] [CrossRef]
- Lyne, A.L.; Krivosheeva, O.; Birgisson, B. Adhesion between bitumen and aggregate: Implementation of spectroscopic ellipsometry characterisation and estimation of Hamaker’s constant. Mater. Struct. 2013, 46, 1737–1745. [Google Scholar] [CrossRef]
- Schellenberger, W. Haftung zwischen Bitumen und Mineralstoff [Adhesion between bitumen and mineral aggregates]. In Asphalt; Germany, 2004; p. 8. [Google Scholar]
- Nehrings, A. Affinitätsproblem zwischen Gestein und Bitumen Lösungsansatz: Einsatz von Haftvermittlern. In Zeitschrift für Asphalt; Germany, 2009; p. 8. Available online: https://docplayer.org/33746588-Affinitaetsproblem-zwischen-gestein-und-bitumen-loesungsansatz-einsatz-von-haftvermittlern.html (accessed on 9 September 2019).
- Aguiar-Moya, J.P.; Loria-Salazar, L.; Salazar, J.; Villegas, E.; Corrales-Azofeifa, J.P.; Hajj, E.Y. Evaluation of Adhesion Properties of Costa Rican Asphalt Mixtures Using Bitumen Bond Strength and Contact-Angle Measurement Tests. Available online: https://www.lanamme.ucr.ac.cr/repositorio/bitstream/handle/50625112500/545/TRB%202013%20Evaluation%20of%20Adhesion%20Properties%20of%20Costa%20Rican%20Asphalt%20Mixtures.pdf?sequence=1&isAllowed=y (accessed on 9 September 2019).
- Aranowski, R.; Wojewodka, P.; Blazejowski, K. Determination of binder-aggregate adhesion by contact angle measurement. In Asphalt Pavements; Kim, Y.R., Ed.; Taylor&Francis Group: London, UK, 2014; pp. 617–624. [Google Scholar] [CrossRef]
- Apeagyei, A.K.; Grenfell, J.R.A.; Airey, G.D. Durability of asphalt mixtures exposed to long-term moisture conditioning. In Proceedings of the TRB 93rd Annual Meeting, Washington, DC, USA, 12–16 January 2014; pp. 1–16. Available online: https://www.researchgate.net/publication/260002328_Durability_of_asphalt_mixtures_exposed_to_long-term_moisture_conditioning (accessed on 27 January 2020).
- EN 12697-11. Bituminous Mixtures–Test Methods for Hot Asphalt–Part 11: Determination of the Affinity between Aggregates and Bitumen. European Committee for Standardization: Brussels, Belgium, 2012. [Google Scholar]
- AASHTO T283. Standard Method of Test for Resistance of Compacted Asphalt Mixtures to Moisture-Induced Damage; AASHTO: Washington, DC, USA, 2014. [Google Scholar]
- ASTM D 1664-80. Test Method for Coating and Stripping of Bitumen Aggregates Mixtures; ASTM International: West Conshohocken, PA, USA, 1985. [Google Scholar]
- ASTM D 3625-96. Standard Practice for Effect of Water on Bituminous-Coated Aggregate Using Boiling Water; ASTM International: West Conshohocken, PA, USA, 2005. [Google Scholar]
- EN 1097-7:2008. Tests for mechanical and physical properties of aggregates. In Determination of the Particle Density of Filler. Pyknometer Method; European Committee for Standardization: Brussels, Belgium, 2009. [Google Scholar]
- ASTM D 4541-17. Standard Test Method for Pull-Off Strength of Coatings Using Portable Adhesion Testers; ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar]
- Moghadas Nejad, F.; Asadi, M.; Hamedi, G.H.; Esmaeeli, M.R. Using hydrophobic coating on aggregate surfaces to reduce moisture damage in asphalt mixture. J. Mater. Civ. Eng. 2018, 30, 04018238. [Google Scholar] [CrossRef]
- Zhang, J.; Airey, G.D.; Grenfell, J.; Apeagyei, A.K.; Barrett, M. Development of a composite substrate peel test to assess moisture sensitivity of aggregate–bitumen bonds. Int. J. Adhes. Adhes. 2016, 68, 133–141. [Google Scholar] [CrossRef]
- Cordon, W.A. Properties, Evaluation and Control of Engineering Materials; McGraw-Hill College: New York, NY, USA, 1979; p. 550. ISBN 9780070131231. [Google Scholar]
- Lu, X.; Sjövall, P.; Soenen, H. Structural and chemical analysis of bitumen using time-of-flight secondary ion mass spectrometry (TOF-SIMS). Fuel 2017, 199, 206–218. [Google Scholar] [CrossRef]
- Blom, J.; Soenen, H.; Katsiki, A.; Van den Brande, N.; Rahier, H.; Van den bergh, W. Investigation of the bulk and surface microstructure of bitumen by atomic force microscopy. Constr. Build. Mater. 2018, 177, 158–169. [Google Scholar] [CrossRef]
- Ramm, A.; Downer, M.C.; Sakib, N.; Bhasin, A. Morphology and kinetics of as-phalt binder microstructure at gas, liquid, and solid interfaces. J. Microsc. 2019, 109–117. [Google Scholar] [CrossRef]
- Awaja, F.; Gilbert, M.; Kellya, G.; Foxa, B.; Pigram, P.J. Adhesion of polymers. Prog. Polym. Sci. 2009, 34, 948–968. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).