Benchmarking Image Processing Algorithms for Unmanned Aerial System-Assisted Crack Detection in Concrete Structures
Abstract
:1. Introduction
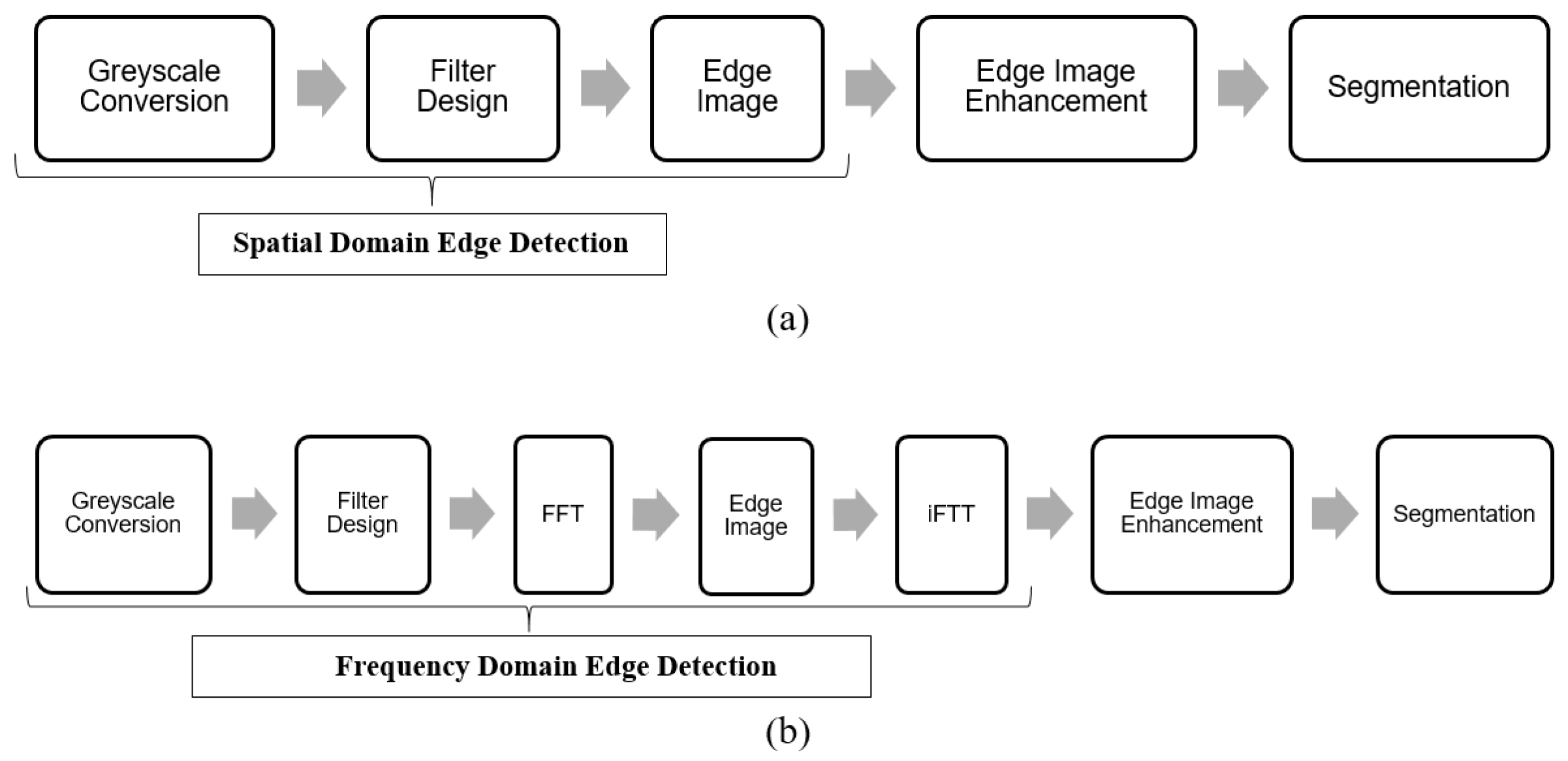
2. Analytical Program
2.1. Greyscale Conversion
2.2. Edge Detection in the Spatial Domain
2.3. Edge Detection in the Frequency Domain
2.4. Edge Image Enhancement
2.5. Segmentation
3. Experimental Program
4. Results
4.1. Spatial Domain, Roberts Filter
4.2. Spatial Domain, Prewitt Filter
4.3. Spatial Domain, Sobel Filter
4.4. Spatial Domain, Laplacian of Gaussian (LoG) Filter
4.5. Frequency Domain, Butterworth Filter
4.6. Frequency Domain, Gaussian Filter
4.7. Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- FHWA (Federal Highway Administration). Tables of Frequently Requested NBI Information. Available online: https://www.fhwa.dot.gov/bridge/britab.cfm (accessed on 16 January 2018).
- Dorafshan, S.; Maguire, M.; Hoffer, N.V.; Coopmans, C. Challenges in bridge inspection using small unmanned aerial systems: Results and lessons learned. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1722–1730. [Google Scholar]
- Dorafshan, S.; Maguire, M. Bridge inspection: Human performance, unmanned aerial systems and automation. J. Civ. Struct. Health Monit. 2018, 8, 443–476. [Google Scholar] [CrossRef]
- Gucunski, N.; Boone, S.D.; Zobel, R.; Ghasemi, H.; Parvardeh, H.; Kee, S.H. Nondestructive evaluation inspection of the Arlington Memorial Bridge using a robotic assisted bridge inspection tool (RABIT). In Nondestructive Characterization for Composite Materials, Aerospace Engineering, Civil Infrastructure, and Homeland Security 2014; International Society for Optics and Photonics: Bellingham, WA, USA, 2014; Volume 9063, p. 90630N. [Google Scholar]
- Lattanzi, D.; Miller, G. Review of robotic infrastructure inspection systems. J. Infrastruct. Syst. 2017, 23, 04017004. [Google Scholar] [CrossRef]
- Le, T.; Gibb, S.; Pham, N.; La, H.M.; Falk, L.; Berendsen, T. Autonomous robotic system using non-destructive evaluation methods for bridge deck inspection. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3672–3677. [Google Scholar]
- Dorafshan, S.; Thomas, R.J.; Maguire, M. Fatigue crack detection using unmanned aerial systems in fracture critical inspection of steel bridges. J. Bridge Eng. 2018, 23, 04018078. [Google Scholar] [CrossRef]
- Khaloo, A.; Lattanzi, D.; Cunningham, K.; Dell’Andrea, R.; Riley, M. Unmanned aerial vehicle inspection of the Placer River Trail Bridge through image-based 3D modelling. Struct. Infrastruct. Eng. 2018, 14, 124–136. [Google Scholar] [CrossRef]
- Dorafshan, S.; Maguire, M.; Hoffer, N.; Coopmans, C. Fatigue Crack Detection Using Unmanned Aerial Systems in Under-Bridge Inspection; RP 256; Final Report; Idaho Department of Transportation: Boise, ID, USA, 2017. Available online: http://apps.itd.idaho.gov/apps/research/Completed/RP256.pdf (accessed on 30 January 2019).
- Omar, T.; Nehdi, M.L. Remote sensing of concrete bridge decks using unmanned aerial vehicle infrared thermography. Autom. Constr. 2017, 83, 360–371. [Google Scholar] [CrossRef]
- Omar, T.; Nehdi, M.L.; Zayed, T. Infrared thermography model for automated detection of delamination in RC bridge decks. Constr. Build. Mater. 2018, 168, 313–327. [Google Scholar] [CrossRef]
- Sony, S.; Laventure, S.; Sadhu, A. A literature review of next-generation smart sensing technology in structural health monitoring. Struct. Control. Health Monit. 2019, 26, e2321. [Google Scholar] [CrossRef]
- Hiasa, S.; Karaaslan, E. Infrared and High-definition Image-based Bridge Scanning Using UAVs without Traffic Control. In Proceedings of the 27th ASNT Research Symposium, Orlando, FI, USA, 26 March 2018; pp. 116–127. [Google Scholar]
- Farhidzadeh, A.; Ebrahimkhanlou, A.; Salamone, S. A vision-based technique for damage assessment of reinforced concrete structures. In Health Monitoring of Structural and Biological Systems 2014; International Society for Optics and Photonics: Bellingham, WA, USA, 2014; Volume 9064, p. 90642H. [Google Scholar]
- Dorafshan, S.; Maguire, M.; Qi, X. Automatic Surface Crack Detection in Concrete Structures Using OTSU Thresholding and Morphological Operations; Paper 1234; Civil and Environmental Engineering Faculty Publications: Logan, UT, USA, 2016. Available online: https://digitalcommons.usu.edu/cee_facpub/1234 (accessed on 30 January 2019).
- Liu, X.; Ai, Y.; Scherer, S. Robust image-based crack detection in concrete structure using multi-scale enhancement and visual features. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 2304–2308. [Google Scholar]
- Gopalakrishnan, K.; Gholami, H.; Vidyadharan, A.; Choudhary, A.; Agrawal, A. Crack Damage Detection in Unmanned Aerial Vehicle Images of Civil Infrastructure Using Pre-Trained Deep Learning Model. Int. J. Traffic Transp. Eng. 2018, 8, 1–14. [Google Scholar]
- Yang, L.; Li, B.; Li, W.; Liu, Z.; Yang, G.; Xiao, J. A robotic system towards concrete structure spalling and crack database. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 5–8 December 2017; pp. 1276–1281. [Google Scholar]
- Vaghefi, K.; Ahlborn, T.M.; Harris, D.K.; Brooks, C.N. Combined imaging technologies for concrete bridge deck condition assessment. J. Perform. Constr. Facil. 2013, 29, 04014102. [Google Scholar] [CrossRef]
- Ellenberg, A.; Kontsos, A.; Moon, F.; Bartoli, I. Bridge related damage quantification using unmanned aerial vehicle imagery. Struct. Control Health Monit. 2016, 23, 1168–1179. [Google Scholar] [CrossRef]
- Dorafshan, S.; Thomas, R.J.; Maguire, M. SDNET2018: An annotated image dataset for non-contact concrete crack detection using deep convolutional neural networks. Data Brief 2018, 21, 1664–1668. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimkhanlou, A.; Farhidzadeh, A.; Salamone, S. Multifractal analysis of crack patterns in reinforced concrete shear walls. Struct. Health Monit. 2016, 15, 81–92. [Google Scholar] [CrossRef]
- Graybeal, B.A.; Phares, B.M.; Rolander, D.D.; Moore, M.; Washer, G. Visual inspection of highway bridges. J. Nondestruct. Eval. 2002, 21, 67–83. [Google Scholar] [CrossRef]
- Phares, B.M.; Washer, G.A.; Rolander, D.D.; Graybeal, B.A.; Moore, M. Routine highway bridge inspection condition documentation accuracy and reliability. J. Bridge Eng. 2004, 9, 403–413. [Google Scholar] [CrossRef]
- Agdas, D.; Rice, J.A.; Martinez, J.R.; Lasa, I.R. Comparison of visual inspection and structural-health monitoring as bridge condition assessment methods. J. Perform. Constr. Facil. 2015, 30, 04015049. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Liu, M. Maintenance and management of civil infrastructure based on condition, safety, optimization, and life-cycle cost∗. Struct. Infrastruct. Eng. 2007, 3, 29–41. [Google Scholar] [CrossRef]
- Dorafshan, S.; Thomas, R.J.; Coopmans, C.; Maguire, M. Deep learning neural networks for sUAS-assisted structural inspections: Feasibility and application. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 874–882. [Google Scholar]
- Dorafshan, S.; Thomas, R.J.; Maguire, M. Comparison of deep convolutional neural networks and edge detectors for image-based crack detection in concrete. Constr. Build. Mater. 2018, 186, 1031–1045. [Google Scholar] [CrossRef]
- Abdel-Qader, I.; Abudayyeh, O.; Kelly, M.E. Analysis of edge-detection techniques for crack identification in bridges. J. Comput. Civ. Eng. 2003, 17, 255–263. [Google Scholar] [CrossRef]
- Kim, H.; Ahn, E.; Cho, S.; Shin, M.; Sim, S. Comparative analysis of image binarization methods for crack identification in concrete structures. Cem. Concr. Res. 2017, 99, 53–61. [Google Scholar] [CrossRef]
- Dorafshan, S.; Maguire, M. Autonomous detection of concrete cracks on bridge decks and fatigue cracks on steel members. In Proceedings of the Digital Imaging 2017, Mashantucket, CT, USA, 26–28 June 2017; pp. 33–44. [Google Scholar]
- Hoang, N.-D. Detection of surface crack in building structures using image processing technique with an improved Otsu method for image thresholding. Adv. Civ. Eng. 2018, 195, 3924120. [Google Scholar] [CrossRef]
- Luo, Q.; Ge, B.; Tian, Q. A fast adaptive crack detection algorithm based on a double-edge extraction operator of FSM. Constr. Build. Mater. 2019, 204, 244–254. [Google Scholar] [CrossRef]
- Hoang, N.-D.; Nguyen, Q.-L. Metaheuristic Optimized Edge Detection for Recognition of Concrete Wall Cracks: A Comparative Study on the Performances of Roberts, Prewitt, Canny, and Sobel Algorithms. Adv. Civ. Eng. 2018, 2018, 7163580. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Nakamura, S.; Saegusa, R.; Hashimoto, S. Image-based crack detection for real concrete surfaces. IEEJ. Trans. Electr. Electron. Eng. 2008, 3, 128–135. [Google Scholar] [CrossRef]
- Yang, C.; Geng, M. The crack detection algorithm of pavement image based on edge information. AIP Conf. Proc. 2018, 1967, 040023. [Google Scholar]
- Li, Y.; Liu, Y. High-accuracy crack detection for concrete bridge based on sub-pixel. In Proceedings of the 2017 IEEE International Conference on Real-time Computing and Robotics (RCAR), Okinawa, Japan, 14–18 July 2017; pp. 234–239. [Google Scholar]
- Oh, J.; Jang, G.; Oh, S.; Lee, J.H.; Yi, By.; Moon, Y.S.; Lee, J.S.; Choi, Y. Bridge inspection robot system with machine vision. Autom. Constr. 2009, 18, 929–941. [Google Scholar] [CrossRef]
- Ali, R.; Gopal, D.L.; Cha, Y. Vision-based concrete crack detection technique using cascade features. In Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2018; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; Volume 10598, p. 105980L. [Google Scholar]
- Van Nguyen, L.; Gibb, S.; Pham, H.X.; La, H.M. A Mobile Robot for Automated Civil Infrastructure Inspection and Evaluation. In Proceedings of the 2018 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Philadelphia, PA, USA, 6–8 August 2018; pp. 1–6. [Google Scholar]
- Rimkus, A.; Podviezko, A.; Gribniak, V. Processing digital images for crack localization in reinforced concrete members. Procedia Eng. 2015, 122, 239–243. [Google Scholar] [CrossRef]
- Talab, A.M.A.; Huang, Z.; Xi, F.; HaiMing, L. Detection crack in image using Otsu method and multiple filtering in image processing techniques. Opt. Int. J. Light Electron Opt. 2016, 127, 1030–1033. [Google Scholar] [CrossRef]
- Mohan, A.; Poobal, S. Crack detection using image processing: A critical review and analysis. Alex. Eng. J. 2018, 57, 787–798. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Wintz, P. Digital image processing. In Applied Mathematics and Computation 1997; Addison-Wesley Publishing Co., Inc.: Reading, MA, USA, 1977; Volume 13, p. 451. [Google Scholar]
- Butterworth, S. On the theory of filter amplifiers. Wirel. Eng. 1930, 7, 536–541. [Google Scholar]
- Blinchikoff, H.; Krause, H. Filtering in the Time and Frequency Domains; The Institution of Engineering and Technology: Stevenage, UK, 2001. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Manand Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Washer, G.; Hammed, M.; Brown, H.; Connor, R.; Jensen, P.; Fogg, J.; Salazar, J.; Leshko, B.; Koonce, J.; Karper, C. Guidelines to Improve the Quality of Element-Level Bridge Inspection Data; No. NCHRP Project 12-104; NCHRP: Washington, DC, USA, 2018. [Google Scholar]
- Dorafshan, S.; Maguire, M.; Hoffer, N.V.; Coopmans, C.; Thomas, R.J. Unmanned Aerial Vehicle Augmented Bridge Inspection Feasibility Study; No. CAIT-UTC-NC31; Rutgers University: Piscataway, NJ, USA, 2017. [Google Scholar]









| Domain | Edge Detector | TPR1 (%) | TNR2 (%) | FPR3 (%) | FNR4 (%) | Ac.5 (%) | Pr.6 (%) | MCW7 (mm) | Time (s) |
|---|---|---|---|---|---|---|---|---|---|
| Spatial | Roberts | 64 | 90 | 10 | 36 | 77 | 86 | 0.4 | 1.67 |
| Spatial | Prewitt | 82 | 82 | 18 | 18 | 82 | 82 | 0.2 | 1.4 |
| Spatial | Sobel | 86 | 84 | 16 | 14 | 85 | 84 | 0.2 | 1.4 |
| Spatial | Laplacian of Gaussian (LoG) | 98 | 86 | 14 | 2 | 92 | 88 | 0.1 | 1.18 |
| Frequency | Butterworth | 80 | 86 | 14 | 20 | 83 | 85 | 0.2 | 1.81 |
| Frequency | Gaussian | 80 | 88 | 12 | 20 | 84 | 87 | 0.2 | 1.92 |
| Edge Detector | Defected Dataset | Sound Dataset | |||||||
|---|---|---|---|---|---|---|---|---|---|
| J1 | J2 | T1 | T2 | J1 | J2 | T1 | T2 | Average N/S (%) | |
| Roberts | 0.204 | 0.251 | 0.70 | 25 | 0.21 | 0.25 | 0.64 | 21 | 0.41 |
| Prewitt | 0.232 | 0.290 | 0.66 | 76 | 0.23 | 0.29 | 0.59 | 53 | 0.32 |
| Sobel | 0.230 | 0.291 | 0.67 | 75 | 0.23 | 0.29 | 0.59 | 53 | 0.33 |
| LoG | 0.534 | 0.590 | 0.71 | 58 | 0.62 | 0.69 | 0.63 | 32 | 0.90 |
| Butterworth | 0.581 | 0.631 | 0.89 | 10 | 0.57 | 0.64 | 0.93 | 6 | 1.74 |
| Gaussian | 0.594 | 0.640 | 0.89 | 8 | 0.58 | 0.64 | 0.93 | 5 | 1.76 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dorafshan, S.; Thomas, R.J.; Maguire, M. Benchmarking Image Processing Algorithms for Unmanned Aerial System-Assisted Crack Detection in Concrete Structures. Infrastructures 2019, 4, 19. https://doi.org/10.3390/infrastructures4020019
Dorafshan S, Thomas RJ, Maguire M. Benchmarking Image Processing Algorithms for Unmanned Aerial System-Assisted Crack Detection in Concrete Structures. Infrastructures. 2019; 4(2):19. https://doi.org/10.3390/infrastructures4020019
Chicago/Turabian StyleDorafshan, Sattar, Robert J. Thomas, and Marc Maguire. 2019. "Benchmarking Image Processing Algorithms for Unmanned Aerial System-Assisted Crack Detection in Concrete Structures" Infrastructures 4, no. 2: 19. https://doi.org/10.3390/infrastructures4020019
APA StyleDorafshan, S., Thomas, R. J., & Maguire, M. (2019). Benchmarking Image Processing Algorithms for Unmanned Aerial System-Assisted Crack Detection in Concrete Structures. Infrastructures, 4(2), 19. https://doi.org/10.3390/infrastructures4020019






