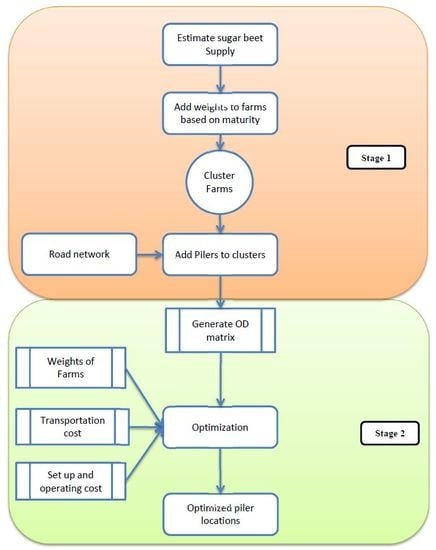
1. Introduction
The sugar beet is considered as one of the most important crops in Red River Valley of North Dakota and Minnesota in the United States. According to Farahmand et al. [
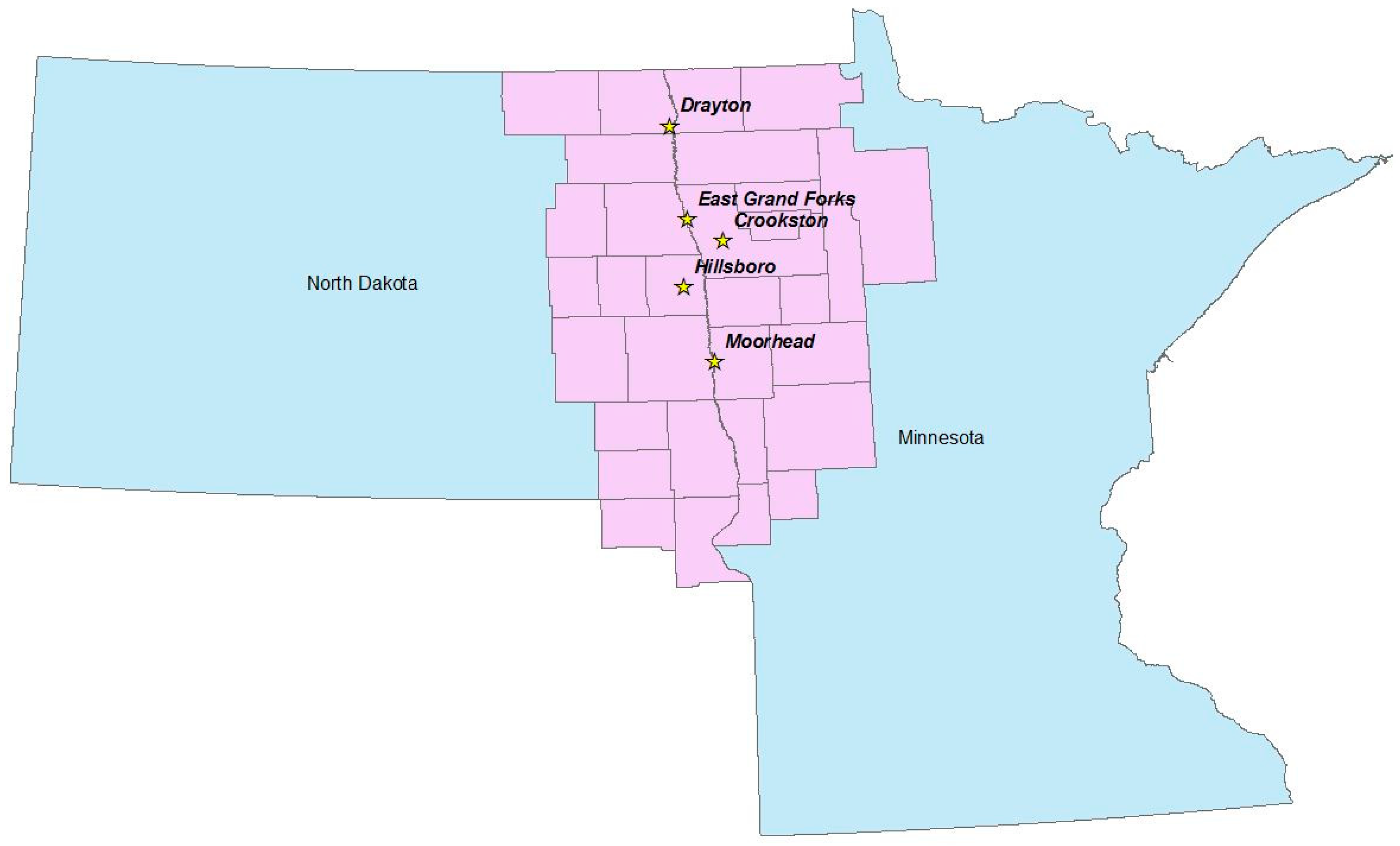
1] this sugar beet co-op operation is the largest sugar beet producer in the United States. The co-op is owned by about 2800 shareholders who raise nearly 40% of the nation’s sugar beet acreage. They also mentioned that the last seeding usually takes place on June 20 while full stockpile harvest starts on October 1st. This explains the seasonal nature of sugar beet harvesting. American Crystal Sugar Company (ACSC) manages this co-op. ACSC has five processing facilities in the Red River Valley as shown in
Figure 1.
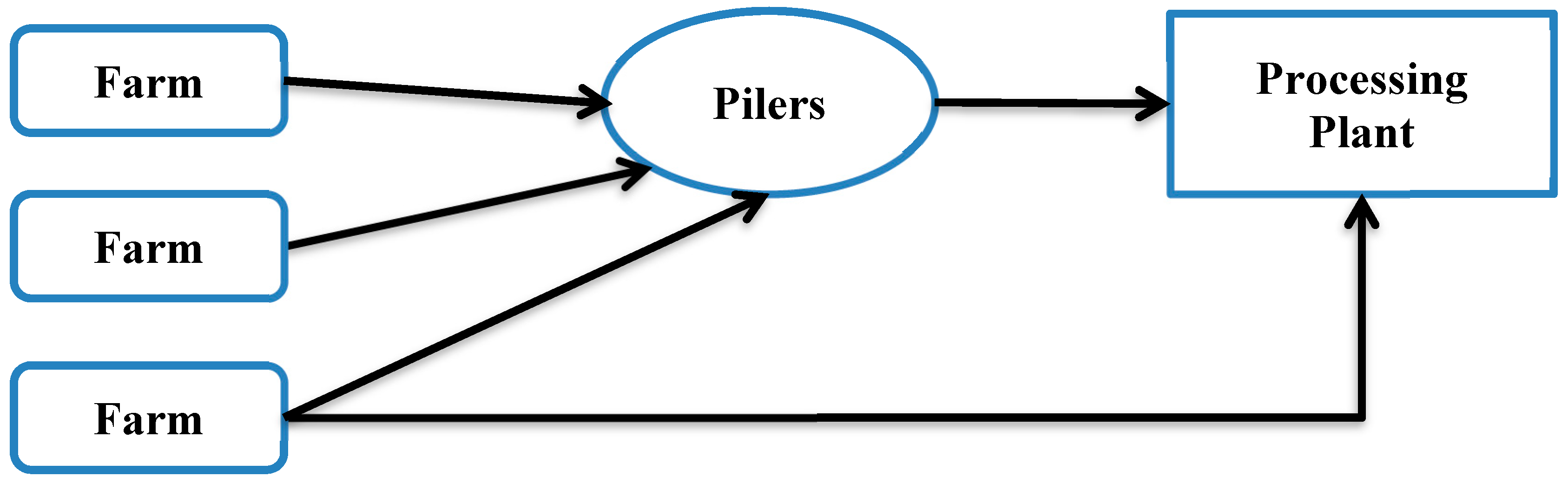
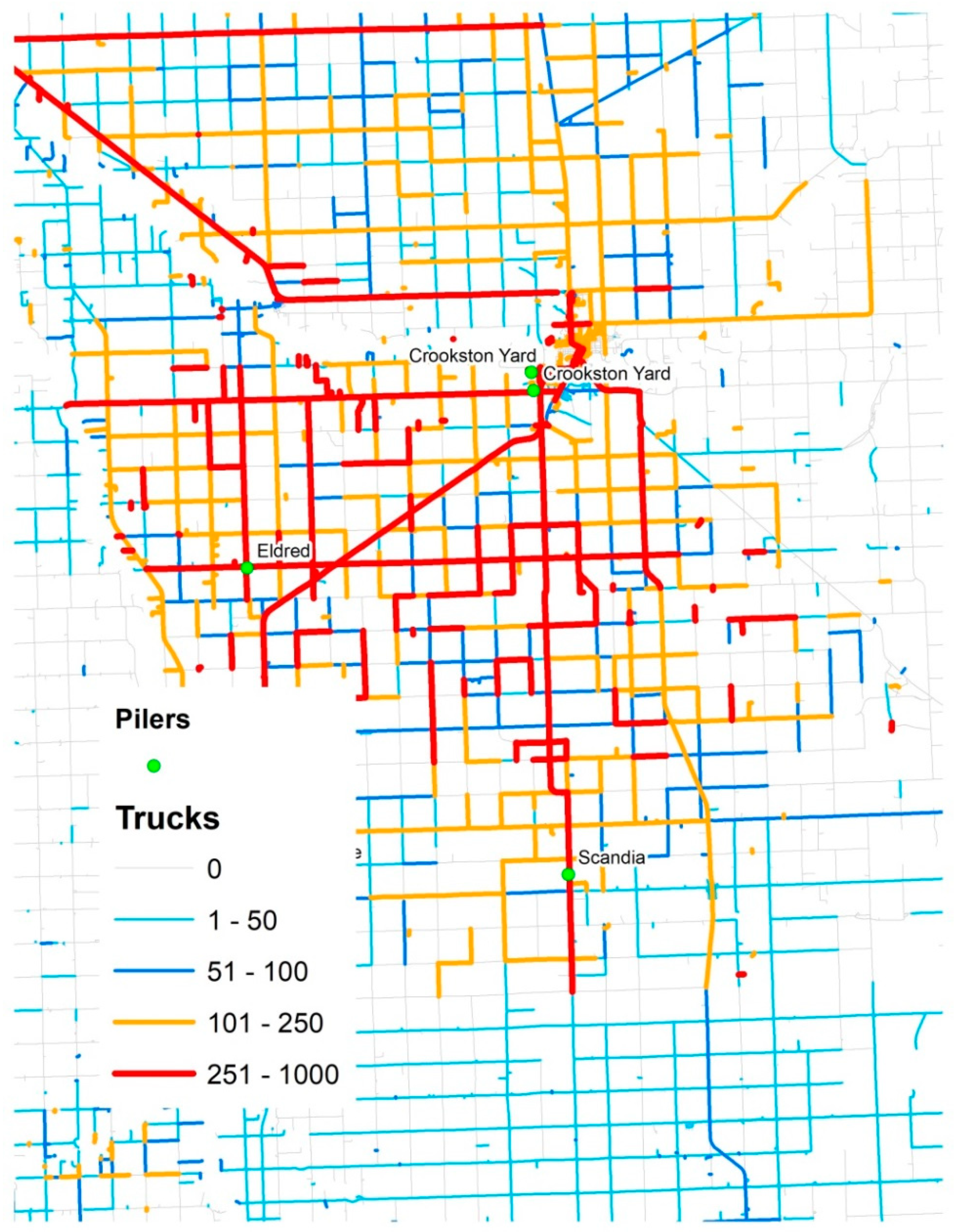
Growers are responsible for delivering the crop to the piling centers. ACSC operates the piling centers for growers to deliver the load to five processing factories. Beets get unloaded at the piling center (piler) in piles and the responsibility shifts from grower to the ACSC. At the pilers, sugar beets are cleaned and are piled 30′ tall x 240′ long for long term storage through the winter. The beets need to stay cold and frozen for long term storage or otherwise they will rot. At processing time, these beets are loaded on the truck using conveyors. Once the truck is full, a new truck takes over loading the beets. The loaded trucks drive to the nearest sugar beet processing plant or receiving station.
Figure 2 depicts this logistics system of sugar beet transportation from farms to processing plants.
Some beets are directly transported to the processing plants without storing them. This process is dependent on different factors. Farmers and ACSC decide whether to store beets or to take them to processing plant directly. This decision is mainly based on the maturity of the beets. The mature beet has the highest sugar content. The payment received by the farmer is based on sugar content thus farmers want to keep the beets in the ground to maximize sugar content. ACSC desires to start the harvest at an optimal time to ensure the processing plants are busy and remain at capacity throughout the season. This balance is important based on the planting time and harvesting time in order to minimize cost and maximize profit to the growers.
Pilers are considered as natural refrigerators to save beets from rotting. The colder temperatures in Red River Valley in winter helps the beets to stay at pilers for a longer time after harvest. Sugar beet roots should be cleaned from excessive dirt, and properly defoliated and cleaned from weed or leaves to allow for proper ventilation while stored in piles. Sugar beets may be stored up to 4 months, and during this storage period the roots will decay and ferment. As a result, the sugar beet roots will heat up and the respiration leads to around 70% loss of sucrose. Decay and fermentation during storage could also cause sucrose loss of up to 10% and 20%. Some of the sucrose losses caused by the storage have been reduced through the utilization of forced-air ventilation, cooling in hotter areas and subsequent freezing of storage piles after mid-December in colder areas. Ensuring the root temperature never reaches 55° F will keep the roots from decay. During harvest, if air temperature is rising and the root temperature increases past 55° F, the harvest will stop, and no sugar beets will be accepted at the pilers. This will prevent storage rot. Cold weather and frost could also damage the roots. Foliage and leaves have proven to provide a natural barrier to frost conditions thus protecting the roots and the crown area. Exposed roots during a frost shutdown, experience a higher degree of frost damage.
This situation is ideal for a location allocation problem. The locations of the pilers are to be optimized to minimize the transportation and storage cost.
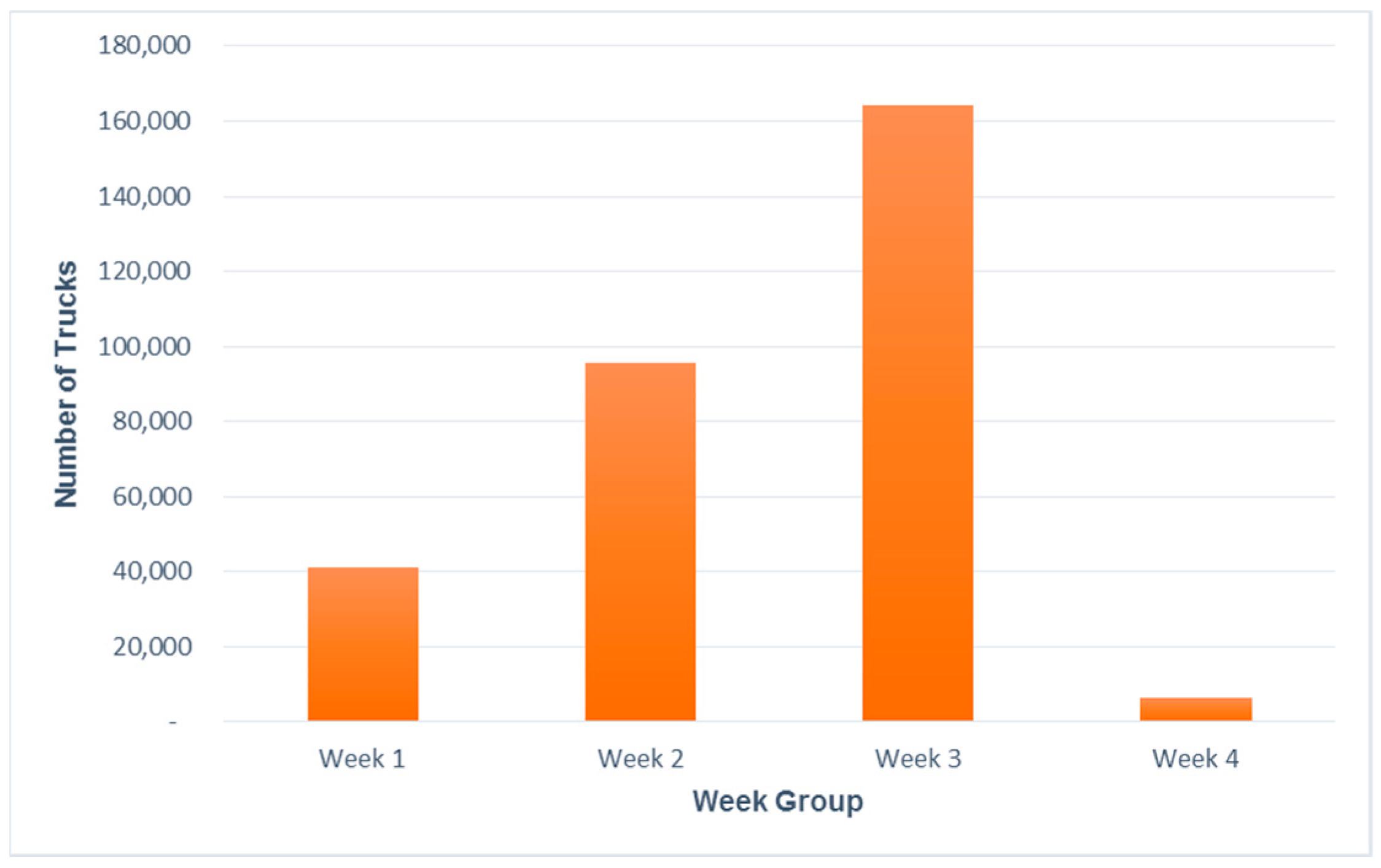
It is really hard for planners and engineers to predict the truck volume on the rural roads. For infrastructure decisions such as where to add lanes or which road needs widening needs data for the truck volume. This method will help to predict the truck volume thus it will be an important method for infrastructure decision makers.
This article is organized as follows.
Section 2 studies the literature available for location allocation problems in agriculture and other settings.
Section 3 describes the methodology and algorithm used for solution.
Section 4 discusses a case study.
Section 5 presents sensitivity analysis.
Section 6 presents conclusions along with the path to future research.
2. Literature Review
Kondor [
2] presented the initial problem of the sugar beet transportation. They tried to find the economic optimum results using the mathematical modeling of the problem. They established the relation between the processor starting date and the scheduling of the beet arrival. They provide the case study of Hungary. Scarpari and de Beauclair [
3] developed a linear programing model for sugarcane farm planning. Their model delivered profit maximization and harvest time schedule optimization. They used GAMS
® programing language to solve the problem. They solve this problem based on the case study of sugarcane farming in Brazil.
The location problem in a different setting is solved by Esnaf and Küçükdeniz [
4]. They presented the multi-facility location problem (mflp) in logistical network. Their objective is to optimally serve set of customers by locating facilities. They studied the fuzzy clustering method and developed a hybrid method. Their method is a two-step method in which the first step uses fuzzy clustering for mflp and the second step further determines the optimum location using single facility location problem (sflp). The fuzzy clustering step uses MATLAB
® for geographical clustering based on plant customer assignment. They compared their method with other clustering methods. Costs generated by the hybrid method are less than other methods. Zhang, Johnson, and Sutherland [
5] presented a two-step method to find the optimum location for biofuel production. Step one uses Geographical Information System (GIS) to identify feasible facility locations and step two employs total transportation cost model to select the preferred location. They presented a sensitivity analysis of location study in the Upper Peninsula of Michigan.
Houck, Joines, and Kay [
6] present the location allocation problem and its solution methodologies. They examine the applications of genetic algorithm to solve the problem. They propose that these problems are difficult to solve by traditional optimization techniques thus requiring the use of heuristic methods. Zhou and Liu [
7] propose different stochastic models for the capacitated location allocation problem. They also propose a hybrid algorithm which integrates network simplex algorithm, stochastic simulation, and genetic algorithm. They test the effectiveness of this algorithm with numerical examples. In the further research Zhou and Liu [
8] study the location allocation problem with fuzzy demands. They model this problem in three different minimization models. They propose another hybrid algorithm to solve these models.
Lucas and Chhajed [
9] provided a detailed review of literature in the field of location allocation involving agricultural problems. They express that there are a lot of location allocation problem solutions available but there is a lack of application-based research articles. They study six real world examples. Pathumnakul et al. [
10] considered the different maturity times of sugarcane to find the optimal locations of the loading stations. They modify the fuzzy c-means method to consider cane maturity time as well as cane supply. Their objective is to minimize the total transportation and utilization cost. They compare the performance of their method with the traditional fuzzy c-means method to conclude their method provides a better solution for the problem. They test these methods with the help of a case study in sugarcane farming in Thailand.
Another location problem of sugarcane loading stations is studied by Khamjan, Khamjan, and Pathumnakul [
11]. They compare the solution times of the mathematical model and the heuristic algorithm. Their objective function includes minimization of various costs such as investment cost, transportation cost, and cost of the sugarcane yield loss. They also applied their model to a case study to solve the industrial problem. In a recent study Kittilertpaisan and Pathumnakul [
12] present a multiple year crop routing decision problem. Their model includes heuristic algorithm for a three-year period of sugarcane harvesting. They solve their problem to design the planting and routing such as sugarcane becomes mature in three years for harvesting.
Yeh and Chow [
13] present an integrated location allocation approach for public facilities planning. They discuss integration of GIS and location allocation model. They use Hong Kong as an example. They provide an extensive review of earlier GIS and other location allocation studies. They also provide an alternating heuristic algorithm.
Church [
14] discusses role of GIS in the location modeling. He presents the history of the use of GIS in location modeling. He states that GIS provide a richer dataset which can be used to find the optimal solution of location modeling.
Murray [
15] enlists the contribution of GIS to location science in terms of input data, visualization, problem solution, and advances in theories. His focus is to showcase the contribution of GIS towards the advancements of the location allocation modeling theories. He reviews numerous studies showing the usefulness of GIS in the case of location allocation problem solutions.
Tolliver et al. [
16] present a methodology to estimate the flows from crop zones to elevators and plants. They also forecast improvement and maintenance costs for roads. They provide a model with nodes, links, and paths. They provide a simplified grain distribution system. They provide an exhaustive GIS analysis. They describe the creation of the travel time matrix. They also discuss how the shortest path between origins and destinations is calculated in GIS using Dijkstra’s algorithm.
This literature study shows that there are very few articles about sugar production and location problems and there are nearly zero articles about sugar beet harvesting and location problems involved in it. The use of GIS is well established for the solution of the location allocation problems as shown in the literature review. As the numbers of sugar beet fields are large, optimization algorithms suggested in some of the articles are not applicable in this situation. Also, there are very few articles studying the seasonal nature of the sugar beet harvest. Based on these problems this article tries to solve the location allocation problem for sugar beet harvesting using a two-stage GIS based Multi Facility Fuzzy Clustering (MFFC) algorithm.
5. Sensitivity Analysis
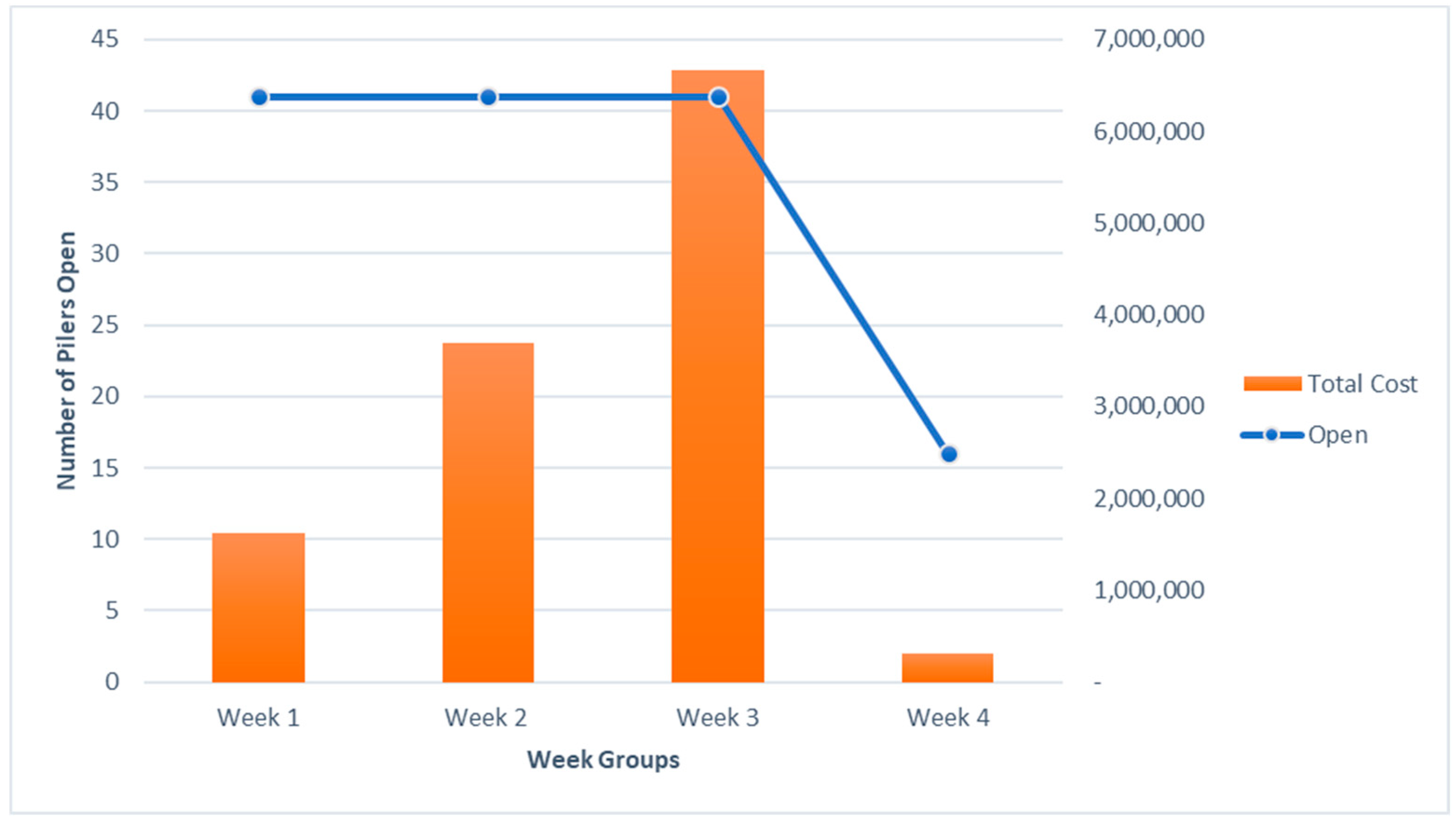
The sensitivity analysis is carried out to check if the model is performing as expected. It is also important to examine the assumed values and how they perform. Week group 4 model is used to perform two types of sensitivity analyses. First analysis is carried out to test the changes in the yield whereas the second analysis is performed to check the effects of changing piler set up costs.
Different percentages of yield changes are assumed for performing the sensitivity analysis. The optimization model is run for these different yield values. The results of running these models are shown in
Figure 10. The number of open pilers reduces as the yield at each farm is reduced by 50% and 75%. At the same time, the number of open pilers increases as the yield at each farm is increased from original yield to 300%. But this piler opening is not immediate and happens as a gradual increase. Number of open pilers are constant for original yield including a 10%–25% yield increase. As the yield increases from 25% to 50%, the number remains the same as it does for yield increases from 50% and 100%. A gradual increase in the total cost is also seen in the
Figure 10.
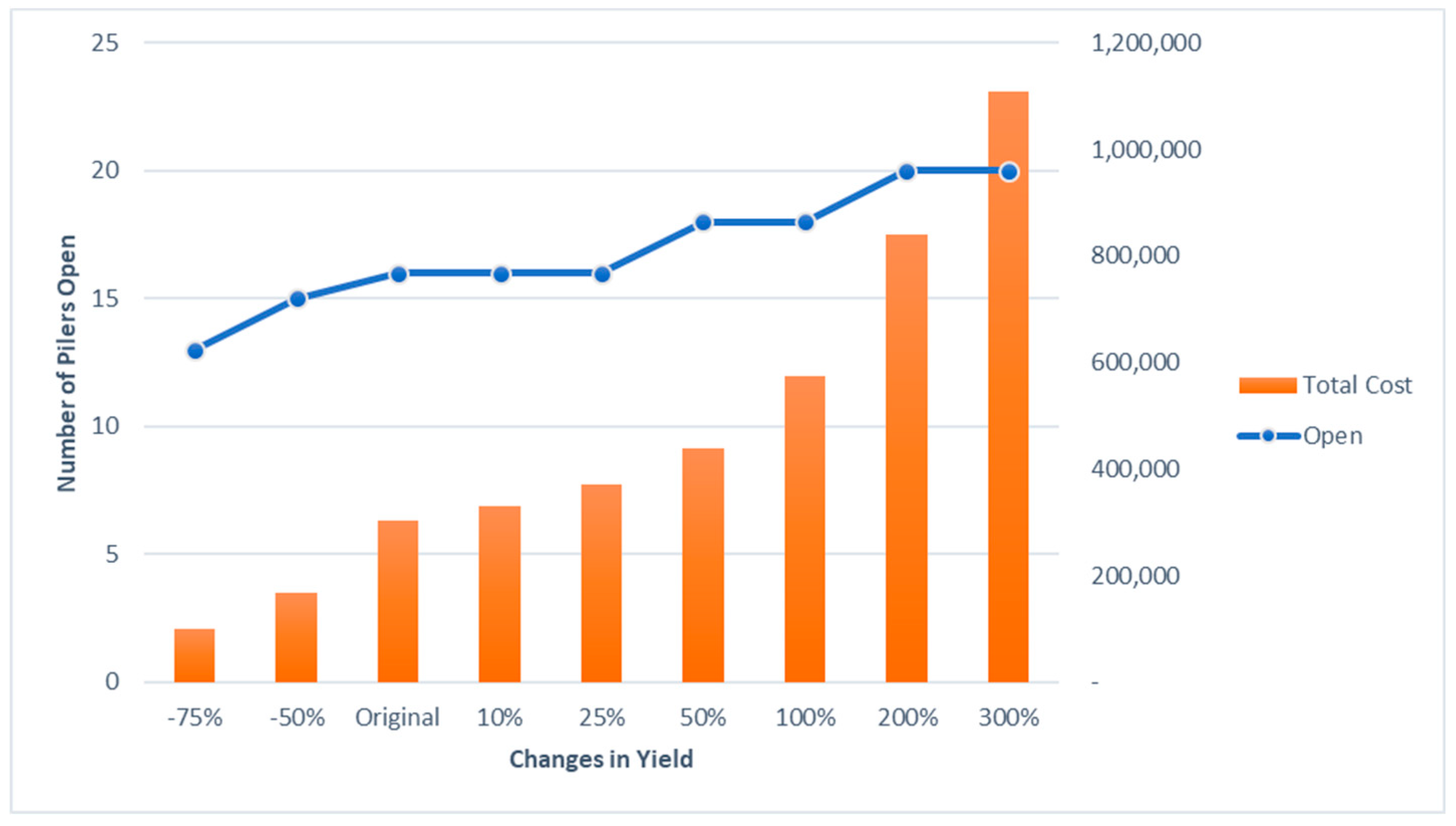
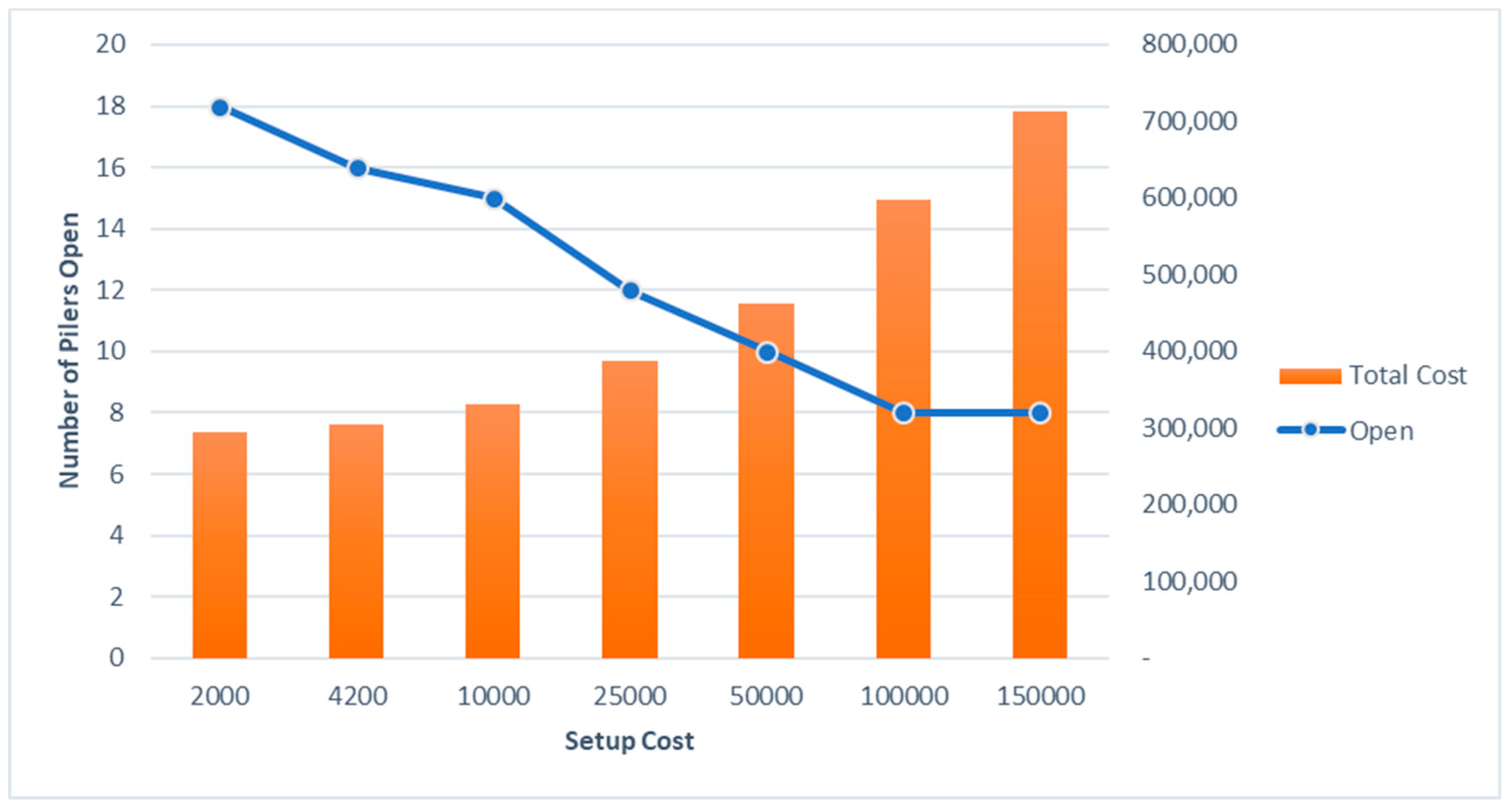
Figure 11 shows the effects of changes in the piler set up costs on the number of open pilers and total cost. As the setup cost reduces, the number of open pilers increases. Even though the number of open pilers increases, the total cost decreases. As the setup cost increases the number of open pilers is reduced. There is a gradual pattern in this decrease. But it settles at eight for the number of open pilers finally. Eight is the minimum required number of open pilers to satisfy all supply at the farms in week 4. The total cost increases as the setup cost increases.
6. Conclusions
This study shows that a two-step method using GIS and optimization can be used to allocate the sugar beet piler locations. This method can be used to save the total transportation cost. This method is also useful for transportation planners and engineers to predict the truck volume on the rural roads. It is hard to predict the truck volume so this will be one of the useful tools to make the infrastructure funding decisions.
As the farm to the piler cost is incurred by the farmers, this method can be helpful for farmers to save more money and reduce overall cost. At the same time this method considers the maturity period of sugar beets thus helping ACSC to transport beets at the peak of their maturity and receive highest sugar content. As seen in the sensitivity analysis as yield changes the number of pilers changes which can attribute to the supply variation. This method is also useful to find the optimal piler locations in this scenario. A reduced time interval such as half a week or less can be used for clustering to get better assessment of piler locations.
This study does not consider the computational time saving by comparing different studies, but it can be done in the future. While designing this type of study, additional consideration of the GIS component needs to be taken in to account. This study is a starting point which can be expanded into a complex model with additional steps of piler to processing plant, and processing plant to market. In the future, this method can be used with the results from Dharmadhikari et al. [
20]. Their research performs yield forecasting which can be used as inputs for this study. Yield forecasting can become a very useful tool for predicting the harvest times and the yield at each farm, which can be used for weight assignment and clustering in GIS analysis. This study can also be a part of a comprehensive economic model of sugar beet production suggested in Farahmand et al. [
1]. This model can be modified to be used as a base model for crops other than sugar beet.