Stability Assessment of Earth Retaining Structures under Static and Seismic Conditions
Abstract
:1. Introduction
2. Seismic Active Thrust Using the Pseudo-Dynamic Method
3. Seismic Active Thrust Using the Modified Pseudo-Dynamic Method
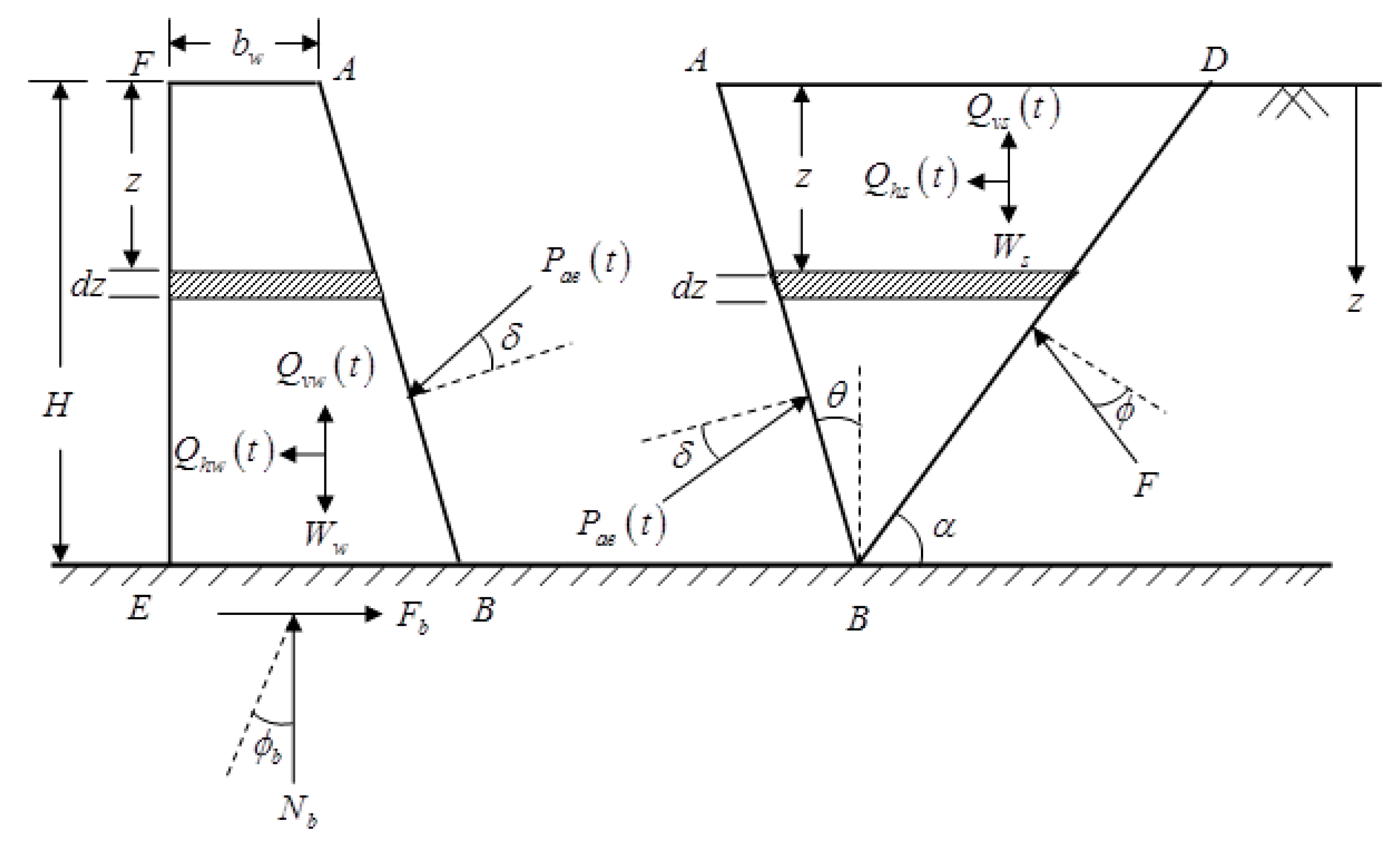
3.1. Stability of Rigid Retaining Wall Under Seismic Conditions Using the Modified Pseudo-Dynamic Method
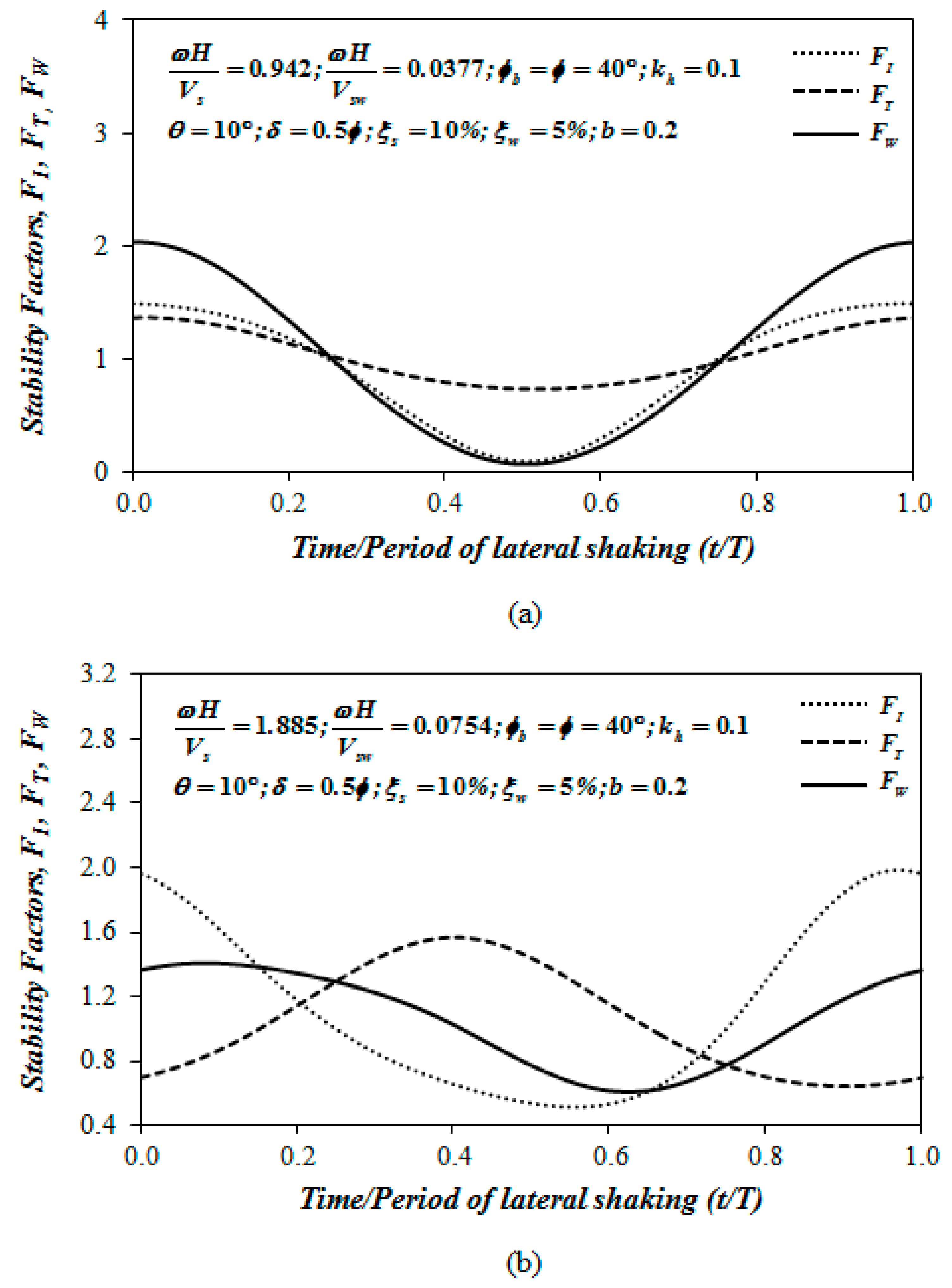
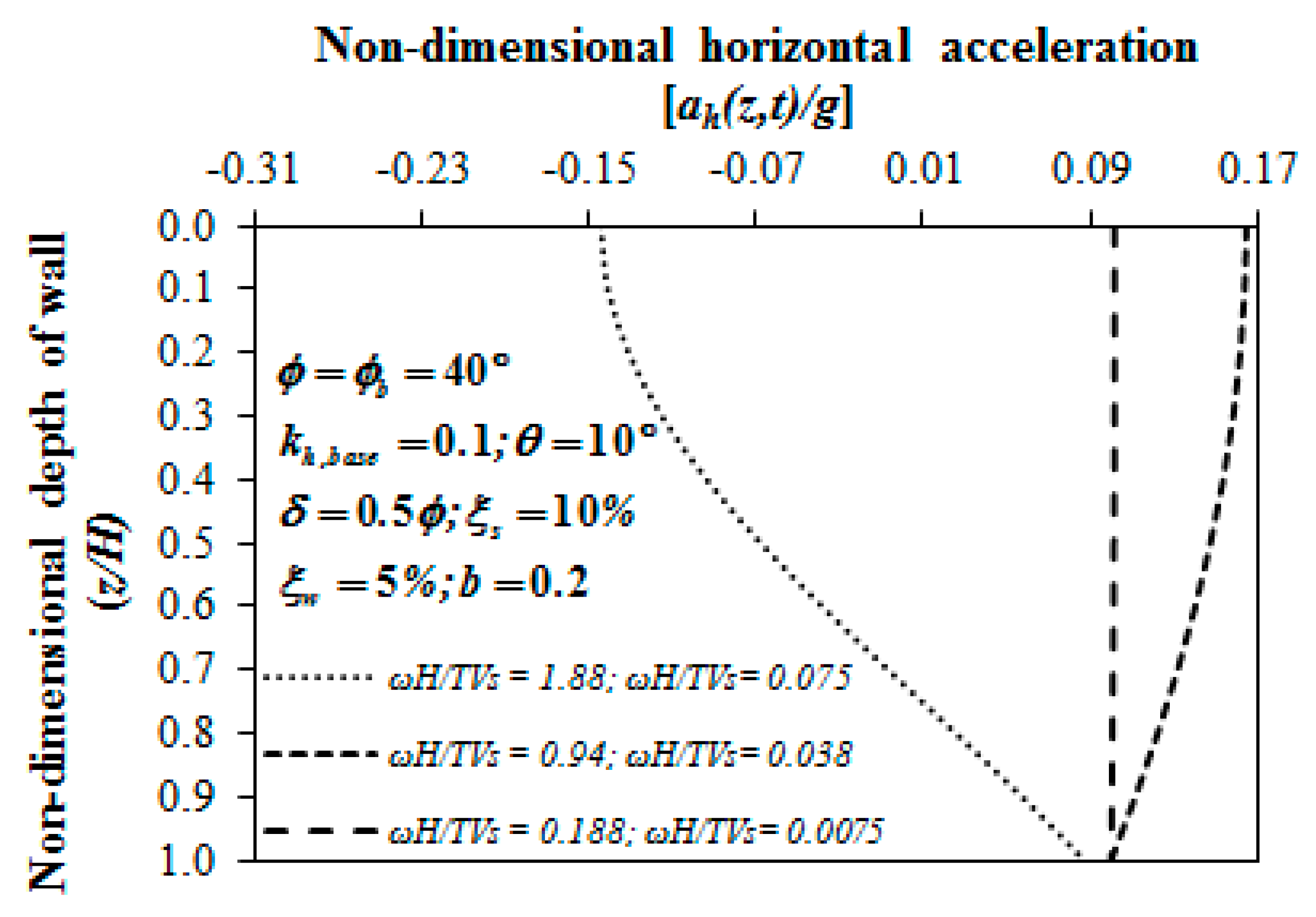
3.2. Results and Discussion
4. Effect of Soil Arching on the Stability of Retaining Structures
4.1. Analytical Model
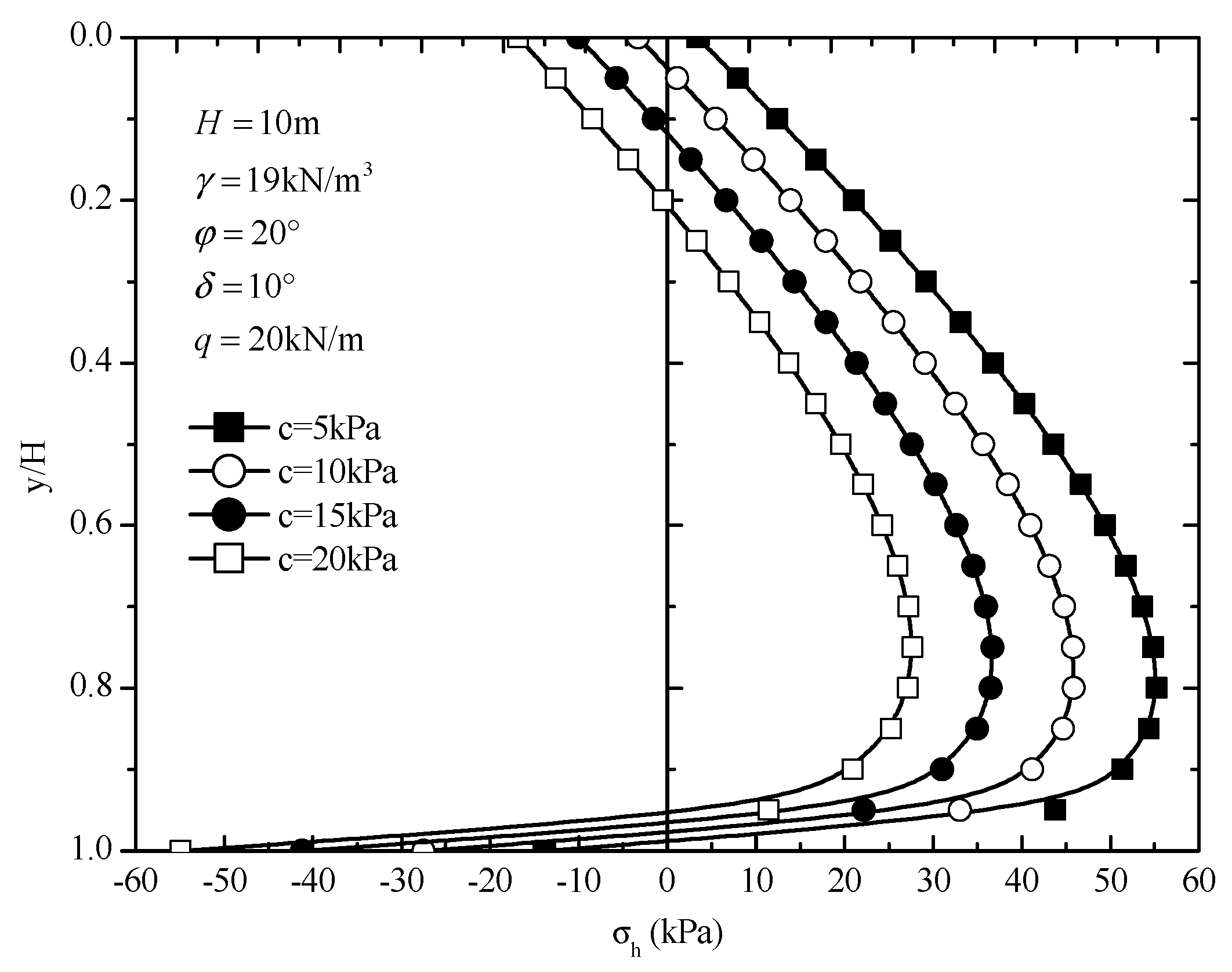
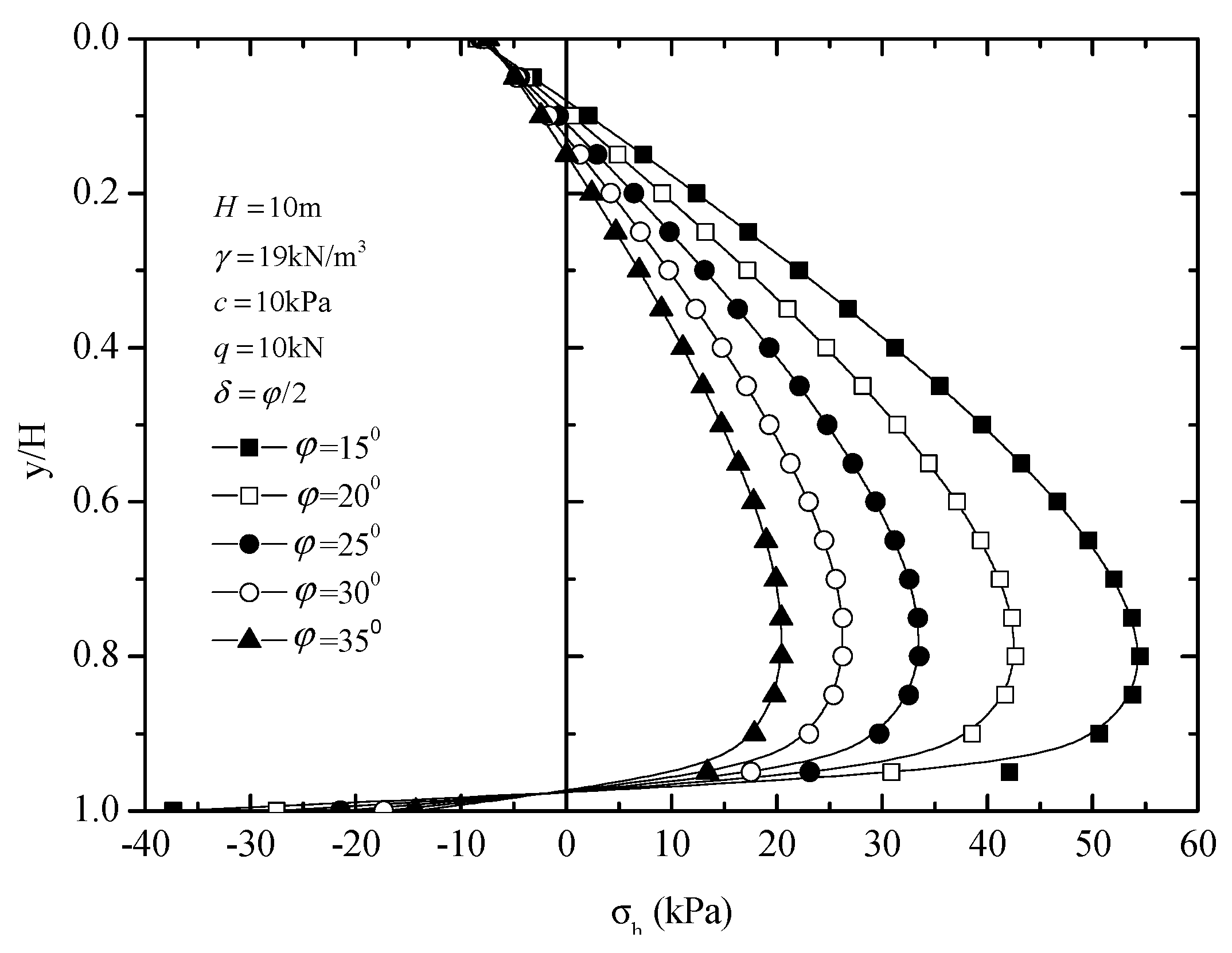
4.2. Results and Discussion
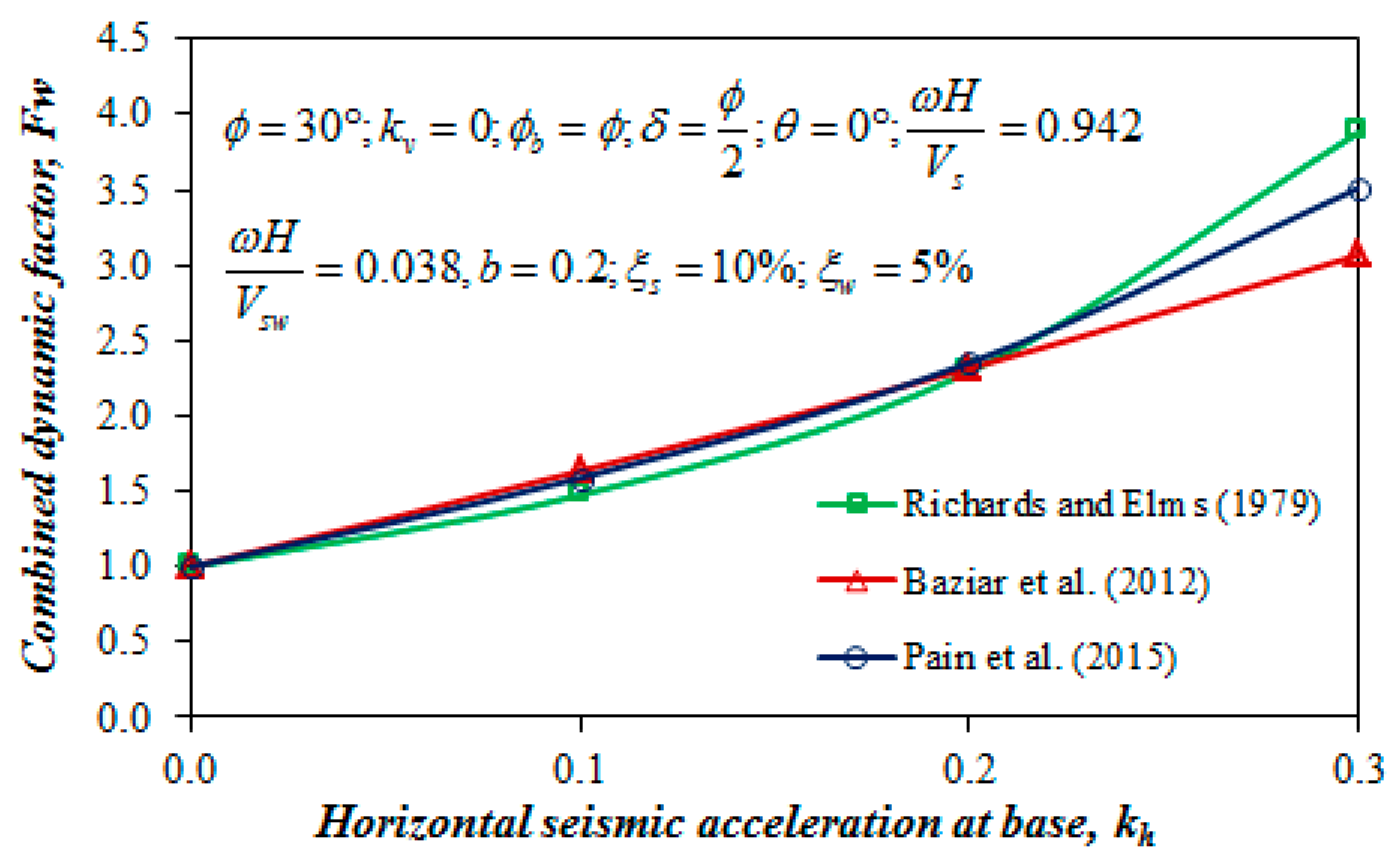
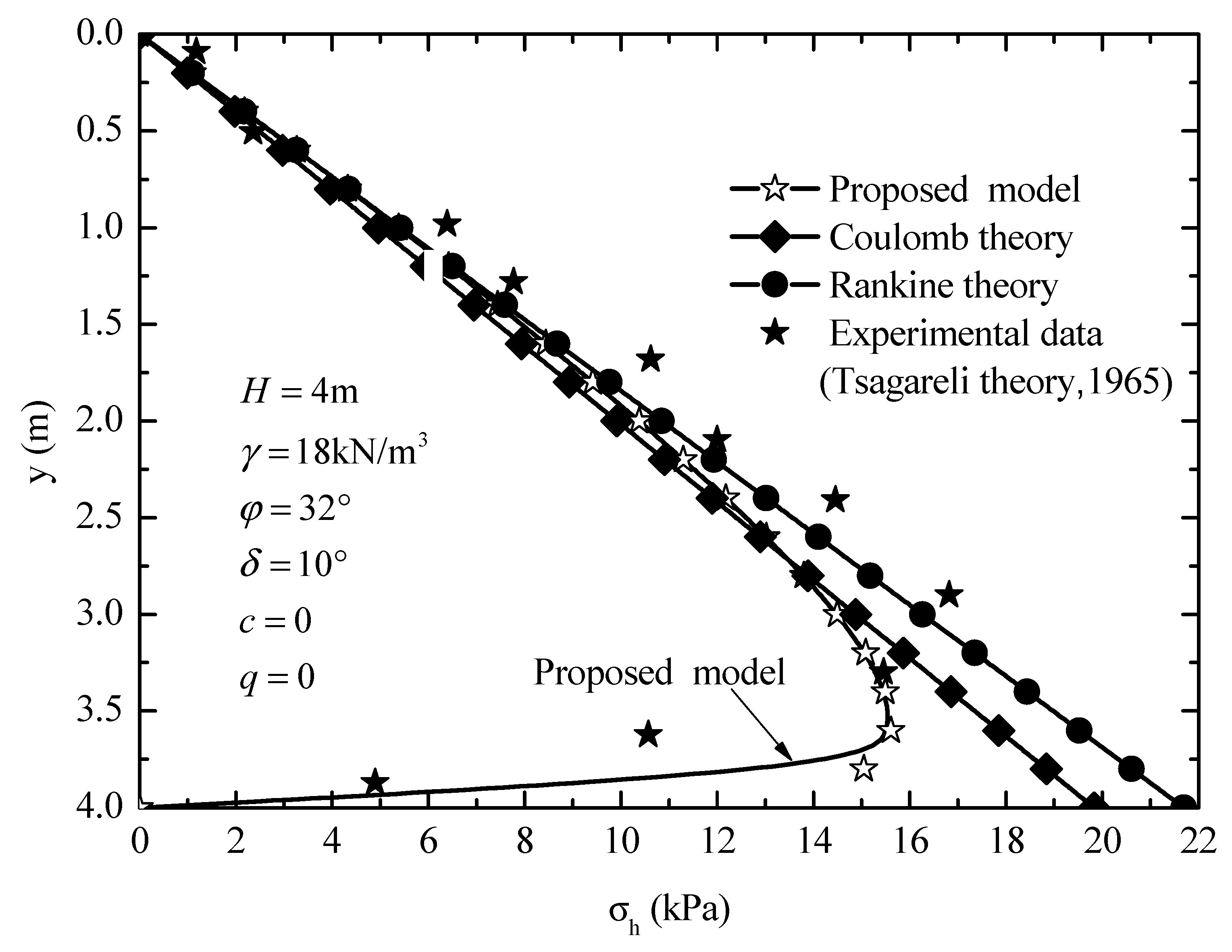
4.3. Comparison with Other Studies
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Caltabiano, S.; Cascone, E.; Maugeri, M. Seismic stability of retaining walls with surcharge. Soil Dyn. Earthq. Eng. 2000, 20, 469–476. [Google Scholar] [CrossRef]
- Caltabiano, S.; Cascone, E.; Maugeri, M. Static and seismic limit equilibrium analysis of sliding retaining walls under different surcharge conditions. Soil Dyn. Earthq. Eng. 2012, 37, 38–55. [Google Scholar] [CrossRef]
- Huang, C.C. Seismic displacements of soil retaining walls situated on slopes. J. Geotech. Geoenviron. Eng. 2005, 131, 1108–1117. [Google Scholar] [CrossRef]
- Huang, C.C.; Wu, S.H.; Wu, H.J. Seismic displacement criterion for soil retaining walls based on soil shear strength mobilization. J. Geotech. Geoenviron. Eng. 2009, 135, 74–83. [Google Scholar] [CrossRef]
- Shukla, S.K. Dynamic active thrust from c–ϕ soil backfills. Soil Dyn. Earthq. Eng. 2011, 31, 526–529. [Google Scholar] [CrossRef]
- Conti, R.; Viggiani, G.M.B.; Cavallo, S. A two-rigid block model for sliding gravity retaining walls. Soil Dyn. Earthq. Eng. 2013, 55, 33–43. [Google Scholar] [CrossRef]
- Choudhury, D.; Ahmad, S.M. Stability of waterfront retaining wall subjected to pseudo-static earthquake forces. Ocean Eng. 2007, 26, 291–301. [Google Scholar] [CrossRef]
- Choudhury, D.; Ahmad, S.M. Design of waterfront retaining wall for the passive case under earthquake and tsunami. Appl. Ocean Res. 2007, 29, 37–44. [Google Scholar] [CrossRef]
- Choudhury, D.; Ahmad, S.M. Stability of waterfront retaining wall subjected to pseudodynamic earthquake forces. J. Waterw. Port Coast. Ocean Eng. 2008, 134, 252–260. [Google Scholar] [CrossRef]
- Ahmad, S.M.; Choudhury, D. Pseudo-dynamic approach of seismic design for waterfront reinforced soil-wall. Geotext. Geomembr. 2008, 26, 291–301. [Google Scholar] [CrossRef]
- Shamsabadi, A.; Xu, S.Y.; Taciroglu, E. A generalized log-spiral-Rankine limit equilibrium model for seismic earth pressure analysis. Soil Dyn. Earthq. Eng. 2013, 49, 197–209. [Google Scholar] [CrossRef]
- Zhang, F.; Leshchinsky, D.; Gao, Y.F. Required unfactored strength of geosynthetics in reinforced 3D slopes. Geotext. Geomembr. 2014, 42, 576–585. [Google Scholar] [CrossRef]
- Yang, X.-L.; Li, Z.-W. Upper bound analysis of 3D static and seismic active earth pressure. Soil Dyn. Earthq. Eng. 2018, 108, 18–28. [Google Scholar] [CrossRef]
- Mylonakis, G.; Kloukinas, P.; Papantonopoulos, C. An alternative to the Mononobe–Okabe equations for seismic earth pressures. Soil Dyn. Earthq. Eng. 2007, 27, 957–969. [Google Scholar] [CrossRef]
- Li, X.; Wu, Y.; He, S. Seismic stability analysis of gravity retaining walls. Soil Dyn. Earthq. Eng. 2010, 30, 875–878. [Google Scholar] [CrossRef]
- Veletsos, A.S.; Younan, A.H. Dynamic response of cantilever retaining walls. J. Geotech. Geoenviron. Eng. 1997, 123, 161–172. [Google Scholar] [CrossRef]
- Gazetas, G.; Psarropoulos, P.N.; Anastasopoulos, I.; Gerolymos, N. Seismic behaviour of flexible retaining systems subjected to short-duration moderately strong excitation. Soil Dyn. Earthq. Eng. 2004, 24, 537–550. [Google Scholar] [CrossRef]
- Psarropoulos, P.N.; Klonaris, G.; Gazetas, G. Seismic earth pressures on rigid and flexible retaining wall. Soil Dyn. Earthq. Eng. 2005, 25, 795–809. [Google Scholar] [CrossRef]
- Jung, C.; Bobet, A.; Fernández, G. Analytical solution for the response of a flexible retaining structure with an elastic backfill. Int. J. Numer. Anal. Methods Geomech. 2010, 34, 1387–1408. [Google Scholar] [CrossRef]
- Kloukinas, P.; Langousis, M.; Mylonakis, G. Simple Wave Solution for Seismic Earth Pressures on Nonyielding Walls. J. Geotechn. Geoenviron. Eng. 2012, 138, 1514–1519. [Google Scholar] [CrossRef]
- Richards, R.; Elms, D.G. Seismic behavior of gravity retaining walls. J. Geotech. Eng. Divis. ASCE 1979, 105, 449–464. [Google Scholar]
- Whitman, R.V.; Liao, S. Seismic design of gravity retaining walls. In Proceedings of the 8th World Conference on Earthquake Engineering, San Francisco, CA, USA, 21–28 July 1984; Volume 3, pp. 533–540. [Google Scholar]
- Saran, S.; Viladkar, M.N.; Reddy, R.K. Displacement dependent earth pressures. Indian Geotech. J. 1985, 17, 121–141. [Google Scholar]
- Saran, S.; Viladkar, M.N.; Tripathi, O.P. Displacement dependent earth pressures in retaining walls. Indian Geotech. J. 1990, 20, 260–287. [Google Scholar]
- Bakr, J.; Ahmad, S.M. A finite element performance-based approach to correlate movement of a rigid retaining wall with seismic earth pressure. Soil Dyn. Earthq. Eng. 2018, 114, 460–479. [Google Scholar] [CrossRef]
- Steedman, R.S.; Zeng, X. The influence of phase on the calculation of pseudo-static earth pressure on a retaining wall. Géotechnique 1990, 40, 103–112. [Google Scholar] [CrossRef]
- Choudhury, D.; Nimbalkar, S. Pseudo-dynamic approach of seismic active earth pressure behind retaining wall. Geotech. Geol. Eng. 2006, 24, 1103–1113. [Google Scholar] [CrossRef]
- Ghosh, P. Seismic active earth pressure behind non-vertical retaining wall using pseudo-dynamic analysis. Can. Geotech. J. 2008, 45, 117–123. [Google Scholar] [CrossRef]
- Kolathayar, S.; Ghosh, P. Seismic active earth pressure on walls with bilinear backface using pseudo-dynamic approach. Comput. Geotech. 2009, 36, 1229–1236. [Google Scholar] [CrossRef]
- Ghanbari, A.; Ahmadabadi, M. Pseudo-dynamic active earth pressure analysis of inclined retaining walls using horizontal slices method. Sci. Iran. Trans. A Civ. Eng. 2010, 17, 118–130. [Google Scholar]
- Ghosh, S.; Sharma, R.P. Seismic Active Earth Pressure on the Back of Battered Retaining Wall Supporting Inclined Backfill. Int. J. Geomech. 2012, 12, 54–63. [Google Scholar] [CrossRef]
- Handy, R.L. The arch in soil arching. J. Geotech. Eng. 1985, 111, 302–318. [Google Scholar] [CrossRef]
- Paik, K.H.; Salgado, R. Estimation of active earth pressure against rigid retaining walls considering arching effect. Géotechnique 2003, 53, 643–653. [Google Scholar] [CrossRef]
- Goel, S.; Patra, N.R. Effect of arching on active earth pressure for rigid retaining walls considering translation mode. Int. J. Geomech. 2008, 8, 123–133. [Google Scholar] [CrossRef]
- Khosravi, M.H.; Pipatpongsa, T.; Takemura, J. Experimental analysis of earth pressure against rigid retaining walls under translation mode. Géotechnique 2013, 63, 1020–1028. [Google Scholar] [CrossRef]
- Rao, P.; Chen, Q.; Zhou, Y.; Nimbalkar, S.; Chiaro, G. Determination of active earth pressure on rigid retaining wall considering arching effect in cohesive backfill soil. Int. J. Geomech. 2015. [Google Scholar] [CrossRef]
- Nakamura, S. Reexamination of Mononobe–Okabe theory of gravity retaining walls using centrifuge model tests. Soils Found. 2006, 46, 135–146. [Google Scholar] [CrossRef]
- Athanasopoulos-Zekkos, A.; Vlachakis, V.S.; Athanasopoulos, G.A. Phasing issues in the seismic response of yielding, gravity-type earth retaining walls—Overview and results from a FEM study. Soil Dyn. Earthq. Eng. 2013, 55, 59–70. [Google Scholar] [CrossRef]
- Al Atik, L.; Sitar, N. Seismic Earth Pressures on Cantilever Retaining Structures. J. Geotech. Geoenviron. Eng. 2010, 136, 1324–1333. [Google Scholar] [CrossRef]
- Tiznado, J.C.; Rodríguez-Roa, F. Seismic lateral movement prediction for gravity retaining walls on granular soils. Soil Dyn. Earthq. Eng. 2011, 31, 391–400. [Google Scholar] [CrossRef]
- Baziar, M.H.; Habib, S.; Moghadam, M.R. Sliding stability analysis of gravity retaining walls using the pseudo-dynamic method. Proc. Inst. Civ. Eng. Geotech. Eng. 2012, 166, 389–398. [Google Scholar] [CrossRef]
- Choudhury, D.; Nimbalkar, S. Seismic rotational displacement of gravity walls by pseudodynamic method. Int. J. Geomech. 2008, 8, 169–175. [Google Scholar] [CrossRef]
- Zeng, X.; Steedman, R.S. Rotating block method for seismic displacement of gravity walls. J. Geotech. Geoenviron. Eng. 2000, 126, 709–717. [Google Scholar] [CrossRef]
- Pain, A.; Choudhury, D.; Bhattacharyya, S.K. Computation of rotational displacements of gravity retaining walls by pseudo-dynamic method. In Proceedings of the 4th GeoChina International Conference: Sustainable Civil Infrastructures: Innovative Technologies for Severe Weathers and Climate Changes, Jinan, China, 25–27 July 2016. [Google Scholar]
- Basha, B.M.; Babu, G.L.S. Optimum design of bridge abutments under high seismic loading using modified pseudo-static method. J. Earthq. Eng. 2010, 14, 874–897. [Google Scholar] [CrossRef]
- Bellezza, I. A new pseudo-dynamic approach for seismic active soil thrust. Geotech. Geol. Eng. 2014, 32, 561–576. [Google Scholar] [CrossRef]
- Bellezza, I. Seismic active soil thrust on walls using a new pseudo-dynamic approach. Geotech. Geol. Eng. 2015, 33, 795–812. [Google Scholar] [CrossRef]
- Harop-Williams, K. Arch in soil arching. J. Geotech. Eng. 1989, 15, 415–419. [Google Scholar] [CrossRef]
- Wang, Y.Z. The active earth pressure distribution and the lateral pressure coefficient of Retaining wall. Rock Soil Mech. 2005, 26, 1019–1022. [Google Scholar]
- Li, J.; Wang, M. Simplified method for calculating active earth pressure on rigid retaining walls considering the arching effect under translational mode. Int. J. Geomech. 2014, 14, 282–290. [Google Scholar] [CrossRef]
- Yuan, C.; Peng, S.; Zhang, Z.; Liu, Z. Seismic wave propagation in Kelvin-Voigt homogeneous visco-elastic media. Sci. China Ser. D Earth Sci. 2006, 49, 147–153. [Google Scholar] [CrossRef]
- Pain, A.; Choudhury, D.; Bhattacharyya, S.K. Seismic stability of retaining wall-soil sliding interaction using modified pseudo-dynamic method. Geotech. Lett. 2015, 5, 56–61. [Google Scholar] [CrossRef]
- Tsagareli, Z.V. Experimental investigation of the pressure of a loose medium on retaining wall with vertical backface and horizontal backfill surface. Soil Mech. Found. Eng. 1965, 91, 197–200. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nimbalkar, S.; Pain, A.; Ahmad, S.M.; Chen, Q. Stability Assessment of Earth Retaining Structures under Static and Seismic Conditions. Infrastructures 2019, 4, 15. https://doi.org/10.3390/infrastructures4020015
Nimbalkar S, Pain A, Ahmad SM, Chen Q. Stability Assessment of Earth Retaining Structures under Static and Seismic Conditions. Infrastructures. 2019; 4(2):15. https://doi.org/10.3390/infrastructures4020015
Chicago/Turabian StyleNimbalkar, Sanjay, Anindya Pain, Syed Mohd Ahmad, and Qingsheng Chen. 2019. "Stability Assessment of Earth Retaining Structures under Static and Seismic Conditions" Infrastructures 4, no. 2: 15. https://doi.org/10.3390/infrastructures4020015
APA StyleNimbalkar, S., Pain, A., Ahmad, S. M., & Chen, Q. (2019). Stability Assessment of Earth Retaining Structures under Static and Seismic Conditions. Infrastructures, 4(2), 15. https://doi.org/10.3390/infrastructures4020015







