Abstract
Detection of early-stage corrosion on slender steel members is crucial for preventing buckling failures of steel structures. An active photoacoustic fiber optic sensor (FOS) system is reported herein for the early-stage steel corrosion detection of steel plates and rebars using surface ultrasonic waves. The objective of this study is to investigate a potential method for detecting surface corrosion/rust of steel rods using numerically simulated surface ultrasonic waves. The finite element method (FEM) was applied in the simulation of propagating ultrasonic waves on steel rod models. The pitch-catch mode of damage detection was adopted, in which one source (transmitter) and one sensor (receiver) were considered. In this research, radial displacements at the receiver were simulated and analyzed by short-time Fourier transform (STFT) for detecting, locating, and quantifying surface rust located between the transmitter and the receiver. From our time domain and frequency domain analyses, it was found that the presence, location, and dimensions (length, width, and depth) of surface rust can be estimated by ultrasonic wave propagation.
1. Introduction
Slender steel members, such as steel rods and bars, are widely used structural components in civil infrastructure (e.g., prestressed tendons and cables, steel rebars, temporary support structures, and traffic signs). Unlike other construction materials, such as bricks and lumber, steel is vulnerable to corrosion. Steel corrosion can take place when certain environmental conditions (e.g., temperature, pH, oxygen, moisture, chloride ions) are met. As a result, premature failures of steel structures can occur if one or more critical members are corroded. Corrosion of steel members reduces the effective cross-sectional area of the member by replacing steel (ferrite) with rust (ferrite oxides). Consequently, structural stiffness and bearing capacity of corroded steel members are reduced. In order to detect early-stage corrosion of steel members, localized miniature sensors must be installed on their surface. Furthermore, corrosion of slender steel members increases the likelihood of their instability (buckling) due to the change in boundary conditions at the support or within each member.
Detection of early-stage corrosion on slender steel members is crucial for preventing their premature failures. Various nondestructive evaluation/testing (NDE/T) and structural health monitoring (SHM) techniques have been applied to steel structures []. Example techniques include visual testing [], modal analysis [], eddy current testing [], thermal infrared testing [], and ultrasonic testing [,]. Among these techniques, piezoelectric transducers (PZTs) and fiber optic sensors (FOSs) are widely used in SHM for corrosion detection. PZT can be applied for both transmitting and receiving acoustic/ultrasonic waves [], while FOSs are mostly used for measuring acoustic/ultrasonic waves []. When instrumenting these sensors, surface mounting or subsurface installation can be used for both PZTs [] and FOSs [,]. While PZTs can function as both generator and receiver, they have limited applicability (size) and are vulnerable to electromagnetic and moisture interference []. On the other hand, FOSs have demonstrated their great potential for detecting, locating, and quantifying steel rebar corrosion in concrete structures. FOSs are a popular approach for long-term monitoring of steel structures [,]. While FOSs have been applied to many steel structures in the past, most of the damage-detection algorithms have been based on the passive response of FOSs. In other words, either corrosion-induced cracking or loading-induced dynamic responses must be generated from the monitored steel members such that the FOS can passively detect the presence of corrosion. An active fiber optic transmitter (FOT) made of gold nanocomposite has been proposed as a point-source ultrasonic wave generator to overcome the limitation of passive FOS sensors []. Such an FOT is attached to the surface of an optical fiber at various locations and used to generate ultrasonic waves, owing to the photoacoustic effect of the gold nanocomposite. Gold nanocomposite can produce ultrasonic waves by its thermal expansion and contraction upon the illumination of a nanosecond pulse laser through the optical fiber []. Propagating ultrasonic waves can be practically measured by using a fiber Bragg grating (FBG) sensor as a receiver []. Different from traditional passive FOS techniques, active FOSs can generate acoustic/ultrasonic waves to probe monitored steel members for early-stage corrosion detection. Meanwhile, installed FOSs allow engineers to assess the conditions (e.g., temperature) of structures without the use of a couplant and “adapters” [,,]. With a compact size, active FOSs can be installed onto irregular/curved surfaces of structures.
In this study, our objective is to investigate the detection of surface rust in a cylindrical geometry (slender steel rod) using ultrasonic waves in pitch-catch mode, and to develop a surface rust detection algorithm as a basis for the practical application of an active photoacoustic FOS system. Steel rods were chosen as an example of slender steel members. The finite element method (FEM) was applied to simulate the propagation of ultrasonic waves at 1 MHz on steel rod models. Surface rust was simulated by a rectangular prism, which is characterized by its location (), length (d), width (w), and depth (h). The pitch-catch mode of damage detection was adopted, in which one source (transmitter) and one sensor (receiver) are considered. In this study, radial displacements () at the receiver were simulated and analyzed by short-time Fourier transform (STFT) for detecting, locating, and quantifying surface rust located between the transmitter and the receiver. Time domain and frequency domain analyses were conducted for developing a damage detection algorithm. In what follows, the details of the finite element (FE) simulation are first provided.
2. Finite Element Simulation
In the past, FEM has been employed for simulating ultrasonic wave propagation for damage detection [,,]. To simulate the photoacoustic fiber optic sensors, described in Section 1, for corrosion detection of steel rods and rebars, six FE cylinder models were created. In each FE model, excitation of ultrasonic waves was introduced by applying time-dependent displacement boundary conditions within a 1 mm × 1 mm area to simulate the photoacoustic fiber optic sensors. Along the longitudinal axis at a given distance, radial displacement was numerically collected to simulate the behavior of an FBG receiver. Among various signal processing techniques, STFT has been demonstrated as an applicable approach for analyzing the transient response of ultrasonic wave propagation in the time-frequency domain []. In this research, cylindrical geometry was numerically modeled by six steel rod models (one intact and five corroded) in a commercially available FE package (ABAQUS 2016) []; 705, 600 linear hexahedral elements (C3D8) were used in all six models. Five corroded steel rod models were created by introducing a rectangular prism/anomaly to the surface of the intact steel rod model. The pitch-catch mode of damage detection was applied for data collection by using one transmitter (source or T) and one receiver (R) in each model, as shown in Figure 1. An explicit solver was used to obtain the time domain radial displacement () at the receiver for all six models. The design of the intact and corroded FE models is described in the following sections.
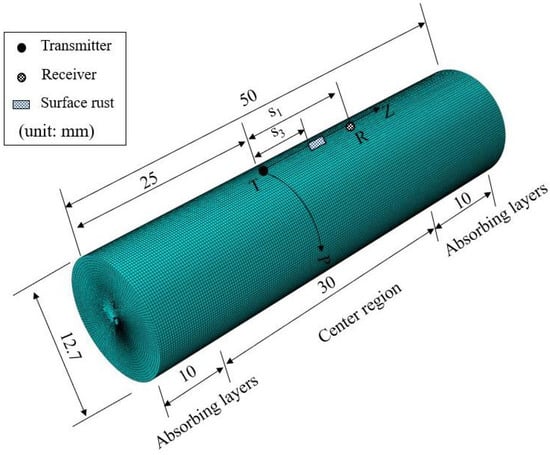
Figure 1.
Intact steel rod model.
2.1. Intact Steel Rod Model
An intact steel rod model (denoted by IM) was created by using a cylinder with 12.7 mm diameter (D) and 50 mm length, as shown in Figure 1. The material properties of the steel used in the intact steel rod model are provided in Table 1. A transmitter (T) was located at mid-span, and a receiver (R) was located 10 mm away from T along the longitudinal axis (z-axis) of the model. The distance between T and R was denoted as . The intact steel rod model was fixed at both ends. To suppress unnecessary reflections from both ends, 10 absorbing layers [] were used at each end of the model such that ultrasonic waves propagating into the absorbing layers can be damped out. As shown in Figure 2, a sinusoidal pulse was introduced at T, and the time domain radial displacement () was collected at R.

Table 1.
Material’s properties.
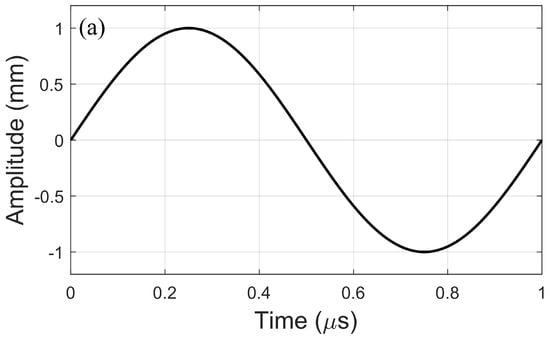
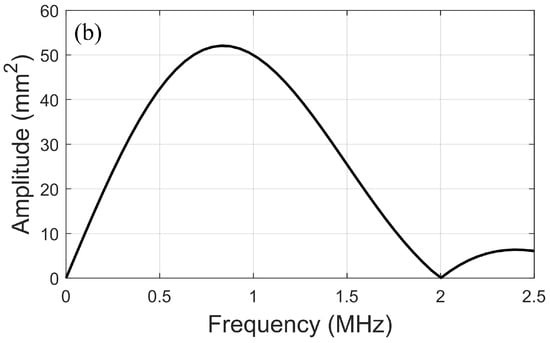
Figure 2.
(a) Designed loading function in the time domain and; (b) designed loading function in the frequency domain.
2.2. Corroded Steel Rod Models
Five corroded steel rod models (denoted by CM) were generated by substituting the material properties of steel with those of rust at a corroded region. This simulated the introduction of surface rust to the intact steel rod model, as shown in Table 2. Four attributes were used to characterize the corroded region (surface rust): location (), length (d), width (w), and thickness (h). Two values were considered for each attribute.

Table 2.
Five corroded steel rod models.
3. Research Hypotheses and Approach
3.1. Hypotheses of Ultrasonic Wave Propagation in Intact and Corroded Rod Models
Five hypotheses of ultrasonic waves propagation in intact and corroded steel rod models were formulated for the damage detection problem in this paper. A Mercator projection of cylindrical geometry for steel rod models is provided in Figure 3 to better illustrate these hypotheses.
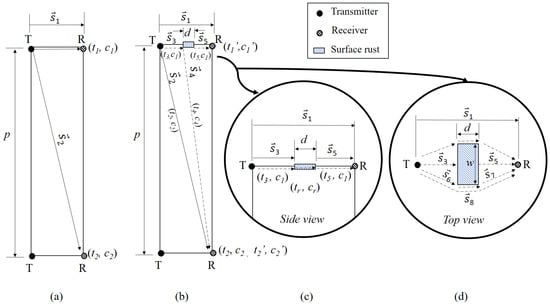
Figure 3.
(a) Mercator projection of intact steel rod model surface; (b) Mercator projection of corroded steel rod model surface; (c) side view of ultrasonic wave propagation paths around the surface rust; and (d) top view of ultrasonic wave propagation paths around the surface rust.
- In the intact steel rod model, the time domain radial displacement is collected at R. The first ultrasonic wave packet is the one propagating along the path at a velocity of and arriving at time . The second ultrasonic wave packet propagates along the path and arrives at time with a velocity of . Both the first and the second wave packets are surface waves (fundamental mode of Rayleigh waves). These surface waves were chosen for surface rust detection, rather than bulk waves [] and guided waves [], because bulk waves attenuate much faster than surface waves, and guided waves require multiple sensors to be in place.
- In the corroded steel rod models (CM1~CM5), the ultrasonic waves propagating along the path are affected by the presence of surface rust. As shown in Figure 3c, some of the ultrasonic waves propagate through the surface rust and arrive at time (i.e., > , since the ultrasonic wave velocity is slower in rust than it is in steel).
- Some of the ultrasonic waves are scattered from the surface rust and propagate along the path . Time is the total time of flight (TOF) of the scattered ultrasonic wave propagating along path (). The propagation velocities of ultrasonic waves on path and path are respectively and .
- In Figure 3d, path is the path of ultrasonic waves diffracted by the surface rust (). TOF of these ultrasonic waves is (i.e., ).
- Higher frequencies are affected more than lower frequencies by the presence of surface rust. This is because the effective depth of each frequency is approximately its wavelength []. With a ‘shallow’ effective depth, higher frequencies interact with the surface rust more than lower frequencies.
3.2. Damage Detection Algorithm
Based on the five aforementioned hypotheses, surface rust detection, localization, and quantification were carried by the following approach.
3.2.1. Damage Detection
In this study, detection of surface rust can be accomplished by determining the reduction of the centroid frequency () in the spectrogram of by using STFT. The steps for obtaining are illustrated in Figure 4 and summarized in the following.
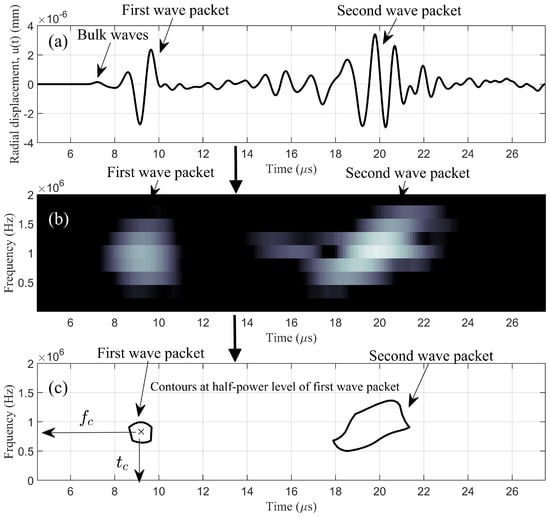
Figure 4.
(a) Time domain radial displacement collected at receiver R; (b) spectrogram obtained by applying short-time Fourier transform (STFT) to ; (c) contours at half-power level of the first wave packet ( is the centroid of the contour for the first wave packet).
- Generate/introduce ultrasonic waves at transmitter T of model IM.
- Collect the time domain radial displacement at receiver R.
- Apply STFT to in order to convert it to its spectrogram .
- In the spectrogram , show the half-power contour at −3 dB from the maximum amplitude of the first wave packet.
- Determine the centroid of the half-power contour for the first wave packet by finding its coordinates in the spectrogram .
- The centroid frequency of this FE simulation is thus found. For the intact model (IM), .
- Repeat the steps for an artificially corroded model. For corroded models, .
Figure 4 illustrates the parameters defined in the steps for damage detection, using model CM1 as an example. Equation (1) shows the damage detection criterion for detecting the presence of surface rust.
where = difference in the centroid frequency between intact and corroded steel rod models (in MHz), = centroid frequency of model IM (in MHz), and = centroid frequency of corroded steel rod models (in MHz). In this research, a steel rod model was considered intact (no damage) if there is no reduction of centroid frequency or and vice versa.
3.2.2. Damage Localization
To locate surface rust, TOF of scattered ultrasonic waves was used. In this paper, the location of surface rust is defined by the length of the path or . The value of indicates the location of surface rust.
The TOF of a scattered wave () traveling through a path and is defined by
where and = TOF of ultrasonic waves propagating on paths and (μs)), respectively.
Equivalently,
where = length of path (mm), = length of path (mm) = , p = perimeter of the rod model (mm), = propagation velocity on path (mm/μs), and = propagation velocity on path (mm/μs). From our previous study, a propagation velocity model (Equation (4)) based on the length of a path with cylindrical geometry was reported [].
where a and b = model parameters. By substituting Equation (4) and rearranging terms, we have
where = length of path (mm). In Equation (5), , p, and must be provided. Parameters a and b are from reported literature []. Time is measured from a corroded model. Once time is measured, Equation (5) can be solved by the graphic method. Equation (5) also represents the damage localization criterion in our algorithm. Finding the value of locates the surface rust.
3.2.3. Damage Quantification
For damage quantification, dimensions of surface rust (length d, width w, and thickness h) are to be found. To find the length d of surface rust, TOF () of ultrasonic waves propagating through surface rust and arriving at receiver R is used. Time denotes the total propagation time along path , which consists of path , surface rust (length d), and path . In other words,
where = total TOF of ultrasonic wave propagating on path (μs), = TOF of ultrasonic wave traveling on path (μs), = TOF of ultrasonic wave traveling on path (μs)), and = TOF of ultrasonic wave traveling within surface rust (μs). Since , we have
where = propagation velocity on the z-axis in rust (mm/μs). By rearranging Equation (7), surface rust length d can be directly determined by
Equation (7) represents the length estimation criterion in our algorithm.
Once (from damage localization, Equation (5)) and d (from Equation (8)) are determined, the width of surface rust (w) can be obtained by using the delayed arrival time of first wave packet (), as shown in Figure 3d. Equation (9) describes the relationship between and w.
where , = TOF of ultrasonic wave propagating on path and
in a corroded steel rod model (μs), = length of path (mm) and = length of path (mm). Equation (9) represents the width estimation criterion in our algorithm.
From our fifth hypothesis (Section 3.1), lower-frequency ultrasonic waves have ‘deeper’ effective depths. It suggests that more frequencies in the STFT spectrogram will be affected when increasing the thickness h of surface rust. This phenomenon is illustrated by the reduction of the spectrograms’ curvature or and modeled by an empirical equation, as shown in Equation (11).
where h = thickness of surface rust (mm), = second-order partial derivative of the first wave packet’s frequency domain projection, and e and g = model parameters. approximates the curvature of the first wave packet. Equation (11) represents the thickness estimation criterion in our algorithm.
4. Simulation Results
The time domain radial displacement () of each model at receiver R was collected from six FE simulation cases (one for the intact model and five for corroded models). Spectrograms () of each were obtained by STFT. Comparison of and between intact and corroded steel rod models was made to study the effects of surface rust on and .
4.1. Time Domain Response
In each model, radial displacement at receiver R was collected as shown in Figure 5. In Figure 5, the time domain radial displacements of models IM, CM1, CM2, CM3, CM4, and CM5 are provided. Two wave packets were observed. While the first wave packets of intact and corroded responses are different, the time domain radial displacement response does not provide sufficient information for damage quantification. As predicted by the first hypothesis, two wave packets were observed. The first wave packet was the ultrasonic wave propagating along the longitudinal direction (z-axis). The second wave packet was the ultrasonic wave propagating in the helical direction (i.e., in Figure 3). The waveform of the second wave packet is more complicated than that of the first wave packet in the spectrogram, owing to the geometric dispersion (in the second wave packet) caused by the cylindrical geometry of FE models.
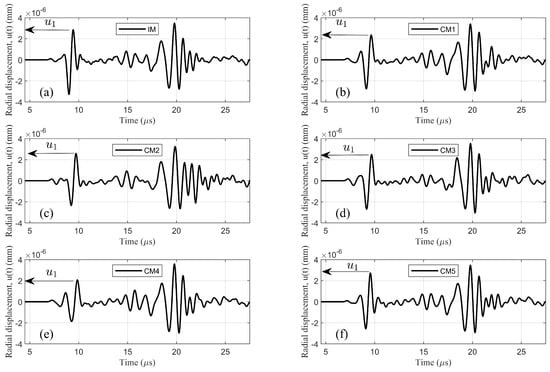
Figure 5.
Time domain radial displacement in (a) intact model (IM); (b) corroded model 1 (CM1); (c) model CM2; (d) model CM3; (e) model CM4; and (f) model CM5.
In Figure 5, for corroded steel rod models (CM1∼CM5), the first peak amplitude () was reduced after interacting with surface rust and propagating on path . While the presence of surface rust can be detected by the reduction of , quantification of surface rust using can be very difficult due to the geometric dispersion effect on . In reality, peak amplitudes can also be contaminated by background noise (e.g., ambient vibration). Therefore, frequency domain analysis of was applied, and the results are described in the next section.
4.2. Time-Frequency Domain Response
By applying STFT to , the frequency change in over time was shown on the resulting spectrograms. A frequency range on the STFT spectrogram between 0.1 MHz and 2 MHz was selected, since this frequency range included most of the kinetic energy of the transmitted ultrasonic waves.
Figure 6 shows the STFT spectrogram of at transmitter T of model IM. In Figure 6, the first wave packet (white-colored vertical shape) represents the transmitted ultrasonic wave traveling in the longitudinal direction or path (without geometric dispersion), whose amplitudes confirmed our choice of frequency range. The second wave packet (gray-colored tilted shape) represents the transmitted ultrasonic wave traveling in the helical direction (with geometric dispersion) and returning to transmitter T. Due to the geometric dispersion in this FE simulation, ultrasonic waves at lower frequencies ( MHz) travel faster than those at higher frequencies ( MHz). This explains the tilted shape of the second wave packet.
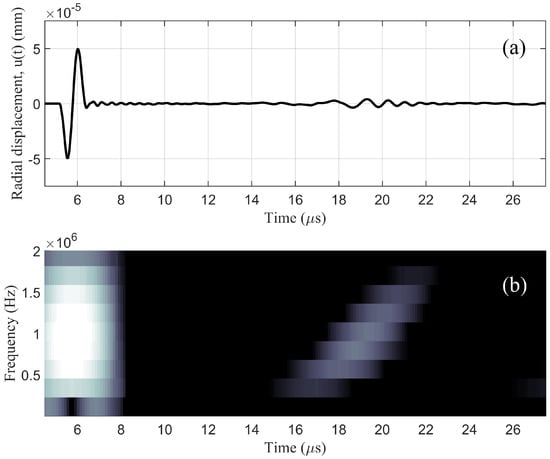
Figure 6.
(a) Time domain radial displacement at transmitter T of model IM and (b) spectrogram obtained by applying STFT to .
Figure 7 shows the STFT spectrograms of at receiver R of all six models. In Figure 7, two wave packets were observed within the time window of 4.5–27.5 μs. The first wave packet centering at 8 μs represents the ultrasonic wave (vertical shape) propagating from transmitter T to receiver R along the longitudinal direction (z-axis). The second wave packet (tilted shape) represents the ultrasonic wave propagating along the helical direction or path . Figure 8 shows the contours at the half-power level of the first wave packet in each spectrogram. In corroded steel rod models (CM1–CM5), higher frequencies in the first wave packet were reduced due to smaller effective depth. In addition, the shape of the second wave packet changed due to the size change of surface rust, as shown in Figure 8.
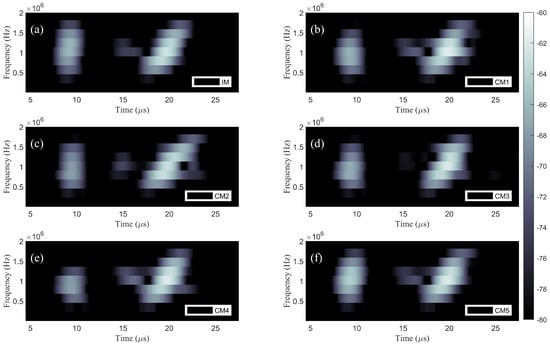
Figure 7.
Spectrogram of (a) model IM; (b) model CM1; (c) model CM2; (d) model CM3; (e) model CM4; and corroded steel rod models at receiver R(f) model CM5.
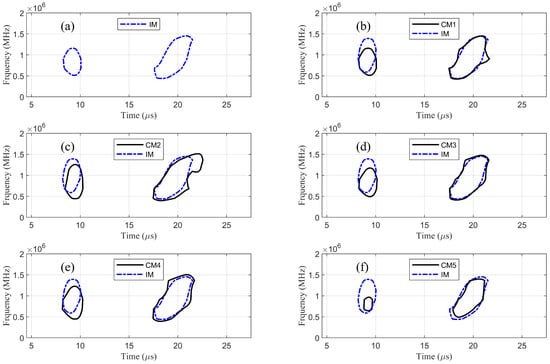
Figure 8.
Half-power contours in STFT spectrograms for the six models at receiver R.
4.3. Surface Rust Detection
Detection of surface rust in a corroded steel rod model was accomplished by comparing its centroid frequency with that of an intact model (IM). Figure 9 compares the half-power contours of intact (model IM) and corroded (models CM1∼CM5) FE models in individual STFT spectrograms at receiver R. The center of the half-power contour of model IM is denoted by centroid frequency . For the five corroded models, their centroid frequency is denoted by with different values. After finding and , their difference was calculated and is reported in Table 3. Based on Equation (1), the presence of surface rust in these models was detected.
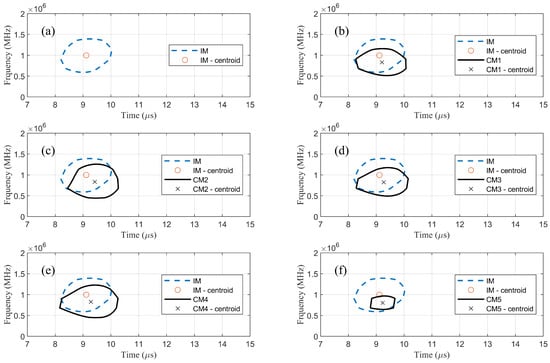
Figure 9.
Half-power contours of the first wave packet at receiver R.

Table 3.
Centroid frequency () of half-power contour for all models.
4.4. Surface Rust Localization
Equation (3) was used to locate surface rust in our simulations. In view of the presence of geometric dispersion in , measuring TOF in the time domain became challenging. To avoid the problem of chasing multiple frequencies at a time, the center frequency of the transmitted ultrasonic waves in the STFT spectrogram (i.e., 1 MHz in this study) was chosen.
Figure 10 shows the STFT spectrogram (at 1 MHz) of model IM at receiver R to demonstrate how to calculate the TOF of the scattered wave () traveling through paths and . In Figure 10a, the 1 MHz curves on the STFT spectrograms of model IM and model CM1 were extracted. Time denotes the TOF of the first wave packet and time denotes the second wave packet for model IM.
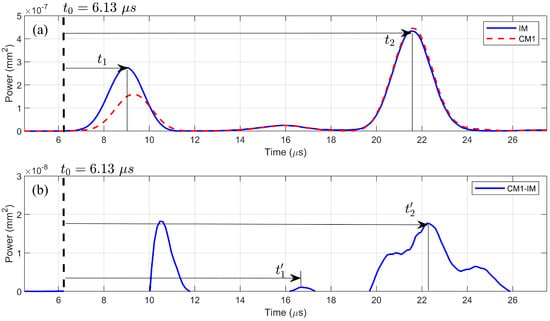
Figure 10.
Spectrograms of model IM and model CM1 at 1 MHz.
In Figure 10, and were measured from the time, , when the ultrasonic wave was introduced at transmitter T; in this study, μs. Since the peak amplitude of the first wave packet was 9.01 μs, μs = 2.88 μs. With traveling distance, being 10 mm, the wave velocity can be calculated by
This wave velocity can be compared with the theoretical surface wave velocity . can be approximated by []
with E = 210,000 MPa, = 7850 kg/m, and = 0.3. The approximated theoretical value was found to be 3.03 mm/μs. Consequently, the theoretical TOF for the first wave packet was found to be
where = distance from the center of transmitter T to receiver R (mm) (= 10 mm), and = distance from the center of transmitter T to the edge of loading area at T (mm) (= 0.5 mm). An error of 8.2% was obtained between the approximated theoretical value and the numerical value.
A subtracted/differential 1 MHz curve (subtract model IM from model CM1) was generated and is shown in Figure 10b, from where differential TOF values of the first wave packet and of the second packet were determined to be μs and μs, respectively. In our algorithm, differential TOF of the second wave packet was used for surface rust localization.
From the differential 1 MHz curve in Figure 10b, a propagation velocity model from the literature [] for elastic waves on a cylindrical geometry was used.
In all six FE models, p = 12.7 = 39.9 mm. From the Mercator projection shown in Figure 3, it is clear that
with = 10 mm, p = 39.9 mm, = 3.47 mm/μs, a = 3.47, . Equation (5) could be written as
Equation (21) provides the condition between and . With differential TOF , surface rust location can be found from Equation (21). Since Equation (21) cannot be solved analytically, the graphic method was applied, and its result is shown in Figure 11. Equation (21) represents a model for locating the surface rust in our algorithm.
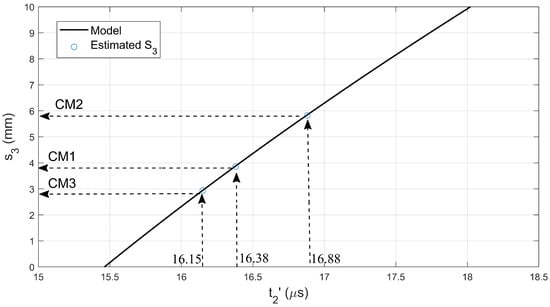
Figure 11.
Relationship between and .
Following the same procedure, 1 MHz curves of models CM2 and CM3 were generated (similar to Figure 10b for model CM1) in order to determine the different TOFs for models CM2 and CM3. For model CM2, was found by μs. For model CM3, was found by μs. Once was found, Equation (21) was used for finding surface rust location .
Estimated surface rust locations () in corroded steel rod models are reported in Table 4.

Table 4.
Comparison between predicted and actual location and dimensions.
4.5. Surface Rust Quantification
For surface rust quantification, Equation (8) was used to determine surface rust length d for models CM1 and CM2 by using measured time . Equation (9) was applied to determine surface rust width w for models CM1 and CM4 by using measured time . Equation (11) was utilized to determine surface rust depth h for models CM1 and CM5 by using measured curvature .
For determining surface rust length d using Equation (8): = 10 mm and propagation velocity in steel = 3.47 mm/μs (from Equation (13)). Propagation velocity in rust was calculated by mm/μs from []. Therefore, Equation (8) became
For model CM1, was found by μs. For model CM2, was found by μs. With Equation (23), estimated surface rust length d for models CM1 and CM2 were determined to be 1.97 mm and 3.69 mm, respectively.
With (from surface rust localization) and d found, surface rust width w values for models CM1 and CM4 were determined by solving Equation (9) with measured (TOF of the first wave wave packet, as shown in Figure 12 ).
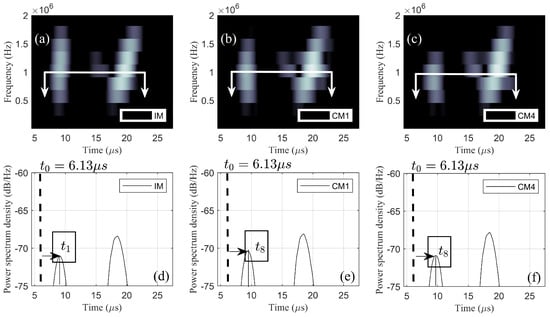
Figure 12.
(a) Spectrogram of model IM; (b) spectrogram of model CM1; (c) spectrogram of model CM4; (d) spectrogram of model IM at 1 MHz; (e) spectrogram of model CM1 at 1 MHz; (f) spectrogram of model CM4 at 1 MHz.
For surface rust width w quantification, estimated and d were substituted into Equation (9). For example, in model CM1, Equation (9) became
where was found by μs. Surface rust width w values for model CM1 was hence determined to be 2.36 mm. Similarly,
was obtained for models CM4. was found by μs in CM4. Predicted w is 4.2 mm, as shown in Table 4.
At last, curvature values of the first wave packet for models IM (), CM1 (), and CM5 () were calculated from Figure 13a. These curvature values were modeled with surface rust depth h by Equation (11) to obtain model parameters and (). Therefore, Equation (11) was written as
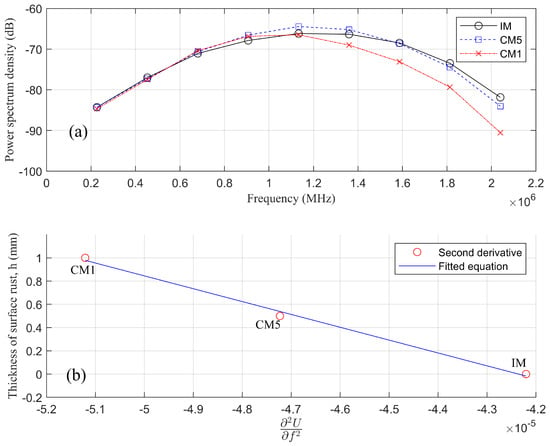
Figure 13.
(a) Ridge of the first wave packets and; (b) second-order derivatives of the first wave packets.
5. Conclusions
This paper reports an FE study of utilizing point-source-generated ultrasonic waves for detecting surface rust in steel rod models. By conducting the FE analysis of ultrasonic wave propagation in intact and corroded steel rod models, the following research findings were obtained: (1) in the time domain, the first peak amplitude () was reduced due to the presence of surface rust; (2) in the STFT spectrogram, the shape of the second wave packet in the spectrogram was tilted due to the geometric dispersion in ultrasonic waves; (3) the first wave packet in corroded steel rod models suffered from high frequency components loss, because higher frequencies have smaller effective depths and are affected by surface rust more than lower frequencies. As a result, non-zero centroid frequency reduction occurred for corroded steel rod models; (4) when measuring TOF from dispersive ultrasonic waves, a single frequency was used on the STFT spectrogram (e.g., 1 MHz in this paper); (5) ultrasonic wave propagation velocity on different curved paths could be estimated by the empirical model described in Equation (4); (6) six empirical equations are proposed for detecting (Equation (1)), locating (Equation (21)), and quantifying (Equations (23)–(26)) surface rust on a steel rod model. Based on the aforementioned findings, a surface rust detection algorithm is proposed, as summarized in Figure 14.
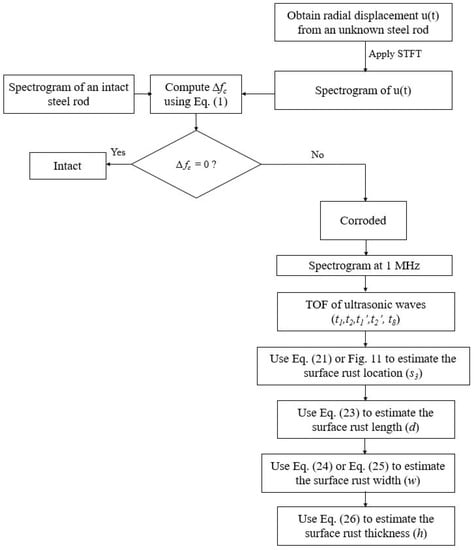
Figure 14.
Surface rust detection algorithm.
Methods of detecting, locating, and quantifying the surface rust are achieved by using the STFT (short-time Fourier transform) spectrogram of radial displacement collected on the surface of corroded steel rod models. We have concluded the following.
- The presence of surface rust can be detected by the reduction of centroid frequency of the first wave packet in the STFT spectrogram of corroded steel rod models.
- The location of surface rust is estimated by finding the difference in arrival time (TOF) between helically propagating ultrasonic waves and scattered ultrasonic waves (due to surface rust).
- The length of surface rust can be predicted by calculating the difference in TOF between longitudinally propagating ultrasonic waves of intact and corroded steel rod models. This difference in TOF is related to the longitudinal dimension (length) of surface rust.
- The width of surface rust can be determined by calculating the difference in TOF of the first wave packet between intact and corroded steel rods in the STFT spectrogram at a fixed frequency (e.g., 1 MHz in this paper).
- The thickness of surface rust can be estimated by utilizing the second-order derivative of the first wave packet of corroded steel rod models.
In conclusion, this paper presents our FE analysis of ultrasonic waves on intact and corroded steel rod models for detecting, locating, and quantifying surface rust in a systematic approach. While this research resulted in several empirical equations, it is believed that our proposed damage detection algorithm can be applied to other corrosion detection problems using distributed photoacoustic fiber optic sensors on steel rods or steel rebars.
Author Contributions
Q.T. and T.Y. conceived and designed the simulation; Q.T., J.H. and C.D. analyzed the data; X.W. and T.Y. contributed analysis tools; Q.T. drafted the manuscript.
Funding
This research was funded by National Science Foundation (NSF), United States grant number [1401369].
Acknowledgments
The authors would like to thank the National Science Foundation (NSF), Division of Civil, Mechanical and Manufacturing Innovation (CMMI) for partially supporting this research through Grant CMMI-1401369.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huston, D. Structural Sensing, Health Monitoring, and Performance Evaluation; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- American Society for Testing & Materials (ASTM). Metals Test Methods and Analytical Procedures. In 1999 Annual Book of ASTM Standards; American Society for Testing & Materials (ASTM): West Conshohocken, PA, USA, 1999; Volume 3. [Google Scholar]
- Tang, Q.; Yu, T.; Jen, M. Finite element analysis for the damage detection of light pole structures. Proc. SPIE 2015, 9437. [Google Scholar] [CrossRef]
- Cheng, W. Pulsed Eddy Current Testing of Carbon Steel Pipes’ Wall-thinning Through Insulation and Cladding. J. Nondestruct. Eval. 2012, 31, 215–224. [Google Scholar] [CrossRef]
- Wallbrink, C.; Wade, S.A.; Jones, R. The effect of size on the quantitative estimation of defect depth in steel structures using lock-in thermography. J. Appl. Phys. 2007, 101, 104907. [Google Scholar] [CrossRef]
- Cook, D.; Berthelot, Y. Detection of small surface-breaking fatigue cracks in steel using scattering of Rayleigh waves. NDT E Int. 2001, 34, 483–492. [Google Scholar] [CrossRef]
- Resch, M.T.; Nelson, D.V. An ultrasonic method for measurement of size and opening behavior of small fatigue cracks. In Small-Crack Test Methods; ASTM International: West Conshohocken, PA, USA, 1992; pp. 169–196. [Google Scholar]
- Giurgiutiu, V. Tuned Lamb Wave Excitation and Detection with Piezoelectric Wafer Active Sensors for Structural Health Monitoring. J. Intell. Mater. Syst. Struct. 2005, 16, 291–305. [Google Scholar] [CrossRef]
- Betz, D.C.; Thursby, G.; Culshaw, B.; Staszewski, W.J. Acousto-ultrasonic sensing using fiber Bragg gratings. Smart Mater. Struct. 2003, 12, 122. [Google Scholar] [CrossRef]
- Lu, Y.; Li, J.; Ye, L.; Wang, D. Guided waves for damage detection in rebar-reinforced concrete beams. Constr. Build. Mater. 2013, 47, 370–378. [Google Scholar] [CrossRef]
- Glisic, B.; Inaudi, D. Development of method for in-service crack detection based on distributed fiber optic sensors. Struct. Health Monit. 2012, 11, 161–171. [Google Scholar] [CrossRef]
- Leung, C.K.Y.; Wan, K.T.; Inaudi, D.; Bao, X.; Habel, W.; Zhou, Z.; Ou, J.; Ghandehari, M.; Wu, H.C.; Imai, M. Review: Optical fiber sensors for civil engineering applications. Mater. Struct. 2015, 48, 871–906. [Google Scholar] [CrossRef]
- Furukawa, T.; Ishida, K.; Fukada, E. Piezoelectric properties in the composite systems of polymers and PZT ceramics. J. Appl. Phys. 1979, 50, 4904–4912. [Google Scholar] [CrossRef]
- Rodríguez, G.; Casas, J.; Villalba, S. SHM by DOFS in civil engineering: A review. Struct. Monit. Maint. 2015, 2, 357–382. [Google Scholar] [CrossRef]
- Li, H.N.; Li, D.S.; Song, G.B. Recent applications of fiber optic sensors to health monitoring in civil engineering. Eng. Struct. 2004, 26, 1647–1657. [Google Scholar] [CrossRef]
- Wu, N.; Tian, Y.; Zou, X.; Silva, V.; Chery, A.; Wang, X. High-efficiency optical ultrasound generation using one-pot synthesized polydimethylsiloxane-gold nanoparticle nanocomposite. J. Opt. Soc. Am. B 2012, 29, 2016–2020. [Google Scholar] [CrossRef]
- Zou, X.; Wu, N.; Tian, Y.; Wang, X. Broadband miniature fiber optic ultrasound generator. Opt. Express 2014, 22, 18119–18127. [Google Scholar] [CrossRef] [PubMed]
- Du, C.; Owusu Twumasi, J.; Tang, Q.; Guo, X.; Zhou, J.; Yu, T.; Wang, X. All-Optical Photoacoustic Sensors for Steel Rebar Corrosion Monitoring. Sensors 2018, 18, 1353. [Google Scholar] [CrossRef] [PubMed]
- Zou, X.; Chao, A.; Tian, Y.; Wu, N.; Yu, T.; Wang, X. A novel Fabry-Perot fiber optic temperature sensor for early age hydration heat study in Portland cement concrete. Smart Struct. Syst. 2013, 12. [Google Scholar] [CrossRef]
- Wu, N.; Zou, X.; Zhou, J.; Wang, X. Fiber optic ultrasound transmitters and their applications. Measurement 2016, 79, 164–171. [Google Scholar] [CrossRef]
- Tang, Q.; Yu, T. Finite element simulation for damage detection of surface rust in steel rebars using elastic waves. Proc. SPIE 2016, 9804. [Google Scholar] [CrossRef]
- Sansalone, M.; Carino, N.J. Detecting Delaminations in Reinforced Concrete Slabs with and without Asphalt Concrete Overlays Using the Impact-Echo Method. Natl. Bur. Stand. J. Res. 1987, 86, 369–381. [Google Scholar] [CrossRef]
- Tang, Q.; Yu, T. Finite element simulation of ultrasonic waves in corroded reinforced concrete for early-stage corrosion detection. Proc. SPIE 2017, 10169. [Google Scholar] [CrossRef]
- Zhang, S.; Shen, W.; Li, D.; Zhang, X.; Chen, B. Nondestructive Ultrasonic Testing in Rod Structure with a Novel Numerical Laplace Based Wavelet Finite Element Method. Latin Am. J. Sol. Struct. 2018, 15, 7. [Google Scholar] [CrossRef]
- Tang, Q.; Twumasi, J.O.; Hu, J.; Wang, X.; Yu, T. Finite element simulation of photoacoustic fiber optic sensors for surface corrosion detection on a steel rod. Proc. SPIE 2018, 10599, 10599-13. [Google Scholar] [CrossRef]
- Abaqus/CAE User’s Manual Version 6.12; Dassault Systémes: Vélizy-Villacoublay, France, 2011.
- Liu, G.R.; Quek, S.S. A non-reflecting boundary for analyzing wave propagation using the finite element method. Finite Elem. Anal. Des. 2003, 39, 403–417. [Google Scholar] [CrossRef]
- Liang, M.T.; Su, P.J. Detection of the corrosion damage of rebar in concrete using impact-echo method. Cem. Concr. Res. 2001, 31, 1427–1436. [Google Scholar] [CrossRef]
- Lohr, K.R.; Rose, J.L. Ultrasonic guided wave and acoustic impact methods for pipe fouling detection. J. Food Eng. 2003, 56, 315–324. [Google Scholar] [CrossRef]
- Bergmann, L. Ultrasonics and Their Scientific and Technical Applications; Wiley: New York, NY, USA, 1948. [Google Scholar]
- Viktorov, I. Rayleigh Waves and Lamb waves-Physical Theory and Application; Plenum: New York, NY, USA, 1967. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).